Simulation of Dynamic Urban Growth with Partial Least Squares Regression-Based Cellular Automata in a GIS Environment

Abstract

We developed a geographic cellular automata (CA) model based on partial least squares (PLS) regression (termed PLS-CA) to simulate dynamic urban growth in a geographical information systems (GIS) environment. The PLS method extends multiple linear regression models that are used to define the unique factors driving urban growth by eliminating multicollinearity among the candidate drivers. The key factors (the spatial variables) extracted are uncorrelated, resulting in effective transition rules for urban growth modeling. The PLS-CA model was applied to simulate the rapid urban growth of Songjiang District, an outer suburb in the Shanghai Municipality of China from 1992 to 2008. Among the three components acquired by PLS, the first two explained more than 95% of the total variance. The results showed that the PLS-CA simulated pattern of urban growth matched the observed pattern with an overall accuracy of 85.8%, as compared with 83.5% of a logistic-regression-based CA model for the same area. The PLS-CA model is readily applicable to simulations of urban growth in other rapidly urbanizing areas to generate realistic land use patterns and project future scenarios.

1. Introduction

Cellular automata (CA) method is a discrete dynamic modeling technique that has been widely applied in fields related to spatiotemporal distributions [1,2,3,4]. Classical CA formalism has been extended to accommodate the complexity of many systems [5,6]. Geographical information systems (GIS) based CA models have attracted extensive attention because of their ability to simulate urban growth and land use change [7,8,9], following the pioneering work of Tobler [10].

Over the past two decades, remarkable achievements have been made in geographical CA-based dynamic urban growth and land use change modeling, particularly in rapidly urbanizing areas [11,12,13,14,15,16]. Substantial progress has also been made in CA methodology, including transition rules retrieval, neighborhood configuration, scale effects, and results assessment [17,18,19,20]. One important issue in CA modeling is the quantification of the impacts of the factors that drive urban growth and land use change at both global and local scales. Many approaches have been developed to define CA transition rules and each is aimed at improving the overall accuracy and reducing errors of simulation [21,22,23,24]. These approaches vary widely in theoretical assumptions, underlying methodologies, and spatio-temporal resolutions and extents [25]. For example, a CA model based on artificial neural networks (ANN) was developed to calculate land conversion probabilities and model dynamic land use in a GIS environment [21]. This model was used to simulate the multiple land use changes in a rapidly growing area of Guangdong Province, China. A heuristic CA model of urban land use change was proposed based on a simulated annealing (SA) algorithm and was successfully applied to simulate the urban growth in one of Shanghai’s outer suburbs [22]. This model was built around a function that minimizes the difference (residual) between observed and simulated land use patterns, resulting in improved locational accuracy when compared to a logistic-regression-based CA model (named logistic-CA). Other heuristic optimization algorithms such as genetic algorithms (GA) and particle swarm optimization (PSO) have been used to optimize CA parameters from logistic regression and calibrate CA models [22,26,27,28]. A landscape expansion index was incorporated into CA (LEI-CA) to simulate both the adjacent and outlying urban growth of Dongguan City in southern China [15]. This approach demonstrated an improvement when compared to the logistic-CA model in terms of urban simulation accuracy. A random forest based CA model was used to simulate urban growth in Harare Metropolitan Province, Zimbabwe from 1984 to 2013 [24]. This model outperformed CA models based on support vector machine (SVM) and logistic regression in the study area. Markov chain integrated CA (CA-Markov) models are another class of methods developed in the last decade to simulate multiple land use changes [29,30]. The CA-Markov has become increasingly popular in geographical modeling since it was included in IDRISI. Most of these proposed new models perform better than earlier models, substantially advancing CA-based modeling of urban growth/expansion and land use change across the world. Current trends of CA model calibration, such as ANN, SVM, GA, SA and PSO, have become more complex [2,27,29]. Therefore, reconsideration of the statistical approaches is necessary for CA-based urban modeling.

Statistical approaches such as logistic regression and principal components analysis (PCA) are relatively simple and easy to implement using modern software packages. As a classical method, logistic regression has proved to be reliable in CA modeling [11,18,31,32]; however, most of the studies were conducted without consideration of correlation among variables. Moreover, the logistic regression method is incapable of eliminating the negative effects of the multicollinearity among variables [21,28]. By adding an auto-covariate term, logistic regression can be used to reduce the effect of correlation and, hence, increase its predictive accuracy in modeling land use change. A case study of the Paochiao watershed region in Taiwan shows that auto-logistic regression performs better than logistic regression [33]. PCA was used to reduce the effect of multicollinearity among spatial variables and obtain more reasonable CA parameters [34], yielding an improvement in performance when compared to the logistic-CA model. Statisticians have pointed out that the PCA method produces principal components that reflect only the covariance structure between the independent variables [35], and, as a consequence, the extracted components may only weakly explain the variance of the independent variable corresponding to the dependent variable in the regression.

The issue of variable multicollinearity, therefore, has continuously pushed researchers to develop more accurate, justifiable, and defensible models for simulating urban growth. Partial least squares (PLS) regression appears to be useful in addressing correlation because it integrates and generalizes features from PCA and multiple regression methods [36,37]. The method offers three advantages: (1) it removes data redundancies and extracts components from highly correlated spatial variables that better represent and explain the dependent variables (land conversion); (2) it avoids the detrimental effects in modeling due to multicollinearity and can regress when the number of observations is less than the number of variables; and (3) it integrates the basic functions of regression models, PCA, and canonical correlation analysis. In summary, PLS searches for the principal components that explain as much as possible of the covariance between the independent and dependent variables. The parameters obtained using the PLS method might then better explain the dependent variables, i.e., the conversion probability of urban growth.

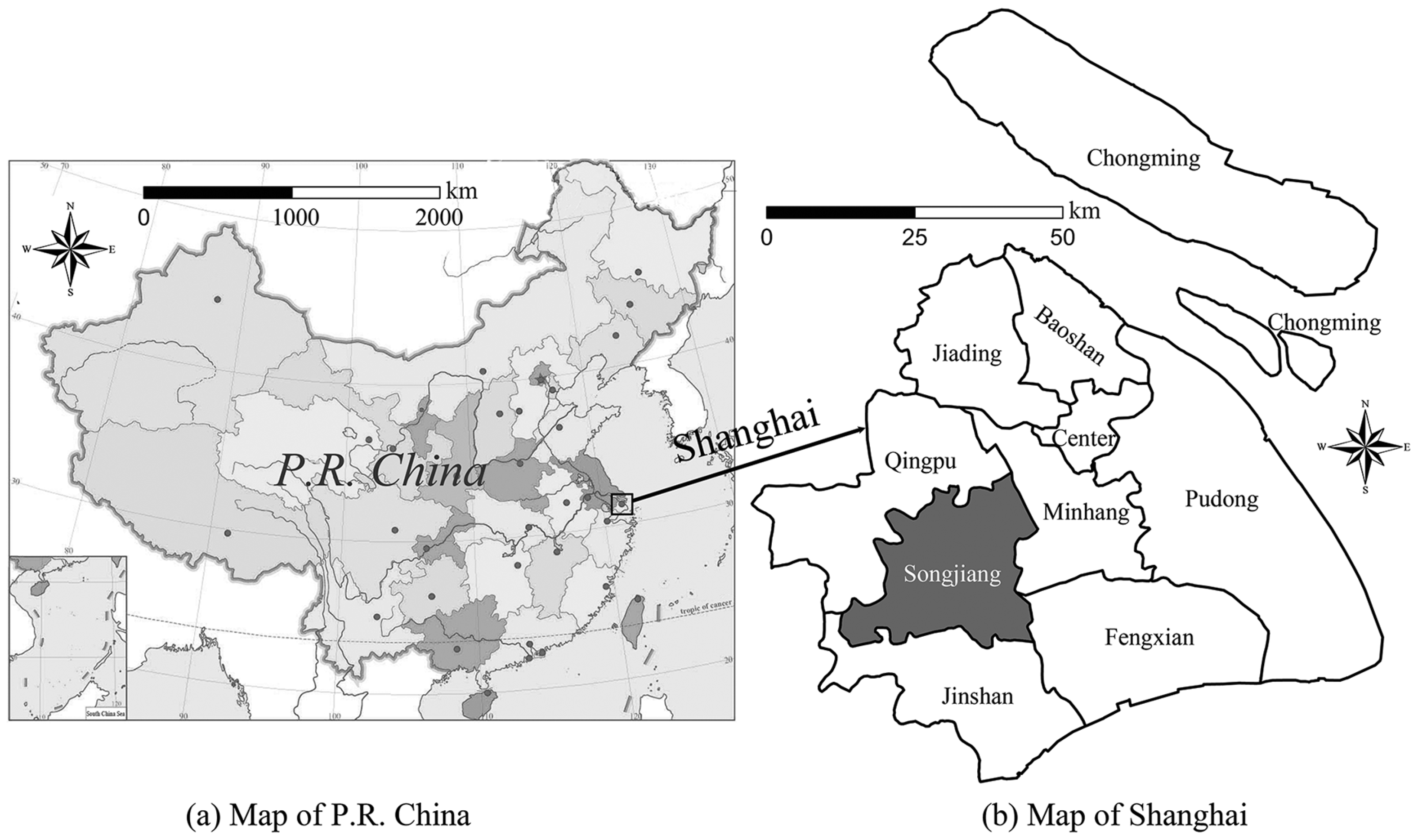
This paper presents a novel CA model based on the PLS approach that we call PLS-CA. This approach was used to derive principal components of the spatial variables for regressing CA parameters. Compared to logistic-CA, PLS can extract variables that are uncorrelated amongst the explanatory variables, and also between the explanatory and response variables. The result is the discovery of important transition rules from a number of driving factors that may be highly correlated. Our PLS-CA model was applied to simulate urban growth in the Songjiang district, an outer suburb of Shanghai Municipality, from 1992 to 2008. For comparison, a logistic-CA model was also applied to simulate the urban growth in the same study area.

2. Material

2.1. Study Area and Data

Songjiang is an outer suburb in the southwest part of Shanghai Municipality that is centered at 121°45′ E and 31°00′ N. Songjiang has a total area of 598.5 km², 15.5 km² of which is water (Figure 1). Over the past two decades, the urban area of Songjiang has grown rapidly with a significant increase in economic activity and concomitant dramatic land use change. According to the local government census, the total registered population has increased from 498,600 in 1995 to 1,074,200 in 2008. Rapid population growth has resulted in an explosive expansion of the urban area [38]. Such large-scale land use change and rapid urban growth have led to the degradation of the landscape, environment, and ecosystem [39,40].

Two Landsat-5 TM/ETM+ images acquired on 18 July 1992 and 24 March 2008 were collected to derive the changes in patterns in the study area. Other, essential ancillary datasets including 1:5000 administrative, topographic, and transportation maps were also collected from the local government. A total of 21 ground control points (GCPs) were identified on the remote sensing images using the topographic map as a reference source. A polynomial method was adopted for geometric rectification and the resulting accuracy obtained was 0.34 and 0.28 pixels for 1992 and 2008, respectively. Finally, the areal extent of Songjiang was clipped from the rectified Landsat images using the administrative map as the boundary.

2.2. Input Variables

Nine factors affecting land use change were chosen to model urban growth in Songjiang from 1992 to 2008. These factors were distance-based variables, neighborhood, constraints, and a stochastic factor (

Table 1. The spatial variables used to simulate urban growth in the partial least squares-based cellular automata (PLS-CA) model.

Variable	Meaning	Type	Acquisition Method
y	Conversion probability	Criterion variable	Remote sensing classification
Durban	Distance to urban center	Spatial variable	Euclidean Distance tool in ArcGIS
Dtown	Distance to town centers
Dmrd	Distance to main roads
Dagri	Distance to agricultural land
Dgs	Distance to green space
Neighborhood	3 × 3 neighborhood	Local variable	Retrieved dynamically during simulation
Constraints	Local constraints
	Global constraints
Stochastic	Stochastic factors	Global variable	Assigned randomly

); all are closely related to urban development and land use changes [2,41,42]. We then visualized the spatial variables and constraints in ArcGIS and produced them as input layers for the PLS-CA model (Figure 2).

Topographic data play an important role in generating spatial variables for CA models. As an example, it is sometimes difficult to convert rural land on a steep slope into urban use. As a result, a slope factor should be included in any credible model. However, the Songjiang study area lies on a very flat land in the Yangtze River Delta [43], and, therefore, the impact of slope can be omitted in the modeling. Distance-based variables and neighborhood reflect the agglomerative effect of urban development and the attractive power of infrastructure [44]. Spatial variables used in the PLS-CA model can be categorized as positive and negative distances. Positive distances include distances to urban center, town centers, and main roads; these factors are significant “push” forces to urban growth. Conversely, the negative distances, such as distances to agricultural land and green space, yield a “repellent” effect on urban development.

Apart from the aforementioned quantifiable factors, there are still many uncertainties and errors in modeling urban growth, resulting in the departure of actual urban growth from some well-known trajectories. Some of these uncertainties are intangible and can be difficult to identify and/or quantify. To represent these uncertainties, a stochastic factor was introduced into our CA model (Table 1). The real values of these spatial variables were acquired from both remotely sensed imagery and vector maps. The conversion probability (y) was calculated by detecting land use change using the thematic mapper (TM) images from 1992 to 2008.

3. The PLS-CA Model

3.1. A Generic CA Model

The global conversion probability of land conversion from non-urban to urban can be calculated as the combined effect of the static probability, neighborhood effect, constraints, and random impact [9,45]. A general form of the global conversion probabilities for u × v cells (in a lattice) is:

$${\left[P_{ij}^t\right]}_{u\times v}={\left[P_d\times con(S_{ij}^t=suitable)\times P_{\mathrm{\Omega },ij}^t\times (1+(-\ln \left(Rnd\right){)}^{\beta })\right]}_{u\times v}$$

(1)

where $P_{ij}^t$ is the global probability of rural-to-urban conversion for cell ij at time t; $P_d$ is the static probability determined by spatial distances [11,34]; con() is a constraint function which returns either 0 or 1 [46]; $P_{\mathrm{\Omega },ij}^t$ is the effect for cell ij at time t within ${\mathrm{\Omega }}_{l\times l}$ neighborhood and it is calculated by $P_{\mathrm{\Omega },ij}^t=\frac{{{\displaystyle \sum }}_{l\times l}con\left(S_{ij}=urban\right)}{l\times l-1}$ where $con(S_{ij}^t=suitable)$ returns 1 if the state of the cell ij is urban, otherwise, it returns 0; $(1+(-\ln \left(Rnd\right){)}^{\beta })$ is the stochastic factor [47], where Rnd is a random real number ranging from 0 to 1, and $\beta$ is a parameter ranging from 0 to 10 that adjusts the influence of the stochastic factor.

The global conversion probability, therefore, consists of: (1) the conversion probability based on spatial variables, (2) cell conversion constraints including planning regulation, protected farmland, and water bodies, (3) neighborhood effects, and (4) a stochastic factor. The first component is the observed conversion probability P_d [18,41]:

$${\left[P_d\right]}_{u\times v}={\left[\frac{1}{1+\exp \left(-\left({\alpha }_0+{\alpha }_1{x}_1+\dots +{\alpha }_p{x}_p\right)\right)}\right]}_{u\times v}$$

(2)

where ${\alpha }_0+{\alpha }_1{x}_1+\dots +{\alpha }_p{x}_p$ represents the comprehensive impacts of distance-based variables on cell ij, $x_i\left(i=1,\dots ,p\right)$ are the distances from the cell ij to a key point such as the urban center, town centers, main roads, etc.; and $a_i\left(i=0,1,\dots ,p\right)$ are their corresponding parameters. These distances are also defined as spatial or independent variables in our CA modeling.

3.2. The PLS Method

We assume that $\mathit{y}={(y_1,\dots ,y_q)}_{n\times q}$ is a set of dependent variables (i.e., the observed rural-to-urban conversion), where n is the size of samples and q is the number of dependent variables, $\mathit{x}={(x_1,\dots ,x_q)}_{n\times p}$ is a set of independent variables with p as the number of independent variables. We also assume that $\mathit{E}={(E_{01},\dots ,E_{0p})}_{n\times p}$ and $\mathit{F}={(F_{01},\dots ,F_{0p})}_{n\times p}$ are the normalized (mean-centered and variance-scaled) matrix forms of x and y, respectively, $t_1$ is the first principal component vector of $E_0$, i.e., $t_1=E_0{w}_1$, $w_1$ is the corresponding unit weight vector of $E_0$ and $\left|\right|w_1\left|\right|=1$, and that $u_1$ is the first principal component vector of $F_0$, i.e., $u_1=F_0{c}_1$, $c_1$ is the corresponding unit weight vector of $F_0$ and $\left|\right|c_1\left|\right|=1$.

In PLS regression, the goal is to obtain a first pair of vectors $t_1=E_0{w}_1$ and $u_1=F_0{c}_1$ under the condition that $\left|\right|w_1\left|\right|=1$ and $\left|\right|c_1\left|\right|=1$, and maximizing $t_i^T{u}_1$. The objective can be re-written as an optimization problem [36,37]:

$$\{\begin{array}{l}ma{x}_{w_1,c_1}\langle E_0{w}_1,F_0{c}_1\rangle \\ subjectto\{\begin{array}{c}{w}_1^T{w}_1=1\\ c_1^T{c}_1=1\end{array}\end{array}$$

(3)

By applying the Lagrange algorithm, we obtained eigenvalue equations resolving a first pair of weight vectors $w_1$ and $c_1$ as follows:

$$\{\begin{array}{l}{E}_0^T{F}_0{F}_0^T{E}_0{w}_1={\theta }_1^2{w}_1\\ F_0^T{E}_0{E}_0^T{F}_0{c}_1={\theta }_1^2{c}_1\end{array}$$

(4)

where $w_1$ and $c_1$ are the unit eigenvectors of the matrices $E_0^T{F}_0{F}_0^T{E}_0$ and $F_0^T{E}_0{E}_0^T{F}_0$, respectively, ${\theta }_1^2$ is the corresponding eigenvalue, and ${\theta }_1=F_0^T{E}_0^T{F}_0{c}_1$. According to Equation (1), ${\theta }_1$ is supposed to be maximal in the sense of PLS regression.

We compute the first pair of component vectors $t_1=E_0{w}_1$ and $u_1=F_0{c}_1$, and run the regression of $E_0$ and $F_0$ with respect to $t_1$ and $u_1$, respectively. The equation is:

$$\{\begin{array}{l}{E}_0=t_1{p}_1^T+E_1\\ F_0=t_1{r}_1^T+F_1\end{array}$$

(5)

where $E_1$ and $F_1$ are the residual matrices, and $p_1$ and $r_1$ are the coefficient vectors that can be given by:

$$\{\begin{array}{l}{p}_1=\frac{E_0^T{t}_1}{{||t_1||}^2}\\ r_1=\frac{F_0^T{t}_1}{{||t_1||}^2}\end{array}$$

(6)

Substituting the residual matrices $E_1$ and $F_1$ for $E_0$ and $F_0$ and repeating the above method, we obtained the second component vectors $t_2$ and $u_2$ as:

$$\{\begin{array}{l}{t}_2=E_1{w}_2\\ u_2=F_1{c}_2\\ {\theta }_2=\langle t_2,u_2\rangle =w_2^T{E}_1^T{F}_1{c}_2\end{array}$$

(7)

where $w_2$ and $c_2$ are the unit eigenvectors of matrices $E_1^T{F}_1{F}_1^T{E}_1$ and $F_1^T{E}_1{E}_1^T{F}_1,$ respectively, corresponding to the maximum eigenvalue ${\theta }_2^2$.

Running the regression of $E_1$ and $F_1$ with respect to $t_2$ and $u_2$, respectively, we have:

$$\{\begin{array}{l}{E}_1=t_2{p}_2^T+E_2\\ F_1=t_2{r}_2^T+F_2\end{array}$$

(8)

where the coefficient vectors $p_2$ and $r_2$ are calculated from:

$$\{\begin{array}{l}{p}_2=\frac{E_1^T{t}_2}{{||t_2||}^2}\\ r_2=\frac{F_1^T{t}_2}{{||t_2||}^2}\end{array}$$

(9)

The procedure is iterated until $E_0$ becomes a null matrix, and the final components $t_i\left(i=1,\dots ,m\right)$ are determined by cross-validation. Therefore, we have the following equations:

$$\{\begin{array}{l}{E}_0=t_1{p}_1^T+\dots +t_m{p}_m^T\\ F_0=t_1{r}_1^T+\dots +t_m{r}_m^T+F_m\end{array}$$

(10)

Since $t_1,\dots ,t_m$ can be represented as the linear combination of the original variables $E_{01},\dots ,E_{0p}$, and $F_0$ in Equation (10) is recovered by the regression equation of $y_j^{*}=F_{ok}\left(k=1,\dots ,q\right)$ with respect to $x_j^{*}=E_{oj}\left(j=1,\dots ,p\right)$as follows:

$$y_k^{*}={\alpha }_{k_1}{x}_1^{*}+\dots +{\alpha }_{k_p}{x}_p^{*}+F_{mk}\left(k=1,\dots ,q\right)$$

(11)

where ${\alpha }_{k_1},\dots ,{\alpha }_{k_p}$ are the corresponding coefficients and F_mk is the k^th column of residual matrix F_m.

Cross-validation checks the contributions of the extracted principal components to determine how well the regression model predicts the data. The cross-validation for the component t_n is:

$$Q_h^2=1-\frac{PRES{S}_h}{S{S}_{h-1}}$$

(12)

where PRESS_h is the sum of squares of prediction error with a total of h components (t₁, …, t_h), and SS_h−1 is the sum of squares of combination error of y with the first (h−1) components (t₁, …, t_h−1).

If $\frac{PRES{S}_h}{S{S}_{h-1}}\le {0.95}^2$, the contribution margin of the newly added component t_n is significant, and as a result, iteration stops when $Q_h^2\ge 0.00975$ [36,37].

3.3. PLS-Based CA Model

Since the conversion probability of each cell in CA is a single decimal variable, Equation (11) can be re-written as [36,37]:

$$\widehat{y}={\alpha }_0+{\alpha }_1{x}_1+\dots +{\alpha }_p{x}_p$$

(13)

where ${\alpha }_i\left(\mathrm{i}=0,1,\dots ,p\right)$ is the $i^{th}$ regression estimator.

The form of Equation (13) retrieved by PLS method is similar to that from PCA method but the regression estimator α_p obtained from the PLS method contains information about the dependent variable y as shown in Equation (7), while α_p obtained by PCA does not contain any contribution of the responsive variable y [34,36,37]. Although data redundancy can be eliminated by PCA, the regression estimators obtained are not related to the independent variables and, thus, have less strong ability to interpret the independent variable y. PLS is more robust than PCA at explaining the responsive variable y.

Integrating Equations (1), (2) and (13), we derived the global conversion probability in the PLS-CA model:

$${\left[P_{ij}^t\right]}_{u\times v}={\left[\begin{array}{c}\frac{1}{1+exp\left[-\left({\alpha }_0+{\alpha }_1{x}_1+\dots +{\alpha }_p{x}_p\right)\right]}\times \frac{{{\displaystyle \sum }}_{l\times l}con\left(S_{ij}=urban\right)}{l\times l-1}\\ \times con\left(cel{l}_{ij}^t=suitable\right)\times \left(1+{\left(-\ln \left(Rnd\right)\right)}^{\beta }\right)\end{array}\right]}_{u\times v}$$

(14)

If the calculated global probability $P_{ij}^t$ exceeds the predefined threshold ranging from 0 to 1, the cell ij at time t will be converted to urban land use at time t + 1. Otherwise, it will retain its current state at next time t + 1 [18,41].

3.4. Structure of the PLS-CA Model

The PLS-CA model workflow consists of five steps: raw data collection, data processing, CA rule discovery with PLS, determination of other CA factors, and model implementation and results assessment (Figure 3). Each step of the model plays a distinct role in the modeling as follows:

(1) Raw data collection: Data used in the model include historical raster images such as remotely sensed images, an administrative vector map, a topographic map, and a transportation map.

(2) Data processing: Spatial variables were extracted from raw data using the ArcGIS Spatial Analyst tool. These spatial variables included the distance to the urban center (D_urban), town centers (D_town), main roads (D_mrd), agricultural land (D_agri), and green space (D_gs). The five spatial variables were normalized by:

$$D_{norm}=\frac{D_{ori}}{D_{max}}$$

(15)

where D_max is the maximum value of the spatial variable, D_ori is the original distance value from the raw data, and D_norm is the normalized value in the range (0, 1). Normalization enables a precise interpretation of the geographic meaning of the parameters. For instance, if a cell is situated at the urban center, its normalized D_urban value will be 0, where if the cell is situated far from the urban center, its normalized D_urban will approach 1.

(3) CA rule discovery: This module derives uncorrelated spatial components using PLS. It determines whether the derived spatial variables satisfy the cross-validation of $Q_h^2\ge 0.0975$ and, hence, it is used to define CA parameters (i.e., weights of spatial variables) by which the land conversion probability $P_d$ under variables can be obtained. The PLS regression was conducted using the “PLSR” package of R-language [48].

(4) Other CA factors: These include non-spatial factors such as neighborhood effect, constraints of basic farmland, and a stochastic factor.

(5) PLS-CA implementation and assessment: This module enables the simulation of the PLS-CA model and incorporates simulation accuracy assessment by generating overall accuracy, producer’s accuracy, user’s accuracy, Kappa coefficient, and the compared urban growth rate (CUGR). The module also displays and exports simulation outcomes.

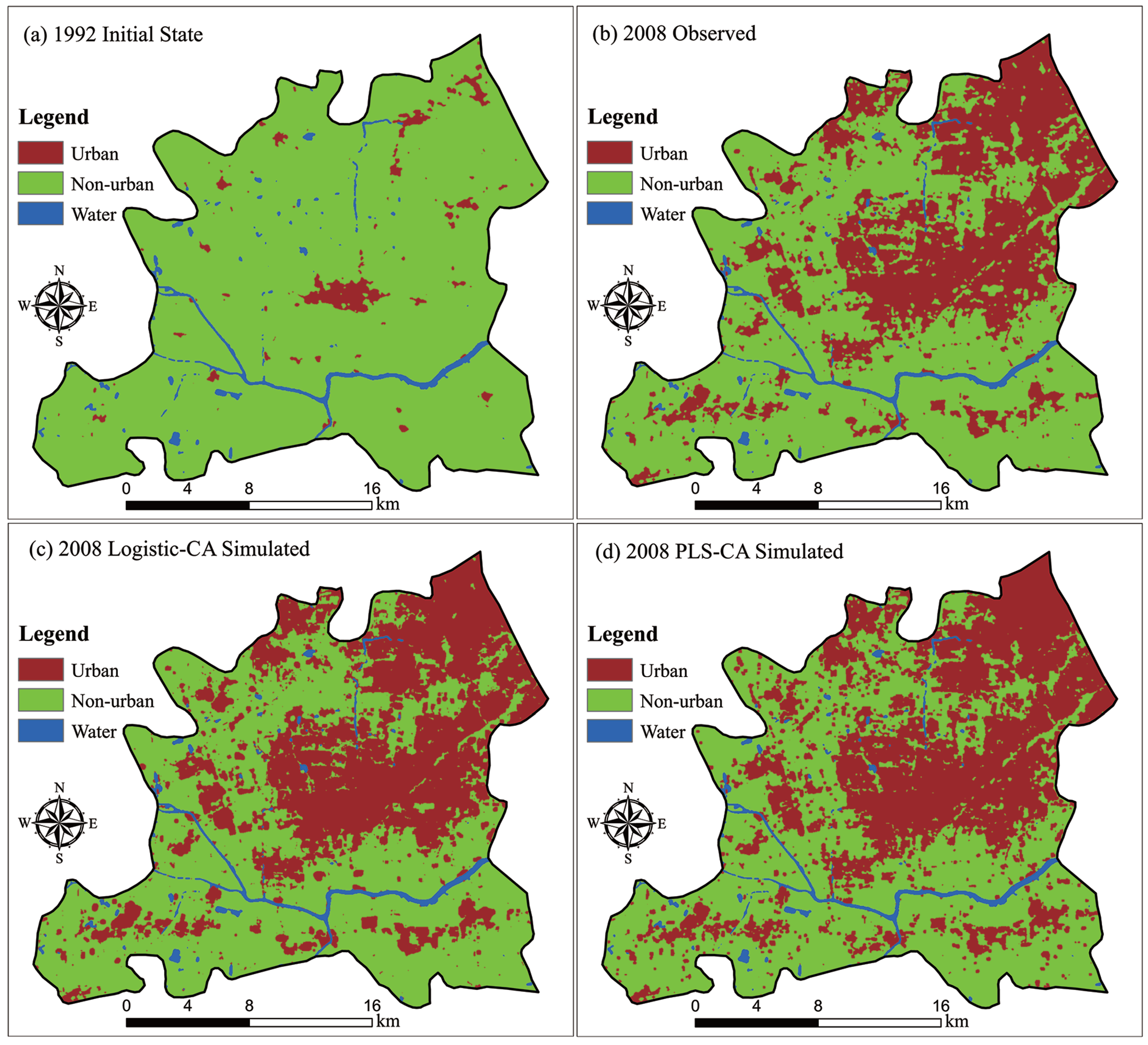
The simulated area of each category from the CA modeling was not exactly equal to the actual area. Therefore, an indicator termed the compared urban growth rate (CUGR) is calculated to assess the accuracy of the PLS-CA model by comparing the observed and simulated urban growth rates. The CUGR indicator was computed as:

$$CUGR=\frac{S_{sim2008}}{S_{obs2008}}\times 100\%$$

(16)

where CUGR is the difference between the observed and simulated areas of each category in terms of growth rate, S_sim2008 is the simulation area of the urban or non-urban category at 2008, and S_obs2008 is the statistical areas of observed urban growth in 2008 or non-urban loss in 1992, respectively.

4. Results and Discussion

4.1. Assessment of Correlation

A total of 5000 samples were randomly selected from spatial variables and the classified land use patterns in 1992 and 2008 to determine the CA transition rules. The correlation matrix of spatial variables was calculated using the samples (

Table 2. Correlation matrix of spatial variables.

Variable	Dtown	Dmrd	Dagri	Dgs	y
Durban	0.6462	0.6109	−0.5372	−0.5280	0.2264
Dtown		0.7058	−0.4496	−0.7754	0.5635
Dmrd			−0.4714	−0.4971	0.2518
Dagri				0.8537	−0.1572
Dgs					−0.1893

), showing significant correlations among these spatial variables. Traditional methods, such as multi-criteria evaluation (MCE) technique and logistic regression, are not able to avoid the negative effects of multicollinearity and are relatively weak in providing correct weights for the variables. We, therefore, applied PLS to extract the uncorrelated principal components from spatial variables to achieve more reasonable CA transition rules and improve the performances of the CA model.

4.2. CA Transition Rules

Among the three components acquired by PLS regression, only the first two satisfied the cross-validation requirement but explained more than 95% of the total variance (

Table 3. Principal components derived from PLS.

Component	Cross-Validation			Spatial Variables
	R	${\mathit{Q}}_{\mathit{h}}^2$	Critical Value	Urban Center	Town Center	Main Road	Agricultural Land	Green Space
1	0.8625	0.8517	−0.0975	−0.8156	−0.4744	0.3012	−0.2290	−0.2967
2	0.3240	0.1054	−0.0975	−0.3694	−0.2536	−0.5515	0.6557	0.3553
3	0.1572	−0.0092	−0.0975	−0.0916	0.1228	0.2031	0.1232	0.0802

). The first component is mainly related to urban center, and the second component is principally related to main roads. For the third component, its $Q_h^2$ is less than the critical value and, therefore, it is not a valid component. By comparison, PCA can reduce data redundancy but it extracts exactly five components for the same samples used in this research. Its first three explained 84.268% of the variance, lower than that of the PLS regression. Based on PLS regression, suitable weights for CA models can be easily defined, since the principal components are independent, avoiding the repeated counting that may occur in general MCE [21]. The CA parameters acquired by logistic regression are quite different with D_mrd (1.7590) being very large and D_town (0.5846) relatively small (

Table 4. Comparison of CA parameters generated by PLS and logistic regression.

Models	Variable
	Durban	Dtown	Dmrd	Dagri	Dgs
PLS-CA	−1.1063	−0.5841	−0.8274	0.1924	0.1513
logistic-CA	−0.5846	−0.2837	−1.7590	2.0263	1.5978

) as compared with those in the PLS regression. This indicates that the logistic-CA model over-weights D_mrd but undervalues D_urban. In contrast, PLS regression generated CA parameters that more reasonably reflect the actual urban growth in Songjiang. In the PLS approach, the negative weights for the distance factors are: D_urban (−1.1063), D_mrd (−0.8274), D_town (−0.5841), followed by the positive weights of D_agri and D_gs which reflect the factors that tend to prevent non-urban land from being developed. The land conversion potential was produced as map layers based on the calibrated logistic regression and PLS methods (Figure 4), which varied from 0.38 to 0.72 for logistic-CA and from 0.34 to 0.70 for PLS-CA.

4.3. Simulation Results

The PLS-CA model was applied to simulate urban growth of Songjiang from 1992 to 2008 (Figure 5). In the simulation, land use types were generalized as urban, non-urban, and water body.

Before running the model, the best combination of threshold value P_thd and the number of iterations was determined for the calibration of the PLS-CA model. The meaning of each iteration should also be defined. As an initial trial, a P_thd value of 0.40 was used to test if a non-urban cell can be converted to an urban cell. By running the model, simulated results that approximated the actual urban growth were realized within a certain number of iterations. For the next trial, P_thd was increased by 0.02 and a simulation result with the highest overall accuracy was acquired with another number of iterations. P_thd increased by 0.02 from 0.40 to 0.80, indicating that there were 21 trials for this model. After comparing the results of all trials with different P_thd values, the PLS-CA model generated the highest overall simulation accuracy of 85.8% at P_thd = 0.68 and Iteration = 16. By comparison, a logistic-CA model was also calibrated with the best overall simulation accuracy of 83.5% at P_thd = 0.66 and Iteration = 16.

Visual inspection demonstrates a good match between the observed and simulated patterns, for both the logistic-CA and PLS-CA models (Figure 5). Further, all three observed and simulated urban patterns in 2008 show that urban growth of Songjiang occurred around the urban centers and northeastern areas in the late 1990s to early 2000s.

4.4. Accuracy Analysis

To quantitatively evaluate the simulation accuracy and the performance of the PLS-CA model, a pixel-by-pixel comparison was used to calculate a confusion matrix about the concordance between the simulated results and the observed pattern [11,21,49,50]. The reference land use map illustrating the observed urban growth was the classified result using a supervised minimum distance classifier in ENVI 5.2. The confusion matrix derived from the simulated results and the observed reference map was produced for comparison (

Table 5. Confusion matrix between remote sensing-based classification and simulated urban pattern using the PLS-CA model for Songjiang in 2008.

Item		Observed (%)
		Urban	Non-Urban	Total
Simulated (%)	Urban	33.6	12.5	46.1
	Non-Urban	1.7	52.2	53.9
	Total	35.3	64.7	100
User’s Accuracy				Commission error
Non-urban	= 33.6/46.1 = 72.9%			27.1%
Urban	= 52.2/53.9 = 96.8%			3.2%
Producer’s Accuracy				Omission error
Non-urban	= 33.6/35.3 = 95.2%			4.8%
Urban	= 52.2/64.7 = 80.7%			19.3%
Overall accuracy	85.8%
Kappa coefficient	70.9%

). Kappa coefficients were also calculated to quantify their actual degree of agreement [51,52].

User’s accuracy was 72.9% for non-urban areas and 96.8% for urban areas in 2008, while the producer’s accuracies for non-urban and urban categories were 95.2% and 80.7%, respectively (Table 5). The user’s accuracy of urban informs that, of all the observed cells considered as urban in the classified patterns, 96.8% were correctly classified in the simulated pattern, and the probability of identification of urban mislabeled as non-urban (i.e., commission error) was 3.2% [53]. For the same urban category in Table 5, of all the urban cells in the simulation result, 80.7% actually correspond to urban in the classified pattern. In other words, the probability of identification of a cell erroneously labeled as urban category (i.e., an omission error) was 19.3%. The overall accuracy shows that 85.8% of all the cells under assessment were correctly categorized in the simulation result. The Kappa coefficient means that the simulation achieved an accuracy that was 70.9% better than what would be expected from the chance assignment of cells to categories.

4.5. Discussion

The detailed simulation accuracies were calculated for Songjiang in 2008 for the logistic-CA and PLS-CA models for Songjiang (Figure 6). The user’s accuracy for non-urban generated by the PLS-CA model was 3.5% greater than that of the logistic-CA model, and the producer’s accuracy for non-urban from the PLS-CA model was nearly equal to that of the logistic-CA model (94.9%). For the urban category, the user’s and producer’s accuracies of the logistic-CA model were 96.5% and 77.3%, respectively, lower than those of the PLS-CA model. The overall accuracy of the simulation results in 2008 was 83.5% for the logistic-CA model, 2.3% less than the new PLS-CA model. The Kappa coefficient of the PLS-CA model was 70.9%, which outperforms the logistic-CA model (66.6%). The comparison suggests that the PLS-CA model generated more accurate results compared to the logistic-CA model.

The CUGR indicator illustrates the growth rate of the simulated urban area compared with the actual urban development. A CUGR for urban areas larger 100% indicates that the simulated growth exceeds the observed growth; otherwise, the simulation growth is slower than the observed growth. A CUGR value approaching 100% suggests that the CA model performs well in terms of the area control. Statistics for observed urban growth (excluding water bodies) were retrieved from remote sensing, corrected by the data from the local government of Songjiang. Logistic-CA and PLS-CA models both simulated more urban growth than actually occurred (

Table 6. Observed and simulated urban growth rates from 1992–2008 (CUGR stands for compared urban growth rate).

Urban Growth		Urban	Non-urban
Observed	Area 1992 (km2)	17.9	565.1
	Area 2008 (km2)	205.2	377.8
logistic-CA	Area 2008 (km2)	248.4	334.6
	CUGR (%)	121.1	88.6
PLS-CA	Area 2008 (km2)	234.3	348.7
	CUGR (%)	114.2	92.3

). The CUGR of the urban category was 114.2% for the PLS-CA model, lower than that of the logistic-CA model (121.1%). The CUGR of the non-urban was 92.3% for the PLS-CA model, which is closer to 100% than that for the logistic-CA model (88.6%). This result suggests that the overall area control performance of the PLS-CA model was better than that of the logistic-CA model, while still overestimating urban growth and underestimating the persistence of non-urban.

Urban development is a complex open system whose trajectory is affected by drivers that may be significantly, spatially correlated. Integrated with the analytical functions of GIS, logistic regression can be used to evaluate the impact of these factors on urban growth. However, logistic regression cannot eliminate the correlation of spatial variables, while PCA can eliminate spatial correlation only to a certain degree, and the principal components found in the independent variables may not adequately explain the dependent variables [35]. The proposed PLS method can extract variables that are uncorrelated from amongst the explanatory variables, and also between the explanatory and response factors [36,37], resulting in the discovery of transition rules from a number of driving factors that are usually highly correlated. This relationship could explain why PLS-CA modeling outperformed the traditional logistic-CA model, at least from a theoretical point of view. Our results show that the simulated patterns of urban growth accord well with the actual urban pattern of Songjiang. Compared with the logistic-CA model, the PLS-CA model achieved better simulation accuracies in modeling the urban growth of Songjiang through time. We speculate that our model is better than the PCA-based CA model as inferred by the principal components, but not necessarily better than auto-logistic regression which performs nearly as well as ANN [33]. It still needs to be tested whether the PLS-CA model is more or less accurate than other CA models based on artificial intelligence and machine learning. However, our new model poses the advantages that it is simpler than these models and generates parameters having clear physical meanings.

In addition, CA models contain various types of uncertainty caused by several other factors such as sampling, neighborhood configuration, constraints, stochastic perturbation, and spatial scale [19,47,54,55]. We took only one group of samples for training the PLS-CA model in this study. Like any other CA models, our PLS-CA could be sensitive to samples that are determined by both sampling method and sample grouping [9]. The effect of sampling on the simulation results is reflected by the CA parameters of drivers. Such an effect is relatively greater for statistically significant drivers, whereas it is much smaller for statistically non-significant drivers which can even be excluded in modeling [32,56]. Neighborhood configuration such as the shape and number of neighbors influences the CA models by local interactions [19,57]. A stochastic factor in CA transition rules is to simulate less tangible uncertainties and perturbations that may affect the simulation results [11,42,47]. Moreover, raster-based CA models are also sensitive to cell size (grain size) in terms of simulation accuracy and landscape structure [39,55,58,59]. The proposed PLS-CA model is no exception because it depends on a rasterized space.

5. Conclusions

This paper demonstrates that CA models can accurately simulate urban growth using global and local constraints that reflect various environmental concerns. The advantages of urban growth simulation by GIS-based CA modeling include the identification of the driving factors of land use change and the identification of spatial patterns across space and over time. The most important part of developing these new models is to discover mature CA transition rules. Our PLS-CA model is capable of extracting uncorrelated factors from the candidate explanatory variables. Thus, PLS-CA can well eliminate redundancy of the input data and, thus, allow for the discovery of better and more reasonable transition rules. The PLS-CA model was successfully applied to simulate the urban growth in Songjiang, demonstrating better simulation accuracy than a conventional logistic-CA model.

Further improvements could be made by testing the response and robustness of the PLS-CA model on sampling, neighborhood configuration, constraints, and spatial scale. In addition, advanced CA models could be packaged with simple, robust, and easily implementable modules such as real-time and dynamic display of simulation results.