Exploring the Influence of Neighborhood Characteristics on Burglary Risks: A Bayesian Random Effects Modeling Approach
Abstract
:1. Introduction
2. Study Region and Data
2.1. Study Region
2.2. Data
3. Methods
3.1. Modeling Strategy
3.2. Prior Specification
3.3. Implementation
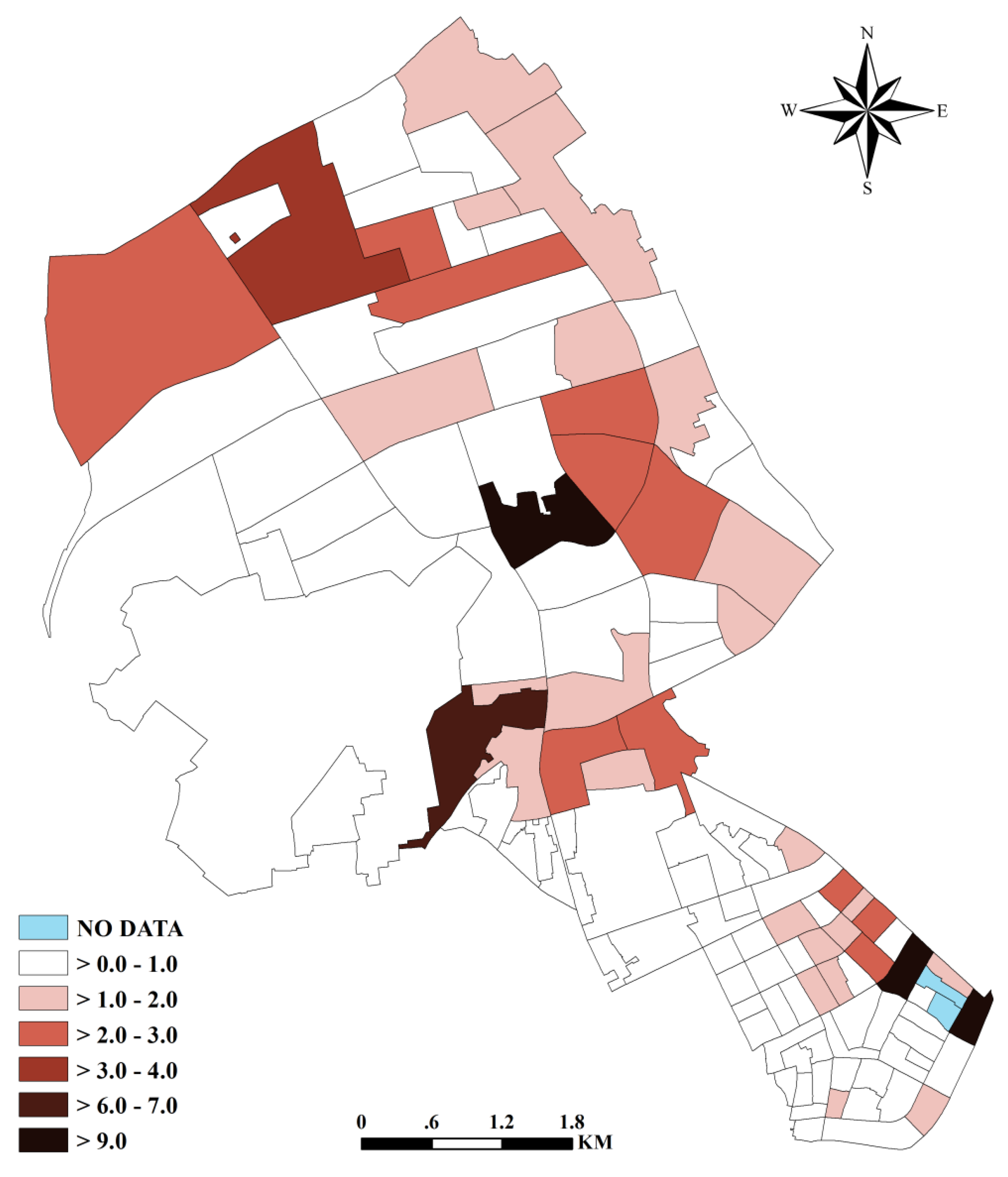
4. Results
5. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Weisburd, D.; Bruinsma, G.J.; Bernasco, W. Units of analysis in geographic criminology: Historical development, critical issues, and open questions. In Putting Crime in Its Place; Springer: Berlin, Germany, 2009; pp. 3–31. [Google Scholar]
- Weir, R.; Bangs, M.; Britain, G. The Use of Geographic Information Systems by Crime Analysts in England and Wales; Home Office: London, UK, 2007. [Google Scholar]
- Archer, D.; Gartner, R. Violence and Crime in Cross-national Perspective; Yale University Press: New Haven, CT, USA, 1987. [Google Scholar]
- Faggiani, D.; Bibel, D.; Brensilber, D. Regional problem solving using the national incident based reporting system. In Solving Crime and Disorder Problems; Police Executive Research Forum: Washington, DC, USA, 2001; pp. 155–174. [Google Scholar]
- Baller, R.D.; Anselin, L.; Messner, S.F.; Deane, G.; Hawkins, D.F. Structural covariates of us county homicide rates: Incorporating spatial effects. Criminology 2001, 39, 561–588. [Google Scholar] [CrossRef]
- Cork, D. Examining space–time interaction in city-level homicide data: Crack markets and the diffusion of guns among youth. J. Quant. Criminol. 1999, 15, 379–406. [Google Scholar] [CrossRef]
- Baumer, E.; Lauritsen, J.L.; Rosenfeld, R.; Wright, R. The influence of crack cocaine on robbery, burglary, and homicide rates: A cross-city, longitudinal analysis. J. Res. Crime Delinquency 1998, 35, 316–340. [Google Scholar] [CrossRef]
- Taylor, R.B. Social order and disorder of street blocks and neighborhoods: Ecology, microecology, and the systemic model of social disorganization. J. Res. Crime Delinquency 1997, 34, 113–155. [Google Scholar] [CrossRef]
- Martin, D. Spatial patterns in residential burglary assessing the effect of neighborhood social capital. J. Contemp. Criminal Justice 2002, 18, 132–146. [Google Scholar] [CrossRef]
- Groff, E.R.; Weisburd, D.; Yang, S.-M. Is it important to examine crime trends at a local “micro” level?: A longitudinal analysis of street to street variability in crime trajectories. J. Quant. Criminol. 2010, 26, 7–32. [Google Scholar] [CrossRef]
- Smith, W.R.; Frazee, S.G.; Davison, E.L. Futhering the integration of routine activity and social disorganization theories: Small units of analysis and the study of street robbery as a diffusion process. Criminology 2000, 38, 489–524. [Google Scholar] [CrossRef]
- Law, J.; Haining, R. A bayesian approach to modeling binary data: The case of high-intensity crime areas. Geogr. Anal. 2004, 36, 197–216. [Google Scholar] [CrossRef]
- Morenoff, J.D.; Sampson, R.J.; Raudenbush, S.W. Neighborhood inequality, collective efficacy, and the spatial dynamics of urban violence. Criminology 2001, 39, 517–558. [Google Scholar] [CrossRef]
- Andresen, M.A. A spatial analysis of crime in vancouver, british columbia: A synthesis of social disorganization and routine activity theory. Can. Geogr./Le Géographe canadien 2006, 50, 487–502. [Google Scholar] [CrossRef]
- Malczewski, J.; Poetz, A. Residential burglaries and neighborhood socioeconomic context in london, ontario: Global and local regression analysis. Prof. Geogr. 2005, 57, 516–529. [Google Scholar] [CrossRef]
- Stein, R.E.; Conley, J.F.; Davis, C. The differential impact of physical disorder and collective efficacy: A geographically weighted regression on violent crime. GeoJournal 2015, 81, 1–15. [Google Scholar] [CrossRef]
- Anselin, L. Spatial Econometrics: Methods and Models; Kulwer Academic: Dordrecht, The Netherlands, 1988. [Google Scholar]
- Carlin, B.P.; Louis, T.A. Bayes and Empirical Bayes Methods for Data Analysis, 2nd ed.; Chapman and Hall: London, UK, 2000. [Google Scholar]
- Spiegelhalter, D.J.; Thomas, A.; Best, N.G.; Gilks, W.R. Bugs: Bayesian Inference Using Gibbs Sampling, version 0.50; Cambridge University, MRC Biostatistics Unit: Cambridge, UK, 1995. [Google Scholar]
- Clayton, D.; Kaldor, J. Empirical bayes estimates of age-standardized relative risks for use in disease mapping. Biometrics 1987, 43, 671–681. [Google Scholar] [CrossRef] [PubMed]
- Bernardinelli, L.; Clayton, D.; Pascutto, C.; Montomoli, C.; Ghislandi, M.; Songini, M. Bayesian analysis of space-time variation in disease risk. Stat. Med. 1995, 14, 2433–2443. [Google Scholar] [CrossRef] [PubMed]
- Lawson, A.B. Bayesian Disease Mapping: Hierarchical Modeling in Spatial Epidemiology; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Kim, H.; Oleson, J.J. A bayesian dynamic spatio-temporal interaction model: An application to prostate cancer incidence. Geogr. Anal. 2008, 40, 77–96. [Google Scholar] [CrossRef]
- Haining, R.; Law, J. Combining police perceptions with police records of serious crime areas: A modelling approach. J. R. Stat. Soc. Ser. A (Stat. Soc.) 2007, 170, 1019–1034. [Google Scholar] [CrossRef]
- Freisthler, B.; Weiss, R.E. Using bayesian space-time models to understand the substance use environment and risk for being referred to child protective services. Subst. Use Misuse 2008, 43, 239–251. [Google Scholar] [CrossRef] [PubMed]
- Wheeler, D.C.; Waller, L.A. Comparing spatially varying coefficient models: A case study examining violent crime rates and their relationships to alcohol outlets and illegal drug arrests. J. Geogr. Syst. 2009, 11, 1–22. [Google Scholar] [CrossRef]
- Levine, N.; Block, R. Bayesian journey-to-crime estimation: An improvement in geographic profiling methodology. Prof. Geogr. 2011, 63, 213–229. [Google Scholar] [CrossRef]
- Yu, Q.; Scribner, R.; Carlin, B.; Theall, K.; Simonsen, N.; Ghosh-Dastidar, B.; Cohen, D.; Mason, K. Multilevel spatio-temporal dual changepoint models for relating alcohol outlet destruction and changes in neighbourhood rates of assaultive violence. Geosp. Health 2008, 2, 161–172. [Google Scholar] [CrossRef] [PubMed]
- Cunradi, C.B.; Mair, C.; Ponicki, W.; Remer, L. Alcohol outlets, neighborhood characteristics, and intimate partner violence: Ecological analysis of a california city. J. Urban Health 2011, 88, 191–200. [Google Scholar] [CrossRef] [PubMed]
- Law, J.; Chan, P.W. Bayesian spatial random effect modelling for analysing burglary risks controlling for offender, socioeconomic, and unknown risk factors. Appl. Spat. Anal. Policy 2012, 5, 73–96. [Google Scholar] [CrossRef]
- Law, J.; Quick, M. Exploring links between juvenile offenders and social disorganization at a large map scale: A bayesian spatial modeling approach. J. Geogr. Syst. 2013, 15, 89–113. [Google Scholar] [CrossRef]
- Gracia, E.; López-Quílez, A.; Marco, M.; Lladosa, S.; Lila, M. Exploring neighborhood influences on small-area variations in intimate partner violence risk: A bayesian random-effects modeling approach. Int. J. Environ. Res. Public Health 2014, 11, 866–882. [Google Scholar] [CrossRef] [PubMed]
- Law, J.; Quick, M.; Chan, P. Bayesian spatio-temporal modeling for analysing local patterns of crime over time at the small-area level. J. Quant. Criminol. 2014, 30, 57–78. [Google Scholar] [CrossRef]
- Law, J.; Quick, M.; Chan, P.W. Analyzing hotspots of crime using a bayesian spatiotemporal modeling approach: A case study of violent crime in the greater toronto area. Geogr. Anal. 2015, 47, 1–19. [Google Scholar] [CrossRef]
- Gracia, E.; López-Quílez, A.; Marco, M.; Lladosa, S.; Lila, M. The spatial epidemiology of intimate partner violence: Do neighborhoods matter? Am. J. Epidemiol. 2015, 182, 58–66. [Google Scholar] [CrossRef] [PubMed]
- Knorr-Held, L. Bayesian modelling of inseparable space-time variation in disease risk. Stat. Med. 1999, 19, 2555–2567. [Google Scholar] [CrossRef]
- Mollié, A.; Gilks, W.; Richardson, S.; Spiegelhalter, D. Bayesian mapping of disease. Markov Chain Monte Carlo Pract. 1996, 1, 359–379. [Google Scholar]
- Wakefield, J.; Best, N.; Waller, L. Bayesian approaches to disease mapping. Spat. Epidemiol. Methods Appl. 2000. [Google Scholar] [CrossRef]
- Wuhan Municipal Bureau of Statistics. Wuhan Statistical Yearbook 2014; China Statistics Press: Beijing, China, 2014.
- Shaw, C.R.; McKay, H.D. Juvenile Delinquency and Urban Areas; University of Chicago Press: Chicago, IL, USA, 1942. [Google Scholar]
- Cohen, L.E.; Felson, M. Social change and crime rate trends: A routine activity approach. Am. Sociol. Rev. 1979, 44, 588–608. [Google Scholar] [CrossRef]
- Bursik, R.J. Social disorganization and theories of crime and delinquency: Problems and prospects. Criminology 1988, 26, 519–552. [Google Scholar] [CrossRef]
- Ackerman, W.V. Socioeconomic correlates of increasing crime rates in smaller communities. Prof. Geogr. 1998, 50, 372–387. [Google Scholar] [CrossRef]
- Felson, M.; Cohen, L.E. Human ecology and crime: A routine activity approach. Hum. Ecol. 1980, 8, 389–406. [Google Scholar] [CrossRef]
- Sherman, L.W.; Gartin, P.R.; Buerger, M.E. Hot spots of predatory crime: Routine activities and the criminology of place. Criminology 1989, 27, 27–56. [Google Scholar] [CrossRef]
- Jacobs, J. The Death and Life of Great American Cities; Random House: New York, NY, USA, 1961. [Google Scholar]
- Beasley, R.W.; Antunes, G. The etiology of urban crime an ecological analysis. Criminology 1974, 11, 439–461. [Google Scholar] [CrossRef]
- Rotolo, T.; Tittle, C.R. Population size, change, and crime in US cities. J. Quant. Criminol. 2006, 22, 341–367. [Google Scholar] [CrossRef]
- Roncek, D.W. Dangerous places: Crime and residential environment. Soc. Forces 1981, 60, 74–96. [Google Scholar] [CrossRef]
- Stark, R. Deviant places: A theory of the ecology of crime. Criminology 1987, 25, 893–910. [Google Scholar] [CrossRef]
- Roncek, D.W.; Maier, P.A. Bars, blocks, and crimes revisited: Linking the theory of routine activities to the empiricism of “hot spots”. Criminology 1991, 29, 725–753. [Google Scholar] [CrossRef]
- Evans, J.D. Straightforward Statistics for the Behavioral Sciences; Brooks/Cole Publishing: Pacific Grove, CA, USA, 1996. [Google Scholar]
- Dormann, C.F.; Elith, J.; Bacher, S.; Buchmann, C.; Carl, G.; Carré, G.; Marquéz, J.R.G.; Gruber, B.; Lafourcade, B.; Leitão, P.J. Collinearity: A review of methods to deal with it and a simulation study evaluating their performance. Ecography 2013, 36, 27–46. [Google Scholar] [CrossRef]
- Montgomery, D.C.; Peck, E.A.; Vining, G.G. Introduction to Linear Regression Analysis; John Wiley & Sons: New York, NY, USA, 2015. [Google Scholar]
- Bizeti, H.S.; de Carvalho, C.G.P.; de Souza, J.R.P.; Destro, D. Path analysis under multicollinearity in soybean. Braz. Arch. Biol. Technol. 2004, 47, 669–676. [Google Scholar] [CrossRef]
- Thomas, A.; Best, N.; Lunn, D.; Arnold, R.; Spiegelhalter, D. Geobugs User Manual; Medical Research Council Biostatistics Unit: Cambridge, UK, 2004. [Google Scholar]
- Besag, J.; York, J.; Mollié, A. Bayesian image restoration, with two applications in spatial statistics. Ann. Inst. Stat. Math. 1991, 43, 1–20. [Google Scholar] [CrossRef]
- Besag, J.; Kooperberg, C. On conditional and intrinsic autoregressions. Biometrika 1995, 82, 733–746. [Google Scholar]
- Gelman, A. Prior distributions for variance parameters in hierarchical models. Bayesian Anal. 2006, 1, 515–534. [Google Scholar]
- Best, N.G.; Arnold, R.A.; Thomas, A.; Waller, L.A.; Conlon, E.M. Bayesian models for spatially correlated disease and exposure data. In Proceedings of the Sixth Valencia International Meeting on Bayesian Statistics, Alcossebre, Spain, 6–10 June 1999; pp. 131–156.
- Spiegelhalter, D.J.; Best, N.G.; Carlin, B.P.; Van der Linde, A. Bayesian Deviance, the Effective Number of Parameters, and the Comparison of Arbitrarily Complex Models. Available online: http://www.sph.umn.edu/faculty1/wp-content/uploads/2012/11/rr98-009.pdf (accessed on 10 January 2016).
- Spiegelhalter, D.J.; Best, N.G.; Carlin, B.P.; Van Der Linde, A. Bayesian measures of model complexity and fit. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2002, 64, 583–639. [Google Scholar] [CrossRef]
- Akaike, H. Information theory and an extension of the maximum likelihood principle. In Selected Papers of Hirotugu Akaike; Springer: Berlin, Germany, 1998; pp. 199–213. [Google Scholar]
- Gelman, A.; Rubin, D.B. Inference from iterative simulation using multiple sequences. Stat. Sci. 1992, 7, 457–472. [Google Scholar] [CrossRef]
- Richardson, S.; Thomson, A.; Best, N.; Elliott, P. Interpreting posterior relative risk estimates in disease-mapping studies. Environ. Health Perspect. 2004, 112, 1016–1025. [Google Scholar] [CrossRef] [PubMed]
- Roncek, D.W.; Bell, R. Bars, blocks, and crimes. J. Environ. Syst. 1981, 11, 35–47. [Google Scholar] [CrossRef]
- Groff, E.R.; La Vigne, N.G. Mapping an opportunity surface of residential burglary. J. Res. Crime Delinq. 2001, 38, 257–278. [Google Scholar] [CrossRef]
- Robinson, M.B.; Mullen, K.L. Crime on campus: A survey of space users. Crime Prev. Community Saf. 2001, 3, 33–46. [Google Scholar] [CrossRef]



| Population Density | Unemployment Rate | Bar Density | Department Store Density | Policing | |
|---|---|---|---|---|---|
| Population density | 1.000 | ||||
| Unemployment rate | 0.420 *** | 1.000 | |||
| Bar density | −0.261 *** | 0.181 | 1.000 | ||
| Department store density | −0.194 ** | −0.218 ** | −0.031 | 1.000 | |
| Policing | −0.048 | −0.052 | −0.098 | −0.080 | 1.000 |
| Variables | Model 1 (Equation 3) | Model 2 (Equation 5) | Model 3 (Equation 4) |
|---|---|---|---|
| Mean (95% CI) | Mean (95% CI) | Mean (95% CI) | |
| Intercept | −0.2075 (−0.2531, −0.1628) | −0.4777 (−0.6677, −0.2960) | −0.5025 (−0.6402, −0.3676) |
| Population density | −0.7205 (−0.7740, −0.6672) | −0.4204 (−0.6423, −0.2018) | −0.3020 (−0.5677, −0.0380) |
| Unemployment rate | 0.0440 (0.0020, 0.0857) | 0.0551 (−0.1613, 0.2745) | 0.0268 (−0.2258, 0.2751) |
| Bar density | −0.0184 (−0.1310, 0.0860) | 0.3094 (0.1020, 0.5181) | 0.3831 (0.1688, 0.6003) |
| Department store density | −0.0625 (−0.1593, 0.0234) | 0.1928 (0.0027, 0.3797) | 0.2119 (0.0338, 0.3878) |
| Policing | −0.1618 (−0.2489, −0.0794) | −0.0138 (−0.2151, 0.1853) | 0.0264 (−0.1896, 0.2386) |
| NA | NA | 0.5493 (0.2784, 0.8108) | |
| DIC | 4,982.890 | 742.030 | 736.462 |
| 5.963 | 102.164 | 101.470 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Zhu, X. Exploring the Influence of Neighborhood Characteristics on Burglary Risks: A Bayesian Random Effects Modeling Approach. ISPRS Int. J. Geo-Inf. 2016, 5, 102. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi5070102
Liu H, Zhu X. Exploring the Influence of Neighborhood Characteristics on Burglary Risks: A Bayesian Random Effects Modeling Approach. ISPRS International Journal of Geo-Information. 2016; 5(7):102. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi5070102
Chicago/Turabian StyleLiu, Hongqiang, and Xinyan Zhu. 2016. "Exploring the Influence of Neighborhood Characteristics on Burglary Risks: A Bayesian Random Effects Modeling Approach" ISPRS International Journal of Geo-Information 5, no. 7: 102. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi5070102






