3.1. Background
Different spectral characteristics elicit different spectral responses. Theoretically, the intrinsic characteristics of any type of object can be reflected by its spectral curve. Discrepancies in spectral curve shape always exist due to distinctive material composition and structure among different types of land covers such as vegetation, soil, water, etc. However, the reflectance spectrum of a natural surface is very complex with the facts that different objects have the same spectrum and the same object has different spectra. This is a common problem in the remotely sensed classification field. Taking the shape analysis into the classification research may be an idea for solving this problem. Our work is motivated by the observation of small shape variations between different objects. As is shown in
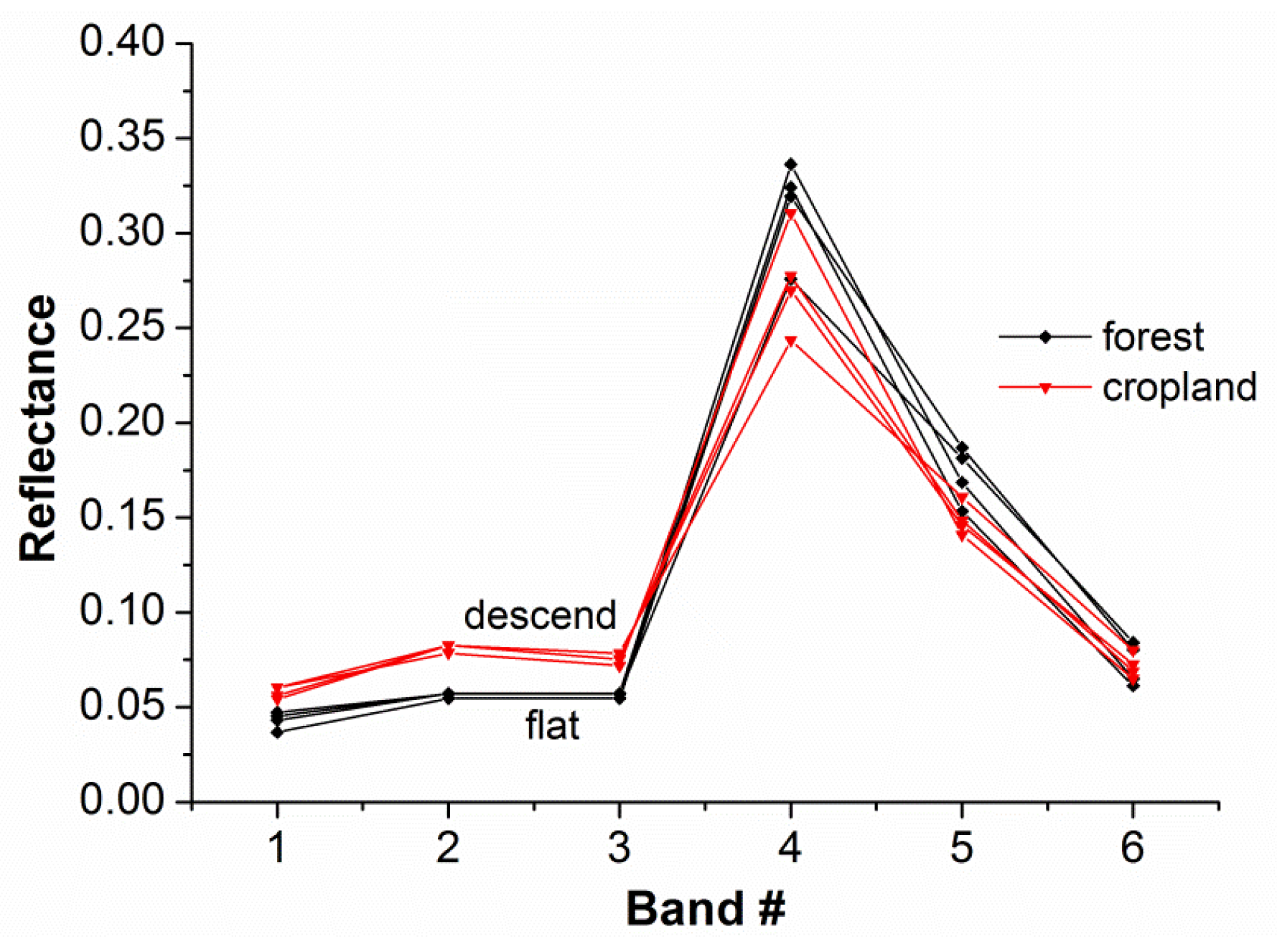
Figure 2, despite the fact that the cropland and the forest classes show the almost equal spectral mean values (both classes between 0.1165 and 0.1221), the subtle difference in reflectance within a certain spectral range can be found for different objects. We are interested in the shape difference between band 2 and band 3. It is apparent from the figure that the curve corresponding to cropland class shows a descending trend while the gradient of the curve corresponding to forest class is zero. The shape analysis will offer benefit over this by decomposition of the spectral curve into a number of consecutive segments, which denote the shape varying trends (such as ascending, descending and flat branches), while the subtle difference is often hard to detect with algorithms based on the spectral value characteristics of the whole spectrum [
28]. Therefore, this study uses the factor of “similarity/difference between spectral curve shapes” as the basis of remotely sensed image classification. To do this, the spectral curve shape must be quantified using the methods described below.
3.2. Symbolization of Curve Morphology
On the basis of the curve morphology principle, a spectral curve can be decomposed to two different morphemes, i.e., fundamental and extended morphemes [
24,
25,
28,
29]. The fundamental morpheme describes the segments of the spectral curve, including ascending, descending and flat segments. The extended morpheme is defined as the extreme value at the peak and/or valley of the spectral curve. These morphemes can be symbolized using codes: ascending segment represented as “0”, descending segment “1”, flat segment “2”, and peak and valley of the spectral curve “3” and “4”, respectively.
Figure 3 shows an example of the symbolization of a spectral curve.
Based on the above symbolization, the basic variation characteristics (ascending/descending) of a spectral curve can be described. Additionally, a morpheme vector is needed to correctly quantify the spectral curve. Thus, we defined the morpheme vector as B = (T, C0, C1, ..., Cn-1), where T is the morpheme code, and C0,C1, …, Cn-1 denote the n attributes of the morpheme, these are, the numerical values that describe the curve. As mentioned previously, there are two types of morphemes. Therefore, the morpheme vectors were also grouped into a fundamental morpheme vector and an extended morpheme vector that were labeled as Bb and Bs, respectively. Through use of the morpheme vectors, a spectral curve was easily transformed into a 2-D table composed of a series of characteristics. In the 2-D table, the second and subsequent rows refer to the types of various morpheme vectors, and the columns denote the attribute characteristics of each vector. Each vector is composed as follows:
Bb (the basic morpheme vector) = (the morpheme code, the beginning position of morpheme, the ending position of morpheme, and the mean value of morpheme); Bs (the expanded morpheme vector) = (the morpheme code, the sequence number of peak/valley, the position of morpheme, and the value of morpheme).
Specific to the remotely sensed data, such as the TM data, the spectral curve shown in
Figure 4 is composed of two ascending segments (from bands 1 to 2 and bands 3 to 4, respectively), two descending segments (from bands 2 to 3 and bands 4 to 6, respectively), two peaks (located at bands 2 and 4, respectively) and one valley (located at band 3). Whether bands j to k is the ascending, descending or flat segments is determined by the following criteria outlined in
Table 1. Specifically, the ascending, descending or flat segment is between two inflection points, at which the curve changes from decreasing trend to increasing trend, or to flat, and vice versa. Through use of the symbolization method and the attribute composition of each morpheme vector as defined above, the values in
Table 2, which show the numerical description of the reflectance spectrum shown in
Figure 4, can be obtained.
3.3. Matching of Spectral Shape
Use of the spectral matching method is necessary to efficiently classify pixels into the known categories. This matching algorithm defines the manner in which unknown or target spectra are compared with the known reference [
15]. Here, the characteristics of known reference are called identification templates. Morpheme vector definition for the identification template is similar to those for
Table 2, but the last column of the identification template shows the upper and lower limits of a range of measurable characteristic. The design of an identification template requires selection of classification samples that are representative of the spectral characteristics of the classes. It should be noted that remotely sensed image data are known for their high degree of complexity and irregularity [
6]. It is necessary to adjust the ranges in the identification template according to the initial identification results to ensure the representativeness of the identification template. Otherwise, the sample data cannot be representative of the spectral variation of that kind of land cover type. Finally, the optimal threshold, which is based on the training samples statistics, must maintain a low number of false alarms and a high number of correct classifications.
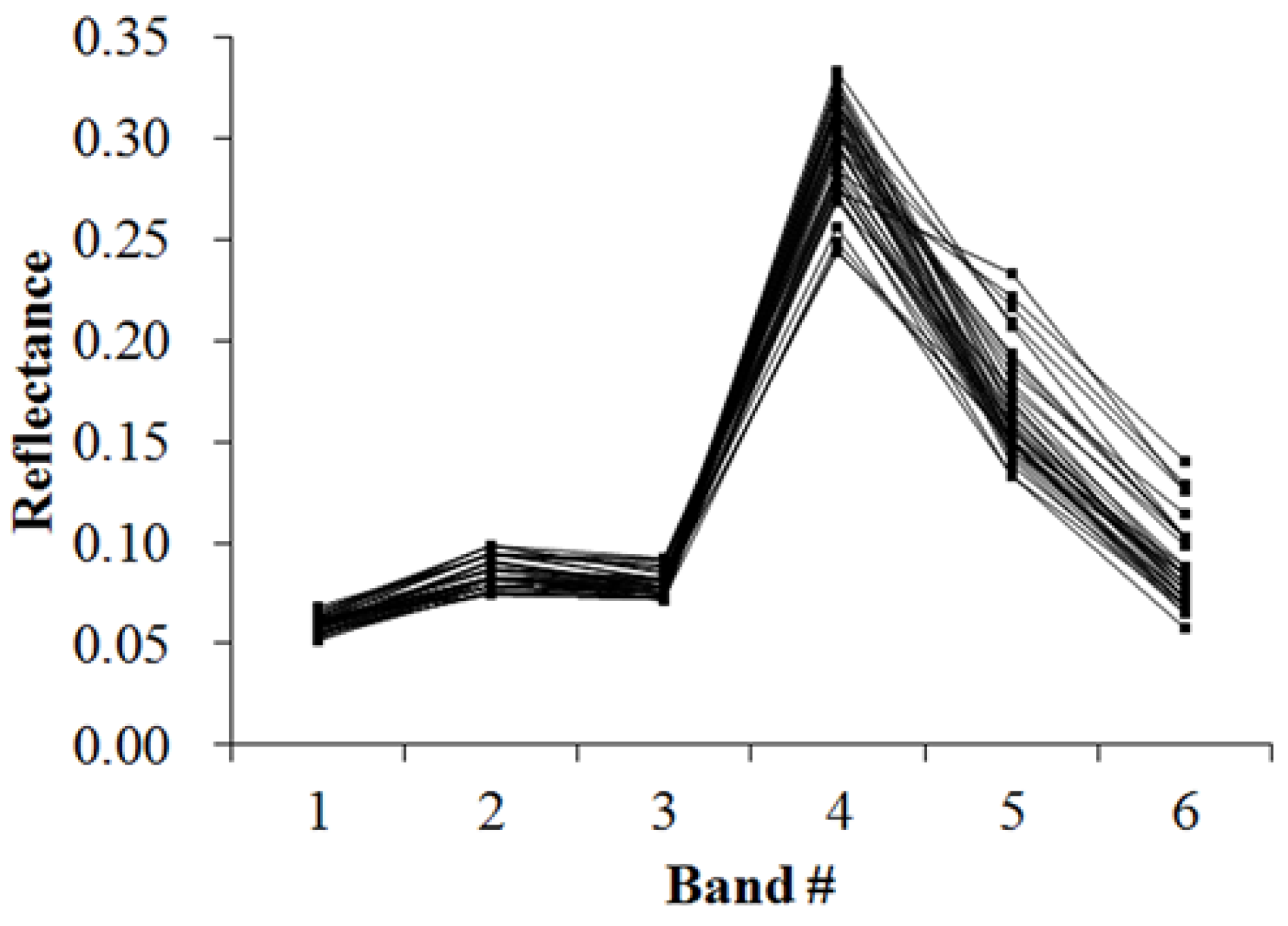
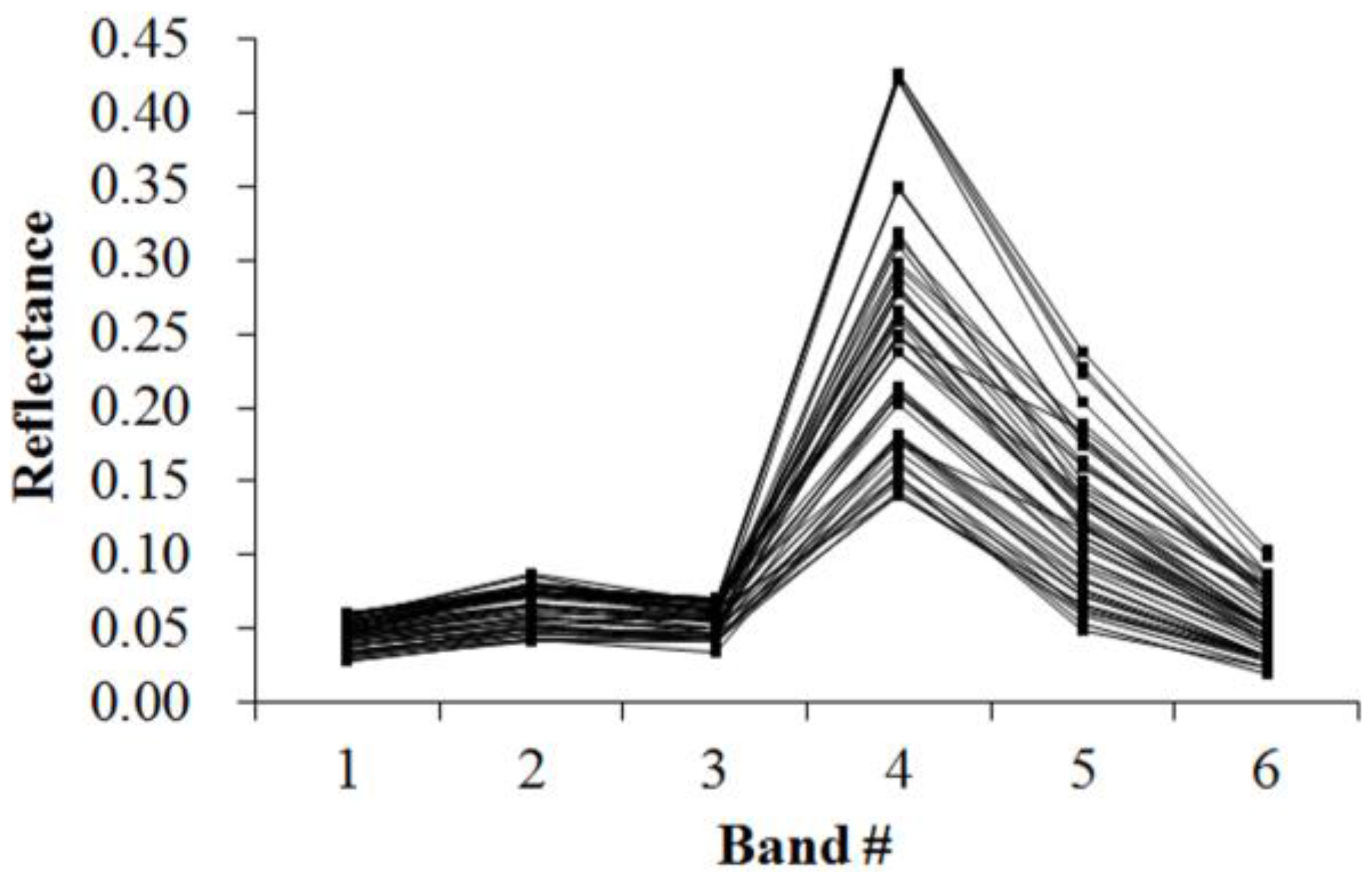
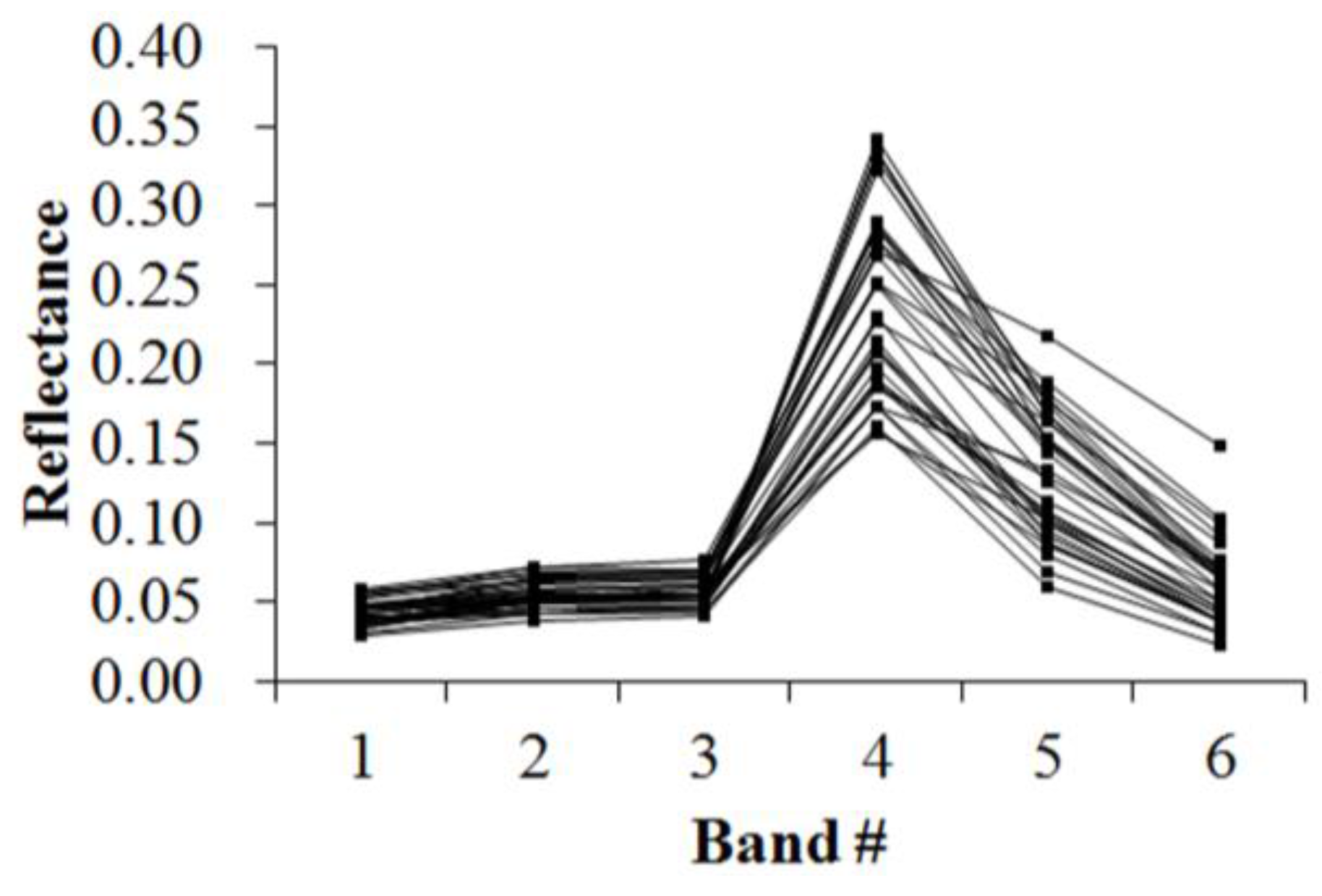
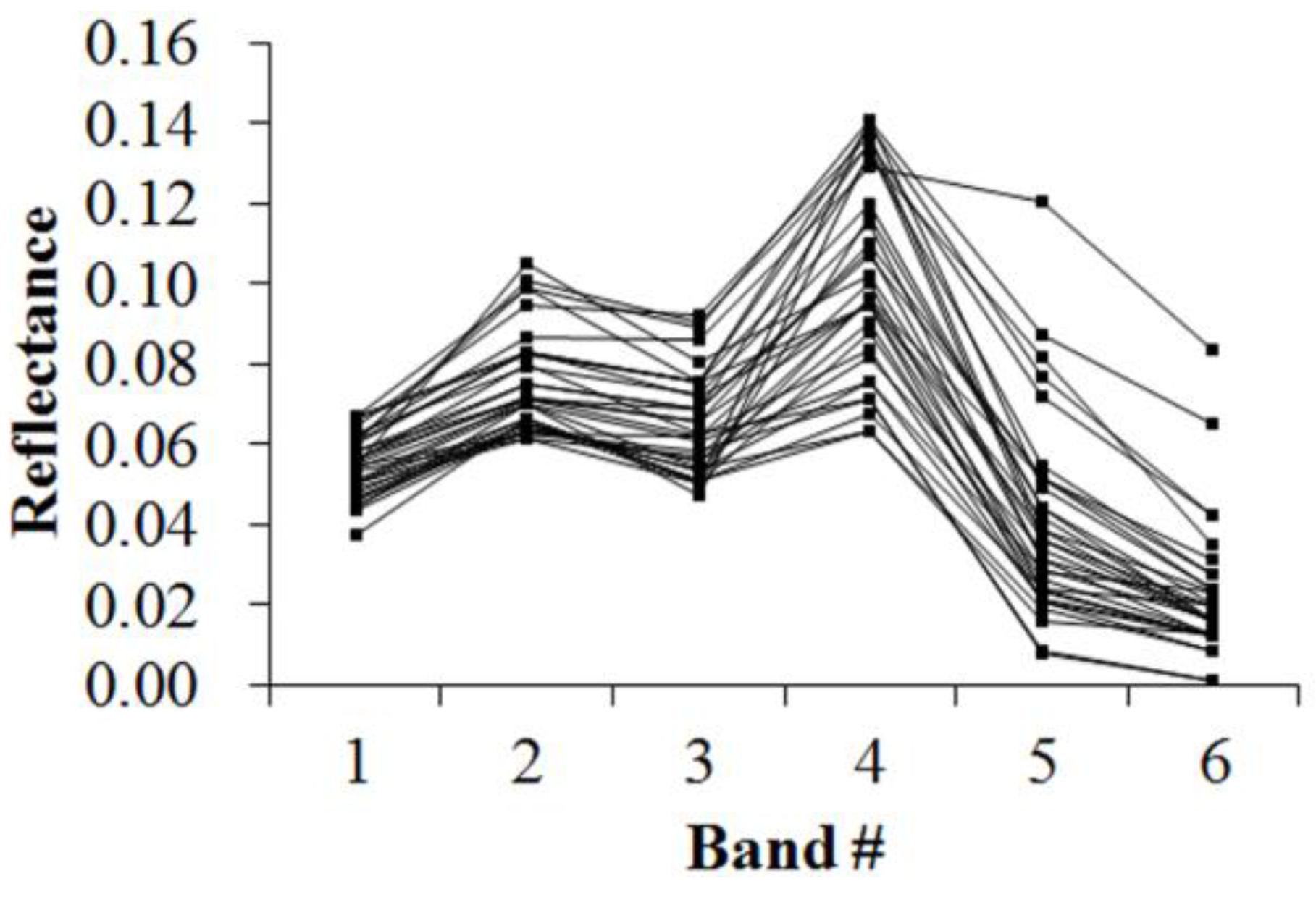
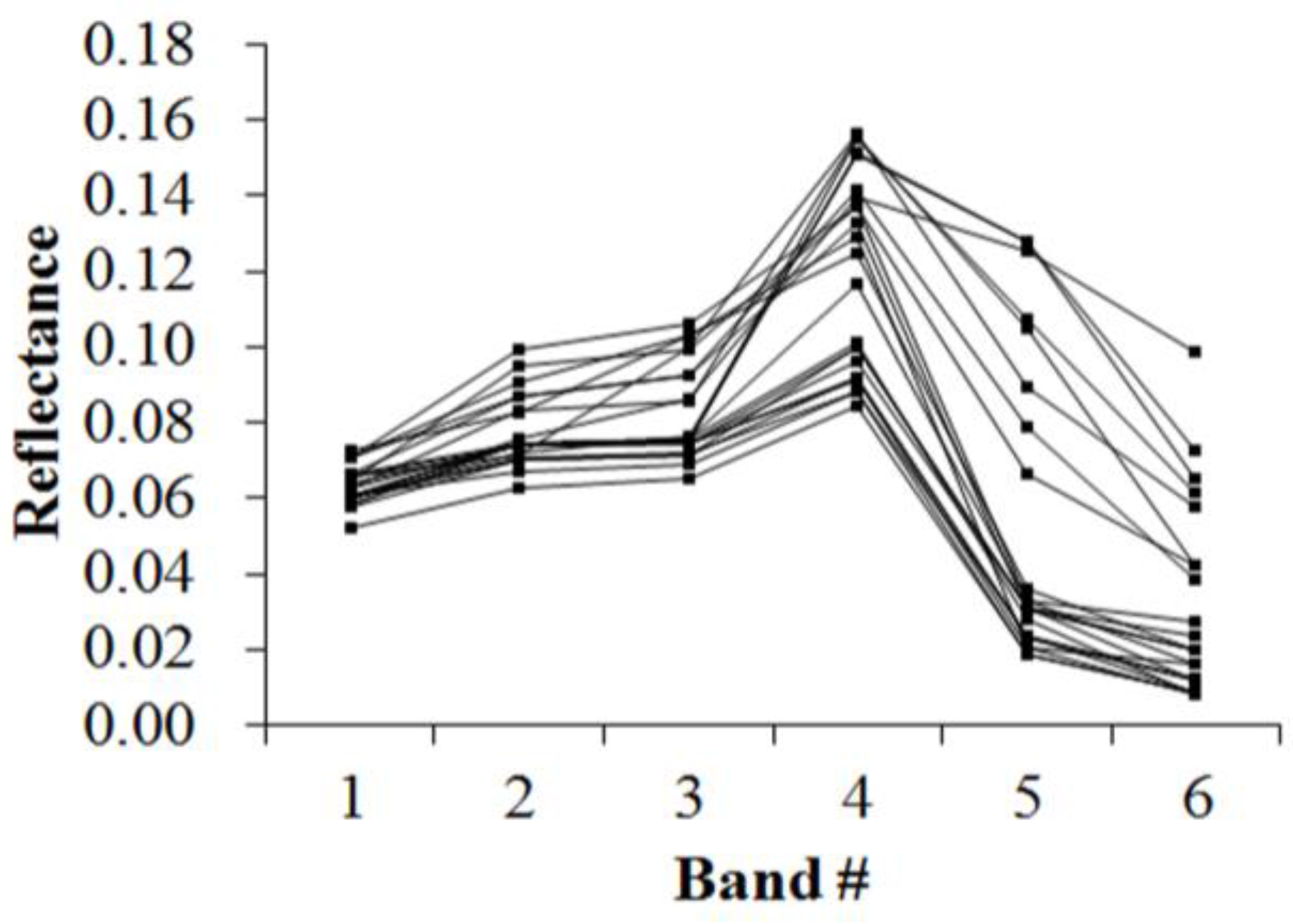
Figure 5,
Figure 6,
Figure 7,
Figure 8,
Figure 9,
Figure 10,
Figure 11 and
Figure 12 display the spectral curves collected from the samples to determine these identification templates (
Table 3,
Table 4,
Table 5,
Table 6,
Table 7,
Table 8,
Table 9 and
Table 10). By symbolizing the curves in
Figure 5,
Figure 6,
Figure 7,
Figure 8,
Figure 9,
Figure 10,
Figure 11 and
Figure 12 using the symbolization method descripted in
Section 3.2, the corresponding table can be obtained. For the study area B, the identification templates are similar with those of area A, but the suitable thresholds in the last column for area B. The total sample numbers used to determine these identification temples are 224 for area A and 209 for area B. Image objects within the defined limits of identification template are assigned to a specific class, while those outside of the limits are assigned to other classes.
Because of the natural complexity and the fact that the same object has different spectra, more than one identification templates were designed for one kind of object. Meanwhile, one may note that identification templates in
Table 3,
Table 5 and
Table 8 for cropland, forest and water classes, respectively, are similar. The same phenomenon occurs in
Table 4,
Table 6 and
Table 9. This also indicates that different objects have the same spectrum. However, the differences between them lie in the different threshold ranges in the last column in a certain row. Specifically,
Table 3 holds the lowest threshold of 0.0718 in the fifth row vs.
Table 5 with highest value of 0.0717, and
Table 3 holds the lowest threshold of 0.1553 in the seventh row vs.
Table 8 with highest value of 0.1408. The different thresholds in similar identification templates, which made the different objects to be separable, were in bold.
Table 7 and
Table 10, which indicate the unique spectral curve shapes for forest and water classes, respectively, are different from others.
To perform the classification process, a matching algorithm that allows for multilevel matching was used in this study. For a target curve S and the known identification template M, this algorithm is executed according to the following steps: (1) Extract the morpheme vectors (the second to fourth columns) from the 2-D Table describing the target curve S and identification template M, respectively. Each column is represented by a string. Thus, six strings were generated in this step, three for the target curve S and three for the identification template M. (2) Compare the strings for the target curve S with the ones for the identification template M. The same strings indicates the similar shape variation between the target curve S and identification template M. (3) Judge whether the values in the last column of 2-D Table corresponding to the target curve S is within the threshold ranges in the last column of the identification template M. If so, the final match with template M is finished. Matching pixel corresponding to target curve S belongs to the corresponding category of identification template M. The above steps are executed for each pixel. The advantages of this matching algorithm lie in its flexibility and the initial identification by shape variation. If the spectral shape variety of the target curve disaccords with the one of identification template, then the target curve is not assigned to that specific class, despite the similar spectral values.
3.4. Accuracy Assessment
The error matrix method, which is the most common approach for accuracy assessment of categorical classes [
30,
31], was used in this study to evaluate the accuracy of classified images, with high resolution images from Google Earth as references. To generate the error matrix, a number of samples that are distributed randomly within areas A and B were required. The polynomial distribution-based method was used to calculate the sample number [
16]:
where
si is the area proportion of class i that is closest to 50% among all classes,
bi is the desired accuracy of class
i, Γ is the χ
2-distribution value with the degree of freedom of 1 and the probability of 1 − (1 − α)/n, α is the confidence level, and n is the number of classes.
Due to the lack of the information on the area proportion of each class, the polynomial distribution algorithm was under the worst case. Following the work of Hu et al. [
16], we assumed that the area proportion of each class was 50% of the study area. Equation (1) was then rewritten as:
In this study, α was set to 85%, and b
i was set to 5%. According to
Figure 13 and
Figure 14, n was 4 and 5 for areas A and B, respectively. Thus,
N is 433 and 471 for areas A and B, respectively. The following statistics will be adopted to evaluate the accuracy of image classification [
32]: user’s accuracy (UA), producer’s accuracy (PA), overall accuracy (OA) and Kappa coefficient.