1. Introduction
Rock surface includes joints, fractures, faults and other geological structures; the properties of which govern the overall behavior of the rock masses. A detailed investigation aiming at the corresponding geological environment is necessary for a rock engineering research. The geometrical information, distribution and combination condition of the rock surface are the basis on which rock mass classification and engineering geological evaluation can proceed well. Therefore, it is vital for hydropower engineering, transportation engineering and mining engineering to extract rock surface accurately, efficiently and fully, which has important realistic significance for engineering exploration, design, evaluation and construction.
However, most basic engineering construction projects focus on alpine and gorge regions, which are so dangerous and inaccessible that the traditional contact measurements cannot proceed efficiently, safely, and quickly. Instead of the traditional contact measurements, the non-contact active measurements, mainly including close-range photogrammetry and TLS, could collect image or point cloud data and then finish rock surface extraction more conveniently and comprehensively in a virtual digital environment generated from these data.
Terrestrial laser scanning (TLS), emerging in the mid-1990s, allows capturing an accurate 3D model of an object in short time, which could be used for several purposes. TLS is an active and non-contact measurement technique, which can obtain the spatial coordinates of an object with high speed and accuracy by measuring the time-of-flight of laser signals [
1]. High temporal resolution, high spatial resolution and uniform accuracy make the TLS data rather appropriate for many applications, including dangerous and inaccessible regions. However, TLS data are poor at expressing the object features due to characteristics such as unstructured 3D point clouds. Photogrammetric techniques processing stereoscopic images may be considered largely complementary to TLS, delivering RGB data plus possibly further spectral channel information. Thus, integrating the TLS data with digital image data may achieve complementary advantages of spatial information as well as spectrum information. This integration may be very valuable for geology research.
One crucial problem that the research of geological information extraction based on the integration of TLS data and image data involves is about the registration between point cloud and digital image. Because of the different sensor sources and reference systems, a spatial similarity transformation is essential to achieve registration. At present, many domestic and international scholars carried on a great deal of research on this, which can mainly be divided into four groups: (1) registration with the digital image and the intensity image generated by point cloud data; (2) registration with the point cloud data respectively acquired by TLS and generated by digital images; (3) registration through corresponding features extracted from both the TLS point cloud and the images; and (4) registration through artificial targets (e.g., retro-reflective targets). As each of the above methods has its pros and cons in certain application, it is important to find the tradeoff that is best suited for geology applications. Compared with the first two groups, the latter two implement the registration based on the original data sources, which effectively reduces error accumulation. However, for geological research objects, the irregular appearance and indeterminate distribution of rock surface make it difficult to directly extract corresponding primitives from the two data either by interactive methods or by automatic methods.
As a primary technique of computer vision to reconstruct 3D scene geometry and camera motion from a set of images of a static scene, Structure from Motion (SfM) has been applied in more and more areas, including geomorphology, medical science, archaeology and cultural heritage [
2,
3,
4,
5,
6]. SfM has the potential to provide both a low cost and time efficient method for collecting data on the object surface [
7]. SfM technique neither needs any prior knowledge about camera positions and orientation, nor targets with known 3D coordinates, all of which can be solved simultaneously using a highly redundant, iterative bundle adjustment procedure, based on a database of features automatically extracted from a set of multiple overlapping images [
8,
9]. Therefore, it seems more feasible to indirectly register digital images and TLS point cloud by use of the SfM point cloud from images and TLS point cloud.
Because of the complicated and irregular geological structure, it is difficult for registration to directly and automatically extract primitives from SfM point cloud and TLS point cloud, such as point-based, regular line segment-based and planar-based. In recent years, a novel 4-points congruent base has been proposed for 3D point clouds registration [
10]. Instead of more than three corresponding points’ selection, these algorithms calculate the rigid transformation parameters by use of 4-points congruent base sets, the advantages of which could be concluded as follows: (1) There is no need to assume both the initial position and orientation of the two point clouds. (2) It is unnecessary to depend on any regular geometrical features from the research object itself. (3) The overlap between the two point clouds does not need to be known in advance. (4) It is robust to noise and outliers, thus it does not require preprocessing such as filtering or noise reduction. In consideration of all the above advantages, the registration theory of the 4-points congruent base is especially suitable for the geological objects. The existing algorithms, such as 4PCS and Super4PCS, are limited to those data sets from the same sensor. However, the geological data sources in this paper are r acquired by a digital camera and a terrestrial laser scanner, and with different scales. Therefore, to use 4-points congruent base sets for registration, the scales between the two point clouds should be unified first.
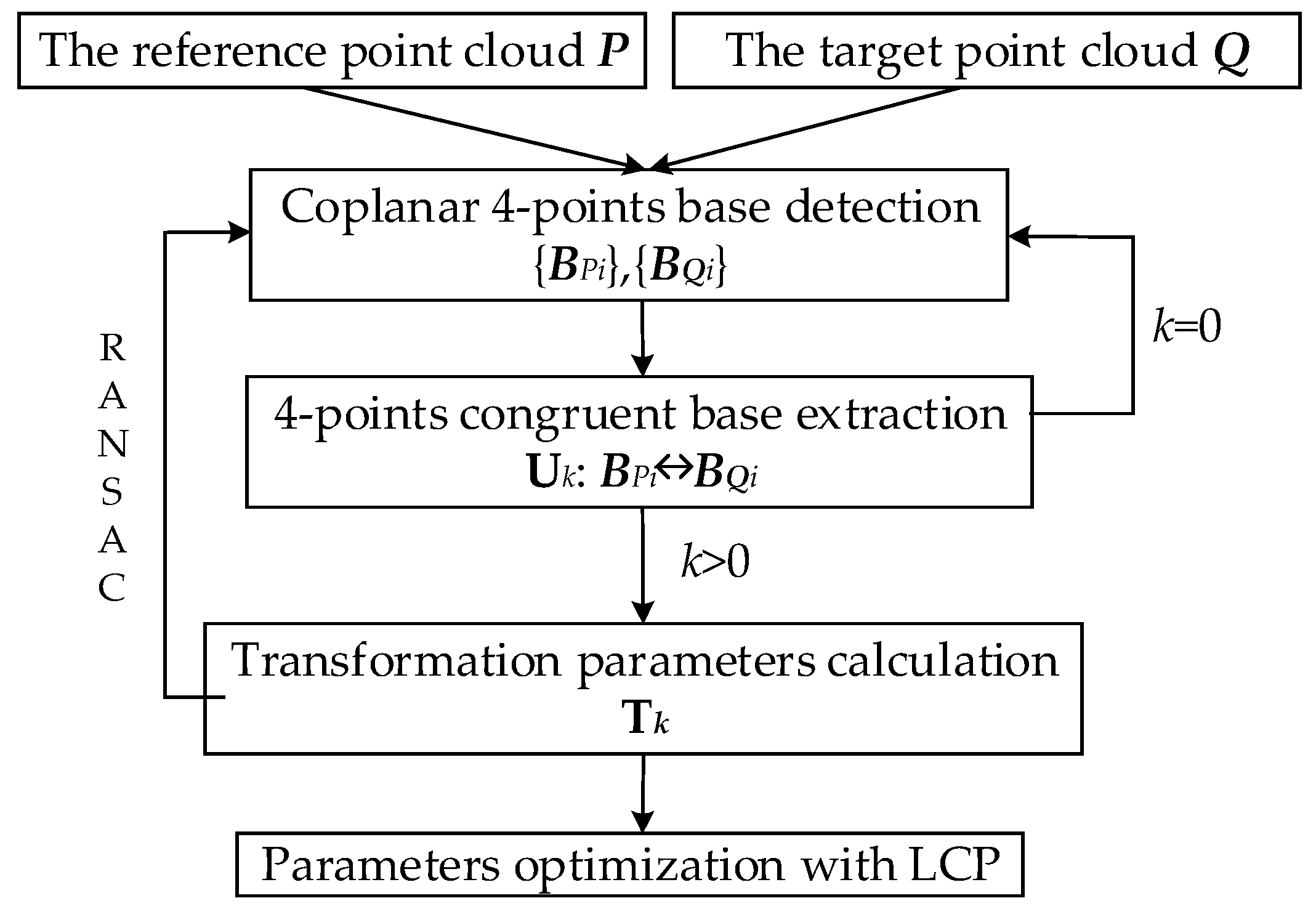
Based on all the above analysis, this paper presents a fully automated method, G-Super4PCS, for indirect registration of digital images and TLS point cloud data. This algorithm firstly takes the SfM and TLS key point clouds, respectively, extracted from digital images and the original TLS point cloud for rigid transformation parameters rough estimation, and then takes the dense SfM point cloud from images and the original TLS point cloud for fine registration. Finally, the developed method was verified by use of the columnar basalt data acquired in Guabushan National Geopark in Jiangsu Province, China. The experimental results demonstrate that the G-Super4PCS registration algorithm could achieve fine registration between digital images and TLS point cloud without any manual interactions, the result of which provides a crucial data basis for further integration research.
The rest of this paper is organized as follows:
Section 2 reviews the existing 4PCS and Super4PCS algorithms.
Section 3 introduces the detailed methodology of the proposed G-Super4PCS algorithm for registration between digital images and TLS point cloud. The feasibility of the algorithm and its applicability in geology are illustrated through an experiment with the columnar basalt data acquired by digital camera and terrestrial laser scanner in
Section 4.
Section 5 presents the conclusion.
3. Methodology
For 4PCS and Super4PCS algorithms, the coplanar 4-points congruent base sets are extracted under some condition constraints, including the same distance of point-pairs, the same affine invariant ratios and the same angles. In the strict sense, the coplanar 4-points congruent base is just a special congruent base, which means that both 4PCS and Super4PCS registration algorithms are only suitable for those point clouds with the same scale. Moreover, in the process of the 4-points congruent base set extraction, some local features associations of point clouds have not been considered, which may have some effect on the efficiency and precision. Therefore, a new Generalized Super 4-points Congruent Sets (G-Super4PCS) registration algorithm has been proposed in this paper. The new algorithm firstly introduces a key-scale rough estimation approach for SfM and TLS key point clouds.; Instead of the traditional 4-points congruent base, this algorithm defines a new generalized super 4-points congruent base which combines geometric relationship and local features including local roughness and normal vector of rock surface. Then scale adaptive optimization and candidate point-pairs extraction could be finished by combination of local roughness and distance constraint condition. The congruent base set could be further filtered with the local normal vector, which largely reduces times of rigid transformation verification, and improves the efficiency and precision of the registration algorithm. The flowchart of G-Super4PCS algorithm is shown as
Figure 5.
3.1. Key-Scales Rough Estimation for SfM and TLS Key Point Clouds
Scale estimation is the key and precondition for registration of point clouds with different scales. The scale estimation methods could be divided into two groups [
15]: the first one is to directly estimate the scale ratio of the two point clouds; and the second one is to estimate the scale for each point cloud. In this paper, a key-scale rough estimation approach based on spin images and cumulative contribution rate of PCA has been used for registration of SfM and TLS point clouds.
3.1.1. Spin Images
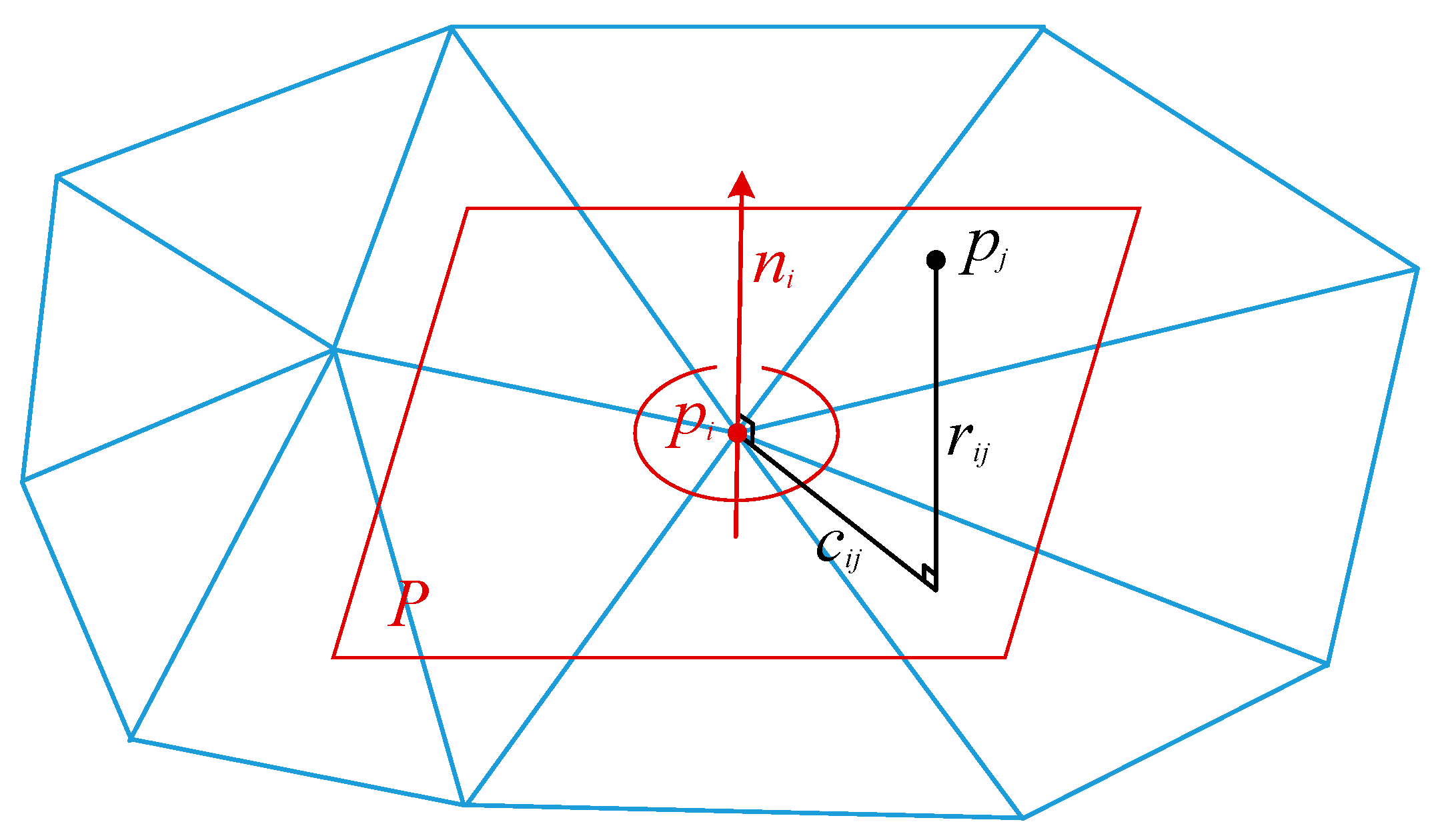
A spin image is a local feature descriptor for a 3D point, which describes local geometry by a 2D distance histogram about the 3D point and its neighbors. The generation of spin image is closely associated to point cloud normal vectors. An oriented-point is defined by a point
in a point cloud
P as well as its unit normal vector
, which is used to be the central axis of cylindrical coordinates. For any other point
near
,
and
, respectively, denote distances along the unit normal vector
and the tangent plane at
, the graph of which is shown as
Figure 6.
and
could be calculated by Equation (4).
where
,
. Let
w denote the spin image width, then
and
. Discretize distances
into a
grid and vote to a 2D distance histogram of
bins, and then a spin image is generated.
Generally, the spin image width is related to the grid size () and its cell size. The grid size decides the spin image resolution, and the larger the grid size is, the higher the resolution is. However, the grid size should be set neither too large nor too small, which would not well describe the difference of spin images. For the experimental data in this paper, the grid size is set to . Therefore, the spin image width changes with the cell size. As the key-scales rough estimation method only needs to obtain the scale ratio between the two point clouds, the spin image width is actually represented by the cell width in this paper.
3.1.2. Relationship of Spin Image and Point Cloud Scale
As a spin image is a feature descriptor which is not scale invariant, the image width has a large effect on local geometry description.
Figure 7a shows an original point cloud, and
Figure 7b shows the corresponding spin images (
Spin 1,
Spin 2, …,
Spin 6) at different image widths.
When the image width is too small, as shown in the top row of
Figure 7b, the local geometry cannot be expressed correctly with spin images, the reason of which is that for any object, its surface can be regarded as flat in an extremely small locality. In this case, all spin images look the same or very similar to each other, because they all describe a plane. Conversely, as shown in the bottom row of
Figure 7b, the local geometry still cannot be described correctly with spin images when the image width is too large. In this case, all 3D points may fall in the same bin (or just in few bins) of a histogram for a spin image, which would make all spin images very similar to each other. Therefore, it can be concluded that the similarity between spin images has a minimum at a certain width. Moreover, spin images keep the most difference from each other at the minimum (as shown in the middle row of
Figure 7b). That is to say, the real scale of point cloud could be estimated according to the optimal width of spin images.
3.1.3. Cumulative Contribution Rate of PCA Based on Spin Image
Principal Components Analysis (PCA) is a statistical procedure that uses an orthogonal transformation to convert a set of observations of possibly correlated variables into a set of values of linearly uncorrelated variables [
16]. The similarity between spin images could be described by the cumulative contribution rate of PCA in special dimension as well as special space. The lower the cumulative contribution rate is, the more dissimilar spin images are. Let
denote a spin image with
bins, then it can be described with an
m2-dimension vector
. After performing PCA on a set of spin images
,
m2 eigenvectors with
m2-dimension,
, as well as corresponding real eigenvalues,
, could be obtained. Let
, then the cumulative contribution rate of the first
d-dimension principal components,
, could be defined as follows:
3.1.4. Key-Scale Estimation of Point Clouds
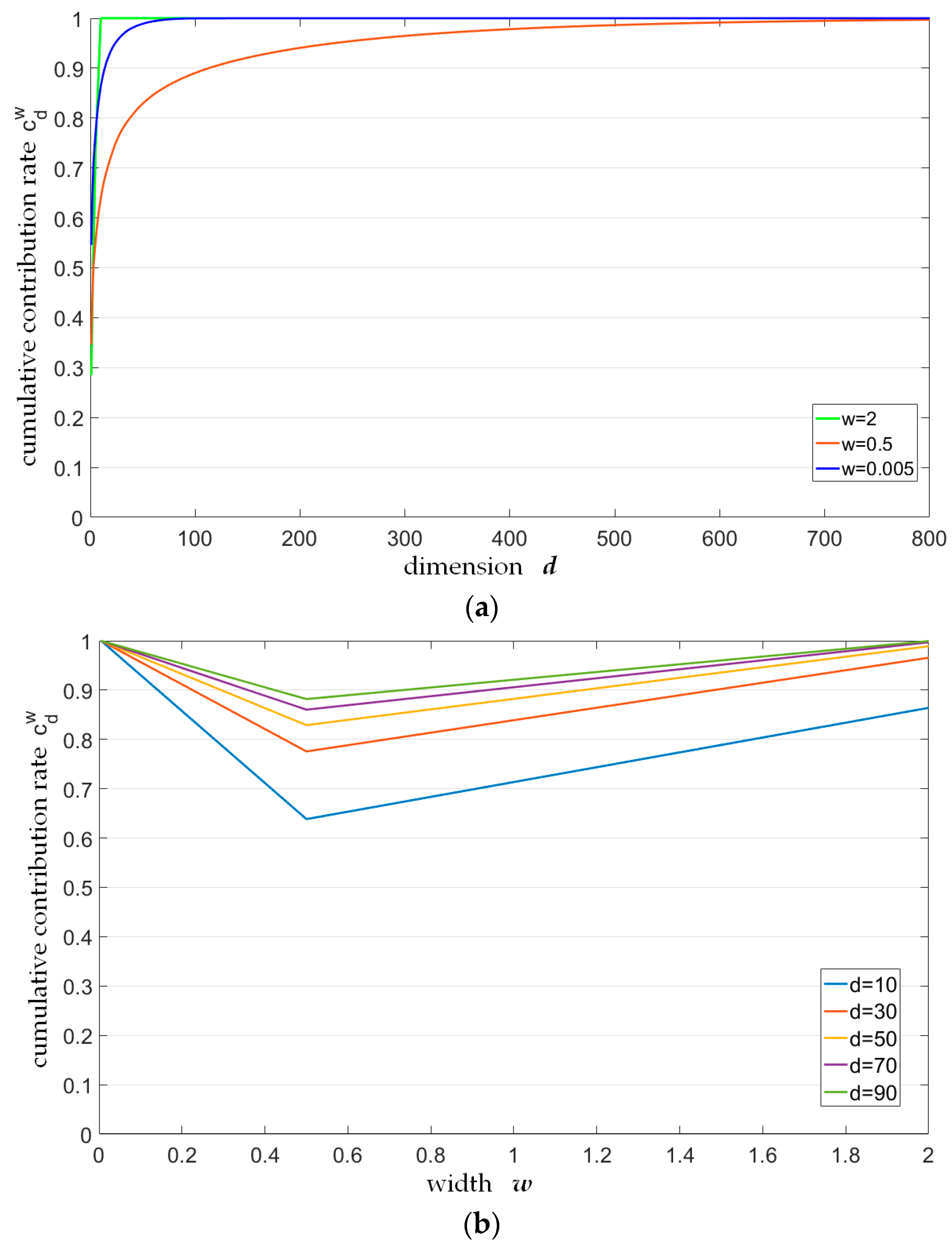
The idea of key-scale estimation is to determine the optimal spin image width when the value of cumulative contribution rate is minimum. It is difficult to show the dissimilarity between spin images if the spin image width w is too large or too small compared to the object itself.
Figure 8 describes how the cumulative contribution rate changes with dimension
d and spin image width
w. In
Figure 8a, it is obvious that the cumulative contribution rate increases monotonically with dimension
d when spin image width
w is fixed. Besides, the cumulative contribution rate curves quickly approach 1 when
and
, while the curve at
increases more slowly, which means that spin images are very dissimilar with each other. In other words, when dimension
d is fixed (such as
d = 100), the figure visually shows that the value of the cumulative contribution rate at
is lower than that at
and
.
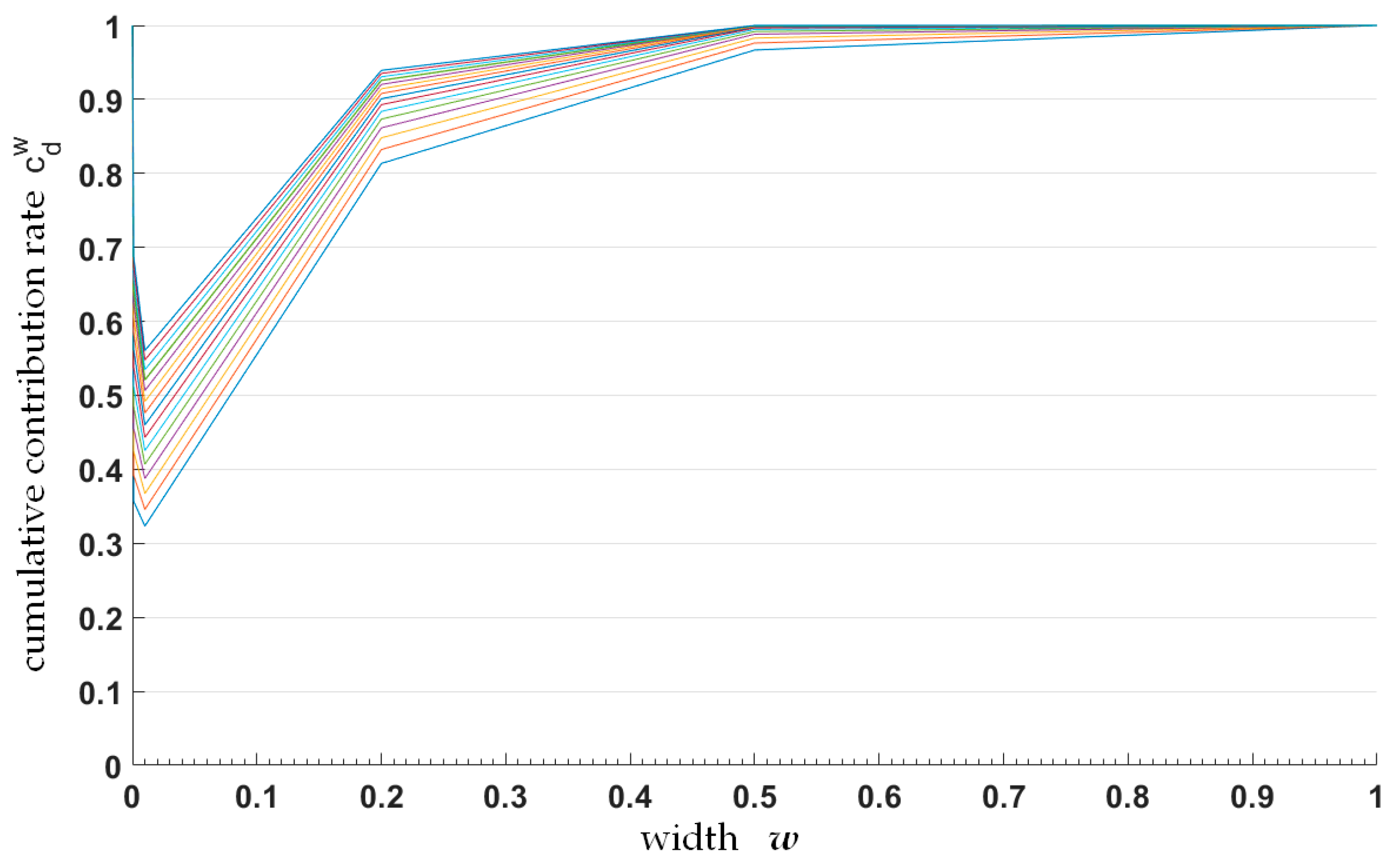
Figure 8b describes a group of cumulative contribution rate curves change with different spin image width
w for fixed dimensions
d (
d = 10, 30, 50, 70 and 90), which shows the above results more clearly. In this figure, all contribution rate curves get the minimum at
, where the corresponding spin images are most dissimilar. Therefore,
corresponds to the key-scale of the point cloud. With the relationship between the key-scale and the spin image width, it is not difficult to conclude that the spin image width is a variable for the key-scale rough estimation, the optimal value range of which appears near the minimum of cumulative contribution rate.
With the scale rough estimation method mentioned above, the key-scales of the SfM and TLS key point clouds could be estimated; the results of which would be used for further registration process.
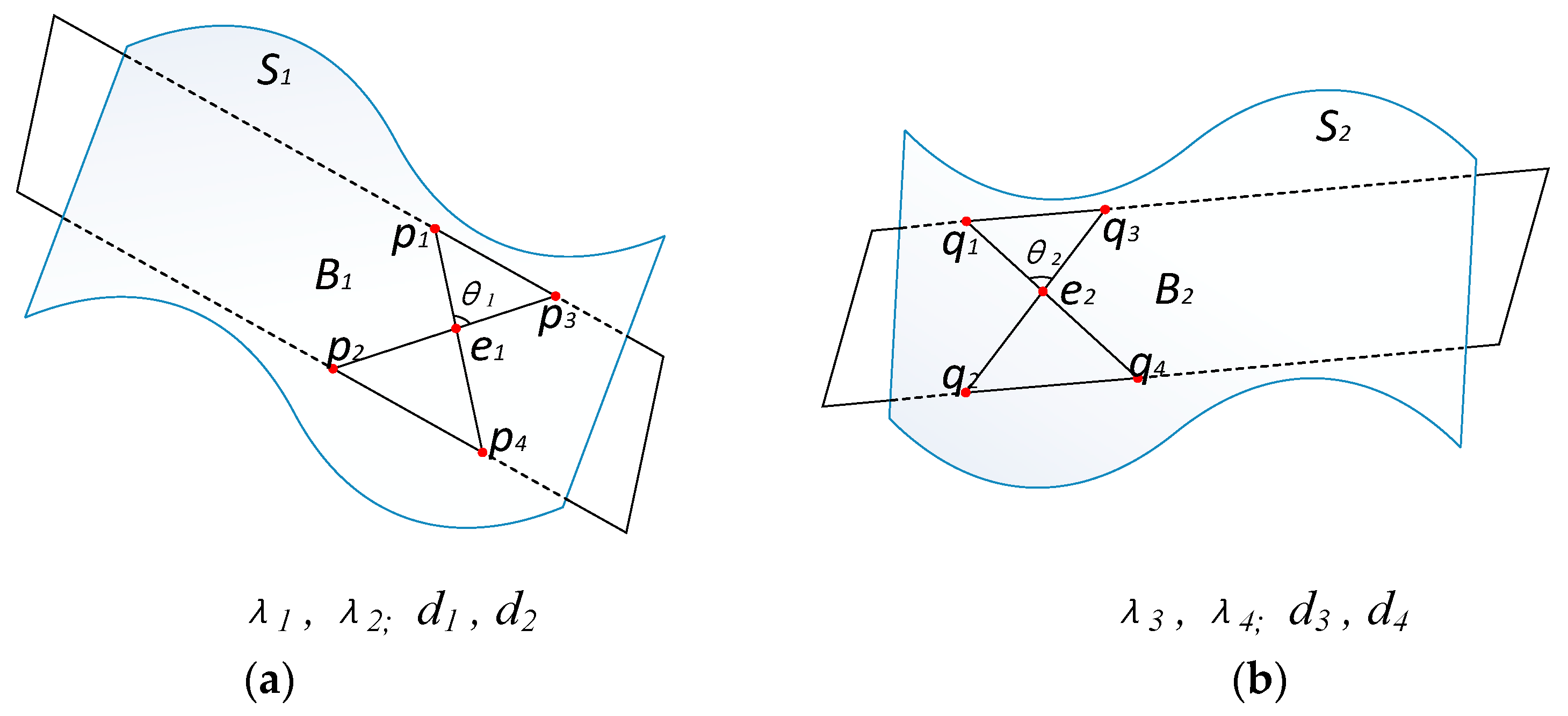
3.2. Definition for Generalized Super 4-Points Congruent Base Set
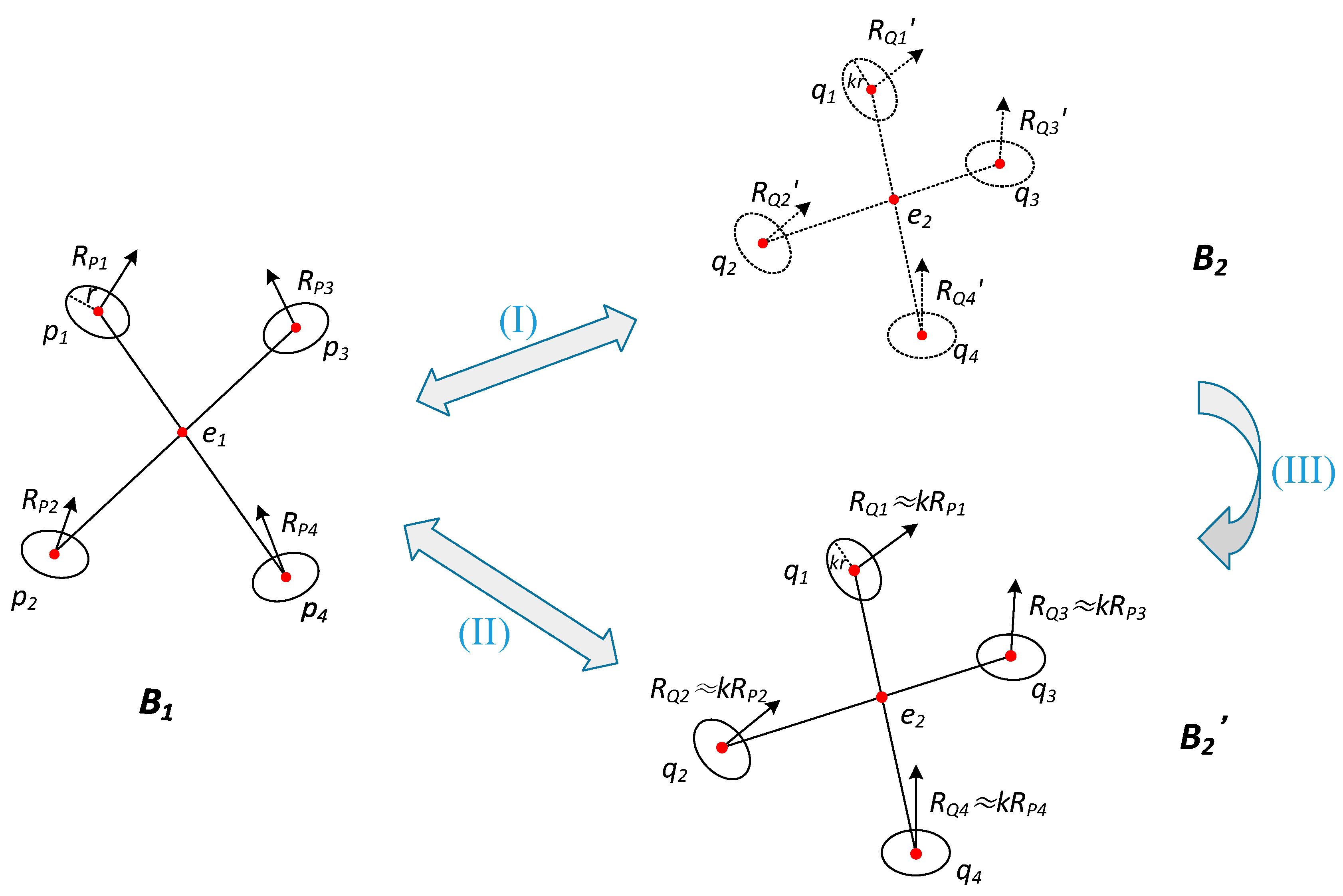
In order to extract generalized super 4-points congruent base set more accurately, this paper introduces local roughness of rock surface, which is defined as the distance between each point in point cloud and the plane fitted by all of its nearest points in the spherical neighborhood of radius r centered at . Suppose the radius r is changed with the scale of point cloud; then the local roughness of point is proportional to the scale. The above characteristic contributes to improving the precision of candidate point-pairs extraction.
Based on the coplanar 4-points congruent base, generalized super 4-points congruent base can be defined as follows: Let
P and
Q denote two point clouds with different scales under rigid transformation, and
and
denote corresponding surfaces.
Figure 9 shows the graph of a pair of generalized super 4-points congruent base, and lines with arrow mean normal vectors of points.
Let
and
denote the key-scales of two point clouds estimated with the scale rough estimation method introduced in
Section 3.1. For one given coplanar 4-points base
in surface
and another coplanar 4-points base
in surface
, if
and
are the generalized super 4-points congruent base, they have to satisfy the following fundamental conditions:
The affine invariant ratios of and are equal to each other, i.e., and , where have been defined in Equation (2).
The angles between the two point-pairs in and are equal to each other, i.e.,.
The distance of corresponding point-pairs in and are proportional, i.e., and , where have been defined in Equation (3).
The normal vector angles of corresponding points in
and
are equal to each other, which is shown as Equation (6).
The local roughness
and
of corresponding points in
and
are proportional to each other in spherical neighborhoods of radius
r and
kr, which is shown as Equation (7).
Let
, then Equation (7) could be written as follows:
Figure 10 reflects the relationship of generalized super 4-points congruent base, local roughness and scales of point clouds. In the figure,
denotes the given 4-points base in point cloud
P,
denotes the corresponding congruent base in point cloud
Q, and
denotes the base
performed scale adjustment.
3.3. Scale Adaptive Optimization and Candidate Point-Pairs Extraction
The key-scale estimation method for point clouds determines the optimal width w by searching the minimum of cumulative contribution rate based on spin images. As the optimal width w may be valid in an extremely small range, it is difficult to get the exact value with this method. Therefore, this paper makes a further adaptive optimization process about the width w during the candidate point-pairs extraction.
Figure 11a shows a coplanar 4-points base
in point cloud
P, and
Figure 11b shows the distance indexing sphere of the two corresponding point-pairs in point cloud
Q. After rasterization for distance indexing sphere, the candidate point-pairs could be extracted. The 2D profile of the rasterized sphere is shown as
Figure 12.
Suppose a refined scale ratio
, where
denotes a slack variable, which could be set according to the experimental data and the result of key-scales rough estimation. The scale adaptive optimization is to find the optimal
in the range of
. The errors of local roughness and distance are both closely related with the value of
. The total error can be expressed as Equation (9).
where
means the deviation of mean distance;
means the deviation of normalized distance between the given point-pairs in point cloud
P and the
i-th candidate point-pairs in point cloud
Q; and
. The candidate point-pairs here are extracted at
, which satisfy Condition 3 of generalized super 4-points congruent base definition.
means the deviation of mean local roughness. Similarly,
and
mean the deviation of normalized local roughness between the given point-pairs in point cloud
P and the
i-th candidate point-pairs in point cloud
Q, and
.
The total error has the minimum at the optimal accurate scale, which can be calculated by parabola fitting. Correspondingly, the candidate point-pairs are the optimal ones for generalized super 4-points congruent base set extraction.
3.4. Extraction of Generalized Super 4-Points Congruent Base Set
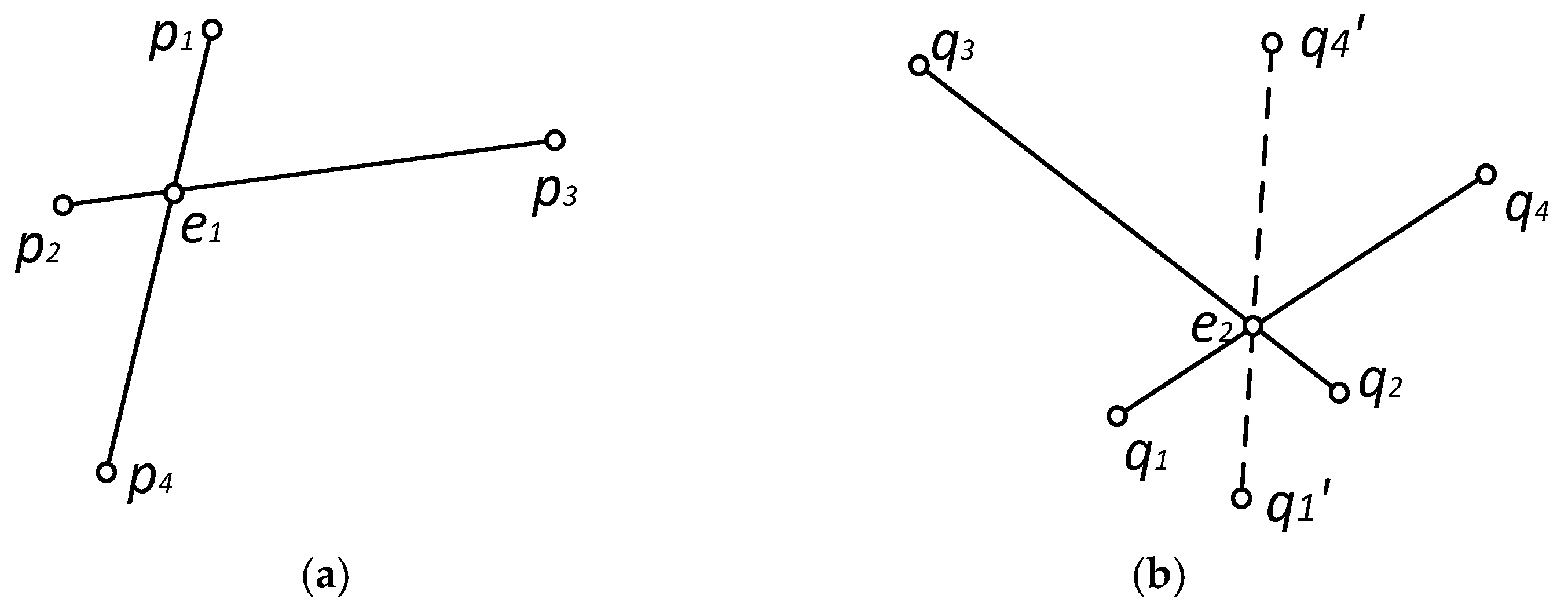
In this paper, a two-step method has been proposed in order to extract generalized super 4-points congruent base set from two groups of candidate point-pairs and with high efficiency and high accuracy.
The first step filters candidate point-pairs according to the constraint condition that the angles of normal vectors between the point-pairs in the given base and the corresponding ones in the candidate point-pairs are equal to each other.
Figure 13 plots a graph for the angles of normal vectors between point-pairs in given base and the corresponding ones in the candidate point-pairs sets. For a given base
in point cloud
P, normal vectors of each point are respectively denoted by
,
,
and
, where,
denotes the angle of normal vectors
and
, and
denotes the angle of normal vectors
and
. Similarly, for candidate point-pairs sets
and
in point cloud
Q,
denotes the angle of corresponding normal vectors
and
, and
denotes the angle of corresponding normal vectors
and
. For point-pairs from the candidate point-pairs sets, if
or
, the point-pairs are preserved; otherwise, they are rejected.
In the second step, in combination of the affine invariant ratios of the given base and the two corresponding candidate point-pairs, two sets of possible intersections {
} and
in point cloud
Q are obtained. Both intersections {
} and
as well as vectors of their corresponding point-pairs are, respectively, stored in a 3D grid G and vector indices. Then, with the unit sphere rasterization approach mentioned in
Section 2.2, let each intersection
in {
} be the center of a unit sphere, and find the intersection
from
which fall in or on the edge of the rasterized unit sphere according to the mapping relationship between angles and vector indices. If
is not empty, the point-pairs correspond to
and
in point cloud
Q constitute a coplanar 4-points base which is congruent with the given base in point cloud
P. With the above process, all generalized super 4-points congruent bases could be extracted successfully.
3.5. Algorithm Description of G-Super4PCS
Having stated the above, the procedures of G-Super4PCS could be described as follows:
Build multi-dimension eigenvectors with spin images, and estimate key-scales of SfM and TLS key point clouds according to the relationship between the similarity of spin images and cumulative contribute rate curves of PCA.
Extract candidate point-pairs from the target point cloud, the distances of which are proportional to the ones of the given base in the reference point cloud. Meanwhile, the accuracy of candidate point-pairs extraction has been improved greatly by the local roughness constraint as well as scale adaptive optimization.
Extract all generalized super 4-points congruent bases from candidate point-pairs according to Constraint Conditions 1, 2 and 4 mentioned in
Section 3.2, and then calculate the rigid transformation parameters.
Select L groups of generalized super 4-points congruent bases with RANSAC to test, and find the optimal registration parameters with the LCP.
Perform ICP algorithm on the SfM dense point cloud and TLS point cloud registered with the parameters calculated by Steps 1–4 in order to refine the registration results.
4. Experiment and Discussion
In this Section, the developed algorithm would be verified by use of the columnar basalt data acquired in Guabushan National Geopark in Jiangsu Province, China. The experiment data include digital images and TLS point cloud, which are, respectively, acquired by Fujifilm X-T10 digital camera (produced by Japan’s Fuji Photo Film) and FARO Focus
3D X330 terrestrial laser scanner (produced by FARO company in Lake Mary, Florida), the resolution (point spacing on the object surface) and the ranging precision of which were, respectively, set to 0.006 m and 0.002 m. The dimensions of the measured geological research area are approximately
, which is shown as
Figure 14.
The experiment firstly takes the SfM key point cloud and the TLS key point cloud, respectively, extracted from digital images and the original TLS point cloud as data sources for rough registration, on the basis of which performs ICP algorithm on the SfM dense point cloud and the original TLS point cloud in order to refine the registration results. The SfM key point cloud (
Figure 15a) and TLS key point cloud (
Figure 15b) are shown as
Figure 15. The SfM key point cloud, as the reference point cloud, has about 5194 points, and the TLS key point cloud, as the target point cloud, includes approximately 5326 points.
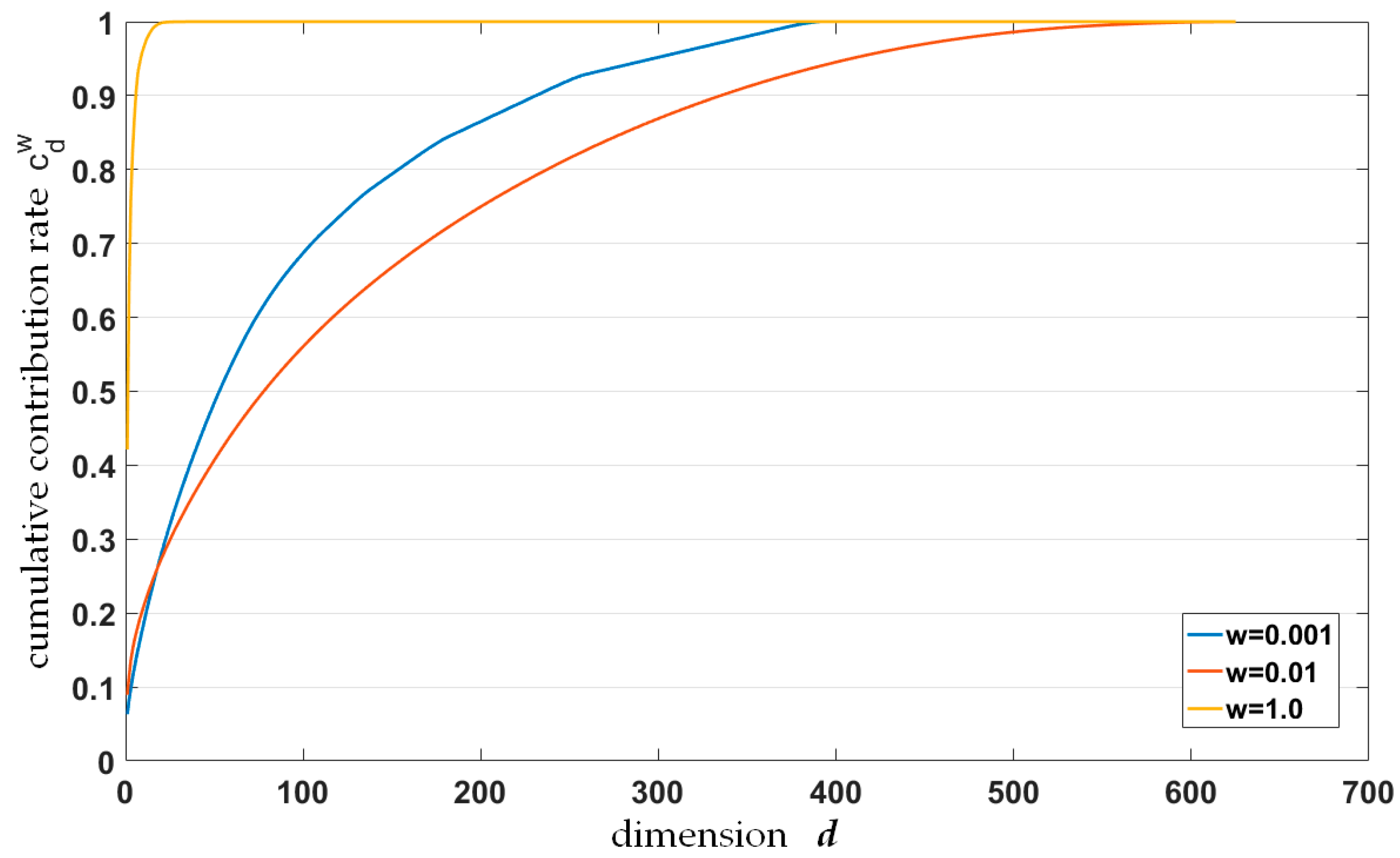
A scale rough estimation is performed on the two point clouds. The size of spin image is set to
pixels.
Figure 16 and
Figure 17 show spin images (
Spin 1,
Spin 2, …,
Spin 8) of some 3D points at different image width (
w = 10
−4, 0.005 and 0.5 for SfM key point cloud;
w = 0.001, 0.01 and 1.0 for TLS key point cloud). In the figures, it can be seen that spin images of the two key point clouds change with the image width, and are rather dissimilar at
w = 0.005 (for SfM key point cloud) and
w = 0.01 (for TLS key point cloud), which possibly approach the real key-scales.
Each spin image generates a
eigenvector. The cumulative contribution rate could be calculated by performing PCA on these eigenvectors, the curves of which are shown in
Figure 18 (for SfM key point cloud) and
Figure 19 (for TLS key point cloud). The curve charts depict the relationship between cumulative contribution rates
and dimension
d at different image width
w. The cumulative contribute rate curves for SfM and TLS key point cloud show a slowly rising trend at
w = 0.005 and
w = 0.01, respectively. Moreover, for the same dimension, the cumulative contribute rate is lower than that at other image widths. That is to say, the optimal key-scales of the two point clouds correspond to
w = 0.005 and
w = 0.01. The key-scale ratio is approximately 1/2.
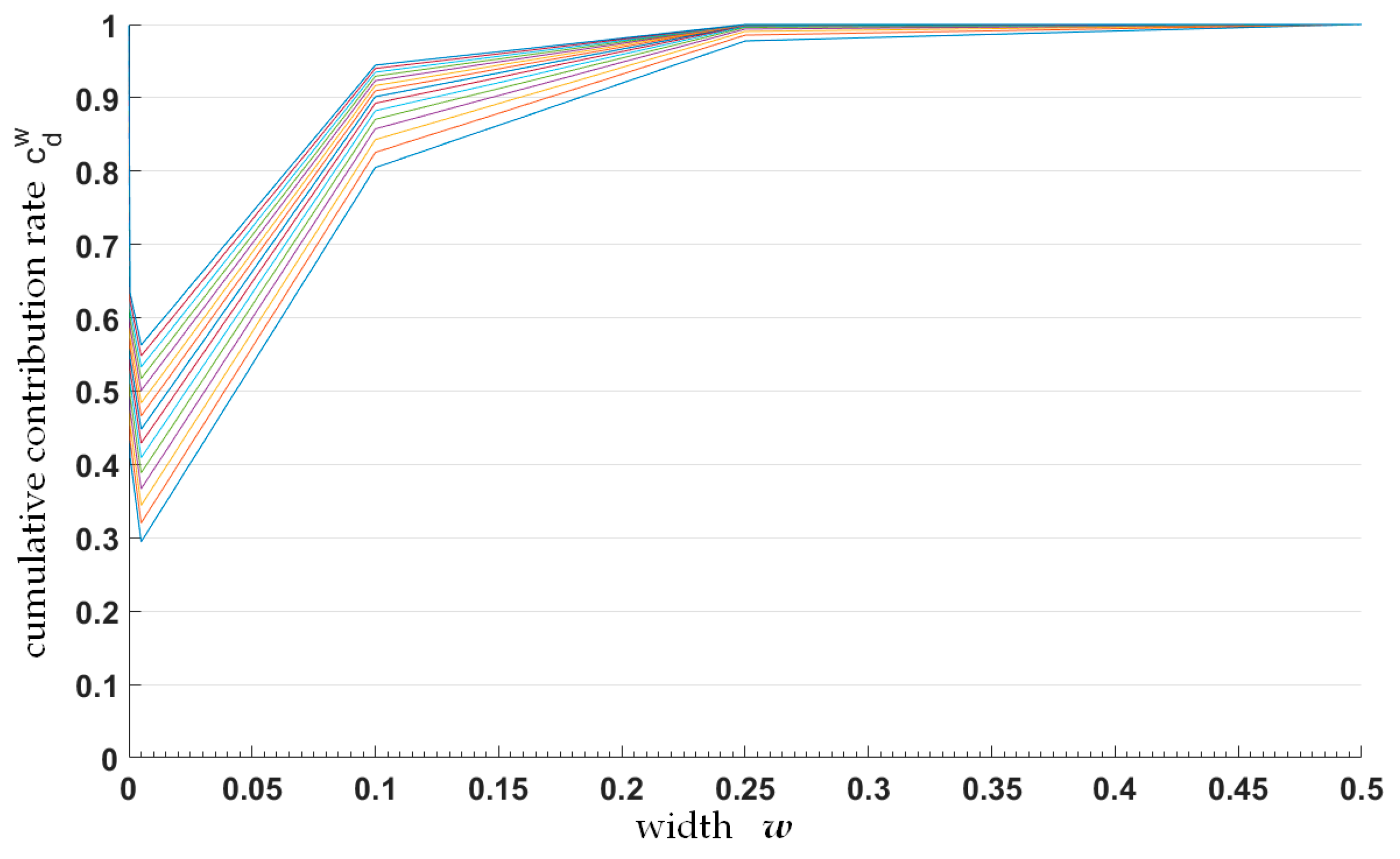
The line graphs in
Figure 20 and
Figure 21 depict the relationship between cumulative contribution rate and image width at different dimensions. Each broken line in the figure corresponds to a special dimension. The dimension value
d is in the range of
with an interval of 5. Obviously, the cumulative contribution rate has the minimum at
w = 0.005 (for SfM key point cloud) and
w = 0.01 (for TLS key point cloud), i.e., the key-scale ratio of SfM and TLS key point cloud is about 1/2. Therefore, the results of the scale ratio estimated with the two different groups of line charts are consistent.
The SfM and TLS key point clouds are unified in the same scale, as shown in
Figure 22. The red one represents the original SfM key point cloud, and the blue one represents the TLS key point cloud after scale adjustment.
The SfM key point cloud is taken as the reference point cloud, and the TLS key point cloud is taken as the target point cloud. In this experiment, the overlap between the two key point clouds is set to 0.8, and the threshold of registration precision is set to 0.1. The whole registration process is performed iteratively. The registration results of key point clouds are shown as
Table 1, where LCP responses the accuracy of registration.
The registration results of SfM and TLS key point clouds are shown as
Figure 23.
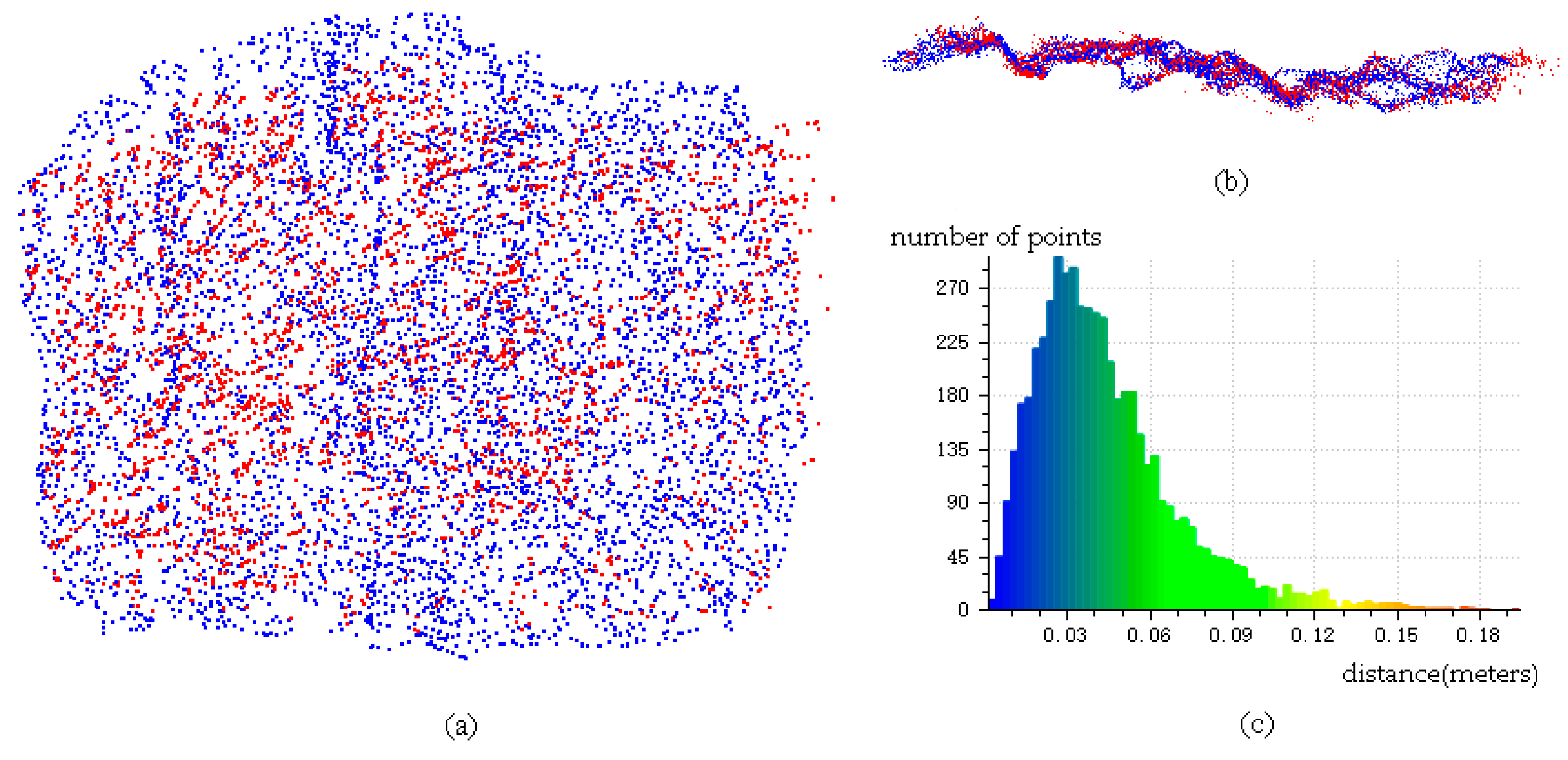
Figure 23a,b, respectively, shows the front and the bottom view of the point clouds after registration.
Figure 23c shows the distance distribution histogram about 5326 points in registered TLS key point cloud as well as their nearest neighbor points in SfM key point cloud. The histogram is composed of 72 bins, and the mean value and standard deviation are 0.044 m and 0.027 m, respectively.
In order to improve the registration precision, taking the registration parameters of key point clouds as inputs, ICP algorithm is performed on the SfM dense point cloud and the original TLS point cloud for further registration optimization. An overlapping display for the SfM dense point cloud as well as the transformed TLS point cloud is shown as
Figure 24. A hierarchical display of distances about the two registered point clouds is shown as
Figure 25a, and the corresponding distance histogram is shown as
Figure 25b. The mean value and standard deviation of the distance statistic results about the SfM dense point cloud and the transformed TLS point cloud are 0.022 m and 0.023 m. It can be concluded that the distances between the points and their nearest neighbor points in the overlapping part of the two point clouds are all less than 2 cm.
After fine registration with ICP algorithm, the results of registration parameters are listed in
Table 2. The overlapping display of the SfM dense point cloud and the original TLS point cloud after fine registration with ICP is shown in
Figure 26.
The corresponding distance hierarchical display result and the distance distribution histogram are shown as
Figure 27. The mean value and standard deviation are 0.003 m and 0.005 m, respectively. According to the statistic results of the distance histogram, there are approximately 95.86% point-pairs whose distances are less than 0.01 m, which demonstrates the registration precision has been improved greatly.
With the registration result, the corresponding 3D point-pairs between the SfM dense point cloud generated from the digital images and the TLS point cloud could be obtained. Moreover, as there is a one-to-one correspondence between pixels in the digital images and 3D points in the SfM dense point cloud, the mapping relationship between the digital images and the TLS point cloud could be built, and the 2D visualization result of which is shown in
Figure 28. The green rectangles represent the locations of pixels in different digital images corresponding to the same 3D point in TLS point cloud.
Figure 29 projects the texture information of seven digital images into the TLS point cloud according to the mapping relationship between pixels in the digital images and 3D points in the TLS point cloud. The final 3D visualization result by the fusion of spatial information of TLS point cloud and texture information of digital images is shown in
Figure 30.
All of the above experimental results demonstrate that the G-Super4PCS registration algorithm could achieve fine registration between digital images and TLS point cloud without any manual interactions, and the result of which provides a crucial data basis for further integration research.
5. Conclusions
Some traditional methods usually select more than three pairs of corresponding feature points as registration primitives, and calculate the registration transformation parameters. However, such registration methods are not appropriate for some special application fields, especially for geological objects with the characteristics of complicated and irregular distribution. In recent years, 4PCS and Super4PCS algorithms have been applied more broadly, which register two point clouds that are not dependent on corresponding feature points, but on 4-points base sets satisfying the 3D affine invariant transformation. While the above algorithms are limited for those point clouds from different sensors and with various scales, this paper proposed a new registration algorithm, G-Super4PCS, for digital images and TLS point cloud in geology. This algorithm combines spin images with cumulative contribute rate for key-scale rough estimation, defines a new generalized super 4-point congruent base, and introduces the rock surface feature constraints for the scale adaptive optimization as well as high efficient extraction of the bases. The feasibility of the algorithm was validated by use of the columnar basalt data acquired in Guabushan National Geopark in Jiangsu Province, China. The results indicate that it is unnecessary for the proposed method to depend on any regular feature information of the research object itself. Moreover, although the digital images and TLS point cloud data are acquired by different sensors and with different scales, they can be registered automatically with the proposed algorithm in high efficiency and high precision. The registration results would be used for further research on rock surface extraction integrating spatial and optical information. For geological objects, the whole algorithm only involves the local orientation and roughness of point clouds, which could be calculated by point clouds normal vectors and neighbor relationship. Therefore, for point clouds data acquired by other techniques, the algorithm would be appropriate if point clouds normal vectors are provided. Besides geological objects, the registration method proposed in this paper may be valuable for some other potential application fields.