Statistical Evaluation of No-Reference Image Quality Assessment Metrics for Remote Sensing Images
Abstract
:1. Introduction
2. Commonly Employed No-Reference Image Quality Metrics: An Overview
- Auto correlation (AC): Derived from the auto-correlation function. The AC metric uses the difference between auto-correlation values at two different distances along the horizontal and vertical directions, respectively. If an image is blurred or the edges are smoothed, the correlation between neighboring pixels becomes high.
- Average gradient (AG): Reflects the contrast and the clarity of the image. It can be used to measure the spatial resolution of a test image, where a larger AG indicates better spatial resolution [18].
- Blind image quality index (BIQI): A two-step framework based on natural scene statistics. Once trained, the framework requires no knowledge of the distortion process, and the framework is modular, in that it can be extended to any number of distortions [19].
- Blind image quality assessment through anisotropy (BIQAA): Measures the averaged anisotropy of an image by means of a pixel-wise directional entropy. A pixel-wise directional entropy is obtained by measuring the variance of the expected Rényi entropy and the normalized pseudo-Wigner distribution of the image for a set of predefined directions. BIQAA is capable of distinguishing the presence of noise in images [20].
- Blind image integrity notator using discrete cosine transform (DCT) statistics (BLIINDS-II): Relies on Bayesian model to predicate image quality scores given certain extracted features. The features are based on natural scene statistics model of the image DCT coefficients [21].
- Blur metric (BM): Based on the discrimination between different levels of blur perceptible on the same image [22].
- Blind/referenceless image spatial quality evaluator (BRISQE): A distortion-generic blind image quality assessment model based on natural scene statistics, which operates in the spatial domain. Scene statistics of locally normalized luminance coefficients are employed to quantify possible losses of naturalness in the image due to the presence of distortions, thereby leading to a holistic measure of quality [23].
- Cumulative probability of blur detection (CPBD): Based on the cumulative probability of blur detection, which is used to classify the visual quality of images into a finite number of quality classes [24].
- Distortion measure (DM): Computes the deviation of frequency distortion from an allpass response of unity gain, and then the deviation is weighted by a model of the frequency response of the human visual system and integrated over the visible frequencies [25].
- Edge intensity (EI): Calculated by the gradient of the Sobel filtered edge image.
- Entropy metric (EM): Measures the information content of an image. If the probability of occurrence of each gray level is low, the entropy is high, and vice versa [26].
- Block-based fast image sharpness (FISH): Computed by taking the root mean square of the 1% largest values of the local sharpness indices. FISH is based on wavelet transforms for estimating both global and local image sharpness [27].
- Just noticeable blur metric (JNBM): Integrates the concept of just noticeable blur into a probability summation model that is able to predict the relative amount of blurriness in images with different contents [3].
- Laplacian derivative (LD): Includes the first-order (gradient) and second-order (Laplacian) derivative metrics. These metrics act as a high-pass filter in the frequency domain. Image sharpness increases with increasing LD.
- Mean metric (MM): Calculated as the mean pixel value of the image, which indicates its average brightness level. For equivalent scenery, image brightness increases with increasing MM.
- Naturalness image quality evaluator (NIQE): A quality-aware collection of statistical features based on a simple and successful space domain natural scene statistic model. These features are derived from a corpus of natural, undistorted images [32].
- Quality aware clustering (QAC): Distorted images are partitioned into overlapping patches, and a percentile pooling strategy is used to estimate the local quality of each patch. Then, a centroid for each quality level is learned by quality aware clustering. These centroids are then used as a codebook to infer the quality of each patch in a given image, and a perceptual quality score can be obtained subsequently for the entire image [33].
- Standard deviation (SD): Calculated as the square root of the image variance. SD reflects the contrast of the image, where the image contrast increases with increasing SD.
- Skewness metric (SM): Skewness is a statistical measure of the direction and extent to which a dataset deviates from a distribution. For a standard normal distribution, high skewness indicates asymmetry of the data. In this case, the data contains a greater amount of information.
3. Test Images and Degradation Methods
3.1. Test Images
3.2. Degradation Methods
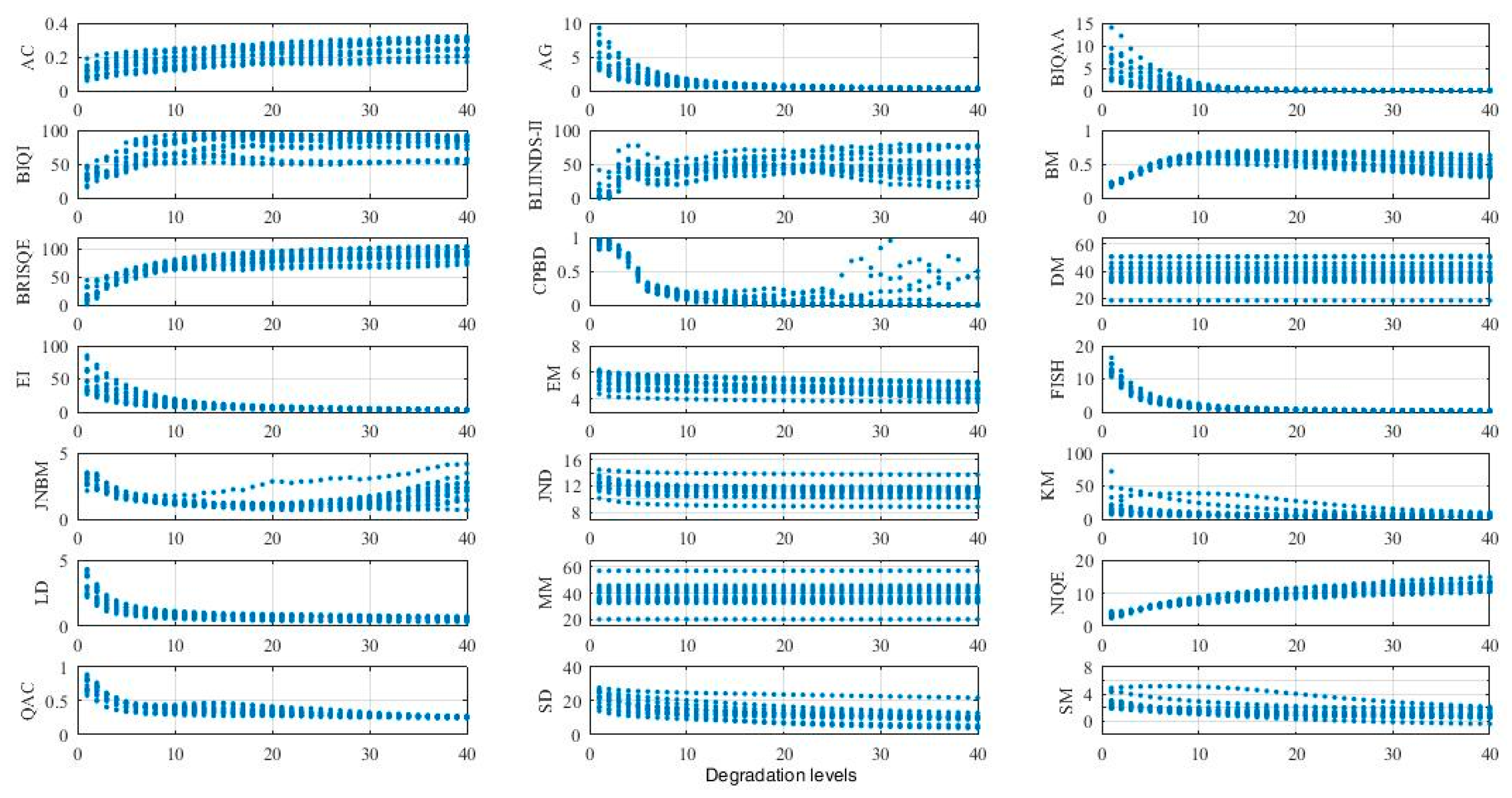
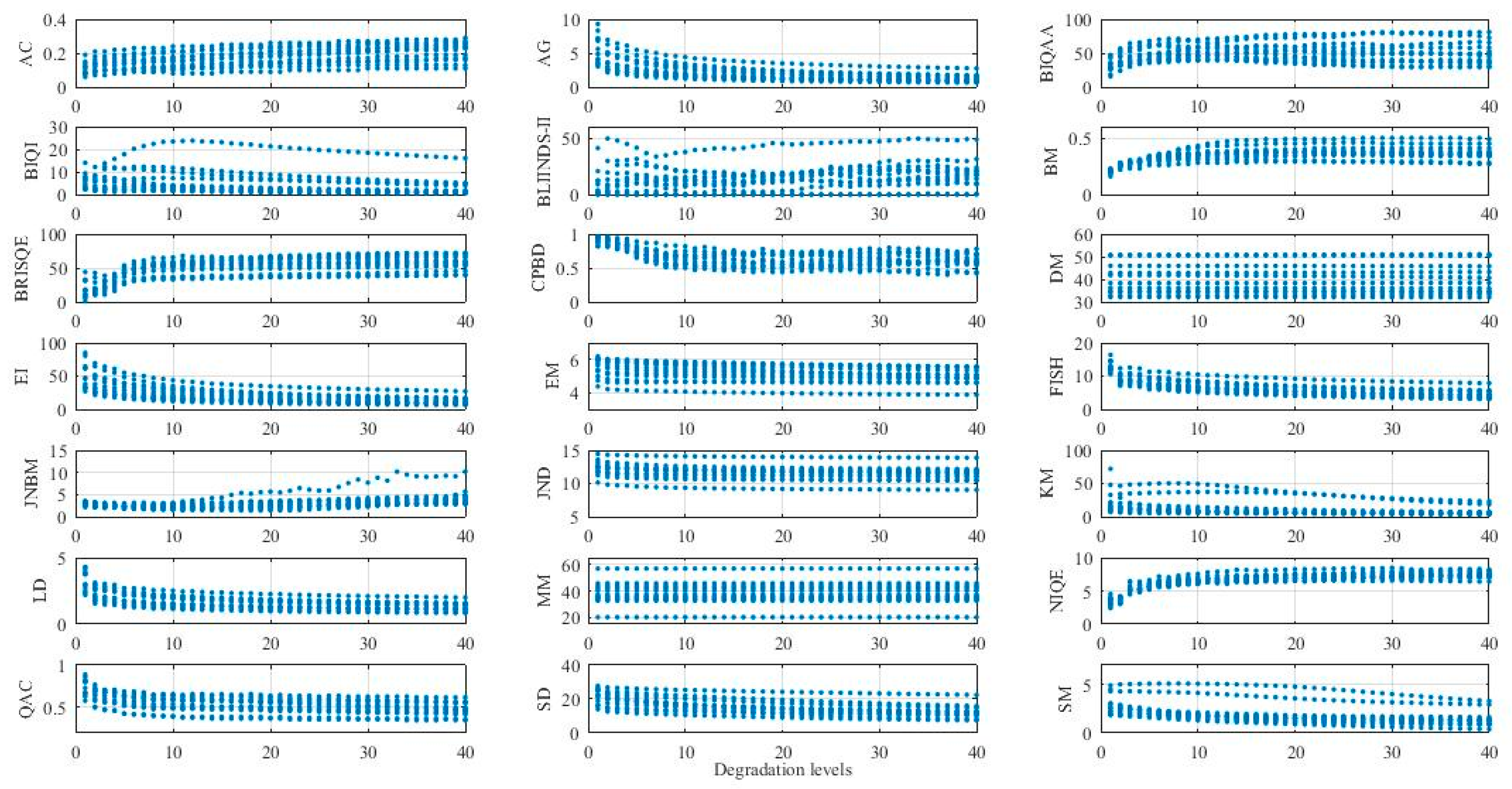
4. Statistical Analysis of Evaluation Results
4.1. Robustness of No-Reference Image Quality Metrics for Remote Sensing Images
4.1.1. Prediction Accuracy
4.1.2. Prediction Monotonicity
4.1.3. Prediction Consistency
4.2. Cluster Analysis of Robust Image Quality Metrics
5. Results and Discussion
5.1. Results of Robustness Analysis
5.1.1. Prediction Accuracy
5.1.2. Prediction Monotonicity
5.1.3. Prediction Consistency
5.1.4. Summary of the Robustness of Image Quality Metrics
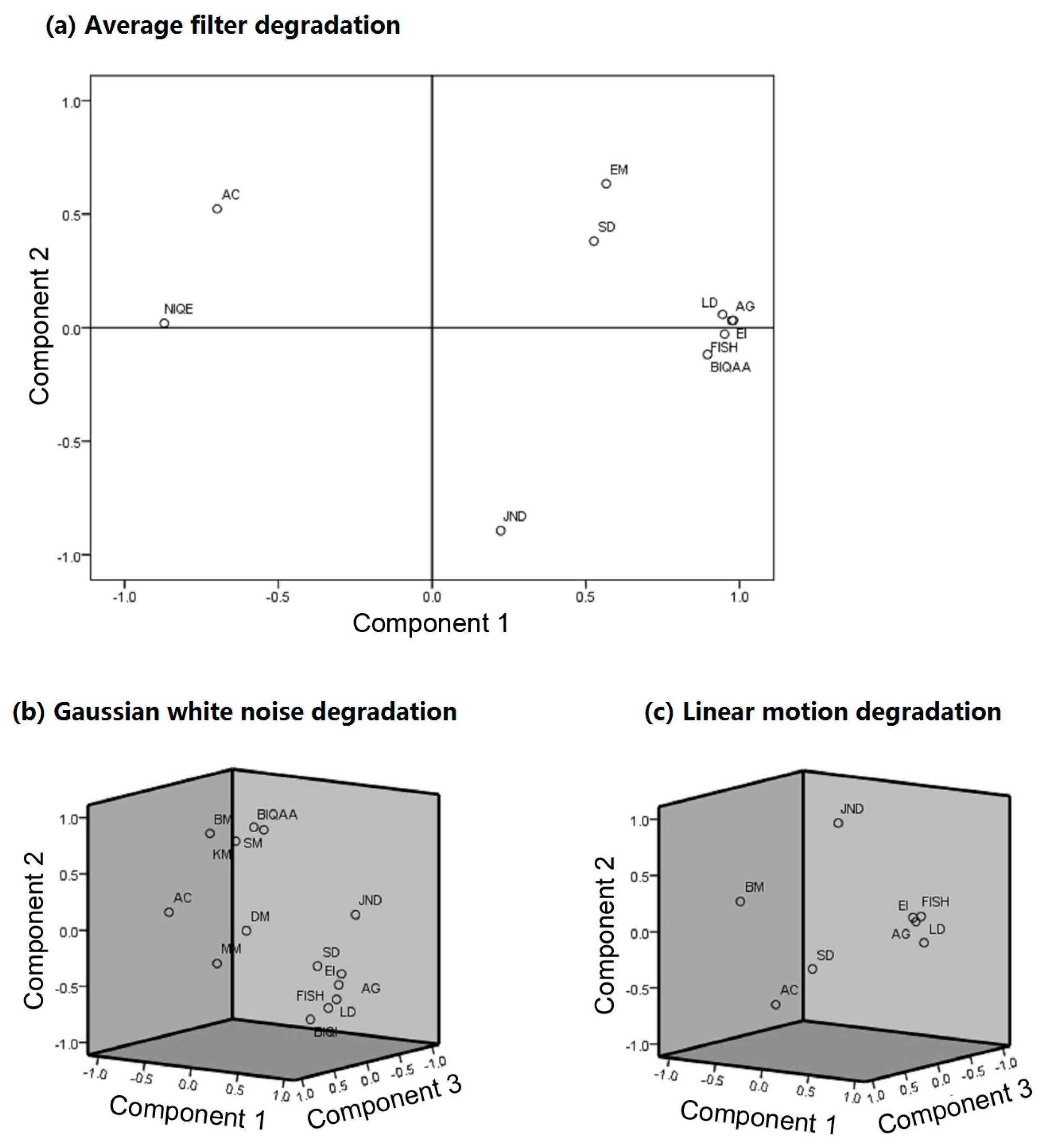
5.2. Factor Analysis of Robust Image Quality Metrics
- Average filter degradationComponent 1: EI, AG, FISH, LD, BIQAA, NIQE, AC, SD.Component 2: JND, EM.
- Gaussian white noise degradationComponent 1: EI, AG, LD, SD, AC.Component 2: BIQAA, SM, BM, BIQI, KM, FISH.Component 3: MM, JND, DM.
- Linear motion degradationComponent 1: LD, AG, FISH, EI, BM.Component 2: JND, AC.Component 3: SD.
- All degradation typesComponent 1: EI, LD, AG, FISH, SD, AC, JND.
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Cohen, E.; Yitzhaky, Y. No-reference assessment of blur and noise impacts on image quality. Signal Image Video Process. 2010, 4, 289–302. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C. Modern image quality assessment. Synth. Lect. Image Video Multimed. Process. 2006, 2, 1–156. [Google Scholar] [CrossRef]
- Ferzli, R.; Karam, L.J. A no-reference objective image sharpness metric based on the notion of just noticeable blur (JNB). IEEE Trans. Image Process. 2009, 18, 717–728. [Google Scholar] [CrossRef] [PubMed]
- Chandler, D.M. Seven challenges in image quality assessment: Past, present, and future research. ISRN Signal Process. 2013, 2013, 905685. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C. Mean squared error: Love it or leave it? A new look at signal fidelity measures. IEEE Signal Process. Mag. 2009, 26, 98–117. [Google Scholar] [CrossRef]
- Ismail, A.; Bulent, S.; Sayood, K. Statistical evaluation of image quality measures. J. Electron. Imaging 2002, 11, 206–223. [Google Scholar]
- Ong, E.; Lin, W.; Lu, Z.; Yao, S.; Yang, X.; Jiang, L. No-reference JPEG-2000 image quality metric. In Proceedings of the International Conference on Multimedia and Expo, Baltimore, MD, USA, 6–9 July 2003; pp. 545–548. [Google Scholar]
- Cohen, E.; Yitzhaky, Y. Blind image quality assessment considering blur, noise, and JPEG compression distortions. In Proceedings of the Applications of Digital Image Processing XXX, San Diego, CA, USA, 26 August 2007. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Simoncelli, E.P. Reduced-reference image quality assessment using a wavelet-domain natural image statistic model. In Proceedings of the Society of Photo-optical Instrumentation Engineers, Human Vision and Electronic Imaging, San Jose, CA, USA, 17–20 January 2005; pp. 149–159. [Google Scholar]
- Carnec, M.; Le Callet, P.; Barba, D. Objective quality assessment of color images based on a generic perceptual reduced reference. Signal Process. Image Commun. 2008, 23, 239–256. [Google Scholar] [CrossRef]
- Eskicioglu, A.M.; Fisher, P.S. Image quality measures and their performance. IEEE Trans. Commun. 1995, 43, 2959–2965. [Google Scholar] [CrossRef]
- Chen, M.J.; Bovik, A.C. No-reference image blur assessment using multiscale gradient. EURASIP J. Image Video Process. 2011. [Google Scholar] [CrossRef]
- Ciancio, A.; da Costa, A.T.; da Silva, E.A.; Said, A.; Samadani, R.; Obrador, P. No-reference blur assessment of digital pictures based on multifeature classifiers. IEEE Trans. Image Process. 2011, 20, 64–75. [Google Scholar] [CrossRef] [PubMed]
- Shen, H.; Zhao, W.; Yuan, Q.; Zhang, L. Blind Restoration of Remote Sensing Images by a Combination of Automatic Knife-Edge Detection and Alternating Minimization. Remote Sens. 2014, 6, 7491–7521. [Google Scholar] [CrossRef]
- Rodger, J.A. Toward reducing failure risk in an integrated vehicle health maintenance system: A fuzzy multi-sensor data fusion Kalman filter approach for IVHMS. Expert Syst. Appl. 2012, 3, 9821–9836. [Google Scholar] [CrossRef]
- Sazzad, Z.P.; Kawayoke, Y.; Horita, Y. No reference image quality assessment for JPEG2000 based on spatial features. Signal Process. Image Commun. 2008, 23, 257–268. [Google Scholar] [CrossRef]
- Yang, X.H.; Jing, Z.L.; Liu, G.; Hua, L.Z.; Ma, D.W. Fusion of multi-spectral and panchromatic images using fuzzy rule. Commun. Nonlinear Sci. Numer. Simul. 2007, 12, 1334–1350. [Google Scholar] [CrossRef]
- Moorthy, A.K.; Bovik, A.C. A two-step framework for constructing blind image quality indices. IEEE Signal Process. Lett. 2010, 17, 513–516. [Google Scholar] [CrossRef]
- Gabarda, S.; Cristóbal, G. Blind image quality assessment through anisotropy. JOSA A 2007, 24, B42–B51. [Google Scholar] [CrossRef] [PubMed]
- Saad, M.A.; Bovik, A.C.; Charrier, C. A DCT statistics-based blind image quality index. IEEE Signal Process. Lett. 2010, 17, 583–586. [Google Scholar] [CrossRef]
- Crete, F.; Dolmiere, T.; Ladret, P.; Nicolas, M. The blur effect: Perception and estimation with a new no-reference perceptual blur metric. In Proceedings of the Human Vision and Electronic Imaging XII, San Jose, CA, USA, 28 January 2007. [Google Scholar]
- Mittal, A.; Moorthy, A.; Bovik, A. No-reference image quality assessment in the spatial domain. IEEE Trans. Image Process. 2012, 21, 4695–4708. [Google Scholar] [CrossRef] [PubMed]
- Narvekar, N.D.; Karam, L.J. A no-reference image blur metric based on the cumulative probability of blur detection (CPBD). IEEE Trans. Image Process. 2011, 20, 2678–2683. [Google Scholar] [CrossRef] [PubMed]
- Damera-Venkata, N.; Kite, T.D.; Geisler, W.S.; Evans, B.L.; Bovik, A.C. Image quality assessment based on a degradation model. IEEE Trans. Image Process. 2000, 9, 636–650. [Google Scholar] [CrossRef] [PubMed]
- Karathanassi, V.; Kolokousis, P.; Ioannidou, S. A comparison study on fusion methods using evaluation indicators. Int. J. Remote Sens. 2007, 28, 2309–2341. [Google Scholar] [CrossRef]
- Vu, P.V.; Chandler, D.M. A fast wavelet-based algorithm for global and local image sharpness estimation. IEEE Signal Process. Lett. 2012, 19, 423–426. [Google Scholar] [CrossRef]
- Yang, X.; Ling, W.; Lu, Z.; Ong, E.P.; Yao, S. Just noticeable distortion model and its applications in video coding. Signal Process. Image Commun. 2005, 20, 662–680. [Google Scholar] [CrossRef]
- Wei, Z.; Ngan, K.N. Spatio-temporal just noticeable distortion profile for grey scale image/video in DCT domain. IEEE Trans. Circuits Syst. Video Technol. 2009, 19, 337–346. [Google Scholar]
- Caviedes, J.; Oberti, F. A new sharpness metric based on local kurtosis, edge and energy information. Signal Process. Image Commun. 2004, 19, 147–161. [Google Scholar] [CrossRef]
- Zhang, J.; Ong, S.H.; Le, T.M. Kurtosis-based no-reference quality assessment of JPEG2000 images. Signal Process. Image Commun. 2011, 26, 13–23. [Google Scholar] [CrossRef]
- Mittal, A.; Soundararajan, R.; Bovik, A.C. Making a “Completely Blind” Image Quality Analyzer. IEEE Signal Process. Lett. 2013, 20, 209–212. [Google Scholar] [CrossRef]
- Xue, W.; Zhang, L.; Mou, X. Learning without Human Scores for Blind Image Quality Assessment. In Proceedings of the 2013 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Portland, OR, USA, 23–28 June 2013. [Google Scholar]
- Feichtenhofer, C.; Fassold, H.; Schallauer, P. A Perceptual Image Sharpness Metric Based on Local Edge Gradient Analysis. IEEE Signal Process. Lett. 2013, 20, 379–382. [Google Scholar] [CrossRef]
- Li, S.; Li, Z.; Gong, J. Multivariate statistical analysis of measures for assessing the quality of image fusion. Int. J. Image Data Fusion 2010, 1, 47–66. [Google Scholar] [CrossRef]
- MacCallum, R. A comparison of factor analysis programs in SPSS, BMDP, and SAS. Psychometrika 1983, 48, 223–231. [Google Scholar] [CrossRef]
- Kim, J.O.; Mueller, C.W. Introduction to Factor Analysis: What It Is and How to Do It; Sage: Thousand Oaks, CA, USA, 1978. [Google Scholar]






| Average | Gaussian | Motion | |
|---|---|---|---|
| AC | 36.37 | 38.2 | 36.67 |
| AG | 36.47 | 89.2 | 13.46 |
| BIQAA | 24.82 | 7.13 | 0.5 |
| BIQI | 13.34 | 112.48 | 3.54 |
| BLIINDS-II | 7.62 | 47.11 | 0.6 |
| BM | 32.8 | 37.53 | 34.63 |
| BRISQE | 63.34 | 123.48 | 14.42 |
| CPBD | 36.78 | 28.42 | 31.03 |
| DM | 3.7 | 5.41 | 3.68 |
| EI | 40.37 | 66.11 | 11.15 |
| EM | 2.49 | 0.59 | 1.21 |
| FISH | 1246.83 | 517.63 | 26.63 |
| JNBM | 16.11 | 6.6 | 4.78 |
| JND | 4.85 | 13.48 | 5.01 |
| KM | 3.17 | 7.67 | 1.14 |
| LD | 33.9 | 63.29 | 33.9 |
| MM | 3.84 | 5.47 | 3.84 |
| NIQE | 57.37 | 42.77 | 18.21 |
| QAC | 35.04 | 29.49 | 32.21 |
| SD | 5.65 | 31.38 | 5.14 |
| SM | 8.66 | 16.59 | 5.59 |
| Average | Gaussian | Motion | |
|---|---|---|---|
| AC | 0.670 | −0.744 | 0.463 |
| AG | −0.664 | 0.917 | −0.594 |
| BIQAA | −0.595 | −0.473 | −0.193 |
| BIQI | 0.445 | 0.778 | 0.083 |
| BLIINDS-II | 0.374 | 0.755 | 0.181 |
| BM | 0.056 | 0.169 | 0.402 |
| BRISQE | 0.763 | 0.767 | 0.510 |
| CPBD | −0.536 | 0.045 | −0.435 |
| DM | −0.004 | 0.910 | 0 |
| EI | −0.690 | 0.351 | −0.596 |
| EM | −0.425 | 0.192 | −0.232 |
| FISH | −0.704 | 0.736 | −0.776 |
| JNBM | −0.011 | 0.018 | 0.440 |
| JND | −0.193 | −0.701 | −0.166 |
| KM | −0.420 | −0.481 | −0.279 |
| LD | −0.617 | −0.538 | −0.553 |
| MM | 0.001 | 0.159 | 0 |
| NIQE | 0.886 | 0.865 | 0.686 |
| QAC | −0.759 | 0.873 | −0.425 |
| SD | −0.519 | 0.774 | −0.481 |
| SM | −0.467 | −0.485 | −0.341 |
| Average | Gaussian | Motion | |||||||
|---|---|---|---|---|---|---|---|---|---|
| PA | PM | PC | PA | PM | PC | PA | PM | PC | |
| AC | √ | √ | √ | √ | √ | √ | √ | √ | √ |
| AG | √ | √ | √ | √ | √ | √ | √ | √ | √ |
| BIQAA | √ | √ | √ | √ | √ | √ | × | × | √ |
| BIQI | √ | × | √ | √ | √ | √ | √ | × | × |
| BLIINDS-II | √ | × | √ | √ | × | √ | × | × | √ |
| BM | √ | × | × | √ | √ | √ | √ | √ | √ |
| BRISQE | √ | × | √ | √ | × | √ | √ | × | √ |
| CPBD | √ | × | √ | √ | × | × | √ | × | √ |
| DM | √ | × | × | √ | √ | √ | √ | × | × |
| EI | √ | √ | √ | √ | √ | √ | √ | √ | √ |
| EM | √ | √ | √ | × | × | √ | × | √ | √ |
| FISH | √ | √ | √ | √ | √ | √ | √ | √ | √ |
| JNBM | √ | × | × | √ | × | × | √ | × | √ |
| JND | √ | √ | √ | √ | √ | √ | √ | √ | √ |
| KM | √ | × | √ | √ | √ | √ | × | × | √ |
| LD | √ | √ | √ | √ | √ | √ | √ | √ | √ |
| MM | √ | × | × | √ | √ | √ | √ | × | × |
| NIQE | √ | √ | √ | √ | × | √ | √ | × | √ |
| QAC | √ | × | √ | √ | × | √ | √ | × | √ |
| SD | √ | √ | √ | √ | √ | √ | √ | √ | √ |
| SM | √ | × | √ | √ | √ | √ | √ | × | √ |
| Degradation | Robust IQMs |
|---|---|
| Average | AC, AG, BIQAA, EI, EM, FISH, JND, LD, NIQE, SD. |
| Gaussian | AC, AG, BIQAA, BIQI, BM, DM, EI, FISH, JND, KM, LD, MM, SD, SM. |
| Motion | AC, AG, BM, EI, FISH, JND, LD, SD. |
| Unknown | AC, AG, EI, FISH, JND, LD, SD. |
| Average | Gaussian | Motion | All | ||
|---|---|---|---|---|---|
| KMO | 0.699 | 0.727 | 0.689 | 0.742 | |
| Bartlett’s test | Approximate chi squared | 8556.255 | 14,746.642 | 6576.038 | 25,101.243 |
| Freedom | 45 | 91 | 28 | 21 | |
| Significance | 0.000 | 0.000 | 0.000 | 0.000 | |
| Component | ||
|---|---|---|
| 1 | 2 | |
| EI | 0.980 | 0.032 |
| AG | 0.975 | 0.032 |
| FISH | 0.951 | −0.028 |
| LD | 0.944 | 0.058 |
| BIQAA | 0.895 | −0.118 |
| NIQE | −0.871 | 0.019 |
| AC | −0.699 | 0.523 |
| SD | 0.526 | 0.382 |
| JND | 0.223 | −0.894 |
| EM | 0.566 | 0.634 |
| Component | |||
|---|---|---|---|
| 1 | 2 | 3 | |
| EI | 0.921 | −0.328 | 0.113 |
| AG | 0.880 | −0.431 | 0.101 |
| LD | 0.805 | −0.579 | 0.026 |
| SD | 0.787 | −0.245 | 0.293 |
| AC | −0.700 | 0.105 | 0.449 |
| BIQAA | −0.001 | 0.843 | −0.008 |
| SM | −0.251 | 0.813 | −0.212 |
| BM | −0.408 | 0.806 | 0.238 |
| BIQI | 0.518 | −0.787 | 0.018 |
| KM | −0.365 | 0.693 | −0.095 |
| FISH | 0.631 | −0.691 | −0.098 |
| MM | 0.169 | −0.190 | 0.952 |
| JND | 0.351 | −0.007 | −0.914 |
| DM | 0.401 | 0.107 | 0.834 |
| Component | |||
|---|---|---|---|
| 1 | 2 | 3 | |
| LD | 0.978 | −0.044 | 0.018 |
| AG | 0.967 | 0.157 | 0.126 |
| FISH | 0.960 | 0.190 | 0.037 |
| EI | 0.953 | 0.195 | 0.150 |
| BM | −0.595 | 0.246 | 0.593 |
| JND | −0.002 | 0.909 | −0.065 |
| AC | −0.588 | −0.748 | 0.059 |
| SD | 0.337 | −0.227 | 0.815 |
| Component | |
|---|---|
| 1 | |
| EI | 0.984 |
| LD | 0.983 |
| AG | 0.980 |
| FISH | 0.964 |
| SD | 0.898 |
| AC | −0.888 |
| JND | 0.726 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Yang, Z.; Li, H. Statistical Evaluation of No-Reference Image Quality Assessment Metrics for Remote Sensing Images. ISPRS Int. J. Geo-Inf. 2017, 6, 133. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi6050133
Li S, Yang Z, Li H. Statistical Evaluation of No-Reference Image Quality Assessment Metrics for Remote Sensing Images. ISPRS International Journal of Geo-Information. 2017; 6(5):133. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi6050133
Chicago/Turabian StyleLi, Shuang, Zewei Yang, and Hongsheng Li. 2017. "Statistical Evaluation of No-Reference Image Quality Assessment Metrics for Remote Sensing Images" ISPRS International Journal of Geo-Information 6, no. 5: 133. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi6050133





