Uncovering Distribution Patterns of High Performance Taxis from Big Trace Data
Abstract
:1. Introduction
2. Related Work
3. Taxi Performance Evaluation
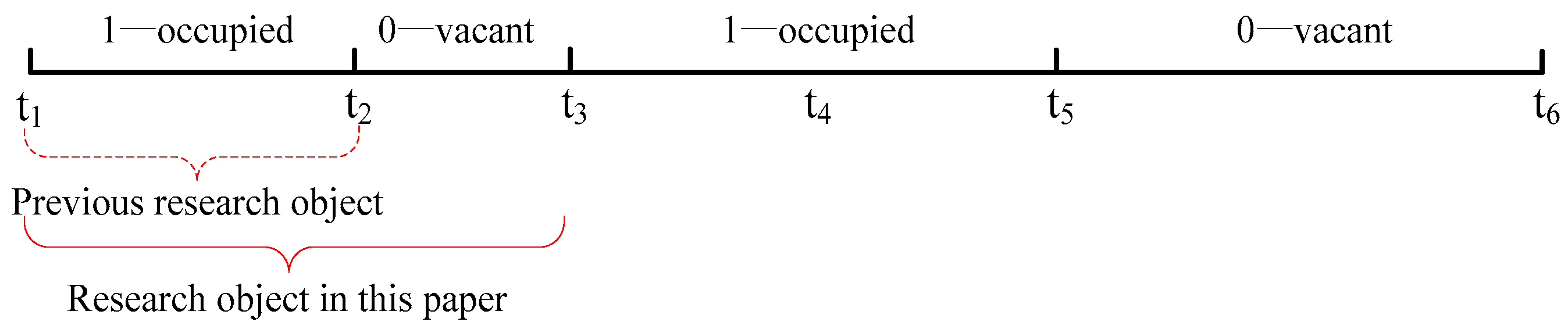
3.1. Data Preprocessing
- ROADID: unique ID for the matched road segment of the GPS trace point
- CARID: unique ID for the taxi
- LONGITUDE: the longitude of the sampled GPS point
- LATITUDE: the latitude of the sampled GPS point
- TIME: the timestamp in the format of seconds
- ISCARRY: the current status of the taxi, 0 for vacant and 1 for occupied.
3.2. Taxi Single Trip Efficiency
3.3. Taxi Performance Evaluation
4. Space-Time Distribution of Top and Ordinary Drivers
4.1. Ranking Taxi Drivers
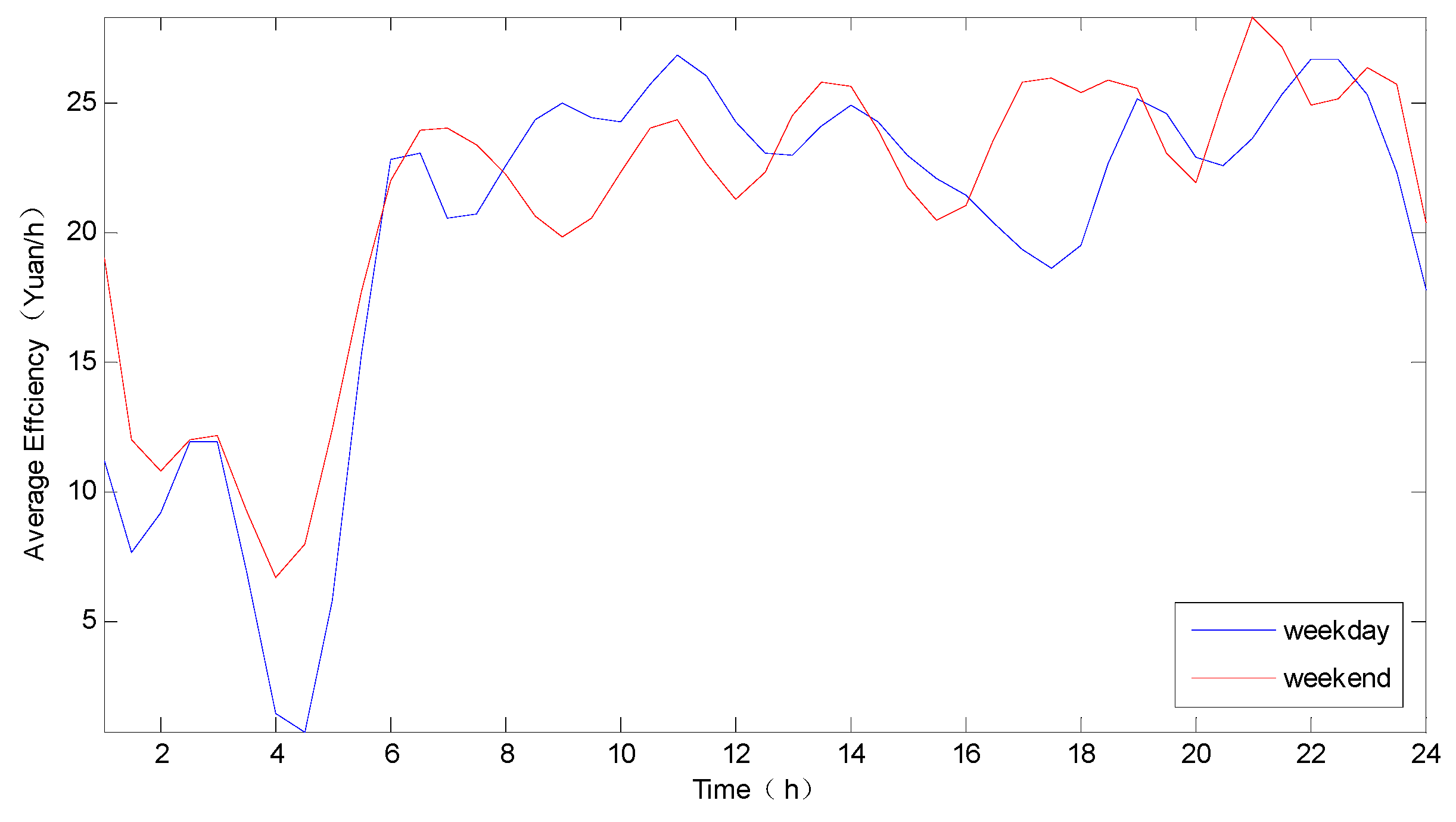
4.2. Space-Time Distribution of Top Drivers
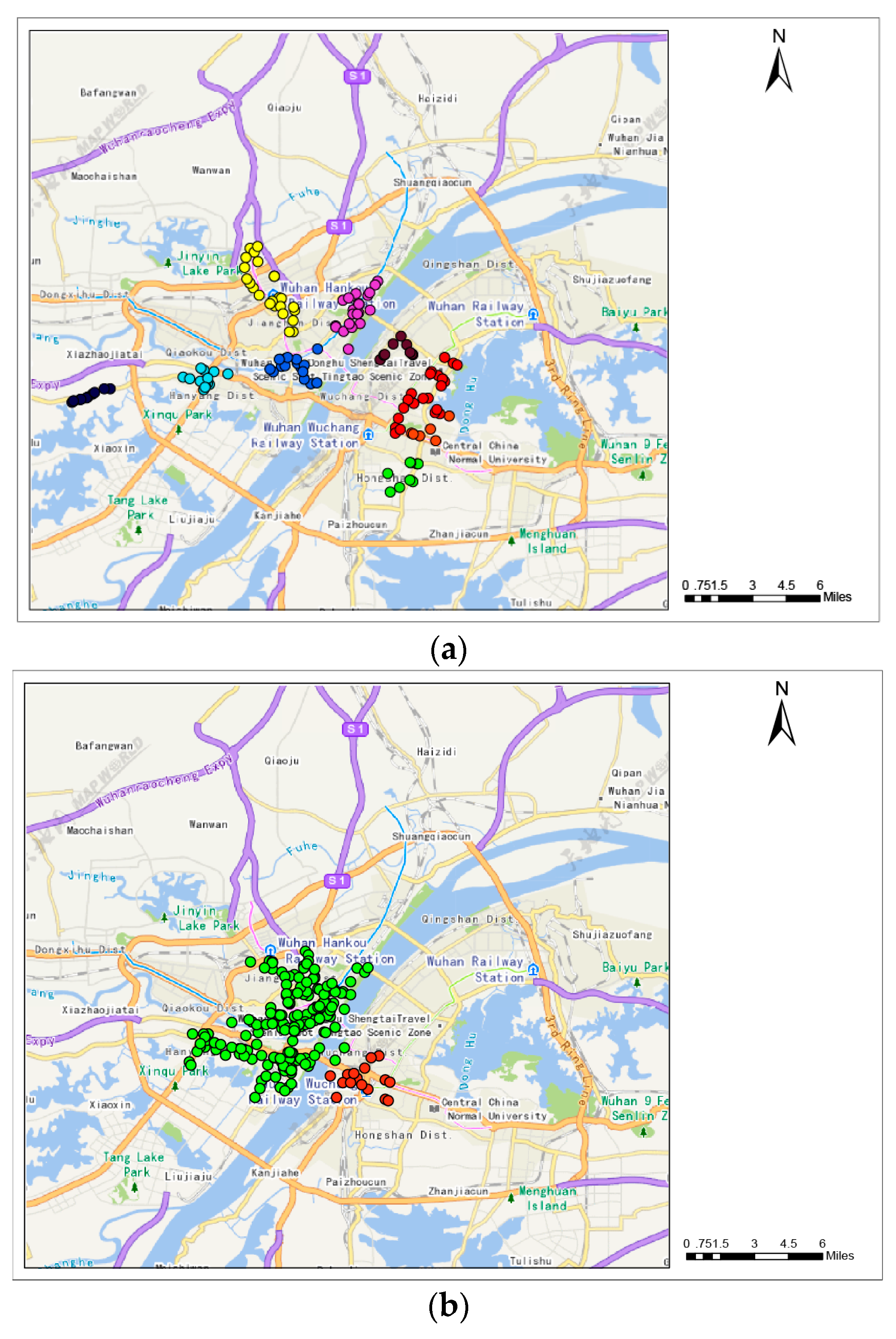
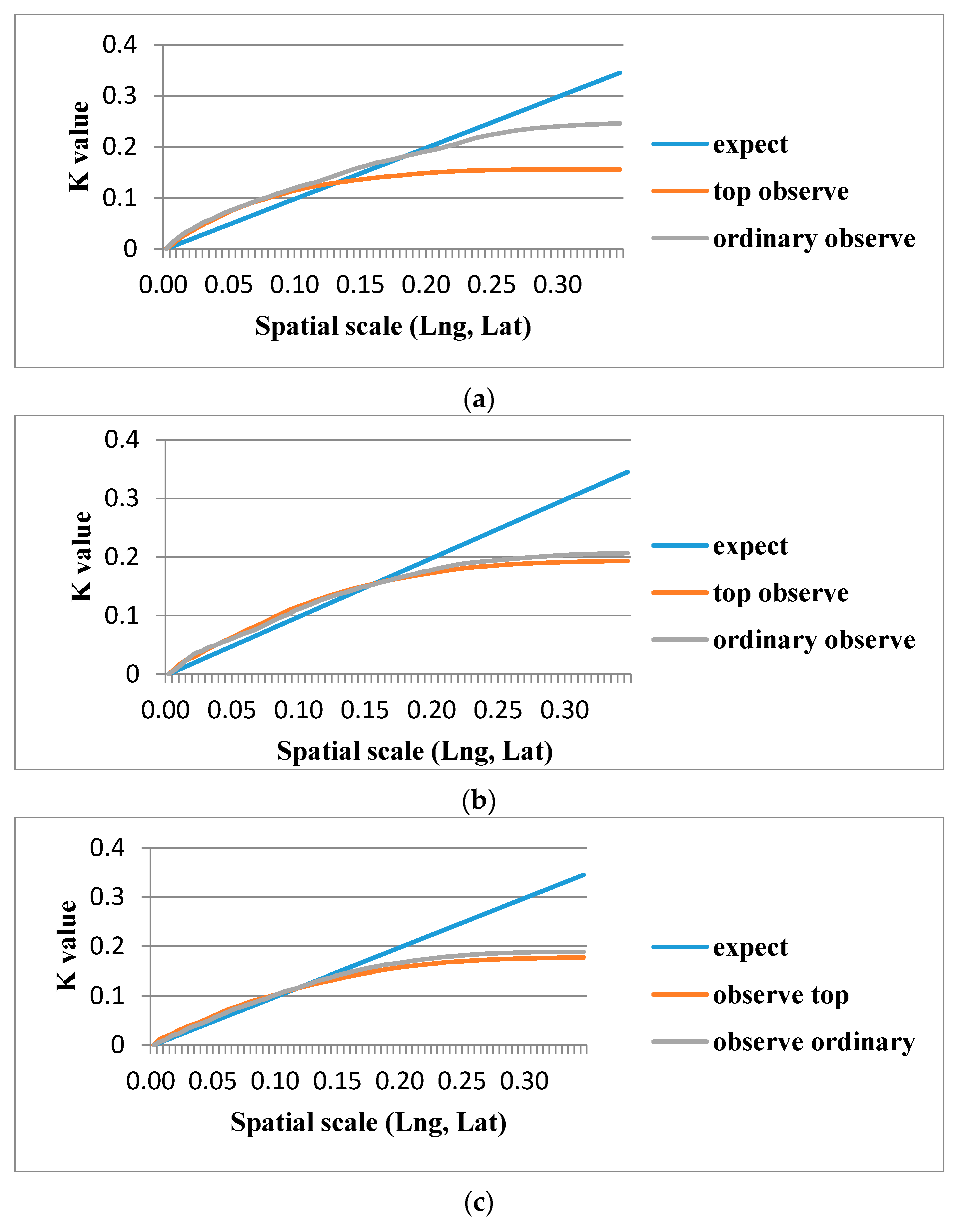
4.3. Spatial Clustering of Operational Points
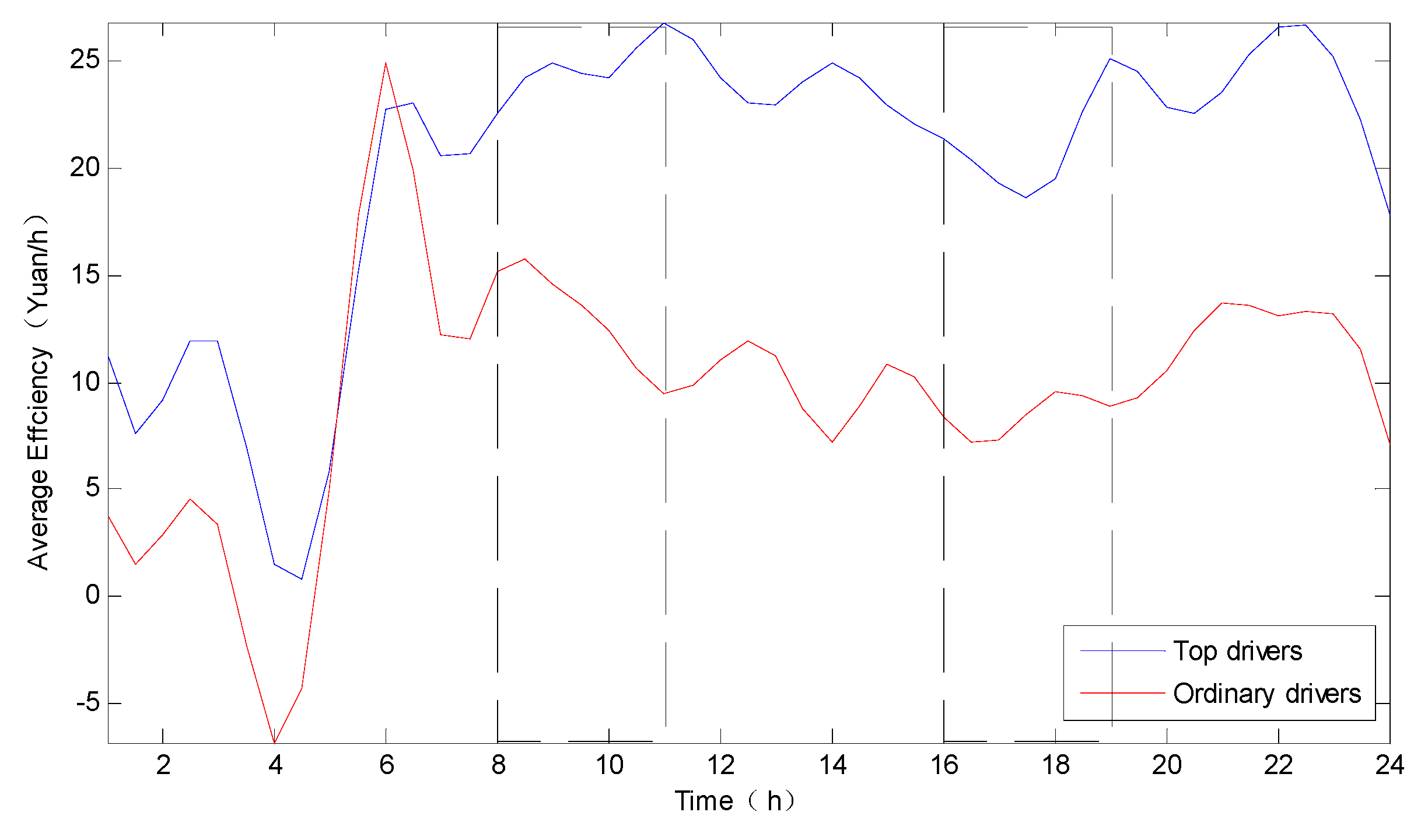
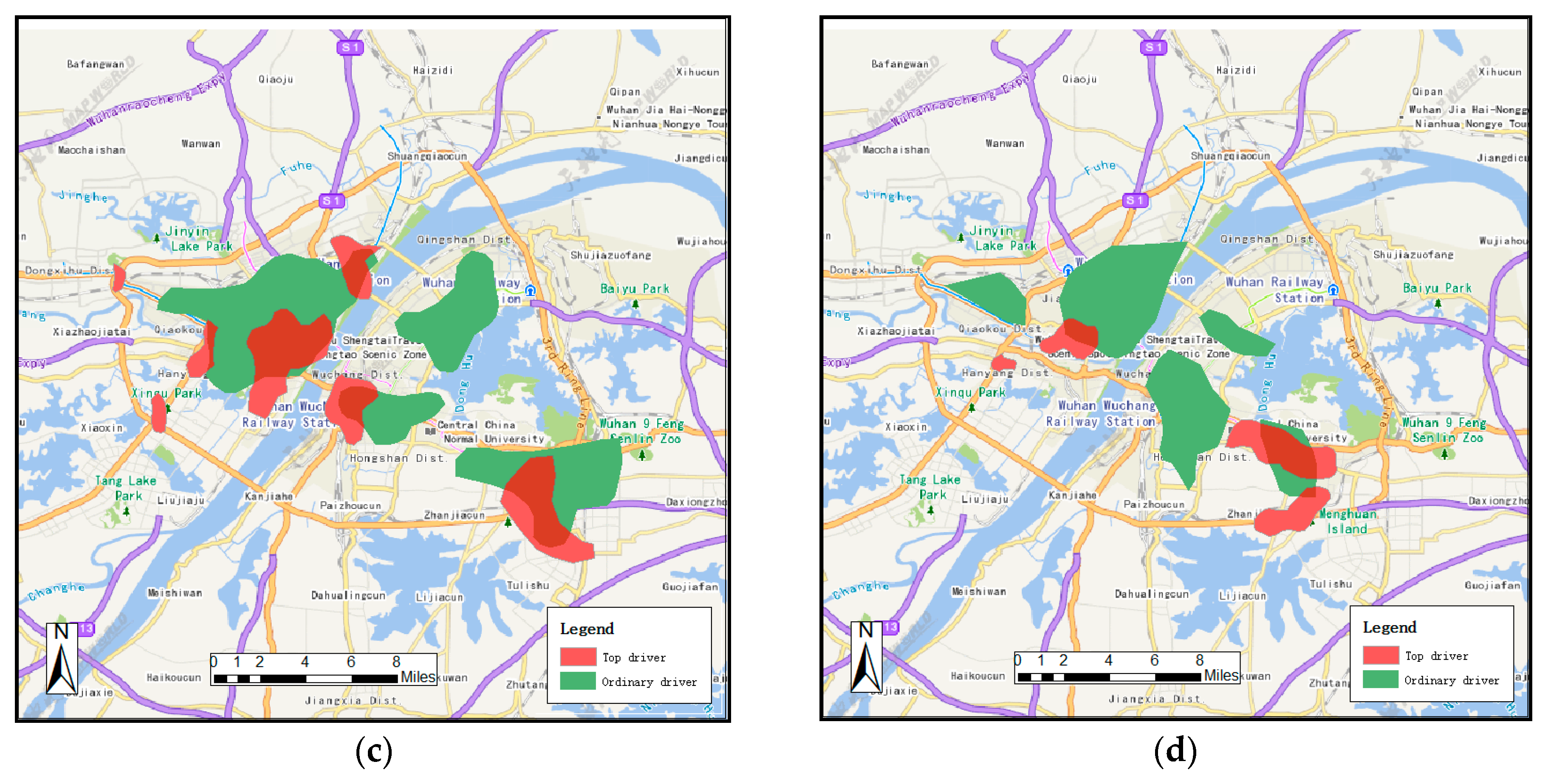
4.4. Comparison of Space-Time Distribution between Top Drivers and Ordinary Drivers
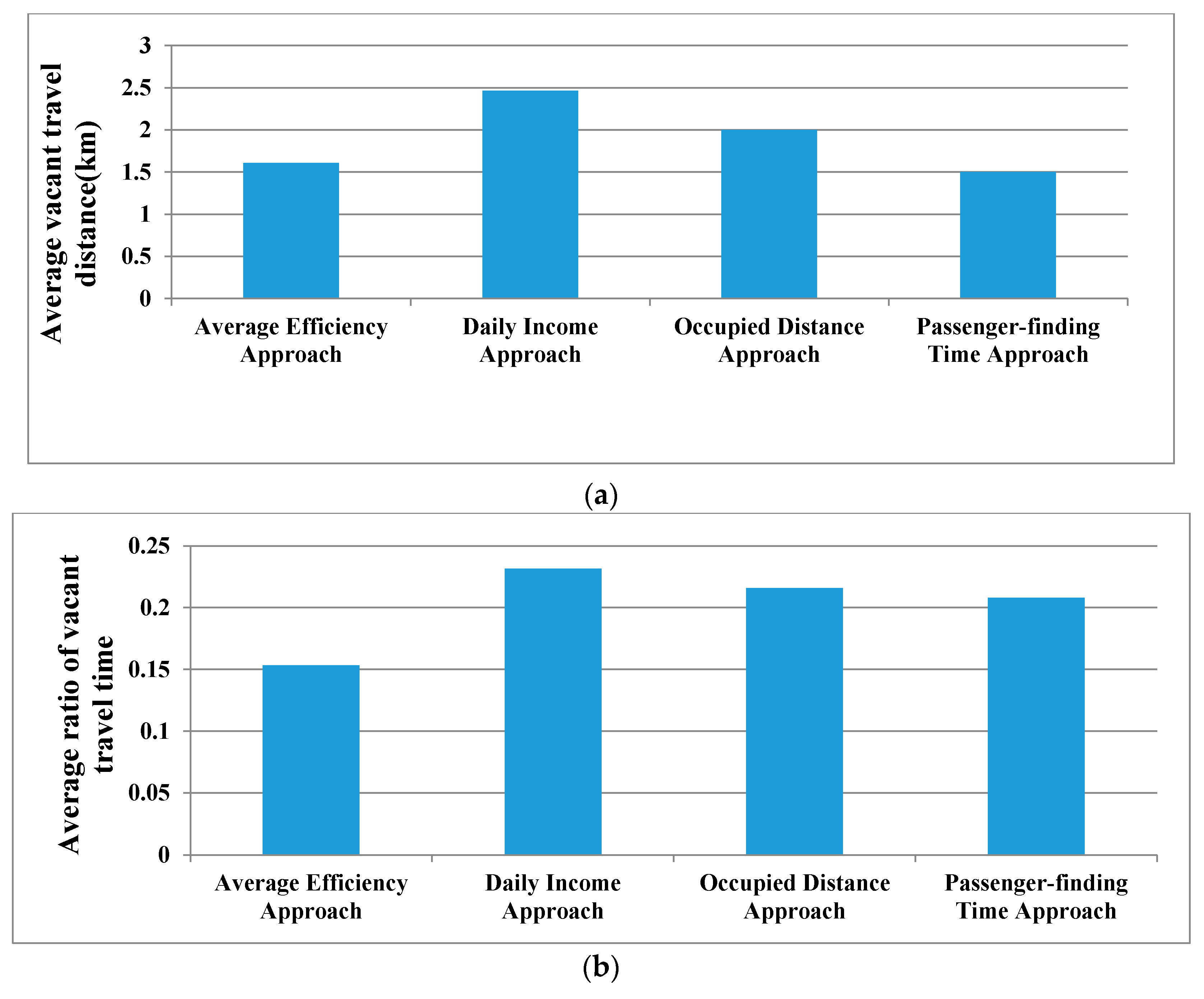
5. Comparison of Different Taxi Ranking Approaches
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Castro, P.S.; Zhang, D.; Chen, C.; Li, S.; Pan, G. From taxi GPS traces to social and community dynamics: A survey. ACM Comput. Surv. 2014, 46, 1167–1182. [Google Scholar] [CrossRef]
- Moreira-Matias, L.; Mendes-Moreira, J.; de Sousa, J.F.; Gama, J. Improving mass transit operations by using AVL-based systems: A survey. IEEE Trans. Intell. Transp. Syst. 2015, 16, 1636–1653. [Google Scholar] [CrossRef]
- Tang, L.; Kan, Z.; Zhang, X.; Sun, F.; Yang, X.; Li, Q. A network kernel density estimation for linear features in space–time analysis of big trace data. Int. J. Geogr. Inf. Sci. 2016, 30, 1–21. [Google Scholar] [CrossRef]
- Tang, L.; Kan, Z.; Zhang, X.; Yang, X.; Huang, F.; Li, Q. Travel time estimation at intersections based on low-frequency spatial-temporal GPS trajectory big data. Cartogr. Geogr. Inf. Sci. 2016, 43, 417–426. [Google Scholar] [CrossRef]
- Zhang, D.; Guo, B.; Yu, Z. The emergence of social and community intelligence. Computer 2011, 44, 21–28. [Google Scholar] [CrossRef]
- Ratti, C.; Frenchman, D.; Pulselli, R.M.; Williams, S. Mobile landscapes: Using location data from cell phones for urban analysis. Environ. Plan. B Plan. Des. 2006, 33, 727–748. [Google Scholar] [CrossRef]
- Zhu, H.; Zhu, Y.; Li, M.; Ni, L.M. SEER: Metropolitan-Scale traffic perception based on lossy sensory data. In Proceedings of the IEEE International Conference on Computer Communications, Joint Conference of the IEEE Computer and Communications Societies, Rio de Janeiro, Brazil, 19–25 April 2009. [Google Scholar]
- Girardin, F.; Calabrese, F.; Fiore, F.D.; Ratti, C.; Blat, J. Digital footprinting: Uncovering tourists with user-generated content. IEEE Pervasive Comput. 2008, 7, 36–43. [Google Scholar] [CrossRef]
- Li, B.; Zhang, D.; Sun, L.; Chen, C.; Li, S.; Qi, G. Hunting or waiting? Discovering passenger-finding strategies from a large-scale real-world taxi dataset. In Proceedings of the IEEE International Conference on Pervasive Computing and Communications Workshops (PERCOM Workshops), Seattle, WA, USA, 21–25 March 2011; pp. 63–68. [Google Scholar]
- Liu, L.; Andris, C.; Ratti, C. Uncovering cabdrivers’ behavior patterns from their digital traces. Comput. Environ. Urban Syst. 2010, 34, 541–548. [Google Scholar] [CrossRef]
- Liu, L.; Andris, C.; Biderman, A.; Ratti, C. Revealing taxi driver’s mobility intelligence through his trace. IEEE Pervasive Comput. 2009, 160, 1–17. [Google Scholar]
- Yuan, J.; Zheng, Y.; Xie, X.; Sun, G. Driving with knowledge from the physical world. In Proceedings of the 17th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Diego, CA, USA, 21–24 August 2011. [Google Scholar]
- Moreira-Matias, L.; Fernandes, R.; Gama, J.; Ferreira, M.; Mendes-Moreira, J.; Damas, L. An online recommendation 450 system for the taxi stand choice problem (poster). In Proceedings of the IEEE Vehicular Networking Conference (VNC), Seoul, Korea, 14–16 November 2012; pp. 173–180. [Google Scholar]
- Qian, S.; Cao, J.; Fr, L.; Le, R.; Sahel, I.; Li, M. SCRAM: A sharing considered route assignment mechanism for fair taxi route recommendations. In Proceedings of the 21th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Sydney, NSW, Australia, 10–13 August 2015. [Google Scholar]
- Li, X.; Pan, G.; Wu, Z.; Qi, G.; Li, S.; Zhang, D.; Zhang, W.; Wang, Z. Prediction of urban human mobility using large-scale taxi traces and its applications. Front. Comput. Sci. 2012, 6, 111–121. [Google Scholar]
- Li, X.; Lv, Z.; Wang, W.; Zhang, B.; Hu, J.; Yin, L.; Feng, S. WebVRGIS based traffic analysis and visualization system. Adv. Eng. Softw. 2016, 93, 1–8. [Google Scholar] [CrossRef]
- Lv, Z.; Li, X.; Zhang, B.; Wang, W.; Zhu, Y.; Hu, J.; Feng, S. Managing big city information based on WebVRGIS. IEEE Access 2016, 4, 407–415. [Google Scholar] [CrossRef]
- Lv, Z.; Li, X.; Hu, J.; Yin, L.; Zhang, B.; Feng, S. Virtual geographic environment based coach passenger flow forecasting. In Proceedings of the 2015 IEEE International Conference on Computational Intelligence and Virtual Environments for Measurement Systems and Applications (CIVEMSA), Shenzhen, China, 12–14 June 2015. [Google Scholar]
- Ge, Y.; Xiong, H.; Tuzhilin, A.; Xiao, K.; Gruteser, M.; Pazzani, M. An energy-efficient mobile recommender system. In Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 25–28 July 2010. [Google Scholar]
- Gan, J.; An, B.; Wang, H.; Sun, X.; Shi, Z. Optimal pricing for improving efficiency of taxi systems. In Proceedings of the 23th International Joint Conference on Artificial Intelligence, Beijing, China, 3–9 August 2013. [Google Scholar]
- Song, L.J.; Zhang, D.X.; Chen, J.C.; Ju, A.N.; Yin, S.U. Analysis of taxi operation characteristics with traffic control. J. Transp. Syst. Eng. Inf. Technol. 2008, 8, 127–131. [Google Scholar] [CrossRef]
- Wong, K.I.; Wong, S.C.; Bell, M.G.H.; Yang, H. Modeling the bilateral micro-searching behavior for urban taxi services using the absorbing markov chain approach. J. Adv. Transp. 2005, 39, 81–104. [Google Scholar] [CrossRef]
- Moreira-Matias, L.; Gama, J.; Mendes-Moreira, J. Concept neurons–handling drift issues for real-time industrial data mining. In Proceedings of the Joint European Conference on Machine Learning and Knowledge Discovery in Databases, Riva del Garda, Italy, 19–23 September 2016; pp. 96–111. [Google Scholar]
- Khiari, J.; Moreira-Matias, L.; Cerqueira, V.; Cats, O. Automated setting of Bus schedule coverage using unsupervised machine learning. In Pacific-Asia Conference on Knowledge Discovery and Data Mining; Bailey, J., Ed.; Springer: New York, NY, USA, 2016; pp. 552–564. [Google Scholar]
- Dijkstra, E.W. A note on two problems in connexion with graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef]
- Santani, D.; Balan, R.K.; Woodard, C.J. Spatio-temporal efficiency in a taxi dispatch system. In Research Collection School of Information Systems; Singapore Management University: Singapore, 2008; p. 9. [Google Scholar]
- Xie, Z.; Yan, J. Kernel density estimation of traffic accidents in a network space. Comput. Environ. Urban Syst. 2008, 32, 396–406. [Google Scholar] [CrossRef]
- Rodgers, A.R.; Kie, J.G.; Wright, D.; Beyer, H.L.; Carr, A.P. HRT: Home Range Tools for ArcGIS. Version 2.0; Ontario Ministry of Natural Resources and Forestry, Centre for Northern Forest Ecosystem Research: Thunder Bay, ON, Canada, 2015.
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise. In Proceedings of the Second International Conference Knowledge Discovery and Data Mining (KDD’96), Portland, OR, USA, 2–4 August 1996; pp. 226–231. [Google Scholar]
- Dixon, P.M. Ripley’s K Function. In Encyclopedia of Environmetrics; El-Shaarawi, A.H., Piegorsch, W.W., Eds.; John Wiley & Sons, Ltd.: New York, NY, USA, 2002; pp. 1796–1803. [Google Scholar]
- Yamada, I.; Thill, J.C. Comparison of planar and network k-functions in traffic accident analysis. J. Transp. Geogr. 2004, 12, 149–158. [Google Scholar] [CrossRef]




© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, L.; Sun, F.; Kan, Z.; Ren, C.; Cheng, L. Uncovering Distribution Patterns of High Performance Taxis from Big Trace Data. ISPRS Int. J. Geo-Inf. 2017, 6, 134. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi6050134
Tang L, Sun F, Kan Z, Ren C, Cheng L. Uncovering Distribution Patterns of High Performance Taxis from Big Trace Data. ISPRS International Journal of Geo-Information. 2017; 6(5):134. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi6050134
Chicago/Turabian StyleTang, Luliang, Fei Sun, Zihan Kan, Chang Ren, and Luling Cheng. 2017. "Uncovering Distribution Patterns of High Performance Taxis from Big Trace Data" ISPRS International Journal of Geo-Information 6, no. 5: 134. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi6050134





