Within Skyline Query Processing in Dynamic Road Networks
Abstract
:1. Introduction
- We address the issue of efficiently processing the continuous within skyline query in dynamic road networks, where three types of time-varying information, the time-varying object attribute, the time-varying edge length and the time-varying query path, are taken into account in query processing.
- Three data structures, OADM, RDSL and SOET, are designed to adequately maintain the information of objects and the road network, in order to efficiently handle the time-varying information.
- We propose the within skyline object updating algorithm, combined with the three data structures, to rapidly evaluate the new query result affected by the time-varying information.
- A comprehensive set of experiments is conducted to demonstrate the merits of the proposed approaches.
2. Related Works
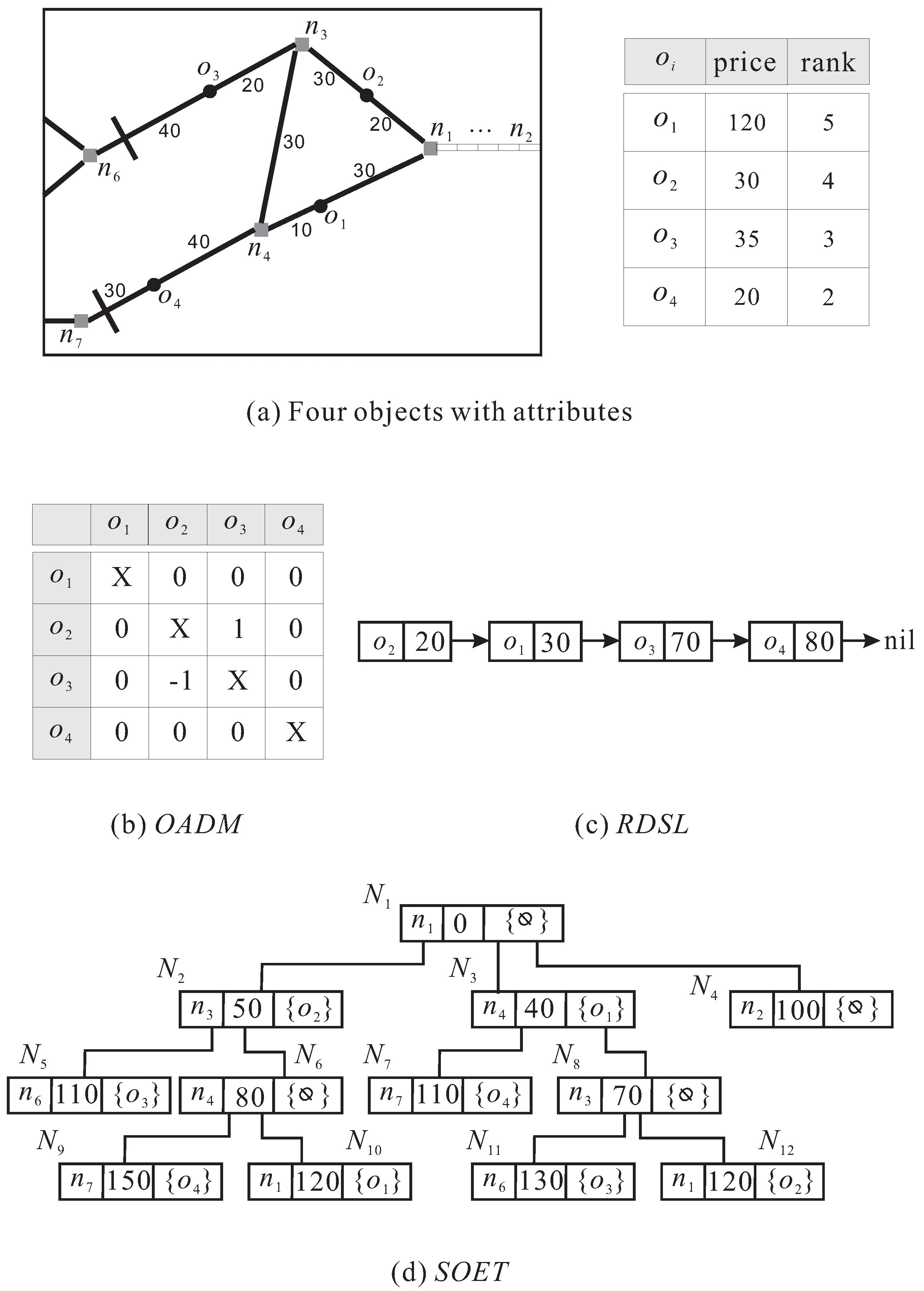
3. Data Structures
3.1. Object Attribute Dominating Matrix
- For the time-varying object attribute of an object o where o’s attribute is changed from to : if object o appears in the OADM, then the dominance relationships between o and the other objects in the OADM are re-checked based on , so as to update the values of entries in the row and the column containing o. Otherwise, the OADM need not be updated as o does not appear in the OADM.
- For the time-varying edge length of an edge e where the length of e is changed from to ∞ (or ∞ to ): in the case that e’s length is changed from to ∞, the road distances of some objects to n would increase. Conversely, changing e’s length from ∞ to would decrease some objects’ road distances. As a result, the objects whose road distances updated by the time-varying edge length are less (greater) than or equal to d need to be added into (removed from) the OADM. Then, the values of new entries in the OADM are determined using Equation (1).
- For the time-varying query path where the query path is changed to : if the edge e connecting node n belongs to , then the OADM of n is still usable because e is not affected by the time-varying query path. Otherwise, e belongs to , and thus, the OADM of n is removed as n is not on the query path.
3.2. Road Distance Sorted List
- For the time-varying object attribute of an object o: changing o’s attribute from to affects only the dominance relationship between o and the other objects, in terms of object attributes. The road distances of objects to node n remain unchanged so that the order of objects in the RDSL is not affected by the time-varying object attribute.
- For the time-varying edge length of an edge e: if the length of e is changed from to ∞ (i.e., e is temporarily closed), then the distances of some objects to n increase. For each object in the RDSL of n, once its road distance affected by e is greater than d, it needs to be removed. In the case that e’s length is changed from ∞ to , some objects would have decreasing distances to n because e is now passable. Therefore, such objects can be added into the RDSL if their decreasing distances do not exceed d. In addition to increasing or decreasing the road distance of the object, the time-varying edge length of e may also result in an adjustment in the order of objects in the RDSL.
- For the time-varying query path where the query path is changed to : similar to the process of updating the OADM of node n mentioned in Section 3.1, the RDSL of n is removed only if n is not on the new query path .
3.3. Skyline Object Expansion Tree
- For the time-varying object attribute of an object o: for the continuous within skyline query, the SOET of n remains valid regardless of the time-varying object attribute, because of the unchanged distance d.
- For the time-varying edge length of an edge e: the process of updating the SOET of node n needs to first determine which objects are affected by e and then re-compute their road distances to n. For the case that the length of edge e connecting nodes and is changed from to ∞ (i.e., e is temporarily closed), the SOET of node n is traversed from its root down to leaf level so as to check whether there are parent-child relationships between the tree nodes containing and . If no such parent-child relationship exists, then the SOET of n remains valid because edge e connecting and falls out of the distance range d. Otherwise, the subtrees rooted at the tree nodes containing and are affected by e and need to be removed from the SOET. For the case that the length of edge e connecting nodes and is changed from ∞ to , some objects’ road distances can further decrease because e now is passable. As such, we perform a grown expansion starting from and to include the objects whose decreasing distances are less than or equal to d. Then, the subtree rooted at the tree node containing (or ) is updated accordingly to contain information of such objects. Here, we explain the two cases using a concrete example, continuing the previous example in Figure 2. Assume that the edge connecting nodes and is temporarily closed (corresponding to the first case), as shown in Figure 3a. Having traversed the SOET of node , we know that both the tree nodes and ( and ) contain node (). As there is a parent-child relationship between and ( and ), the subtree rooted at () is removed from the SOET (the shaded part in Figure 3a), so that the road distances of objects and are re-computed as ∞ (because is on e) and 120, respectively. As a result, objects and are removed from the OADM and the RDSL of . Going back to the example in Figure 2, assume that the edge connecting nodes and is passable, and its length is equal to 30 (corresponding to the second case), as shown in Figure 3b. Starting from the tree nodes and containing node , two new subtrees have been included into the SOET (the bold part in Figure 3b) because their updated distances do not exceed the distance 100.
- For the time-varying query path where the query path is changed to : if the node n is not on the new query path , then the SOET of n is removed.
4. Within Skyline Object Updating Algorithm
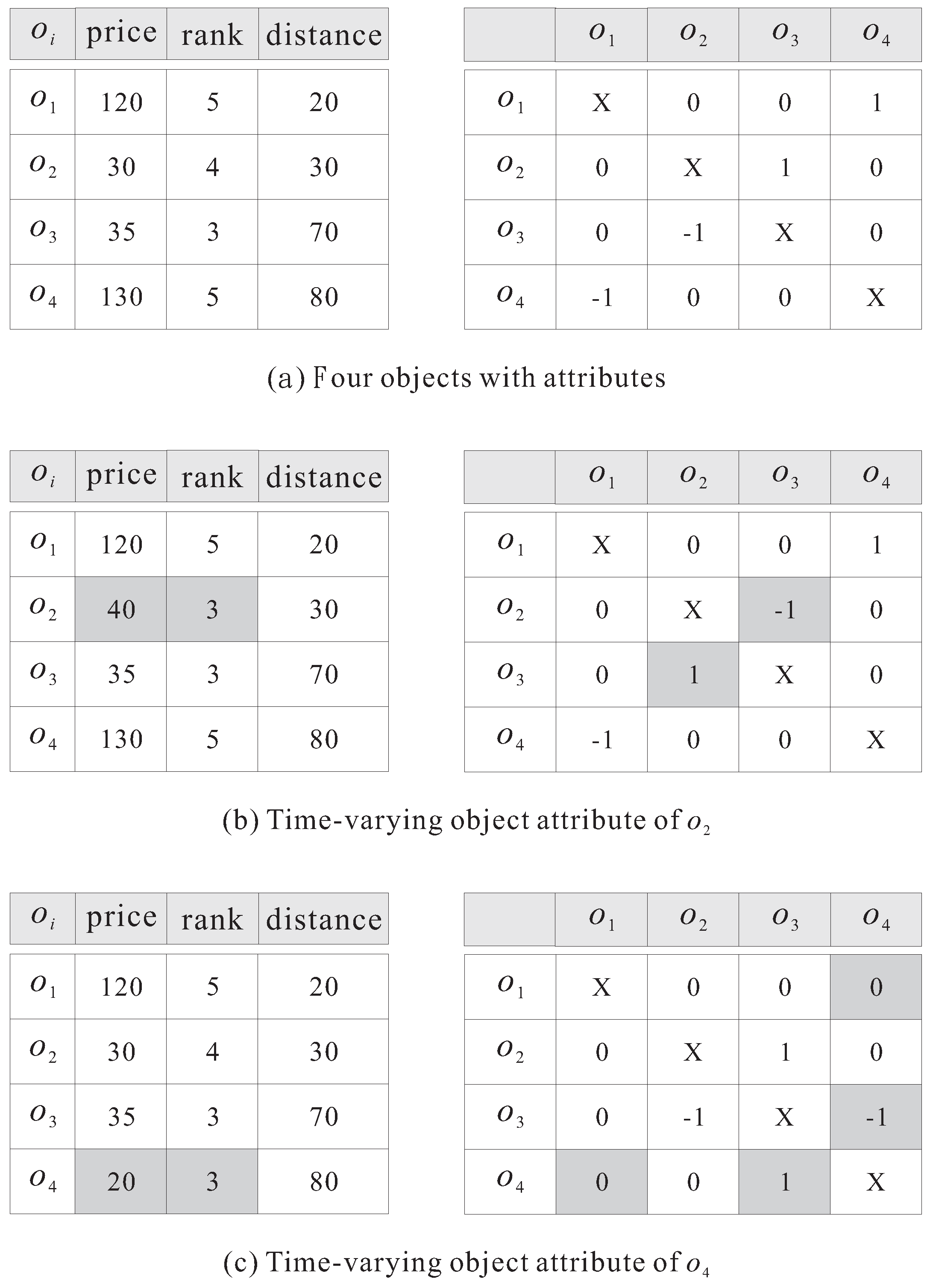
4.1. Processing of Time-Varying Object Attribute
- is changed from to zero: this means that there is no longer a dominance relationship between o and (i.e., o and cannot dominate each other). Because o and are still contained in the , changing from –0 cannot affect the and can be ignored.
- is changed from one to zero: same as the first condition, the is not affected even though is changed to zero.
- is changed from to one: o now can dominate in terms of the object attributes. Note that since o is previously dominated by in terms of the object attributes (), but still can be a WSO, o must be closer to n than (i.e., o is in front of in the RDSL). Therefore, when , needs to be removed from the .
- is changed from one to : similar to the third condition, o has to be removed from the because it is dominated by in terms of the object attributes and the “distance” attribute.
- is changed from zero to : as , o now is dominated by in terms of the object attributes. By checking the order of o and in the RDSL, o should be removed from the if it is behind (otherwise, o is still kept in the because of its better “distance” attribute).
- is changed from zero to one: same as the fifth condition, is removed from the as long as o has a better order than in the RDSL.
- is changed from to one: means that o is no longer dominated by , which will not affect the objects in the . Thus, the change of can be ignored.
- is changed from one to zero: as the dominance relationship between o and does not exist, can be promoted to a WSO (i.e., is added to the ) if (1) does not appear in the OADM or (2) appears, but is in front of in the RDSL. Otherwise, can still dominate , so that the remains unchanged.
- is changed from to one: similar to the first condition, the is not affected by changing to one.
- is changed from one to : it implies that (1) can dominate o if it has a better “distance” attribute, and (2) can be a WSO if no object dominates it. For (1), we only need to check the positions of o and in the RDSL. If o is behind , then o is removed from the . Otherwise, o is still kept in the . For (2), the process for the second condition can be applied to determine whether becomes a WSO.
- is changed from zero to : because o now is dominated by in terms of the object attributes, o should be removed from the once is better than o in the “distance” attribute. By checking the order of o and in the RDSL, o is removed from (kept in) the if it is behind (in front of) .
- is changed from zero to one: same as the third condition, the is not affected by the change of .
- is changed from to zero: means that o is no longer dominated by in terms of the object attributes, and thus, o can be a WSO if is the only object previously dominating o. In other words, if there still exists an object that leads to and is in front of o in the RDSL, then o cannot be added to the . Otherwise, o becomes a new WSO and is added to the .
- is changed from one to zero: even though the dominance relationship between o and is affected by changing from one to zero, the remains unchanged (that is, and ).
- is changed from to one: because o now can dominate in terms of the object attributes, there is a chance that o () is added to (removed from) the . Here, the process for the first condition can be applied to determine whether o is added to the or not. On the other hand, whether is removed from the can be determined by checking the order of o and in the RDSL.
- is changed from one to : similar to the second condition, the would not be affected regardless of the change of .
- is changed from zero to : means that o now is dominated by in terms of the object attribute. As (that is, an object can dominate o), the changed dominance relationship between o and cannot affect the .
- is changed from zero to one: due to , o can be used to dominate by checking whether it is in front of in the RDSL. If so, is removed from the . Otherwise, the need not be updated.
- is changed from to zero: if is the object previously dominating o (i.e., ) and there is no other object whose in the OADM and in front of o in the RDSL, then o can be added to the . Otherwise, the is not affected by changing from to zero.
- is changed from one to zero: although is no longer dominated by o, it cannot be promoted to a WSO based on the following reasons: (1) if , then the object previously dominating o is still better than in the object attributes and the “distance” attribute, even though the dominance relationship between o and has been changed, or (2) if , then there is an object dominating .
- is changed from to one: similar to the first condition, o can be a new WSO and added to the when is the only object previously dominating o in terms of the object attributes and the “distance” attribute.
- is changed from one to : same as the second condition, there must be an object dominating in terms of the object attributes and the “distance” attribute, regardless of the change of .
- is changed from zero to : even if the dominance relationship between o and is changed, an object (or ) can still dominate o (or ) so that (or ).
- is changed from zero to one: means that o now can dominate , which, however, cannot affect the because both o and are not contained in the .
4.2. Processing of Time-Varying Edge Length
- Object o does not appear in the RDSL: this means that the road distance of object o to node n is greater than the distance d. As , object o cannot appear in the RDSL. Therefore, the need not be updated.
- Object o appears in the RDSL, but : if the updated distance of object o exceeds d, then o is directly removed from the OADM and the RDSL of node n (while the remains unchanged). Otherwise (i.e., ), the order of the RDSL has to be adjusted according to . As for the OADM and the obtained by previous, they are still valid because o’s dominance relationship is not affected and .
- Object o appears in the RDSL and : in the case where the updated distance is greater than d, object o needs to be removed from the OADM, the RDSL and the of node n (meaning that the WSOs result has been changed). In addition, some object, say , that appears in the RDSL, but not in the , can be promoted to the skyline object if it is dominated only by object o (i.e., in the OADM and o is in front of in the RDSL). By looking up the row containing o in the previous OADM, we know the objects with . For each object , if there is no object such that in the OADM and is in front of in the RDSL, then can be added to as it is now a skyline object, and its distance to n is within the distance range d. In the case where the updated distance , object o is still kept in the OADM and the RDSL, but it has a higher position in the RDSL than before. In this case, object o could be removed from the because of its increasing . Conversely, the objects previously dominated by o have a chance to be added to the if they are no longer dominated. To determine whether object o is removed from the or not, the row containing o in the OADM is first checked to find each object with , and then, the updated position of o in the RDSL is compared to that of . Object o is removed from the only when is in front of o. On the other hand, to determine whether object previously dominated by object o can be added to the , each object that has in the OADM and is behind o in the RDSL is considered. Once is now in front of o (that is, is no longer dominated by o) and no object in front of and can be found, is added to the . Otherwise, is still dominated by , so that .
- Object o does not appear in the RDSL: as the updated road distance of object o to node n is less than or equal to d, object o has to be added into the OADM (where the values of entries in the row and the column containing o are computed using Equation (1)) and the RDSL (in which the order of o is determined according to its ), resulting in that (a) object o could be added into the and (b) some object could be removed from the . For (a), if there is an object with in the OADM and in front of o in the RDSL, then o is still dominated by and, thus, cannot be added to the . Otherwise, . For (b), object is removed from the only when o is better than in terms of the object attributes and the “distance” attribute. Therefore, if the entry exists in the OADM and o is in front of in the RDSL, then is removed from .
- Object o appears in the RDSL, but : as , object o has a better order in the RDSL than before. As a result, there is a chance that object behind o’s current position in the RDSL (meaning that o is better than in the “distance” attribute) is now dominated by o. Having checked the row containing o in the OADM, such an object can be removed from the if exists in the OADM (that is, o is also better than in the object attributes). On the other hand, due to the decreasing distance , all of the objects in front of o may no longer dominate o so that o can be added to the . Consider again the row containing o in the OADM. If no entry , where is in front of o in the RDSL, can be found, then o is promoted to a skyline object (i.e., ).
- Object o appears in the RDSL and : in this case, object o would still be kept in the because its road distance decreases to . Furthermore, o may dominate the other objects in the , as it now has a better “distance” attribute. For each object , once the two conditions that in the OADM and o is in front of in the RDSL hold, is removed from the .
4.3. Processing of the Time-Varying Query Path
| Algorithm 1: The within skyline object updating algorithm. |
 |
5. Performance Evaluation
5.1. Experimental Settings
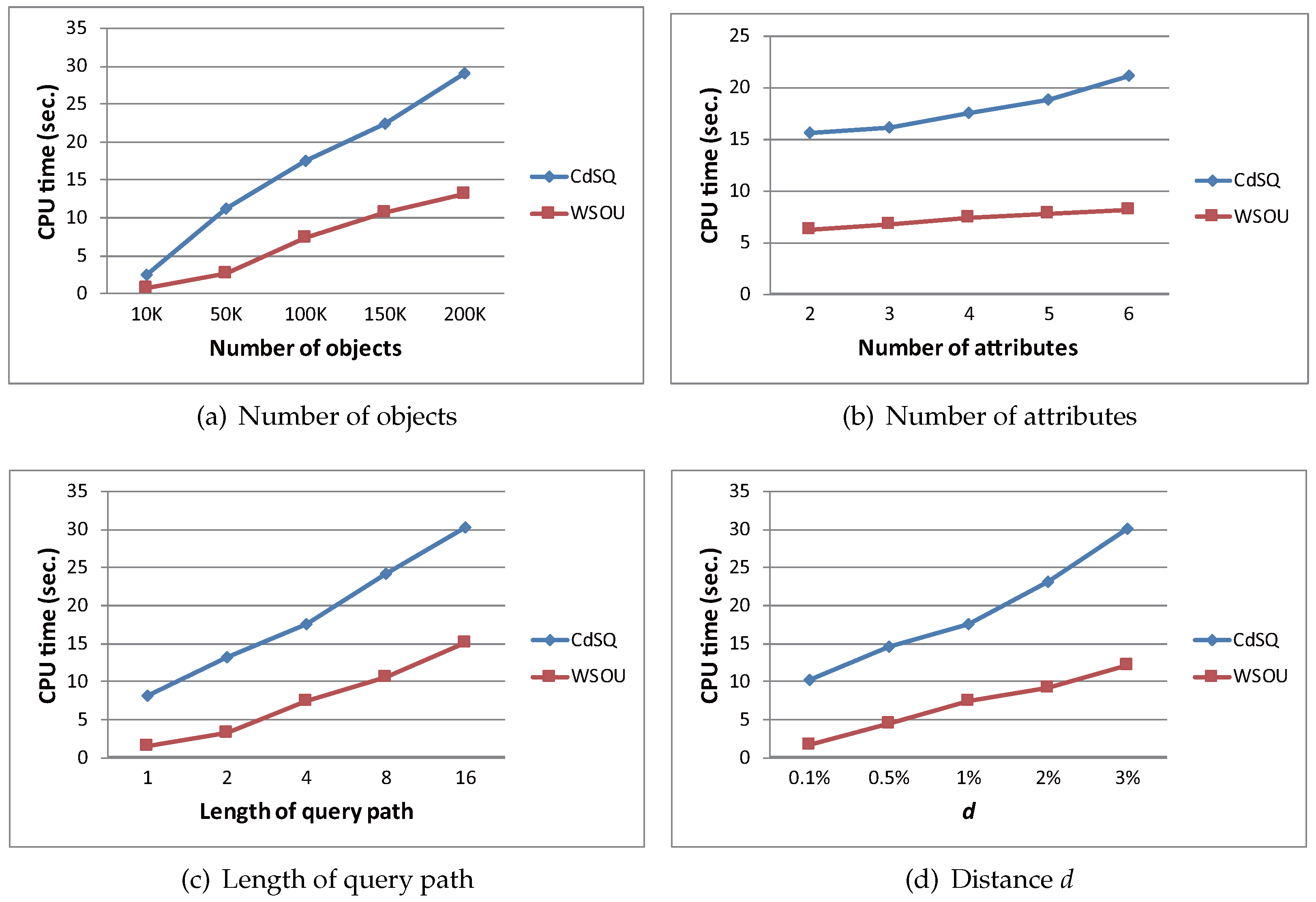
5.2. Effect of Four Important Factors
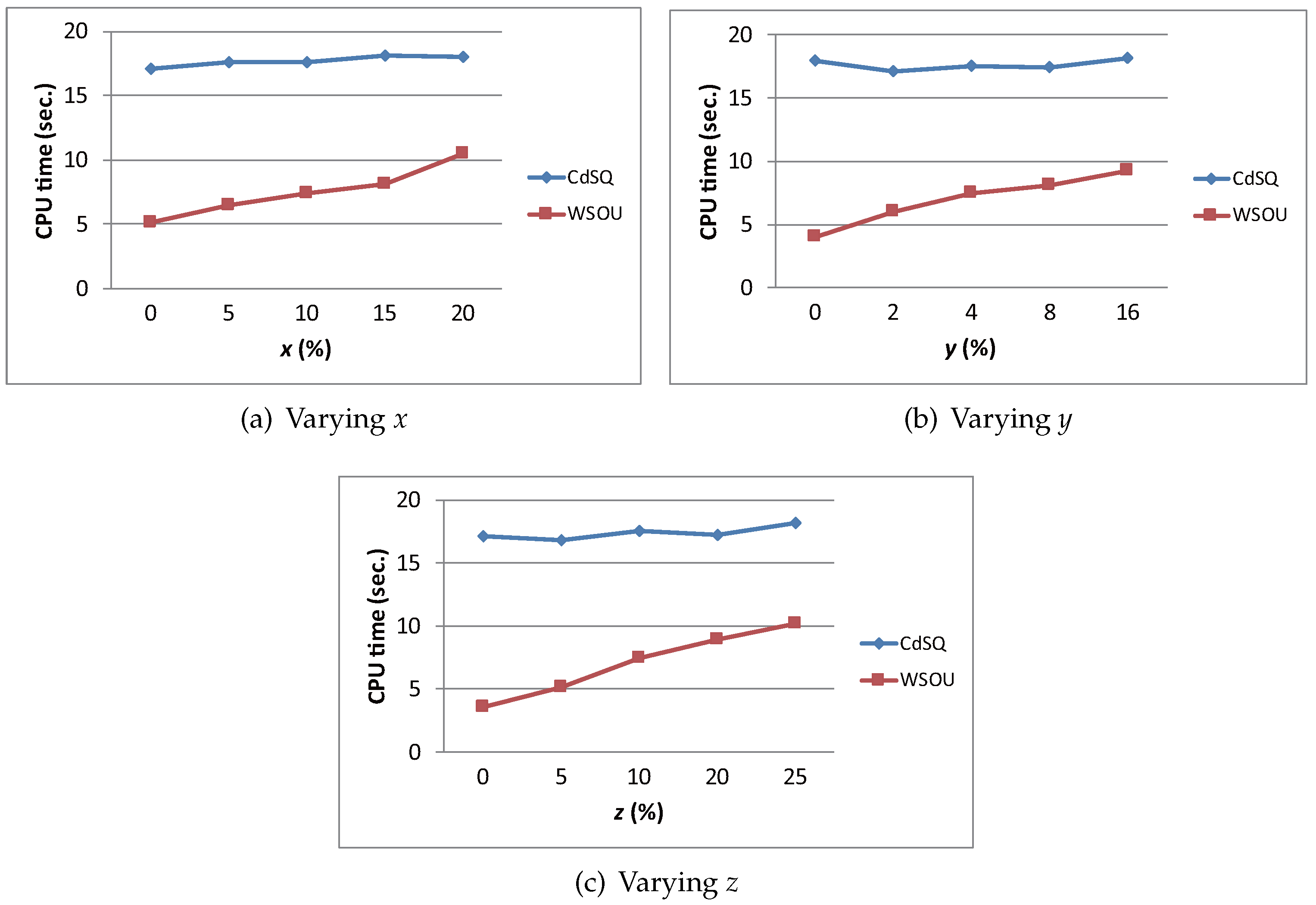
5.3. Effect of Time-Varying Information
5.4. Discussion of the Space Requirement
6. Conclusions
Acknowledgments
Conflicts of Interest
References
- Benetis, R.; Jensen, C.S.; Karciauskas, G.; Saltenis, S. Nearest Neighbor and Reverse Nearest Neighbor Queries for Moving Objects. VLDB J. 2006, 15, 229–249. [Google Scholar] [CrossRef]
- Huang, Y.K.; Kuo, W.H.; Lee, C.; Wang, T.H. Shortest Average-Distance Query on Heterogeneous Neighboring Objects. In Proceedings of the International Conference on IDEAS, Yokohoma, Japan, 13–15 July 2015; pp. 116–125. [Google Scholar]
- Mokbel, M.F.; Xiong, X.; Aref, W.G. SINA: Scalable Incremental Processing of Continuous Queries in Spatio-temporal Databases. In Proceedings of the ACM SIGMOD, Paris, France, 13–18 June 2004; pp. 623–634. [Google Scholar]
- Tao, Y.; Papadias, D. Time-parameterized queries in spatio-temporal databases. In Proceedings of the ACM SIGMOD, Madison, WI, USA, 2–6 June 2002; pp. 334–345. [Google Scholar]
- Borzsonyi, S.; Kossmann, D.; Stocker, K. The skyline operator. In Proceedings of the 17th International Conference on Data Engineering, Heidelberg, Germany, 2–6 April 2001; pp. 421–430. [Google Scholar]
- Huang, Z.; Lu, H.; Ooi, B.C.; Tung, A. Continuous Skyline Queries for Moving Objects. IEEE Trans. Knowl. Data Eng. 2006, 18, 1645–1658. [Google Scholar] [CrossRef]
- Sharifzadeh, M.; Shahabi, C. The Spatial Skyline Queries. In Proceedings of the International Conference on Very Large Data Bases, Seoul, Korea, 12–15 September 2006; pp. 751–762. [Google Scholar]
- Huang, Y.K.; Chang, C.H.; Lee, C. Continuous distance-based skyline queries in road networks. Inf. Syst. 2012, 37, 611–633. [Google Scholar] [CrossRef]
- Bentley, J.L.; Kung, H.T.; Schkolnick, M.; Thompson, C.D. On the average number of maxima in a set of vectors and applications. J. ACM 1978, 25, 536–543. [Google Scholar] [CrossRef]
- Chomicki, J.; Ciaccia, P.; Meneghetti, N. Skyline Queries, Front and Back. ACM SIGMOD Rec. 2013, 42, 6–18. [Google Scholar] [CrossRef]
- Hsueh, Y.L.; Hascoet, T. Caching Support for Skyline Query Processing with Partially Ordered Domains. IEEE Trans. Knowl. Data Eng. 2014, 26, 2649–2661. [Google Scholar] [CrossRef]
- Kung, H.T.; Luccio, F.; Preparata, F.P. On finding the maxima of a set of vectors. J. ACM 1975, 22, 469–476. [Google Scholar] [CrossRef]
- Mortensen, M.L.; Chester, S.; Assent, I.; Magnani, M. Efficient caching for constrained skyline queries. In Proceedings of the International Conference on Extending Database Technology, Brussels, Belgium, 23–27 March 2015. [Google Scholar]
- Cheema, M.A.; Lin, X.; Zhang, W.; Zhang, Y. A Safe Zone Based Approach for Monitoring Moving Skyline Queries. In Proceedings of the International Conference on Extending Database Technology, Genoa, Italy, 18–22 March 2013. [Google Scholar]
- Zheng, J.; Chen, J.; Wang, H. Efficient Geometric Pruning Strategies for Continuous Skyline Queries. ISPRS Int. J. Geo-Inf. 2017, 6, 91. [Google Scholar] [CrossRef]
- Vu, K.; Zheng, R. Efficient Algorithms for Spatial Skyline Query With Uncertainty. In Proceedings of the 21st ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems (ACM SIGSPATIAL), Orlando, FL, USA, 5–8 November 2013. [Google Scholar]
- Deng, K.; Zhou, X.; Shen, H.T. Multi-source skyline query processing in road networks. In Proceedings of the 23rd International Conference on Data Engineering, Istanbul, Turkey, 11–15 April 2007; pp. 796–805. [Google Scholar]
- Zou, L.; Chen, L.; Ozsu, M.T.; Zhao, D. Dynamic Skyline Queries in Large Graphs. In Proceedings of the International Conference on Database Systems for Advanced Applications, Tsukuba, Japan, 1–4 April 2010. [Google Scholar]
- Kriegel, H.P.; Renz, M.; Schubert, M. Route Skyline Queries: A Multi-Preference Path Planning Approach. In Proceedings of the International Conference on Data Engineering, Long Beach, CA, USA, 1–6 March 2010. [Google Scholar]
- Mouratidis, K.; Lin, Y.; Yiu, M.L. Preference Queries in Large Multi-Cost Transportation Networks. In Proceedings of the International Conference on Data Engineering, Long Beach, CA, USA, 1–6 March 2010. [Google Scholar]
- Huang, X.; Jensen, C.S. In-Route Skyline Querying for Location-based Services. In Proceedings of the International Workshop on Web and Wireless Geographical Information Systems, Goyang, Korea, 26–27 November 2004; pp. 120–135. [Google Scholar]
- Jang, S.M.; Yoo, J.S. Processing Continuous Skyline Queries in Road Networks. In Proceedings of the International Symposium on Computer Science and its Applications, Hobart, Australia, 13–15 October 2008. [Google Scholar]
- TIGER. Available online: http://www.census.gov/geo/www/tiger/ (accessed on 28 April 2017).
- Brinkhoff, T. A Framework for Generating Network-Based Moving Objects. GeoInformatica 2002, 6, 153–180. [Google Scholar] [CrossRef]
- Cheema, M.A.; Zhang, W.; Lin, X.; Zhang, Y.; Li, X. Continuous reverse k nearest neighbors queries in Euclidean space and in spatial networks. VLDB J. 2012, 21, 69–95. [Google Scholar] [CrossRef]
- Guting, R.H.; de Almeida, V.T.; Ding, Z. Modeling and querying moving objects in networks. VLDB J. 2006, 15, 165–190. [Google Scholar] [CrossRef]
- Mouratidis, K.; Yiu, M.L.; Papadias, D.; Mamoulis, N. Continuous Nearest Neighbor Monitoring in Road Networks. In Proceedings of the International Conference on VLDB, Seoul, Korea, 12–15 September 2006. [Google Scholar]
- Buonanno, A.; D’Urso, M.; Prisco, G.; Felaco, M.; Meliado, E.F.; Mattei, M.; Palmieri, F.; Ciuonzo, D. Mobile Sensor Networks based on Autonomous Platforms for Homeland Security. In Proceedings of the Tyrrhenian Workshop on Advances in Radar and Remote Sensing, Naples, Italy, 12–14 September 2012. [Google Scholar]
- Ciuonzo, D.; Buonanno, A.; D’Urso, M.; Palmieri, F.A. Distributed Classification of Multiple Moving Targets with Binary Wireless Sensor Networks. In Proceedings of the International Conference on Information Fusion, Chicago, IL, USA, 5–8 July 2011. [Google Scholar]
- Tsiligkaridis, T.; Sadler, B.M.; Hero, A.O. On Decentralized Estimation with Active Queries. IEEE Trans. Signal Process. 2015, 63, 2610–2622. [Google Scholar] [CrossRef]



| Notation | Description |
|---|---|
| a set of data objects | |
| a path along which the query object moves | |
| d | a user-defined distance |
| WSOs | the within skyline objects |
| Time-varying object attribute | o changes its attribute from to |
| Time-varying edge length | e’s length is changed from to ∞ or from ∞ to |
| Time-varying query path | is changed to |
| Parameter | Default | Range |
|---|---|---|
| Number of objects | 100 (K) | 10, 50, 100, 150, 200 (K) |
| Number of attributes | 4 | 2, 3, 4, 5, 6 |
| Length of path length | 4 | 1, 2, 4, 8, 16 |
| Distance d | 0.1, 0.5, 1, 2, 3 | |
| Time-varying object attribute x | 0, 5, 10, 15, 20 | |
| Time-varying edge length y | 0, 2, 4, 8, 16 | |
| Time-varying query path z | 0, 5, 10, 20, 25 |
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.-K. Within Skyline Query Processing in Dynamic Road Networks. ISPRS Int. J. Geo-Inf. 2017, 6, 137. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi6050137
Huang Y-K. Within Skyline Query Processing in Dynamic Road Networks. ISPRS International Journal of Geo-Information. 2017; 6(5):137. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi6050137
Chicago/Turabian StyleHuang, Yuan-Ko. 2017. "Within Skyline Query Processing in Dynamic Road Networks" ISPRS International Journal of Geo-Information 6, no. 5: 137. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi6050137






