Topographic Spatial Variation Analysis of Loess Shoulder Lines in the Loess Plateau of China Based on MF-DFA
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Topographical Data
2.3. Methods
2.3.1. EEMD
2.3.2. MF-DFA
2.3.3. DCCA
3. Results
3.1. Multi-Fractal Analysis of Loess Shoulder Line
3.2. Spatial Variation of Loess Shoulder Line
3.3. Scale Effect of Loess Shoulder-Line Topographic Variation
4. Discussion
4.1. Influence Factors of Loess Shoulder-Line
4.2. Correlation Analysis with Other Geographical Agents
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Tang, G.; Li, F.; Liu, X.; Long, Y.; Yang, X. Research on the slope spectrum of the Loess Plateau. Sci. China Ser. E Technol. Sci. 2008, 51, 175–185. [Google Scholar] [CrossRef]
- Liu, D.; Ding, Z.; Guo, Z. Loess, Environment, and Global Change; Science Press: Beijing, China, 1991. [Google Scholar]
- Ding, Z.; Sun, J.; Liu, T.; Zhu, R.; Yang, S.; Guo, B. Wind-blown origin of the Pliocene red clay formation in the central Loess Plateau, China. Earth Planet. Sci. Lett. 1998, 161, 135–143. [Google Scholar] [CrossRef]
- Guo, Z.; Ruddiman, W.F.; Hao, Q.; Wu, H.; Qiao, Y.; Zhu, R.X.; Peng, S.; Wei, J.; Yuan, B.; Liu, T. Onset of Asian desertification by 22 Myr ago inferred from loess deposits in China. Nature 2002, 416, 159–163. [Google Scholar] [CrossRef] [PubMed]
- Moore, I.D.; Gessler, P.; Nielsen, G.; Peterson, G. Soil attribute prediction using terrain analysis. Soil Sci. Soc. Am. J. 1993, 57, 443–452. [Google Scholar] [CrossRef]
- Quine, T.A.; Govers, G.; Walling, D.E.; Zhang, X.; Desmet, P.J.; Zhang, Y.; Vandaele, K. Erosion processes and landform evolution on agricultural land—New perspectives from caesium—137 measurements and topographic—Based erosion modelling. Earth Surf. Process. Landf. 1997, 22, 799–816. [Google Scholar] [CrossRef]
- Zhou, Y.; Tang, G.; Yang, X.; Xiao, C.; Zhang, Y.; Luo, M. Positive and negative terrains on northern Shaanxi Loess Plateau. J. Geogr. Sci. 2010, 20, 64–76. [Google Scholar] [CrossRef]
- Wu, Y.; Cheng, H. Monitoring of gully erosion on the Loess Plateau of China using a global positioning system. Catena 2005, 63, 154–166. [Google Scholar] [CrossRef]
- Hessel, R.; van Asch, T. Modelling gully erosion for a small catchment on the Chinese Loess Plateau. Catena 2003, 54, 131–146. [Google Scholar] [CrossRef]
- Zhu, T. Gully and tunnel erosion in the hilly Loess Plateau region, China. Geomorphology 2012, 153, 144–155. [Google Scholar] [CrossRef]
- Xiubin, H.; Tang, K.; Zhang, X. Soil erosion dynamics on the Chinese Loess Plateau in the last 10,000 years. Mt. Res. Dev. 2004, 24, 342–347. [Google Scholar] [CrossRef]
- Fu, B.; Zhao, W.; Chen, L.; Zhang, Q.; Lü, Y.; Gulinck, H.; Poesen, J. Assessment of soil erosion at large watershed scale using RUSLE and GIS: A case study in the Loess Plateau of China. Land Degrad. Dev. 2005, 16, 73–85. [Google Scholar] [CrossRef]
- Wu, F.; Fang, X.; Ma, Y.; An, Z.; Li, J. A 1.5 Ma sporopollen record of paleoecologic environment evolution in the central Chinese Loess Plateau. Chin. Sci. Bull. 2004, 49, 295–302. [Google Scholar] [CrossRef]
- Jahn, B.-M.; Gallet, S.; Han, J. Geochemistry of the Xining, Xifeng and Jixian sections, Loess Plateau of China: Eolian dust provenance and paleosol evolution during the last 140 ka. Chem. Geol. 2001, 178, 71–94. [Google Scholar] [CrossRef]
- Goulden, T.; Hopkinson, C.; Jamieson, R.; Sterling, S. Sensitivity of DEM, slope, aspect and watershed attributes to LiDAR measurement uncertainty. Remote Sens. Environ. 2016, 179, 23–35. [Google Scholar] [CrossRef]
- Bolstad, P.V.; Stowe, T. An evaluation of DEM accuracy: Elevation, slope, and aspect. Photogramm. Eng. Remote Sens. 1994, 60, 1327–1332. [Google Scholar]
- Xiong, L.-Y.; Tang, G.-A.; Zhu, A.-X.; Li, J.-L.; Duan, J.-Z.; Qian, Y.-Q. Landform-derived placement of electrical resistivity prospecting for paleotopography reconstruction in the loess landforms of China. J. Appl. Geophys. 2016, 131, 1–13. [Google Scholar] [CrossRef]
- Bi, L.; He, H.; Wei, Z.; Shi, F. Fractal properties of landforms in the Ordos Block and surrounding areas, China. Geomorphology 2012, 175, 151–162. [Google Scholar] [CrossRef]
- Cheng, W.; Zhou, C.; Li, B.; Shen, Y.; Zhang, B. Structure and contents of layered classification system of digital geomorphology for China. J. Geogr. Sci. 2011, 21, 771–790. [Google Scholar] [CrossRef]
- Xiong, L.Y.; Tang, G.A.; Strobl, J.; Zhu, A. Paleotopographic controls on loess deposition in the Loess Plateau of China. Earth Surf. Process. Landf. 2016, 41, 1155–1168. [Google Scholar] [CrossRef]
- Bergonse, R.; Reis, E. Reconstructing pre-erosion topography using spatial interpolation techniques: A validation-based approach. J. Geogr. Sci. 2015, 25, 196–210. [Google Scholar] [CrossRef]
- Zhu, H.; Tang, G.; Qian, K.; Liu, H. Extraction and analysis of gully head of Loess Plateau in China based on digital elevation model. Chin. Geogr. Sci. 2014, 24, 328–338. [Google Scholar] [CrossRef]
- Tian, J.; Tang, G.-A.; Zhou, Y. Points Group of Topographical Feature Based On SOFM. In Proceedings of the 2012 2nd International Conference on Remote Sensing, Environment and Transportation Engineering (RSETE), Nanjing, China, 1–3 June 2012; pp. 1–4. [Google Scholar]
- Li, J.; Tang, G.-A.; Zhang, T.; Xiao, C.-C. Conflux threshold of extracting stream networks from DEMs in north Shaanxi province of Loess Plateau. Bull. Soil Water Conserv. 2007, 2, 75–78. [Google Scholar]
- Song, X.D.; Tang, G.A.; Li, F.Y.; Jiang, L.; Zhou, Y.; Qian, K.J. Extraction of loess shoulder-line based on the parallel GVF snake model in the loess hilly area of China. Comput. Geosci. 2013, 52, 11–20. [Google Scholar] [CrossRef]
- Yan, S.-J.; Tang, G.A.; Li, F.-Y.; Zhang, L. Snake model for the extraction of loess shoulder-line from DEMs. J. Mt. Sci. 2014, 11, 1552–1559. [Google Scholar] [CrossRef]
- Bai, R.; Li, T.; Huang, Y.; Li, J.; Wang, G. An efficient and comprehensive method for drainage network extraction from DEM with billions of pixels using a size-balanced binary search tree. Geomorphology 2015, 238, 56–67. [Google Scholar] [CrossRef]
- Chen, Y.-G.; Yang, C.-J.; Chen, X.-Y.; Ma, T.-W.; Wang, L.; Du, J.-Y. A new method of tree structure for analysing nested watershed shape. Geomorphology 2016, 265, 98–106. [Google Scholar] [CrossRef]
- Li, T.; Wang, G.; Chen, J. A modified binary tree codification of drainage networks to support complex hydrological models. Comput. Geosci. 2010, 36, 1427–1435. [Google Scholar] [CrossRef]
- Liu, K.; Ding, H.; Tang, G.; Na, J.; Huang, X.; Xue, Z.; Yang, X.; Li, F. Detection of catchment-scale gully-affected areas using unmanned aerial vehicle (UAV) on the Chinese Loess Plateau. ISPRS Int. J. Geo-Inf. 2016, 5, 238. [Google Scholar] [CrossRef]
- Li, F.; Tang, G.; Wang, C.; Cui, L.; Zhu, R. Slope spectrum variation in a simulated loess watershed. Front. Earth Sci. 2016, 10, 328–339. [Google Scholar] [CrossRef]
- Zhu, S.; Tang, G.A.; Li, F.; Xiong, L. Spatial variation of hypsometric integral in the Loess Plateau based on DEM. Acta Geogr. Sin. 2013, 7, 921–932. [Google Scholar]
- Qian, Y.; Xiong, L.; Li, J.; Tang, G. Landform planation index extracted from DEMs: A case study in Ordos platform of China. Chin. Geogr. Sci. 2016, 26, 314–324. [Google Scholar] [CrossRef]
- Jiang, S.; Tang, G.; Liu, K. A new extraction method of loess shoulder-line based on marr-hildreth operator and terrain mask. PLoS ONE 2015, 10, e0123804. [Google Scholar] [CrossRef] [PubMed]
- Jiang, L.; Tang, G.; Liu, X.; Song, X.; Yang, J.; Liu, K. Parallel contributing area calculation with granularity control on massive grid terrain datasets. Comput. Geosci. 2013, 60, 70–80. [Google Scholar] [CrossRef]
- Liu, K.; Tang, G.; Jiang, L.; Zhu, A.-X.; Yang, J.; Song, X. Regional-scale calculation of the LS factor using parallel processing. Comput. Geosci. 2015, 78, 110–122. [Google Scholar] [CrossRef]
- Gagnon, J.-S.; Lovejoy, S.; Schertzer, D. Multifractal earth topography. Nonlinear Process. Geophys. 2006, 13, 541–570. [Google Scholar] [CrossRef]
- Ramisch, A.; Bebermeier, W.; Hartmann, K.; Schütt, B.; Alexanian, N. Fractals in topography: Application to geoarchaeological studies in the surroundings of the necropolis of Dahshur, Egypt. Q. Int. 2012, 266, 34–46. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. How long is the coast of Britain. Science 1967, 156, 636–638. [Google Scholar] [CrossRef] [PubMed]
- Xu, T.; Moore, I.D.; Gallant, J.C. Fractals, fractal dimensions and landscapes—A review. Geomorphology 1993, 8, 245–262. [Google Scholar] [CrossRef]
- Chase, C.G. Fluvial landsculpting and the fractal dimension of topography. Geomorphology 1992, 5, 39–57. [Google Scholar] [CrossRef]
- Kantelhardt, J.W.; Zschiegner, S.A.; Koscielny-Bunde, E.; Havlin, S.; Bunde, A.; Stanley, H.E. Multi-fractal detrended fluctuation analysis of nonstationary time series. Phys. A Stat. Mech. Its Appl. 2002, 316, 87–114. [Google Scholar] [CrossRef]
- Lee, H.; Chang, W. Multi-fractal regime detecting method for financial time series. Chaos Solitons Fractals 2015, 70, 117–129. [Google Scholar] [CrossRef]
- Stošić, D.; Stošić, T.; Stanley, H.E. Multi-fractal properties of price change and volume change of stock market indices. Phys. A Stat. Mech. Its Appl. 2015, 428, 46–51. [Google Scholar] [CrossRef]
- Dewandaru, G.; Masih, R.; Bacha, O.I.; Masih, A.M.M. Developing trading strategies based on fractal finance: An application of MF-DFA in the context of Islamic equities. Phys. A Stat. Mech. Its Appl. 2015, 438, 223–235. [Google Scholar] [CrossRef]
- Chamoli, A.; Yadav, R. Multi-fractality in seismic sequences of NW Himalaya. Nat. Hazards 2015, 77, 19–32. [Google Scholar] [CrossRef]
- Michas, G.; Sammonds, P.; Vallianatos, F. Dynamic multi-fractality in earthquake time series: Insights from the corinth rift, Greece. Pure Appl. Geophys. 2015, 172, 1909–1921. [Google Scholar] [CrossRef]
- Telesca, L.; Matcharashvili, T.; Chelidze, T.; Zhukova, N.; Javakhishvili, Z. Investigating the dynamical features of the time distribution of the reservoir-induced seismicity in Enguri area (Georgia). Nat. Hazards 2015, 77, 117–125. [Google Scholar] [CrossRef]
- Wan, L.; Zhu, Y.; Deng, X. Multi-fractal characteristics of gold grades series in the Dayingezhuang Deposit, Jiaodong Gold Province, China. Earth Sci. Inf. 2015, 8, 843–851. [Google Scholar] [CrossRef]
- Liu, D.; Luo, M.; Fu, Q.; Zhang, Y.; Imran, K.M.; Zhao, D.; Li, T.; Abrar, F.M. Precipitation complexity measurement using multi-fractal spectra empirical mode decomposition detrended fluctuation analysis. Water Resour. Manag. 2016, 30, 505–522. [Google Scholar] [CrossRef]
- Shao, Z.-G.; Ditlevsen, P.D. Contrasting scaling properties of interglacial and glacial climates. Nat. Commun. 2016, 7, 10951. [Google Scholar] [CrossRef] [PubMed]
- Mali, P. Multi-fractal characterization of global temperature anomalies. Theor. Appl. Climatol. 2015, 121, 641–648. [Google Scholar] [CrossRef]
- Lana, X.; Burgueño, A.; Martínez, M.; Serra, C. Monthly rain amounts at Fabra Observatory (Barcelona, NE Spain): Fractal structure, autoregressive processes and correlation with monthly western Mediterranean Oscillation index. Int. J. Climatol. 2016, 37, 1557–1577. [Google Scholar] [CrossRef]
- Lana, X.; Burgueño, A.; Martínez, M.; Serra, C. Complexity and predictability of the monthly western Mediterranean Oscillation index. Int. J. Climatol. 2016, 36, 2435–2450. [Google Scholar] [CrossRef]
- Yin, Y.; Shang, P. Multiscale multi-fractal detrended cross-correlation analysis of traffic flow. Nonlinear Dyn. 2015, 81, 1329–1347. [Google Scholar] [CrossRef]
- Xu, M.; Shang, P.; Xia, J. Traffic signals analysis using qSDiFF and qHDiFF with surrogate data. Commun. Nonlinear Sci. Numerical Simul. 2015, 28, 98–108. [Google Scholar] [CrossRef]
- Zhao, H.; He, S. Analysis of speech signals’ characteristics based on MF-DFA with moving overlapping windows. Phys. A Stat. Mech. Its Appl. 2016, 442, 343–349. [Google Scholar] [CrossRef]
- Wang, F.; Liao, D.-W.; Li, J.-W.; Liao, G.-P. Two-dimensional multi-fractal detrended fluctuation analysis for plant identification. Plant Methods 2015, 11, 1. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Ni, Z.; Ni, L.; Li, J.; Zhou, L. Asymmetric multi-fractal detrending moving average analysis in time series of PM2.5 concentration. Phys. A Stat. Mech. Its Appl. 2016, 457, 322–330. [Google Scholar] [CrossRef]
- Xue, Y.; Pan, W.; Lu, W.-Z.; He, H.-D. Multi-fractal nature of particulate matters (PMS) in Hong Kong urban air. Sci. Total Environ. 2015, 532, 744–751. [Google Scholar] [CrossRef] [PubMed]
- Bhaduri, A.; Ghosh, D. Quantitative assessment of heart rate dynamics during meditation: An ECG based study with multi-fractality and visibility graph. Front. Physiol. 2016, 7, 44. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z.; Huang, N. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. A study of the characteristics of white noise using the empirical mode decomposition method. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 2004, 460, 1597–1611. [Google Scholar] [CrossRef]
- Ihlen, E.A.F. Introduction to multifractal detrended fluctuation analysis in Matlab. Front. Psychol. 2012, 3, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Podobnik, B.; Stanley, H.E. Detrended cross-correlation analysis: A new method for analyzing two nonstationary time series. Phys. Rev. Lett. 2008, 100, 084102. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.K.; Ho, D.S.; Yu, C.C.; Wang, C.C.; Hsiao, Y.H. Simple multi-fractal cascade model for air pollutant concentration (APC) time series. Environmetrics 2003, 14, 255–269. [Google Scholar] [CrossRef]
- Lee, C.-K.; Juang, L.-C.; Wang, C.-C.; Liao, Y.-Y.; Yu, C.-C.; Liu, Y.-C.; Ho, D.-S. Scaling characteristics in ozone concentration time series (OCTS). Chemosphere 2006, 62, 934–946. [Google Scholar] [CrossRef] [PubMed]
- Fu, B. Soil erosion and its control in the Loess Plateau of China. Soil Use Manag. 1989, 5, 76–82. [Google Scholar] [CrossRef]
- Zhao, G.; Kondolf, G.M.; Mu, X.; Han, M.; He, Z.; Rubin, Z.; Wang, F.; Gao, P.; Sun, W. Sediment yield reduction associated with land use changes and check dams in a catchment of the Loess Plateau, China. Catena 2017, 148, 126–137. [Google Scholar] [CrossRef]
- Wei, Y.; He, Z.; Li, Y.; Zhao, G.; Mu, X. Sediment Yield Deduction from Check-dams Deposition in the Weathered Sandstone Watershed on the North Loess Plateau, China. Land Degrad. Dev. 2017, 28, 217–231. [Google Scholar] [CrossRef]
- Zhao, G.; Mu, X.; Han, M.; An, Z.; Gao, P.; Sun, W.; Xu, W. Sediment yield and sources in dam-controlled watersheds on the northern Loess Plateau. Catena 2017, 149, 110–119. [Google Scholar] [CrossRef]




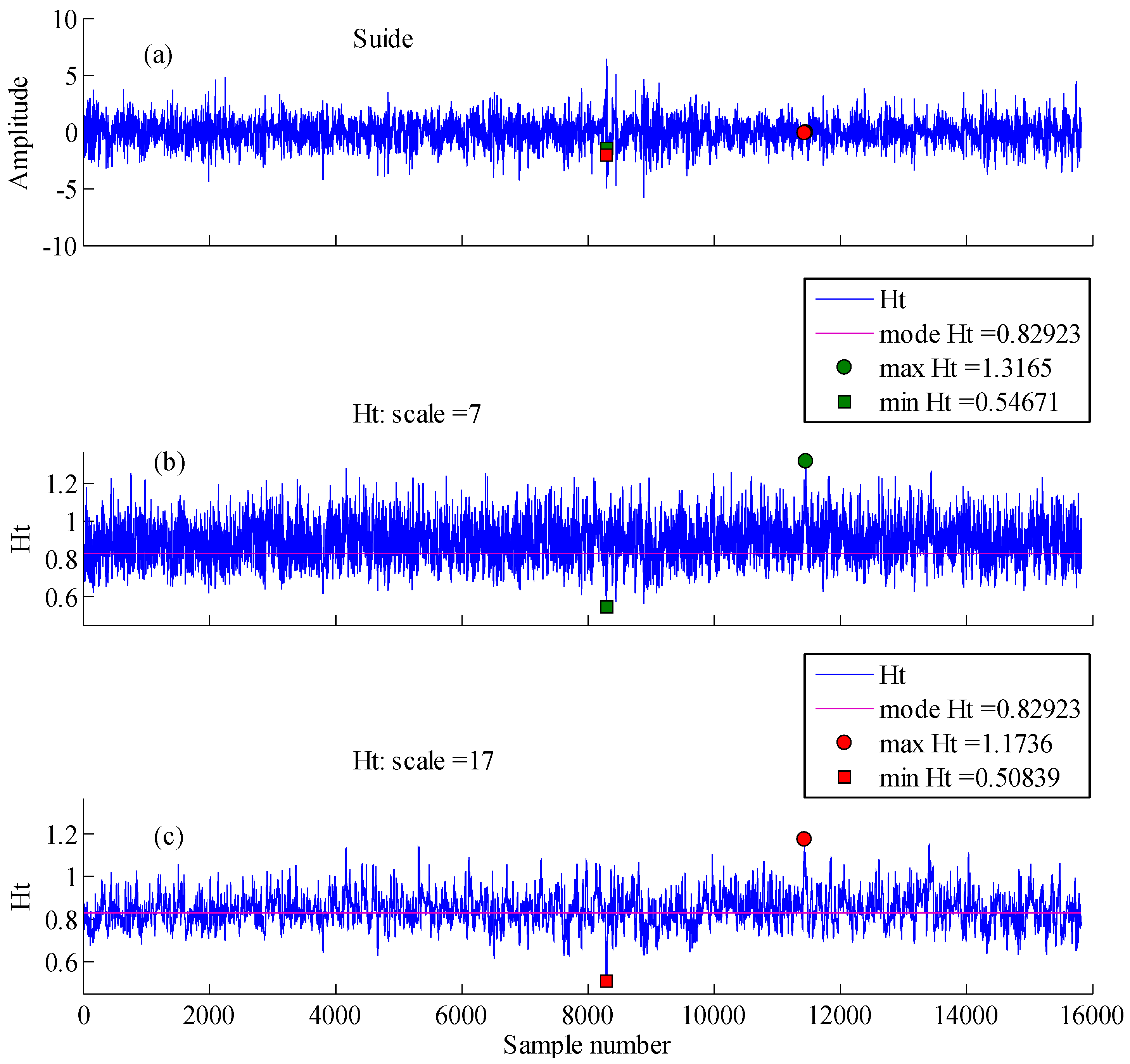



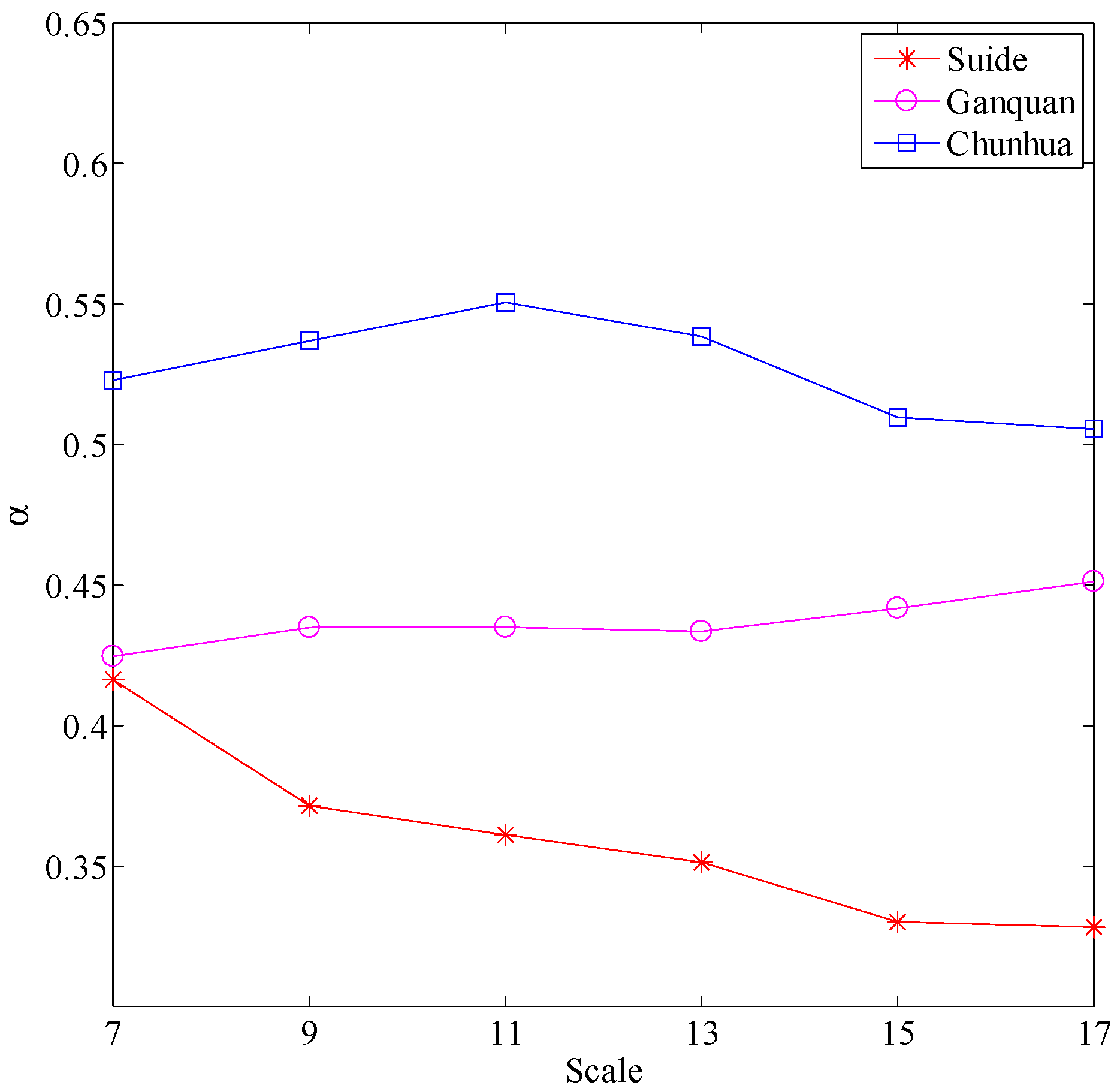
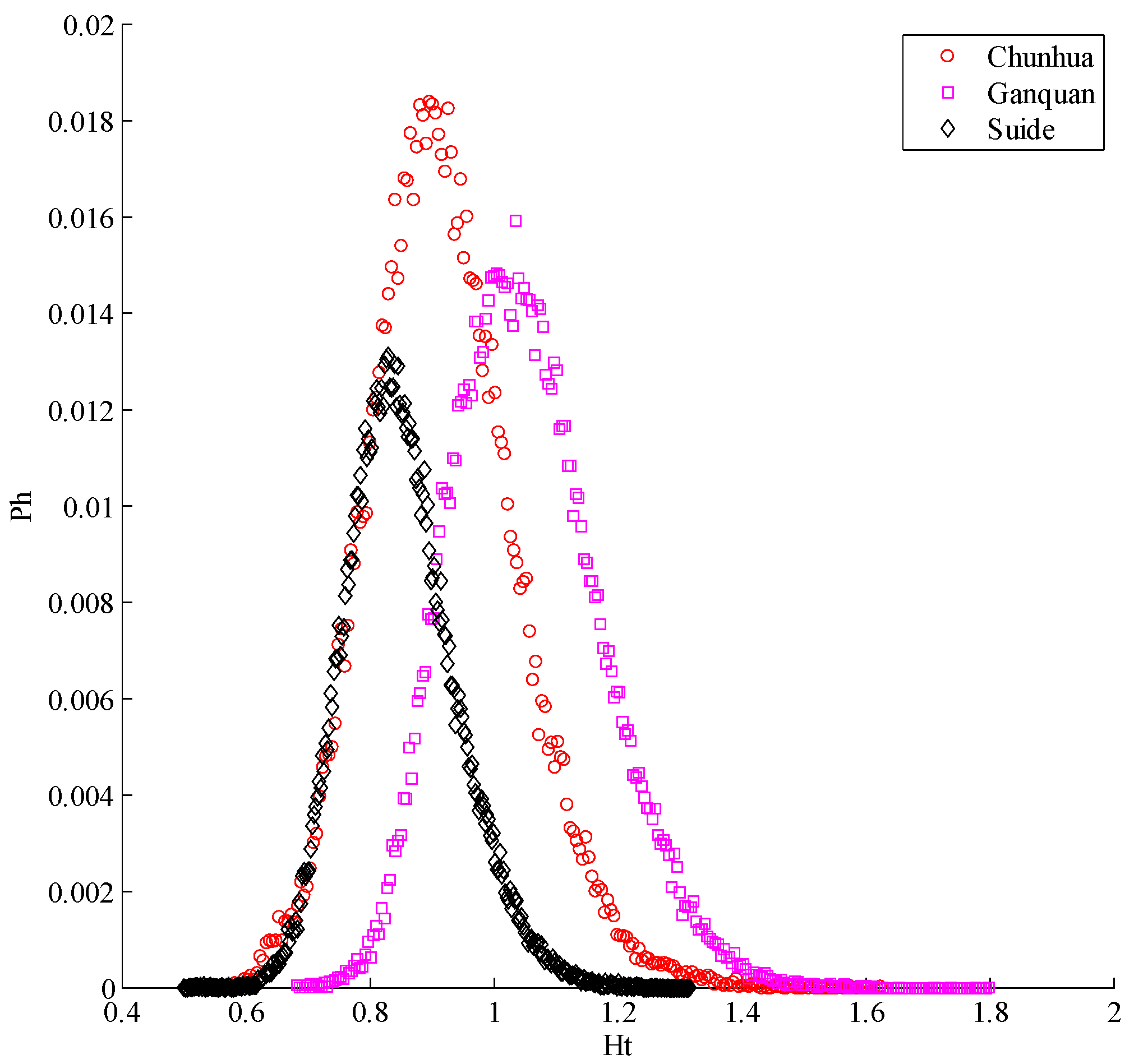
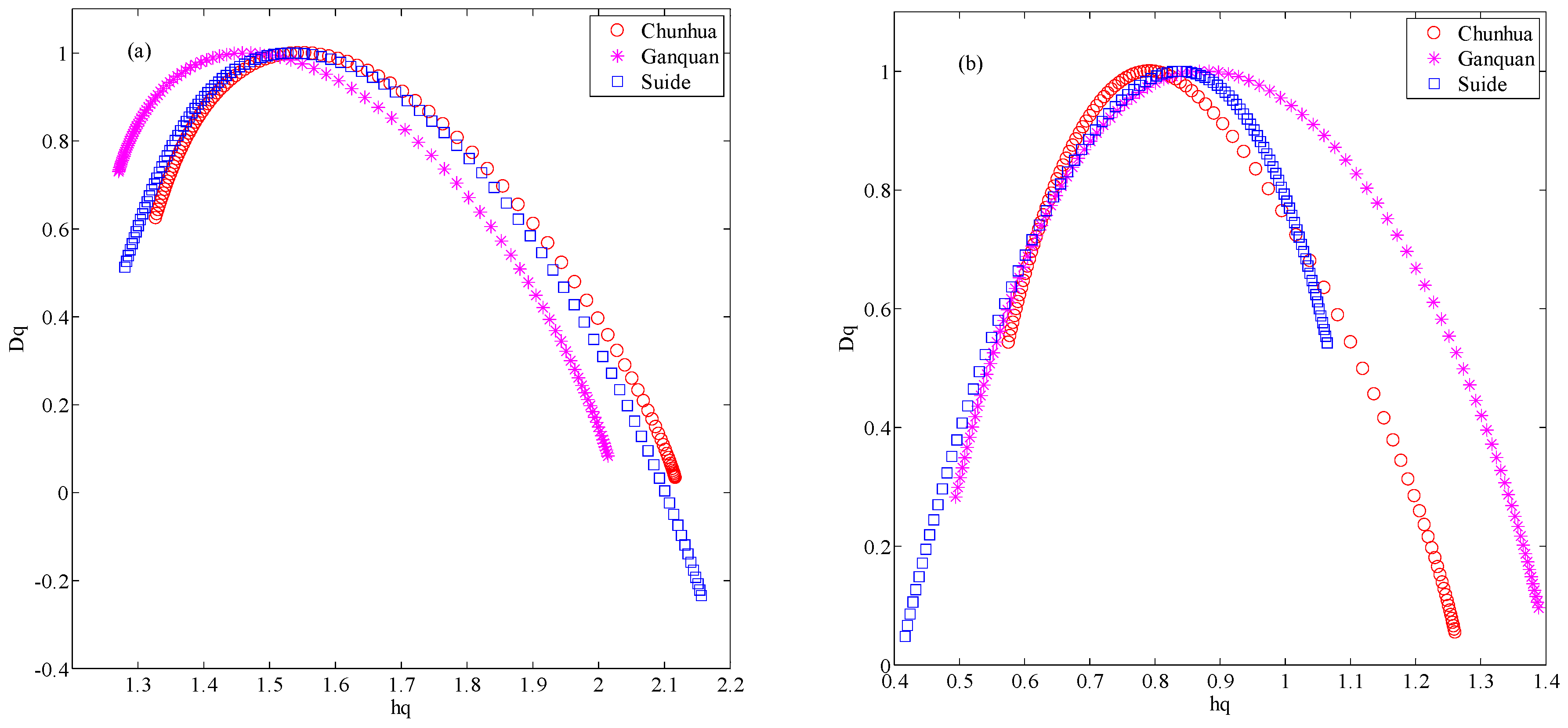
| Landform | Location | Geographic Descriptions |
|---|---|---|
| Loess hill | 110°15′00′′–110°22′30′′ E; 37°32′30′′–37°37′30′′ N | Located in Suide county, Shaanxi province with an elevation between 814 and 1188 m, an average slope inclination of 29° and 9.39 km−1 of gully destiny. The intensive soil erosion in this area characterizes the fragmented land, which have a strong self-like morphology. |
| Loess ridge | 110°18′30′′–110°22′00′′ E; 37°33′00′′–36°35′00′′ N | Located in Ganquan, Shaanxi province, with an elevation between 990 and 1404 m, an average slope inclination of 27° and 7.74 km−1 of gully density. This area is characterized by an irregular bank-shaped distribution in morphology, which is almost a loess ridge with 200–300 m in width. |
| Loess tableland | 108°22′30′′–108°30′00′′ E; 34°50′00′′–34°55′00′′ N | Located in Chunhua, Shaanxi province, with an average elevation between 768 and 1188 m, an average slope inclination of 12, and 1.79 km−1 of gully density. The gentle slopes of land surface decreased the total soil loss by erosion. |
| Sites | q | tq | hq | Dq | Hq | |
|---|---|---|---|---|---|---|
| Suide | −5 | −5.8647 | 1.0645 | 0.5423 | 0.9729 | 0.6479 |
| 0 | −1 | 0.8344 | 1 | 0.8381 | ||
| 5 | 2.0348 | 0.4166 | 0.0482 | 0.6070 | ||
| Ganquan | −5 | −7.0391 | 1.3885 | 0.0965 | 1.2078 | 0.8945 |
| 0 | −1 | 0.8683 | 1 | 0.8755 | ||
| 5 | 2.1873 | 0.4940 | 0.2829 | 0.6375 | ||
| Chunhua | −5 | −6.3584 | 1.2607 | 0.0549 | 1.0717 | 0.6852 |
| 0 | −1 | 0.7890 | 1 | 0.7918 | ||
| 5 | 2.3343 | 0.5755 | 0.5431 | 0.6669 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, J.; Na, J.; Li, J.; Tang, G.; Fang, X.; Xiong, L. Topographic Spatial Variation Analysis of Loess Shoulder Lines in the Loess Plateau of China Based on MF-DFA. ISPRS Int. J. Geo-Inf. 2017, 6, 141. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi6050141
Cao J, Na J, Li J, Tang G, Fang X, Xiong L. Topographic Spatial Variation Analysis of Loess Shoulder Lines in the Loess Plateau of China Based on MF-DFA. ISPRS International Journal of Geo-Information. 2017; 6(5):141. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi6050141
Chicago/Turabian StyleCao, Jianjun, Jiaming Na, Jilong Li, Guoan Tang, Xuan Fang, and Liyang Xiong. 2017. "Topographic Spatial Variation Analysis of Loess Shoulder Lines in the Loess Plateau of China Based on MF-DFA" ISPRS International Journal of Geo-Information 6, no. 5: 141. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi6050141








