Toward Model-Generated Household Listing in Low- and Middle-Income Countries Using Deep Learning
Abstract
:1. Introduction
Related Work
2. Data and Methods
2.1. Data
2.1.1. Building Detection Data
2.1.2. Alive and Thrive Survey Data
2.2. Methods
2.2.1. Building Detection Models
2.2.2. Model Evaluation Metrics
3. Results
3.1. Building Detection
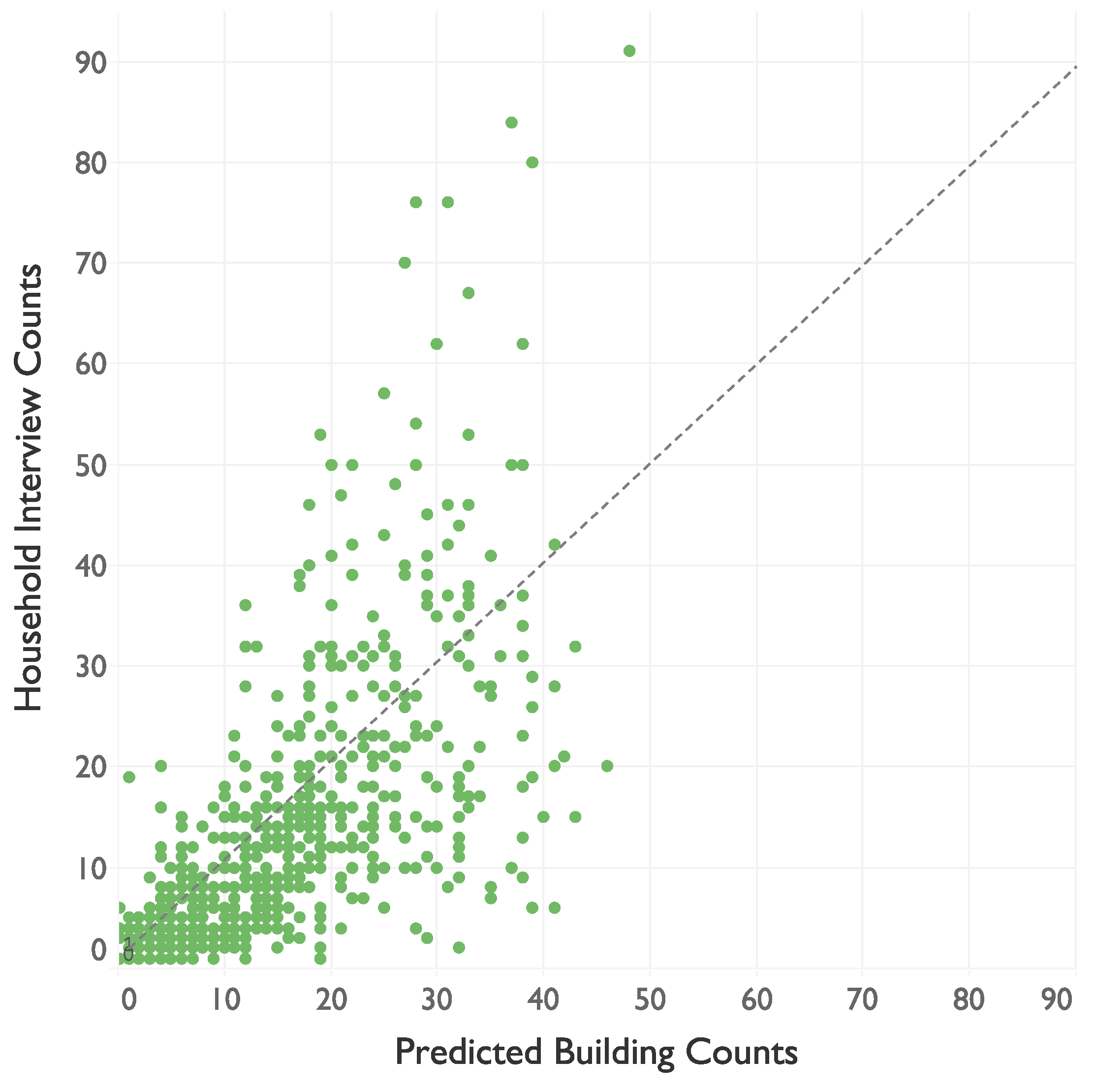
3.2. Correlation between A&T Households and Predicted Building Counts
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Predicted Building Counts versus Building Density
| Maximum Buildings in Image | Test Images | Percent of Test Images | Average Building Count | Average Predicted Building Count | Mean Absolute Error |
|---|---|---|---|---|---|
| <10 | 16 | 23% | 5.19 | 5.88 | 1.44 |
| <20 | 37 | 52% | 10.16 | 9.68 | 1.78 |
| <30 | 44 | 62% | 12.43 | 11.23 | 2.30 |
| <40 | 50 | 70% | 14.82 | 13.02 | 2.76 |
| <50 | 62 | 87% | 20.47 | 16.08 | 5.16 |
| <60 | 64 | 90% | 21.52 | 16.39 | 5.88 |
| <70 | 69 | 97% | 24.58 | 17.62 | 7.65 |
| <80 | 72 | 100% | 25.97 | 18.20 | 8.45 |
References
- About the Sustainable Development Goals. Available online: https://www.un.org/sustainabledevelopment/sustainable-development-goals/ (accessed on 12 May 2018).
- United Nations Statistical Commission (UNSD). Report of the Inter-agency and Expert Group on Sustainable Development Goal Indicators; UNSD: New York, NY, USA, 2017. [Google Scholar]
- The Economist. The 169 Commandments: The Proposed Sustainable Development Goals Would Be Worse than Useless. Available online: https://www.economist.com/leaders/2015/03/26/the-169-commandments (accessed on 12 May 2018).
- Renwick, D. Sustainable Development Goals. The Council on Foreign Relations. Available online: https://www.cfr.org/backgrounder/sustainable-development-goals (accessed on 12 May 2018).
- Organisation for Economic Co-operation and Development. Measuring Distance to the SDG Targets: An Assessment of Where OECD Countries Stand; OECD: Paris, France, 2017. [Google Scholar]
- United Nations Statistical Commission. Report of the Intersecretariat Working Group on Household Surveys; UNSD: New York, NY, USA, 2017. [Google Scholar]
- Groves, R.M. Survey Errors and Survey Costs; John Wiley and Sons: New York, NY, USA, 1989. [Google Scholar]
- Groves, R.M.; Lyberg, L. Total survey error: Past, present, and future. Public Opin. Q. 2010, 74, 849–879. [Google Scholar] [CrossRef]
- Biemer, P.P. Total survey error: Design, implementation, and evaluation. Public Opin. Q. 2010, 74, 817–848. [Google Scholar] [CrossRef]
- Alkire, S.; Samman, E. Mobilising the Household Data Required to Progress toward the SDGs; OPHI Working Paper 72; Oxford University: Oxford, UK, 2014. [Google Scholar]
- Demographic and Health Surveys Program. SDG Indicators in DHS Surveys. Available online: https://dhsprogram.com/Topics/upload/SDGs%20in%20DHS%2018May2017.pdf (accessed on 15 May 2018).
- Shannon, H.S.; Hutson, R.; Kolbe, A.; Stringer, B.; Haines, T. Choosing a survey sample when data on the population are limited: A method using Global Positioning Systems and aerial and satellite photographs. Emerg. Themes Epidemiol. 2012, 9, 5. [Google Scholar] [CrossRef] [PubMed]
- Burnham, G.; Lafta, R.; Doocy, S.; Roberts, L. Mortality after the 2003 invasion of Iraq: A cross-sectional cluster sample survey. Lancet 2006, 368, 1421–1428. [Google Scholar] [CrossRef]
- Eckman, S.; Eyerman, J.; Temple, D. Unmanned Aircraft Systems Can Improve Survey Data Collection; RTI Press: Research Triangle Park, NC, USA, 2018. [Google Scholar] [CrossRef]
- Zhu, X.X.; Tuia, D.; Mou, L.; Xia, G.S.; Zhang, L.; Xu, F.; Fraundorfer, F. Deep learning in remote sensing: A comprehensive review and list of resources. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–36. [Google Scholar] [CrossRef]
- Cheng, G.; Han, J.; Lu, X. Remote sensing image scene classification: Benchmark and state of the art. Proc. IEEE 2017, 105, 1865–1883. [Google Scholar] [CrossRef]
- Basu, S.; Ganguly, S.; Mukhopadhyay, S.; DiBiano, R.; Karki, M.; Nemani, R. Deepsat: A learning framework for satellite imagery. In Proceedings of the 23rd SIGSPATIAL International Conference on Advances in Geographic Information Systems, Seattle, WA, USA, 3–6 November 2015; p. 37. [Google Scholar]
- Castelluccio, M.; Poggi, G.; Sansone, C.; Verdoliva, L. Land use classification in remote sensing images by convolutional neural networks. arXiv, 2015; arXiv:1508.00092. [Google Scholar]
- Han, X.; Zhong, Y.; Cao, L.; Zhang, L. Pre-trained AlexNet architecture with pyramid pooling and supervision for high spatial resolution remote sensing image scene classification. Remote Sens. 2017, 9, 848. [Google Scholar] [CrossRef]
- Hu, F.; Xia, G.S.; Hu, J.; Zhang, L. Transferring deep convolutional neural networks for the scene classification of high-resolution remote sensing imagery. Remote Sens. 2015, 7, 14680–14707. [Google Scholar] [CrossRef]
- Zhong, Y.; Fei, F.; Liu, Y.; Zhao, B.; Jiao, H.; Zhang, L. SatCNN: Satellite image dataset classification using agile convolutional neural networks. Remote Sens. Lett. 2017, 8, 136–145. [Google Scholar] [CrossRef]
- Chew, R.F.; Amer, S.; Jones, K.; Unangst, J.; Cajka, J.; Allpress, J.; Bruhn, M. Residential scene classification for gridded population sampling in developing countries using deep convolutional neural networks on satellite imagery. Int. J. Health Geogr. 2018, 17, 12. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jiang, T.; Xia, G.S.; Lu, Q. Sketch-based aerial image retrieval. In Proceedings of the 2017 IEEE International Conference on Image Processing (ICIP), Beijing, China, 17–20 September 2017; pp. 3690–3694. [Google Scholar]
- Zhou, W.; Newsam, S.; Li, C.; Shao, Z. Learning low dimensional convolutional neural networks for high-resolution remote sensing image retrieval. Remote Sens. 2017, 9, 489. [Google Scholar] [CrossRef]
- Yang, H.L.; Lunga, D.; Yuan, J. Toward country scale building detection with convolutional neural network using aerial images. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 870–873. [Google Scholar]
- Dickenson, M.; Gueguen, L. Rotated Rectangles for Symbolized Building Footprint Extraction. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Salt Lake City, UT, USA, 18–22 June 2018; pp. 225–228. [Google Scholar]
- Bischke, B.; Helber, P.; Folz, J.; Borth, D.; Dengel, A. Multi-task learning for segmentation of building footprints with deep neural networks. arXiv, 2017; arXiv:1709.05932. [Google Scholar]
- Yuan, J. Automatic building extraction in aerial scenes using convolutional networks. arXiv, 2015; arXiv:1602.06564. [Google Scholar]
- Zhang, A.; Liu, X.; Gros, A.; Tiecke, T. Building Detection from Satellite Images on a Global Scale. arXiv, 2017; arXiv:1707.08952. [Google Scholar]
- Tiecke, T.G.; Liu, X.; Zhang, A.; Gros, A.; Li, N.; Yetman, G.; Kilic, T.; Murray, S.; Blankespoor, B.; Prydz, E.B. Mapping the world population one building at a time. arXiv, 2017; arXiv:1712.05839. [Google Scholar]
- Jean, N.; Burke, M.; Xie, M.; Davis, W.M.; Lobell, D.B.; Ermon, S. Combining satellite imagery and machine learning to predict poverty. Science 2016, 353, 790–794. [Google Scholar] [CrossRef] [PubMed]
- Gebru, T.; Krause, J.; Wang, Y.; Chen, D.; Deng, J.; Aiden, E.L.; Li, F.-F. Using deep learning and Google Street View to estimate the demographic makeup of neighborhoods across the United States. arXiv, 2017; arXiv:1702.06683. [Google Scholar] [CrossRef] [PubMed]
- Oshri, B.; Hu, A.; Adelson, P.; Chen, X.; Dupas, P.; Weinstein, J.; Burke, M.; Lobell, L.; Ermon, S. Infrastructure Quality Assessment in Africa using Satellite Imagery and Deep Learning. arXiv, 2018; arXiv:1806.00894. [Google Scholar]
- Eyerman, J.; Krotki, K.; Amer, S.; Gordon, R.; Evans, J.; Snyder, K.; Zajkowski, T. Drone-Assisted Sample Design for Developing Countries. In Proceedings of the FedCASIC Workshops, Washington, DC, USA, 4–5 March 2015. [Google Scholar]
- Haenssgen, M.J. Satellite-aided survey sampling and implementation in low- and middle-income contexts: A low-cost/low-tech alternative. Emerg. Themes Epidemiol. 2015, 12. [Google Scholar] [CrossRef] [PubMed]
- State Development Plan: 2014–2018. Kaduna State Government, Ministry of Economic Planning. Available online: http://www.sparc-nigeria.com/RC/files/1.1.9_Kaduna_Development_Plan_2014_2018.pdf (accessed on 2 November 2018).
- Cajka, J.; Amer, S.; Ridenhour, J.; Allpress, J. Geo-sampling in developing nations. Int. J. Soc. Res. Methodol. 2018, 21, 729–746. [Google Scholar] [CrossRef]
- Huang, J.; Rathod, V.; Sun, C.; Zhu, M.; Korattikara, A.; Fathi, A.; Fischer, I.; Wojna, Z.; Song, Y.; Guadarrama, S.; et al. Speed/accuracy trade-offs for modern convolutional object detectors. In Proceedings of the IEEE Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; Volume 4. [Google Scholar]
- Szegedy, C.; Ioffe, S.; Vanhoucke, V.; Alemi, A.A. Inception-v4, inception-resnet and the impact of residual connections on learning. In Proceedings of the Association for the Advancement of Artificial Intelligence (AAAI), San Francisco, CA, USA, 4–9 February 2017. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster r-cnn: Towards real-time object detection with region proposal networks. In Advances in Neural Information Processing Systems; The MIT Press: Cambridge, MA, USA, 2015; pp. 91–99. [Google Scholar]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the inception architecture for computer vision. arXiv, 2015; arXiv:1512.00567. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. arXiv, 2015; arXiv:1512.03385. [Google Scholar]
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.; Fu, Y.; Berg, A.C. SSD: Single shot multibox detector. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 8–16 October 2016; pp. 21–37. [Google Scholar]
- Pan, S.J.; Yang, Q.A. Survey on transfer learning. IEEE Trans. Knowl. Data Eng. 2010, 22, 1345–1359. [Google Scholar] [CrossRef]
- Lin, T.Y.; Maire, M.; Belongie, S.; Hays, J.; Perona, P.; Ramanan, D.; Dollár, C.; Zitnick, C.L. Microsoft COCO: Common Objects in Context. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; pp. 740–755. [Google Scholar]
- Liang, K.J.; Heilmann, G.; Gregory, C.; Diallo, S.O.; Carlson, D.; Spell, G.P.; Sigman, J.B.; Roe, K.; Carin, L. Automatic threat recognition of prohibited items at aviation checkpoint with X-ray imaging: A deep learning approach. In Proceedings of the Anomaly Detection and Imaging with X-rays (ADIX) III, Orlando, FL, USA, 27 April 2018. [Google Scholar]
- Arcos-García, Á.; Álvarez-García, J.A.; Soria-Morillo, L.M. Evaluation of Deep Neural Networks for traffic sign detection systems. Neurocomputing 2018, 316, 332–344. [Google Scholar] [CrossRef]
- Everingham, M.; Van Gool, L.; Williams, C.K.; Winn, J.; Zisserman, A. The PASCAL Visual Object Classes (VOC) challenge. Int. J. Comput. Vis. 2010, 88, 303–338. [Google Scholar] [CrossRef]
- Hu, X.; Weng, Q. Impervious surface area extraction from IKONOS imagery using an object-based fuzzy method. Geocarto Int. 2011, 26, 3–20. [Google Scholar] [CrossRef]
- Belgiu, M.; Tomljenovic, I.; Lampoltshammer, T.J.; Blaschke, T.; Höfle, B. Ontology-based classification of building types detected from airborne laser scanning data. Remote Sens. 2014, 6, 1347–1366. [Google Scholar] [CrossRef]
- Rodriguez, M.; Laptev, I.; Sivic, J.; Audibert, J.Y. Density-aware person detection and tracking in crowds. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Barcelona, Spain, 6–13 November 2011; pp. 2423–2430. [Google Scholar]
- Sindagi, V.A.; Patel, V.M. Generating high-quality crowd density maps using contextual pyramid CNNs. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 1879–1888. [Google Scholar]
- Cohen, J.P.; Boucher, G.; Glastonbury, C.; Lo, H.Z.; Bengio, Y. Count-ception: Counting by fully convolutional redundant counting. In Proceedings of the IEEE International Conference on Computer Vision Workshop (ICCVW), Venice, Italy, 22–29 October 2017; pp. 18–26. [Google Scholar]
- Xie, W.; Noble, J.A.; Zisserman, A. Microscopy cell counting and detection with fully convolutional regression networks. Comput. Methods Biomech. Biomed. Eng. Imaging Vis. 2018, 6, 283–292. [Google Scholar] [CrossRef]
- Dyachia, Z.S.; Permana, A.S.; Ho, C.S.; Baba, A.N.; Agboola, O.P. Implications of Present Land Use Plan on Urban Growth and Environmental Sustainability in a Sub Saharan Africa City. Int. J. Built Environ. Sustain. 2017, 4. [Google Scholar] [CrossRef]
- Bredl, S.; Storfinger, N.; Menold, N. A Literature Review of Methods to Detect Fabricated Survey Data (No. 56); Discussion Paper; Zentrum für Internationale Entwicklungs-und Umweltforschung: Gießen, Genmany, 2011. [Google Scholar]
- Murphy, J.; Baxter, R.; Eyerman, J.; Cunningham, D.; Kennet, J. A system for detecting interviewer falsification. In Proceedings of the American Association for Public Opinion Research 59th Annual Conference, Phoenix, Arizona, 20–23 May 2004; pp. 4968–4975. [Google Scholar]
- Shook-Sa, B.; Harter, R.; McMichael, J.; Ridenhour, J.; Dever, J. The CHUM: A Frame Supplementation Procedure for Address-Based Sampling; RTI Press: Research Triangle Park, NC, USA, 2016. [Google Scholar] [CrossRef]
- Yates, F.; Grundy, P.M. Selection without replacement from within strata with probability proportional to size. J. R. Stat. Soc. 1953, 15, 253–261. [Google Scholar]


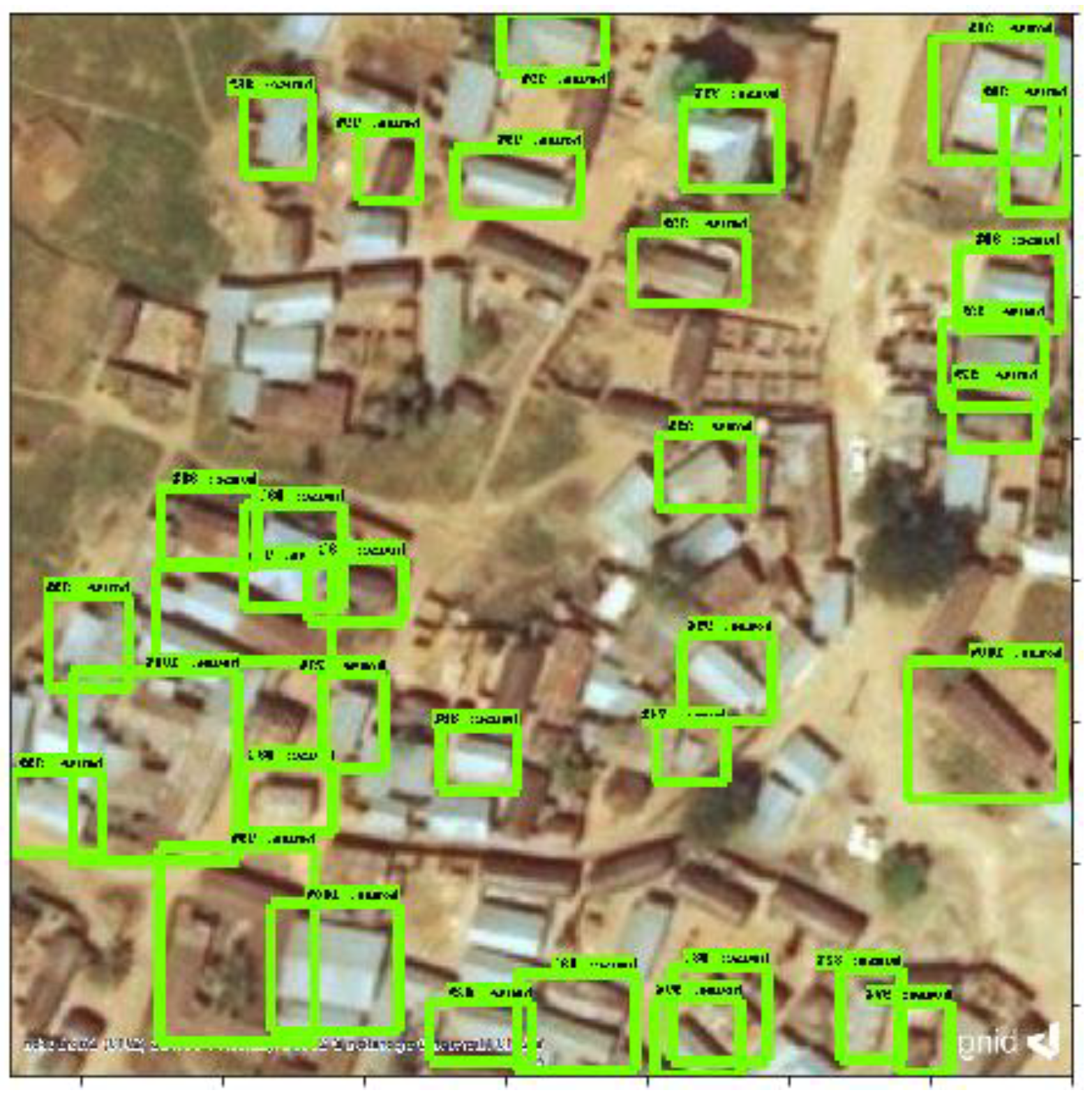


| Summary Statistic | Training | Test |
|---|---|---|
| Total images | 128 | 72 |
| Total annotated buildings | 2711 | 1844 |
| Annotated buildings per image | ||
| Mean | 22.5 | 26 |
| Min | 1 | 1 |
| Median | 18 | 18 |
| Max | 107 | 76 |
| Cut-Off | 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1 | mAP |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Precision | 1 | 0.86 | 0.86 | 0.86 | 0.85 | 0.85 | 0 | 0 | 0 | 0 | 0 | 0.48 |
| Cut-Off | 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1 | mAP |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Precision | 1 | 0.89 | 0.89 | 0.89 | 0.88 | 0.87 | 0.85 | 0.9 | 0 | 0 | 0 | 0.65 |
| Type | Correlation |
|---|---|
| Pearson | 0.702 |
| Spearman | 0.806 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chew, R.; Jones, K.; Unangst, J.; Cajka, J.; Allpress, J.; Amer, S.; Krotki, K. Toward Model-Generated Household Listing in Low- and Middle-Income Countries Using Deep Learning. ISPRS Int. J. Geo-Inf. 2018, 7, 448. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi7110448
Chew R, Jones K, Unangst J, Cajka J, Allpress J, Amer S, Krotki K. Toward Model-Generated Household Listing in Low- and Middle-Income Countries Using Deep Learning. ISPRS International Journal of Geo-Information. 2018; 7(11):448. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi7110448
Chicago/Turabian StyleChew, Robert, Kasey Jones, Jennifer Unangst, James Cajka, Justine Allpress, Safaa Amer, and Karol Krotki. 2018. "Toward Model-Generated Household Listing in Low- and Middle-Income Countries Using Deep Learning" ISPRS International Journal of Geo-Information 7, no. 11: 448. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi7110448





