1. Introduction
Urban land-use mapping is of great significance for various urban applications, such as urban planning and designing, urban-environment monitoring, and urban-land surveys [
1,
2]. Traditional methods for urban land-use mapping are based on the visual interpretation of high-resolution optical remote-sensing imagery and field surveys, which can be quite time-consuming and laborious. Therefore, it is very important to investigate the automatic classification methods for fragmented and complex urban land-use types.
With the development of remote-sensing technology, some researchers started to use multispectral optical imagery and machine-learning methods to automatically extract urban and-cover and land-use information [
3,
4,
5,
6]. For instance, Lu et al. [
3] combined textural and spectral images with the traditional supervised classification method for urban land-cover classification based on multispectral QuickBird remote-sensing data. Powell et al. [
4] utilized spectral-mixture analysis for subpixel urban land-cover mapping based on Landsat imagery. Pu et al. [
5] adopted an object-based method and IKONOS imagery for urban land-cover classification. However, due to the complicated composition of urban landscapes and the low spectral resolution of multispectral remote-sensing data, it is very difficult to yield very high classification accuracy. Compared with multispectral remote sensing, hyperspectral remote sensing can obtain hundreds of narrow contiguous spectral bands, which is capable of separating objects with subtle spectral differences. Recent studies also show the great potential of hyperspectral remote sensing in the differentiation of complex urban land-use types [
6,
7]. Demarchi et al. [
6] used APEX 288-band hyperspectral data for urban land-cover mapping based on unsupervised dimensionality-reduction techniques and several machine-learning classifiers. Tong et al. [
7] discussed which features of airborne hyperspectral data to use for urban land-cover classification and showed that the synthetic use of shape, texture and spectral information can improve the classification accuracy.
Meanwhile, due to the availability of diverse remote sensors, researchers began to integrate multisource and multisensor data for better characterization of the land surface [
8,
9,
10,
11,
12,
13]. Since then, the combined use of HSI and Light Detection and Ranging (LiDAR) data has been an active topic [
8,
9,
10,
11,
12,
13]. The addition of LiDAR data can provide detailed height and shape information of the scene, which can improve classification accuracy when compared with the use of hyperspectral data alone. For instance, roofs and roads that are both made of concrete are difficult to distinguish in hyperspectral images, but they can easily be separated using LiDAR-derived height information due to the significant difference in altitude. Based on the above points, researchers investigated the fusion methods of multisource hyperspectral and LiDAR data. Debes et al. [
8] highlighted two methods for hyperspectral and LiDAR data fusion, including a combined unsupervised and supervised classification scheme, and a graph-based method for the fusion of spectral, spatial, and elevation information. Man et al. [
9] discussed both the pixel- and feature-level fusion of hyperspectral and LiDAR data for urban land-use classification and showed that the combination of pixel- and object-based classifiers can increase the classification precision. Moreover, the fusion of hyperspectral and LiDAR data has also been applied in many other fields, such as forest monitoring [
10,
11], volcano mapping [
12], and crop-species classification [
13].
As for the approaches of multisource remote sensing data fusion, the widely used methods mainly include feature-level fusion and decision-level fusion. Specifically, in the procedure of feature-level fusion, remote sensing data from different sources are firstly processed to extract the relevant features and then fused through feature stacking or feature reconstructing. Man et al. [
9] stacked LiDAR features, i.e., nDSM, Intensity and HSI features, i.e., spectral indices and textures to improve the performance of urban land-use classification. Gonzalez et al. [
14] also stacked multisource features from color infrared imagery and LiDAR data for object-based mapping of forest habitats. Similar feature stacking approaches can be also found in the studies of Sankey et al. [
11] and Sasaki et al. [
15]. Different from above studies, Debes et al [
8] utilized a fusion graph to project all the original multisource features into a low-dimensional subspace to increase the robustness of the fused features. Compared with feature-level fusion, multisource datasets are separately classified and then fused or integrated in the process of decision-level fusion to generate the final classification results. Sturari et al. [
16] proposed a decision-level fusion method for the fusion of LiDAR and multispectral optical data, where the LiDAR classified objects were used as a posteriori in the object rule-based winner-takes-all fusion step.
In addition, all the above studies are based on shallow architectures and hand-crafted feature descriptors, which cannot obtain the fine and abstract high-level features of a complex urban landscape. Deep learning, on the other hand, is capable of modeling high-level feature representations through a hierarchical learning framework [
17]. Abstract and invariant features, together with the classifiers, can be simultaneously learned with a multilayer cascaded deep neural network, which outperforms hand-crafted shallow features in computer-vision tasks, such as image classification [
18,
19], object detection [
20], and landmark detection [
21,
22]. Deep-learning methods have also been a hot topic in remote sensing [
23], and have been successfully applied to building and road extraction [
24], wetland mapping [
25], cloud detection [
26], and land-cover classification [
27].
Recently, researchers have started to utilize deep learning for multisource remote-sensing data fusion [
28,
29,
30]. A typical framework for multisource data fusion based on deep learning is to construct a two-branch network [
28,
29,
30]. Features from different data sources are first separately extracted via each branch and then fused through feature stacking or feature concatenation. The fused features are passed to the classifier layer to generate the final classification results. For instance, Xu et al. [
28] proposed a two-branch convolutional neural network (CNN) for multisource remote-sensing data classification, and the network can achieve better classification performance than existing methods. Huang et al. [
29] used a two-branch CNN for extracting both spatial and spectral features of urban land objects for improved urban land-use mapping performance. Hughes et al. [
30] adopted a pseudo-Siamese CNN, which also had a two-branch structure, to identify corresponding patches in SAR (Synthetic Aperture Radar) and optical images.
Nevertheless, the above studies that use a two-branch network have two drawbacks that could be improved. Firstly, the data-fusion method of simply stacking or concatenating different features does not consider the importance or contribution of each feature to the final classification task, which could be improved by assigning a specific weight to each feature. Secondly, the backbone of the network is conventional, e.g., AlexNet [
18], which can be replaced by other recent network structures.
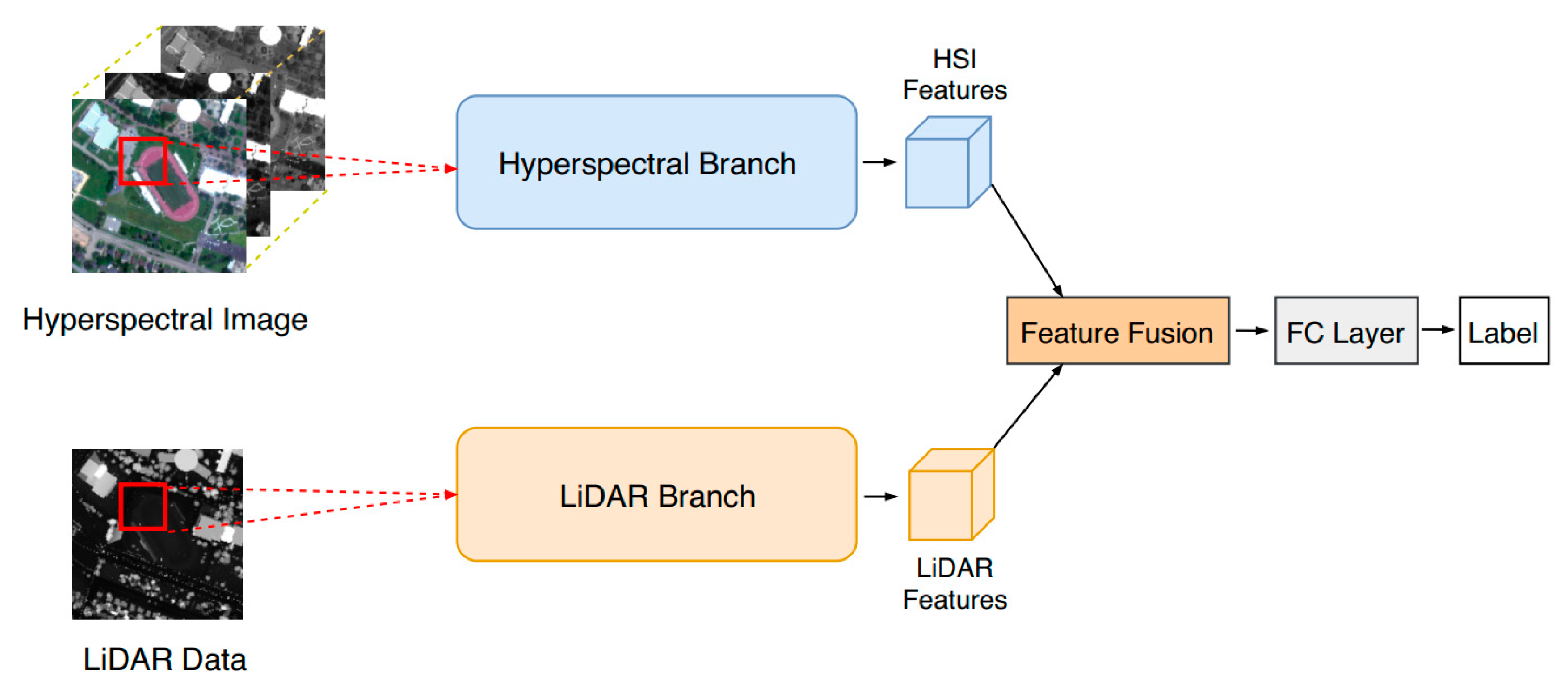
To tackle these problems, this paper modified the original two-branch neural network [
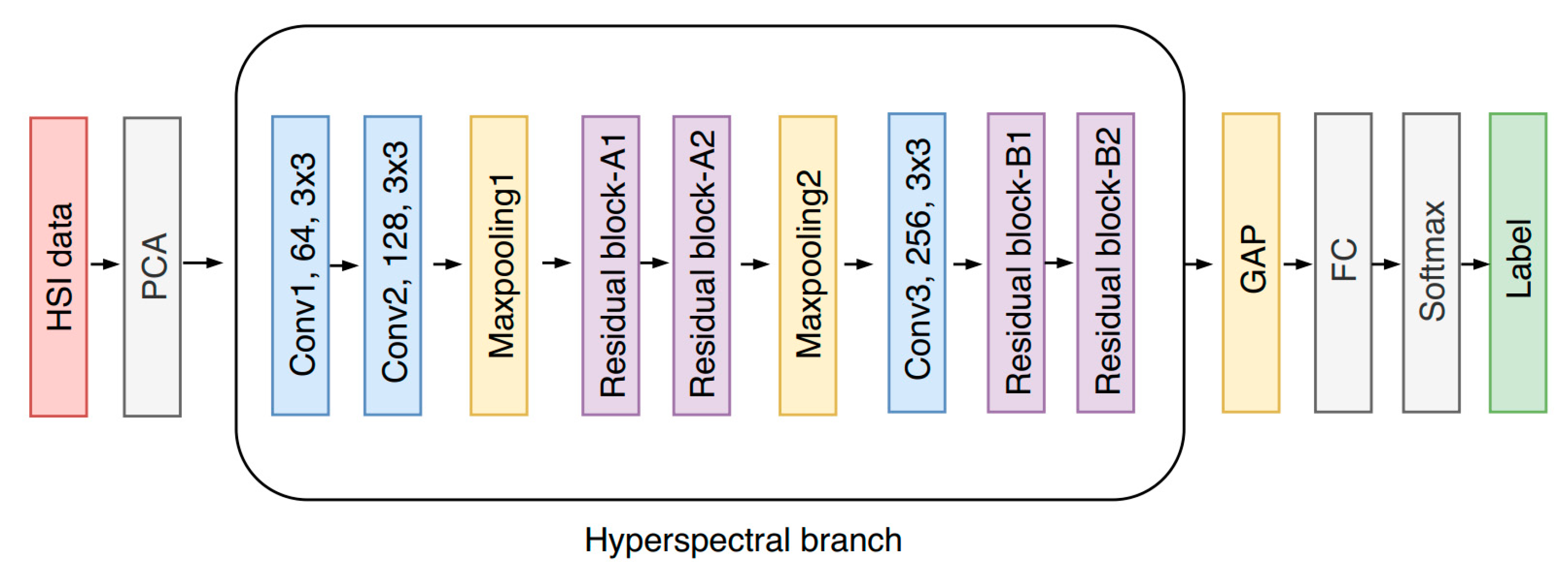
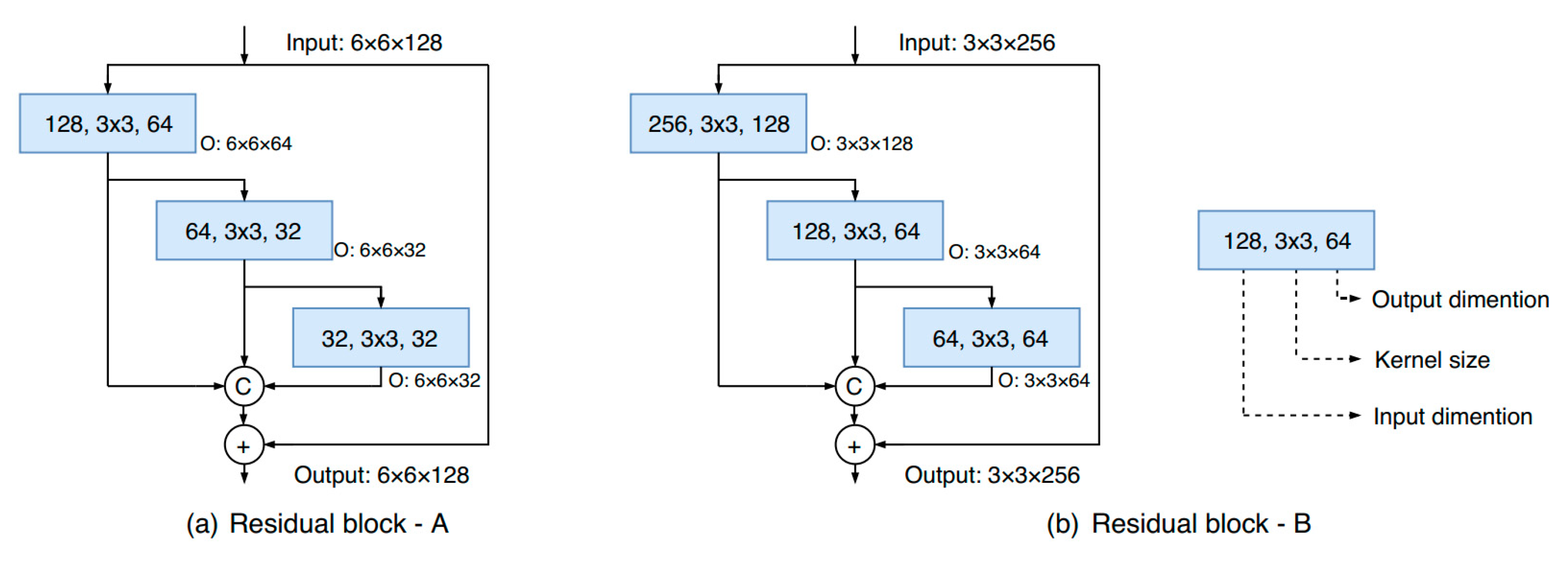
28] to adaptively fuse hyperspectral and LiDAR data for urban land-use classification. The proposed model mainly consists of three parts, i.e., the hyperspectral-imagery (HSI) branch for spatial–spectral feature extraction, the LiDAR branch for height-relevant feature extraction, and a fusion module for the adaptive feature fusion of the two branches. Specifically, the HSI branch and LiDAR branch share the same network structure, which is based on the cascade of a new multiscale residual block in order to reduce the burden of network design. During the training procedure, each branch is first separately trained, and the whole network is then fine-tuned based on each trained branch.
The rest of the paper is organized as follows.
Section 2 introduces the study area and dataset.
Section 3 presents the detailed architecture of the modified two-branch network.
Section 4 shows the experimental results and discussion, and
Section 5 provides the main concluding remarks.
2. Study Area and Dataset
The study area was the University of Houston campus and its neighboring urban areas, which are located in the southeast of Texas, United States. The hyperspectral and LiDAR data were from the 2013 IEEE (Institute of Electrical and Electronic Engineers) GRSS (Geoscience and Remote Sensing Society) Data Fusion Contest [
8]. Specifically, the hyperspectral imagery was acquired on 23 June 2012, which consisted of 144 spectral bands ranging from 380 to 1050 nm, with a spectral resolution of 4.8 nm. The spatial resolution was 2.5 m, while the height and width were 349 and 1905 m, respectively.
The LiDAR data were acquired on 22 June 2012 and had already been co-registered with hyperspectral imagery. The spatial resolution of the LiDAR-derived DSM (Digital Surface Model) was also 2.5 m.
Figure 1 shows a true-color composite representation of the hyperspectral imagery and the corresponding LiDAR-derived DSM.
All the training and testing samples are from the Data Fusion Contest. The spatial distribution of training and testing samples are depicted in
Figure 1c,d, respectively. There are 15 classes of interest in this study: grass-healthy, grass-stressed, grass-synthetic, tree, soil, water, residential, commercial, road, highway, railway, parking lot 1, parking lot 2, tennis court, and running track. It should be noted that parking lot 1 includes parking garages at both the ground level and elevated areas, while parking lot 2 corresponds to parked vehicles.
The numbers of training and testing samples together with colors for each class are shown in
Table 1. As can been seen, the number of training samples is quite limited, which makes it very difficult to achieve high classification accuracy.
4. Results and Discussion
4.1. Results of Urban Land-Use Classification
In order to evaluate the performance of the proposed two-branch neural network for urban land-use mapping, a series of classification maps are depicted in
Figure 7 including the following cases:
(a) HSI branch only, i.e., using only HSI data and the HSI branch for classification;
(b) LiDAR branch only, i.e., using only LiDAR data and the LiDAR branch for classification;
(c) the proposed two-branch CNN.
It is evident that the synthetic use of HSI and LiDAR data leads to a classification map with a better visual effect and higher quality when compared with the results of only the HSI branch and only the LiDAR branch.
Meanwhile, the HSI branch yields a better classification map with fewer errors than that of the LiDAR branch. However, due to the large spectral variance of different urban land-use types, hyperspectral data alone could also result in inaccurate classification results. For instance, the eastern area of the image is covered by some clouds, which leads to the spectral distortion of certain land-use types, resulting in more classification errors. The LiDAR data alone also do not contain enough information to differentiate complicated urban objects, especially for different objects with the same or similar elevation. Nonetheless, the fusion of HSI and LiDAR data can avoid the above demerits and benefit from both the spectral characteristics of the HSI image and the geometric information of the LiDAR data, which could lead to a better classification map.
4.2. Accuracy-Assessment Results
In order to quantitatively evaluate the proposed approach in the study, the confusion matrix, together with the overall accuracy (OA) and Kappa coefficient, were calculated based on the testing samples. Results are shown in the
Table 4.
The proposed two-branch network shows good performance, with an OA of 91.87% and a Kappa of 0.9117. However, the highway class had the lowest producer accuracy (PA) with 80.89%, while all the other classes had a higher PA of more than 83%. This could be due to the spectral mixture between highway and other impervious surface types, such as railway and commercial areas, since they all consist of concrete materials. It should also be noted that all highway training samples are outside the cloud-covered regions, while nearly half of the highway testing samples are from the cloud-covered regions. This could cause the spectral inconsistency between training and testing samples of the highway class, which could result in relatively lower classification accuracy.
In addition, the confusion matrix indicates that most classification errors occurred among the following land-use types: Highway, railway, road, and parking lot 1. This is mainly because all those land-use categories belong to impervious surfaces that share similar spectral properties. Highway, railway, and road also share similar shape features, which could increase the difficulty in separating between them using a patch-based CNN model, since the CNN takes spatial contextual information into consideration when classifying each pixel. Other errors occurred where several healthy-grass and stressed-grass pixels were misclassified as the railway. This is uncommon in remote-sensing image classification, since grass and railway share different spectral characteristics. However, when checking the classification map, it is in the eastern cloud-covered regions that several grass areas were misclassified as railway. This is mainly because the existence of heavy cloud distorted the spectral curves of the grass, which led to the uncommon classification errors.
4.3. Ablation Analysis
To further evaluate the performance of the proposed method, a series of ablation experiments were done including: (a) only the HSI branch, (b) only the LiDAR branch, and (c) feature-stacking (i.e., using stacked or concatenated features of HSI and LiDAR instead of adaptive fusion for classification). The results of class-level classification accuracy are illustrated in
Table 5 including all the above three cases together with the proposed two-branch network.
Table 5 indicates that the LiDAR branch alone achieved the lowest classification accuracy with an OA of 53.42% and a Kappa of 0.4967. This is mainly due to the fact that height information alone can hardly separate different land-use types in complicated urban regions. Meanwhile, the HSI branch alone achieved much higher accuracy than that of only the LiDAR branch, with an OA of 83.83% and a Kappa of 0.8244. The reason why the HSI branch alone outperformed the LiDAR branch alone is that HSI images can provide much more abundant spectral and spatial information of land surfaces than LiDAR-derived DSMs, leading to a higher capability of differentiating complex urban land-use types.
Table 5 also indicates that, when compared with single-source data alone, the integration of multisource HSI and LiDAR data leads to a significant improvement of classification accuracy for almost each urban land-use class. This is reasonable since the separability of urban objects could increase if we simultaneously integrate multiple spectral and elevation features. Compared with hyperspectral data alone, the integration of LiDAR data improved OA by 4.42% and 8.04% through feature-stacking and the proposed two-branch network, respectively. In terms of class-level accuracy, the main contribution of LiDAR data was in the following classes: Synthetic grass, tree, soil, water, commercial, railway, and parking lot 1 and 2. This is due to some of the classes (e.g., grass and tree) sharing very similar spectral characteristics but having different height values; therefore, the inclusion of LiDAR-derived DSMs could significantly improve the separability between these classes.
It should be noted that the proposed two-branch network, which uses adaptive feature fusion, outperforms the traditional feature-stacking method by improving OA from 88.25% to 91.87%, with an increase of 3.62%. This is because, when simply stacking all features together, the values of each feature can be significantly unbalanced, and the information carried by each feature may not be equally represented. Therefore, we introduced the adaptive squeeze-and-excitation module to automatically assign a weight to each feature according to its importance, which could integrate multiple features in a more natural and reasonable way, resulting in the accuracy improvement of 3.62%.
Since the proposed approach used a pixel-centered patch as input to the networks, more comparative experiments should be done to compare the performance between the pixel-based and patch-based classification, and to investigate the effect of the PCA and non-PCA approaches. Therefore, a series of ablation experiments were performed, and the comparison results are shown in the following table.
Specifically, since the input was changed to 1D pixel vectors, all the 2D convolutional layers of the original patch-based two-branch CNN were replaced by 1D convolutional layers in the pixel-based CNN, while all parameters remained the same. As can be seen from
Table 6, the patch-based models outperformed the pixel-based ones with an accuracy increase of 7.89% and 5.82% for the non-PCA and PCA-based approaches, respectively. This is mainly because, when compared with the patch-based model, the pixel-based model only considers the spectral characteristics of the land object. However, the patch-based model can take both the spectral and spatial contextual information into account, leading to more discriminative and representative features which are essential for classification. When compared with non-PCA approaches, the usage of PCA has a positive effect on classification, leading to an accuracy increase of 4.56% and 2.49% for the pixel-based and patch-based-models, respectively. This is due to the fact that PCA can effectively reduce the data redundancy of the original hyperspectral imagery, which can reduce the overfitting risk of the convolutional neural network and, thus, improve its generalization ability when predicting on new datasets.
Additionally, the proposed approach can be considered as a reference framework for multisource data fusion in the remote-sensing field.
4.4. Comparison with Other Methods
To further justify the performance of the proposed approach, it should be compared with other widely used machine-learning methods, such as random forest (RF) [
35], support vector machines (SVM) [
36], and state-of-the-art methods.
For RF, the Gini coefficient was used as the index for feature selection. For SVM, the Radial Basis Function (RBF) was used as the kernel function. As for the determination of the hyperparameters of RF and SVM, we utilized the grid-search method to find the optimal values. Specifically, the ranges of used parameters for RF are as follows. The number of trees ranged from 50 to 500 with a step of 10, while the max depth had a range of 5 to 15 with a step of 2. For SVM, gamma ranged from 0.001 to 0.1 with a step of 0.001, while punishment coefficient C had a range of 10 to 200 with a step of 10. After the procedure of grid search, RF achieved the best overall accuracy of 83.97% when the number of trees was 200 and the max depth was 13. Meanwhile, SVM achieved the best accuracy of 84.16% with a gamma of 0.01 and a C of 100.
Meanwhile, we selected Xu’s model [
28] as a strong baseline since it first utilized a two-branch CNN for HSI and LiDAR data fusion, and achieved an OA of 87.98%, also on the 2013 IEEE GRSS Data Fusion Contest testing dataset. All the above methods were trained and tested with the same training and testing samples as the proposed method to maintain fairness. The accuracy comparison results are listed in
Table 7.
Table 7 indicates that our proposed modified two-branch CNN outperformed both RF and SVM with an OA improvement of 7.90% and 7.71%, respectively. This was expected since, when compared with traditional machine-learning methods, the CNN could learn high-level spatial features of complicated and fragmented urban land-use types, which led to a more robust and accurate classification result.
When compared with Xu’s state-of-the-art model, the proposed method in this study improved OA from 87.98% to 91.87%, with an increase of 3.89%. However, when using feature-stacking, the modified two-branch CNN in this study only achieved a slight accuracy increase of 0.27% compared to Xu’s model. This indicates that, when compared with the modification of the network structure, the introduction of the feature-fusion module contributed more to the increase of classification accuracy. This is because the feature-fusion module could learn the importance of each feature, which can emphasize more effective features while suppressing the less informative ones, leading to a more reasonable and robust fusion strategy for multisource remote-sensing data. The backbone of the modified two-branch CNN is less effective than the feature-fusion strategy and does not show superior performance to that of Xu’s model.
As stated above, the fusion method of this study is more effective than the model structure itself, therefore, a more comprehensive comparison with existing methods is necessary. In fact, as stated in the Introduction, most of the feature-level fusion studies just simply stacked and concatenated the features from LiDAR and HSI data and then carried out the classification based on machine learning classifiers such as decision tree, support vector machine and random forest. Relevant studies include that of Man et al. [
9], Gonzalez et al. [
14], Sasaki et al. [
16]. However, these approaches gave equal importance to all the features, which could bring in redundant information and extra noise. Different from those feature-stacking methods, the feature fusion approach in this study takes the importance of multisource features into account, which could effectively highlight those most informative features while reduce the noisy ones. Meanwhile, some existing methods designed a feature fusion model to reconstruct the multisource features to increase the classification performance. One concrete example is Debes’s study [
8], in which a graph-based fusion model was used to re-project all the features into a low-dimensional subspace to increase the robustness of the fused features. Actually, the newly reconstructed features were more informative with less noises, however, this method was not that straight-forward when compared with our approach, where all the original features were directly re-weighted in our feature-fusion model. Nonetheless, the graph-based fusion method can be introduced in the deep learning model in future research.
5. Conclusions
This paper proposed a modified two-branch convolutional neural network for urban land-use mapping using multisource hyperspectral and LiDAR data. The proposed two-branch network consists of an HSI branch and a LiDAR branch, both of which share the same network structure in order to reduce the burden and time cost of network design. Within the HSI and LiDAR branches, a hierarchical, parallel, and multiscale residual block was utilized, which could simultaneously increase the receptive field size and improve gradient flow. An adaptive feature-fusion module based on a Squeeze-and-Excitation Net was proposed to fuse the HSI and LiDAR features, which could integrate multisource features in a natural and reasonable way. Experiment results showed that the proposed two-branch network had good performance, with an OA of almost 92% on the 2013 IEEE GRSS Data Fusion Contest dataset. When compared with hyperspectral data alone, the introduction of LiDAR data increased OA from almost 84% to 92%, which indicates that the integration of multisource data could improve classification accuracy in complicated urban landscapes. The proposed adaptive fusion method increased accuracy by more than 3% when compared with the traditional feature-stacking method, which justifies its usefulness in multisource data fusion. The two-branch CNN in this paper also outperformed traditional machine-learning methods, such as random forest and support vector machines.
This paper demonstrates that the modified two-branch network can effectively integrate multisource features from hyperspectral and LiDAR data, showing good performance in urban land-use mapping. Future work should be carried out on more datasets to further justify the performance of the proposed method.