PolySimp: A Tool for Polygon Simplification Based on the Underlying Scaling Hierarchy
Abstract
:1. Introduction
2. Methods
2.1. Related Algorithms for Polygon Simplification
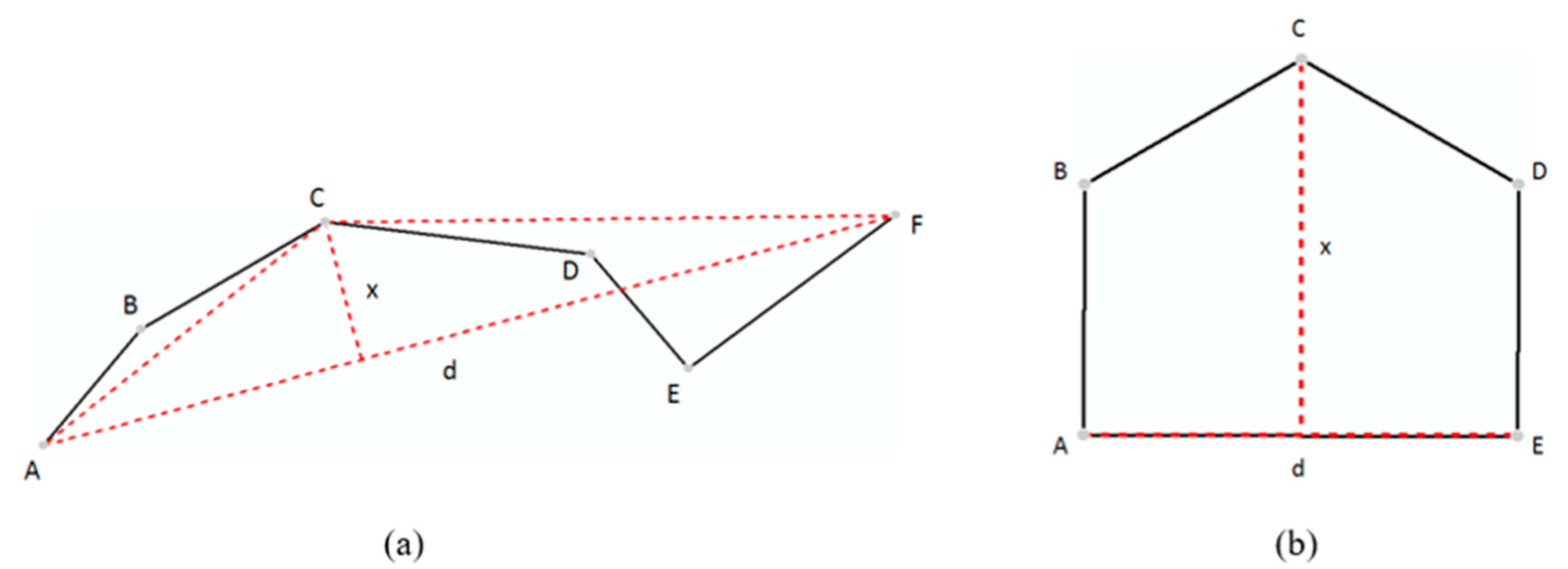
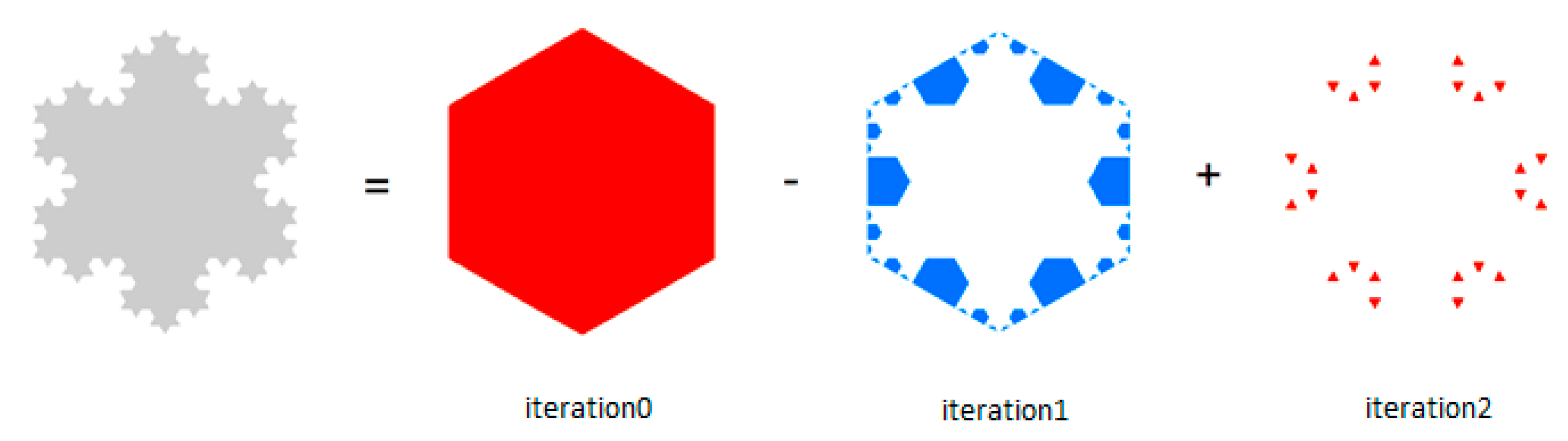
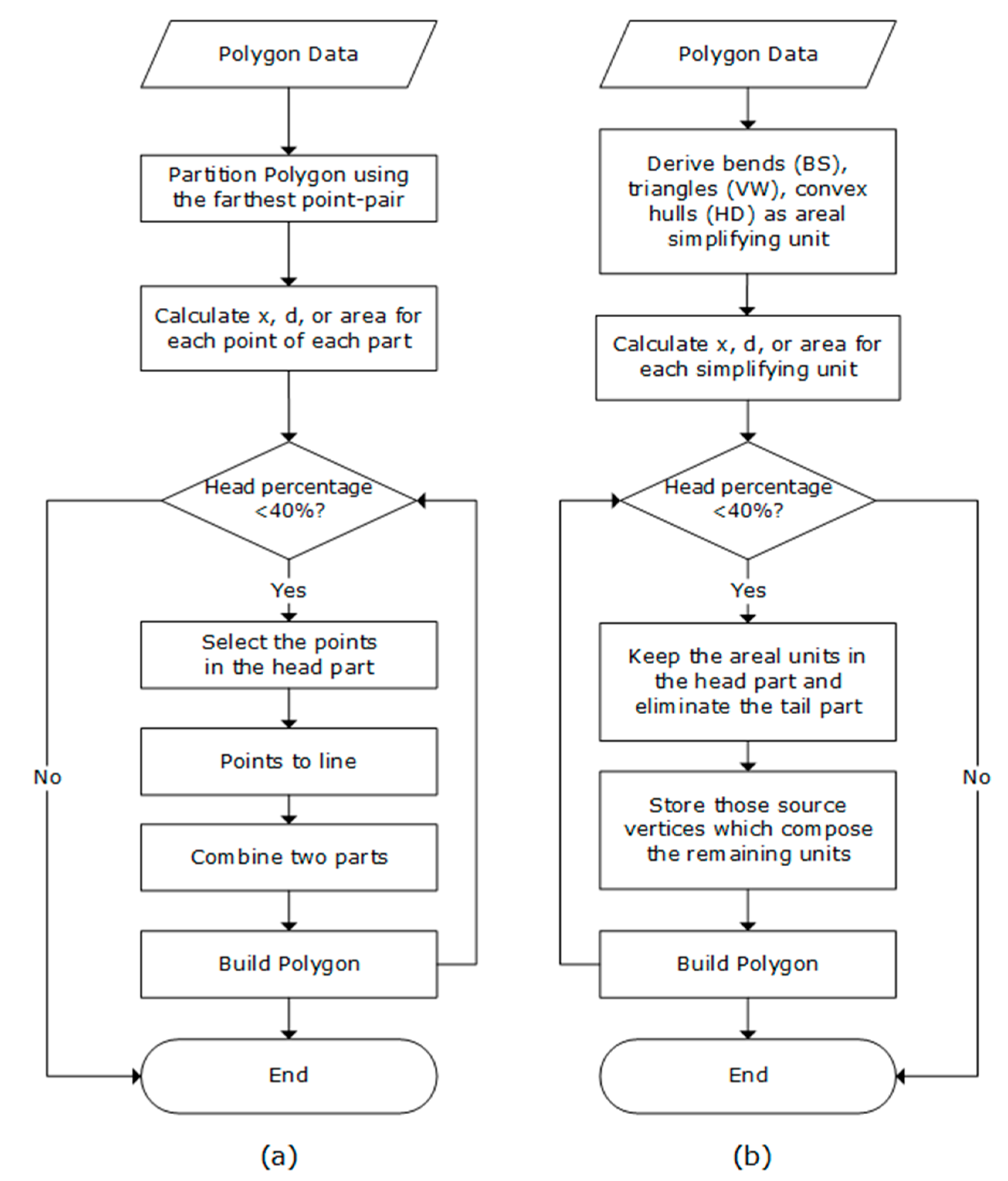
2.2. Polygon Simplification Using Its Inherent Scaling Hierarchy
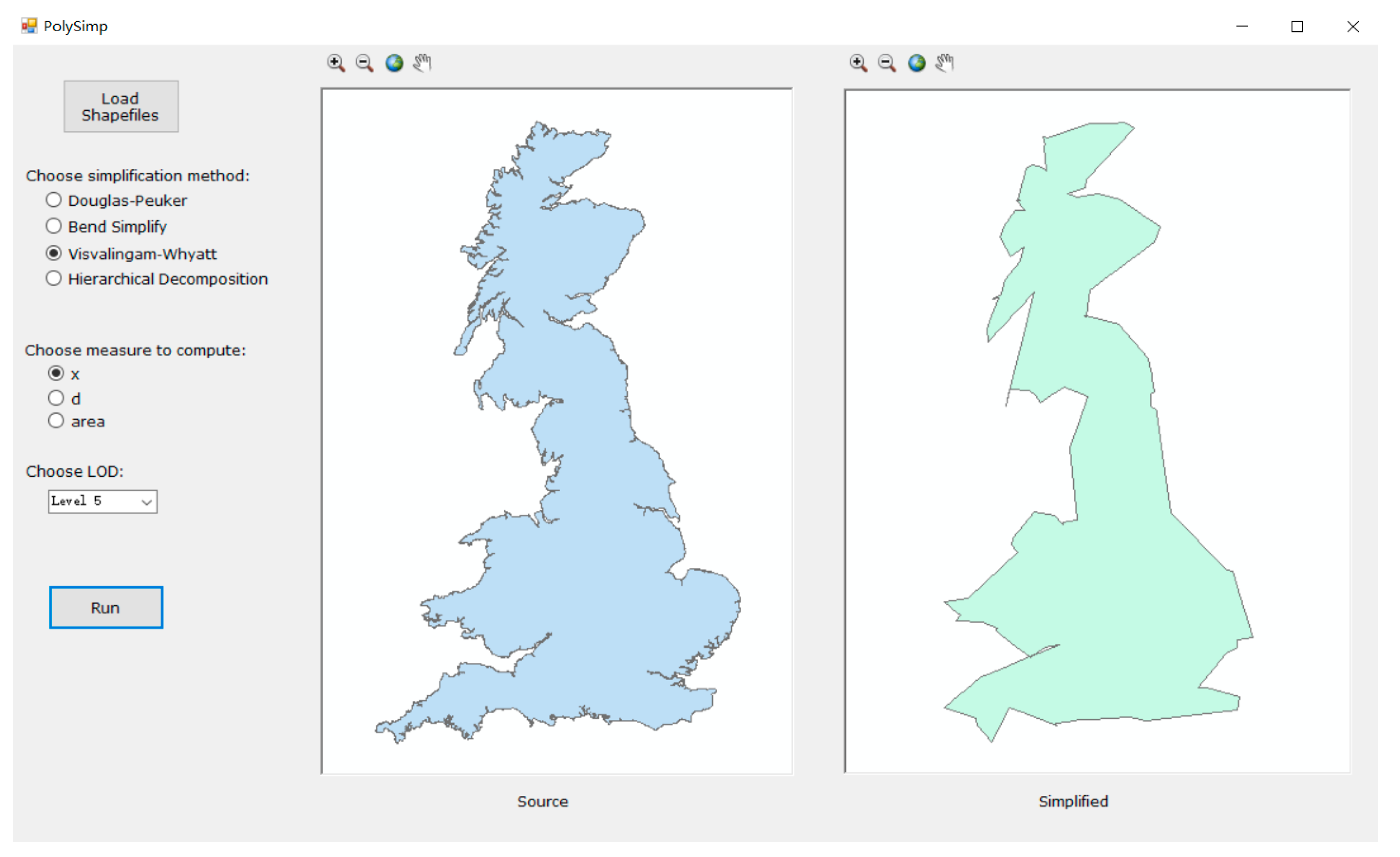
3. Development of a Software Tool: PolySimp
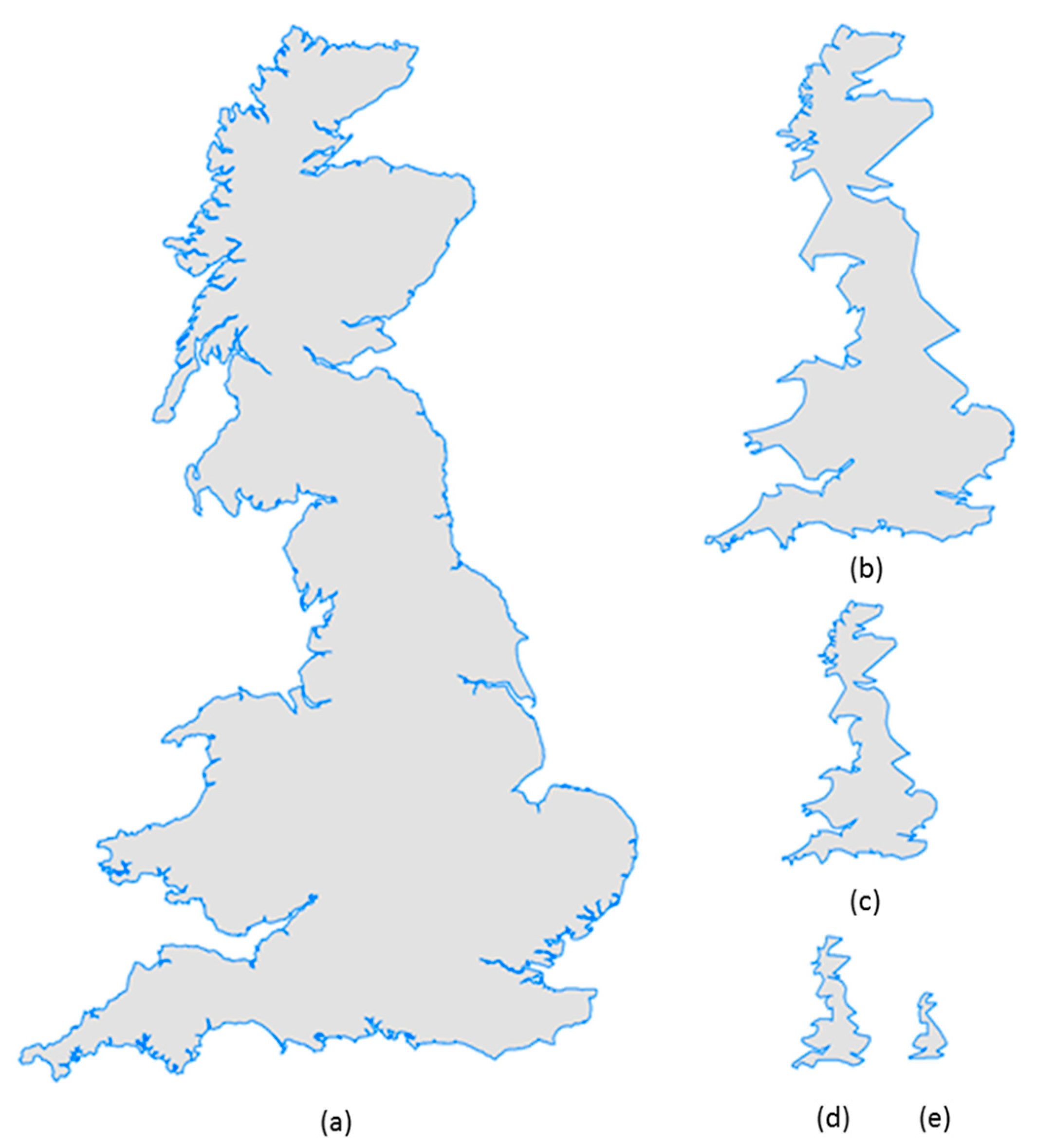
4. Case Study and Analysis
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Appendix A. The Scaling Hierarchy of Geometric Units Derived from DP, BS, and VW Algorithms

References
- Buttenfield, B.P.; McMaster, R.B. Map Generalization: Making Rules for Knowledge Representation; Longman Group: London, UK, 1991. [Google Scholar]
- Mackaness, W.A.; Ruas, A.; Sarjakoski, L.T. Generalisation of Geographic Information: Cartographic Modelling and Applications; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Stoter, J.; Post, M.; van Altena, V.; Nijhuis, R.; Bruns, B. Fully automated generalization of a 1:50k map from 1:10k data. Cartogr. Geogr. Inf. Sci. 2014, 41, 1–13. [Google Scholar] [CrossRef]
- Burghardt, D.; Duchêne, C.; Mackaness, W. Abstracting Geographic Information in a Data Rich World: Methodologies and Applications of Map Generalisation; Springer: Berlin, Germany, 2014. [Google Scholar]
- Jiang, B.; Liu, X.; Jia, T. Scaling of geographic space as a universal rule for map generalization. Ann. Assoc. Am. Geogr. 2013, 103, 844–855. [Google Scholar] [CrossRef] [Green Version]
- Weibel, R.; Jones, C.B. Computational Perspectives on Map Generalization. GeoInformatica 1998, 2, 307–315. [Google Scholar] [CrossRef]
- McMaster, R.B.; Usery, E.L. A Research Agenda for Geographic Information Science; CRC Press: London, UK, 2005. [Google Scholar]
- Tobler, W.R. Numerical Map Generalization; Department of Geography, University of Michigan: Ann Arbour, MI, USA, 1966. [Google Scholar]
- Li, Z.; Openshaw, S. Algorithms for automated line generalization1 based on a natural principle of objective generalization. Int. J. Geogr. Inf. Syst. 1992, 6, 373–389. [Google Scholar] [CrossRef]
- Visvalingam, M.; Whyatt, J.D. Line generalization by repeated elimination of points. Cartogr. J. 1992, 30, 46–51. [Google Scholar] [CrossRef]
- Saalfeld, A. Topologically consistent line simplification with the Douglas-Peucker algorithm. Cartogr. Geogr. Inf. Sci. 1999, 26, 7–18. [Google Scholar] [CrossRef]
- Gökgöz, T.; Sen, A.; Memduhoglu, A.; Hacar, M. A new algorithm for cartographic simplification of streams and lakes using deviation angles and error bands. ISPRS Int. J. Geo-Inf. 2015, 4, 2185–2204. [Google Scholar] [CrossRef] [Green Version]
- Kolanowski, B.; Augustyniak, J.; Latos, D. Cartographic Line Generalization Based on Radius of Curvature Analysis. ISPRS Int. J. Geo-Inf. 2018, 7, 477. [Google Scholar] [CrossRef] [Green Version]
- Ruas, A. Modèle de Généralisation de Données Géographiques à Base de Contraintes et D’autonomie. Ph.D. Thesis, Université Marne La Vallée, Marne La Vallée, France, 1999. [Google Scholar]
- Touya, G.; Duchêne, C.; Taillandier, P.; Gaffuri, J.; Ruas, A.; Renard, J. Multi-Agents Systems for Cartographic Generalization: Feedback from Past and On-going Research. Technical Report; LaSTIG, équipe COGIT. hal-01682131; IGN (Institut National de l’Information Géographique et Forestière): Saint-Mandé, France, 2018; Available online: https://hal.archives-ouvertes.fr/hal-01682131/document (accessed on 6 October 2020).
- Harrie, L.; Sarjakoski, T. Simultaneous Graphic Generalization of Vector Data Sets. GeoInformatica 2002, 6, 233–261. [Google Scholar] [CrossRef]
- Zahn, C.T.; Roskies, R.Z. Fourier descriptors for plane closed curves. IEEE Trans. Comput. 1972, C-21, 269–281. [Google Scholar] [CrossRef]
- Mandelbrot, B. The Fractal Geometry of Nature; W. H. Freeman and Co.: New York, NY, USA, 1982. [Google Scholar]
- Normant, F.; Tricot, C. Fractal simplification of lines using convex hulls. Geogr. Anal. 1993, 25, 118–129. [Google Scholar] [CrossRef]
- Lam, N.S.N. Fractals and scale in environmental assessment and monitoring. In Scale and Geographic Inquiry; Sheppard, E., McMaster, R.B., Eds.; Blackwell Publishing: Oxford, UK, 2004; pp. 23–40. [Google Scholar]
- Batty, M.; Longley, P.; Fotheringham, S. Urban growth and form: Scaling, fractal geometry, and diffusion-limited aggregation. Environ. Plan. A Econ. Space 1989, 21, 1447–1472. [Google Scholar] [CrossRef]
- Batty, M.; Longley, P. Fractal Cities: A Geometry of Form and Function; Academic Press: London, UK, 1994. [Google Scholar]
- Bettencourt, L.M.A.; Lobo, J.; Helbing, D.; Kühnert, C.; West, G.B. Growth, innovation, scaling, and the pace of life in cities. Proc. Natl. Acad. Sci. USA 2007, 104, 7301–7306. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jiang, B. The fractal nature of maps and mapping. Int. J. Geogr. Inf. Sci. 2015, 29, 159–174. [Google Scholar] [CrossRef] [Green Version]
- Töpfer, F.; Pillewizer, W. The principles of selection. Cartogr. J. 1966, 3, 10–16. [Google Scholar] [CrossRef]
- Jiang, B. Head/tail breaks: A new classification scheme for data with a heavy-tailed distribution. Prof. Geogr. 2013, 65, 482–494. [Google Scholar] [CrossRef]
- Jiang, B.; Yin, J. Ht-index for quantifying the fractal or scaling structure of geographic features. Ann. Assoc. Am. Geogr. 2014, 104, 530–541. [Google Scholar] [CrossRef]
- Long, Y.; Shen, Y.; Jin, X.B. Mapping block-level urban areas for all Chinese cities. Ann. Am. Assoc. Geogr. 2016, 106, 96–113. [Google Scholar] [CrossRef] [Green Version]
- Long, Y. Redefining Chinese city system with emerging new data. Appl. Geogr. 2016, 75, 36–48. [Google Scholar] [CrossRef]
- Gao, P.C.; Liu, Z.; Xie, M.H.; Tian, K.; Liu, G. CRG index: A more sensitive ht-index for enabling dynamic views of geographic features. Prof. Geogr. 2016, 68, 533–545. [Google Scholar] [CrossRef]
- Gao, P.C.; Liu, Z.; Tian, K.; Liu, G. Characterizing traffic conditions from the perspective of spatial-temporal heterogeneity. ISPRS Int. J. Geo-Inf. 2016, 5, 34. [Google Scholar] [CrossRef] [Green Version]
- Liu, P.; Xiao, T.; Xiao, J.; Ai, T. A multi-scale representation model of polyline based on head/tail breaks. Int. J. Geogr. Inf. Sci. 2020. [Google Scholar] [CrossRef]
- Müller, J.C.; Lagrange, J.P.; Weibel, R. GIS and Generalization: Methodology and Practice; Taylor & Francis: London, UK, 1995. [Google Scholar]
- Li, Z. Algorithmic Foundation of Multi-Scale Spatial Representation; CRC Press: London, UK, 2007. [Google Scholar]
- ESRI. How Simplify Line and Simplify Polygon Work. Available online: https://desktop.arcgis.com/en/arcmap/latest/tools/cartography-toolbox/simplify-polygon.htm (accessed on 15 July 2020).
- Touya, G.; Lokhat, I.; Duchêne, C. CartAGen: An Open Source Research Platform for Map Generalization. In Proceedings of the International Cartographic Conference 2019, Tokyo, Japan, 15–20 July 2019; pp. 1–9. [Google Scholar]
- CartAGen. Line Simplification Algorithms. 2020. Available online: https://ignf.github.io/CartAGen/docs/algorithms.html (accessed on 6 October 2020).
- Douglas, D.; Peucker, T. Algorithms for the reduction of the number of points required to represent a digitized line or its caricature. Can. Cartogr. 1973, 10, 112–122. [Google Scholar] [CrossRef] [Green Version]
- Zhou, S.; Christopher, B.J. Shape-Aware Line Generalisation with Weighted Effective Area. In Developments in Spatial DataHandling, Proceedings of the 11th International Symposium on Spatial Handling, Zurich, Switzerland; Fisher, P.F., Ed.; Springer-Verlag: Berlin/Heidelberg, Germany, 2005; pp. 369–380. [Google Scholar]
- Wang, Z.; Müller, J.C. Line Generalization Based on Analysis of Shape Characteristics. Cartog. Geogr. Inf. Syst. 1998, 25, 3–15. [Google Scholar] [CrossRef]
- Ai, T.; Li, Z.; Liu, Y. Progressive transmission of vector data based on changes accumulation model. In Developments in Spatial Data Handling; Springer-Verlag: Heidelberg, Germany, 2005; pp. 85–96. [Google Scholar]
- Ma, D.; Jiang, B. A smooth curve as a fractal under the third definition. Cartographica 2018, 53, 203–210. [Google Scholar] [CrossRef] [Green Version]
- Sester, M.; Brenner, C. A vocabulary for a multiscale process description for fast transmission and continuous visualization of spatial data. Comput. Geosci. 2009, 35, 2177–2184. [Google Scholar] [CrossRef]
- Jiang, B. Methods, Apparatus and Computer Program for Automatically Deriving Small-Scale Maps. U.S. Patent WO 2018/116134, PCT/IB2017/058073, 28 June 2018. [Google Scholar]


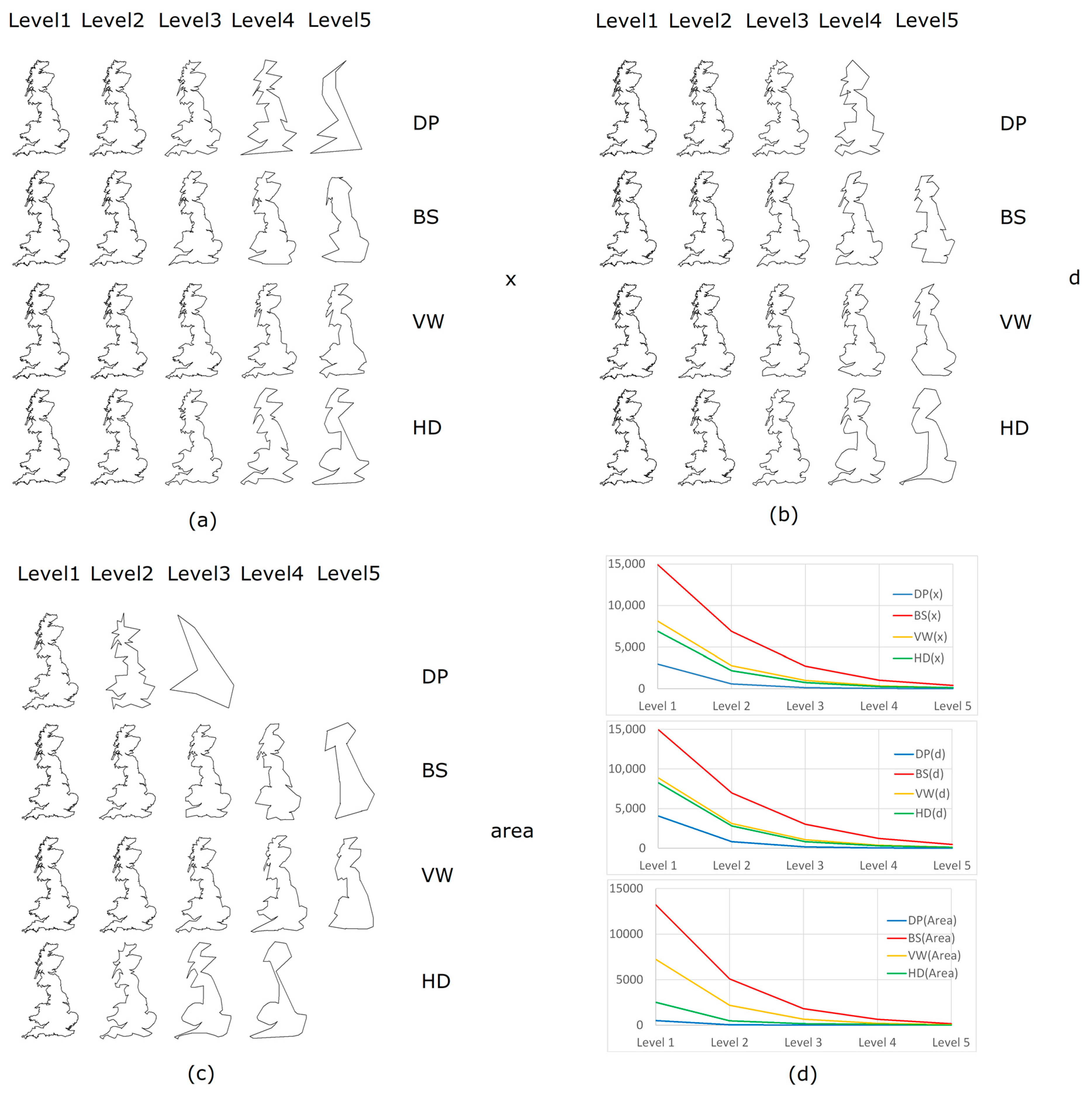
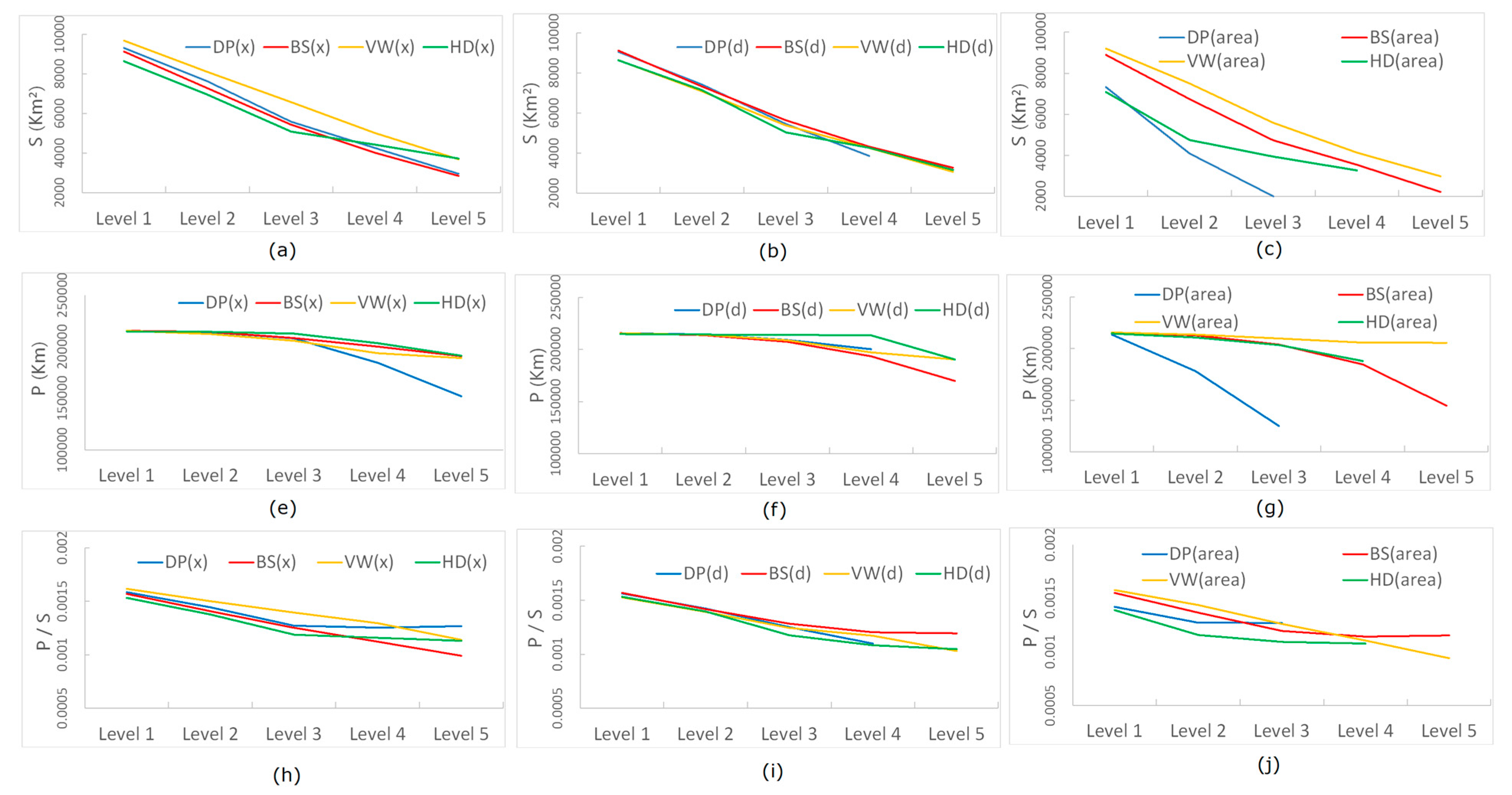

| DP | BS | VW | HD | |
|---|---|---|---|---|
| Time (x) | 1.06 | 4.32 | 0.25 | 103.92 |
| Time (d) | 1.12 | 4.43 | 0.19 | 75.67 |
| Time(area) | 1.08 | 4.31 | 0.24 | 34.83 |
| DP | BS | VW | HD | |
|---|---|---|---|---|
| Ht (x) | 6 | 9 | 10 | 6 |
| Ht (d) | 5 | 6 | 8 | 7 |
| Ht (area) | 4 | 6 | 7 | 5 |
| Level 1 | Level 2 | Level 3 | Level 4 | Level 5 | |
|---|---|---|---|---|---|
| #Pt(x)-DP | 2969 | 583 | 133 | 34 | 12 |
| #Pt(d)-DP | 4074 | 829 | 173 | 45 | NA |
| #Pt(area)-DP | 505 | 48 | 10 | NA | NA |
| #Pt(x)-BS | 14,913 | 6883 | 2706 | 1023 | 395 |
| #Pt(d)-BS | 14,957 | 6970 | 3037 | 1238 | 485 |
| #Pt(area)-BS | 13,234 | 5086 | 1816 | 638 | 159 |
| #Pt(x)-VW | 8112 | 2762 | 990 | 346 | 119 |
| #Pt(d)-VW | 8866 | 3124 | 1078 | 378 | 124 |
| #Pt(area)-VW | 7233 | 2178 | 661 | 192 | 62 |
| #Pt(x)-HD | 6899 | 2162 | 743 | 260 | 127 |
| #Pt(d)-HD | 8262 | 2814 | 827 | 311 | 112 |
| #Pt(area)-HD | 2509 | 483 | 159 | 91 | NA |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, D.; Zhao, Z.; Zheng, Y.; Guo, R.; Zhu, W. PolySimp: A Tool for Polygon Simplification Based on the Underlying Scaling Hierarchy. ISPRS Int. J. Geo-Inf. 2020, 9, 594. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi9100594
Ma D, Zhao Z, Zheng Y, Guo R, Zhu W. PolySimp: A Tool for Polygon Simplification Based on the Underlying Scaling Hierarchy. ISPRS International Journal of Geo-Information. 2020; 9(10):594. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi9100594
Chicago/Turabian StyleMa, Ding, Zhigang Zhao, Ye Zheng, Renzhong Guo, and Wei Zhu. 2020. "PolySimp: A Tool for Polygon Simplification Based on the Underlying Scaling Hierarchy" ISPRS International Journal of Geo-Information 9, no. 10: 594. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi9100594





