Accurate Road Marking Detection from Noisy Point Clouds Acquired by Low-Cost Mobile LiDAR Systems
Abstract
:1. Introduction
- (1)
- Establishing an efficient and reliable strategy to reduce the number of point clouds to be processed, including a pseudo-scan line-based organization data structure that could be used for road marking extraction from dense 3D point clouds.
- (2)
- Presenting a density-based adaptive window median filter to suppress noise in different point-density and intensity-noise levels of MLS point clouds as well as a marker edge constraint detection (MECD) method for road marking edge extraction.
2. Method
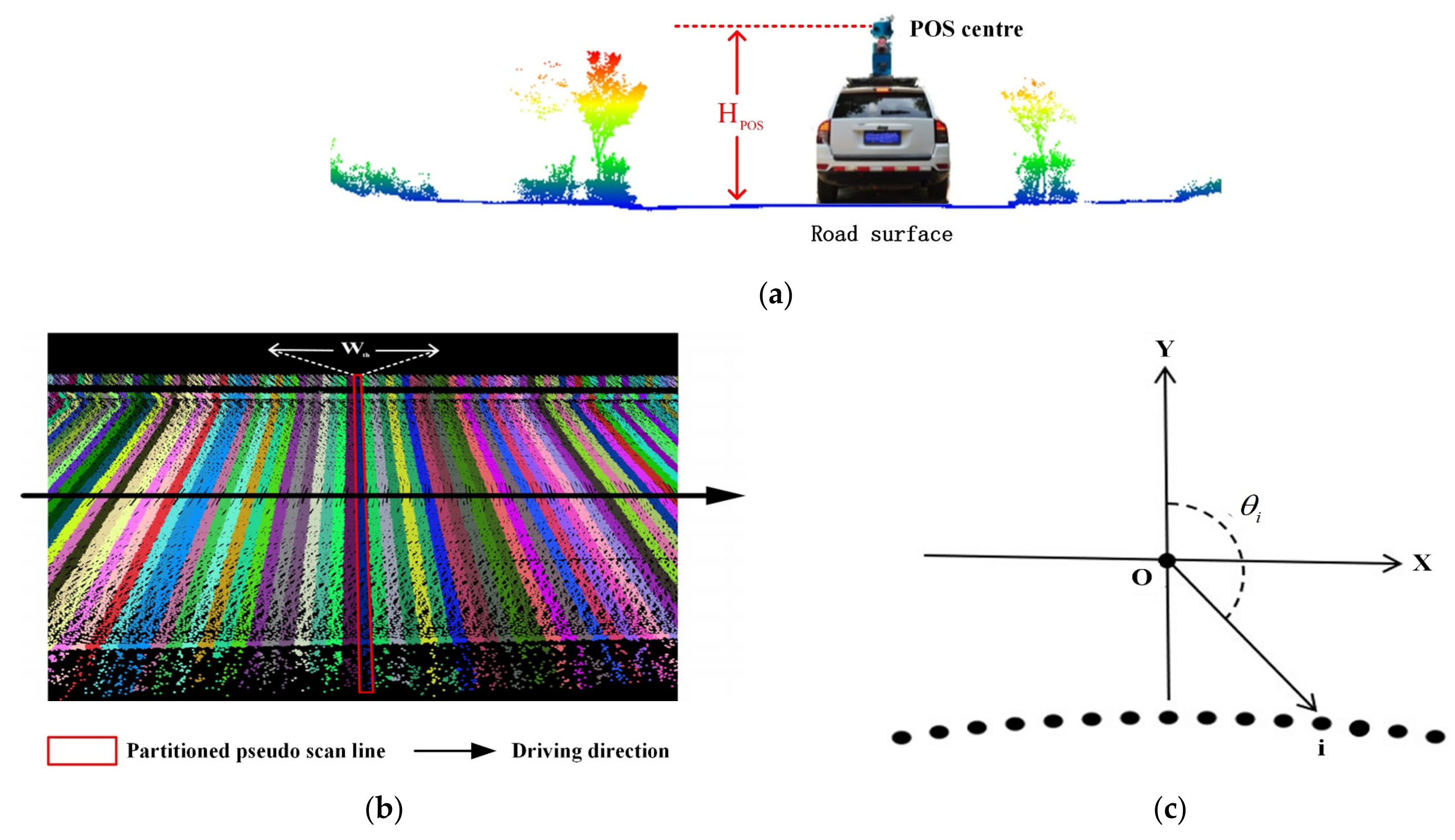
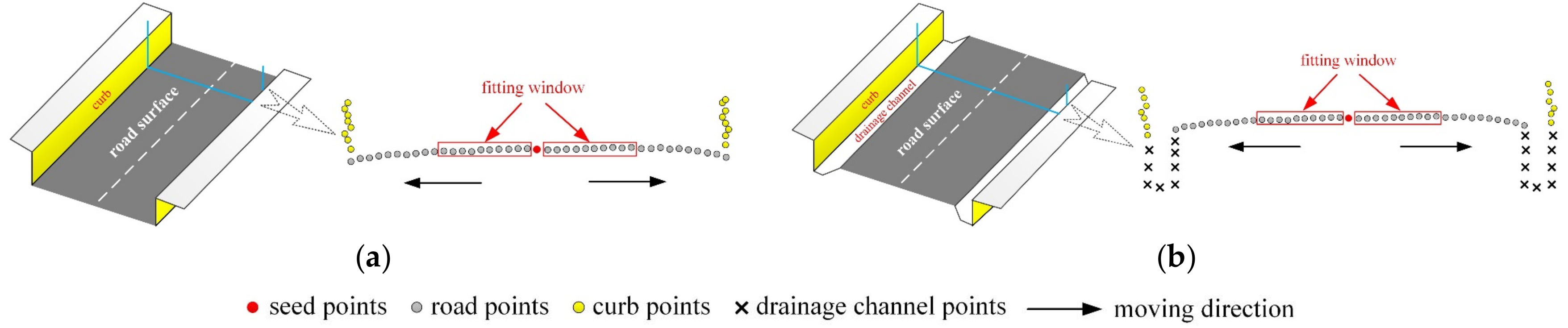
2.1. Road Surface Extraction
- (1)
- Elevation jump criterion. Since the elevations of road points in a local area are almost unchanged, a potential point is determined as a road point if the distance from the point to the fitted line is smaller than the threshold . represents the elevation difference between points at the road boundary and points at the curb, and is set here to 0.04 m.
- (2)
- Horizontal distance jump criterion. The distance from the current point to the outmost point in the window is calculated. The point is determined as a nonroad point if the distance is greater than the threshold . represents the width of the drainage channel and is set here to 0.7 m because the drainage channels are relatively narrow in the road environment of the datasets.
2.2. Road Marking Extraction
2.2.1. Intensity Median Filtering
2.2.2. Marker Edge Constraint Detection
2.3. Road Marking Refinement
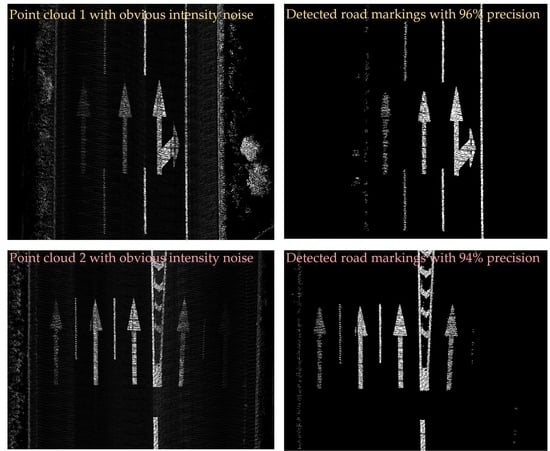
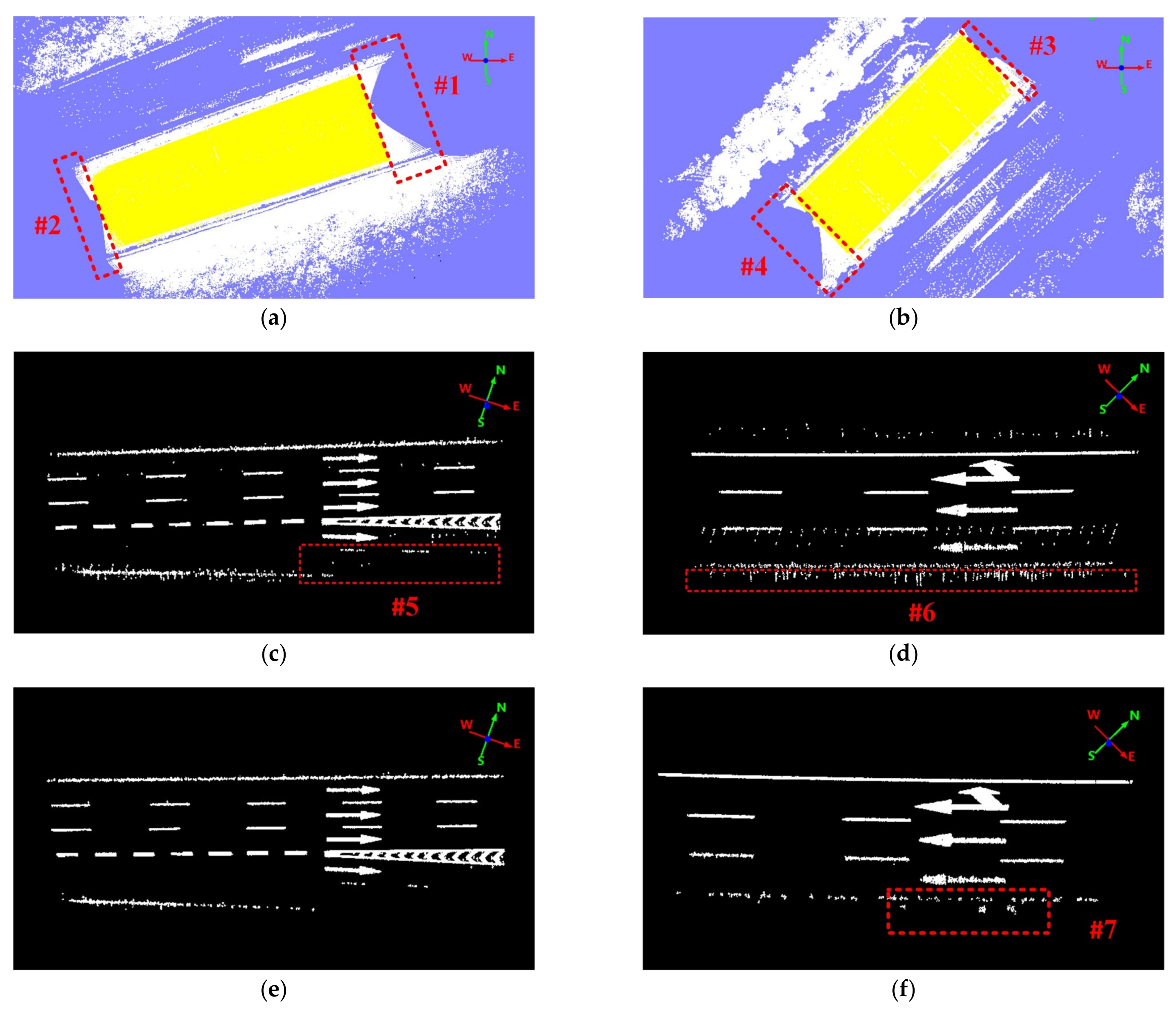
3. Result
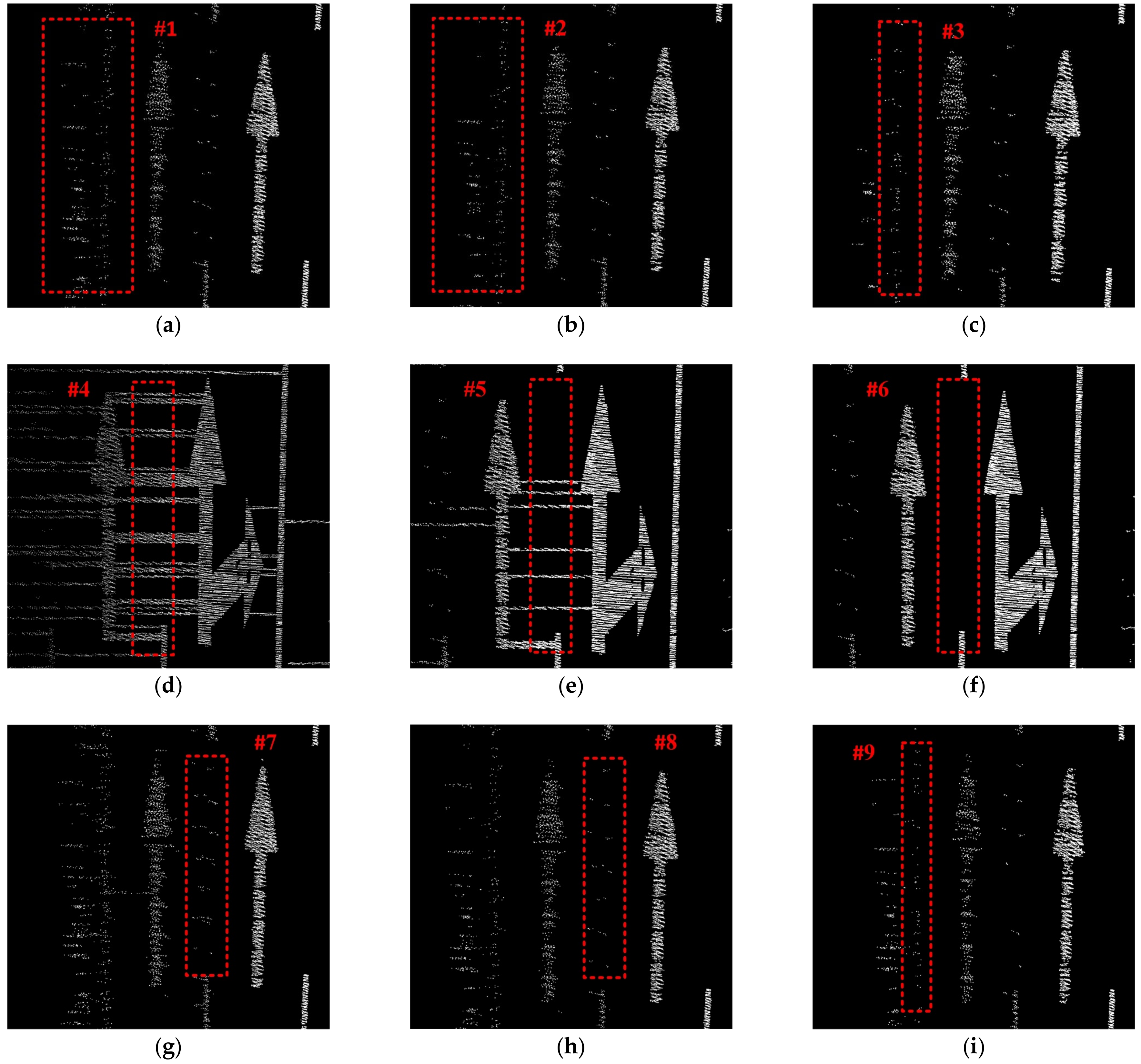
3.1. Parameter Sensitivity Analysis
3.2. Experiments
3.3. Comparative Study
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hoffmann, G.M.; Tomlin, C.J.; Montemerlo, M.; Thrun, S. Autonomous automobile trajectory tracking for off-road driving: Controller design, experimental validation and racing. In Proceedings of the American Control Conference, New York, NY, USA, 9–13 July 2007. [Google Scholar]
- Holgado-Barco, A.; Riveiro, B.; González-Aguilera, D.; Arias, P. Automatic inventory of road cross-sections from mobile laser scanning system. Comput. Aided Civ. Infrastruct. Eng. 2017, 32, 3–17. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Tan, J.; Liu, H. Rigorous boresight self-calibration of mobile and UAV LiDAR scanning systems by strip adjustment. Remote Sens. 2019, 11, 442. [Google Scholar] [CrossRef] [Green Version]
- Mandlburger, G.; Pfennigbauer, M.; Wieser, M.; Riegl, U.; Pfeifer, N. Evaluation of a novel UAV-bornet opo-bathymetric laser profiler. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 41, 933–939. [Google Scholar] [CrossRef]
- Yan, L.; Tan, J.; Liu, H.; Xie, H.; Chen, C. Automatic non-rigid registration of multi-strip point clouds from mobile laser scanning systems. Int. J. Remote Sens. 2018, 39, 1713–1728. [Google Scholar] [CrossRef]
- Glennie, C.L.; Kusari, A.; Facchin, A. Calibration and stability analysis of the VLP-16 laser scanner. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 9, 55–60. [Google Scholar] [CrossRef]
- Pierzchała, M.; Giguère, P.; Astrup, R. Mapping forests using an unmanned ground vehicle with 3D LiDAR and graph-SLAM. Comput. Electron. iAgric. 2018, 145, 217–225. [Google Scholar] [CrossRef]
- Miadlicki, K.; Pajor, M.; Sakow, M. Real-time ground filtration method for a loader crane environment monitoring system using sparse LIDAR data. In Proceedings of the 2017 IEEE International Conference on INnovations in Intelligent SysTems and Applications (INISTA), Gdynia, Poland, 3–5 July 2017. [Google Scholar]
- Yang, B.; Fang, L.; Li, Q.; Li, J. Automated extraction of road markings from mobile LiDAR point clouds. Photogramm. Eng. Remote Sens. 2012, 78, 331–338. [Google Scholar] [CrossRef]
- Guan, H.; Li, J.; Yu, Y.; Ji, Z.; Wang, C. Using mobile LiDAR data for rapidly updating road markings. IEEE Trans. Intell. Transp. Syst. 2015, 16, 2457–2466. [Google Scholar] [CrossRef]
- Kumar, P.; McElhinney, C.P.; Lewis, P.; McCarthy, T. Automated road markings extraction from mobile laser scanning data. Int. J. Appl. Earth Obs. Geoinf. 2014, 32, 125–137. [Google Scholar] [CrossRef] [Green Version]
- Jung, J.; Che, E.; Olsen, M.J.; Parrish, C. Efficient and robust lane marking extraction from mobile lidar point clouds. ISPRS J. Photogramm. Remote Sens. 2019, 147, 1–18. [Google Scholar] [CrossRef]
- Li, L.; Zhang, D.; Ying, S.; Li, Y. Recognition and reconstruction of zebra crossings on roads from mobile laser scanning data. ISPRS Int. J. Geo Inf. 2016, 5, 125. [Google Scholar] [CrossRef]
- Ma, L.; Li, Y.; Li, J.; Wang, C.; Wang, R.; Chapman, M. Mobile laser scanned point-clouds for road object detection and extraction: A Review. Remote Sens. 2018, 10, 1531. [Google Scholar] [CrossRef] [Green Version]
- Yang, B.; Liu, Y.; Dong, Z.; Liang, F.; Li, B.; Peng, X. 3D local feature BKD to extract road information from mobile laser scanning point clouds. ISPRS J. Photogramm. Remote Sens. 2017, 130, 329–343. [Google Scholar] [CrossRef]
- Yu, Y.; Li, J.; Guan, H.; Jia, F.; Cheng, W. Learning hierarchical features for automated extraction of road markings from 3-D mobile LiDAR point clouds. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 709–726. [Google Scholar] [CrossRef]
- Wang, J.; Zhao, H.; Wang, D.; Chen, Y.; Zhang, Z.; Liu, H. GPS trajectory-based segmentation and multi-filter-based extraction of expressway curbs and markings from mobile laser scanning data. Eur. J. Remote Sens. 2018, 51, 1022–1035. [Google Scholar] [CrossRef]
- Yan, L.; Liu, H.; Tan, J.; Li, Z.; Xie, H.; Chen, C. Scan line based road marking extraction from mobile LiDAR point clouds. Sensors 2016, 16, 903. [Google Scholar] [CrossRef] [PubMed]
- Soilan, M.; Riveiro, B.; Martinez-Sanchez, J.; Arias, P. Segmentation and classification of road markings using MLS data. ISPRS J. Photogramm. Remote Sens. 2017, 123, 94–103. [Google Scholar] [CrossRef]
- Wen, C.; Sun, X.; Li, J.; Wang, C.; Guo, Y.; Habib, A. A deep learning framework for road marking extraction, classification and completion from mobile laser scanning point clouds. ISPRS J. Photogramm. Remote Sens. 2019, 147, 178–192. [Google Scholar] [CrossRef]
- Chen, S.; Zhang, Z.; Zhong, R.; Zhang, L.; Ma, H.; Liu, L. A dense feature pyramid network-based deep learning model for road marking instance segmentation using MLS point clouds. IEEE Trans. Geoence Remote Sens. 2020, 1–17. [Google Scholar] [CrossRef]
- Cheng, Y.-T.; Patel, A.; Wen, C.; Bullock, D.; Habib, A. Intensity thresholding and deep learning based lane marking extraction and lane width estimation from mobile light detection and ranging (LiDAR) point clouds. Remote Sens. 2020, 12, 1379. [Google Scholar] [CrossRef]
- Tan, K.; Cheng, X. Intensity data correction based on incidence angle and distance for terrestrial laser scanner. J. Appl. Remote Sens. 2015, 9, 094094. [Google Scholar] [CrossRef]
- Alireza, K.; Michael, O.; Christopher, P.; Nicholas, W. A review of LiDAR radiometric processing: From ad hoc intensity correction to rigorous radiometric calibration. Sensors 2015, 15, 28099–28128. [Google Scholar] [CrossRef] [Green Version]
- Lalonde, J.-F.; Vandapel, N.; Huber, D.F.; Hebert, M. Natural terrain classification using three-dimensional ladar data for ground robot mobility. J. Field Robot. 2006, 23, 839–861. [Google Scholar] [CrossRef]
- Yan, L.; Li, Z.; Liu, H.; Tan, J.; Zhao, S.; Chen, C. Detection and classification of pole-like road objects from mobile LiDAR data in motorway environment. Opt. Laser Technol. 2017, 97, 272–283. [Google Scholar] [CrossRef]
- Pankaj, K.; Paul, L.; Tim, M.C. The potential of active contour models in extracting road edges from mobile laser scanning data. Infrastructures 2017, 2, 9. [Google Scholar] [CrossRef]
- Yang, B.; Dong, Z.; Liu, Y.; Liang, F.; Wang, Y. Computing multiple aggregation levels and contextual features for road facilities recognition using mobile laser scanning data. ISPRS J. Photogramm. Remote Sens. 2017, 126, 180–194. [Google Scholar] [CrossRef]
- Arias, P.; Gonzalez-Jorge, H.; Riveiro, B.; Diaz-Vilarino, L.; Martinez-Sanchez, J. Automatic detection of zebra crossings from mobile LiDAR data. Opt. Laser Technol. 2015, 70, 63–70. [Google Scholar] [CrossRef]
- Yang, B.; Fang, L.; Li, J. Semi-automated extraction and delineation of 3D roads of street scene from mobile laser scanning point clouds. ISPRS J. Photogramm. Remote Sens. 2013, 79, 80–93. [Google Scholar] [CrossRef]




| Yu’s Method | Truth | TP | FN | FP | TN | Recall (%) | Precision (%) | MCC (%) |
|---|---|---|---|---|---|---|---|---|
| Dataset I | 73,429 | 54,575 | 18,854 | 21,919 | 1,115,820 | 74 | 71 | 71 |
| Dataset II | 40,898 | 31,180 | 9718 | 2530 | 589,737 | 76 | 92 | 83 |
| Average | 75 | 82 | 77 |
| Our Method | Truth | TP | FN | FP | TN | Recall (%) | Precision (%) | MCC (%) |
|---|---|---|---|---|---|---|---|---|
| Dataset I | 73,429 | 65,097 | 8332 | 4079 | 1,605,861 | 89 | 94 | 91 |
| Dataset II | 40,898 | 36,752 | 4146 | 1588 | 883,497 | 90 | 96 | 92 |
| Average | 90 | 95 | 92 |
| Datasets | Road Surface Extraction | Road Marking Extraction | Road Marking Refinement | Total Time |
|---|---|---|---|---|
| Dataset I | 1.5 | 1.7 | 1.2 | 4.4 |
| Dataset II | 0.8 | 1.0 | 0.7 | 2.5 |
| Average | 1.15 | 1.35 | 0.95 | 3.45 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, R.; Li, Q.; Tan, J.; Li, S.; Chen, X. Accurate Road Marking Detection from Noisy Point Clouds Acquired by Low-Cost Mobile LiDAR Systems. ISPRS Int. J. Geo-Inf. 2020, 9, 608. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi9100608
Yang R, Li Q, Tan J, Li S, Chen X. Accurate Road Marking Detection from Noisy Point Clouds Acquired by Low-Cost Mobile LiDAR Systems. ISPRS International Journal of Geo-Information. 2020; 9(10):608. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi9100608
Chicago/Turabian StyleYang, Ronghao, Qitao Li, Junxiang Tan, Shaoda Li, and Xinyu Chen. 2020. "Accurate Road Marking Detection from Noisy Point Clouds Acquired by Low-Cost Mobile LiDAR Systems" ISPRS International Journal of Geo-Information 9, no. 10: 608. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi9100608