Investigating the Relationship between the Built Environment and Relative Risk of COVID-19 in Hong Kong
Abstract
:1. Introduction
2. The Built Environment and the Spread of Infectious Disease
3. Data and Methods
3.1. Study Area and Data
3.2. Assessing COVID-19 Risk
3.3. Deriving the Built-Environment Features
3.4. Exploring the Relationship between Built-Environment Features and COVID-19 Risk
4. Results
4.1. Assessing the COVID-19 Risk in Each TPU
4.2. The Relationship between Built-Environment Features and COVID-19 Risk: Results of the GPR Analysis
4.3. The Relationship between Built-Environment Features and COVID-19 Risk: Results of the GWPR Analysis
5. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Guarner, J. Three emerging coronaviruses in two decades: The story of SARS, MERS, and now COVID-19. Am. J. Clin. Pathol. 2020, 153, 420–421. [Google Scholar] [CrossRef]
- World Health Organization. Novel Coronavirus (COVID-19) Situation Report-75. 2020. Available online: https://www.who.int/docs/default-source/coronaviruse/situation-reports/20200404-sitrep-75-covid-19.pdf?sfvrsn=99251b2b_2 (accessed on 12 May 2020).
- Kupferschmidt, K.; Cohen, J. China’s Aggressive Measures Have Slowed the Coronavirus. They May not Work in Other Countries. 2020. Available online: https://www.sciencemag.org/news/2020/03/china-s-aggressive-measures-have-slowed-coronavirus-they-may-not-work-other-countries (accessed on 12 May 2020).
- Tian, H.; Liu, Y.; Li, Y.; Wu, C.H.; Chen, B.; Kraemer, M.U.; Li, B.; Cai, J.; Xu, B.; Yang, Q.; et al. An investigation of transmission control measures during the first 50 days of the COVID-19 epidemic in China. Science 2020, 368, 638–642. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Koo, J.R.; Cook, A.R.; Park, M. Interventions to mitigate early spread of COVID-19 in Singapore: A modelling study. Lancet Infect Dis. 2020, 20, 678–688. [Google Scholar] [CrossRef] [Green Version]
- Wilder-Smith, A.; Freedman, D.O. Isolation, quarantine, social distancing and community containment: Pivotal role for old-style public health measures in the novel coronavirus (2019-nCoV) outbreak. J. Travel Med. 2020, 27, taaa020. [Google Scholar] [CrossRef]
- Del Valle, S.; Hethcote, H.; Hyman, J.M.; Castillo-Chavez, C. Effects of behavioral changes in a smallpox attack model. Math. Biosci. 2005, 195, 228–251. [Google Scholar] [CrossRef]
- Fenichel, E.P.; Castillo-Chavez, C.; Ceddia, M.G.; Chowell, G.; Parra, P.A.G.; Hickling, G.J.; Holloway, G.; Horan, R.; Morin, B.; Perrings, C.; et al. Adaptive human behavior in epidemiological models. Proc. Natl. Acad. Sci. USA 2011, 108, 6306–6311. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, Y.; Atkinson, P.M.; Ettema, D. Analysis of CDC social control measures using an agent-based simulation of an influenza epidemic in a city. BMC Infect. Dis. 2011, 11, 199. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rizzo, A.; Frasca, M.; Porfiri, M. Effect of individual behavior on epidemic spreading in activity-driven networks. Phys. Rev. E 2014, 90, 042801. [Google Scholar] [CrossRef] [PubMed]
- World Health Organization. Non-Pharmaceutical Public Health Measures for Mitigating the Risk and Impact of Epidemic and Pandemic Influenza: Annex: Report of Systematic Literature Reviews. 2019. Available online: https://apps.who.int/iris/bitstream/handle/10665/329439/WHO-WHE-IHM-GIP-2019.1-eng.pdf (accessed on 12 May 2020).
- Bayham, J.; Fenichel, E.P. Impact of school closures for COVID-19 on the US health-care workforce and net mortality: A modelling study. Lancet Public Health 2020, 5, e271–e278. [Google Scholar] [CrossRef]
- Douglas, M.; Katikireddi, S.V.; Taulbut, M.; McKee, M.; McCartney, G. Mitigating the wider health effects of covid-19 pandemic response. BMJ Br. Med. J. 2020, 369, m1557. [Google Scholar] [CrossRef]
- Venkatesh, A.; Edirappuli, S. Social distancing in covid-19: What are the mental health implications? BMJ Br. Med. J. 2020, 369, m1379. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Galea, S.; Merchant, R.M.; Lurie, N. The mental health consequences of COVID-19 and physical distancing: The need for prevention and early intervention. JAMA Intern. Med. 2020, 180, 817–818. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Emeruwa, U.N.; Ona, S.; Shaman, J.L.; Turitz, A.; Wright, J.D.; Gyamfi-Bannerman, C.; Melamed, A. Associations between Built Environment, Neighborhood Socioeconomic Status, and SARS-CoV-2 Infection among Pregnant Women in New York City. JAMA Netw. 2020, 324, 390–392. [Google Scholar] [CrossRef] [PubMed]
- Frank, L.D.; Engelke, P.O. The built environment and human activity patterns: Exploring the impacts of urban form on public health. J. Plan. Lit. 2001, 16, 202–218. [Google Scholar] [CrossRef]
- Hamidi, S.; Sabouri, S.; Ewing, R. Does Density Aggravate the COVID-19 Pandemic? Early Findings and Lessons for Planners. J. Am. Plann. Assoc. 2020, 1–15. [Google Scholar] [CrossRef]
- Weber, D.J.; Rutala, W.A.; Fischer, W.A.; Kanamori, H.; Sickbert-Bennett, E.E. Emerging infectious diseases: Focus on infection control issues for novel coronaviruses (Severe Acute Respiratory Syndrome-CoV and Middle East Respiratory Syndrome-CoV), hemorrhagic fever viruses (Lassa and Ebola), and highly pathogenic avian influenza viruses, A (H5N1) and A (H7N9). Am. J. Infect. Control 2016, 44, e91–e100. [Google Scholar] [CrossRef] [Green Version]
- Casanova, L.; Rutala, W.A.; Weber, D.J.; Sobsey, M.D. Survival of surrogate coronaviruses in water. Water Res. 2009, 43, 1893–1898. [Google Scholar] [CrossRef]
- Peiris, J.S.M.; Chu, C.M.; Cheng, V.C.C.; Chan, K.S.; Hung, I.F.N.; Poon, L.L.; Law, K.I.; Tang, B.S.F.; Hon, T.Y.W.; Chan, C.S.; et al. Clinical progression and viral load in a community outbreak of coronavirus-associated SARS pneumonia: A prospective study. Lancet 2003, 361, 1767–1772. [Google Scholar] [CrossRef] [Green Version]
- Van Doremalen, N.; Bushmaker, T.; Morris, D.H.; Holbrook, M.G.; Gamble, A.; Williamson, B.N.; Tamin, A.; Harcourt, J.L.; Thornburg, N.J.; Gerber, S.I.; et al. Aerosol and surface stability of SARS-CoV-2 as compared with SARS-CoV-1. N. Engl. J. Med. 2020, 382, 1564–1567. [Google Scholar] [CrossRef]
- Handy, S.L.; Boarnet, M.G.; Ewing, R.; Killingsworth, R.E. How the built environment affects physical activity: Views from urban planning. Am. J. Prev. Med. 2002, 23, 64–73. [Google Scholar] [CrossRef]
- Yan, J.; Grantham, M.; Pantelic, J.; de Mesquita, P.J.B.; Albert, B.; Liu, F.; Ehrman, S.; Milton, D.K.; EMIT Consortium. Infectious virus in exhaled breath of symptomatic seasonal influenza cases from a college community. Proc. Natl. Acad. Sci. USA 2018, 115, 1081–1086. [Google Scholar] [CrossRef] [Green Version]
- Zhao, P.; Kwan, M.-P.; Zhou, S. The uncertain geographic context problem in the analysis of the relationships between obesity and the built environment in Guangzhou. Int. J. Environ. Res. Public Health 2018, 15, 308. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Lee, K.; Kwan, M.-P. Environmental influences on leisure-time physical inactivity in the US: An exploration of spatial non-stationarity. ISPRS Int. J. Geoinf. 2018, 7, 143. [Google Scholar] [CrossRef] [Green Version]
- Huang, J.; Liu, X.; Zhao, P.; Zhang, J.; Kwan, M.P. Interactions between bus, metro, and taxi use before and after the Chinese Spring Festival. ISPRS Int. J. Geoinf. 2019, 8, 445. [Google Scholar] [CrossRef] [Green Version]
- Zhao, P.; Xu, Y.; Liu, X.; Kwan, M.-P. Space-time dynamics of cab drivers’ stay behaviors and their relationships with built environment characteristics. Cities 2020, 101, 102689. [Google Scholar] [CrossRef]
- Rundle, A.; Neckerman, K.M.; Freeman, L.; Lovasi, G.S.; Purciel, M.; Quinn, J.; Richards, C.; Sircar, N.; Weiss, C. Neighborhood food environment and walkability predict obesity in New York City. Environ. Health Perspect. 2009, 117, 442–447. [Google Scholar] [CrossRef] [PubMed]
- Bodor, J.N.; Rice, J.C.; Farley, T.A.; Swalm, C.M.; Rose, D. The association between obesity and urban food environments. J. Urban Health 2010, 87, 771–781. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lu, Y. Using Google Street View to investigate the association between street greenery and physical activity. Landsc. Urban Plan. 2019, 191, 103435. [Google Scholar] [CrossRef]
- Lin, T.P.; Tsai, K.T.; Hwang, R.L.; Matzarakis, A. Quantification of the effect of thermal indices and sky view factor on park attendance. Landsc. Urban Plan. 2012, 107, 137–146. [Google Scholar] [CrossRef]
- Carter, S.J.; Baranauskas, M.N.; Fly, A.D. Considerations for obesity, vitamin D, and physical activity amidst the COVID-19 pandemic. Obesity 2020, 28, 1176–1177. [Google Scholar] [CrossRef] [PubMed]
- Gallè, F.; Sabella, E.A.; Molin, G.D.; Giglio, O.D.; Caggiano, G.; Onofrio, V.D.; Ferracuti, S.; Montagna, M.T.; Liguori, G.; Orsi, G.B.; et al. Understanding Knowledge and Behaviors Related to CoViD-19 Epidemic in Italian Undergraduate Students: The EPICO Study. Int. J. Environ. Res. Public Health 2020, 17, 3481. [Google Scholar] [CrossRef] [PubMed]
- Leyden, K.M. Social capital and the built environment: The importance of walkable neighborhoods. Am. J. Public Health 2003, 93, 1546–1551. [Google Scholar] [CrossRef] [PubMed]
- Mouratidis, K. Built environment and social well-being: How does urban form affect social life and personal relationships? Cities 2018, 74, 7–20. [Google Scholar] [CrossRef]
- Chen, H.; Jia, B.; Lau, S. Sustainable urban form for Chinese compact cities: Challenges of a rapid urbanized economy. Habitat Int. 2008, 32, 28–40. [Google Scholar] [CrossRef]
- Pinter-Wollman, N.; Jelić, A.; Wells, N.M. The impact of the built environment on health behaviours and disease transmission in social systems. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2018, 373, 20170245. [Google Scholar] [CrossRef]
- Bajardi, P.; Poletto, C.; Ramasco, J.J.; Tizzoni, M.; Colizza, V.; Vespignani, A. Human mobility networks, travel restrictions, and the global spread of 2009 H1N1 pandemic. PLoS ONE 2011, 6, e16591. [Google Scholar] [CrossRef] [Green Version]
- Chinazzi, M.; Davis, J.T.; Ajelli, M.; Gioannini, C.; Litvinova, M.; Merler, S.; Piontti, A.P.y.; Mu, K.; Rossi, L.; Sun, K.; et al. The effect of travel restrictions on the spread of the 2019 novel coronavirus (COVID-19) outbreak. Science 2020, 368, 395–400. [Google Scholar] [CrossRef] [Green Version]
- Samuelsson, K.; Barthel, S.; Colding, J.; Macassa, G.; Giusti, M. Urban nature as a source of resilience during social distancing amidst the coronavirus pandemic. OSF Prepr. 2020. [Google Scholar] [CrossRef]
- Van Bavel, J.J.; Baicker, K.; Boggio, P.S.; Capraro, V.; Cichocka, A.; Cikara, M.; Crockett, M.J.; Crum, A.J.; Douglas, K.M.; Druckman, J.N.; et al. Using social and behavioural science to support COVID-19 pandemic response. Nat. Hum. Behav. 2020, 4, 460–471. [Google Scholar] [CrossRef] [PubMed]
- Dietz, L.; Horve, P.F.; Coil, D.A.; Fretz, M.; Eisen, J.A.; Van Den Wymelenberg, K. 2019 novel coronavirus (COVID-19) pandemic: Built environment considerations to reduce transmission. mSystems 2020, 5, e00245-20. [Google Scholar] [CrossRef] [Green Version]
- Feng, Y.; Marchal, T.; Sperry, T.; Yi, H. Influence of wind and relative humidity on the social distancing effectiveness to prevent COVID-19 airborne transmission: A numerical study. J. Aerosol Sci. 2020, 147, 105585. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Wong, M.S.; Menenti, M.; Nichol, J. Modeling the effective emissivity of the urban canopy using sky view factor. ISPRS J. Photogramm. Remote Sens. 2015, 105, 211–219. [Google Scholar] [CrossRef]
- Oke, T.R. Street design and urban canopy layer climate. Energy Build. 1988, 11, 103–113. [Google Scholar] [CrossRef]
- Lai, P.-C.; Low, C.-T.; Tse, W.-S.C.; Tsui, C.-K.; Lee, H.; Hui, P.-K. Risk of tuberculosis in high-rise and high density dwellings: An exploratory spatial analysis. Environ. Pollut. 2013, 183, 40–45. [Google Scholar] [CrossRef] [Green Version]
- Alexander, C.; Ishikawa, S.; Silverstein, M. A Pattern Language: Towns, Buildings, Construction; Oxford University Press: Oxford, UK, 1977. [Google Scholar]
- Lee, K.; Park, J.S.; Goh, S.; Choi, M. Accessibility measurement in transportation networks and application to the Seoul bus system. Geogr. Anal. 2019, 51, 339–353. [Google Scholar] [CrossRef]
- Lee, K.; Lee, H.Y. A new algorithm for graph-theoretic nodal accessibility measurement. Geogr. Anal. 1998, 30, 1–14. [Google Scholar] [CrossRef]
- Kauhl, B.; Heil, J.; Hoebe, C.J.; Schweikart, J.; Krafft, T.; Dukers-Muijrers, N.H. The spatial distribution of hepatitis C virus infections and associated determinants—An application of a geographically weighted Poisson regression for evidence-based screening interventions in hotspots. PLoS ONE 2015, 10, e0135656. [Google Scholar] [CrossRef]
- Brunsdon, C.; Fotheringham, A.S.; Charlton, M.E. Geographically weighted regression: A method for exploring spatial nonstationarity. Geogr Anal. 1996, 28, 281–298. [Google Scholar] [CrossRef]
- Desjardins, M.R.; Hohl, A.; Delmelle, E.M. Rapid surveillance of COVID-19 in the United States using a prospective space-time scan statistic: Detecting and evaluating emerging clusters. Appl. Geogr. 2020, 118, 102202. [Google Scholar] [CrossRef]
- Gatto, M.; Bertuzzo, E.; Mari, L.; Miccoli, S.; Carraro, L.; Casagrandi, R.; Rinaldo, A. Spread and dynamics of the COVID-19 epidemic in Italy: Effects of emergency containment measures. Proc. Natl. Acad. Sci. USA 2020, 117, 10484–10491. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, Q.C.; Huang, Y.; Kumar, A.; Duan, H.; Keralis, J.M.; Dwivedi, P.; Meng, H.-W.; Brunisholz, K.D.; Jay, J.; Javanmardi, M.; et al. Using 164 Million Google Street View Images to Derive Built Environment Predictors of COVID-19 Cases. Int. J. Environ. Res. Public Health 2020, 17, 6359. [Google Scholar] [CrossRef]
- Amram, O.; Amiri, S.; Lutz, R.B.; Rajan, B.; Monsivais, P. Development of a vulnerability index for diagnosis with the novel coronavirus, COVID-19, in Washington State, USA. Health Place 2020, 64, 102377. [Google Scholar] [CrossRef] [PubMed]
- Xiong, Y.; Wang, Y.; Chen, F.; Zhu, M. Spatial Statistics and Influencing Factors of the COVID-19 Epidemic at Both Prefecture and County Levels in Hubei Province, China. Int. J. Environ. Res. Public Health 2020, 17, 3903. [Google Scholar] [CrossRef]
- Cowling, B.J.; Ali, S.T.; Ng, T.W.; Tsang, T.K.; Li, J.C.; Fong, M.W.; Liao, Q.; Kwan, M.Y.; Lee, S.L.; Chiu, S.S.; et al. Impact assessment of non-pharmaceutical interventions against coronavirus disease 2019 and influenza in Hong Kong: An observational study. Lancet Public Health 2020, 5, e279–e288. [Google Scholar] [CrossRef]




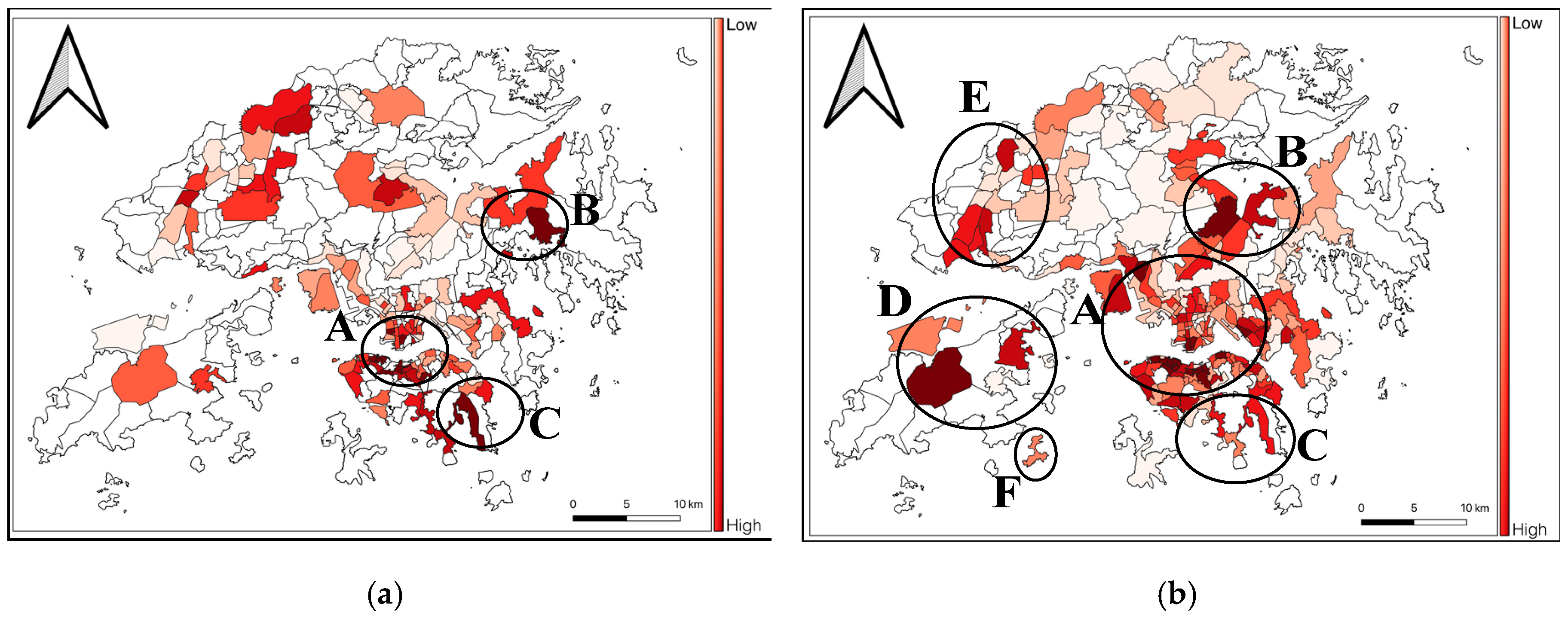


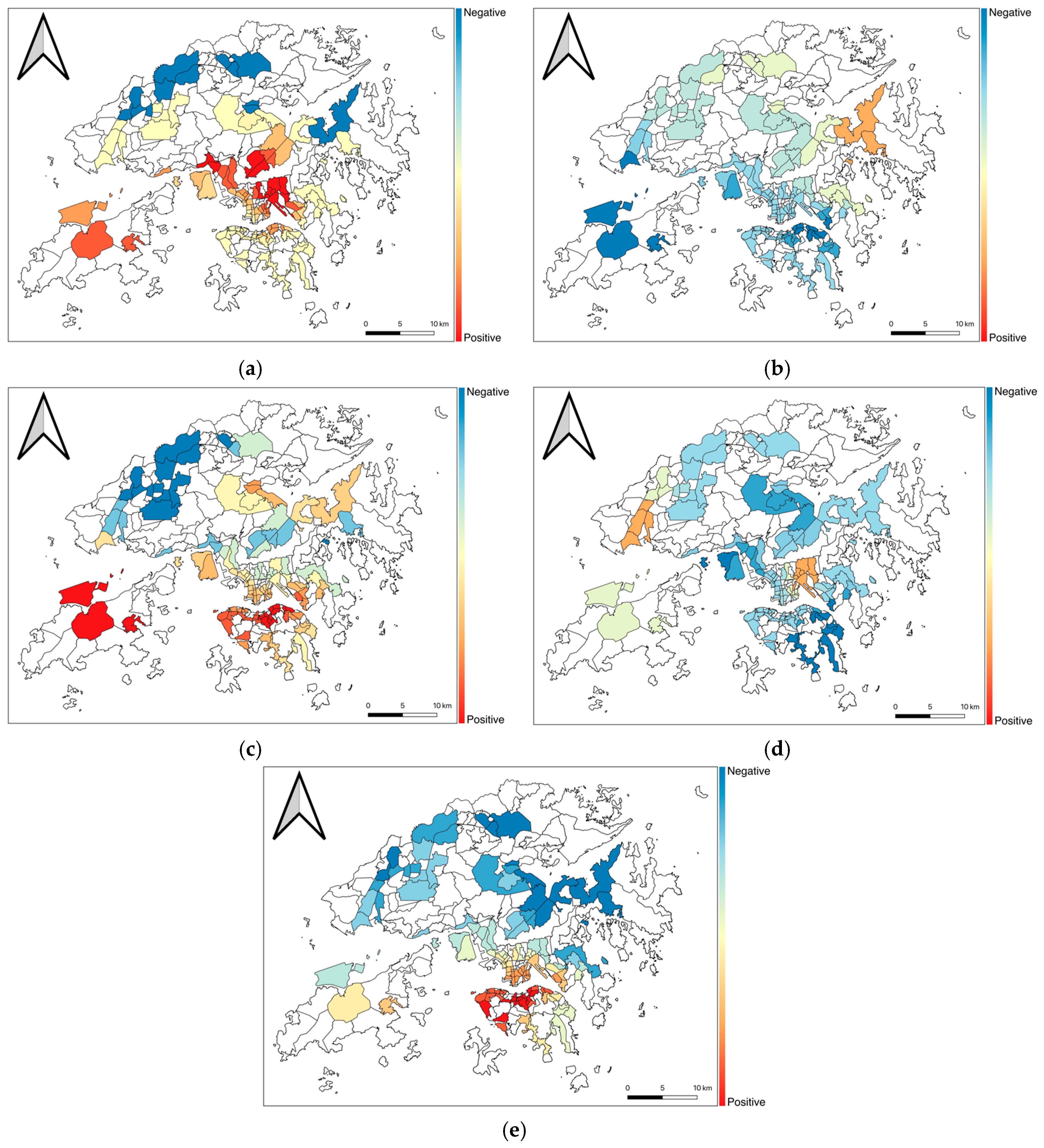
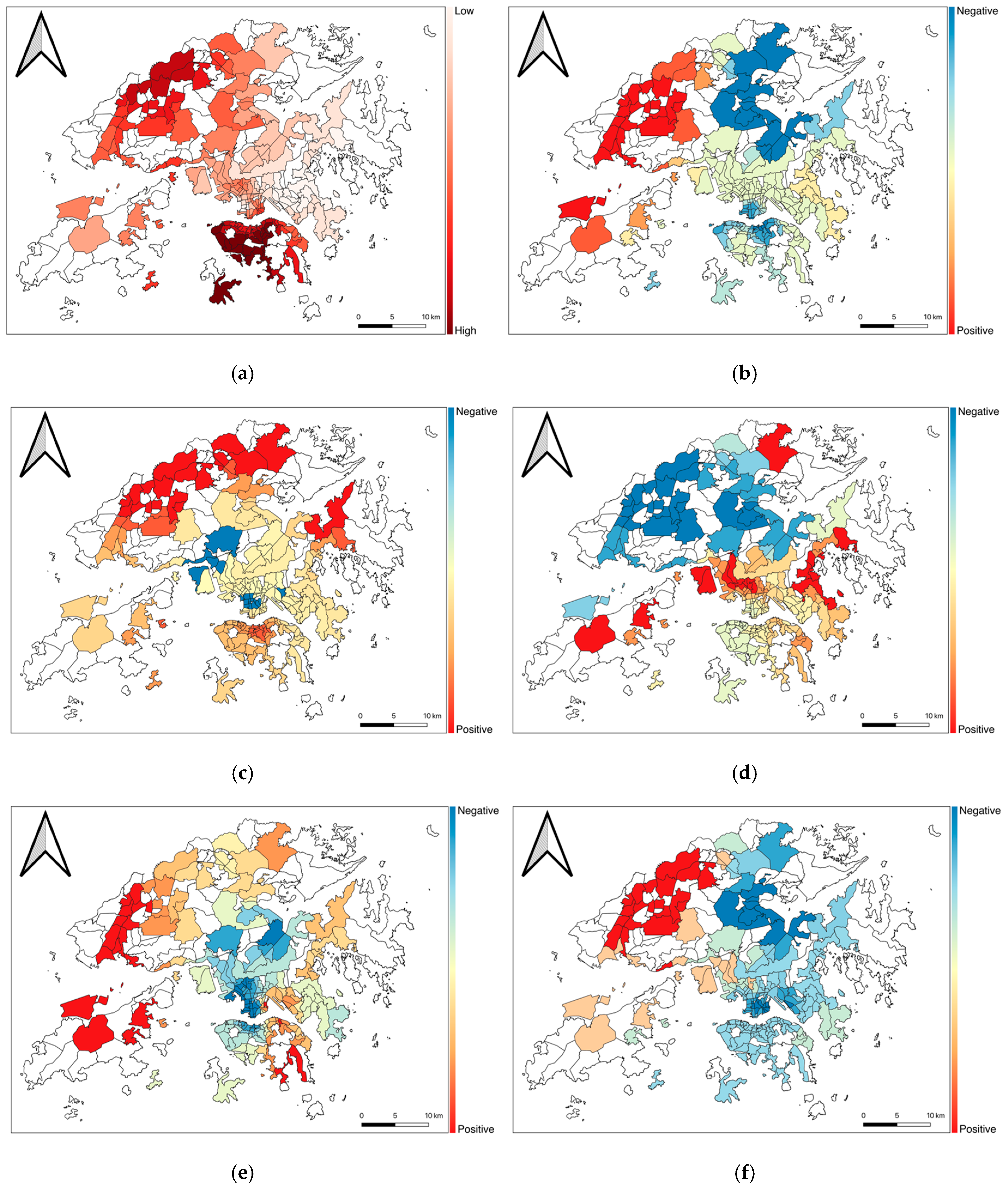
| Name | Abbreviations | Dependent Variables |
|---|---|---|
| Nodal accessibility | NA | R2 |
| Population density | PD | R1 and R2 |
| Private residential | PR | R1 and R2 |
| Commercial density | CD | R2 |
| Green space density | GSD | R2 |
| Building height | BH | R1 |
| Transport facility density | TF | R1 |
| Land-use diversity | LUD | R1 |
| Sky view | SV | R2 |
| Abbreviations | Mean | Standard Deviation | |
|---|---|---|---|
| Independent variables | |||
| Nodal accessibility | NA | 0.20 | 0.23 |
| Population density | PD | 30,042.00 | 40,741.63 |
| Private residential | PR | 0.08 | 0.11 |
| Commercial density | CD | 0.03 | 0.06 |
| Green space density | GSD | 0.42 | 0.34 |
| Building height | BH | 22.71 | 16.04 |
| Transport facility density | TF | 0.13 | 0.13 |
| Land-use diversity | LUD | 0.61 | 0.18 |
| Sky view | SV | 0.78 | 0.14 |
| Dependent variables | |||
| Risk 1 | R1 | 0.18 | 0.23 |
| Risk 2 | R2 | 11.97 | 13.21 |
| GPR Model (R1) | |||||
|---|---|---|---|---|---|
| Variable | Abbreviations | Coef. | S.E. | p-value | VIF |
| Transport facilities density | TF | 2.50 | 0.54 | 0.000 *** | 3.84 |
| Population density | PD | −4.00 | 0.48 | 0.000 *** | 2.35 |
| Private residential | PR | 3.21 | 0.74 | 0.000 *** | 2.76 |
| Land-use diversity | LUD | −1.13 | 0.19 | 0.000 *** | 1.78 |
| Building height | BH | 0.90 | 0.37 | 0.015 ** | 4.68 |
| Residual deviance = 97 | |||||
| Degrees of freedom = 96 | |||||
| AIC = 331.21 | |||||
| Adjusted percent deviance explained = 0.44 | |||||
| GPR Model (R2) | |||||
| Variable | Abbreviations | Coef. | S.E. | p-value | VIF |
| Nodal accessibility | NA | 1.78 | 0.11 | 0.000 *** | 2.48 |
| Population density | PD | −1.59 | 0.17 | 0.000 *** | 3.32 |
| Private residential | PR | 2.58 | 0.28 | 0.000 *** | 2.82 |
| Commercial density | CD | 1.98 | 0.40 | 0.000 *** | 1.27 |
| Green space density | GSD | 0.95 | 0.15 | 0.000 *** | 2.03 |
| Sky view | SV | −4.82 | 0.42 | 0.000 *** | 4.17 |
| Residual deviance = 187 | |||||
| Degrees of freedom = 181 | |||||
| AIC = 1513.14 | |||||
| Adjusted percent deviance explained = 0.58 | |||||
| Goodness of Fit | |||
|---|---|---|---|
| Model | AIC | Percent Deviance Explained | Adjusted Percent Deviance Explained |
| R1 | |||
| GPR | 429.71 | 0.46 | 0.44 |
| GWPR | 149.42 | 0.71 | 0.63 |
| R2 | |||
| GPR | 1513.14 | 0.59 | 0.58 |
| GWPR | 512.93 | 0.81 | 0.74 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, J.; Kwan, M.-P.; Kan, Z.; Wong, M.S.; Kwok, C.Y.T.; Yu, X. Investigating the Relationship between the Built Environment and Relative Risk of COVID-19 in Hong Kong. ISPRS Int. J. Geo-Inf. 2020, 9, 624. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi9110624
Huang J, Kwan M-P, Kan Z, Wong MS, Kwok CYT, Yu X. Investigating the Relationship between the Built Environment and Relative Risk of COVID-19 in Hong Kong. ISPRS International Journal of Geo-Information. 2020; 9(11):624. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi9110624
Chicago/Turabian StyleHuang, Jianwei, Mei-Po Kwan, Zihan Kan, Man Sing Wong, Coco Yin Tung Kwok, and Xinyu Yu. 2020. "Investigating the Relationship between the Built Environment and Relative Risk of COVID-19 in Hong Kong" ISPRS International Journal of Geo-Information 9, no. 11: 624. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi9110624





