Worldwide Detection of Informal Settlements via Topological Analysis of Crowdsourced Digital Maps
Abstract
:1. Introduction
1.1. Context
1.2. Prior Work and Novel Contributions
2. Materials and Methods
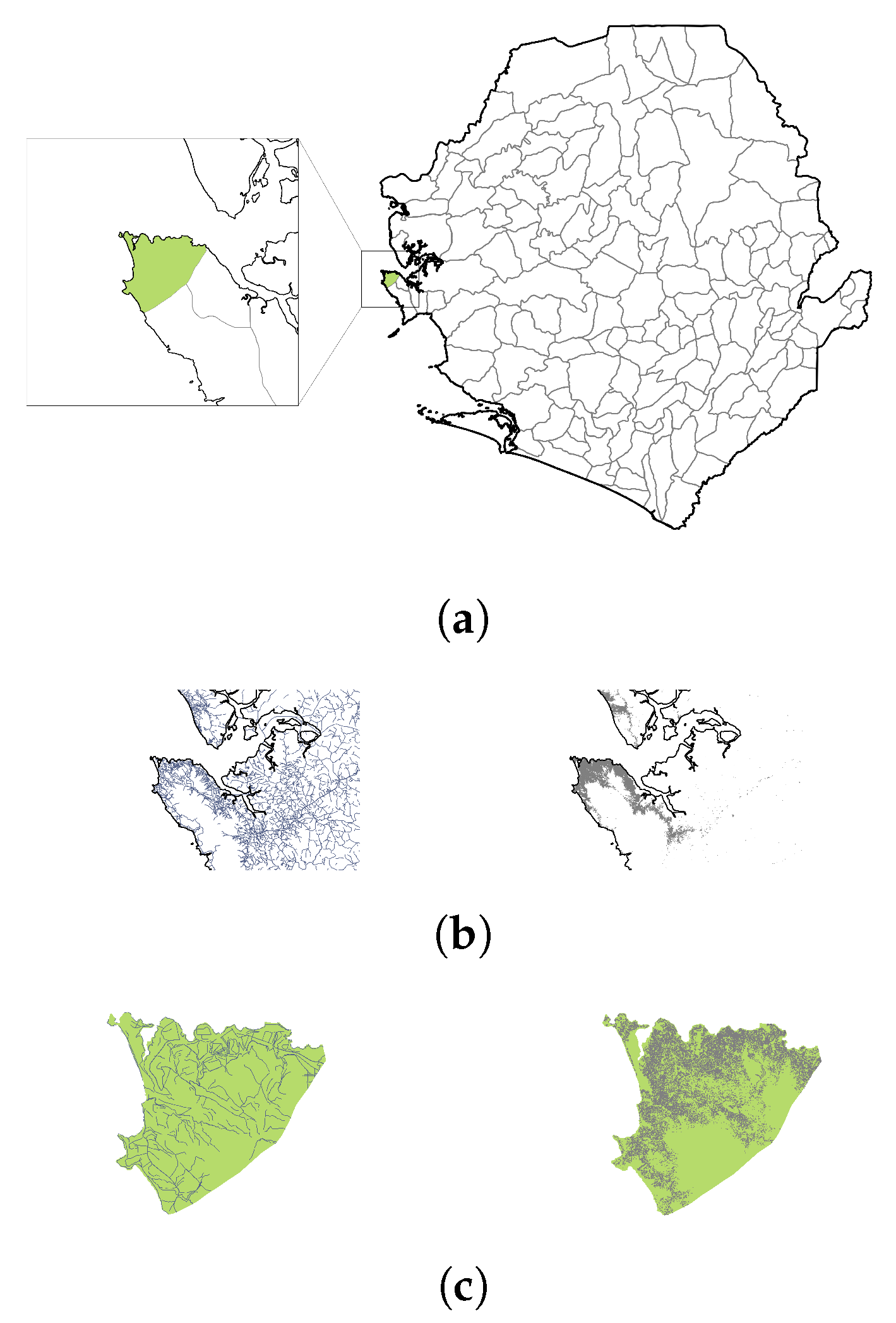
2.1. Geospatial Data and Computation
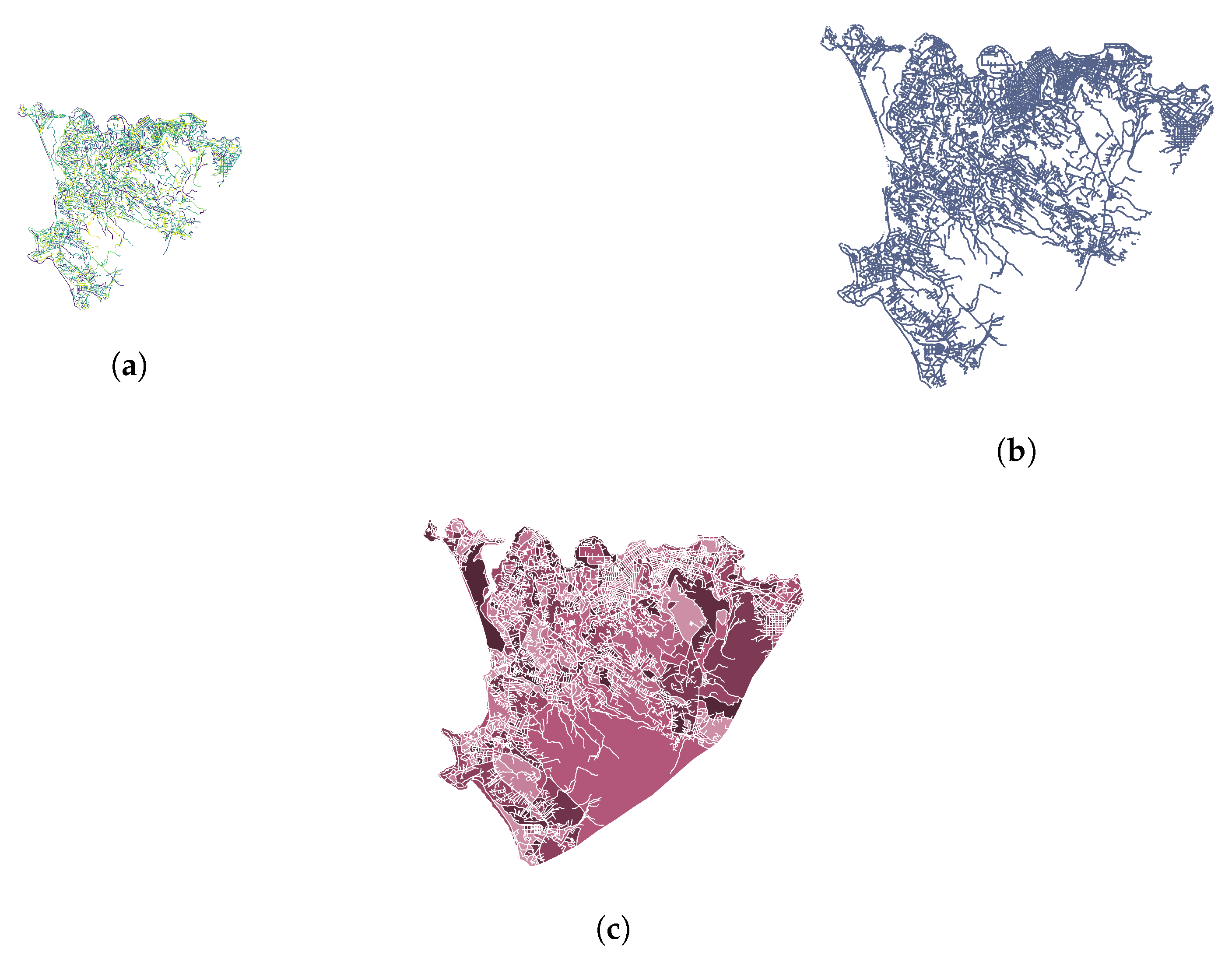
2.2. Street Block Geometry Determination
2.3. Land Parcel Map Construction
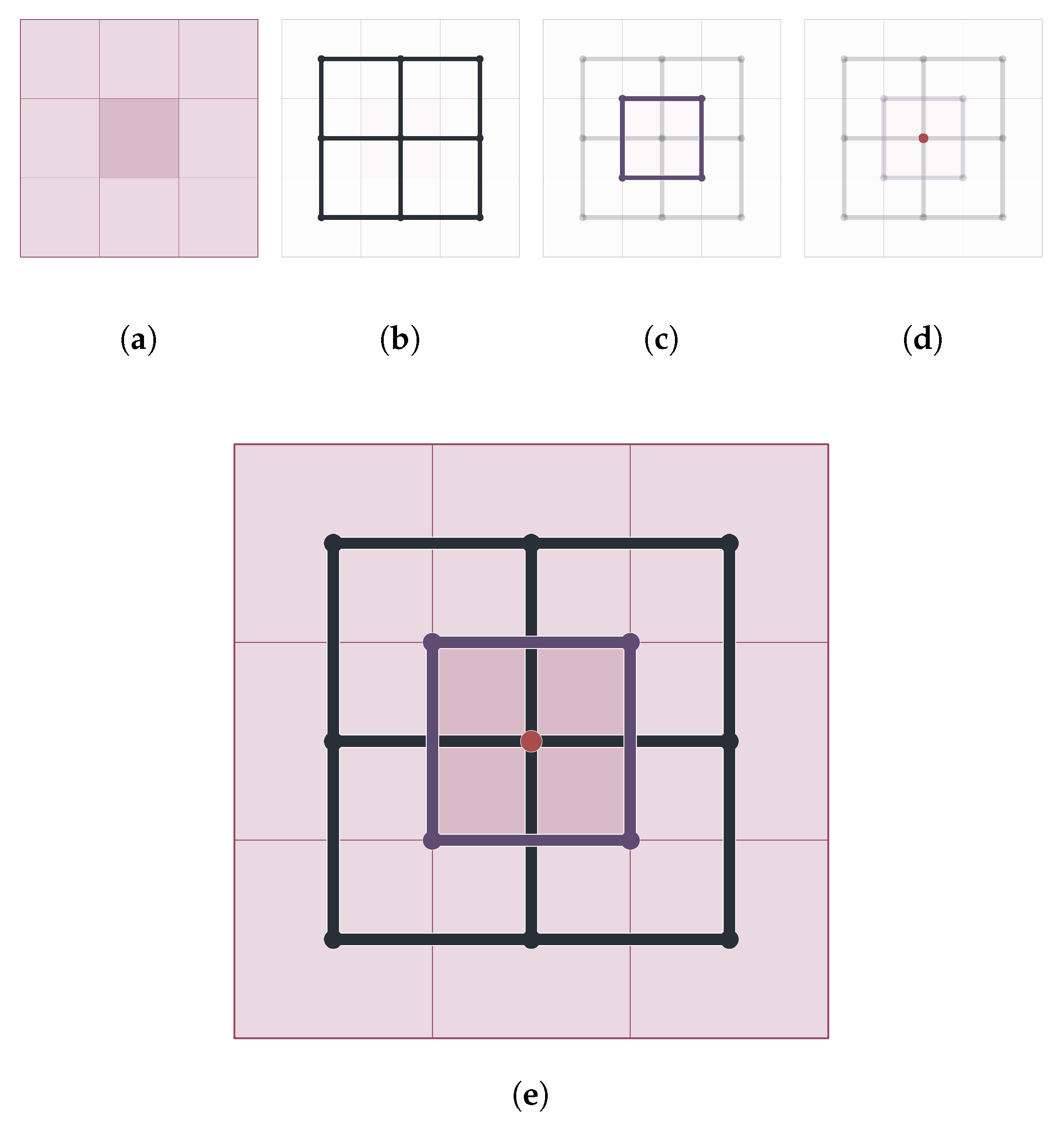
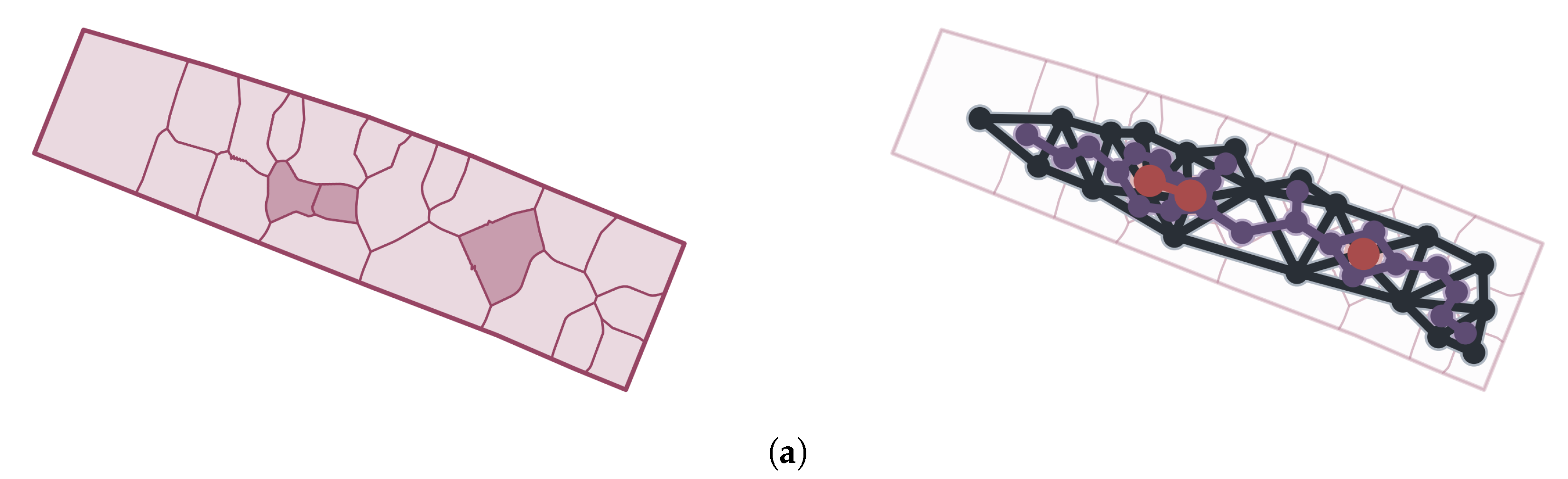
2.4. Estimation of Street Block Topology and Access to Buildings
2.5. Map of Inaccessible and Under-Serviced Neighborhoods
2.6. Estimation of Minimal Street Network Extensions for Universal Connectivity
3. Results
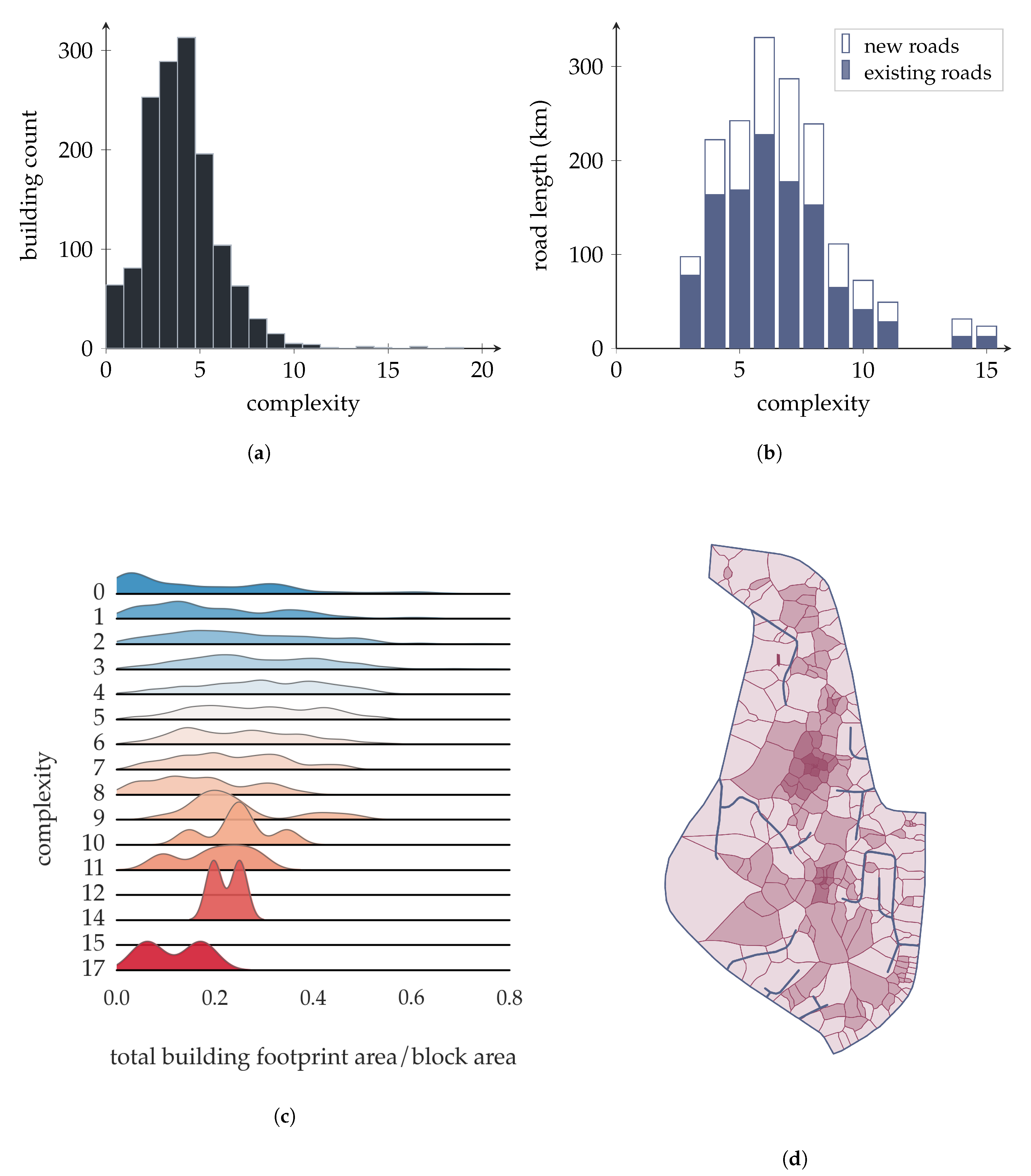
3.1. Analysis of Complexity and Other Block-Level Metrics
3.2. Worldwide Analysis of Block Complexity
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| OSM | OpenStreetMap |
| LMIC | Low- and Middle-Income Country |
| SSA | Sub-Saharan Africa |
| GADM | Database of Global Administrative Areas |
| EO | Earth observation |
| OOA | object-oriented analysis |
| CNN | convolutional neural network |
| NGO | Non-Governmental Organization |
| GIS | Geographic Information System |
References
- United Nations Development Programme. Human Development Indices and Indicators: 2018 Statistical Update; UNDP: New York, NY, USA, 2018. [Google Scholar]
- United Nations Human Settlements Programme (UN-Habitat). Indicator 11.1.1: Proportion of Urban Population Living in Slums, Informal Settlements or Inadequate Housing. Available online: https://unstats.un.org/sdgs/metadata/files/Metadata-11-01-01.pdf (accessed on 12 September 2020).
- UN-Habitat. The challenge of slums: Global report on human settlements 2003. Manag. Environ. Qual. Int. J. 2004, 15, 337–338. [Google Scholar]
- Saunders, D. Arrival City: How the Largest Migration in History Is Reshaping Our World; Vintage: New York, NY, USA, 2011. [Google Scholar]
- United Nations. World Urbanization Prospects: The 2014 Revision; United Nations Department of Economics and Social Affairs, Population Division: New York, NY, USA, 2015; Volume 41. [Google Scholar]
- Satterthwaite, D. The impact of urban development on risk in sub-Saharan Africa’s cities with a focus on small and intermediate urban centres. Int. J. Disaster Risk Reduct. 2017, 26, 16–23. [Google Scholar] [CrossRef]
- De Boeck, F.; Cassiman, A.; Van Wolputte, S. Recentering the City: An Anthropology of Secondary Cities in Africa; Department of Architecture, University of Pretoria: Pretoria, South Africa, 2010; pp. 33–41. [Google Scholar]
- Andreasen, M.H.; Agergaard, J.; Kiunsi, R.B.; Namangaya, A.H. Urban transformations, migration and residential mobility patterns in African secondary cities. Geogr. Tidsskr.-Dan. J. Geogr. 2017, 117, 93–104. [Google Scholar] [CrossRef] [Green Version]
- Pieterse, D.E.; Parnell, S. Africa’s Urban Revolution; Zed Books Ltd.: London, UK, 2014. [Google Scholar]
- Manda, M.Z. Where there is no local government: Addressing disaster risk reduction in a small town in Malawi. Environ. Urban. 2014, 26, 586–599. [Google Scholar] [CrossRef] [Green Version]
- Farouk, B.R.; Owusu, M. “If in doubt, count”: The role of community-driven enumerations in blocking eviction in Old Fadama, Accra. Environ. Urban. 2012, 24, 47–57. [Google Scholar] [CrossRef]
- Makau, J.; Dobson, S.; Samia, E. The five-city enumeration: The role of participatory enumerations in developing community capacity and partnerships with government in Uganda. Environ. Urban. 2012, 24, 31–46. [Google Scholar] [CrossRef]
- Brelsford, C.; Lobo, J.; Hand, J.; Bettencourt, L.M. Heterogeneity and scale of sustainable development in cities. Proc. Natl. Acad. Sci. USA 2017, 114, 8963–8968. [Google Scholar] [CrossRef] [Green Version]
- Brelsford, C.; Martin, T.; Hand, J.; Bettencourt, L.M. Toward cities without slums: Topology and the spatial evolution of neighborhoods. Sci. Adv. 2018, 4, eaar4644. [Google Scholar] [CrossRef] [Green Version]
- Kit, O.; Lüdeke, M. Automated detection of slum area change in Hyderabad, India using multitemporal satellite imagery. ISPRS J. Photogramm. Remote Sens. 2013, 83, 130–137. [Google Scholar] [CrossRef] [Green Version]
- Kohli, D.; Sliuzas, R.; Stein, A. Urban slum detection using texture and spatial metrics derived from satellite imagery. J. Spat. Sci. 2016, 61, 405–426. [Google Scholar] [CrossRef] [Green Version]
- Taubenböck, H.; Kraff, N.J.; Wurm, M. The morphology of the Arrival City—A global categorization based on literature surveys and remotely sensed data. Appl. Geogr. 2018, 92, 150–167. [Google Scholar] [CrossRef]
- Zhu, X.X.; Tuia, D.; Mou, L.; Xia, G.S.; Zhang, L.; Xu, F.; Fraundorfer, F. Deep learning in remote sensing: A comprehensive review and list of resources. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–36. [Google Scholar] [CrossRef] [Green Version]
- Jean, N.; Burke, M.; Xie, M.; Davis, W.M.; Lobell, D.B.; Ermon, S. Combining Satellite Imagery and Machine Learning to Predict Poverty. Science 2016, 353, 790–794. Available online: https://science.sciencemag.org/content/353/6301/790.full.pdf (accessed on 12 September 2020). [CrossRef] [PubMed] [Green Version]
- Suraj, P.K.; Gupta, A.; Sharma, M.; Paul, S.; Banerjee, S. On monitoring development using high resolution satellite images. arXiv 2017, arXiv:abs/1712.02282. [Google Scholar]
- Albert, A.; Kaur, J.; Gonzalez, M.C. Using Convolutional Networks and Satellite Imagery to Identify Patterns in Urban Environments at a Large Scale. In Proceedings of the KDD’17, 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Halifax, NS, Canada, 13–17 August 2017; Association for Computing Machinery: New York, NY, USA, 2017; pp. 1357–1366. [Google Scholar] [CrossRef] [Green Version]
- Maiya, S.; Babu, S. Slum Segmentation and Change Detection: A Deep Learning Approach. arXiv 2018, arXiv:1811.07896. [Google Scholar]
- Demir, I.; Koperski, K.; Lindenbaum, D.; Pang, G.; Huang, J.; Basu, S.; Hughes, F.; Tuia, D.; Raska, R. Deepglobe 2018: A challenge to parse the earth through satellite images. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Salt Lake City, UT, USA, 18–22 June 2018; pp. 172–17209. [Google Scholar]
- Wurm, M.; Stark, T.; Zhu, X.X.; Weigand, M.; Taubenböck, H. Semantic segmentation of slums in satellite images using transfer learning on fully convolutional neural networks. ISPRS J. Photogramm. Remote Sens. 2019, 150, 59–69. [Google Scholar] [CrossRef]
- Zeiler, M.D.; Fergus, R. Visualizing and Understanding Convolutional Networks. In Computer Vision—ECCV 2014; Fleet, D., Pajdla, T., Schiele, B., Tuytelaars, T., Eds.; Springer International Publishing: Cham, Switzerland, 2014; pp. 818–833. [Google Scholar]
- Kuffer, M.; Pfeffer, K.; Sliuzas, R. Slums from Space—15 Years of Slum Mapping Using Remote Sensing. Remote Sens. Rev. 2016, 8, 455. [Google Scholar] [CrossRef] [Green Version]
- Kohli, D.; Sliuzas, R.; Kerle, N.; Stein, A. An ontology of slums for image-based classification. Comput. Environ. Urban Syst. 2012, 36, 154–163. [Google Scholar] [CrossRef]
- Filho, M.; Sobreira, F. Accuracy of lacunarity algorithms in texture classification of high spatial resolution images from urban areas. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, 37, 417–422. [Google Scholar]
- Mahabir, R.; Croitoru, A.; Agouris, P.; Stefanidis, A. A Critical Review of High and Very High-Resolution Remote Sensing Approaches for Detecting and Mapping Slums: Trends, Challenges and Emerging Opportunities. Urban Sci. Rev. 2018, 2, 8. [Google Scholar] [CrossRef] [Green Version]
- Hofmann, P. Detecting informal settlements from IKONOS image data using methods of object oriented image analysis—An example from Cape Town (South Africa). Remote Sens. Urban Areas 2001, 107–118. [Google Scholar]
- Brelsford, C.; Martin, T.; Bettencourt, L.M. Optimal reblocking as a practical tool for neighborhood development. Environ. Plan. B Urban Anal. City Sci. 2019, 46, 303–321. [Google Scholar] [CrossRef]
- OpenStreetMap—About. Available online: https://www.openstreetmap.org/about (accessed on 12 September 2020).
- Barrington-Leigh, C.; Millard-Ball, A. The world’s user-generated road map is more than 80% complete. PLoS ONE 2017, 12, e0180698. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hare, J. OpenStreetMap: Help Us #MapLesotho. Available online: https://opensource.com/government/15/1/virtual-journey-through-maplesotho-shawn-day (accessed on 12 September 2020).
- MapLesotho—Planning and OpenStreetMap Project. Available online: https://www.maplesotho.com/about/ (accessed on 12 September 2020).
- Marx, B.; Stoker, T.; Suri, T. The economics of slums in the developing world. J. Econ. Perspect. 2013, 27, 187–210. [Google Scholar] [CrossRef] [Green Version]
- Mahabir, R.; Agouris, P.; Stefanidis, A.; Croitoru, A.; Crooks, A.T. Detecting and mapping slums using open data: A case study in Kenya. Int. J. Digit. Earth 2020, 13, 683–707. [Google Scholar] [CrossRef]
- Parcel—OpenStreetMap Wiki. Available online: https://wiki.openstreetmap.org/wiki/Parcel (accessed on 12 September 2020).
- Robins, G.; Zelikovsky, A. Improved Steiner Tree Approximation in Graphs. In Proceedings of the SODA’00, Eleventh Annual ACM-SIAM Symposium on Discrete Algorithms, San Francisco, CA, USA, 9–11 January 2000; Society for Industrial and Applied Mathematics: San Francisco, CA, USA, 2000; pp. 770–779. [Google Scholar]
- Highways—OpenStreetMap Wiki. Available online: https://wiki.openstreetmap.org/wiki/Highways (accessed on 12 September 2020).
- Arabindoo, P. Rhetoric of the ‘slum’: Rethinking urban poverty. City 2011, 15, 636–646. [Google Scholar] [CrossRef]
- Brown-Luthango, M.; Reyes, E.; Gubevu, M. Informal settlement upgrading and safety: Experiences from Cape Town, South Africa. J. Hous. Built Environ. 2017, 32, 471–493. [Google Scholar] [CrossRef]
- Tshabalala, T.; Mxobo, S. Reblocking as an Attempt at Reconfiguring and Improving Socio-Economic Conditions in Informal Settlements: The Case of Mtshini Wam, Cape Town. In Planning Africa 2014; Making Great Places: Durban, South Africa, 2014; p. 240. [Google Scholar]
- Alexander, C. The Timeless Way of Building; Oxford University Press: Oxford, UK, 1979. [Google Scholar]
- Kostof, S. The City Shaped: Urban Patterns and Meanings Through History; Bulfinch; Reprint Edition; Thames and Hudson: London, UK, 1993. [Google Scholar]






| Layer | Tags |
|---|---|
| lines | natural = ‘coastline’ |
| non-null waterway | |
| non-null building | |
| multipolygons | non-null building |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soman, S.; Beukes, A.; Nederhood, C.; Marchio, N.; Bettencourt, L.M.A. Worldwide Detection of Informal Settlements via Topological Analysis of Crowdsourced Digital Maps. ISPRS Int. J. Geo-Inf. 2020, 9, 685. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi9110685
Soman S, Beukes A, Nederhood C, Marchio N, Bettencourt LMA. Worldwide Detection of Informal Settlements via Topological Analysis of Crowdsourced Digital Maps. ISPRS International Journal of Geo-Information. 2020; 9(11):685. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi9110685
Chicago/Turabian StyleSoman, Satej, Anni Beukes, Cooper Nederhood, Nicholas Marchio, and Luís M. A. Bettencourt. 2020. "Worldwide Detection of Informal Settlements via Topological Analysis of Crowdsourced Digital Maps" ISPRS International Journal of Geo-Information 9, no. 11: 685. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi9110685





