1. Introduction
When we look at maps, “we see symbols spread out on the space of a document, on paper or a computer screen” and we expect these symbols to refer to geographic space [
1] (p. 21). Through the mediation of signs, maps enable us to relate to spatial phenomena and events from a viewpoint beyond direct experience [
2]. By this, maps enable us to imagine near as well as distant events, some of which we would never encounter otherwise. As such, cartographic maps are a form of communication, a means of conceiving, articulating, and structuring the human world [
3].
However, albeit a map may be designed to convey a single focus of interest, it does not convey a single universal message [
4]. The elements of a map are independent associative signs and symbols with a reference fixed by convention but not fixed by a single, unequivocal reference [
5,
6]. The map-making process must, therefore, follow particularly informed choices and deliberate decisions since the variety of methods and visual variables available to represent information allow for strikingly different results based on a single dataset [
4].
One of the first decisions made by the cartographer concerns the type of symbolization to employ for a given topic [
7]. Yet, to this day, the cartographer faces the challenge—as well as the creative joy—of near-infinite variations of signs and symbols to choose from. This challenging fact is addressed by cartographic semiotic frameworks, which aim to provide theoretical and practical guidance for cartographic design decisions. Still, which visual variables are most suitable for a given context? Which ones most congruent with a given type of spatial information, object, or phenomenon? While existing semiotic frameworks provide some theoretical direction, the selection for the most adequate visual signifier remains a difficult task [
8]. At the same time, cartographic semiotic frameworks have so far predominantly addressed the dimension of cognitive, analytical congruence to help guide the selection between different types of visual variables [
5]. These frameworks, however, do not encompass the dimensions of contextual congruences, such as when to employ a particular shape symbol for a given type of content. Such decisions are, yet, crucial, since they will affect how map-readers respond to the cartographic representation [
9,
10].
This research, therefore, draws attention to cartographic symbols as communication vehicles of contextual congruence. Point symbols in the form of different shapes are considered a core visual variable in cartography as well as over a wide range of visual disciplines [
5,
11,
12]. In cartography, point symbols are prevalently employed in thematic maps to represent nominal data and to refer to and to locate geospatial events and objects. This research introduces the principle of contextual congruence to study the correspondence between shape symbols and different geospatial contents. This paper, first, outlines semiotic perspectives on the dimensions and relations of signs as communication vehicles (see
Section 2). It further reports an empirical study that aimed to identify contextual (in)congruences between cartographic point symbols and different positive, neutral, and negative geospatial topics in monothematic maps (see
Section 3 and
Section 4). Finally, findings and implications for future research are addressed and discussed in
Section 5 and
Section 6.
2. Theoretical Background
Congruence is a quality or state of agreeing or coinciding [
13], a condition of broadly corresponding to something or being in agreement with it in its essentials. Effective graphics are considered to follow the principle of congruence, where “the structure and content of the external representation should correspond to the desired structure and content of the internal representation” [
14] (p. 249). Cartographic maps are such external representations. They depict a particular selection of geographic space on a spatial scale smaller than 1:1 [
15]. As maps are restraint by scale, they require cartographic generalization [
16]. Maps, therefore, simplify and regularize, reduce dimensionality, omit some information, and exaggerate others. The way maps schematize information is considered to be comparable to the way human minds schematize information [
17]. High congruence between external representations and internal representations are recognized to be beneficial, such as to enhance cognitive processing fluency [
17,
18] and problem-solving [
17,
19]. High processing fluency is regarded to even be hedonically marked, i.e., eliciting positive affective reactions [
20]. Contrariwise, “visualizations that do not match the mental schema require cognitive transformations to make the visualization and mental representation align” [
21] (p. 3f). The mental effort needed for correcting mental mismatches and to resolve cognitive discrepancies can increase errors, increase the time to complete a task, and demand higher working memory [
21,
22]. Cartographers, therefore, strive to create cognitively congruent maps, such as by employing map symbols which are somehow associative to the type of information they refer to [
5]. Maps are, however, a result of a myriad of choices, such as towards the type of information to include which to omit, as well as towards how to communicate information through specific cartographic signs. Cartographic maps are, therefore, considered selective representations [
23], never value-free or neutral [
24], but “culturally determined and ethnocentric in origin” [
16] (p. 447).
As such, cartographic communication is a complex process between the map maker and map user [
23,
25,
26], “wherein thought originating in one human mind is converted by that mind into physical forms according to rules developed by the culture in which he [she] lives” [
27] (p. 184). The map and its elements are apprehended by the map reader, who constructs meaning by interpreting its symbols, colors, visual expressions, and the like [
4,
27]. Cartographic communication from a semiotic perspective is considered a triadic, interrelated process between
the sign-vehicle, which refers to the physical sign,
the referent, which stands for the phenomenon or object of reference the sign-vehicle refers to, and
the interpretant, which comprises the sign-vehicle’s effects on the interpreter, such as its meaning [
28,
29,
30]. As meanings are mental events, they are difficult to measure and challenging to distinctively define [
30,
31]. Due to its imprecision, the semiotician Charles Morris even deliberately excluded the concept of meaning from his semiotic theory [
29]. Later, theorists have attempted to decompose the “many meanings of ‘meaning’” [
31] (p. 2), suggesting two core dimensions: the
dimension of reference and the
dimension of sense [
30]. On the dimension of reference, all cartographic sign-vehicles can be considered identifiers which either apprise, inform, state, designate, indicate, label, or denote [
30,
32]. Map signs may, however, also connote, prescribe, express, and stimulate ideas [
2,
32]. Hence, whilst map signs may be analytically congruent with a specific type of content, some may be more—and others less—contextually congruent, such that different map signs may stimulate different associations and ideas about a depicted geospatial phenomenon. Cartographic maps and the signs therein are, therefore, regarded to communicate on both semiotic dimensions of meaning, i.e., on the dimension of reference and on the dimension of sense [
30,
32].
Throughout recent decades, cartographic semioticians have aspired to establish a mutually shared set of signs and semiotic rules to enhance the communication of geospatial information. Yet, most of these frameworks have focused on the dimension of reference, such as to aptly inform, state, indicate, or label geospatial information. One of the most prominent examples of such cartographic semiotic frameworks was established in the 1970s by the French cartographer Jacques Bertin, who appeared to be the first to formally propose semiotic rules aiming to help guide the cartographic design process [
5]. He proposed a set of six fundamental visual variables for two-dimensional maps (i.e., size, color value, texture, color hue, orientation, and shape). He further proposed a set of rules to guide their cartographic employment, such as when they may be considered suitable to represent quantitative, ordinal, or nominal data [
5]. Bertin’s semiotic framework aimed to cover the core “manipulable primitives of graphic sign vehicles from which any information graphic can be built” [
33] (p. 2497).
While Bertin’s framework is still generally accepted in information visualization and cartography [
33], it has also been criticized to be dogmatic, limitedly empirically verified, and incomplete [
32]. Bertin’s semiology has, therefore, been expanded over the years, such as to meet the characteristics of different map types and map uses (e.g., static tactile maps, dynamic visual maps, dynamic audio maps) [
32] as well as for different data characteristics, such as for visualizing geospatial uncertainty [
33,
34]. In recent years, cartographic semiotic research has further begun to empirically assess the effects of cartographic design decisions on human responses. Empirical research, for example, showed that cognitive congruent visualizations, i.e., those of greater cognitive fit, will produce faster and more effective decisions [
21]. A draw to cognitive congruent map symbols can already be found in school children, indicated by the associative and metaphorical use of signs and symbols even at an early age [
8,
35]. Empirical assessments on the influence of cartographic design decisions on human responses further showed that supposedly simple changes of cartographic sign-vehicles can lead to substantially different experiences and responses, such as different visual map styles will influence map readers’ judgments, trust, liking, and recall [
9,
36], as well as emotional responses [
37,
38]. Likewise, the style of line shapes in origin-destination flow maps (e.g., curved versus straight flow lines) showed to significantly impact the map users’ preferences and to influence judgment accuracy [
10]. Empirical research, moreover, highlights a significant impact on map reading intuitiveness, judgments, and preferences towards maps based on how uncertainty is cartographically visualized [
33,
39,
40,
41]. Empirical research on abstract map symbols further suggests a significant influence on detection speed in visual search tasks [
42] as well as on associative and affective responses [
43,
44] based on symbol type.
While cartography allows for a sheer infinite variety of signs and symbols to visualize geospatial information, the aforementioned empirical findings strongly suggest that only a few of those may be considered to be effective and suitable for a given context and content. Cartographic semiotic research has so far strongly focused on the dimension of reference, i.e., on analytic congruences between sign and meaning. Theorists, however, further emphasize the dimension of sense as a crucial factor in cartographic communication processes, such that the meaning of signs may vary by context. Such semiotic differentiations have, however, often been neglected in cartographic research and applications of semiotics. “Despite a large number of papers dealing with communication in cartography, relatively few have pursued in detail the analysis of map symbols, and the relationships between map symbols and semiotic theory” [
2] (p. 179). Consequently, “the difference of what a map sign means and what it represents has become blurred” [
32] (p. 245). Research highlights the persisting need for a differentiated understanding of how visual variables can be used to congruently represent geospatial information by taking into consideration the different dimensions of meaning. The present research, therefore, draws attention to cartographic point symbols employed in thematic maps and explores their congruence with different geospatial contexts.
3. Materials and Methods
An empirical study was carried out to explore how congruent—as well as incongruent—cartographic point symbols are experienced in different geospatial contexts. Geospatial context, in the present study, referred to three types of content, i.e., geospatial topics of positive, neutral, or negative character. For each of the three content groups, monothematic maps were created, in which point symbols for representing a given map topic were systematically varied. The final set of monothematic maps was used as stimulus material and the perceived symbol-content congruence of each map was rated by study participants. The following sections describe the materials and methods of this empirical study in detail.
3.1. Materials and Study Design
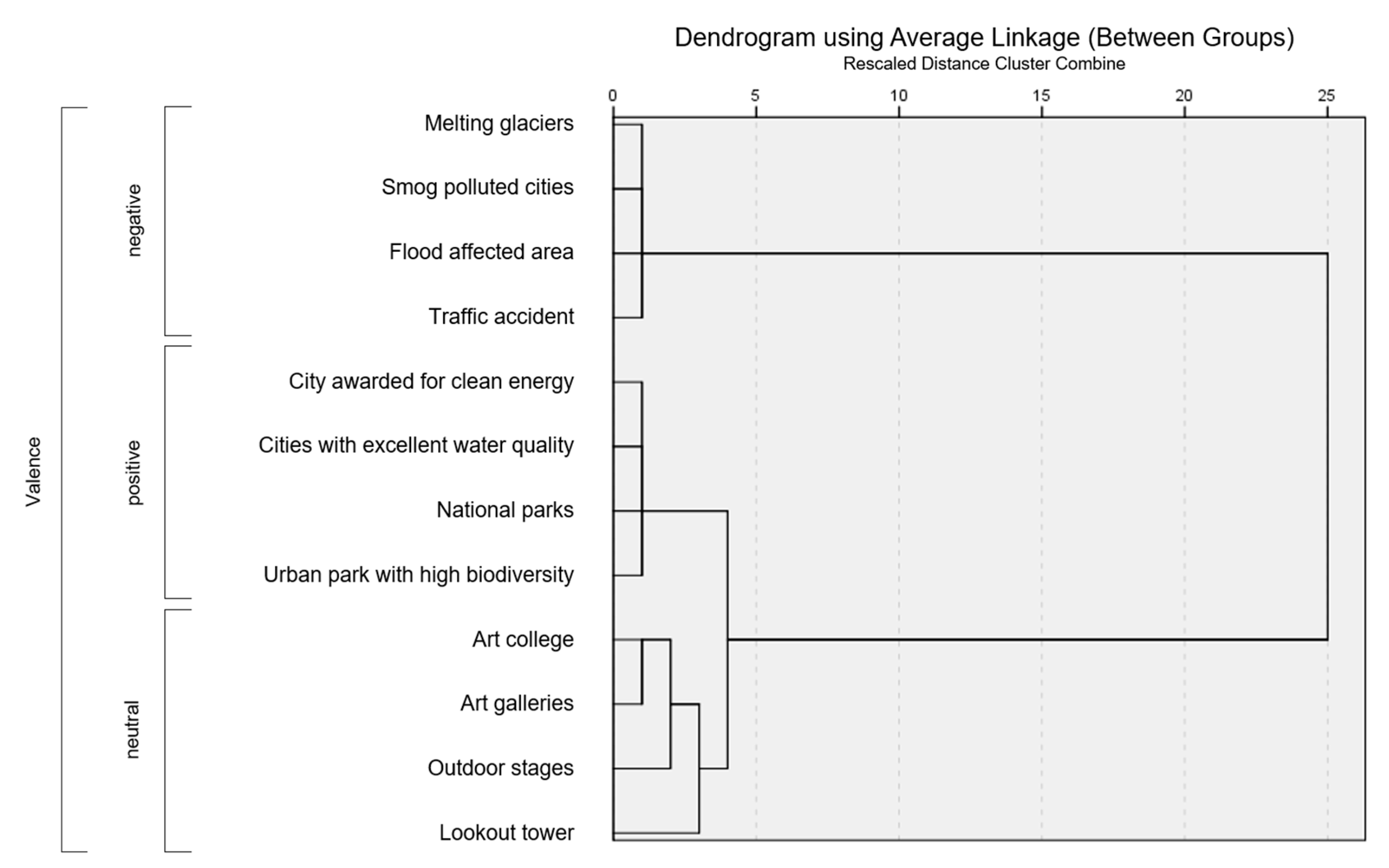
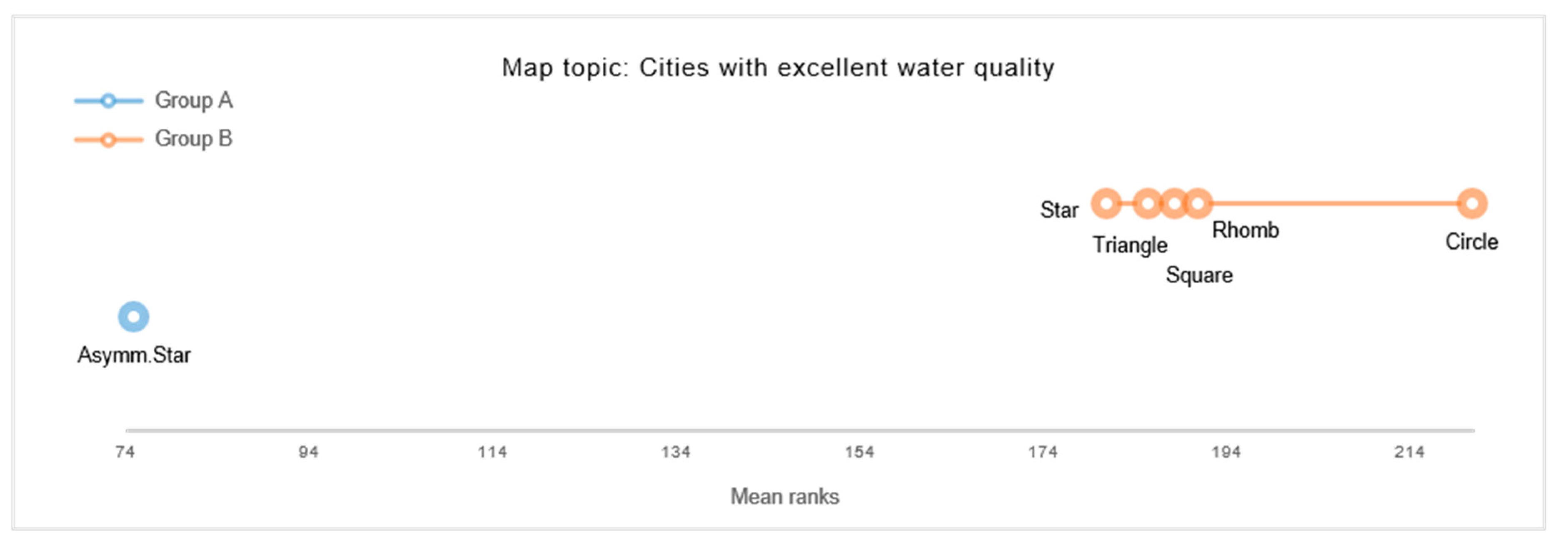
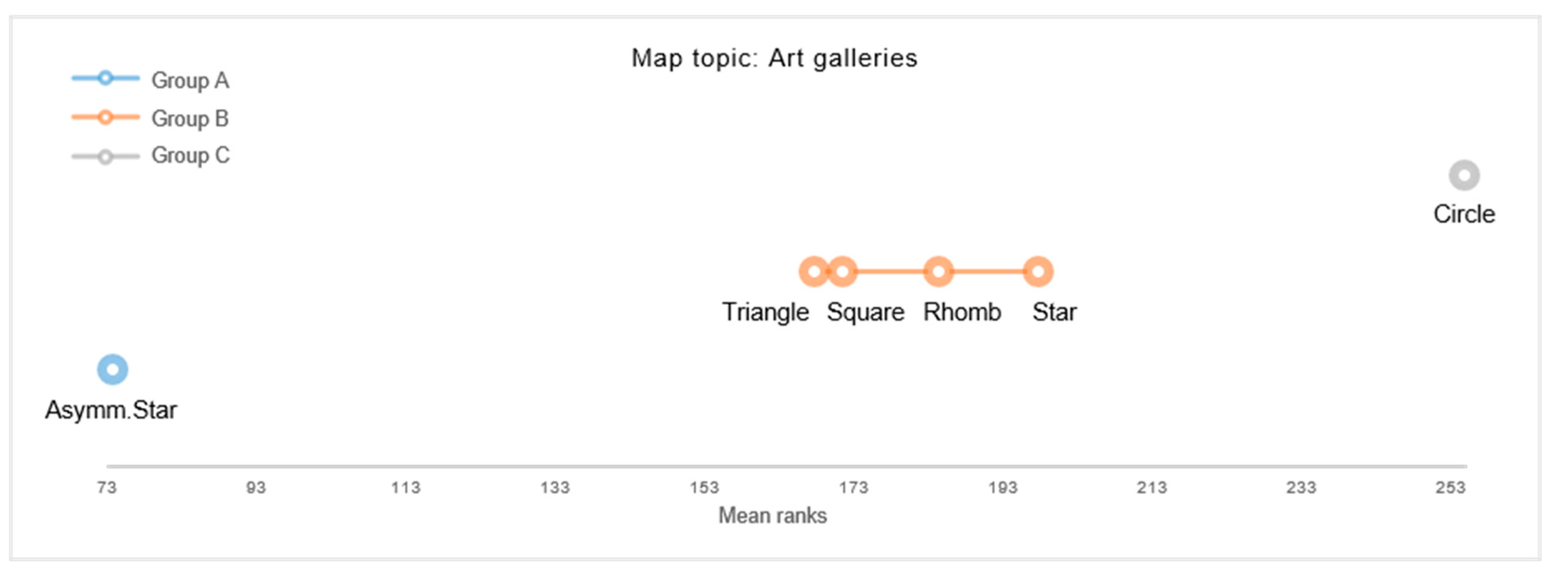
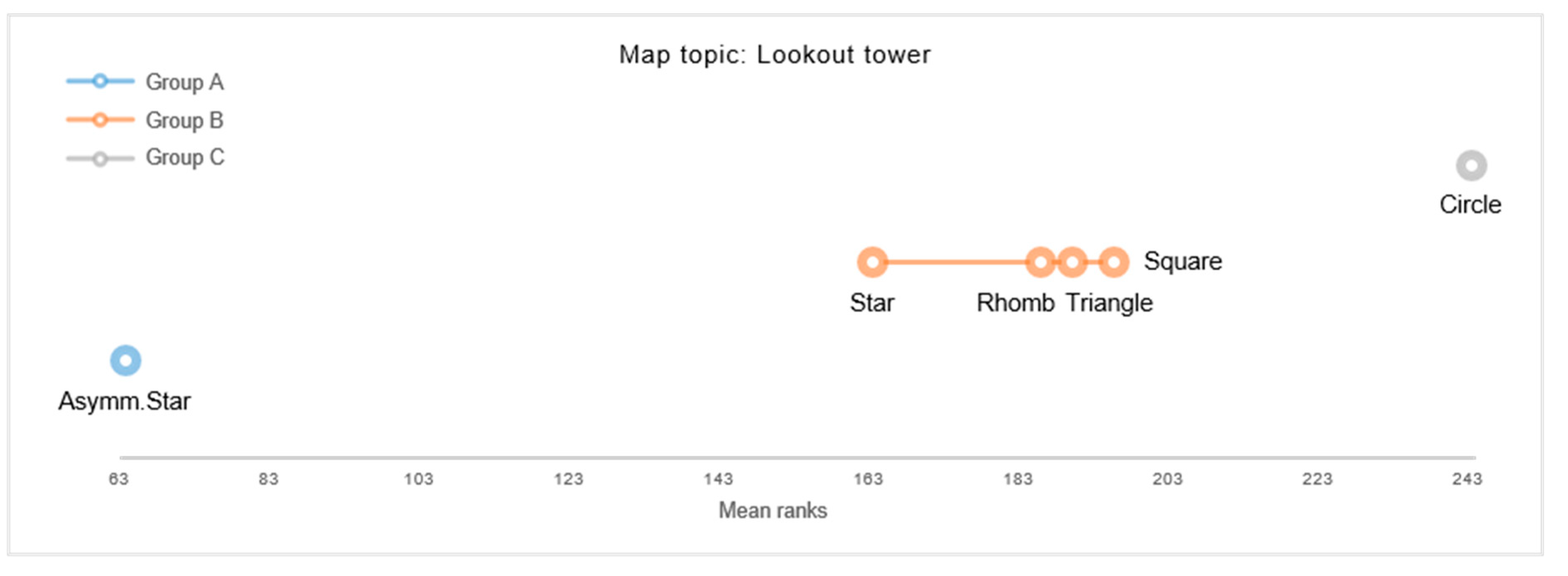
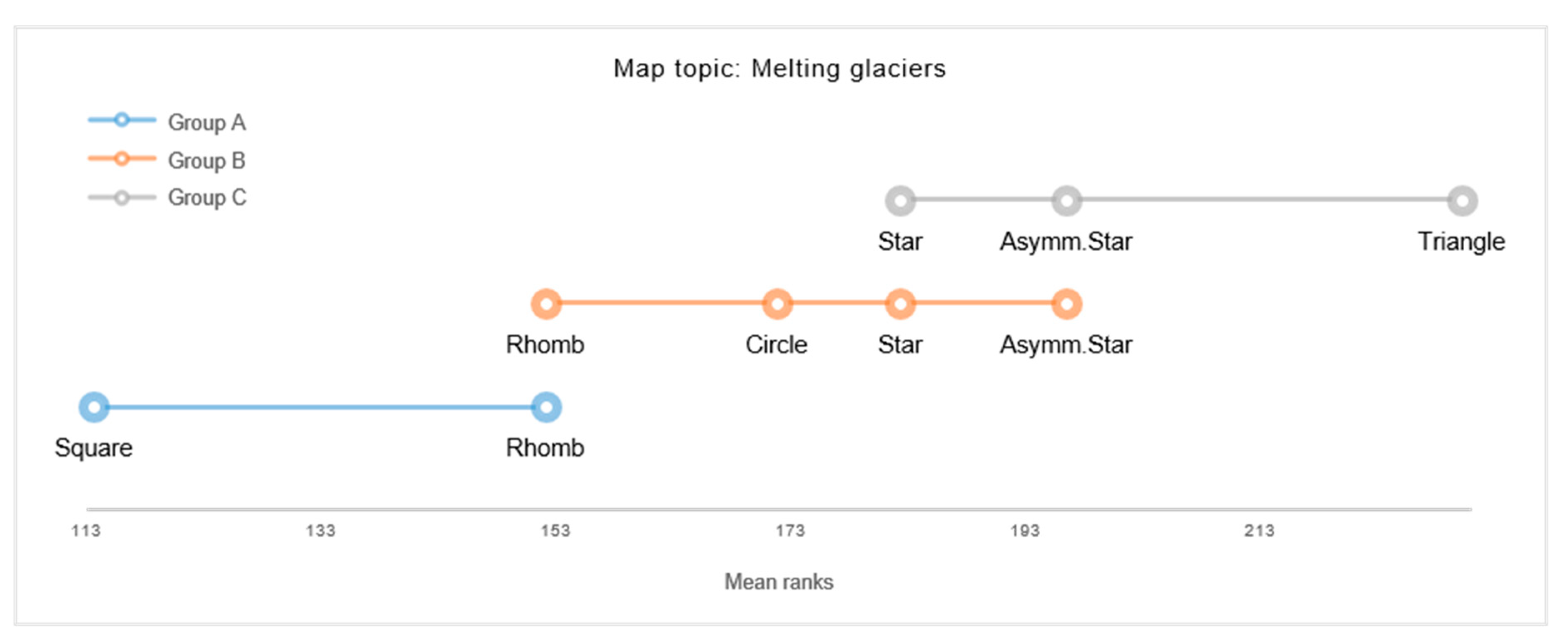
An online survey was set up to empirically assess the (in)congruence of abstract map symbols with respect to different thematic map content. Twelve map topics were selected a priori by the experimenter, i.e., four positive, four neutral, and four negative topics, to test for symbol-content congruences (see
Table 1).
For each map topic, a set of six thematic maps were created, where each map depicted one of six abstract shape symbols, i.e., Circle, Triangle, Square, Rhomb, Star, and Asymmetric Star (for examples see
Figure 1). The map symbols used in the present study refer to commonly used symmetric shapes in thematic cartography and related visual disciplines [
5,
45]. In addition, one asymmetric star shape was incorporated into the stimulus set, as related literature indicates particular perceptual qualities of asymmetric shapes, such as quicker detection times in visual search tasks [
46], and distinct negative hedonic qualities of asymmetric star symbols [
44]. Map symbols were displayed in black in 50 percent transparency, on light-hued basemaps. Basemaps were created to thematically correspond with each map topic. As a result, the basemaps used for the twelve map topics varied by content and scale. For example, the basemap for illustrating a “Traffic accident” displayed a street network, while the basemap for locating a “Lookout tower” indicated urban structures and settlements. Topics that referred to events of a single location were depicted by maps displaying one map symbol, while topics referring to events of multiple locations were represented by three map symbols (see
Figure 1 for examples). The final stimulus set comprised 72 maps, as a result of six map stimuli employed for each of the twelve map topics.
A between-groups design was applied, which randomly assigned participants to one of two stimulus groups. This approach aimed to minimize learning and response transfer across the stimulus conditions. As a result, each participant assessed half of the stimulus set, i.e., 36 maps. The online survey was carried out in the German language by using the software LimeSurvey [
47].
After the survey briefly introduced the aim of the study, which was phrased as to explore how shape symbols and maps are subjectively perceived, participants were instructed to proceed with map evaluation tasks. In these tasks, participants were asked to rate the (in)congruence between each map topic and its cartographic representation on a unipolar 6-point rating scale. The rating scale ranged from 0 (i.e., the cartographic representation does not suit the topic at all) to 5 (i.e., the representation suits the topic very well). Each map stimulus was presented individually, consecutively, and in a randomized order, at a size of 5.
After the map evaluation task, participants rated each map topic on an 11-point Likert scale, from −5 (very negative) to +5 (very positive). These topic ratings were later subjected to empirically identify homogeneous topic clusters of positive, neutral, and negative valence (see
Section 4.1).
Sociodemographic data were gathered at the end of the survey, regarding the participants’ affinity for graphic design (self-evaluation on a unipolar 4-point rating scale, from “not at all” to “very affine”, with the additional option for “no answer”), their affinity for maps or cartography (unipolar 4-point rating scale, from “not at all” to “very affine”, or “no answer”), age, and gender. At the end of the survey, participants were also asked to indicate the devices they used for completing the survey (i.e., desktop PC, laptop, tablet, or smartphone).
3.2. Participants
Bachelor’s students of Regional Planning were recruited from a course on “Thematic Cartography in Regional Planning” held in winter term 2019 at TU Wien—Vienna University of Technology, Austria. Students participated voluntarily and received course credits in the form of bonus points, which counted towards their final grades. The online survey was sent to students in December 2019.
In total, 116 students completed the survey (49 males, 64 females, one person of diverse gender, two missing responses). Participants were randomly assigned to one of two stimulus groups, resulting in 63 participants who completed stimulus material A and 53 individuals who completed stimulus material B, which both comprised a set of 36 map stimuli. Of all participants, 109 persons indicated their age (M = 22.10, SD = 3.29, Min = 18, Max = 35). The majority of participants used laptops to complete the questionnaire (85.3%), followed by desktop PCs (10.3%), tablets (3.4%), and smartphones (0.9%, i.e., one person). Most participants indicated their affinity for graphic design to be moderate to high (somewhat affine = 29.3%; quite affine = 37.9%; very affine = 25.9%), while one person reported to have no interest in graphic design (0.9%). Seven individuals (6.0%) did not answer this question. The participants’ affinity for cartographic design showed to be moderate in most cases (somewhat affine = 30.2%; quite affine = 50.9%) and high in 12.9% of the cases. Seven individuals (6.0%) did not report their affinity for cartographic design.
5. Discussion
As visual means of communication, maps employ signs and symbols to relate to geospatial phenomena and events. As such, maps support the communication and imagination of geographic space and related events from a viewpoint beyond direct experience. At the same time, maps are selective and based on a myriad of decisions. The visual variables employed in maps, such as map signs and symbols, are based on abstractions and generalizations. When using visual variables, cartographers generally strive for congruence, where the schematization of the external representation aims to correspond to structures of the internal representation. Cartography is, therefore, concerned with establishing a mutually shared set of signs and semiotic rules to communicate geospatial information successfully. Yet, in as far as cartographic semiotics provide some guidance for the selection of visual variables from an analytic perspective, such as when to employ visual variables for a given type of data, it does not address contextual congruence, such as when to use a particular shape symbol for a given type of geospatial content. This research, therefore, aimed to contribute to closing this research gap by investigating the contextual congruence of cartographic point symbols with respect to different types of geospatial information.
In detail, the present study empirically assessed the perceived (in)congruence of a set of six-point symbols in monothematic maps of positive, neutral, and negative valence. The six-point symbols comprised five symmetric shapes (i.e., Circle, Triangle, Square, Rhomb, Star) and one Asymmetric Star shape. In an online survey, 72 maps (i.e., twelve map topics in six symbol variations) were evaluated by 116 participants in a between-groups design. Participants evaluated the congruence between each map topic and its depiction by the different point symbols on a 6-point rating scale. Four positive, four neutral, and four negative map topics were assessed by the participants. Participants’ congruency ratings were subjected to statistical analyses. First, symbol-content congruency ratings were analyzed on an aggregated level, i.e., by the three positive, neutral, and negative topic clusters. Second, symbol-content congruency ratings were analyzed individually, i.e., by each of the twelve map topics.
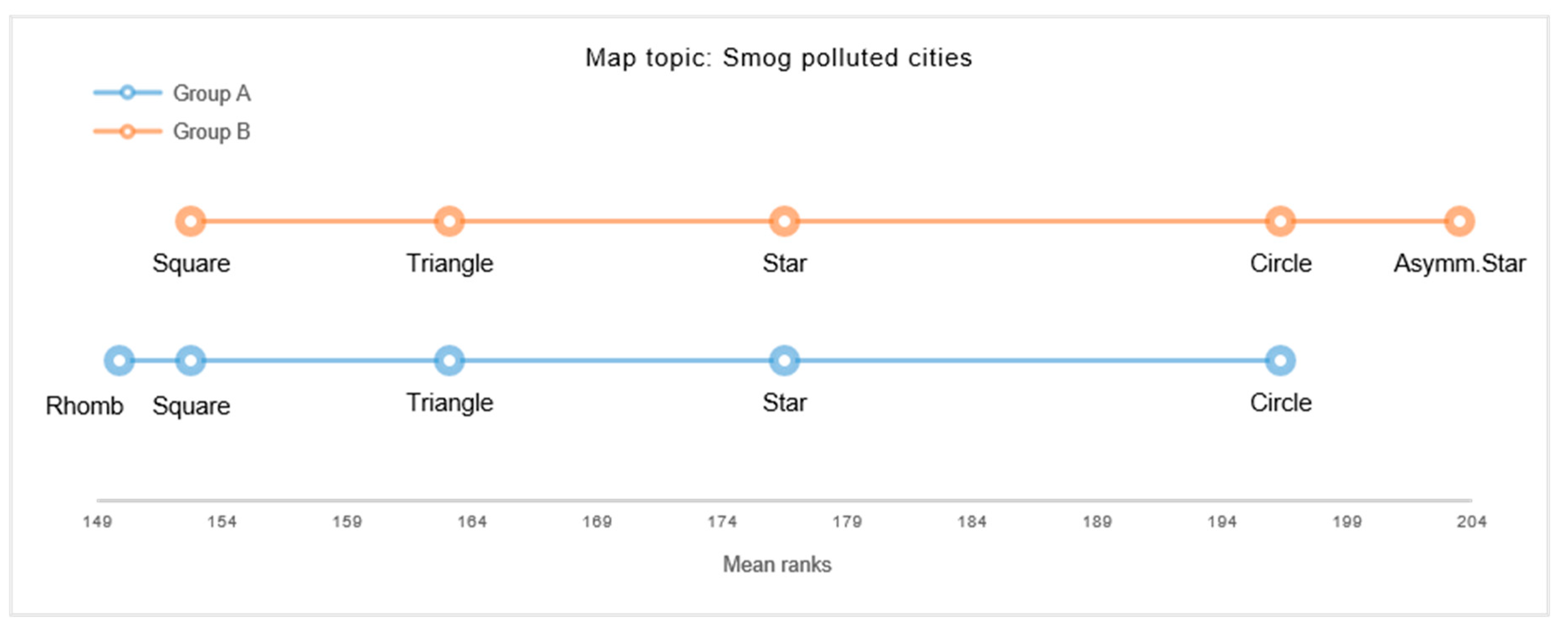
The clustered congruency ratings showed that Asymmetric Stars were rated to be least suitable to cartographically represent positive content. In contrast, the five symmetric shapes were generally found to be of high congruence with positive map topics. Congruency ratings for neutral topics revealed similar results, such as Asymmetric Stars were perceived least congruent, while polygonal, symmetric shapes were found to correspond significantly better with neutral map content. Results further disclosed a significant preference for Circular map symbols for depicting neutral map topics. Hence, results suggest that neutral topics may best be represented by Circular point symbols, while symmetric polygonal map symbols may be considered as second-best alternatives. Whilst incongruent with both positive and neutral topics, Asymmetric Star symbols were significantly preferred for depicting negative events. In contrast, Star, Circle, and Triangle were generally rated as moderately congruent with negative topics, while Square and Rhomb were experienced as least congruent for cartographically referring to negative events.
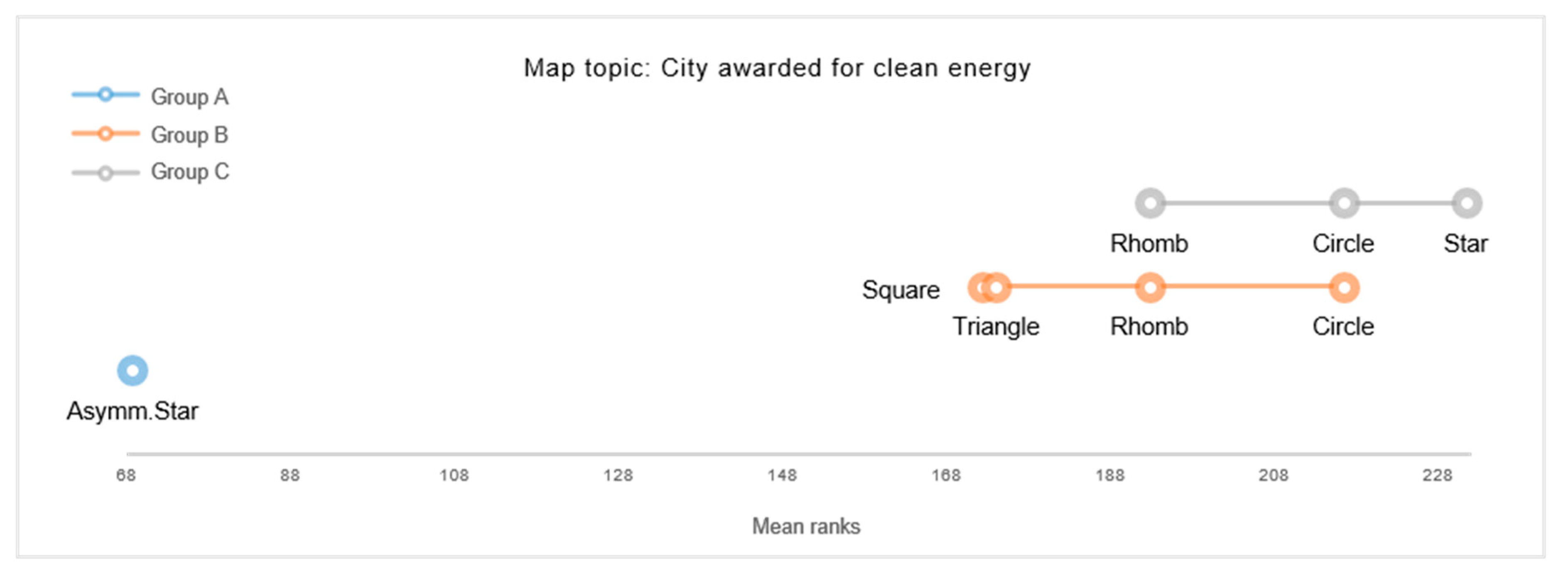
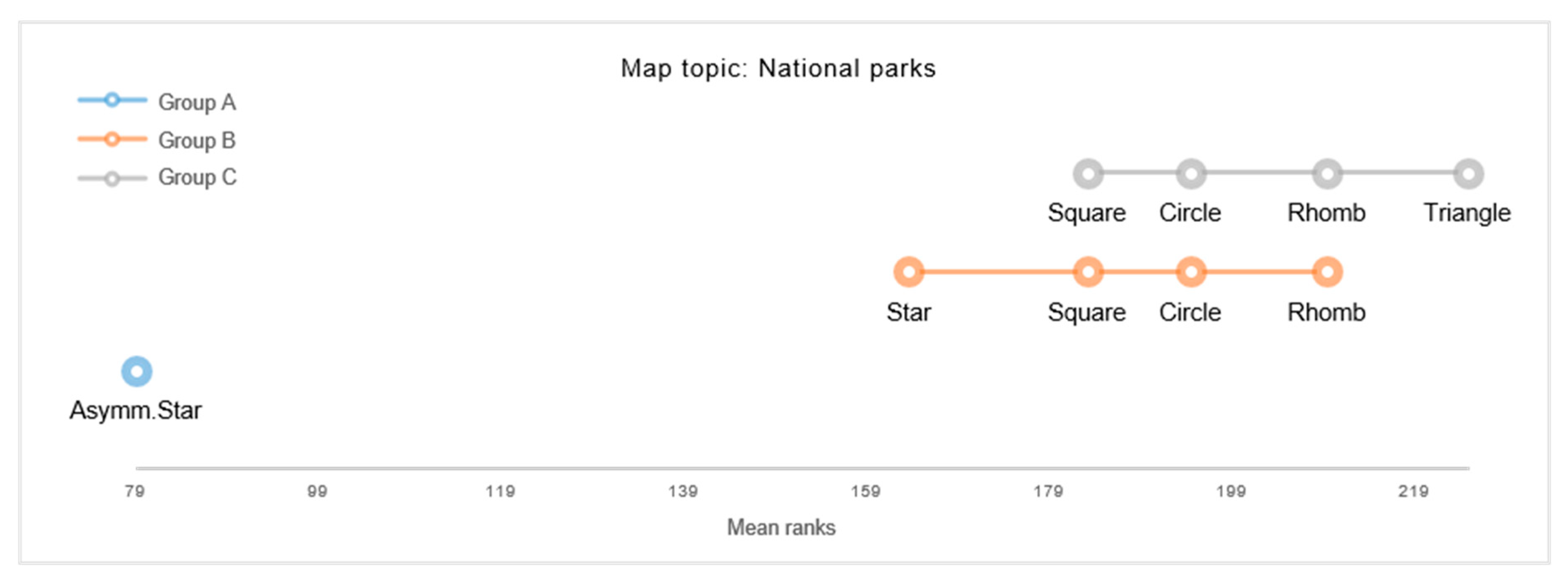
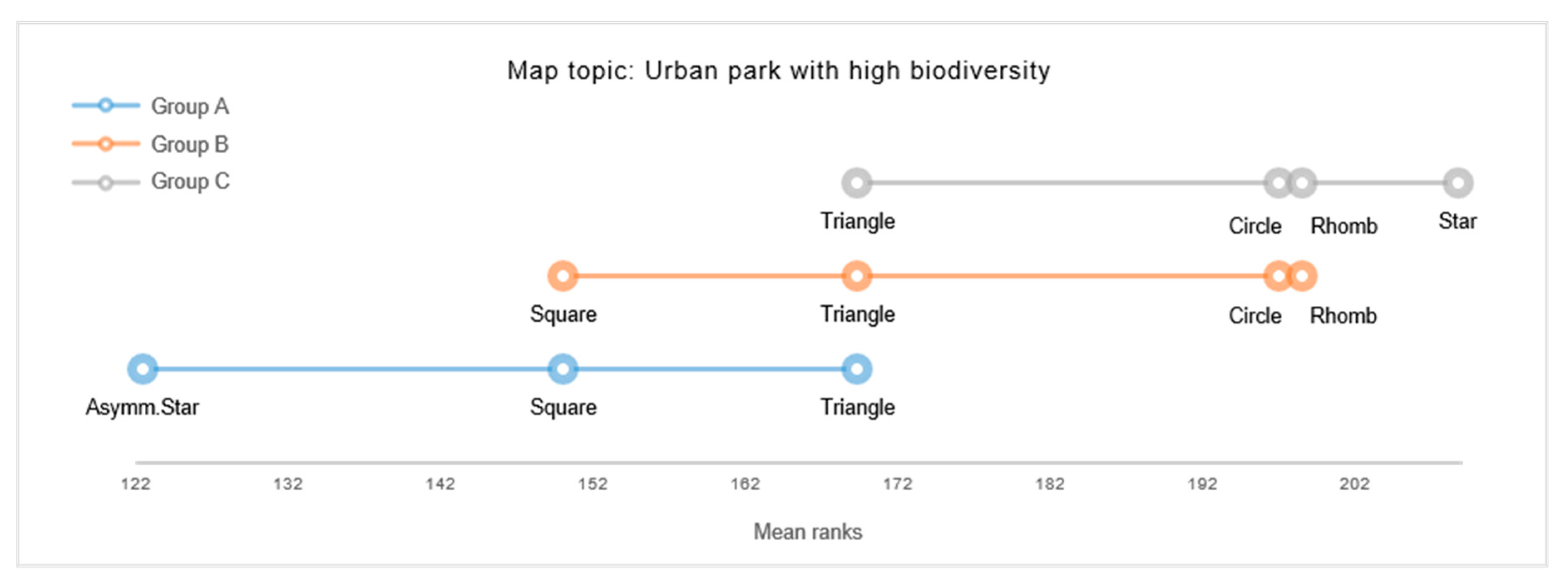
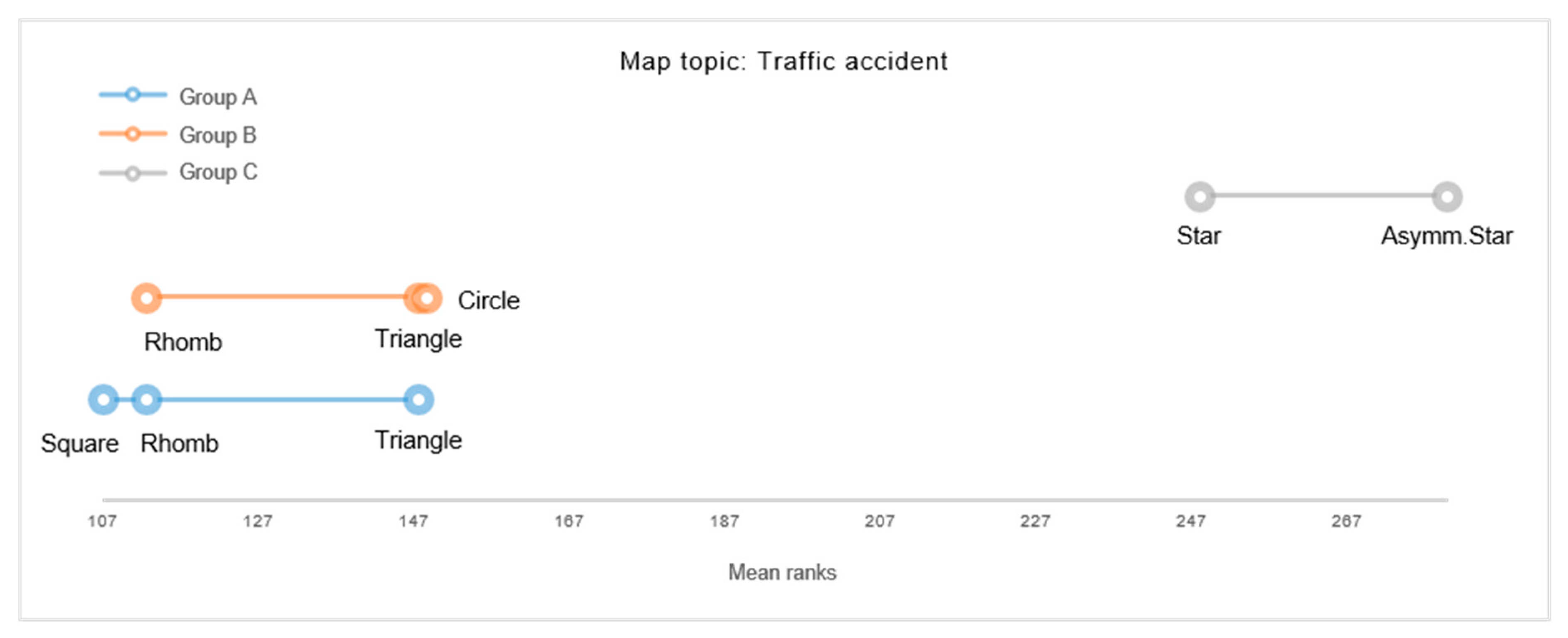
While the present findings on a cluster-level propose general tendencies of symbol-topic relations, some topic-specific visualization preferences were revealed at a more detailed level of analysis. For example, Triangles were rated to best correspond to representing “National parks” and “Melting glaciers”, whilst symmetric Stars showed to be the preferred choice for representing “Cities awarded for clean energy” and “Urban parks with high biodiversity”. For depicting “Traffic accidents”, the Asymmetric Star and symmetric Star were both found to be significantly favored. These findings may imply particular preferences towards iconic map symbols.
Iconicity refers to the conceived similarity or analogy between the form of a sign-vehicle and its meaning. Abstract, geometric shapes are generally considered to be of low iconicity, whilst associative and pictorial point symbols are regarded as moderately to highly iconic [
32]. The results of the present study indicate that the iconicity of abstract map symbols may have been amplified by the cartographic context. The topic of “Melting glaciers”, for example, may have been associated with mountains, which may be visually associated and abstracted by triangular shapes. Traffic accidents, on the other hand, may be associated with collision and conflict, often graphically abstracted by star-like shapes. In the present study, contextually more iconic symbols may have been experienced as more congruent with the given map topics, as participants’ draw towards those map symbols indicate. Yet, as the present findings only allow to conjecture the influence of iconicity on congruence, future research is needed to systematically and empirically explore such an influence in depth.
Related research further suggests that when people make evaluative judgments, they draw on a range of different processes [
20]. Such processes may relate to cognitive as well as to affective responses [
18]. Winkielman et al. even stress that some affective response is always involved in evaluative judgments. These affective responses may be based on stimulus attributes as well as be caused by the dynamics of information processing, i.e., by processing fluency [
20].
Processing fluency is considered to be hedonically marked, such as that high fluency elicits positive affective reactions [
20]. A tendency towards affectively congruent map symbols may also be supported by the findings of this study. Negative map topics in the present study referred to rather dynamic spatiotemporal events (e.g., smog, floods, traffic accident), where in contrast, positive and neutral topics predominantly related to rather static geospatial occurrences (e.g., national parks, biodiversity, art galleries, lookout tower). These different qualities may have influenced participants’ congruence judgments, such as towards favoring symbols of dynamic character for dynamic topics. Osgood et al., for example, referred to such dynamic qualities of stimuli as the affective dimension of
activity, for which he found “some relation to physical sharpness or abruptness” [
31] (p. 38). Such particular stimulus-affect correspondences are moreover supported by related empirical research on map symbols, which found that asymmetric star symbols were experienced as highly dynamic and of negative valence, whereas symmetric shapes were regarded as neutral or slightly positive and of rather static quality [
44]. Related research further showed that point symbols may be experienced visually, associatively, and affectively [
43]. Map topic-specific visualization preferences may therefore result due to either of these dimensions. Hence, while the present findings and related literature strongly suggest that the principle of congruence may be a crucial factor for cartographic communication, such as to enhance map design, future research is needed to dissect its dimensions and explore its effects in greater detail.
So far, the present research provides first empirical insights into symbol-content relations of such kind. Yet, the study also encompasses some shortcomings:
The present study used a limited set of six map symbols. Besides the attempt to incorporate the most common abstract cartographic point symbols, the possible number of map symbols is sheer unlimited. At the same time, cartographic nominal point symbols used in practice may not only be manipulated by shape but also by color, size, and other qualities. Such symbol properties have been excluded deliberately from the present study in order to allow for a systematic study on the influence of shape by controlling for potential confounders, such as different symbol colors and symbol size. Future research may, however, expand on the set of point symbols by considering additional manipulable symbol qualities. Future studies may also consider increasing the complexity and the interaction of different visual map features, as the findings of the present study, are limited to monothematic maps of low visual complexity. In addition, the number of geospatial topics used in the present study was limited to a selection of twelve topics, which certainly limits the findings’ transferability. Hence, despite a greater variety of point symbols and thematic maps of differing visual complexity, a larger set of map topics must also be considered in future studies to expand upon the present findings and to ensure the findings’ external validity.
Another shortcoming refers to the selection of map topics, which was undertaken a priori by the experimenter. Topics were selected to be of positive, neutral, and negative character. Whilst statistical analysis confirmed such three homogenous clusters, results further showed a more proximal relation between the neutral and positive topic clusters with a greater distance towards the negative cluster. Mean ratings further showed that neutral topics in the present study were rated slightly positive and may, therefore, not be considered to be purely neutral. The selection of maps towards a set of distinctively positive, neutral, and negative geospatial topics may be improved in future studies, such as by conducting prestudies for prior topic assessments.
Future research also needs to take into account more heterogeneous groups of participants, as this study relied on students only. Participants of the present study can be characterized as young adults, with high education, and a moderate to high affinity to graphic design and cartography. The findings of the present study must, therefore, be considered to be restricted to this fairly homogeneous user group as the study did not embrace the vast diversity of map users. Social semiotics further stress that “people respond culturally and engage emotionally with data and their visualizations” [
54] (p. 50). This is supported by research in cartography, which found that cultural backgrounds influence map perception and performance in cartographic visual search tasks [
42]. Such findings strongly imply the impact of cultural sign-conventions on map reading performances. It is, therefore crucial to continue exploring the effects of cartographic design decisions from the perspectives and backgrounds of different user groups.
6. Conclusions
Maps are a form of communication: a means of conceiving, articulating, and structuring the human world [
3]. Through cartographic signs and symbols, maps refer to phenomena and entities in geographic space in a generalized and abstracted way. To communicate geospatial information successfully, cartography generally strives for cognitively congruent map design. Cartographic research has, however, only started to understand the myriad of relations between the map as an external representation and internal human processes.
This research, therefore, drew attention to the principle of contextual congruence and empirically explored the cognitive correspondences between cartographic point symbols and different positive, neutral, and negative geospatial contexts. Findings strongly imply that context matters. Overall results revealed high congruences of Asymmetric Star symbols when representing negative map topics, whilst highly incongruent when depicting positive or neutral geospatial content. Symmetric shapes, on the other hand, generally emerged to highly correspond with positive and neutral map topics, whilst incongruent with negative content. As the meaning of point symbols showed to be susceptible to context, the findings lead to the conclusion that cognitive congruence can be enhanced by integrating context-specific information into the cartographic design, such as when form follows content.
Yet, while this research provided first empirical insights, the present findings aim to be expanded upon. Future research is needed to continue exploring the different semiotic dimensions of sign meanings and their role in cartographic communication processes. A profound understanding of the various context-related communication effects of cartographic signs may allow for more deliberate and informed design decisions, and with this, may contribute to enhancing cartographic communication.