1. Introduction
As some of the most significant immovable cultural relics in the world, ancient wooden architecture (AWA) structures are usually considered to have high social, historical and scientific value [
1]. Understanding and modernized elaboration of the architectural and structural characteristics are critical for protecting such historical structures effectively [
2,
3]. Furthermore, the documentation of such characteristics based on three-dimensional (3D) high-fidelity modeling method is preferred. Thus, 3D digital technology has become a vital method for supporting AWA conservation [
4,
5,
6,
7,
8]. For the protection of AWA structures, historical knowledge of the structures, including the construction regulation of assembly guidelines and component specifications, is considered essential [
9,
10]. First, the historical knowledge enhances the understanding of the history of an ancient structure and the knowledge of its construction method. Second, as inevitable damage and deformation will occur in AWA structures, such knowledge is crucial for the performance evaluation and the resulting repair. A 3D digital model which can illustrate such historical knowledge and be updated frequently will be more beneficial in the sustainable protection of AWA structures.
Building information modeling (BIM) fully meets the requirements mentioned above, as it can integrate knowledge from different disciplines, such as architecture, mapping, and civil engineering. In addition, the information of a BIM model can be updated continuously [
11]. Hence, BIM can be used and has been used to protect architectural heritage. Such BIM is called heritage/historic building information modeling (HBIM) [
12,
13,
14]. In comparison with the traditional data collection methods (e.g., two-dimensional (2D) drawings, tables, text, and images), HBIM can express the original appearance of ancient buildings more intuitively and accurately. Similar to modern buildings, AWA buildings were also usually built with standardized components [
15,
16]. For example, Chinese AWA structures constructed during the Liao and Song dynasties followed “Yingzao fashi,” and the corresponding components were highly standardized. Theoretically, the HBIM modeling of AWA structures can be efficiently performed using standardized components.
Various researchers have conducted valuable studies on HBIM and applied it to digitizing architectural heritage. Pocobelli et al. [
17] reviewed the research findings on BIM for heritage and recommended that future studies should focus on the development of new tools that can store and share all the relevant metadata. Baik et al. [
18] used Autodesk
Revit to build a 3D model of a historic building in Jeddah (i.e., Farsi House), and the model was established based on the obtained and processed laser and images survey data. However, a components library was not proposed and introduced in the process, and the entire process was manually operated. Murphy et al. [
19] identified historical details from architectural pattern books and constructed a semi-automatic parameter object library of European classical architecture using a geometric descriptive language. Quattrini et al. [
20] researched irregular and complex Romanesque architecture. A 3D semantic-aware model was developed, which could connect the geometrical-historical survey data with descriptive thematic databases. The HBIM model of the Church of Santa Maria at Portonovo was established using this method. For the application of HBIM in AWA, Park [
21] defined a parametric relationship between the structural elements in Hanok and developed a systematic data library for such elements.
Despite the efforts mentioned above, it is still required that HBIM should be further developed for modeling AWA structures in the following three aspects:
(1) Standardized component libraries for typical components of AWA buildings with an emphasis on historical knowledge, especially commonality and characteristics. The authors have proposed multi-level details of BIM models for different components of AWA buildings, which focused on various requirements at different protection phases [
22]. However, the authors found out that different components with different knowledge exhibited identical appearance (which is illustrated in detail in
Section 2), thus extremely hindering professionals in surveying and civil engineering from understanding the actual information about different components. This feature is quite different from masonry and stone heritage buildings [
23], and currently, is not well considered. A parametric model of typical components with emphasis on commonality and characteristics which intelligently integrates the historical knowledge and can be easily used by conservation workers will be beneficial for dealing with the diversity of practitioners protecting AWA buildings [
24,
25,
26].
(2) Obtaining invisible dimensions due to complicated stacking. Different from modern architecture and other types of historical buildings, the construction of AWA structures is complex [
27]. For example, there are more than 480 dou-gongs in Yingxian Wood Pagoda, with 54 types. Each dou-gong is stacked with more than 20 components [
28]. A highly manual deduction based on historical knowledge is usually applied to calculate the invisible dimension. Although the deduction algorithm may be simple, it is rather time-consuming because experts with specific knowledge are needed, and thousands of components are required for identification and deduction. An intelligent algorithm and a corresponding program, which can integrate the knowledge, should be developed to automatically identify the type of component and deduce the invisible dimensions.
(3) The method for automatically modeling most components. The current trend in practice is the use of advanced automation technology [
6,
7,
15,
18,
29]. However, the automatic modeling of an entire AWA structure or even a single dou-gong remains a significant challenge. An automatic modeling method for most components is more applicable and convenient to check [
30]. If standardized component libraries are established, the corresponding parametric models require two types of input parameters (i.e., visible dimensions, which can be obtained using a surveying method and deduced invisible dimensions, which can be calculated automatically and intelligently). The model of such a component can be established theoretically. However, due to the two issues highlighted above, a systematic method that incorporates intelligent identification of the type of components, deduction of invisible dimensions, and automatic modeling, is rarely reported.
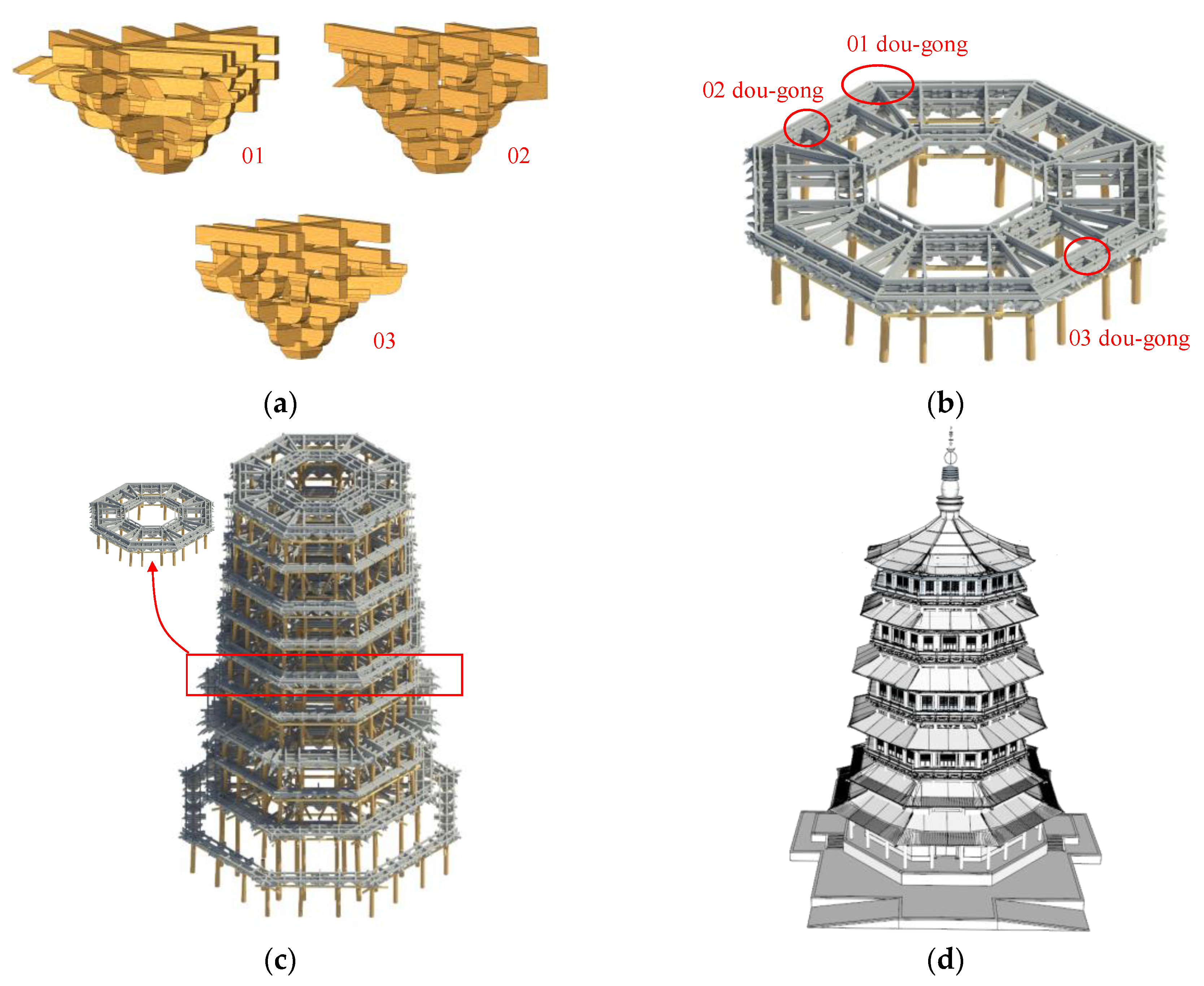
In addressing these issues using the Chinese AWA structures constructed during the Liao and Song dynasties as an example, the knowledge of typical components, with an emphasis on commonality and characteristics, was further identified. The corresponding parametric models for the typical components, with an emphasis on commonality and characteristics, were recommended. Subsequently, an intelligent automated modeling method was developed using Dynamo with three critical functions, which were the intelligent identification of the type of components, deduction of invisible dimensions, and automatic modeling of the structures. A complicated dou-gong was established with surveying data using this method to validate the reliability of the proposed method. Furthermore, the method was applied to establish the HBIM model of the Yingxian Wood Pagoda, which is the oldest and tallest ancient wooden architecture in China with a height of 65.88 m. The research findings will provide an essential reference for the conservation of wooden architectural heritage structures.
2. Parametric Model for Typical Components with Emphasis on Commonality and Characteristics
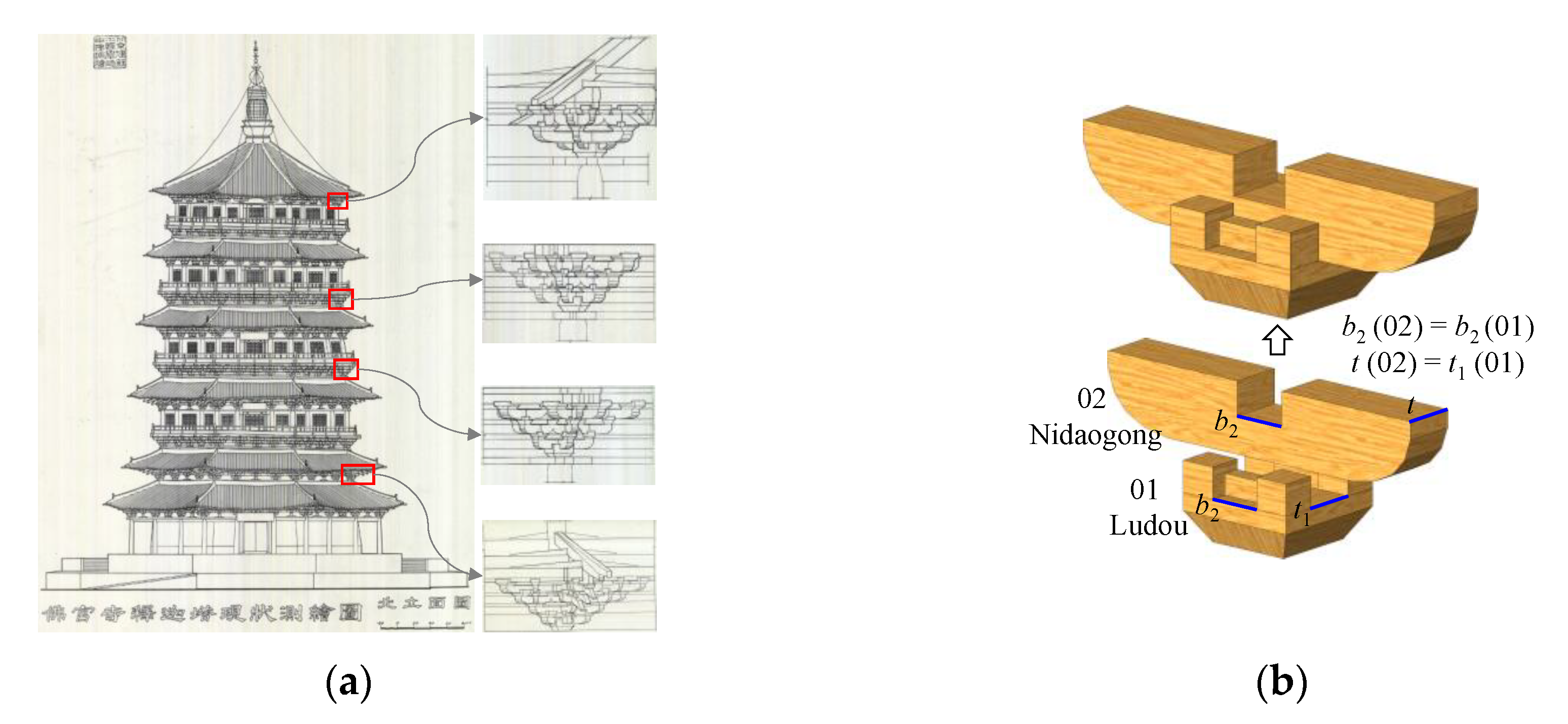
The dou-gong is the most important and sophisticated element in Chinese AWA structures. The dou-gong is composed of four typical components (i.e., dou, gong, ang, and fang) and is assembled by following specific principles (as shown in
Figure 1a). Similar to modern architecture, the Chinese AWA also adopts the fundamental concepts of standardization and modularization. In the AWA structures constructed during the Liao and Song dynasties, the typical components were highly standardized. The “caifen zhi” in “Yingzao fashi” specified the shape and modulus of each component [
31]. Specifically, the absolute value of a specific characteristic size, as well as the proportional relationships between other characteristic sizes and this specific characteristic size, were prescribed. Therefore, parametric models for such components can be developed.
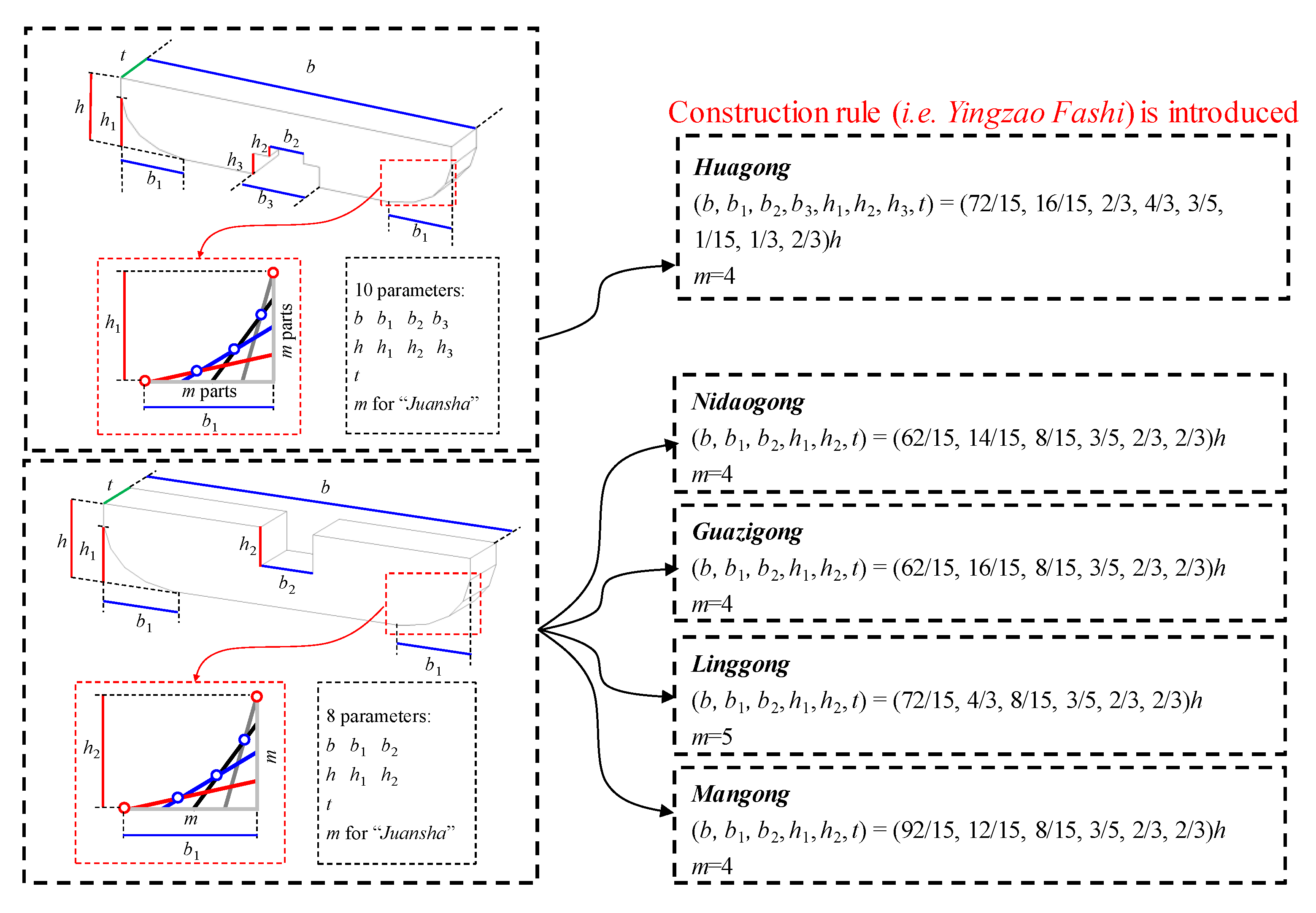
It should be noted that these standard key components exhibit commonalities and characteristics. Taking the gong for instance (Huagong, Linggong, Guazigong, Mangong and Nidaogong as shown in
Figure 1a,b), the gong in different positions of a dou-gong has a particular name due to different proportional relationships, although an identical appearance is observed for different gongs through a parametric modeling view. The identical appearance is the commonality between different gongs, while the various names and proportional relationships can be considered as characteristics, which is essential historical knowledge.
During the digital protection of such AWA structures using BIM, a unified parametric model reflecting commonality, rather than several personalized models reflecting characteristics, is preferred by surveyors and civil engineers [
32,
33,
34,
35,
36]. However, some parameters (i.e., sizes) are invisible and unmeasurable because typical components in a real dou-gong are stacked. The historical knowledge of characteristics, which is not precisely known, should be introduced to determine the type of element and to deduce such sizes.
Consequently, the development of a unified parametric model with intelligent reasoning is required. Specifically, a unified model reflecting commonality is used, and the characteristics are internally integrated for deduction. The commonality and characteristics of such a model should be analyzed comprehensively. Then, the unified parametric model can be proposed, and the characteristics should be mathematically expressed and integrated. Taking “gong” in the ancient wooden heritage of the Liao and Song dynasties as an example, the fundamental idea of the corresponding parametric model, which integrates the commonality and characteristics, is introduced.
2.1. Characteristics of Gong
The gong is a typical component in dou-gong that is located in the notch of “dou” (such as the “Huagong,” “Nidaogong,” “Guazigong,” “Mangong,” and “Linggong1,” as shown in
Figure 1a) or on the “jump” (such as the “Linggong2,” as shown in
Figure 1a). The gong usually has an upward-bowed shape and transfers the vertical and horizontal loads. According to its position in dou-gong and the historical knowledge, the gong can be categorized into five types, which are “Huagong,” “Nidaogong,” “Guazigong,” “Mangong,” and “Linggong,” as shown in
Figure 1a,b. From the perspective of the gong shape, two notable characteristics are observed, including a notch carved in the middle of the gong and “juansha” at both ends. For the notch, the gong is used to connect the upper and lower components through intersection. The notch is a flat notch carved at the top or bottom of the gong. Remarkably, only Huagong carves the notch at the bottom, whereas the other four types of gongs carve at the top.
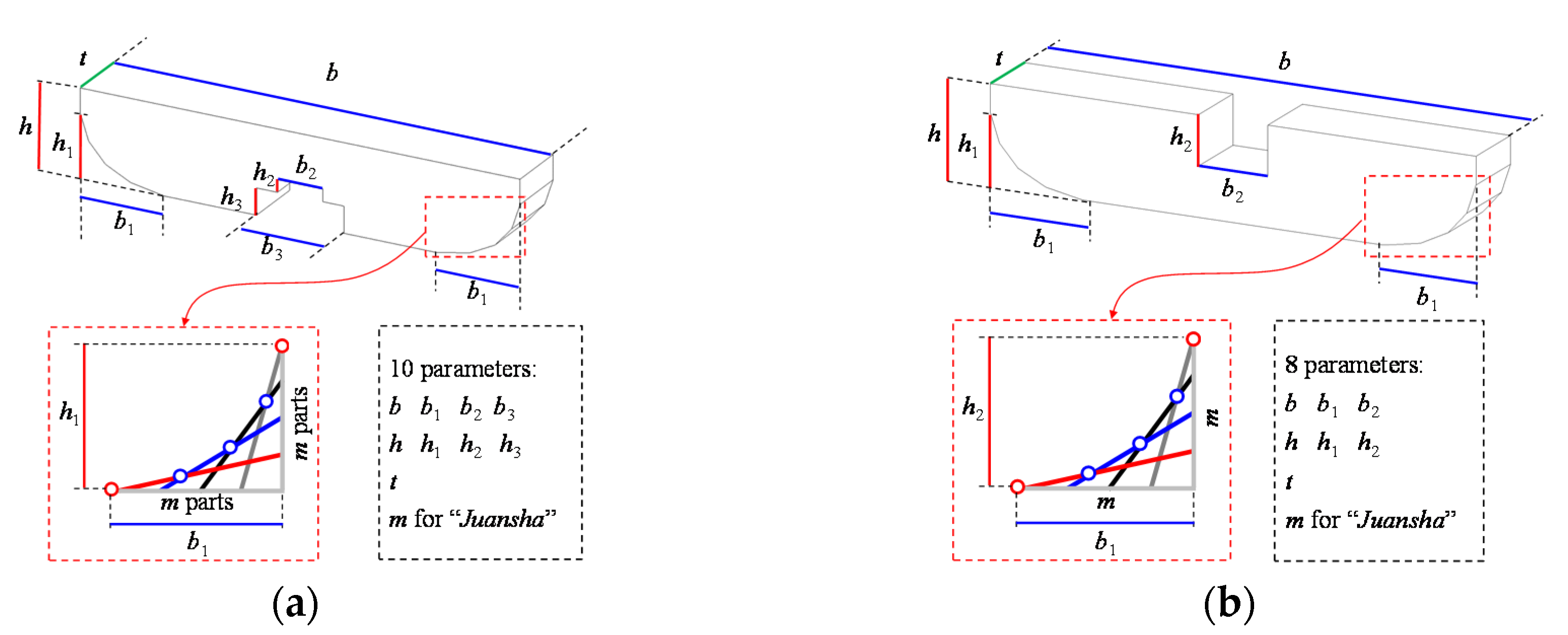
As for the juansha, it is an aesthetic border. To manufacture a “juansha,” the end of the gong is first divided into the same number of parts (noted as a variable
m) along the height and length directions, as shown in
Figure 2. The length and height of “juansha” are denoted as
b1 and
h1, respectively, as shown in
Figure 2. After that,
m points are assigned and numbered along the length and height directions. Specifically, the nodes along the length direction are numbered from
m (the red point shown in
Figure 2) to 1, whereas the nodes along the height direction are numbered from 1 (the blue point shown in
Figure 2) to
m. The
ith point in the height direction and the
ith point in the length direction are connected using a straight line. The
m-minus-one points of intersection (the black points shown in
Figure 2) can be obtained from the two adjacent straight lines. In combination with the two endpoints of “juansha” (i.e., point
m in the length direction and point 1 in the height direction), the outline of “juansha” is determined and presented in multiple linear segments.
2.2. Parametric Model for Gong
From the above discussion, it can be observed that Huagong is significantly different from other types of gongs. Therefore, a unique model is required for Huagong. In contrast, Nidaogong, Guazigong, Mangong and Linggong exhibit significant common characteristics. Specifically, these four types of gongs all have an upward notch at the middle of the gong, and a common model can be developed for these gongs. Hence, two types of common models are required for these five types of gongs.
Before the introduction of these models, the fundamental principle of “caifen zhi” [
31] is briefly introduced. “Cai” refers to a wood member with a height-width ratio of 3:2, and it is categorized into eight grades in Yingzao fashi. Each grade has different absolute sizes, but “cai” is divided into proportional sections in both the height and width directions; the total height and width are divided into 15 and 10 “fen,” respectively. The other dimensions, such as the total length and the dimensions of notch, are also expressed in “fen.” By taking Huagong as an example using the first grade of cai, Huagong is designed such that it has a total height and width of 278.1 and 185.4 mm, respectively. A “fen” in this case is equal to 18.54 mm. The total length of such a component is 72 “fen,” i.e., 1334.88 mm. Using the second grade of cai for the Huagong, it has a total height of 255 mm and a width of 170 mm, and a “fen” in this context is equal to 17 mm. The total length of such a component is also 72 “fen,” but with a value of 1224 mm. Non-professionals may not easily understand the traditional description, and therefore, a modern description method for Yingzao fashi is required.
A parametric model for Huagong, as shown in
Figure 3a, was developed with 10 parameters as follows: total height
h, height of “juansha”
h1, first height of notch
h2, second height of notch
h3, total length
b, length of “juansha”
b1, first length of notch
b2, second length of notch
b3, width
t, and number of parts of “juansha”
m. As mentioned earlier, the historical knowledge should be introduced to deduce the invisible and unmeasurable parameters. The proportional relationships of each parameter specified in “caifen zhi” are elaborated, and the original description can be transformed as follows: (1) the length of Huagong is 72 fen; (2) juansha is divided into four parts (i.e.,
m = 4); (3) the length and height of juansha are 16 and 9 fen, respectively; (4) a notch is carved at the bottom with a total height of 5 fen and a total length 20 fen; (5) the first height and length of the notch are 1 and 10 fen, respectively. The total height and width in the parametric model of Huagong are 15 and 10 fen, respectively. If the grade of the cai is given, the absolute value of the total height and width can be determined. The characteristic parameters in the parametric model of Huagong can be calculated using Equation (1).
In comparison with Huagong, a flat notch in the middle of the top is adopted for the other four types of gongs. A unified parametric model is developed, as shown in
Figure 3b. This model is designed with eight parameters as follows: total height
h, height of “juansha”
h1, height of notch
h2, total length
b, length of “juansha”
b1, length of notch
b2, width
t, and number of parts of “juansha”
m. The proportional relationships of each parameter are also introduced for these four types of gongs as the characteristics. Due to length limitations, the original description of the proportional relationships specified in Yingzao fashi is not converted here, but the proportional relationships are directly presented in
Table 1.
Based on the above discussion, a parametric model system with an emphasis on commonality and characteristics is proposed, as shown in
Figure 4 for the gongs. The common parametric models stated above are illustrated on the left side, which generalize components with an identical appearance and express them from a mathematical point of view. If all the parameters can be obtained through surveying and mapping technologies, the model can then be established directly. However, the parameters cannot be usually obtained owing to stacking. The historical knowledge of Chinese AWA structures is usually introduced to deduce the invisible parameters, and the proportional relationships are integrated, as shown on the right side of
Figure 4. The fundamental idea of the reasoning method is that the component type is identified first through the proportional relationships between the visible dimensions; the invisible dimensions of the component are deduced based on visible dimensions and proportional relationships between the visible and invisible dimensions.
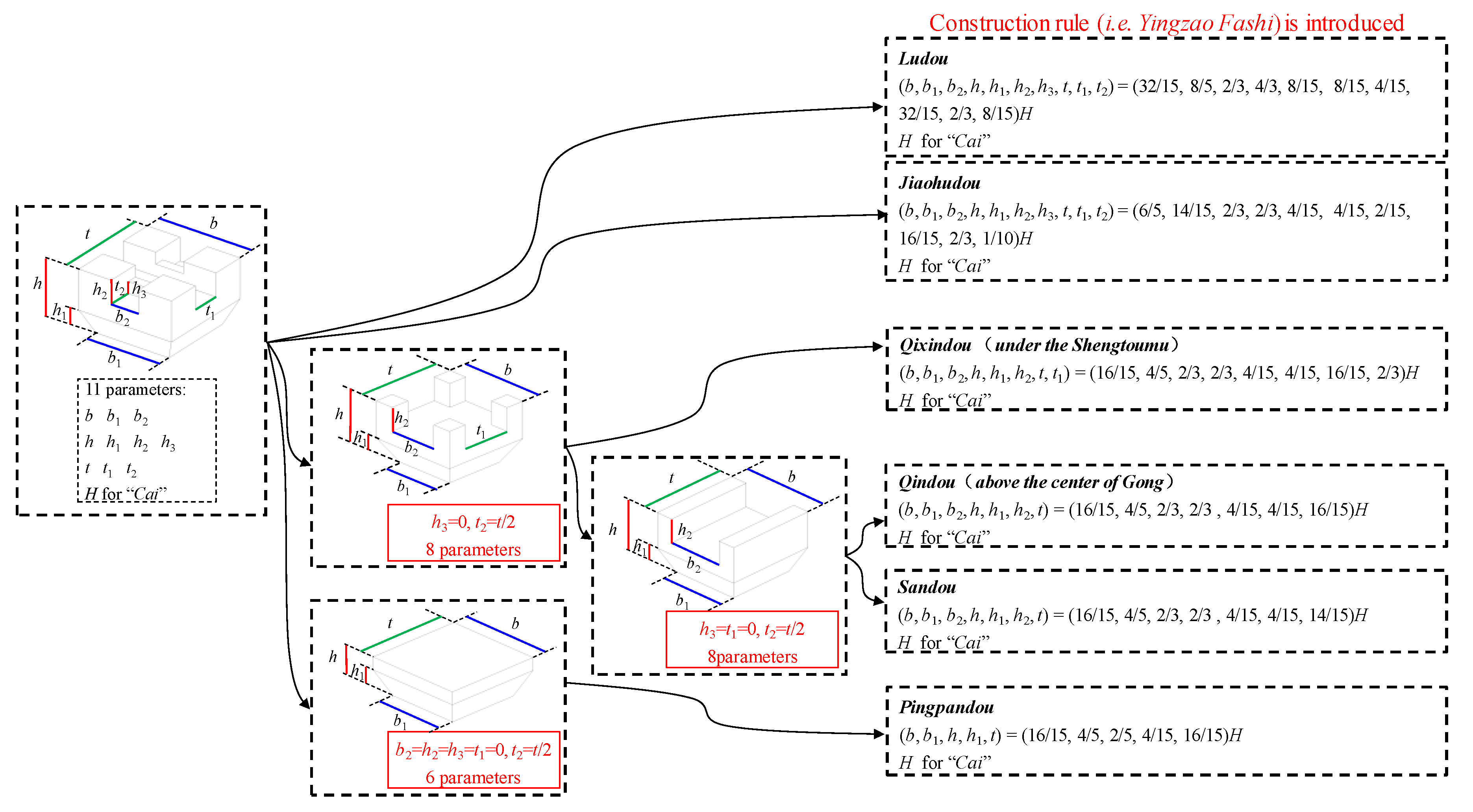
2.3. Parametric Model of the other Components
The dou, as shown in
Figure 5, is a square wooden block with a cross-mortise notch, which supports the weight of the components resting on it. The fang, as shown in
Figure 6, is a horizontal or vertical inserting component with a relatively simple configuration. It is a cuboid with a flat notch in the middle of the top, and the notch is used to connect with other components. Due to the length limitation, the parametric models for the dou with an emphasis on commonality and characteristics are directly presented in
Figure 5, and the corresponding parameters and construction guidelines specified in Yingzao fashi are also determined and introduced, similar to those of the gongs. For the fang, only one type exists; a commonly parametric model is also directly given and presented in
Figure 6.
The ang is located on the central line of the front and back of the dou-gong, and it stretches longitudinally to the front and back of the dou-gong to connect with the inside and outside of the jump, which is schematically illustrated in
Figure 1a. Shuatou is a component that locates the top of the ang or Huagong and is perpendicular to Linggong, as depicted in
Figure 1a,b. Commonality is rarely observed for the ang and shuatou, and they are rarely used. Therefore, the parametric model was not considered here, and the model for the ang and shuatou was separately established using the traditional method.
3. Intelligent Automated Modeling Method Developed Using Dynamo
In actual engineering practice, the dou-gong is stacked, and only some exposed dimensions can be obtained for each component. In developing an intelligent automated modeling method, three issues should be carefully addressed: (1) the type of component should be first determined based on only the appearance (e.g., Nidaogong or Linggong) and the exposed dimensions; (2) then, the invisible dimensions can be automatically deduced according to the component type and exposed dimensions, in which the characteristics (i.e., proportional relationships between the exposed and invisible dimensions) associated with the type of component should be introduced; (3) after all the dimensions of each component are obtained, it is preferred that the model is established automatically.
The traditional “family” in
Revit can be used to construct the common model, but all parameters should be manually inputted to establish the model [
37,
38]. Furthermore, the existing knowledge cannot be integrated to deduce the invisible dimensions, hindering the intelligent modeling.
Dynamo, a built-in visual programming tool in
Revit, can be used to solve these two problems effectively. This solution is attributed to the fact that it is easy to achieve the integration of logical judgment (i.e., the identification of component type) and operation (i.e., the calculation of invisible dimensions based on the exposed dimensions) through programming, leading to intelligent reasoning [
39,
40,
41,
42]. In addition, using
Dynamo supports automated modeling based on parameters [
43,
44].
Dynamo in
Revit 2017 was adopted in this study, and the intelligent automated modeling method was developed using the following typical nodes, including the
Point.ByCoordinates,
Line.ByStartPointEndPoint,
PolyCurve.ByPoints,
Surface.ByPatch, and
Solid.ByJoinedSurfaces. By taking “gong” as an example, the method was introduced in developing the parametric model for these components.
3.1. Identification Method for the Component Type
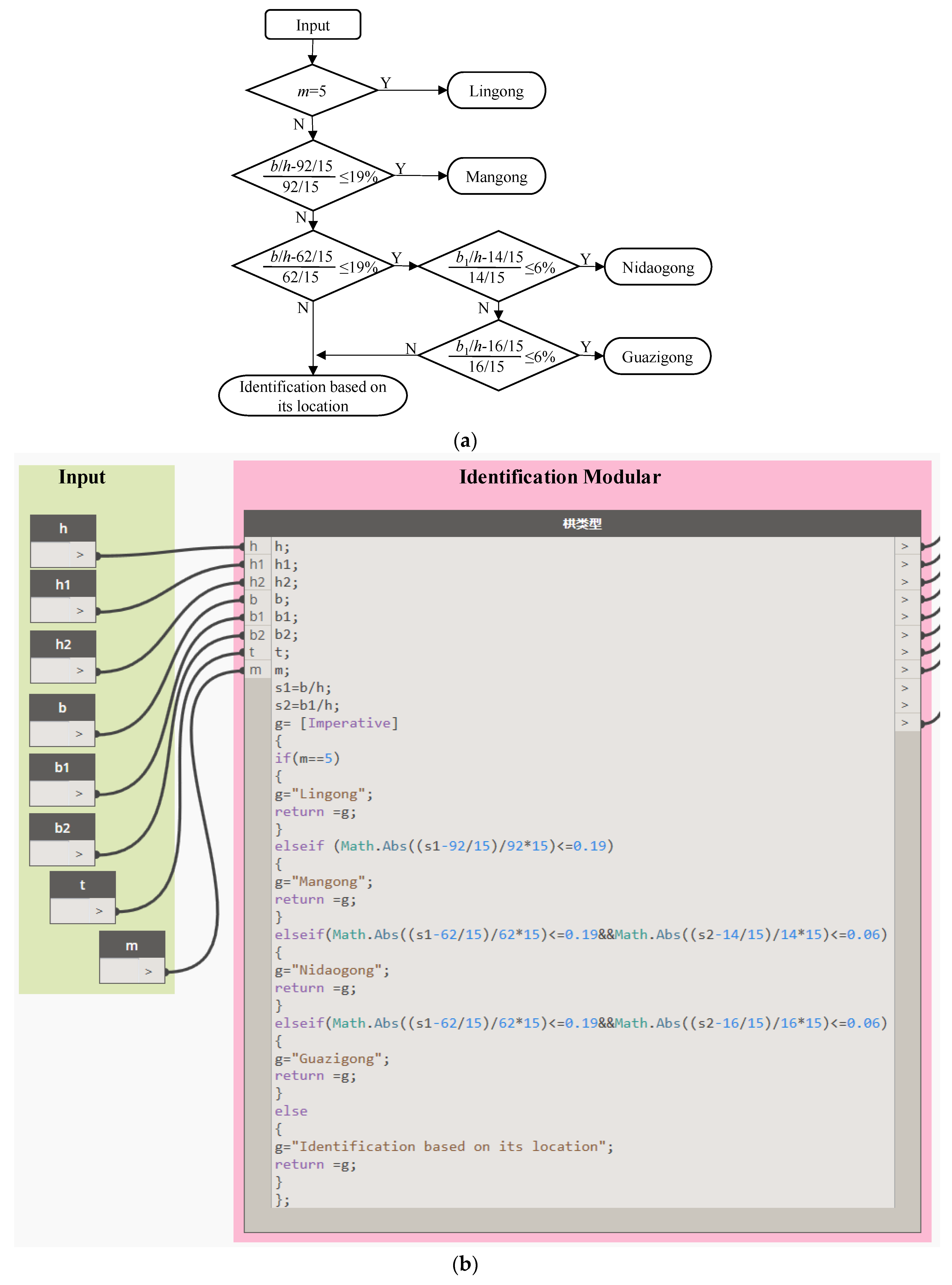
As indicated in
Figure 1a, there are significant differences between the appearances of the dou, gong, ang, and fang, resulting in the convenient identification of these components through visual recognition. However, the specific types of components with similar appearances, such as Nidaogong or Linggong, requires further identification of peculiar characteristics. Two issues should be considered for such identification, which are the variables for identification and the corresponding accepted relative error.
For evaluating the variables, there are different ratios (i.e., proportional relationships) between specific parameters or a particular value for
m. Such ratios and particular values can be regarded as variables and used for identifying the type of the component. For Nidaogong, Linggong, Mangong, and Guazigong, using a common model, seven parameters (i.e.,
h,
h1,
b,
b1,
b2,
t, and
m) in such a model are the exposed and measurable parameters; only
h2 requires deduction.
b/
h,
b1/
h, and
m can be adopted as three variables, resulting in a vector. The expressions, (62/15, 14/15, 4), (62/15, 16/15, 4), (72/15, 4/3, 5), and (92/15, 12/15, 4) are used to identify Nidaogong, Guazigong, Linggong, and Mangong, respectively. Three steps are considered as follows (as shown in
Figure 7): (1)
m is first used for identifying Linggong because only this type of gong is designed with
m equal to 5. (2) The ratio of
b/
h is used for identifying Mangong because the value of
b/
h for Nidaogong and Guazigong is 62/15, which is significantly different from that of Mangong (92/15). (3) The ratio of
b1/
h is adopted to distinguish Nidaogong from Guazigong.
For the accepted relative error of variables, the error between the expected and measured values of the ratios given above exists because manufacturing precision was relatively low during the Liao and Song dynasties. Hence, some thresholds of the relative error need to be introduced to assist in the identification of the component type. The threshold for the error in b/h is adopted as 19%, through which the acceptable values of b/h for Manggong and Nidaogong (as well as Guazigong) range from 4.97–7.3 and 3.35–4.92, respectively, leading to the identification of these components. The threshold for the error in b1/h is taken as 6%, through which the acceptable values of b1/h for Nidaogong and Guazigong range from 0.88–0.99 and 1–1.13, respectively, also resulting in the identification of these two components.
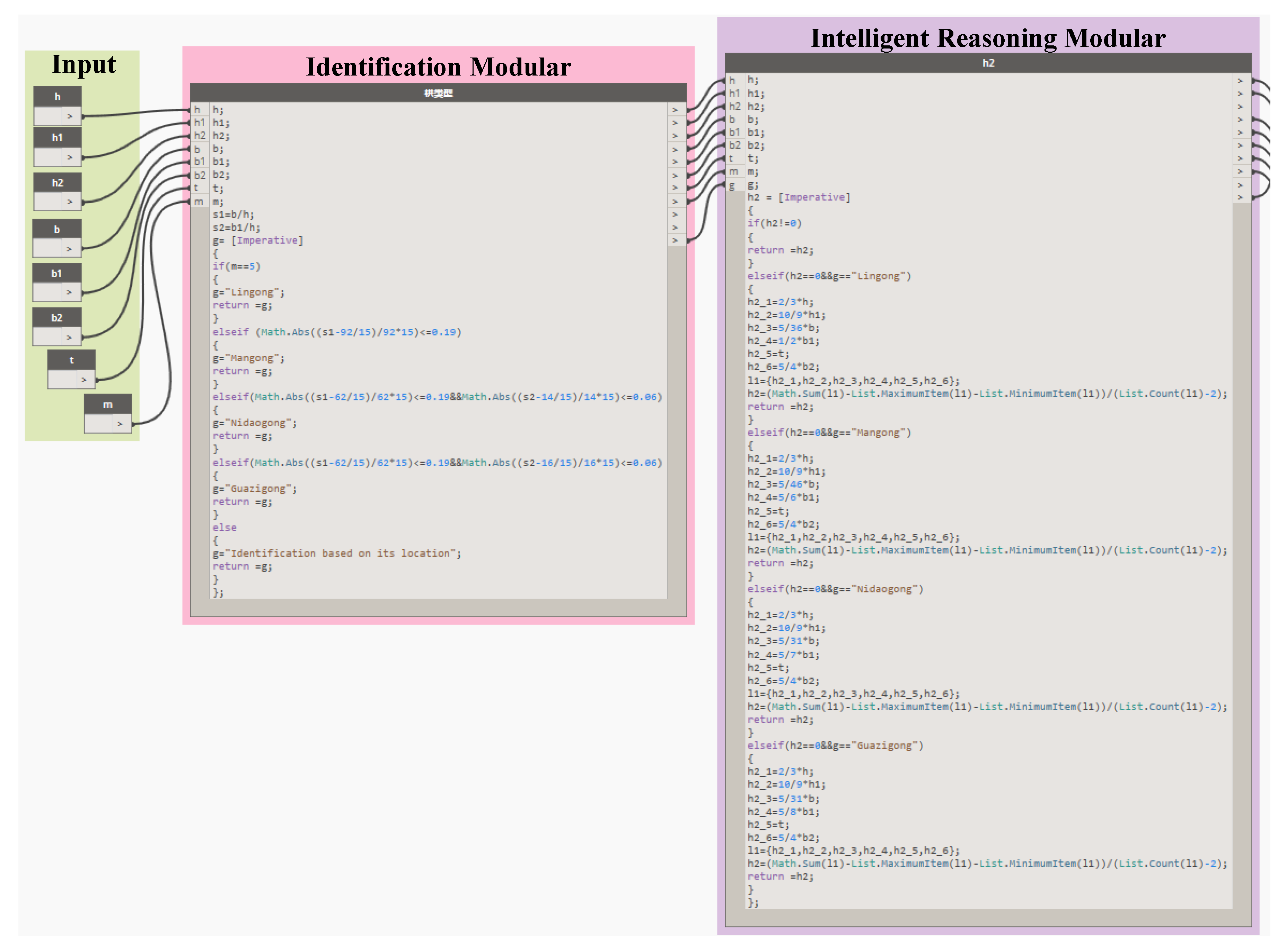
The identification method described above is programmed in
Dynamo. The corresponding logic diagram and implementation diagram in
Dynamo are presented in
Figure 7. Detailed procedures are given as follows. (1) All the available parameters should be input first. (2)
b/
h and
b1/
h are calculated, and the type of gong is defined as a variable named
g. (3) If
m is equal to 5, Linggong is assigned to g; otherwise, the absolute relative error between
b/
h and 92/15 is calculated. If the absolute relative error is not higher than 19%, the type of gong is identified as a Mangong. Otherwise, the absolute relative error between
b/
h and 62/15 is calculated and is mostly not greater than 19%. Then, the absolute relative error between
b1/
h and 14/15 is further calculated, and if this error is not higher than 6%, the component is identified as Nidaogong. Otherwise, the absolute relative error between
b1/
h and 16/15 is calculated, and if it does not exceed 6%, the gong is then identified as Guazigong. (4) If the gong does not belong to any of the situations mentioned above, “identification based on its location” is assigned to
g. (5) Finally, the result is transferred to the “parameters reasoning program.”.
3.2. Intelligent Reasoning Method for the Invisible Dimensions
In actual engineering practice, the dou-gong is usually stacked. The exposed and measurable dimensions (i.e., the input parameters presented in
Section 3.1) in the common model can be obtained, whereas the invisible dimensions are the parameters that should be reasoned in this model. During this procedure, the historical knowledge (i.e., the proportional relationships between each parameter) is required and integrated in
Dynamo as the characteristics.
Through the identification method of the type of component, the component type is transferred to the program using a variable
g. The proportional relationships between the exposed and invisible dimensions are integrated as several functions. Such functions are selected according to “
g” (i.e., the identified type) and called to reason the invisible dimensions.
h2 is the invisible dimension of the gong that is to be deduced. If Linggong is identified, six functions integrated in
Dynamo, which specify the relationships between the exposed dimensions (i.e.,
h,
h1,
b,
b1,
b2, and
t) and the invisible dimension (i.e.,
h2), are used for calculating
h2. Then, excluding the maximum and minimum values of the calculated
h2, the average value of the other four
h2 is calculated and regarded as the acceptable value. The intelligent reasoning method for the invisible dimensions is shown in
Figure 8. It should be noted that currently, there is no universal agreement on the reasoning method. Thus, a simple engineering method is adopted in this study to illustrate the fundamental principle of the intelligent reasoning method. In future studies, the framework described in this study can still be used, while a new algorithm can be introduced to improve the accuracy or expanded to AWA structures built during other dynasties (e.g., Qing dynasty) with different historical knowledge.
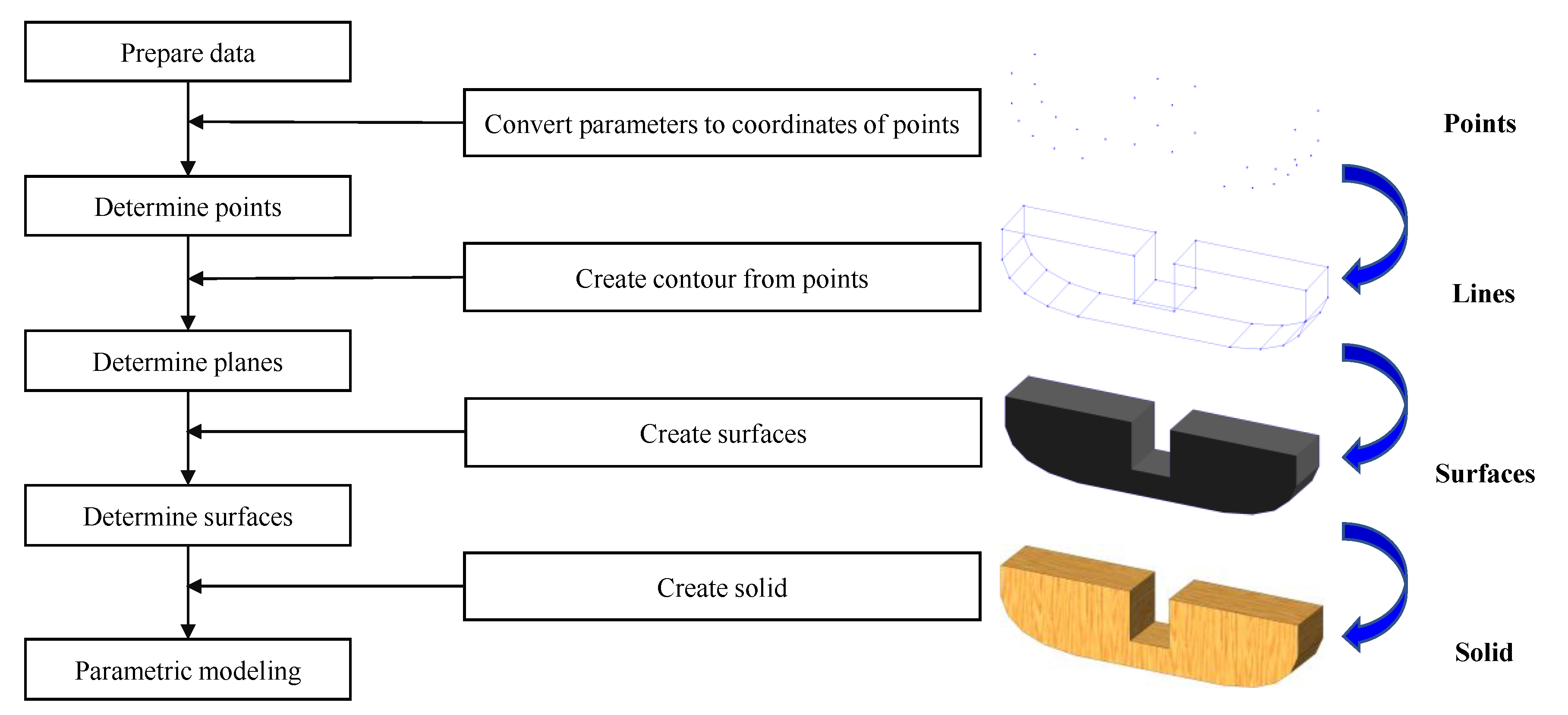
3.3. Automated Modeling Method
All the parameters, including the exposed and deduced parameters, were obtained to establish the model. An automated modeling method was subsequently required. The traditional modeling method in
Revit, i.e., points-to-lines, lines-to-surfaces, and surfaces-to-solid, as shown in
Figure 9, was also programmed based on
Dynamo.
The outline of each component in the dou-gong can be considered as a polyline, and some characteristic points (as shown in
Figure 10a) are defined. In
Dynamo, such points can be represented using coordinate points, and the coordinate values of each point can be determined by the characteristic parameters in the common model. Before the characteristic points are created, such points should be numbered, which will facilitate the resulting definition of the relationships between such points (i.e., the generation of lines). Nidaogong, Mangong, Guazigong, and Linggong are also adopted here as an example to illustrate the method. The characteristic points of the gong are presented in
Figure 10a, and the coordinate values can be determined based on the parameters in the common model. For example, the coordinates of No. 1–5 in
Figure 10a are given as follows: 1 (0, 0,
h1), 2 (0, 0,
h), 3 (0,
t,
h), 4 (0,
t,
h1), and 5 ((
b-
b2)/2,
t,
h).
(1) Creating points
For the gong, two types of characteristic points were considered and defined, which were the points on juansha (e.g., 22, 23, and 26 in
Figure 10b) and the other points (e.g., 1, 2, and 3 in
Figure 10a). For the other points, with all the parameters for the common model, the coordinates of such points can be obtained by simple addition and subtraction. Subsequently,
Point.ByCoordinates in
Dynamo was directly used to create the points. For the points on juansha, taking
m equal to 4 as an example, the process of creating such points involved the following four steps: (1)
h1 (the distance between Point 1 and Point O in
Figure 10b) and
b1 (the distance between Point 19 and Point O in
Figure 10b) were equally divided into four parts.
Point.ByCoordinates in
Dynamo was also used to create the points obtained through such equalization (i.e.,
S1,
S2,
S3,
S4,
S5, and
S6 in
Figure 10b). (2)
Line.ByStartPointEndPoint was called to connect Points 1 and
S4, Points
S3 and
S5, Points
S2 and
S6, and Points
S1 and 19, and four lines were generated. (3) The four generated lines were named
L1,
L2,
L3, and
L4, respectively, and the intersections of
L1 and
L2, L2 and
L3, and
L3 and
L4 were points on juansha that were required for the modeling.
Geometry.intersect was subsequently used to determine the intersections (i.e., Points 22, 23, and 26) of 4 lines. Meanwhile, the corresponding coordinates were also obtained through
Point.X, Point.Y, and
Point.Z. (4) Most components were symmetrical, through which the characteristic points of the other three parts of juansha can be determined using the function,
Translate, in
Dynamo. For example, according to the symmetry in the direction of length
b, Point 26-1 can be determined from Point 26. Based on the symmetry in the direction of thickness
t, Point 25 can be determined from Point 26, and Point 25-1 can be determined from Point 26-1.
(2) Creating lines, surfaces, and solid
After creating the points, the contour of the component was first established. The points on each surface were organized to facilitate the creation of surfaces, and the connection relationships between these points were defined in a single list. The lists for all the surfaces were stored in List.Join in Dynamo. Then, PolyCurve.ByPoints in Dynamo was used to connect the points in the lists, and several closed curves can be generated automatically, leading to the contour of each surface and the component. Subsequently, Surface.ByPatch in Dynamo, which could be used to create a surface based on several closed curves through filling, was used to create all the surfaces. A surface list was defined there to organize all the surfaces attributed to the component. Finally, Solid.ByJoinedSurfaces in Dynamo, which can create a solid based on all surfaces, was called to build the solid.
The procedure described above was programmed in
Dynamo. An example of the intelligent automated modeling of Nidaogong, Mangong, Linggong, and Guazigong is presented in
Figure 11, which all share a common model.
5. Conclusions
A parametric model of the typical components of an ancient wooden architectural structure with emphasis on commonality and characteristics, as well as an intelligent automated method for modeling these components, are two critical issues in the protection of such structures using HBIM.
Using a Chinese AWA building constructed during the Liao and Song dynasties as an example, a parametric model for the typical components with emphasis on commonality and characteristics were first proposed. Subsequently, an intelligent automated modeling method was developed and programmed using Dynamo. Dynamo can intelligently identify the component type and determine the invisible dimensions based on only the measured visible dimension, which is driven by the knowledge highlighted above. Additionally, Dynamo is capable of automatically establishing the corresponding HBIM model. A complicated dou-gong was established with surveying data using this method, thus validating the reliability and efficiency of the proposed method. Furthermore, the method was conclusively used to establish the HBIM model of Yingxian Wood Pagoda. The research findings will be a vital reference for the conservation of wooden architectural heritage structures.
It should be recognized that the actual conditions of AWA structures are complex. In particular, the damage of components was not considered in this study. Further improvements are required for considering the damaged components in future investigations.