A GIS-Based Multi-Criteria Decision Analysis Model for Determining Glacier Vulnerability
Abstract
:1. Introduction
2. Study Area
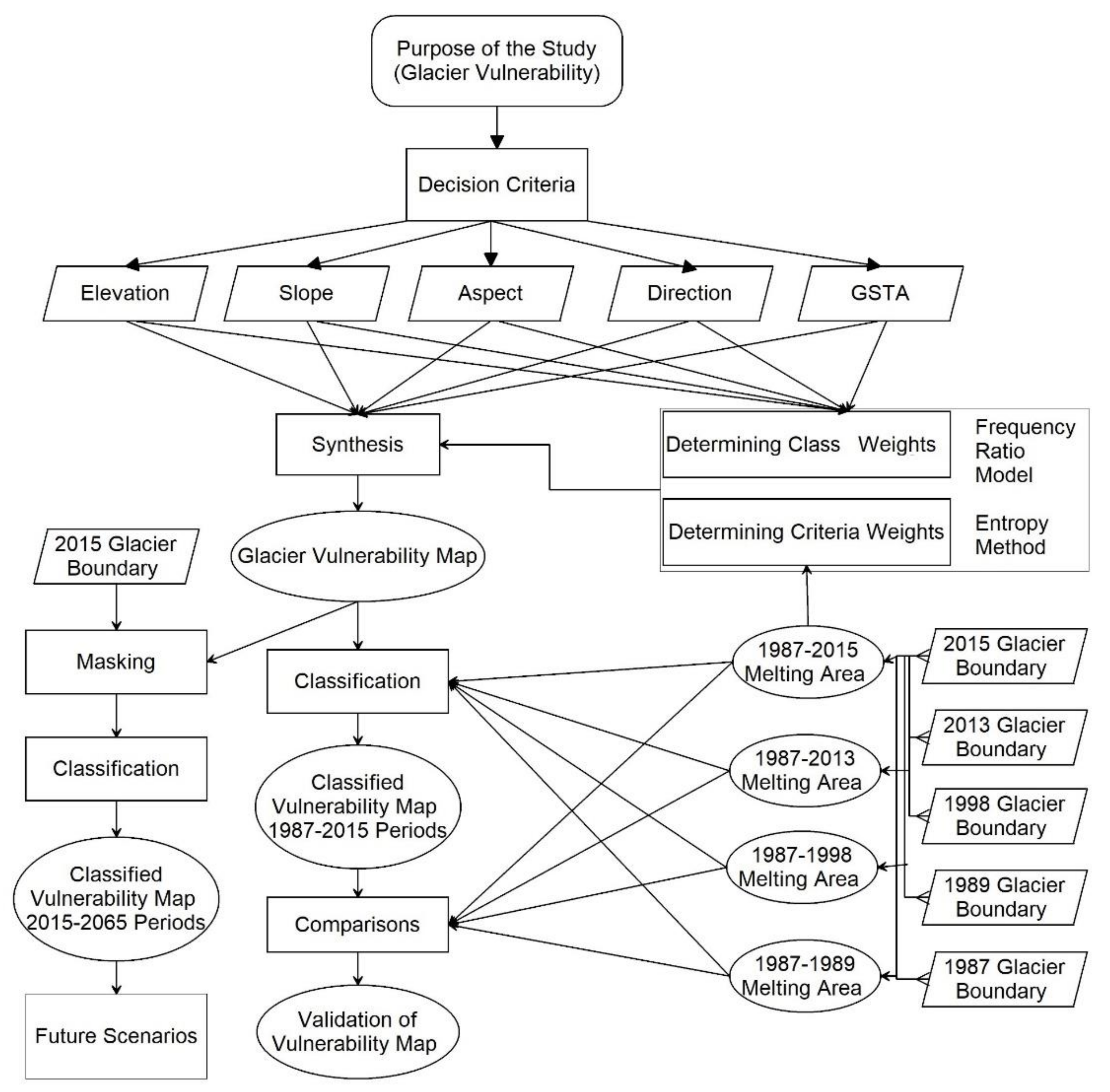
3. Materials and Methods
3.1. Decision Criteria
3.2. Evaluation Criteria
3.3. Weighting
3.4. Synthesizing
4. Results
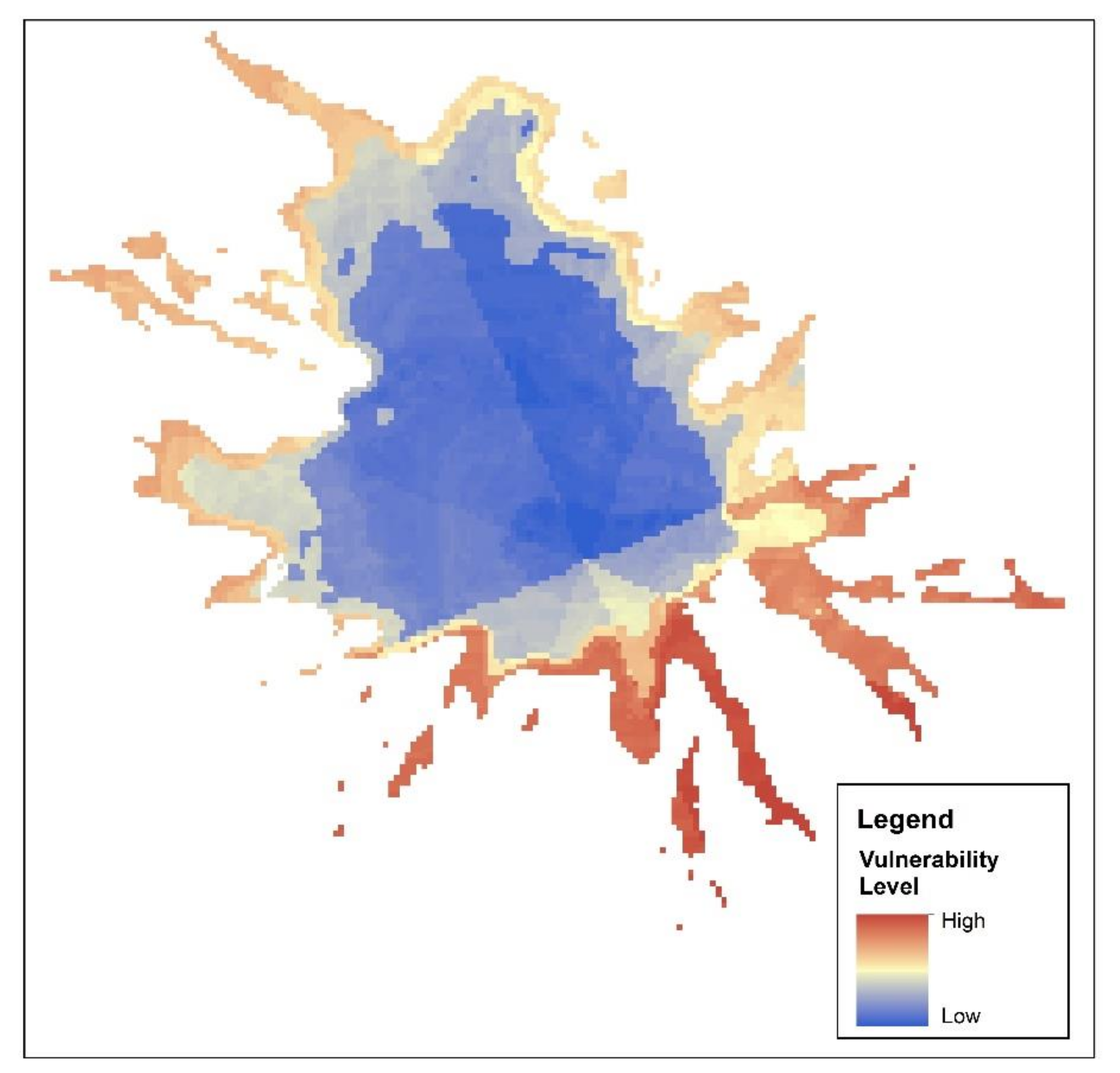
4.1. Glacier Vulnerability Map
4.2. Validation of the Glacier Vulnerability Map
4.3. Future Scenarios
5. Discussion
Funding
Acknowledgments
Conflicts of Interest
References
- Liu, T.; Kinouchi, T.; Ledezma, F. Characterization of recent glacier decline in the Cordillera Real by LANDSAT, ALOS, and ASTER data. Remote Sens. Environ. 2013, 137, 158–172. [Google Scholar] [CrossRef]
- Bishop, M.P.; Olsenholler, J.A.; Shroder, J.F.; Barry, R.G.; Raup, B.H.; Bush, A.B.; Copland, L.; Dwyer, J.L.; Fountain, A.G.; Haeberli, W.; et al. Global Land Ice Measurements from Space (GLIMS): Remote sensing and GIS investigations of the Earth’s cryosphere. Geocarto Int. 2004, 19, 57–84. [Google Scholar] [CrossRef]
- The National Snow and Ice Data Center (NSIDC). Glaciers and Climate Change. Available online: https://nsidc.org/cryosphere/glaciers/questions/climate.html (accessed on 24 July 2019).
- Kaser, G.; Fountain, A.; Jansson, P. A Manual for Monitoring the Mass Balance of Mountain Glaciers; UNESCO: Paris, France, 2003; p. 137. [Google Scholar]
- Tangborn, W.V.; Krimmel, R.M.; Meier, M.F. A comparison of glacier mass balance by glaciological, hydrological and mapping methods, South Cascade Glacier, Washington. Int. Assoc. Hydrol. Sci. Publ. 1975, 104, 185–196. [Google Scholar]
- Østrem, G.; Brugman, M. Glacier-Mass Balance Measurements: A Manual for Field and Office Work; NHRI Science Report; National Hydrology Research Institute: Saskatoon, SK, Canada, 1994. [Google Scholar]
- Imhof, E. The ararat. Die Alpen 1956, 32, 1–14. [Google Scholar]
- Bayr, K.J.; Hall, D.K.; Kovalick, W.M. Observations on glaciers in the eastern Austrian Alps using satellite data. Int. J. Remote Sens. 1994, 15, 1733–1742. [Google Scholar] [CrossRef]
- Paul, F. Evaluation of different methods for glacier mapping using Landsat TM. In Proceedings of the EARSeL-SIG Workshop on Land Ice and Snow, Dresden, Germany, 16–17 June 2000; Volume 16, p. 17. [Google Scholar]
- Paul, F.; Huggel, C.; Kääb, A.; Kellenberger, T.; Maisch, M. Comparison of TM-derived glacier areas with higher resolution data sets. In Proceedings of the EARSeL Workshop on Remote Sensing of Land Ice and Snow, Bern, Switzerland, 11–13 March 2002; Volume 11. [Google Scholar]
- Andreassen, L.M.; Paul, F.; Kääb, A.; Hausberg, J.E. Landsat-derived glacier inventory for Jotunheimen, Norway, and deduced glacier changes since the 1930s. Cryosphere 2008, 2, 131–145. [Google Scholar] [CrossRef] [Green Version]
- Racoviteanu, A.E.; Williams, M.W.; Barry, R.G. Optical remote sensing of glacier characteristics: A review with focus on the Himalaya. Sensors 2008, 8, 3355–3383. [Google Scholar] [CrossRef] [Green Version]
- Strigaro, D.; Moretti, M.; Mattavelli, M.; Frigerio, I.; De Amicis, M.; Maggi, V. A GRASS GIS module to obtain an estimation of glacier behavior under climate change: A pilot study on Italian glacier. Comput. Geosci. 2016, 94, 68–76. [Google Scholar] [CrossRef]
- Garg, P.K.; Shukla, A.; Jasrotia, A.S. Influence of topography on glacier changes in the central Himalaya, India. Glob. Planet. Chang. 2017, 155, 196–212. [Google Scholar] [CrossRef]
- Jones, D.B.; Harrison, S.; Anderson, K.; Selley, H.L.; Wood, J.L.; Betts, R.A. The distribution and hydrological significance of rock glaciers in the Nepalese Himalaya. Glob. Planet. Chang. 2018, 160, 123–142. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.P.; Ding, Y.J.; Liu, S.Y.; Tan, C.P. Vulnerability of mountain glaciers in China to climate change. Adv. Clim. Chang. Res. 2015, 6, 171–180. [Google Scholar] [CrossRef]
- Allen, T.R. Topographic context of glaciers and perennial snowfields, Glacier National Park, Montana. Geomorphology 1998, 21, 207–216. [Google Scholar] [CrossRef]
- Lambrecht, A.; Kuhn, M. Glacier changes in the Austrian Alps during the last three decades, derived from the new Austrian glacier inventory. Ann. Glaciol. 2007, 46, 177–184. [Google Scholar] [CrossRef] [Green Version]
- Gibson, M.J.; Glasser, N.F.; Quincey, D.J.; Mayer, C.; Rowan, A.V.; Irvine-Fynn, T.D. Temporal variations in supraglacial debris distribution on Baltoro Glacier, Karakoram between 2001 and 2012. Geomorphology 2017, 295, 572–585. [Google Scholar] [CrossRef] [Green Version]
- Pandey, A.C.; Ghosh, S.; Nathawat, M.S. Evaluating patterns of temporal glacier changes in Greater Himalayan Range, Jammu & Kashmir, India. Geocarto Int. 2011, 26, 321–338. [Google Scholar]
- Bolch, T. Climate change and glacier retreat in northern Tien Shan (Kazakhstan/Kyrgyzstan) using remote sensing data. Glob. Planet. Chang. 2007, 56, 1–12. [Google Scholar] [CrossRef]
- Kumar, A.; Verma, A.; Gokhale, A.A.; Bhambri, R.; Misra, A.; Sundriyal, S.; Dobhal, D.P.; Kishore, N. Hydrometeorological assessments and suspended sediment delivery from a central Himalayan glacier in the upper Ganga basin. Int. J. Sediment Res. 2018, 33, 493–509. [Google Scholar] [CrossRef]
- Wu, F.; Zhan, J.; Wang, Z.; Zhang, Q. Streamflow variation due to glacier melting and climate change in upstream Heihe River Basin, Northwest China. Phys. Chem. Earth Parts A/B/C 2015, 79, 11–19. [Google Scholar] [CrossRef]
- Li, Z.; Shi, X.; Tang, Q.; Zhang, Y.; Gao, H.; Pan, X.; Déry, S.J.; Zhou, P. Partitioning the contributions of glacier melt and precipitation to the 1971–2010 runoff increases in a headwater basin of the Tarim River. J. Hydrol. 2020, 583, 124579. [Google Scholar] [CrossRef]
- López-Moreno, J.I.; Fontaneda, S.; Bazo, J.; Revuelto, J.; Azorin-Molina, C.; Valero-Garcés, B.; Morán-Tejeda, E.; Vicente-Serrano, S.M.; Zubieta, R.; Alejo-Cochachín, J. Recent glacier retreat and climate trends in Cordillera Huaytapallana, Peru. Glob. Planet. Chang. 2014, 112, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Schauwecker, S.; Rohrer, M.; Acuña, D.; Cochachin, A.; Dávila, L.; Frey, H.; Giráldez, C.; Gómez, J.; Huggel, C.; Jacques-Coper, M.; et al. Climate trends and glacier retreat in the Cordillera Blanca, Peru, revisited. Glob. Planet. Chang. 2014, 119, 85–97. [Google Scholar] [CrossRef]
- Yan, W.; Liu, J.; Zhang, M.; Hu, L.; Chen, J. Outburst flood forecasting by monitoring glacier-dammed lake using satellite images of Karakoram Mountains, China. Quat. Int. 2017, 453, 24–36. [Google Scholar] [CrossRef]
- Mir, R.A.; Jain, S.K.; Lohani, A.K.; Saraf, A.K. Glacier recession and glacial lake outburst flood studies in Zanskar basin, western Himalaya. J. Hydrol. 2018, 564, 376–396. [Google Scholar] [CrossRef]
- Wang, X.; Siegert, F.; Zhou, A.G.; Franke, J. Glacier and glacial lake changes and their relationship in the context of climate change, Central Tibetan Plateau 1972–2010. Glob. Planet. Chang. 2013, 111, 246–257. [Google Scholar] [CrossRef]
- Viani, C.; Machguth, H.; Huggel, C.; Godio, A.; Franco, D.; Perotti, L.; Giardino, M. Potential future lakes from continued glacier shrinkage in the Aosta Valley Region (Western Alps, Italy). Geomorphology 2020, 353, 107068. [Google Scholar] [CrossRef]
- Akhtar, M.; Ahmad, N.; Booij, M.J. The impact of climate change on the water resources of Hindukush–Karakorum–Himalaya region under different glacier coverage scenarios. J. Hydrol. 2008, 355, 148–163. [Google Scholar] [CrossRef]
- Li, Y.; Li, Y. Topographic and geometric controls on glacier changes in the central Tien Shan, China, since the Little Ice Age. Ann. Glaciol. 2014, 55, 177–186. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.; Li, Z.; Li, J.I.A. Slight glacier mass loss in the Karakoram region during the 1970s to 2000 revealed by KH-9 images and SRTM DEM. J. Glaciol. 2017, 63, 331–342. [Google Scholar] [CrossRef] [Green Version]
- Yalcin, M. The impact of topographical parameters to the glaciation and glacial retreat on Mount Ağrı (Ararat). Environ. Earth Sci. 2019, 78, 393. [Google Scholar] [CrossRef]
- Yalcin, M.; Gul, F.K. A GIS-based multi criteria decision analysis approach for exploring geothermal resources: Akarcay basin (Afyonkarahisar). Geothermics 2017, 67, 18–28. [Google Scholar] [CrossRef]
- Ouma, Y.; Tateishi, R. Urban flood vulnerability and risk mapping using integrated multi-parametric AHP and GIS: Methodological overview and case study assessment. Water 2014, 6, 1515–1545. [Google Scholar] [CrossRef]
- Ahmed, B. Landslide susceptibility mapping using multi-criteria evaluation techniques in Chittagong Metropolitan Area, Bangladesh. Landslides 2015, 12, 1077–1095. [Google Scholar] [CrossRef] [Green Version]
- Kougkoulos, I.; Cook, S.J.; Jomelli, V.; Clarke, L.; Symeonakis, E.; Dortch, J.M.; Edwards, L.; Merad, M. Use of multi-criteria decision analysis to identify potentially dangerous glacial lakes. Sci. Total Environ. 2018, 621, 1453–1466. [Google Scholar] [CrossRef] [PubMed]
- Kumar, S.; Srivastava, P.; Snehmani, K. GIS-based MCDA–AHP modelling for avalanche susceptibility mapping of Nubra valley region, Indian Himalaya. Geocarto Int. 2017, 32, 1254–1267. [Google Scholar] [CrossRef]
- Blumenthal, M.M. Vom Ağrı Dag (Ararat) zum Kaçkar Dag. Bergfahrten in nordostanatolischen Glenzlanden (From Mount Ararat to Mount Kaçkar. Mountain trip in the frontier region of northeastern Anatolia). Die Alpen 1958, 34, 125–137. [Google Scholar]
- Çiner, A. Turkish glaciers and glacial deposits. In Developments in Quaternary Sciences; Elsevier: Amsterdam, The Netherlands, 2004; Volume 2, pp. 419–429. [Google Scholar]
- Kurter, A.; Sungur, K. Present glaciation in Turkey. Int. Assoc. Hydrol. Sci. 1980, 126, 155–160. [Google Scholar]
- Sarıkaya, M.A. Recession of the ice cap on Mount Ağrı (Ararat), Turkey, from 1976 to 2011 and its climatic significance. J. Asian Earth Sci. 2012, 46, 190–194. [Google Scholar] [CrossRef]
- Yavasli, D.D.; Tucker, C.J.; Melocik, K.A. Change in the glacier extent in Turkey during the Landsat Era. Remote Sens. Environ. 2015, 163, 32–41. [Google Scholar] [CrossRef]
- Yalcin, M.; Ugur, M.A.; Polat, N.; Dereli, M.A. Gis-Based Temporal Analysis of Glacier Changes on Agri Mountain Using Landsat Data. Int. Multidiscip. Sci. GeoConf. SGEM Surv. Geol. Min. Ecol. Manag. 2017, 17, 133–140. [Google Scholar]
- Malczewski, J. GIS-based multicriteria decision analysis: A survey of the literature. Int. J. Geogr. Inf. Sci. 2006, 20, 703–726. [Google Scholar] [CrossRef]
- JPL. SRTM Mission Statistics. Available online: https://www2.jpl.nasa.gov/srtm/statistics.html (accessed on 9 August 2019).
- Malczewski, J.; Rinner, C. Multicriteria Decision Analysis in Geographic Information Science; Springer: New York, NY, USA, 2015. [Google Scholar]
- MacCrimmon, K.R. Inproving the System Design and Evaluation Process by the Use of Trade-Off Information; Memorandum RM-5877-DOT; The Rand Corporation: Santa Monica, CA, USA, 1969. [Google Scholar]
- Keeney, R.L.; Raiffa, H. Decisions with Multiple Objectives: Preferences and Value Tradeoffs; Wiley: New York, NY, USA, 1976. [Google Scholar]
- Pitz, G.F.; McKillip, J. Decision Analysis for Program Evaluators; SAGE Publications, Incorporated: Thousand Oaks, CA, USA, 1984; Volume 7. [Google Scholar]
- Malczewski, J. GIS and Multicriteria Decision Analysis; John Wiley & Sons: Hoboken, NJ, USA, 1999. [Google Scholar]
- Wu, Y.; Wang, N.; He, J.; Jiang, X. Estimating mountain glacier surface temperatures from Landsat-ETM+ thermal infrared data: A case study of Qiyi glacier, China. Remote Sens. Environ. 2015, 163, 286–295. [Google Scholar] [CrossRef]
- Eastman, J.R. IDRISI: A Grid Based Geographic Analysis System, version 4.1; Graduate School of Geography, Clark University: Worcester, MA, USA, 1991. [Google Scholar]
- Eastman, J.R.; Kyem, P.A.K.; Toledano, J.; Jin, W. GIS and Decision Making; The United Nations Institute for Training and Research (UNITAR): Geneva, Switzerland, 1993. [Google Scholar]
- Bonham-Carter, G.F. Geographic Information Systems for Geoscientists, Modeling with GIS; Pergamon Press: Oxford, UK, 1994. [Google Scholar]
- Al-Abadi, A.M. Modeling of groundwater productivity in northeastern Wasit Governorate, Iraq using frequency ratio and Shannon’s entropy models. Appl. Water Sci. 2017, 7, 699–716. [Google Scholar] [CrossRef] [Green Version]
- Bednarik, M.; Magulová, B.; Matys, M.; Marschalko, M. Landslide susceptibility assessment of the Kraľovany–Liptovský Mikuláš railway case study. Phys. Chem. Earth Parts A/B/C 2010, 35, 162–171. [Google Scholar] [CrossRef]
- Constantin, M.; Bednarik, M.; Jurchescu, M.C.; Vlaicu, M. Landslide susceptibility assessment using the bivariate statistical analysis and the index of entropy in the Sibiciu Basin (Romania). Environ. Earth Sci. 2011, 63, 397–406. [Google Scholar] [CrossRef]
- Jaafari, A.; Najafi, A.; Pourghasemi, H.R.; Rezaeian, J.; Sattarian, A. GIS-based frequency ratio and index of entropy models for landslide susceptibility assessment in the Caspian forest, Northern Iran. Int. J. Environ. Sci. Technol. 2014, 11, 909–926. [Google Scholar] [CrossRef] [Green Version]
- Wang, Q.; Li, W.; Yan, S.; Wu, Y.; Pei, Y. GIS based frequency ratio and index of entropy models to landslide susceptibility mapping (Daguan, China). Environ. Earth Sci. 2016, 75, 780. [Google Scholar] [CrossRef]
- Nesje, A.; Bakke, J.; Dahl, S.O.; Lie, Ø.; Matthews, J.A. Norwegian mountain glaciers in the past, present and future. Glob. Planet. Chang. 2008, 60, 10–27. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2001: The Scientific Basis; Houghton, J.T., Ding, Y., Griggs, D.J., Noguer, M., van der Linden, P.J., Dai, X., Maskell, K., Johnson, C.A., Eds.; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Barry, R.G. The status of research on glaciers and global glacier recession: A review. Prog. Phys. Geogr. 2006, 30, 285–306. [Google Scholar] [CrossRef]
- Kutuzov, S.; Shahgedanova, M. Glacier retreat and climatic variability in the Eastern Terskey–Alatoo, inner Tien Shan between the middle of the 19th century and beginning of the 21st century. Glob. Planet. Chang. 2009, 69, 59–70. [Google Scholar] [CrossRef]
- Gao, H.; Li, H.; Duan, Z.; Ren, Z.; Meng, X.; Pan, X. Modelling glacier variation and its impact on water resource in the Urumqi Glacier No. 1 in Central Asia. Sci. Total Environ. 2018, 644, 1160–1170. [Google Scholar] [CrossRef] [PubMed]
- Ding, Y.; Liu, S.; Li, J.; Shangguan, D. The retreat of glaciers in response to recent climate warming in western China. Ann. Glaciol. 2006, 43, 97–105. [Google Scholar] [CrossRef] [Green Version]
- Wójcik, K.A.; Sobota, I. Spatial and temporal changes in ablation, distribution and evolution of glacial zones on Irenebreen, a small glacier of the High Arctic, Svalbard. Polar Sci. 2020, 23, 100503. [Google Scholar] [CrossRef]
- Da Silva, A.B.; Arigony-Neto, J.; Braun, M.; de Almeida Espinoza, J.M.; Costi, J.; Janã, R. Spatial and temporal analysis of changes in the glaciers of the Antarctic Peninsula. Glob. Planet. Chang. 2019, 184, 103079. [Google Scholar] [CrossRef]
- Narama, C.; Kääb, A.; Duishonakunov, M.; Abdrakhmatov, K. Spatial variability of recent glacier area changes in the Tien Shan Mountains, Central Asia, using Corona (~1970), Landsat (~2000), and ALOS (~2007) satellite data. Glob. Planet. Chang. 2010, 71, 42–54. [Google Scholar] [CrossRef]
- Vijay, S.; Braun, M. Early 21st century spatially detailed elevation changes of Jammu and Kashmir glaciers (Karakoram–Himalaya). Glob. Planet. Chang. 2018, 165, 137–146. [Google Scholar] [CrossRef] [Green Version]
- Peduzzi, P. Landslides and vegetation cover in the 2005 North Pakistan earthquake: A GIS and statistical quantitative approach. Nat. Hazards Earth Syst. Sci. 2010, 10, 623–640. [Google Scholar] [CrossRef]




| Criteria | Classes | Glacial Area (m2) | Glacial Area Ratio (a) | Melting Area (m2) | Melting Area Ratio (b) | FR (b/a) | (Pij) | Pij (Mean) | Hj | Hij max | Ij | Wj |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Elevation (m) | 3600–3700 | 1983 | 0.0002 | 1983 | 0.0006 | 2.5916 | 0.1256 | 0.0625 | 3.6308 | 4.0 | 0.0923 | 0.0058 |
| 3700-3800 | 567,77 | 0.0061 | 567,77 | 0.0158 | 2.5916 | 0.1256 | ||||||
| 3800–3900 | 147,274 | 0.0158 | 132,894 | 0.0370 | 2.3385 | 0.1133 | ||||||
| 3900–4000 | 164,877 | 0.0177 | 117,274 | 0.0327 | 1.8433 | 0.0893 | ||||||
| 4000–4100 | 284,135 | 0.0306 | 232,564 | 0.0648 | 2.1212 | 0.1028 | ||||||
| 4100–4200 | 539,261 | 0.0580 | 392,978 | 0.1096 | 1.8886 | 0.0915 | ||||||
| 4200–4300 | 942,652 | 0.1014 | 540,500 | 0.1507 | 1.4860 | 0.0720 | ||||||
| 4300–4400 | 1,037,116 | 0.1116 | 478,268 | 0.1333 | 1.1951 | 0.0579 | ||||||
| 4400–4500 | 1,008,851 | 0.1085 | 385,540 | 0.1075 | 0.9904 | 0.0480 | ||||||
| 4500–4600 | 974,388 | 0.1048 | 334,714 | 0.0933 | 0.8902 | 0.0431 | ||||||
| 4600–4700 | 872,239 | 0.0938 | 279,672 | 0.0780 | 0.8309 | 0.0403 | ||||||
| 4700–4800 | 1,391,417 | 0.1497 | 259,837 | 0.0724 | 0.4840 | 0.0235 | ||||||
| 4800–4900 | 809,759 | 0.0871 | 241,985 | 0.0675 | 0.7745 | 0.0375 | ||||||
| 4900–5000 | 562,815 | 0.0605 | 131,902 | 0.0368 | 0.6074 | 0.0294 | ||||||
| 5000–5100 | 492,401 | 0.0530 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | ||||||
| 5100–5200 | 9670 | 0.0010 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | ||||||
| Direction | North | 1,848,237 | 0.1987 | 183,727 | 0.0508 | 0.2555 | 0.0226 | 0.1250 | 2.6905 | 3.000 | 0.1032 | 0.0129 |
| Northwest | 2,442,723 | 0.2626 | 598,004 | 0.1652 | 0.6292 | 0.0557 | ||||||
| West | 1,578,162 | 0.1696 | 510,726 | 0.1411 | 0.8317 | 0.0736 | ||||||
| Southwest | 486,716 | 0.0523 | 379,380 | 0.1048 | 2.0033 | 0.1773 | ||||||
| South | 381,942 | 0.0411 | 339,650 | 0.0938 | 2.2855 | 0.2023 | ||||||
| Southeast | 524,154 | 0.0563 | 573,507 | 0.1584 | 2.8121 | 0.2489 | ||||||
| East | 1,114,486 | 0.1198 | 832,588 | 0.2300 | 1.9200 | 0.1699 | ||||||
| Northeast | 926,533 | 0.0996 | 202,099 | 0.0558 | 0.5606 | 0.0496 | ||||||
| Aspect | North | 1,948,777 | 0.2096 | 356,284 | 0.0989 | 0.4720 | 0.0515 | 0.1250 | 2.9057 | 3.000 | 0.0314 | 0.0039 |
| Northwest | 1,496,045 | 0.1609 | 486,202 | 0.1350 | 0.8390 | 0.0916 | ||||||
| West | 1,494,806 | 0.1608 | 585,377 | 0.1626 | 1.0110 | 0.1104 | ||||||
| Southwest | 868,520 | 0.0934 | 490,913 | 0.1363 | 1.4592 | 0.1593 | ||||||
| South | 859,346 | 0.0924 | 544,467 | 0.1512 | 1.6356 | 0.1785 | ||||||
| Southeast | 658,270 | 0.0708 | 392,483 | 0.1090 | 1.5392 | 0.1680 | ||||||
| East | 600,005 | 0.0645 | 331,242 | 0.0920 | 1.4252 | 0.1556 | ||||||
| Northeast | 1,369,846 | 0.1474 | 413,805 | 0.1149 | 0.7798 | 0.0851 | ||||||
| Slope (°) | 0–5 | 184,216 | 0.0198 | 13,636 | 0.0038 | 0.1911 | 0.0147 | 0.0714 | 3.6574 | 3.807 | 0.0394 | 0.0028 |
| 5–10 | 470,087 | 0.0506 | 58,265 | 0.0162 | 0.3200 | 0.0245 | ||||||
| 10–15 | 654,799 | 0.0704 | 122,976 | 0.0342 | 0.4848 | 0.0372 | ||||||
| 15–20 | 959,512 | 0.1032 | 257,110 | 0.0714 | 0.6918 | 0.0530 | ||||||
| 20–25 | 1,340,590 | 0.1442 | 425,210 | 0.1181 | 0.8188 | 0.0628 | ||||||
| 25–30 | 1,483,401 | 0.1596 | 578,930 | 0.1608 | 1.0075 | 0.0773 | ||||||
| 30–35 | 1,380,507 | 0.1485 | 654,551 | 0.1818 | 1.2240 | 0.0939 | ||||||
| 35–40 | 1,184,390 | 0.1274 | 640,419 | 0.1779 | 1.3959 | 0.1070 | ||||||
| 40–45 | 783,973 | 0.0843 | 424,962 | 0.1180 | 1.3994 | 0.1073 | ||||||
| 45–50 | 428,929 | 0.0461 | 222,894 | 0.0619 | 1.3415 | 0.1029 | ||||||
| 50–55 | 233,308 | 0.0251 | 123,224 | 0.0342 | 1.3635 | 0.1046 | ||||||
| 55–60 | 109,836 | 0.0118 | 49,587 | 0.0138 | 1.1655 | 0.0894 | ||||||
| 60–65 | 69,918 | 0.0075 | 25,785 | 0.0072 | 0.9521 | 0.0730 | ||||||
| 65–75 | 12,149 | 0.0013 | 3223 | 0.0009 | 0.6849 | 0.0525 | ||||||
| GSTA (°) | < –4 | 1,530,600 | 0.1646 | 100,500 | 0.0301 | 0.1831 | 0.0250 | 0.1667 | 2.2061 | 2.585 | 0.1466 | 0.0244 |
| –4 - –2 | 2,846,700 | 0.3061 | 225,300 | 0.0676 | 0.2207 | 0.0301 | ||||||
| –2 - 0 | 1,400,700 | 0.1506 | 503,700 | 0.1510 | 1.0027 | 0.1369 | ||||||
| 0 - 2 | 887,100 | 0.0954 | 590,700 | 0.1771 | 1.8567 | 0.2535 | ||||||
| 2 - 4 | 734,100 | 0.0789 | 537,300 | 0.1611 | 2.0409 | 0.2786 | ||||||
| 4< | 1,899,600 | 0.2043 | 1,377,300 | 0.4130 | 2.0217 | 0.2760 |
| Criteria | Relative Importance |
|---|---|
| GSTA | 0.49 |
| Direction | 0.26 |
| Elevation | 0.12 |
| Aspect | 0.08 |
| Slope | 0.06 |
| Periods | Melting Area (m2) | Overlap Area (m2) | Overlap % |
|---|---|---|---|
| 1987–1989 | 1571 | 1223 | 77.8 |
| 1987–1998 | 1117 | 780 | 69.8 |
| 1987–2013 | 2744 | 2401 | 87.5 |
| 1987–2015 | 3223 | 2969 | 92.1 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yalcin, M. A GIS-Based Multi-Criteria Decision Analysis Model for Determining Glacier Vulnerability. ISPRS Int. J. Geo-Inf. 2020, 9, 180. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi9030180
Yalcin M. A GIS-Based Multi-Criteria Decision Analysis Model for Determining Glacier Vulnerability. ISPRS International Journal of Geo-Information. 2020; 9(3):180. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi9030180
Chicago/Turabian StyleYalcin, Mustafa. 2020. "A GIS-Based Multi-Criteria Decision Analysis Model for Determining Glacier Vulnerability" ISPRS International Journal of Geo-Information 9, no. 3: 180. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi9030180





