Geological Map Generalization Driven by Size Constraints
Abstract
:1. Introduction
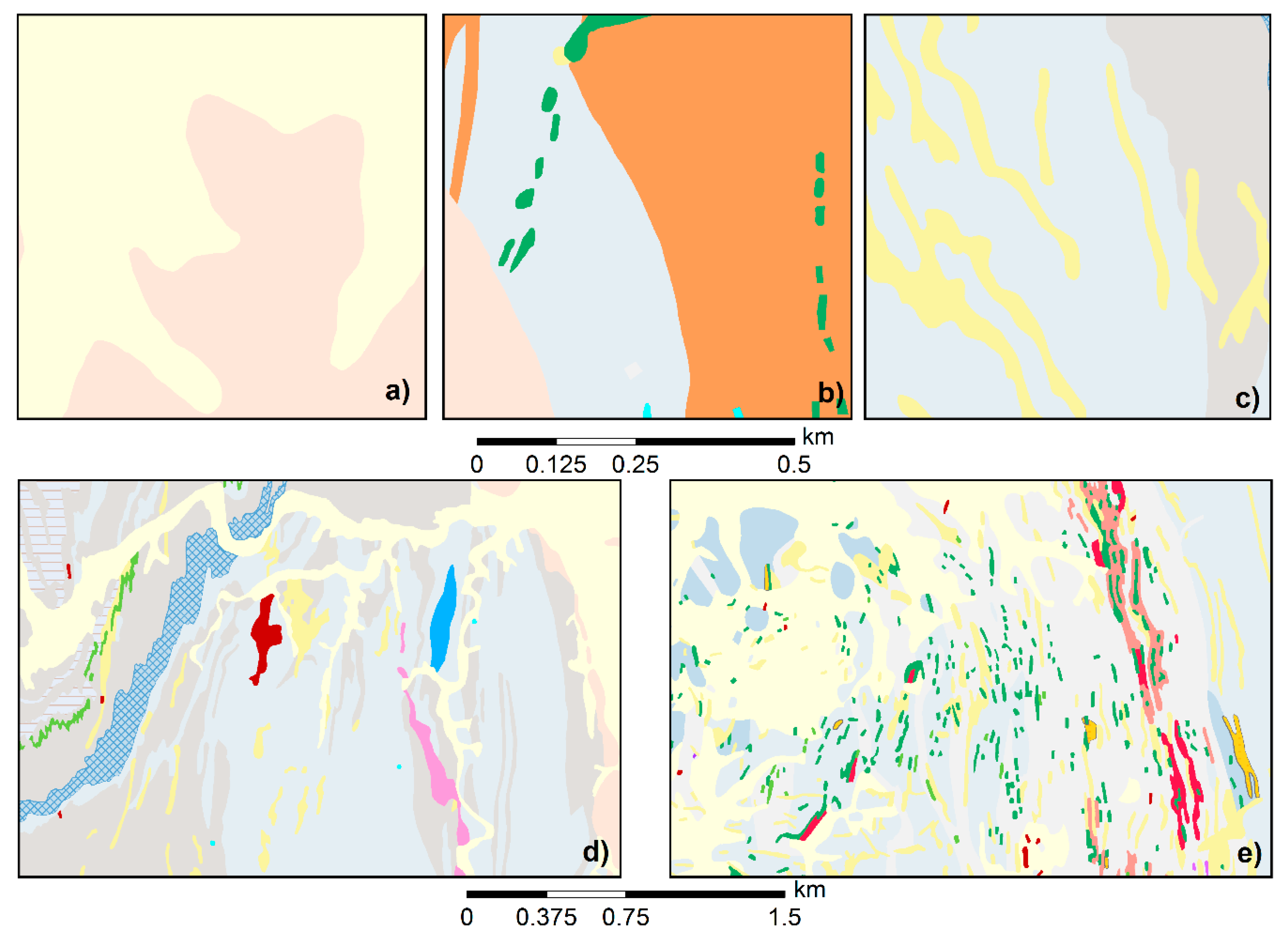
2. Geological Maps: Purpose and Peculiarities
3. Related Work
4. Methodology
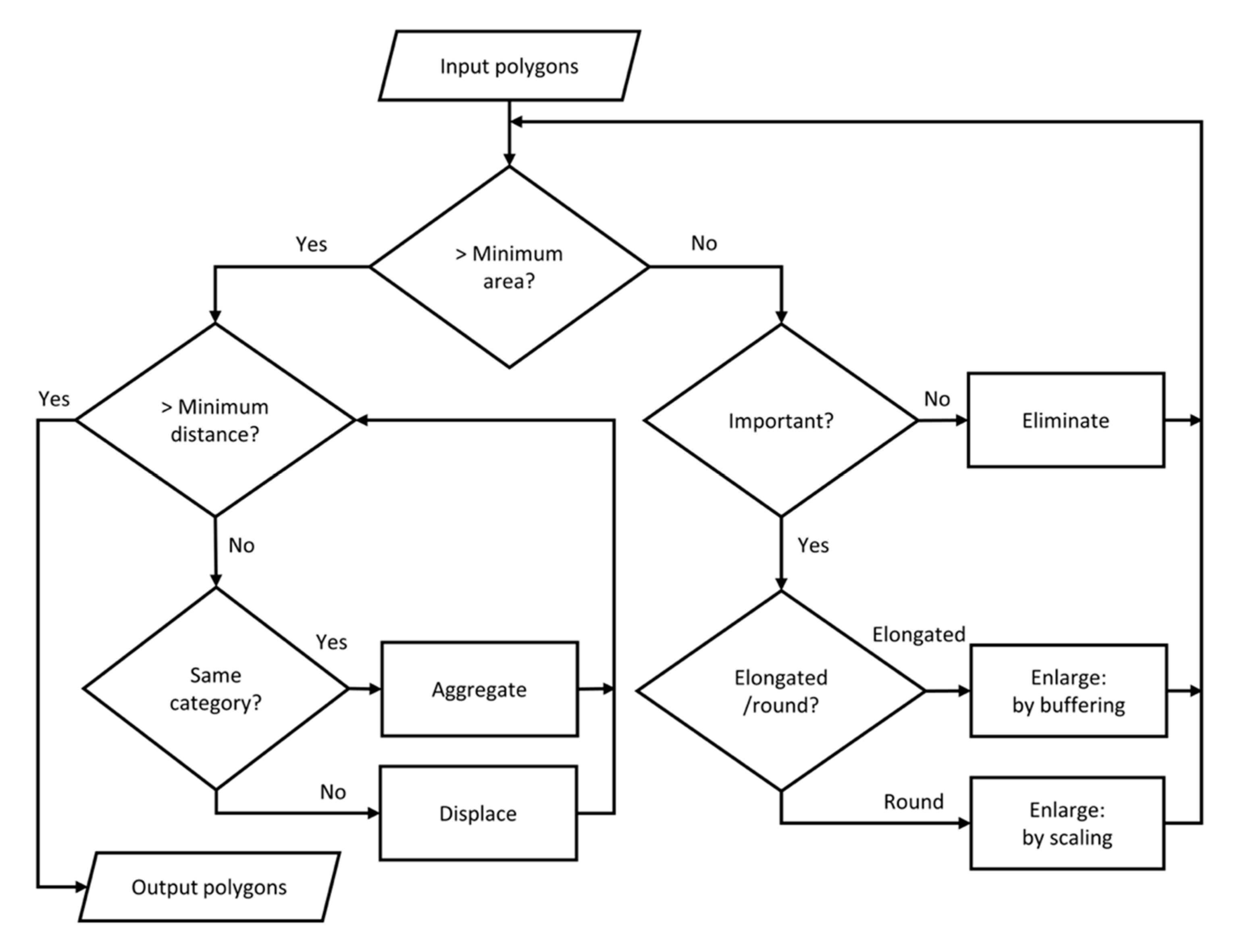
4.1. Overall Workflow
4.2. Identification of Constraints
- Minimum area
- Object separation
- Distance between boundaries
- Consecutive vertices
- Outline granularity
4.3. Constraint Modeling
4.4. Generalization Execution
4.4.1. Generalization Workflow
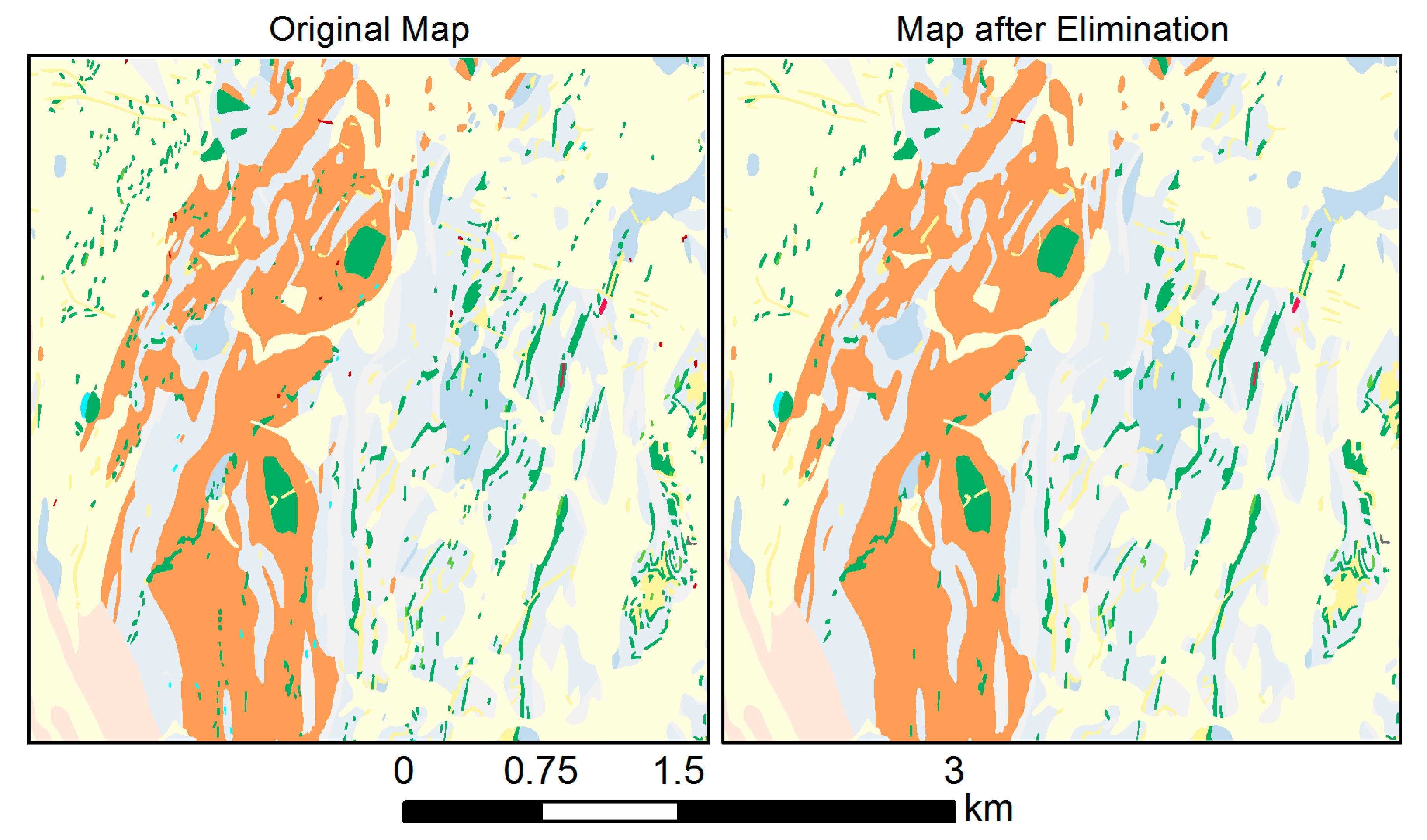
4.4.2. Elimination
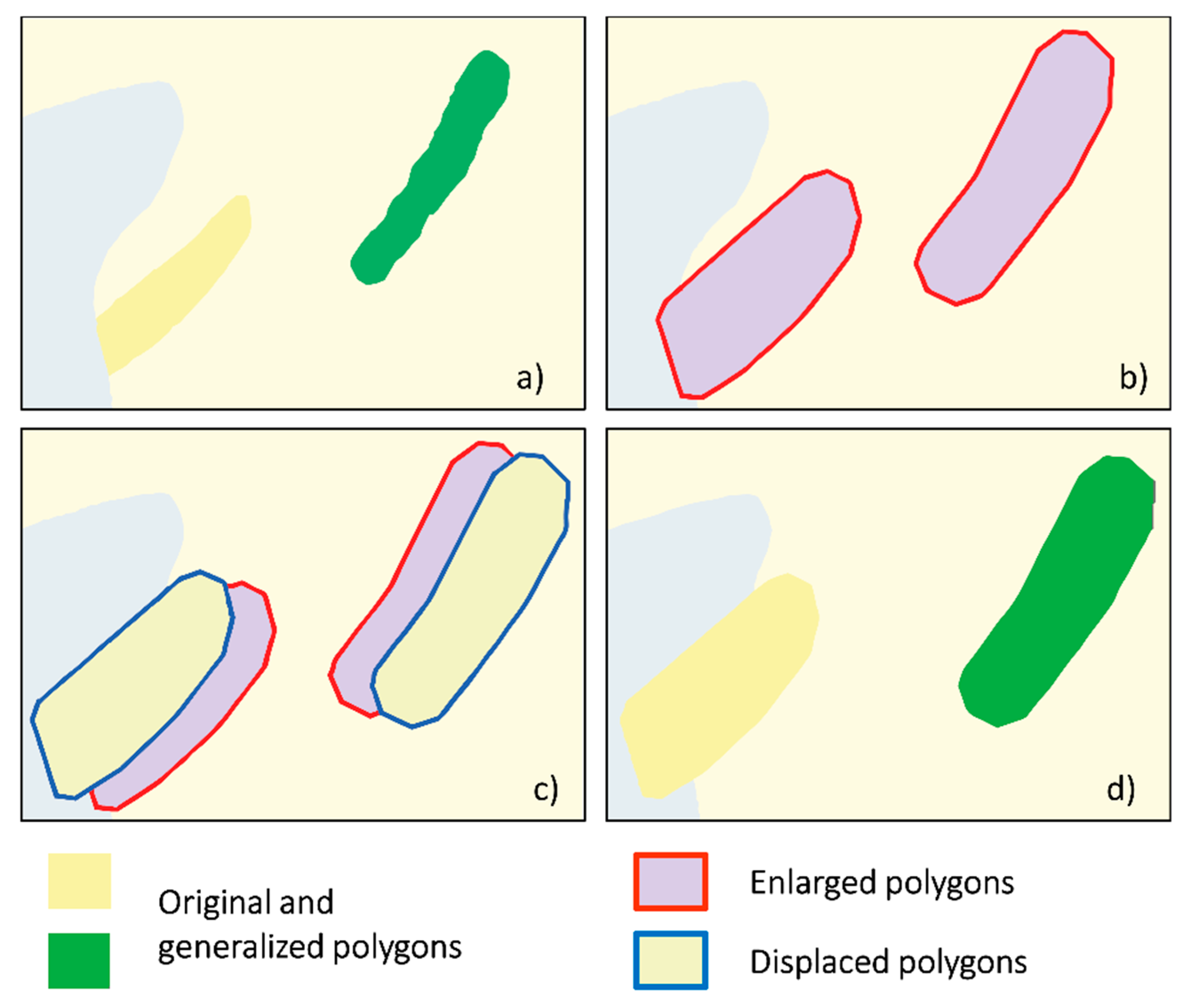
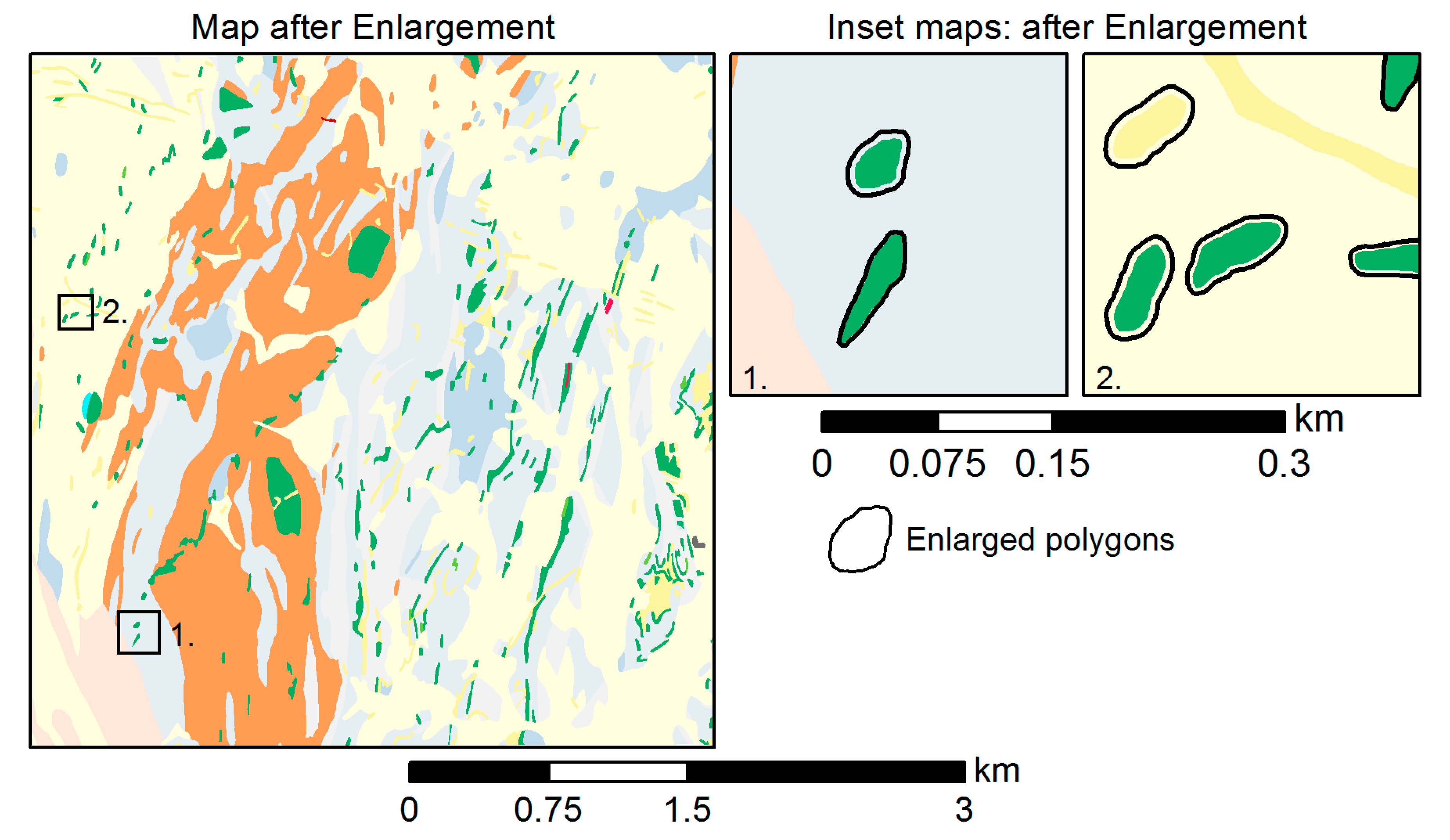
4.4.3. Enlargement
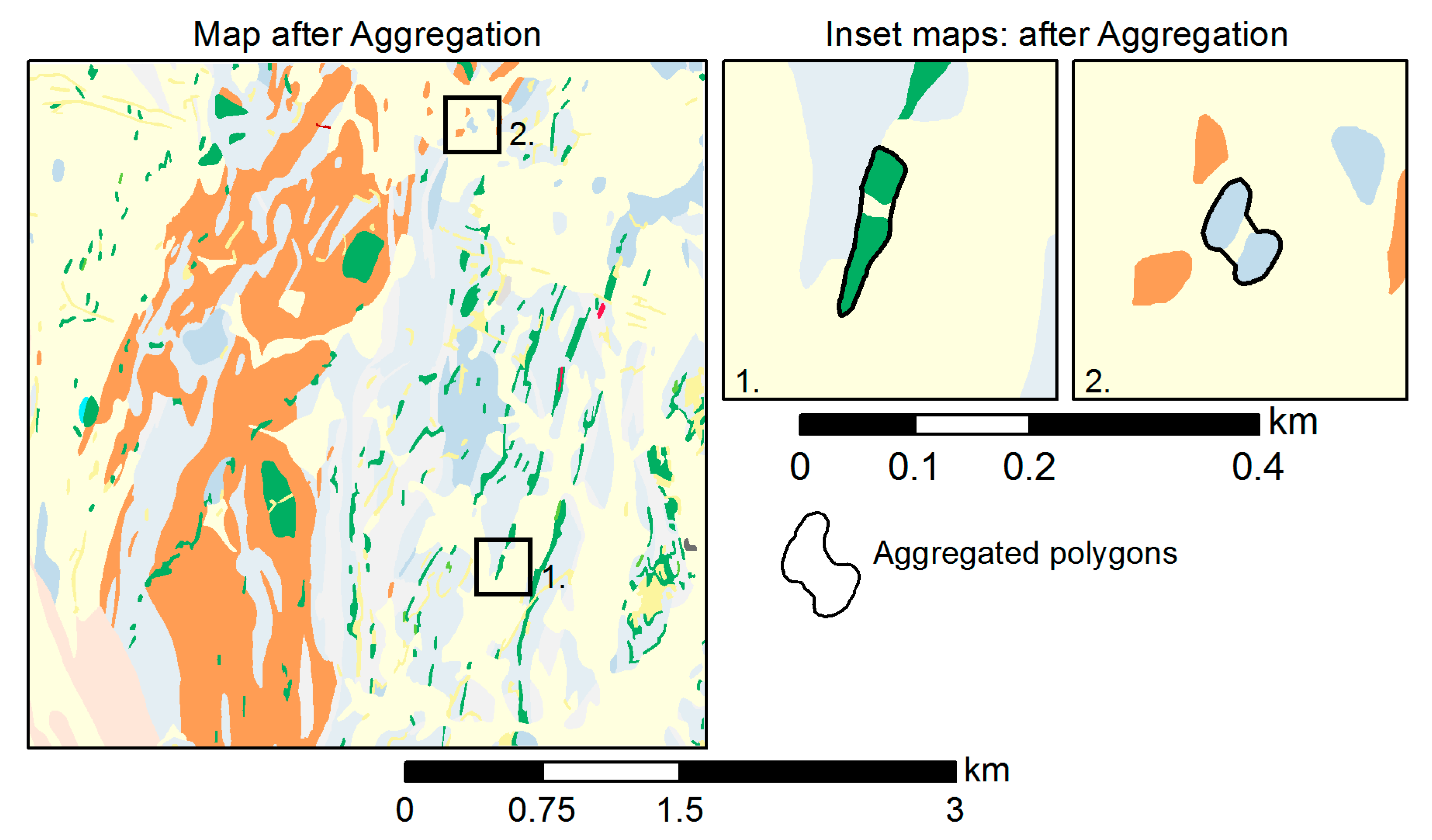
4.4.4. Aggregation
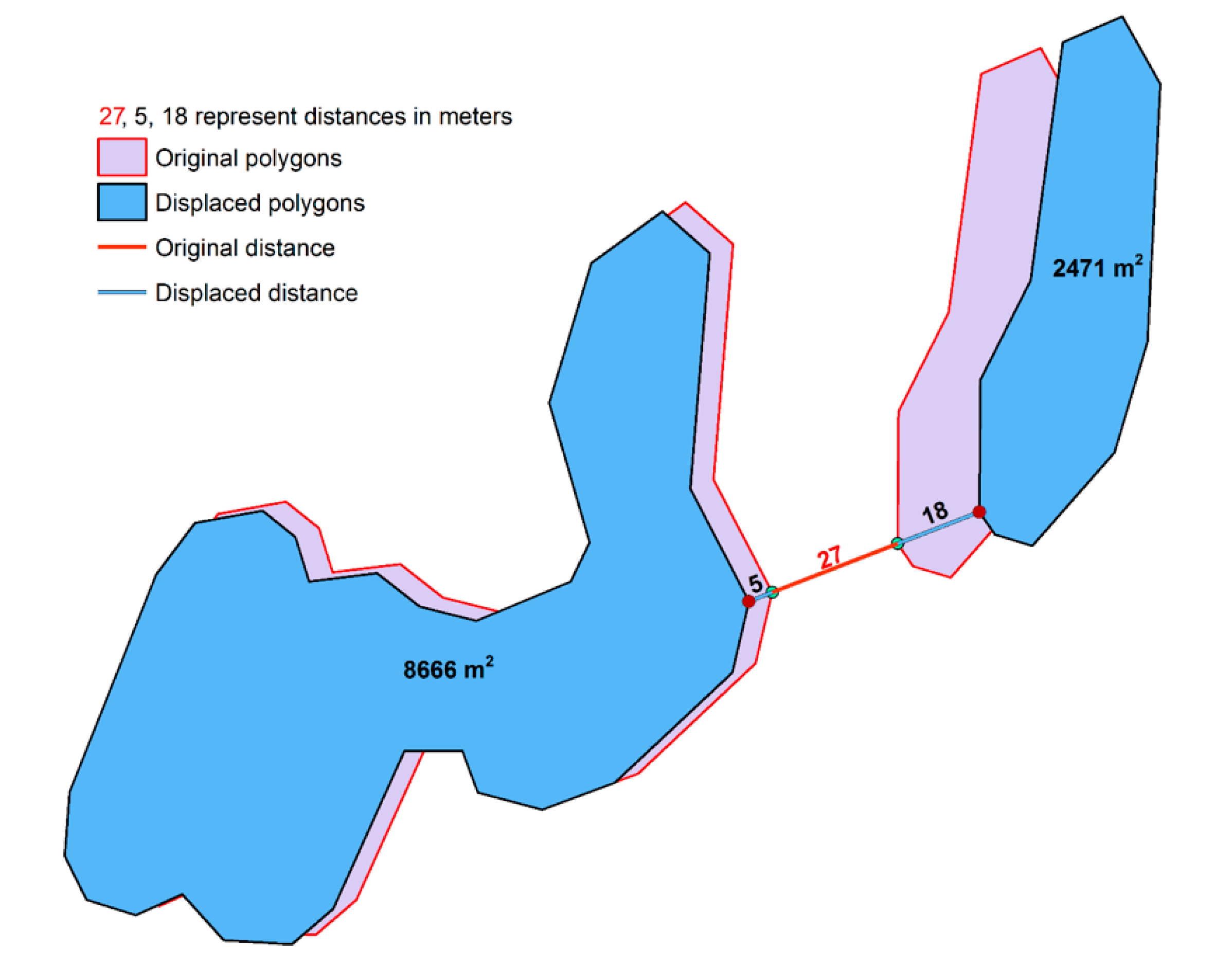
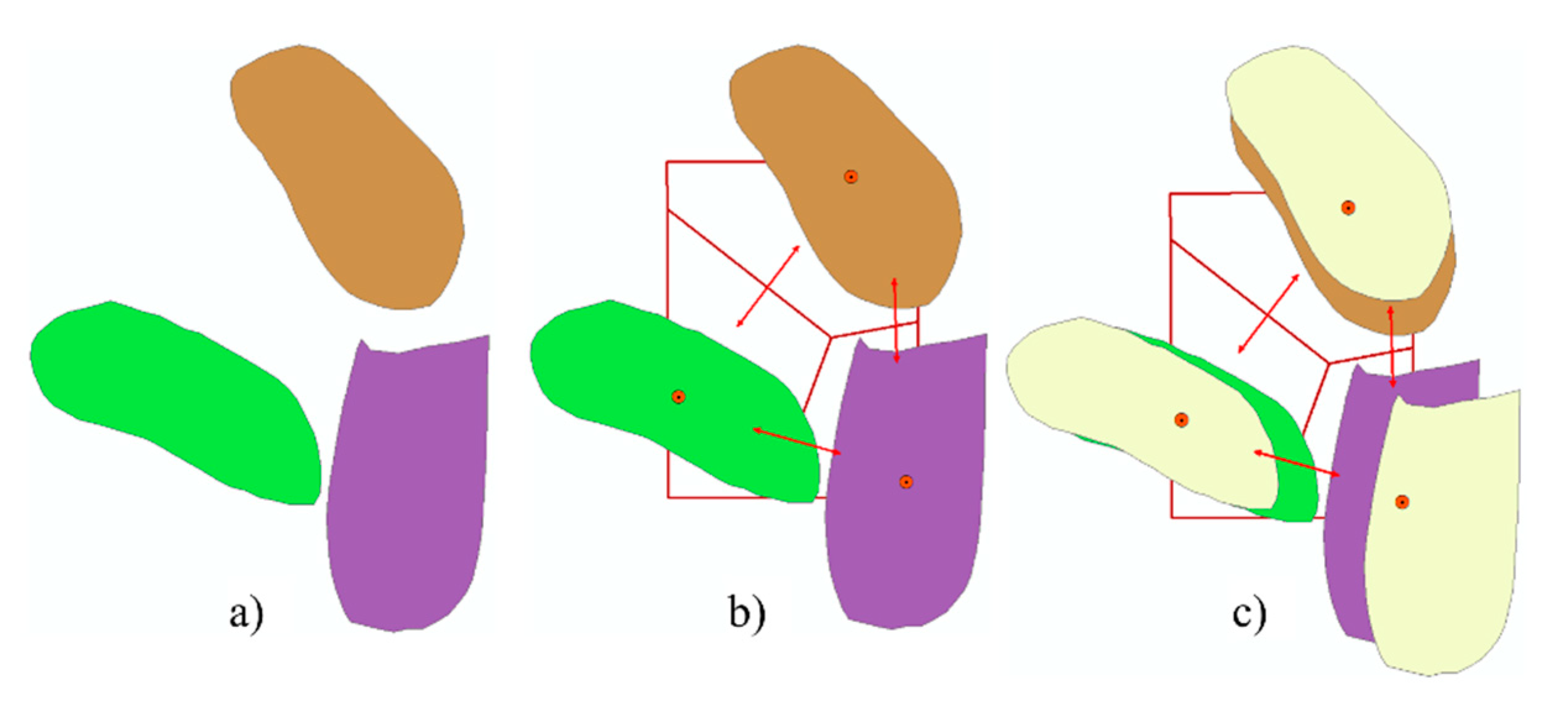
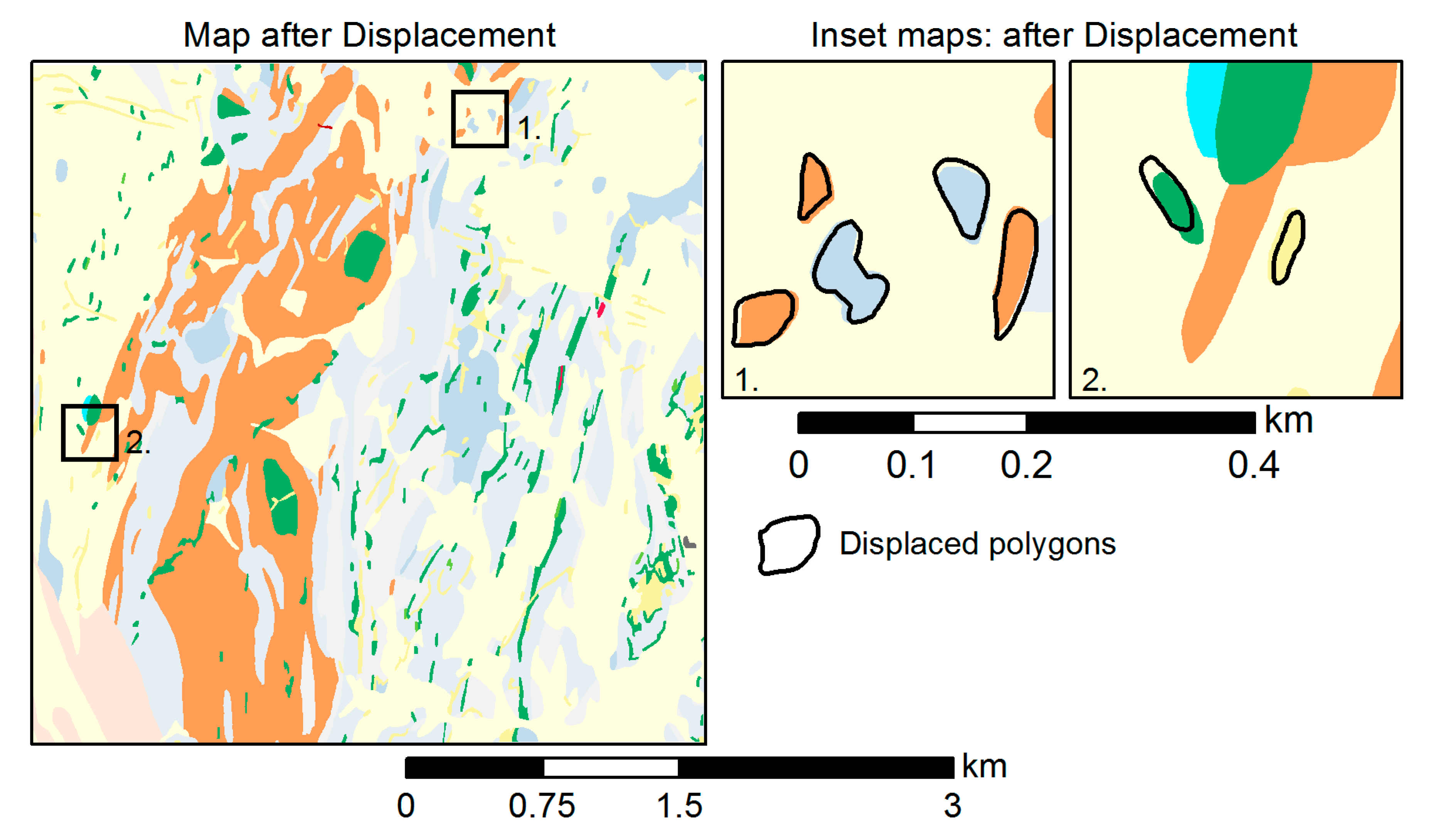
4.4.5. Displacement
4.5. Implementation
5. Experiments and Results
5.1. Data
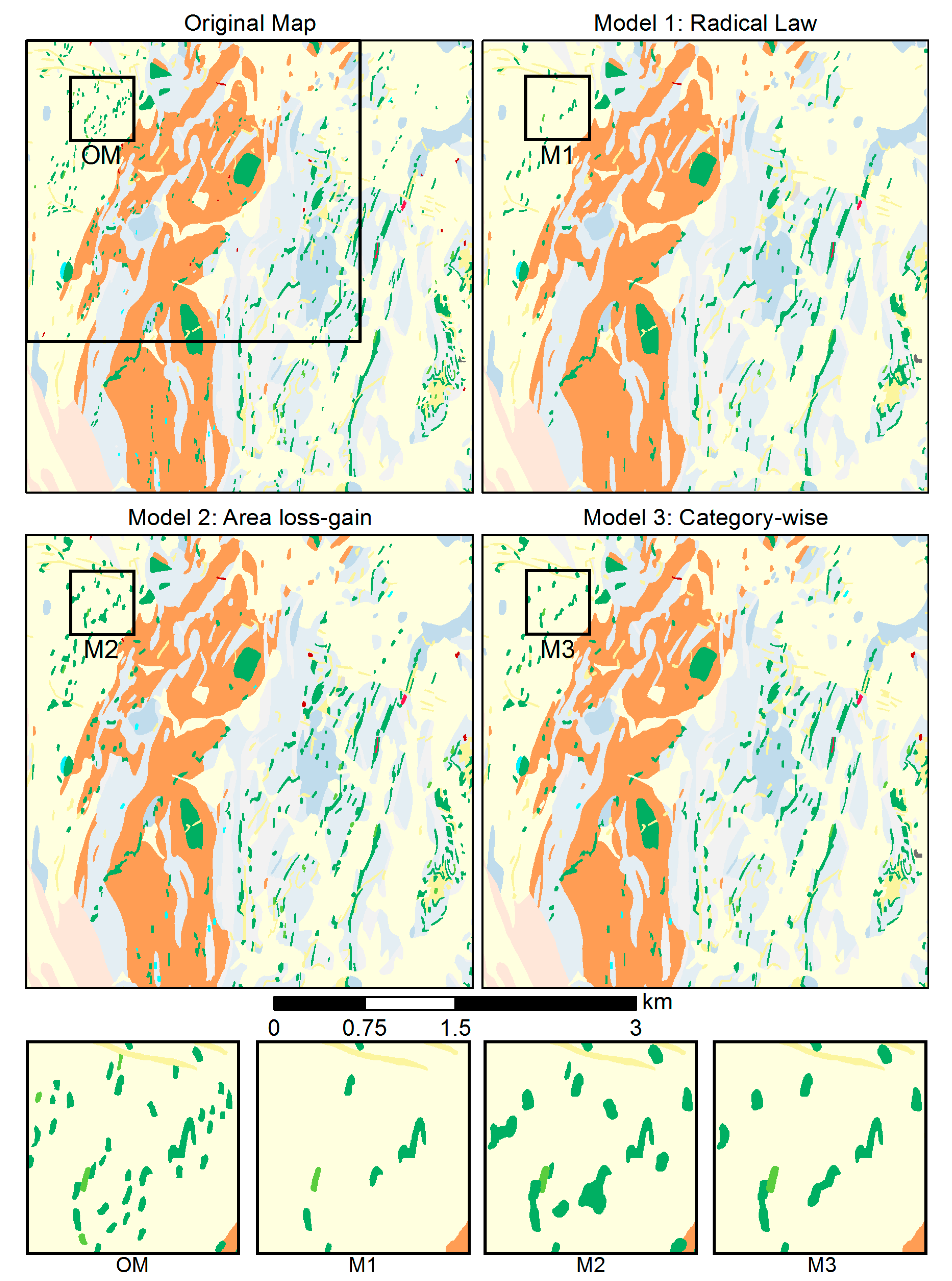
5.2. Elimination
5.3. Enlargement
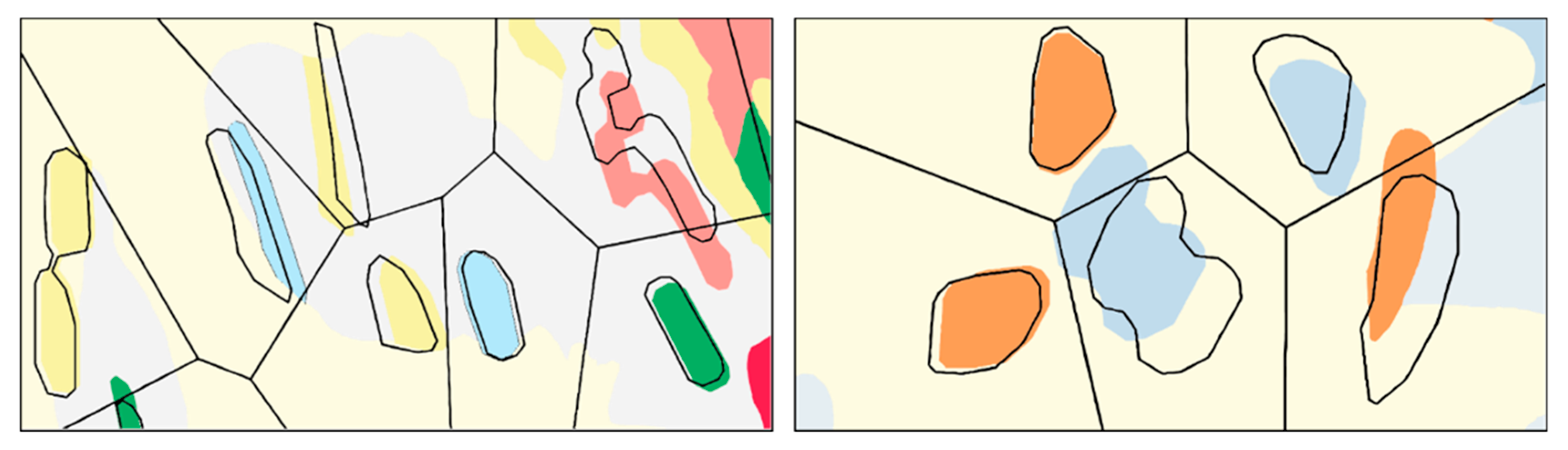
5.4. Aggregation
5.5. Displacement
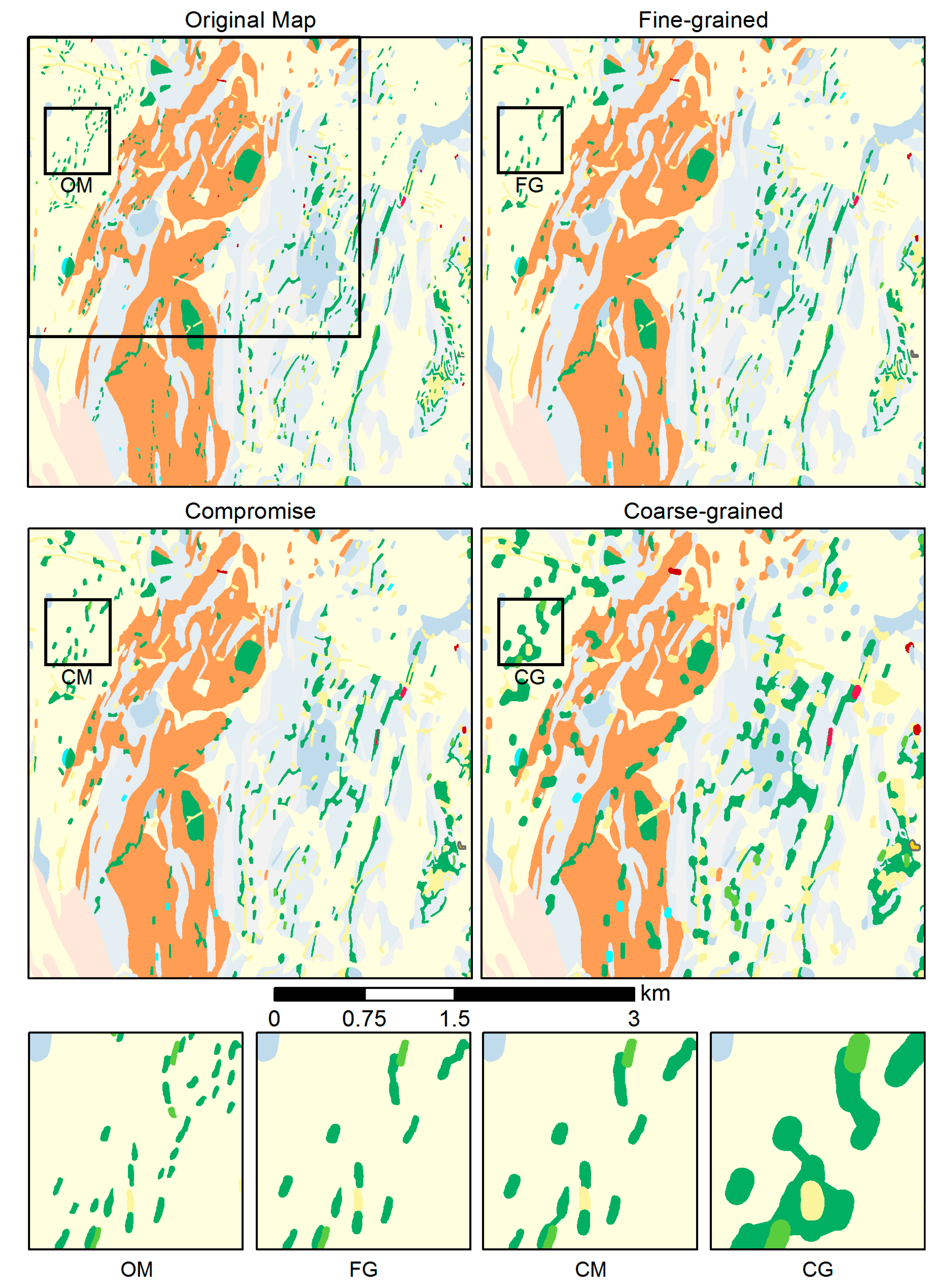
5.6. Sensitivity to Parameter Settings
5.6.1. Test Case 1
5.6.2. Test Case 2
5.6.3. Test Case 3
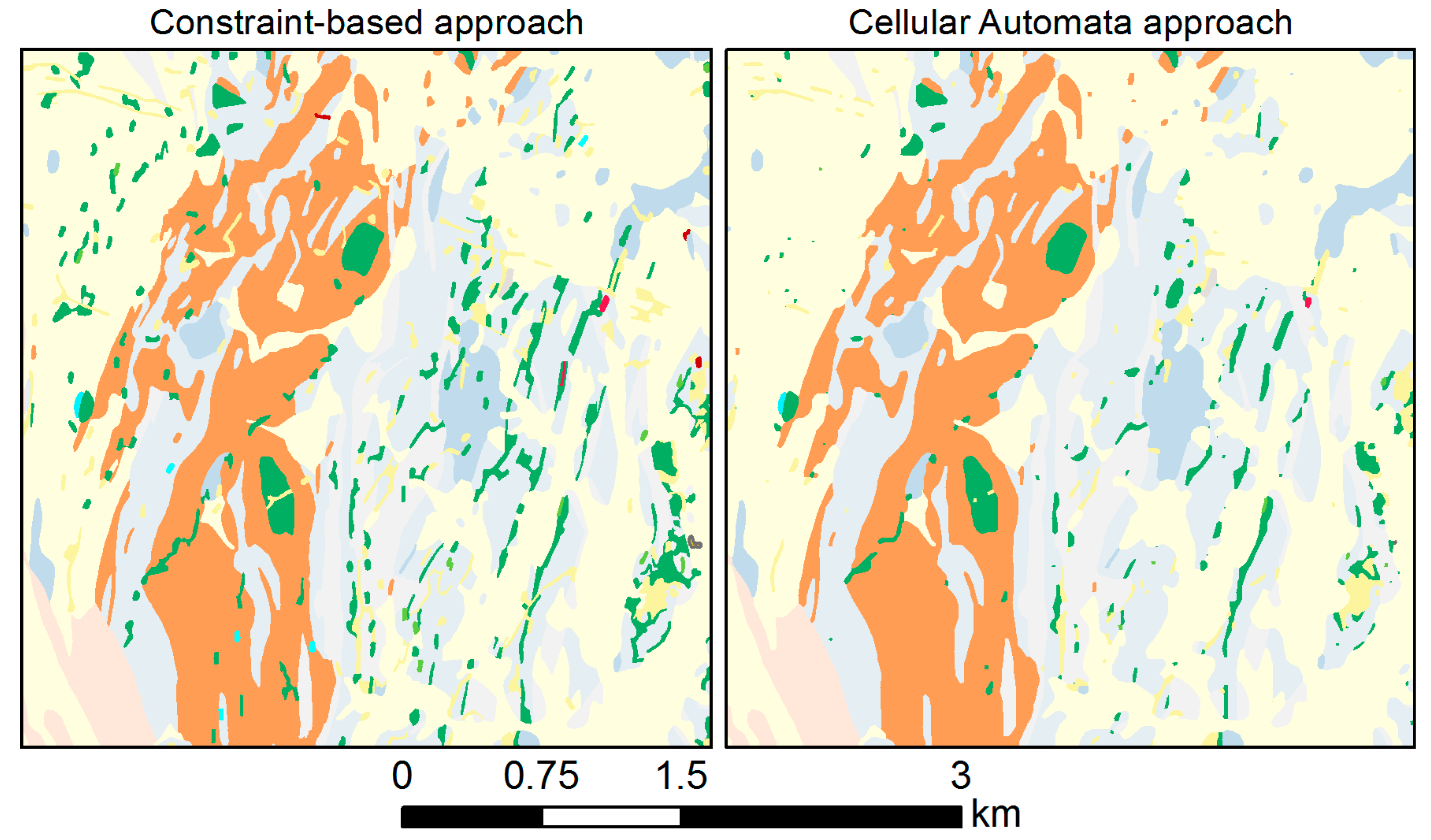
5.6.4. Comparison with Cellular Automata Approach
6. Discussion
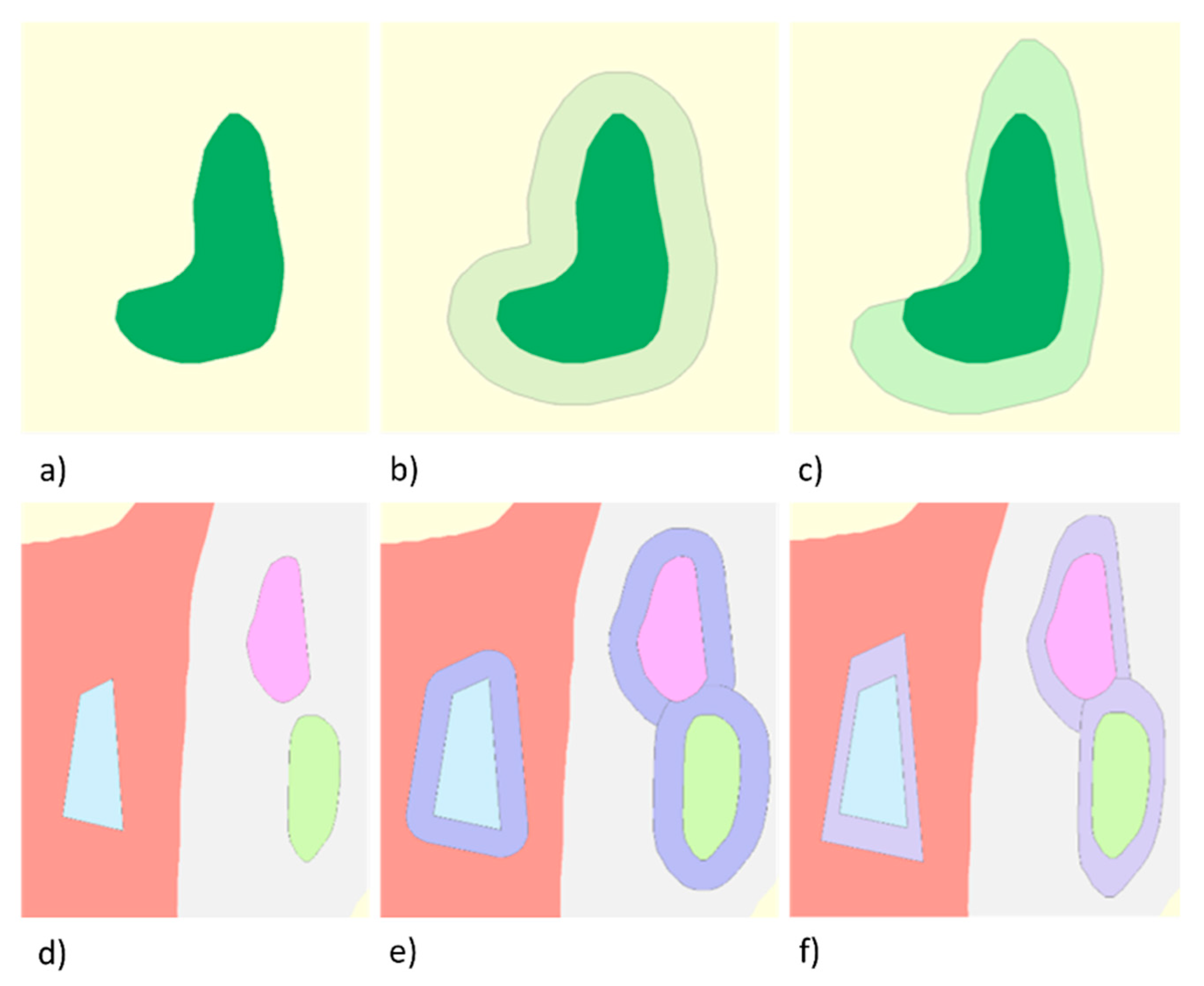
- The proposed methodology resolves the main legibility problems associated with small polygons in a step-by-step manner. The resulting map is more readable, and map features remain distinguishable after generalization (Figure 13).
- Although the goal values of the size constraints are defined globally, each polygon is treated individually to its own, specific properties rather than by a global process such as cellular automata. Hence, by consideration of the semantics of individual polygons, important polygons can be protected by enlargement; by consideration of shape properties, the shape characteristics of the individual polygons are largely maintained.
- Few parameters are required to control the generalization methodology. The process is initially triggered by the MA constraint and further assisted by few additional size constraints (most importantly, the OS constraint). Once the goal values of the size constraints and additional algorithm-specific parameters have been set, the methodology operates automatically, without further human intervention.
- The constraints’ goal values are, first of all, a function of the map legibility at the target scale, and hence allow adapting to the desired scale transition. Furthermore, the goal values also allow for controlling the overall granularity of the output map (Table 4 and Figure 15), depending on the map purpose.
- Despite the rather low number of constraints and control parameters, the methodology is modular and features several generalization operators, thus achieving considerable flexibility.
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sayidov, A.; Weibel, R. Constraint-based approach in geological map generalization. In Proceedings of the 19th ICA Workshop on Generalisation and Multiple Representation, Helsinki, Finland, 14 June 2016. [Google Scholar]
- Sayidov, A.; Weibel, R. Automating geological mapping: A constraint-based approach. In Proceedings of the CEUR (Central Europe) Workshop Proceedings, Leeds, UK, 30 October–2 November 2017. [Google Scholar]
- Ruas, A.; Duchêne, C. A prototype generalisation system based on the multi-agent system paradigm. In Generalisation of Geographic Information: Cartographic Modelling and Applications; Elsevier: Amsterdam, The Netherlands, 2007; pp. 269–283. [Google Scholar]
- Weibel, R.; Dutton, G.H. Constraint-based automated map generalization. In 8th International Symposium on Spatial Data Handling; Taylor & Francis: Columbia, UK, 1998; pp. 214–224. [Google Scholar]
- Barrault, M.; Regnauld, N.; Duchene, C.; Haire, K.; Baeijs, C.; Demazeau, Y.; Hardy, P.; Mackaness, W.; Ruas, A.; Weibel, R. Integrating multi-agent, object-oriented and algorithmic techniques for improved automated map generalization. In Proceedings of the 20th International Cartographic Conference, Beijing, China, 6–10 August 2001; Volume 3, pp. 2110–2116. [Google Scholar]
- Harrie, L.; Weibel, R. Modelling the overall process of generalisation. In Generalisation of Geographic Information: Cartographic Modelling and Applications; Elsevier: Oxford, UK, 2007; pp. 67–87. [Google Scholar]
- Stoter, J.; Burghardt, D.; Duchêne, C.; Baella, B.; Bakker, N.; Blok, C.; Pla, M.; Regnauld, N.; Touya, G.; Schmid, S. Methodology for evaluating automated map generalization in commercial software. Comput. Environ. Urban Syst. 2009, 33, 311–324. [Google Scholar] [CrossRef] [Green Version]
- Galanda, M. Automated Polygon Generalization in a Multi-Agent System. Ph.D. Thesis, University of Zurich, Zurich, Switzerland, 2003. [Google Scholar]
- Ruas, A. Modèle de Généralisation de Données Géographiques à Base de Contraintes et D‘autonomie; Université de Marne-la-Vallée: Champs-sur-Marne, France, 1999. [Google Scholar]
- Sayidov, A.; Weibel, R.; Leyk, S. Recognition of group patterns in geological maps by building similarity networks. Geocarto Int. 2020, 1–20. [Google Scholar] [CrossRef]
- Juliev, M.; Mergili, M.; Mondal, I.; Nurtaev, B.; Pulatov, A.; Hübl, J. Comparative analysis of statistical methods for landslide susceptibility mapping in the Bostanlik District, Uzbekistan. Sci. Total Environ. 2019, 653, 801–814. [Google Scholar] [CrossRef] [PubMed]
- Maine.gov. Maine Geological Survey: Reading Detailed Bedrock Geology Maps. Available online: https://www.maine.gov/dacf/mgs/pubs/mapuse/bedrock/bed-read.htm (accessed on 18 July 2019).
- Jirsa, M.A.; Boerboom, T.J. Components of Geologic Maps. Available online: http://docslide.us/documents/components-of-geologic-maps-by-mark-a-jirsa-and-terrence-j-boerboom-2003.html (accessed on 14 January 2020).
- Dawes, R.L.; Dawes, C.D. Basics-Geologic Structures; Geology of the Pacific Northwest: Wenatchee, WA, USA, 2013. [Google Scholar]
- Graymer, R.W.; Moring, B.C.; Saucedo, G.J.; Wentworth, C.M.; Brabb, E.E.; Knudsen, K.L. Geologic Map of the San Francisco Bay Region; US Department of the Interior, US Geological Survey: Reston, VA, USA, 2006.
- Steiniger, S.; Weibel, R. Relations among map objects in cartographic generalization. Cartogr. Geogr. Inf. Sci. 2007, 34, 175–197. [Google Scholar] [CrossRef]
- Downs, T.C.; Mackaness, W. An integrated approach to the generalization of geological maps. Cart. J. 2002, 39, 137–152. [Google Scholar] [CrossRef]
- Brassel, K.E.; Weibel, R. A review and conceptual framework of automated map generalization. Int. J. Geogr. Inf. Syst. 1988, 2, 229–244. [Google Scholar] [CrossRef]
- Mackaness, W.A.; Edwards, G. The importance of modelling pattern and structure in automated map generalization. In Proceedings of the Joint ISPRS/ICA Workshop on Multi-scale Representations of Spatial Data, Ottawa, ON, Canada, 7–8 July 2002. [Google Scholar]
- Steiniger, S.; Weibel, R. A conceptual framework for automated generalization and its application to geologic and soil maps. In Proceedings of the 22nd International Cartographic Conference, La Coruña, Spain, 11–16 July 2005. [Google Scholar]
- Shea, K.S.; McMaster, R.B. Cartographic Generalization in a Digital Environment: When and How to Generalize; AUTO-CARTO 9: Baltimore, MD, USA, 1989. [Google Scholar]
- McCabe, C.A. Vector Approaches to Generalizing Faults and Polygons in Santa Rosa, California, Case Study. 2007. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.643.17&rep=rep1&type=pdf. (accessed on 14 January 2020).
- Smirnoff, A.; Paradis, S.J.; Boivin, R. Generalizing surficial geological maps for scale change: ArcGIS tools vs. cellular automata model. Comput. Geosci. 2008, 34, 1550–1568. [Google Scholar] [CrossRef]
- Smirnoff, A.; Huot-Vézina, G.; Paradis, S.J.; Boivin, R. Generalizing geological maps with the GeoScaler software: The case study approach. Comput. Geosci. 2012, 40, 66–86. [Google Scholar] [CrossRef]
- Bader, M.; Weibel, R. Detecting and resolving size and proximity conflicts in the generalization of polygonal maps. In Proceedings of the 18th International Cartographic Conference, Stockholm, Sweden, 23–27 June 1997; Volume 23, p. 27. [Google Scholar]
- Galanda, M.; Weibel, R. An agent-based framework for polygonal subdivision generalization. In Advances in Spatial Data Handling, 10th International Symposium on Spatial Data Handling; Richardson, D., van Oosterom, P., Eds.; Springer: Berlin, Germany, 2002; pp. 121–136. [Google Scholar]
- Edwardes, A.; Mackaness, W.A. Modelling knowledge for automated generalisation of categorical maps—A constraint based approach. In Innovations in GIS 7. GIS and Geocomputation; Atkinson, P., Martin, D., Eds.; Taylor & Francis: London, UK, 2000; pp. 161–174. [Google Scholar]
- Müller, J.C.; Wang, Z. Area-patch generalisation: A competitive approach. Cartogr. J. 1992, 29, 137–144. [Google Scholar] [CrossRef]
- Ruas, A.; Plazanet, C. Strategies for automated generalization. In Advances in GIS Research II, Proceedings of the 7th International Symposium on Spatial Data Handling; Kraak, M.J., Molenaar, M., Eds.; Taylor & Francis: London, UK, 1996; pp. 319–336. [Google Scholar]
- Spiess, E.; Baumgartner, U.; Arn, S.; Vez, C. Topographic maps map graphics and generalisation. Cartogr. Publ. Ser. 2005, 17, 121. [Google Scholar]
- Subcommittee, G.D. U.S. Geological Survey FGDC Digital Cartographic Standard for Geologic Map Symbolization (FGDC Document Number FGDC-STD-013-2006); U.S. Geological Survey for the Federal Geographic Data Committee: Reston, VA, USA, 2006.
- Lichtner, W. Computer-assisted processes of cartographic generalization in topographic maps. Geo Process. 1979, 1, 183–199. [Google Scholar]
- Töpfer, F.; Pillewizer, W. The principles of selection. Cartogr. J. 1966, 3, 10–16. [Google Scholar] [CrossRef]
- Osserman, B.Y.R. The isoperimetric inequality. Bull. Amer. Math. Soc. 1978, 6, 1182–1238. [Google Scholar] [CrossRef] [Green Version]
- Touya, G. A road network selection process based on data enrichment and structure detection. Trans. GIS 2010, 14, 595–614. [Google Scholar] [CrossRef] [Green Version]
- Regnauld, N. Contextual building typification in automated map generalization. Algorithmica 2001, 30, 312–333. [Google Scholar] [CrossRef]
- Burghardt, D.; Cecconi, A. Mesh simplification for building typification. Int. J. Geogr. Inf. Sci. 2007, 21, 283–298. [Google Scholar] [CrossRef]
- Moreira, A.; Santos, M.Y. Concave hull: A k-nearest neighbours approach for the computation of the region occupied by a set of points. In Proceedings of the Second International Conference on Computer Graphics Theory and Applications, Algarve, Portugal, 5–7 March 2011; pp. 61–68. [Google Scholar]
- Galanda, M.; Weibel, R. Using an energy minimization technique for polygon generalization. Cartogr. Geogr. Inf. Sci. 2003, 30, 263–279. [Google Scholar] [CrossRef]
- Bader, M.; Barrault, M.; Weibel, R. Building displacement over a ductile truss. Int. J. Geogr. Inf. Sci. 2005, 19, 915–936. [Google Scholar] [CrossRef]
- Mackaness, W.; Purves, R. Automated displacement for large numbers of discrete map objects. Algorithmica 2001, 30, 302–311. [Google Scholar] [CrossRef]
- Ai, T.; Zhang, X.; Zhou, Q.; Yang, M. A vector field model to handle the displacement of multiple conflicts in building generalization. Int. J. Geogr. Inf. Sci. 2015, 29, 1310–1331. [Google Scholar] [CrossRef]
- Basaraner, M. A zone-based iterative building displacement method through the collective use of Voronoi Tessellation, spatial analysis and multicriteria decision making. Bol. Ciências Geodésicas 2011, 17, 161–187. [Google Scholar] [CrossRef] [Green Version]
- Barnes, R.G. Metallogenic Studies of the Broken Hill and Euriowie Blocks. 1. Styles of Mineralisation in the Broken Hill Block. 2. Mineral Deposits of the Southwestern Broken Hill Block; Geological Survey of New South Wales: New South Wales, Australia, 1988.
- Peljo, M. Broken Hill Exploration Initiative: Abstracts of Papers Presented at the July 2003 Conference in Broken Hill; Geoscience Australia, Ed.; Geoscience Australia: Canberra, Australia, 2003; ISBN 978-0-642-46771-3.
- Wilson, J.R. Minerals and Rocks; BookBoon: London, UK, 2010. [Google Scholar]
- Huot-Vézina, G.; Boivin, R.; Smirnoff, A.; Paradis, S.J. GeoScaler: Generalization tool (with a supplementary user guide in French). Geol. Surv. Can. 2012, 6231, 82. [Google Scholar] [CrossRef]

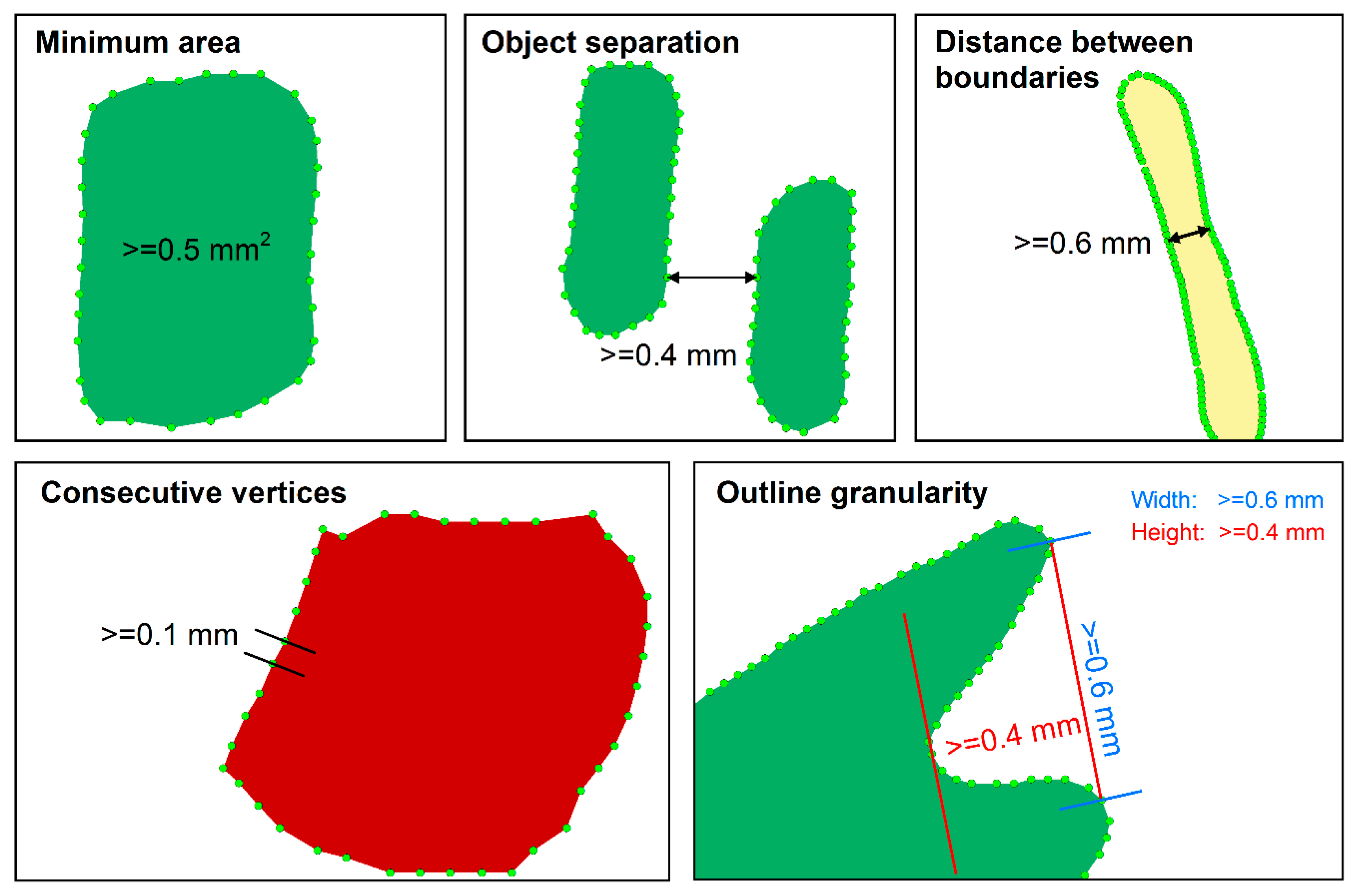
| Constraint | Cause | Goal Value | Measures | Plans/Possible Operators | Impact |
|---|---|---|---|---|---|
| Minimum area | Scale reduction | 0.5 × 0.5 mm | Area | Elimination | Area loss and gain (area constraint), change of the overall configuration of polygons |
| Enlargement | Change of minimum distance between features | ||||
| Aggregation | Loss of overall spatial pattern, shape distortion | ||||
| Object separation | Scale reduction, enlargement | 0.4 mm | Shortest distance | Displacement | Minimum distance between features, positional accuracy |
| Enlargement, exaggeration | Shape distortion, ratio between features | ||||
| Aggregation | Loss of overall spatial pattern, shape distortion | ||||
| Typification | Loss of overall spatial pattern, shape distortion | ||||
| Distance between boundaries | Scale reduction | 0.6 mm | Internal buffer | Enlargement | Minimum distance between features |
| Consecutive vertices | Scale reduction | 0.1 mm | Shortest distance between vertices | Elimination | Shape distortion polygon outline |
| Outline granularity—width | Scale reduction | 0.6 mm | Shortest distance | Simplification, smoothing | Shape distortion |
| Outline granularity—height | Scale reduction | 0.4 mm | Shortest distance | Simplification, smoothing | Shape distortion |
| # | Property | Value Measurement | Normalized Importance |
|---|---|---|---|
| 1 | Area of polygons | 7–625 m2 | 0.0–1.0 |
| 2 | Geological hierarchy | 1–15 | 0.0–1.0 |
| Selection Method | Number of Polygons | ||
|---|---|---|---|
| Source Map (25,000) | Target Map (50,000) | Removed | |
| Radical Law selection | 1877 | 1314 | 563 |
| Area loss–gain selection | 1877 | 1738 | 139 |
| Category-wise selection | 1877 | 1460 | 417 |
| Threshold Set | MA | Avg. Area | #Poly | OS | Source |
|---|---|---|---|---|---|
| Fine-grained (FG) | 0.5 × 0.5 mm | 19,792 m2 | 1265 | 0.4 mm | [30] |
| Compromise (CM) | 0.75 × 0.75 mm | 20,572 m2 | 1217 | 0.6 mm | compromise |
| Coarse-grained (CG) | 2 × 2 mm | 26,244 m2 | 954 | 1.0 mm | [31] |
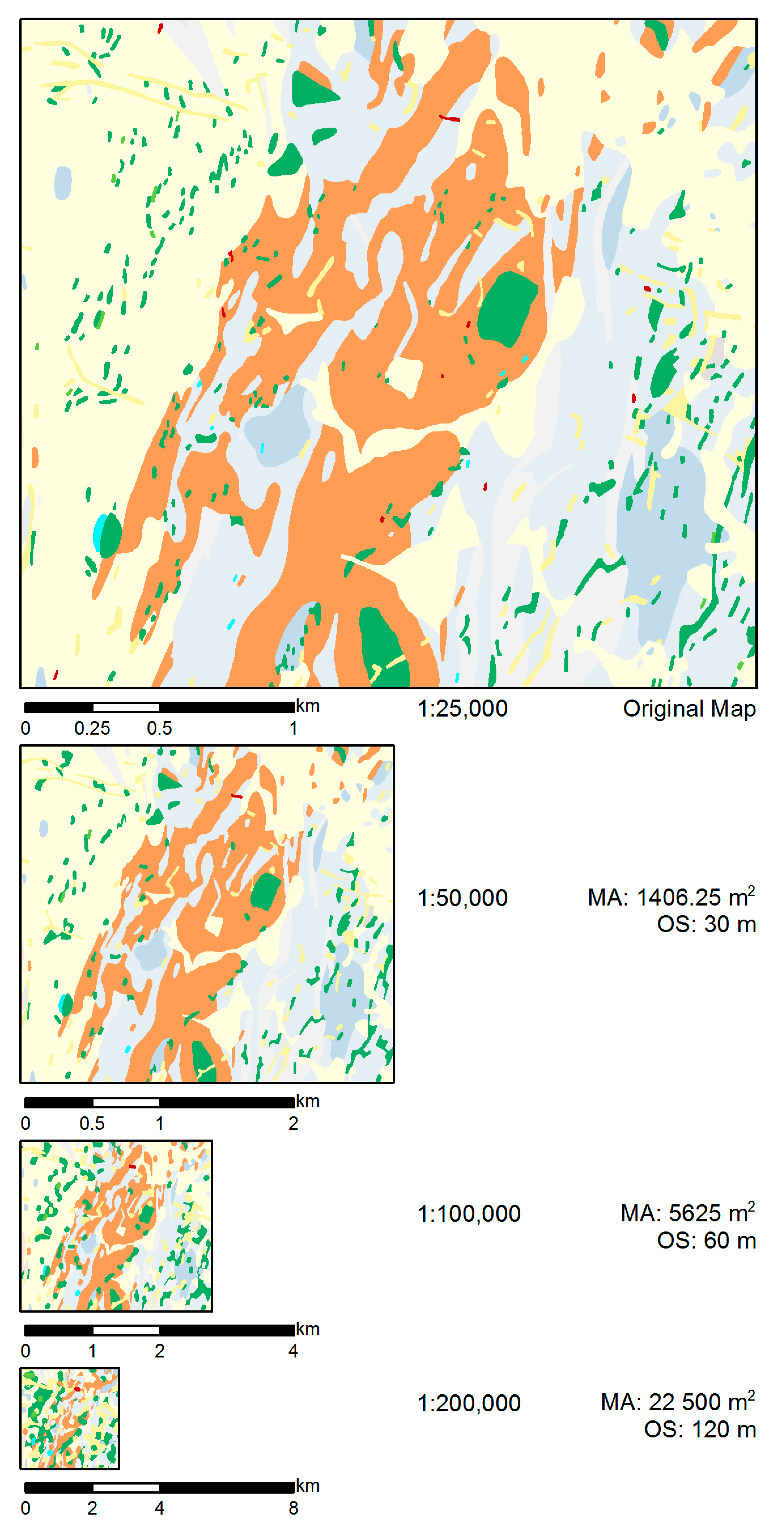
| Scales | Geological Units | Total Area in m2 (%) | Polygons |
|---|---|---|---|
| Original (1:25,000) | All units | 25,032,549 (100%) | 1877 |
| Amphibolite | 1,177,891 (4.71%) | 838 | |
| Pegmatite | 915,132 (3.66%) | 393 | |
| Late Proterozoic | 713,420 (2.85%) | 10 | |
| Soil–sand–gravel–clay | 12,371,617 (49.42%) | 18 | |
| 1:50,000 | All units | 25,032,549 (100%) | 1349 |
| MA—1406.25 m2 OS—30 m | Amphibolite | 1,382,525 (5.52%) | 587 |
| Pegmatite | 888,572 (3.55%) | 276 | |
| Late Proterozoic | 713,020 (2.85%) | 9 | |
| Soil–sand–gravel–clay | 12,333,353 (49.24%) | 17 | |
| 1:100,000 | All units | 25,032,549 (100%) | 953 |
| MA—5625 m2 OS—60 m | Amphibolite | 1,584,974 (6.32%) | 419 |
| Pegmatite | 1,317,895 (5.26%) | 197 | |
| Late Proterozoic | 697,109 (2.78%) | 5 | |
| Soil–sand–gravel–clay | 11,857,308 (47.31%) | 14 | |
| 1:200,000 | All units | 25,032,549 (100%) | 667 |
| MA—22,500 m2 OS—120 m | Amphibolite | 1,766,809 (7.05%) | 294 |
| Pegmatite | 3,126,179 (12.48%) | 138 | |
| Late Proterozoic | 673,570 (2.69%) | 5 | |
| Soil–sand–gravel–clay | 10,120,376 (40.40%) | 7 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sayidov, A.; Aliakbarian, M.; Weibel, R. Geological Map Generalization Driven by Size Constraints. ISPRS Int. J. Geo-Inf. 2020, 9, 284. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi9040284
Sayidov A, Aliakbarian M, Weibel R. Geological Map Generalization Driven by Size Constraints. ISPRS International Journal of Geo-Information. 2020; 9(4):284. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi9040284
Chicago/Turabian StyleSayidov, Azimjon, Meysam Aliakbarian, and Robert Weibel. 2020. "Geological Map Generalization Driven by Size Constraints" ISPRS International Journal of Geo-Information 9, no. 4: 284. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi9040284





