3.1. Study Area
Cracow is a city located in Poland (
Figure 1) and is the capitol of the Małopolska Province. As Głuszak and Marona emphasise [
53], Cracow is an extremely important place for real estate market research. This is because of several reasons. First of all, it is the second largest city in Poland in terms of population. Moreover, the real estate market in Cracow is developing in a dynamic way. In particular, the average transaction price for residential units from 2006 to 2019 increased from 5193 PLN(the Polish Zloty)/m
2 to 7414 PLN/m
2 on the secondary market, and from 6816 PLN/m
2 to 8244 PLN/m
2 on the primary market [
54] (as at 30 April 2020, 1 USD represents approximately 4.17 PLN). Similarly, the average monthly rental price increased from 31.8 PLN/m
2 to 42.7 PLN/m
2 from 2013 to 2019 [
54]. The importance of the real estate market in Cracow is also confirmed by data on the annual number of new flats delivered for use, which is one of the highest in Poland. In 2018, this reached almost ten thousand new dwellings.
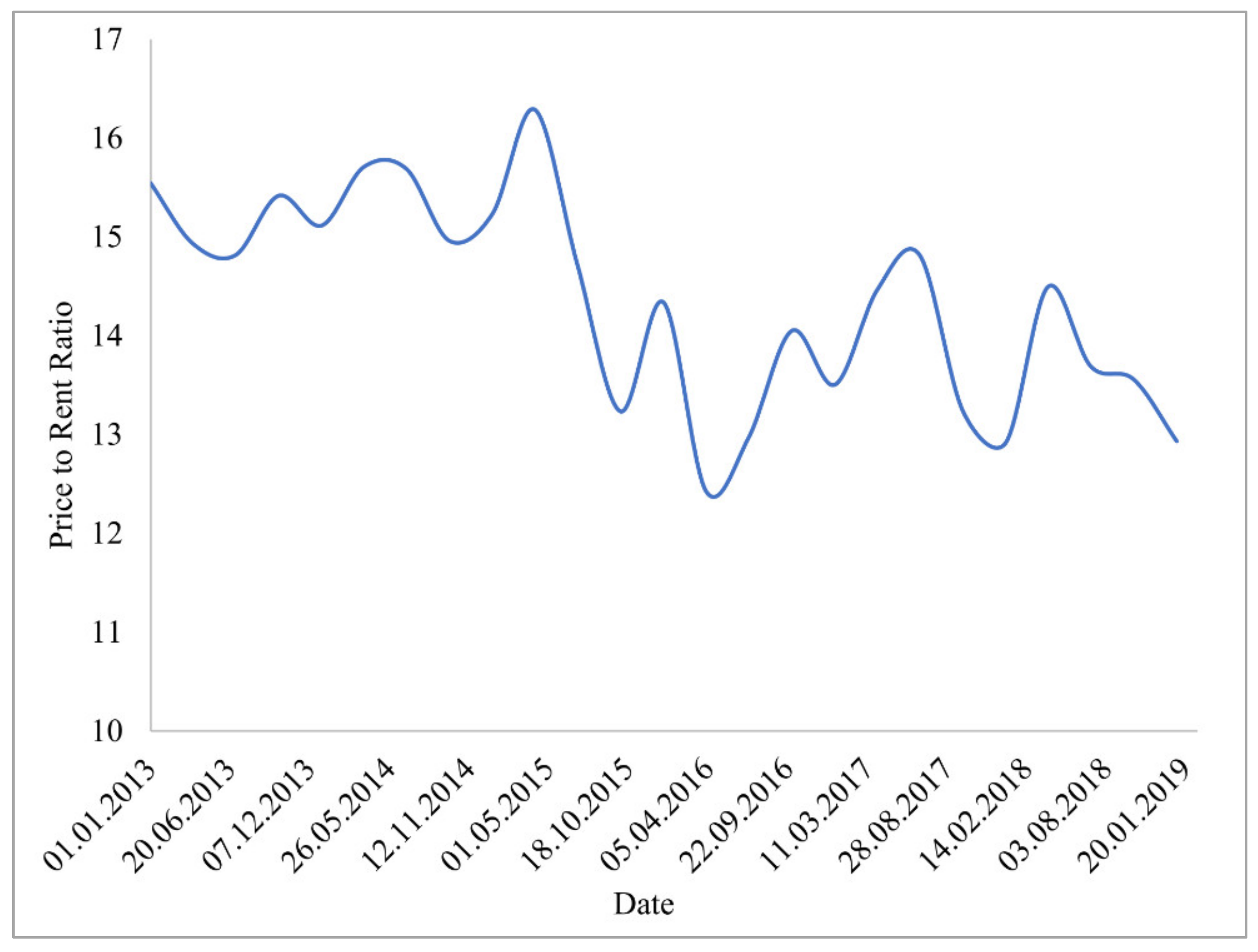
It should also be noted that Cracow is a university town, with large numbers of students, both domestic and foreign, arriving each year. These users are a very strong determinant of prices in the rental market. Additionally, Cracow is also a very popular tourist destination. According to the Małopolska Tourist Organisation, in 2019, the city was visited by 14,050,000 tourists. Such increased tourist traffic is obviously not without significance for the functioning of the rental market. It can be expected that, especially within the city centre, there may be price bubbles caused by the so-called short-term renting. All of the above influence the price-to-rent ratio in Cracow, which has oscillated in recent years between 12 and 16 (
Figure 2). This translates into much less interest among residents in long-term renting.
Moreover, Cracow is an interesting place to study the determinants of residential rents because of the fact that its real estate market has been assessed as the smartest of all provincial cities in Poland [
2]. This should be understood as the presence in a given city of modern online housing platforms or the so-called "automatic" residential rental market.
3.2. Data Collection and Processing
The dependent variable in this study is monthly housing rent (PLN/m
2). However, obtaining data on this subject is very challenging because in Poland lacks both official and private databases on transactional rental prices. This is because of the fact that, unlike real estate purchase transactions, lease agreements are drawn up directly by the parties involved and, in the vast majority of cases, do not have to be officially reported anywhere. Therefore, the analysis of determinant rental prices will be based on offer prices from the most popular portal in Poland containing long-term rental announcements, that is, the internet platform otodom.pl. It should be noted that the use of offer rents in this study will allow reliable conclusions to be drawn. This is because of the fact that, according to data from the National Bank of Poland [
54], approximately from 2018, transaction and offer prices in the residential rental market in Cracow were even identical.
In order to obtain the data, the web scraping technique was used. On 14 February 2020, data on 4185 monthly housing rents in Cracow were collected. It should be noted, however, that very often in Poland, the same flat is posted on an internet platform by both the landlord and the real estate agency cooperating with him. Sometimes, the owner of a flat may collaborate with several agencies at the same time. This leads to the repetition of a large percentage of the data obtained. Therefore, preliminary data processing was carried out and the detected duplicates were removed. Moreover, outlier observations and those for which the exact location of the flat was not given, that is, the geographical coordinates (latitude and longitude), were also eliminated. At the end of this process, 2336 unique observations were collected.
3.3. Spatial Distribution of Housing Rents
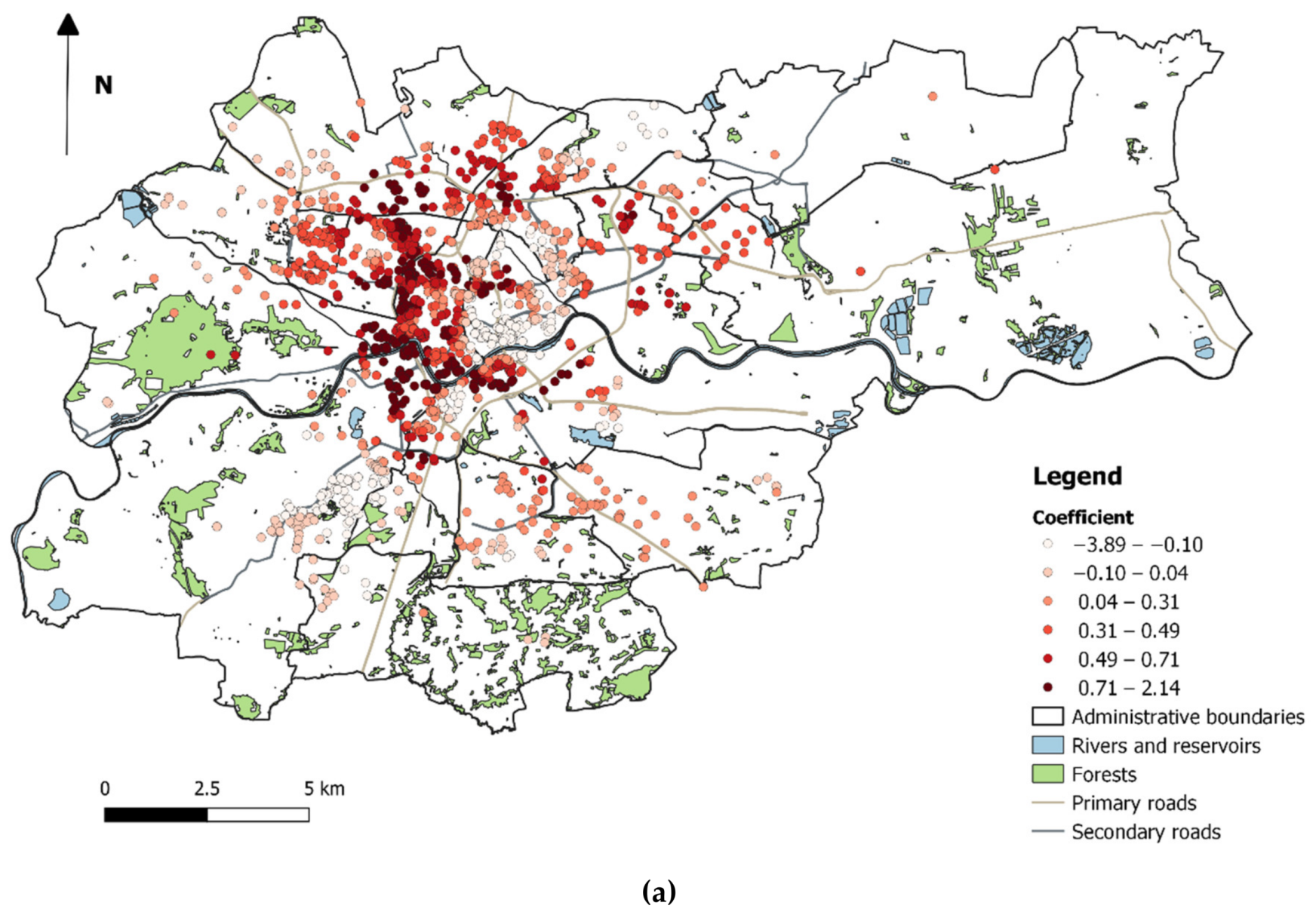
For the initial recognition of the data, information on latitude and longitude, and the spatial distribution of housing rents in Cracow, is presented in
Figure 3. In particular, it can be noted that the vast majority of flats for rent are located at the city centre and along main roads. Conversely, to the east of the city, there are hardly any flats for rent, which is mainly because of the under-developed road network, as well as the presence of large areas with industrial functions, for example, the second largest steelwork plant in Poland. When analysing rental prices, it should be noted that by far the highest level is present in the city centre, reaching as much as 136.36 PLN/m
2. Lower rents can be found in the northern parts of the city, where they oscillate between 20 and 40 PLN/m
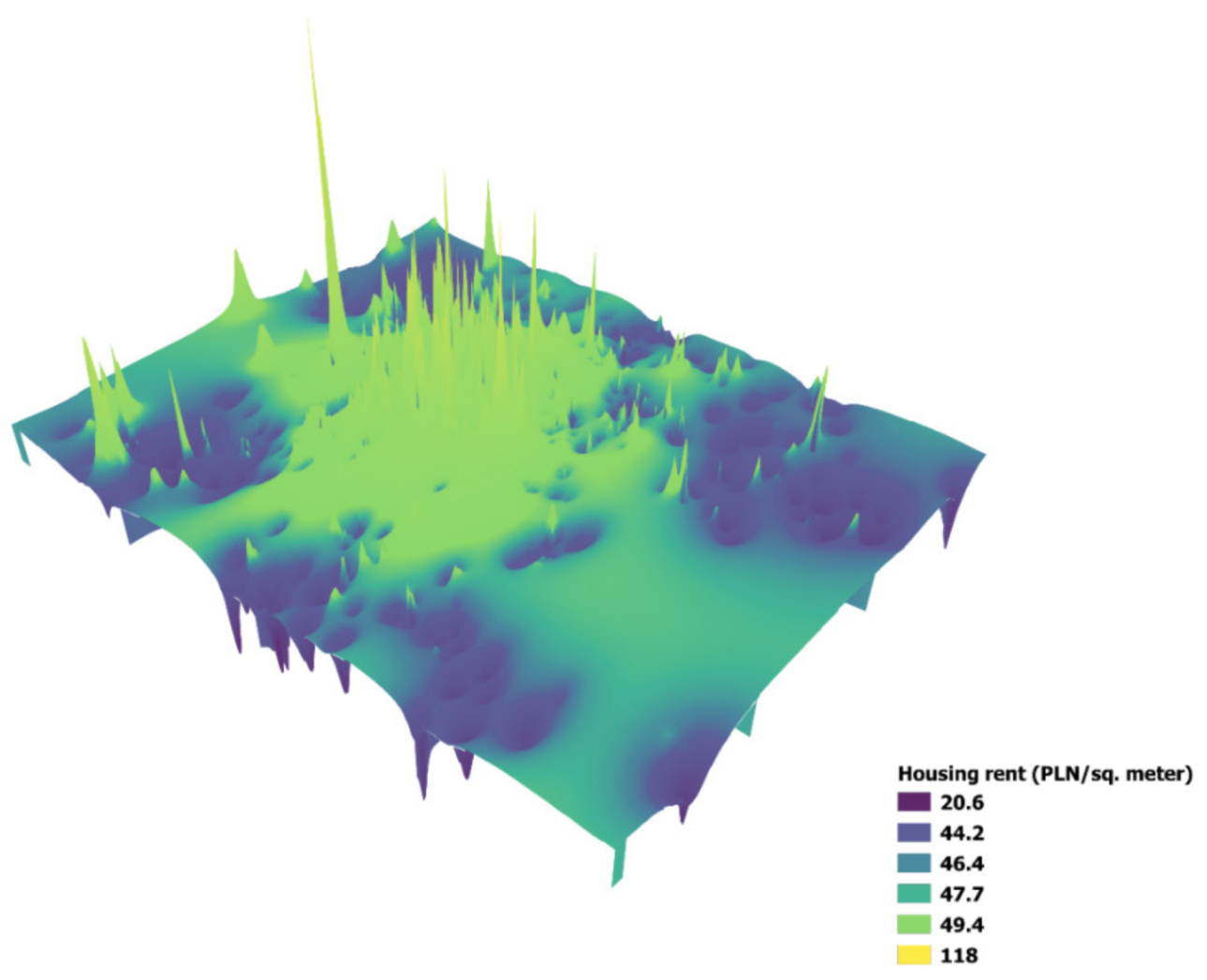
2. In order to get a better understanding of the differentiation of rental prices, 3D IDW interpolation (
Figure 4) was performed for the area marked in
Figure 3. On the basis of
Figure 4, it can be observed that, in some areas of the city centre, there are very large price bubbles. Taking into account the specificity of Cracow, these very high rental prices may occur for properties that have extraordinary features, such as attractive views on the Wisła River or the Wawel Royal Castle.
3.4. Independent Variables
A description of variables used for modelling monthly housing rents is presented in
Table 1. In particular, based on previous studies [
1,
13] and data availability, three groups of independent variables were defined: structural variables, locational variables, and neighbourhood variables. Unfortunately, in this study, it was not possible to take into account variables that characterise the economic aspect, for example, determinants such as wage levels. This type of data is not available at the micro level, either in terms of actual or offered wages.
Prior to establishing the final list of independent variables, they were subjected to preliminary analysis. In particular, the skewness of the variables was checked and the problem of multicollinearity was taken into account. Variables characterised by skewness above 3 were logarithmically transformed [
55]. Then, using OLS regression, VIFs were calculated for the analysed variables. Determinants with a VIF value above 10 were removed from further analysis.
Looking at the final list of variables, the group of structural variables includes determinants that characterise the physical characteristics of both the flat itself and the building in which it is located. As far as locational variables are concerned, attention has been paid primarily to the distance from the nearest means of transport. In terms of neighbourhood variables, the focus was on education; healthcare; and natural, commercial, and public amenities, as well as job opportunities.
3.5. Econometrics Models
In this study, the starting point for identifying rent determinants is the traditional OLS regression, which can be expressed as follows:
where
denotes an
vector of rental prices in the non-logarithmic form (skewness below 3),
is an
matrix of determinants,
is a
vector of coefficients, and
is an
vector of error terms.
It should be noted, however, that ordinary least squares regression is far from sufficient to investigate the determinants of rental prices. First of all, housing rents can be spatially autocorrelated. This is directly because of the behaviour of the real estate market participants, who very often check prices or rents in the immediate vicinity before the flat is put on the market. Moreover, it is obvious that spatial autocorrelation results from the fact that the general location and properties of the neighbourhood similarly influence real estate prices in given areas. These conclusions for the analysed data are confirmed by the value of Moran’s
I test, which is 0.37 and is statistically significant. The type of spatial model can be determined using
tests [
56], the results of which suggested the use of the spatial autoregressive model (SAR):
where
is the spatial autoregressive parameter,
denotes a spatially lagged dependent variable, and
is an
spatial weights matrix. In this study, a row-standardised binary k-nearest-neighbour matrix (with
) was used to calculate
. There are many other proposals for defining the spatial weights matrix in the scientific literature; however, among others, a study on the determinants of house prices carried out by Basile et al. [
57] indicated high robustness of the results to the choice of the weight matrix. Moreover, the use of
gives the best model performance in terms of AIC and AICc criteria (see
Table A1). In addition, the use of a row-standardised matrix enables the interpretation of
as the direct marginal effect, whereas the total marginal effect can be expressed as
) for the SAR model [
58]. Furthermore, row-standardising of
allows to interpret
as the average rental price of the neighbours.
When analysing an area as large as the city of Cracow, it can be expected that the strength of the influence of particular determinants of rental prices may vary in given locations. Therefore, when modelling house or rental prices, one should also take into account spatial heterogeneity. It should be noted that the spatial autoregressive parameter may also be unevenly distributed over space. The occurrence of spatial heterogeneity, however, is not certain for all parameters. Therefore, it is possible that some of the variables may affect rental prices in a global way, that is, the strength of their influence on the dependent variable will be the same at every point of the analysed area. In order to take into account all of the above demands, the MGWR-SAR model outlined by Geniaux and Martinetti [
17] should be used for modelling rental prices. In particular, the model that takes into account the possibility of the existence of global and local variables (including the spatial autoregressive parameter) takes the form:
where
denotes the longitude and latitude of rental price
,
are
independent variables with constant coefficients (
), and
represents
independent variables with spatially varying coefficients (
). It should be noted that
.
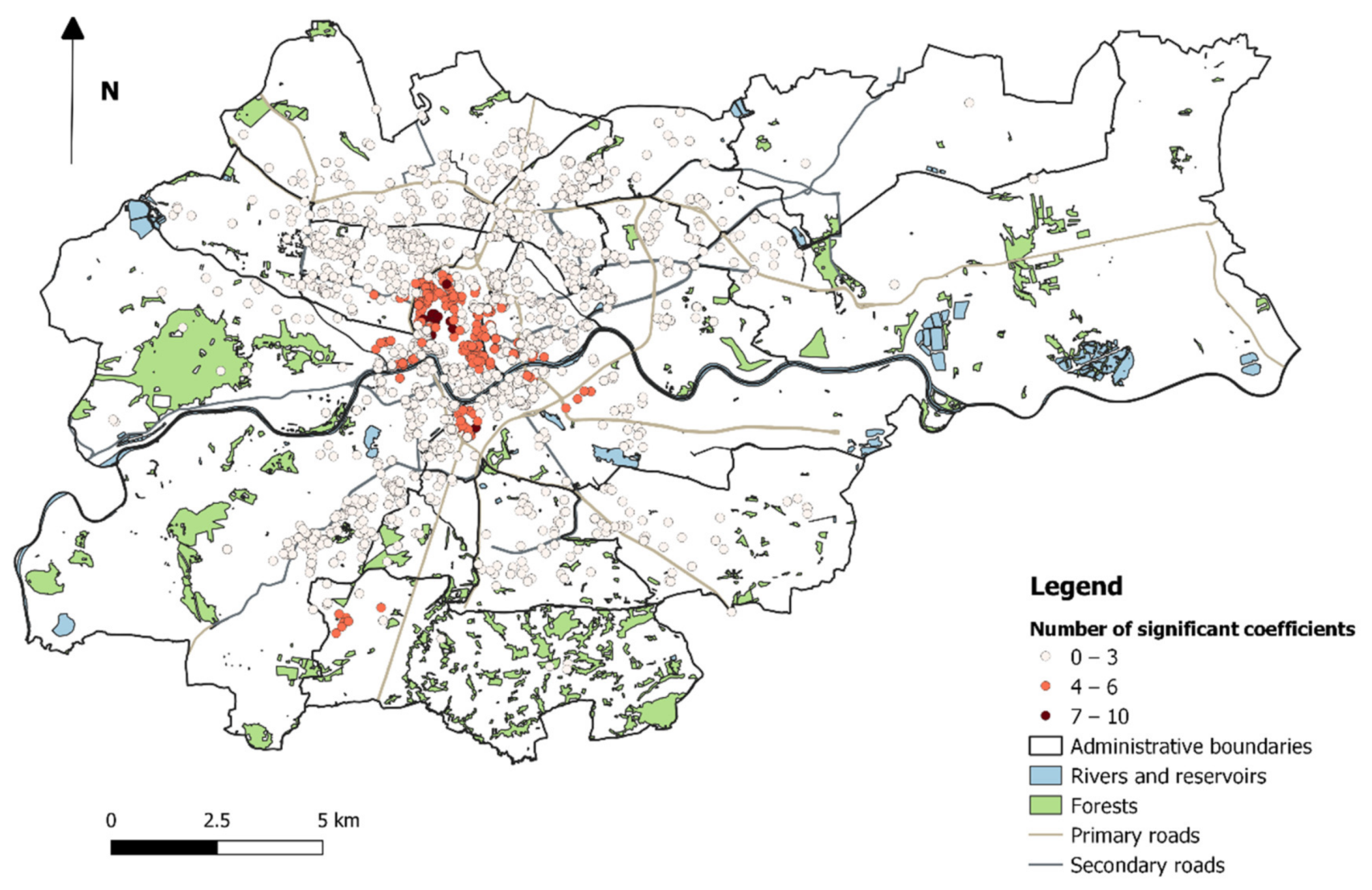
In order to select an appropriate model specification, the spatial non-stationarity of all parameters, both the tested determinants, and the spatial autocorrelation term should be assumed at the first stage (this type of model will be named GWR-SAR in this study, because in this case, there are no global variables). Then, the Monte Carlo test for spatial variability should be performed to identify global variables. With information on global as well as local variables, it is possible to choose an appropriate model and then make its estimation. In this study, in models based on geographically weighted regression (GWR), a bi-square kernel function and an adaptive bandwidth were used. The latter was selected based on the AICc criterion.
Moreover, taking into account the spatially lagged dependent variable, the issue of endogeneity appears. Therefore, in order to estimate models in which spatial autocorrelation occurs, the spatial two-stage least squares technique was used with
and
as a set of instruments [
59].
There is another problem when estimating the GWR model. In particular, the subsamples used in the local GWR estimates often overlap, which artificially increases the t-values obtained [
47]. Therefore, an adjusted significance level for the estimates will be applied in this study, which can be expressed by the following formula [
60]:
where
is the usual
,
is the effective number of parameters, and
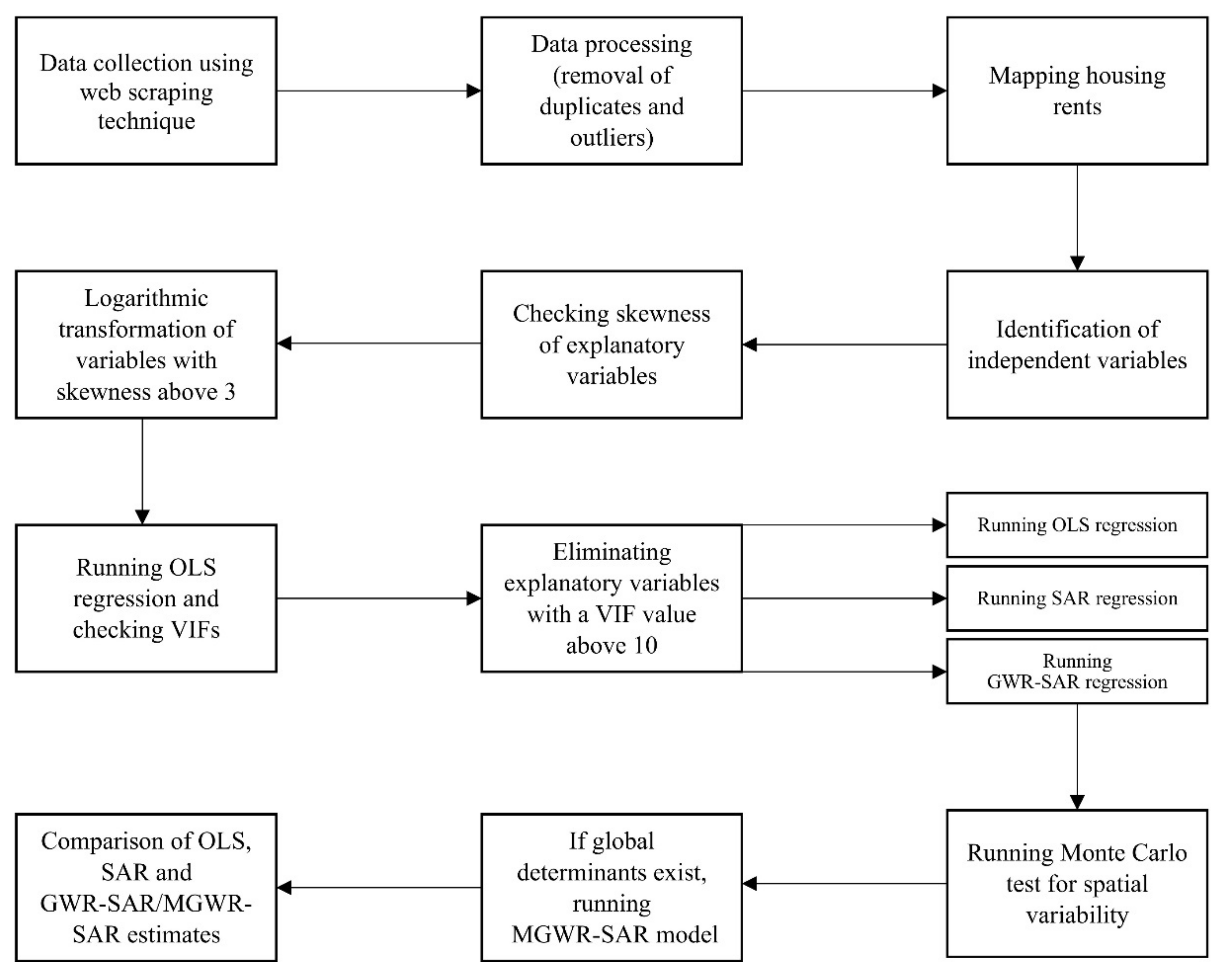
is the number of parameters. In order to synthesise the research methodology presented in
Section 3, and in particular, its subsequent steps, the whole procedure is presented in
Figure 5.