Capacitated Refuge Assignment for Speedy and Reliable Evacuation

Abstract

When a large-scale disaster occurs, each evacuee should move to an appropriate refuge in a speedy and safe manner. Most of the existing studies on the refuge assignment consider the speediness of evacuation and refuge capacity while the safety of evacuation is not taken into account. In this paper, we propose a refuge assignment scheme that considers both the speediness and safety of evacuation under the refuge capacity constraint. We first formulate the refuge assignment problem as a two-step integer linear program (ILP). Since the two-step ILP requires route candidates between evacuees and their possible refuges, we further propose a speedy and reliable route selection scheme as an extension of the existing route selection scheme. Through numerical results using the actual data of Arako district of Nagoya city in Japan, we show that the proposed scheme can improve the average route reliability among evacuees by 13.6% while suppressing the increase of the average route length among evacuees by 7.3%, compared with the distance-based route selection and refuge assignment. In addition, we also reveal that the current refuge capacity is not enough to support speedy and reliable evacuation for the residents.

1. Introduction

When a large-scale disaster, e.g., an earthquake, occurs, each evacuee should move to an appropriate refuge in a speedy and safe manner. Such speedy and reliable evacuation can be achieved by both pre-disaster and post-disaster approaches. The pre-disaster approaches include establishment of refuges [1,2,3,4,5,6], refuge assignment [7,8,9], evacuation planning [10,11,12], and geographical risk analysis [13,14,15,16,17]. From the viewpoint of the refuge assignment, most of the existing studies basically consider the evacuation time and refuge capacity while the safety evacuation is also important.

The pre-disaster approaches can provide us with a global picture of evacuation under predefined assumptions (e.g., refuge locations, geographical population distribution, and road network risk). Since it is difficult to consider all possible disaster situations, the post-disaster approaches are also important to compensate for the mismatch between the assumptions and actual situations.

The post-disaster approaches include evacuation guiding [18,19,20] and signage systems [21,22,23]. In comparison with the pre-disaster approaches, the post-disaster ones can flexibly deal with dynamic environmental changes due to the disaster for supporting the evacuees’ decision making under their high-stressed situation. However, most of the post-disaster approaches implicitly assume that each evacuee selects the nearest refuge for evacuation, which might guide the evacuee to a less reliable route and/or to a filled refuge. In recent years, we can obtain the safety-related information (e.g., geographical risk information) in addition to the capacity-related information (e.g., population distribution and refuge locations and capacities) from governments and some municipalities [13,14,15].

In this paper, we consider the earthquake case study and propose a refuge assignment scheme to achieve speedy and safety evacuations under the refuge capacity constraint. This is a kind of the multi-objective optimization problems, i.e., minimization of route length and maximization of route reliability.

We first formulate the refuge assignment problem as a two-step integer linear program (ILP) under the input of route candidates between evacuees and their possible refuges, which can be solved by the existing solver, CPLEX [24]. As for the route candidates, we also propose a speedy and reliable path selection scheme, which is an extended version of the existing path selection scheme [20] to improve the route reliability.

The proposed scheme can be viewed as either pre-disaster approach or post-disaster one, depending on the knowledge about the locations of evacuees. If the proposed scheme uses the geographical distribution of residents as their initial locations, it can be viewed as pre-disaster refuge assignment for evacuation planning. On the other hand, if it can obtain the actual locations of evacuees under the disaster situations through information and communication technologies (e.g., mobile devices, global positioning systems, and communication networks), it can also achieve post-disaster refuge assignment, which is responsive to the environmental changes.

In this paper, we mainly focus on the pre-disaster refuge assignment under the earthquake case study using actual geographical data (i.e., road blockage probabilities, map of Nagoya city, locations and capacities of refuges, and the distribution of residents), which are provided by the Japanese government and municipality [13,25,26,27].

Through numerical results using the actual data of Arako district of Nagoya city, in Japan, we will show the effectiveness of the proposed refuge assignment scheme in terms of speediness and safety of evacuation under the refuge capacity constraints.

The rest of this paper is organized as follows. Section 2 gives related work. In Section 3, we introduce the proposed scheme. After showing numerical results in Section 4, we finally give conclusions and future work in Section 5.

2. Related Work

2.1. Geographical Risk Analysis and Path Selection

In case of evacuation guiding, the simple shortest path may not be enough for the speedy and safety evacuation. Several studies focused on various metrics for the speedy and reliable path selection: traffic congestion [28,29], obstructions related to the presence of debris [30,31], and road vulnerability [13,15,17,32,33]. From the viewpoint of the evacuation speediness, the selfish behavior of evacuees (i.e., trying to move to their refuges as speedy as possible) may cause heavy congestion. To grasp such congestion caused by the selfish behavior, several studies provide pedestrian flow models [28,29]. In [34], Bernardini analyzed the video recording the real earthquake evacuations and proposed a database for earthquake pedestrian evacuation models, which includes the step-by-step evacuation behavior as well as motion quantities (i.e., speed, acceleration, and distance from obstacles). In [35], Liu et al. proposed a path selection method based on the artificial bee colony algorithm to avoid the congestion during the evacuation in building. Kasai et al. proposed a congestion-aware route selection using collected evacuees’ locations through the device to device communication [36]. For simplicity, we focus on the path length as the metric of speediness, but the proposed approach can also be applied to other speediness metrics if applicable.

From the viewpoint of the evacuation safety, Coutinho-Rodrigues et al. proposed a multi-objective location-routing problem using two kinds of paths (i.e., a main path and a backup one), which aims to minimize the distance and risk during evacuations [2]. In this case study, they conducted a case study analysis under the fire-risk assumption where Fire-Risk Index Method [15] is used as a tool for assessing the fire safety in buildings. The fire-risk index is a weighted sum of multiple risk parameters and ranges from 0.0 to 5.0. The high (resp. low) risk index represents the high (resp. low) level of the fire safety. There are several studies on earthquake emergencies in Italy and Japan [20,32,37]. Bernardini et al., considered multiple safety factors for evacuees (e.g., street vulnerability, street blockages probability, and crowding conditions along paths) and proposed a dynamic guidance tool based on Dijkstra’s algorithm with the integrated safety index [37]. Santrelli et al. developed vulnerability indices for a road network under an earthquake [32]. These two studies assumed the possibility of road blockage caused by debris of collapsed buildings, which is evaluated by the road width, the height of buildings along the road, and the vulnerability of buildings [17].

In Japan, a certain municipality (e.g., Nagoya city) also provides the road blockage probability in a similar manner, which represents the probability that the corresponding road segment will be blocked after an occurrence of a certain magnitude of an earthquake. The detailed definition will be given in Appendix A. In [20], Hara et al. proposed a geographical risk analysis-based path selection scheme that provides a speedy and safe route for each evacuee with the help of the road blockage probability.

In this paper, we extend this path selection scheme to improve the path safety and use it to obtain route candidates between evacuees and their possible refuge candidates.

2.2. Evacuation Guiding and Human Interactions

There have been several studies on the indirect/direct evacuation guiding systems: indirect guiding based on signage systems [21,22,23] and direct evacuation guiding systems [18,19,20]. The signage system is one of the building attributions in emergencies as well as ordinary conditions, and provides evacuees with indirect suggestion about evacuation [21,23]. However, Galea et al. demonstrated that the effectiveness of signage systems for evacuation is limited and only 38% of evacuees use the information about evacuation from the signage system [21]. To tackle this problem, the impact of interactions between people and signages on the relationship among the perception, interpretation, and use has been investigated [22,23].

From viewpoint of the direct evacuation guiding, Fujihara and Miwa proposed an evacuation guiding scheme that can work even when the existing communication infrastructures were highly damaged [18]. In this scheme, evacuees manually register the state information of each road (e.g., passable and blocked) to their mobile devices and share it with others through a delay tolerant network [38], which is composed of the mobile devices. Since such manual operations may be difficult under the emergent situations, Komatsu et al. proposed a mobile-edge collaborative automatic evacuation guiding scheme where the evacuees’ mobile devices automatically estimate the road state information through information sharing with their evacuees [19].

In the field of psychology, it has been pointed out that a small number of leaders can lead many evacuees (e.g., follow-direction method and follow-me method) [39]. In [19], the implicit interactions among evacuees through information sharing can be regarded as a kind of such leader-follower communication. Since such post-disaster approaches implicitly build the cooperative relationship caused by human interactions, it can not only improve the evacuation speediness but also contribute to avoiding roads with high risks in an adaptive manner. However, most of studies on the evacuation guiding are the post-disaster approaches and basically adopted the shortest path selection.

To improve the evacuation safety, Hara et al. proposed a geographical risk analysis-based path selection for automatic evacuation guiding scheme, which provided each evacuee with a speedy and safe route by combining the pre-obtained risk information and the collected information during the evacuation [20]. This approach, however, implicitly assumes that each evacuee selects the nearest refuge, which may cause the overflow of the refuge and/or the selection of routes/refuges in high risk regions. In this paper, we propose a refuge assignment scheme that can consider the capacity limitation as well as the speediness and safety of evacuations.

2.3. Refuge Assignment

There have been several studies on the refuge assignment for speedy evacuation under large-scale disasters [7,8,9]. Ng et al. proposed a refuge assignment scheme that considers the balance between the global refuge assignment for minimizing the total evacuation time and the individual selfish refuge selection under emergent situations [7]. Saadatseresht et al. proposed a refuge assignment scheme considering the evacuation route length, population, and refuge capacity, with the help of the multi-objective evolutionary algorithms and the geographical information system [8]. Bayram proposed a refuge assignment scheme such that the route length of each evacuee does not exceed the length of the shortest route plus a certain threshold [9]. These existing studies focus on the speedy evacuation and the refuge capacity while the safety of the evacuation is not taken account. In terms of the evacuation safety, Coutinho-Rodrigues et al. proposed a multi-objective mixed integer linear programming model to minimize the distance and fire risk during evacuations [2,3]. In this paper, we consider the earthquake case study and address the refuge assignment for speedy and safety evacuation under the refuge capacity constraints.

2.4. Multi-Objective Mathematical Programming

As mentioned above, the appropriate refuge assignment must consider the various aspects (i.e., speediness, safety, and refuge capacity), which indicates it is a kind of the multi-objective optimization problem. There have also been several studies on multi-objective optimization, e.g., weighting method [40,41], $\epsilon$-constraint method [40,41,42], and AUGMECON [43,44]. Their common goal is to derive the representative subset of the Pareto set, which is the set of Pareto optimal solutions (i.e., solutions that cannot improve one objective function without deteriorating the remaining objective functions). The weighting method transforms the original objective functions into a single objective function, i.e., the weighted sum of them [40,41]. It requires the careful design of the weighting parameters that can consider the relative importance of each objective. $\epsilon$-constraint method optimizes the first objective functions under the constraints where each remaining k-th objective function is bounded by a certain threshold ${\epsilon }_k$ [42]. The vector of ${\epsilon }_k$ should be chosen carefully by considering the trade-off among the objectives. The augmented $\epsilon$-constraint method (AUGMECON) provides us with the way to determine the range of ${\epsilon }_k$ [43].

In this paper, inspired by $\epsilon$-constraint method and AUGMECON, we formulate the refuge assignment as a two-step ILP, where the first step ILP is used to determine the range of parameter and the second-step ILP is formulated based on $\epsilon$-constraint method.

3. Capacitated Refuge Assignment for Speedy and Reliable Evacuation

Refuge assignment for evacuees is a kind of combinational optimization problems where we require consideration of multiple important features of evacuation (i.e., speediness, safety, and capacity constraint of refuges).

We first provide notations and criteria for evacuation route, i.e., speediness and reliability, in Section 3.1 and explain the overview of the proposed refuge assignment scheme in Section 3.2. Next, we formulate such refuge assignment as a two-step ILP in Section 3.3. We further propose an algorithm to calculate speedy and reliable route candidates between evacuees and their possible refuges in Section 3.4.

3.1. Preliminaries

Since the refuge assignment is part of the evacuation planning, we focus on the target area for the evacuation planning. In Japan, the unit of the target area is typically a school district and the mayor of municipality must determine designated emergency evacuation site for each disaster type (e.g., earthquake and flood) [45]. $G=(\mathcal{V},\mathcal{E},g)$ denotes the graph representing the internal structure of the target area, where $\mathcal{V}$ is a set of vertices i.e., intersections or refuges, and $\mathcal{E}$ is a set of edges i.e., roads. There are D refuges denoted by $\mathcal{D}=\{1,2,\dots ,D\}$ such that $\mathcal{D}\subset \mathcal{V}$. Suppose that there are $N>0$ evacuees, denoted by $\mathcal{N}=\{1,2,\dots ,N\}$, and each evacuee i is initially located at vertex $l_i$ in the target area.

To calculate the refuge assignment, we require the initial locations of the evacuees. The refuge assignment can be regarded as either pre-disaster approach or post-disaster one, according to the knowledge about the initial locations of the evacuees. From the viewpoint of the pre-disaster refuge assignment, the geographical distribution of residents [27] can be used as possible initial locations of evacuees (residents). We can also adopt the time-varying geographical population distribution (e.g., People Flow Data [14]) to consider the initial locations of evacuees under human life cycle (e.g., commuting period in the morning and returning period in the evening). On the other hand, from the viewpoint of the post-disaster refuge assignment, we can collect the actual locations of the evacuees through their mobile devices at the beginning of a disaster if the terrestrial communication infrastructure (e.g., cellular networks and Wi-Fi) is working.

If the terrestrial communication infrastructures are (partly) damaged and unavailable, we can also use device to device (D2D) communication through evacuees’ mobile devices [38,46] and devices with satellite connectivity [47]. Please note that such post-disaster information collection would be affected not only by communication environments but also by the penetration ratio of the proposed scheme as well as evacuees’ privacy settings for their location information. If the post-disaster refuge assignment cannot obtain the actual locations of evacuees, it can also adopt the above-mentioned statistical information as in the pre-disaster one. In what follows, we mainly focus on the pre-disaster refuge assignment where the geographical distribution of residents is used as the initial locations of the evacuees.

The map matching algorithm [48] can find the nearest vertex of the internal graph from a coordinate-based location. $g:\mathcal{E}\to \mathbb{I}$ is a real-valued function that assigns road blockage probability $p_e$ in closed unit interval $\mathbb{I}=[0,1]$ to each edge $e\in \mathcal{E}$ in the risk map. Road blockage probability $p_e$ is an estimated probability that road segment $e\in \mathcal{E}$ is blocked due to the collapse of building along a road under a certain earthquake [13]. The detailed definition of the road blockage probability is explained in Appendix A.

An evacuation route r can be represented by a vector of roads. We define the length of route r as the sum of the length of each road e in r:

$$\begin{array}{c}\hfill f_{\mathrm{d}}\left(r\right)=\sum _{\forall e\in r}{d}_e,\end{array}$$

(1)

where $d_e$ is the length of road e. In addition, we can also define the route reliability as follows [20]:

$$\begin{array}{c}\hfill f_{\mathrm{p}}\left(r\right)=\prod _{\forall e\in r}(1-p_e),\end{array}$$

(2)

which is the probability that all the roads e along the route r are passable under the assumption that the road blockage probabilities along the routes are independent. The route reliability takes a value in the range of $[0,1]$ and a large (resp. small) value means high (resp. low) reliability. We can obtain the geographical information (e.g., the location of the refuge, the refuge capacity, and the distribution of residents) from the government and the municipalities before the disaster occurs [14,26,27]. Each refuge $j\in \mathcal{D}$ has a capacity of $C_j$ persons. $\mathcal{C}=\{C_1,C_2,\dots ,C_D\}$ denotes a set of refuge capacity.

Table 1. Notation.

Notation	Definition
G	Directed graph of the road network
$\mathcal{V}$	The set of vertices
$\mathcal{E}$	The set of edges
$p_e$	Road blockage probability of road e
$\mathcal{N}$	The set of evacuees $\{1,2,\dots ,N\}$ $\left[\mathrm{persons}\right]$
$ℒ$	The set of initial locations of each evacuee i, $\{l_1,l_2,\dots ,l_N\}$
$\mathcal{D}$	The set of refuges $\{1,2,\dots ,D\}$
$\mathcal{C}$	The set of refuge capacity $\{C_1,C_2,\dots ,C_D\}$ $\left[\mathrm{persons}\right]$
$x_{i,j}$	Decision variable
$r_{i,j}$	Evacuee i’s route to refuge j
$d_e$	The length of road e $\left[\mathrm{m}\right]$
$f_{\mathrm{p}}\left(r\right)$	The reliability of route r
$f_{\mathrm{d}}\left(r\right)$	The length of route r $\left[\mathrm{m}\right]$
$f_{\mathrm{p}}^{*}$	The optimal route reliability
$\epsilon$	The constraint on the decrease of the route reliability

summarizes notations used in this paper.

3.2. Overview of Proposed Refuge Assignment Scheme

In this subsection, we introduce the overview of the proposed refuge assignment scheme. Figure 1 illustrates the flow chart of conducting the refuge assignment and route candidate. We first calculate the initial locations of evacuees from the geographical distribution of residents [27].

Since the geographical distribution of residents gives us the number of persons in each sub-region q, $N_q$, we uniformly allocate $N_q$ evacuees to the vertices in the sub-region q. Let $\mathcal{Q}$ denote the set of sub-regions, and thus ${\sum }_{q\in \mathcal{Q}}{N}_q=N$.

Considering the fact that some of the residents may stay their home or workplace even under the emergency, we further assume that $\beta$ ($0\le \beta \le 1$) ratio of all the residents act as evacuees, denoted by ${\mathcal{N}}_{\beta }$. In such cases, we can regard $\mathcal{N}$ as ${\mathcal{N}}_{\beta }$.

Next, given risk map $G=(\mathcal{V},\mathcal{E},g)$, set of refuges $\mathcal{D}$, set of refuge capacity $\mathcal{C}$, set of evacuees $\mathcal{N}$, and initial locations of evacuees $ℒ$, we obtain the route candidates $r_{i,j}$ between all evacuees $i\in \mathcal{N}$ and all refuges $j\in \mathcal{D}$ using Algorithm 2, which will be described in Section 3.4. Finally, the refuge assignment is obtained by solving ILPs, ${\mathsf{OP}}_{\mathrm{p}}$ and/or ${\mathsf{OP}}_{\mathrm{d}}$, which will be described in Section 3.3.

3.3. Two-Step ILP Formulation for Refuge Assignment

As mentioned above, the refuge assignment must be carefully designed by considering the speediness and safety of evacuation under the refuge capacity constraint. This is a kind of multi-objective optimization problems, and thus we tackle this problem in the following two-step ILP.

3.3.1. First Step: Maximization of Average Route Reliability among Evacuees under Refuge Capacity Constraint

Given route candidates between evacuees and their possible refuges as the input data, which will be explained in Section 3.4, we first aim at maximizing the evacuation safety, i.e., the average route reliability among evacuees. This optimization problem can be represented by the following ILP ${\mathsf{OP}}_{\mathrm{p}}$.

$$\begin{array}{cc}\hfill max& \frac{1}{N}\sum _{i\in \mathcal{N}}\sum _{j\in \mathcal{D}}{f}_{\mathrm{p}}\left(r_{i,j}\right)x_{i,j},\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill \mathrm{s}.\mathrm{t}.& x_{i,j}\in \{0,1\},\forall i\in \mathcal{N},\forall j\in \mathcal{D},\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill & \sum _{j\in \mathcal{D}}{x}_{i,j}=1,\forall i\in \mathcal{N},\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill & \sum _{i\in \mathcal{N}}{x}_{i,j}\le C_j,\forall j\in \mathcal{D}.\hfill \end{array}$$

(6)

The objective function (3) is the maximization of the average road reliability among evacuees, where $r_{i,j}$ is the route candidate between evacuee i and refuge j. The calculation of $r_{i,j}$ will be described in Section 3.4. $x_{i,j}$ is binary decision variable given by (4). If evacuee i is assigned to refuge j, $x_{i,j}=1$. Otherwise, $x_{i,j}=0$. The constraint of (5) guarantees that each evacuee i must be allocated to one refuge. Since the overflow evacuees will be required to move to other refuges [49], such overflow conditions are prohibited by (6), which indicates that the number of evacuees assigned to each refuge does not exceed the corresponding capacity.

Since the objective function and all the constraints are linear with the binary decision variables, ${\mathsf{OP}}_{\mathrm{p}}$ is ILP, which can be solved by the existing solver, e.g., CPLEX.

3.3.2. Second Step: Minimization of Average Route Length among Evacuees under Refuge Capacity Constraint and Average Route Reliability

By solving the problem ${\mathsf{OP}}_{\mathrm{p}}$, we can obtain the optimal value of the average route reliability $f_{\mathrm{p}}^{*}$. The corresponding refuge assignment, however, may have some room to improve in terms of speedy evacuation. To tackle this trade-off between the speediness and reliability, we further propose a second-step optimization as an ILP ${\mathsf{OP}}_{\mathrm{d}}$, which can be formulated by modifying ${\mathsf{OP}}_{\mathrm{p}}$ as follows.

First, the objective function (3) is replaced with

$$\begin{array}{cc}\hfill min& \frac{1}{N}\sum _{i\in \mathcal{N}}\sum _{j\in \mathcal{D}}{f}_{\mathrm{d}}\left(r_{i,j}\right)x_{i,j},\hfill \end{array}$$

(7)

which is the minimization of the average route length among evacuees. In addition to the constraints of ${\mathsf{OP}}_{\mathrm{p}}$, i.e., (4)–(6), ${\mathsf{OP}}_{\mathrm{d}}$ adds the following constraint:

$$\begin{array}{cc}\hfill & \frac{1}{N}\sum _{i\in \mathcal{N}}\sum _{j\in \mathcal{D}}{f}_{\mathrm{p}}\left(r_{i,j}\right)x_{i,j}\ge f_{\mathrm{p}}^{*}-\epsilon .\hfill \end{array}$$

(8)

The constraint of (8) guarantees a certain level of the average route availability by controlling a parameter $\epsilon$$(0\le \epsilon \le f_{\mathrm{p}}^{*})$, which describes the allowable decrease of average route reliability from the optimal value $f_{\mathrm{p}}^{*}$. If $\epsilon$ is small (resp. large), the refuge assignment is designed for reliable (speedy) evacuation.

The appropriate setting for $\epsilon$ will be discussed in Section 4.2. Since the objective function and all the constraints are linear with the binary variables, ${\mathsf{OP}}_{\mathrm{p}}$ is also ILP.

3.4. Calculation of Speedy and Reliable Route Candidates between Evacuees and Their Possible Refuges

The solution, i.e., refuge assignment, of the two-step ILP depends on its input parameters, which are the route candidates between evacuees and their possible refuges, i.e., $r_{i,j}$. We propose a speedy and reliable route selection scheme, which is an extended version of the existing route selection scheme [20].

Algorithm 1 presents a function $\mathsf{candidate}\_\mathsf{paths}(G,i,j,k_{max},{\delta }_{max},{\gamma }_{\mathrm{th}})$ that enumerates at most $k_{max}$$(k_{max}\ge 1)$ shortest route candidates between evacuee i and refuge j under the constraint on route length, ${\delta }_{max}$$({\delta }_{max}\ge 0)$, and route reliability, ${\gamma }_{\mathrm{th}}$$(0\le {\gamma }_{\mathrm{th}}\le 1)$. Given road network $G=(\mathcal{V},\mathcal{E},g)$, evacuee i, refuge j, parameters $(k_{max},{\delta }_{max})$, and ${\gamma }_{\mathrm{th}}$, it first initializes the set of route candidates, ${ℛ}_{i,j}^{k_{max},{\delta }_{max},{\gamma }_{\mathrm{th}}}$, to be empty and the shortest route length $d_{min}$ to be infinity (line 1). Next, it obtains at most $k_{max}$ shortest route candidates between evacuee i and refuge j, $R_{i,j}^{k_{max}}$, by using k$-\mathrm{th}\_\mathrm{shortest}\_\mathrm{paths}(·)$ function based on Yen’s algorithm [50] (line 2). It also calculates the length of the shortest path in $R_{i,j}^{k_{max}}$, $d_{min}$ (line 3). In the next loop of lines 4–8, it extracts speedy and reliable route candidates from $R_{i,j}^{k_{max}}$. Please note that route candidates in $R_{i,j}^{k_{max}}$ are sorted in ascending order of route length. If the length of route r is longer than that of the shortest path, i.e., $d_{min}$, at a certain level, ${\delta }_{max}$, it stops the loop (lines 5–6). If the reliability of route r is equal or greater than a threshold ${\gamma }_{th}$, it adds r to ${ℛ}_{i,j}^{k_{max},{\delta }_{max},{\gamma }_{\mathrm{th}}}$ (line 8). Please note that the existing scheme in [20] does not have this operation, and thus the road reliability is considered in the best effort manner. After the loop, it returns ${ℛ}_{i,j}^{k_{max},{\delta }_{max},{\gamma }_{\mathrm{th}}}$ as the speedy and reliable route candidates.

Algorithm 1$\mathsf{candidate}\_\mathsf{paths}(G,i,j,k_{max},{\delta }_{max},{\gamma }_{\mathrm{th}})$: Enumeration of at most $k_{max}$ shortest route candidates between evacuee i and refuge j under constraint on route length, ${\delta }_{max}$, and route reliability, ${\gamma }_{\mathrm{th}}$.
Require:$G,i,j,k_{max},{\delta }_{max},{\gamma }_{\mathrm{th}}$
Ensure:${ℛ}_{i,j}^{k_{max},{\delta }_{max},{\gamma }_{\mathrm{th}}}$
1: ${ℛ}_{i,j}^{k_{max},{\delta }_{max},{\gamma }_{\mathrm{th}}}\leftarrow \varnothing$, $d_{min}\leftarrow \infty$	▹ Initialization
2: ${ℛ}_{i,j}^{k_{max}}$←k$-\mathrm{shortest}\_\mathrm{paths}(G,i,j,k_{max})$	▹ Calculation of the $k_{max}$-shortest routes
3: $d_{min}\leftarrow {min}_{r\in {ℛ}_{i,j}^{k_{max}}}{f}_{\mathrm{d}}\left(r\right)$	▹ Calculation of the length of the shortest route
4: for $r\in {ℛ}_{i,j}^{k_{max}}$ do
5:     if $f_{\mathrm{d}}\left(r\right)-d_{min}>{\delta }_{max}$ then	▹ Check on the route length condition
6:         break
7:     if $f_{\mathrm{p}}\left(r\right)\ge {\gamma }_{th}$ then	▹ Check on the route reliability condition
8:         ${ℛ}_{i,j}^{k_{max},{\delta }_{max},{\gamma }_{\mathrm{th}}}\leftarrow {ℛ}_{i,j}^{k_{max},{\delta }_{max},{\gamma }_{\mathrm{th}}}\cup \left\{r\right\}$
9: return ${ℛ}_{i,j}^{k_{max},{\delta }_{max},{\gamma }_{\mathrm{th}}}$

The route candidates in ${ℛ}_{i,j}^{k_{max},{\delta }_{max},{\gamma }_{\mathrm{th}}}$ change depending on the parameters $k_{max}$, ${\delta }_{max}$, and ${\gamma }_{\mathrm{th}}$. $k_{max}$ and ${\delta }_{max}$ controls the diversity and speediness of route candidates [20]. $k_{max}$ can be as large as possible under the constraint on the computation overhead. ${\delta }_{max}$ can also be a moderate value by considering both the speedy evacuation and reliable route discovery. On the contrary, the setting of ${\gamma }_{\mathrm{th}}$ tends to be difficult because the feasible route reliability between evacuee i and refuge j can change depending on the pair of i and j.

Considering these features, we propose a function $\mathsf{speedy}\_\mathsf{reliable}\_\mathsf{path}(G,i,j,\eta ,k_{max},{\delta }_{max})$ that calculates the speedy and reliable route candidate $r_{i,j}$ between evacuee i and refuge j (Algorithm 2). Given road network $G=(\mathcal{V},\mathcal{E},g)$, evacuee i, refuge j, and parameters $(k_{max}$,${\delta }_{max})$, it first initializes ${\gamma }_{\mathrm{th}}$ to be the maximum value, i.e., one, and ${ℛ}_{i,j}^{k_{max},{\delta }_{max},{\gamma }_{\mathrm{th}}}$ to be an empty set (line 1). In the next loop of lines 2–6, it searches for the most reliable route candidate $r_{i,j}$ between evacuee i and refuge j under the constraint on $k_{max}$ and ${\delta }_{max}$, by decreasing ${\gamma }_{\mathrm{th}}$ at a certain interval, $\eta$, e.g., $\eta =0.1$. If it succeeds in finding route candidates ${ℛ}_{i,j}^{k_{max},{\delta }_{max},{\gamma }_{\mathrm{th}}}$ using $\mathsf{candidate}\_\mathsf{paths}(·)$ (line 3), it selects the most reliable one as follows (line 5):

$$\begin{array}{c}\hfill r_{i,j}=\underset{r\in {ℛ}_{i,j}^{k_{max},{\delta }_{max},{\gamma }_{\mathrm{th}}}}{\arg \max }{f}_{\mathrm{p}}\left(r\right).\end{array}$$

(9)

Otherwise, If ${ℛ}_{i,j}^{k_{max},{\delta }_{max},{\gamma }_{\mathrm{th}}}$ is empty, it continues searching for the route candidates by setting ${\gamma }_{\mathrm{th}}={\gamma }_{\mathrm{th}}-\eta$ (line 6). As a result, Algorithm 2 provides us with speedy and reliable route candidate $r_{i,j}$ between evacuee i and refuge j.

Algorithm 2$\mathsf{speedy}\_\mathsf{reliable}\_\mathsf{path}(G,i,j,\eta ,k_{max},{\delta }_{max})$: Calculation of speedy and reliable route candidate $r_{i,j}$ between evacuee i and refuge j.
Require:$G,i,j,\eta ,k_{max},{\delta }_{max}$
Ensure:$r_{i,j}$
1: ${\gamma }_{\mathrm{th}}\leftarrow 1$, ${ℛ}_{i,j}^{k_{max},{\delta }_{max},{\gamma }_{\mathrm{th}}}\leftarrow \varnothing$	▹ Initialization
2: while ${\gamma }_{\mathrm{th}}\ge 0$ do
3:    ${ℛ}_{i,j}^{k_{max},{\delta }_{max},{\gamma }_{\mathrm{th}}}\leftarrow \mathsf{candidate}\_\mathsf{paths}(G,i,j,k_{max},{\delta }_{max},{\gamma }_{\mathrm{th}})$	▹ Calculation of the route candidates
4:     if ${ℛ}_{i,j}^{k_{max},{\delta }_{max},{\gamma }_{\mathrm{th}}}\ne \varnothing$ then
5:         return $r_{i,j}$ according to (9)	▹ Calculation of the speedy and reliable route candidate
6:     ${\gamma }_{\mathrm{th}}\leftarrow {\gamma }_{\mathrm{th}}-\eta$	▹ Update of ${\gamma }_{\mathrm{th}}$

4. Numerical Results

In this section, we evaluate the refuge assignment obtained by solving the two-step ILP, ${\mathsf{OP}}_{\mathrm{p}}$ and ${\mathsf{OP}}_{\mathrm{d}}$, using the actual information.

4.1. Evaluation Model

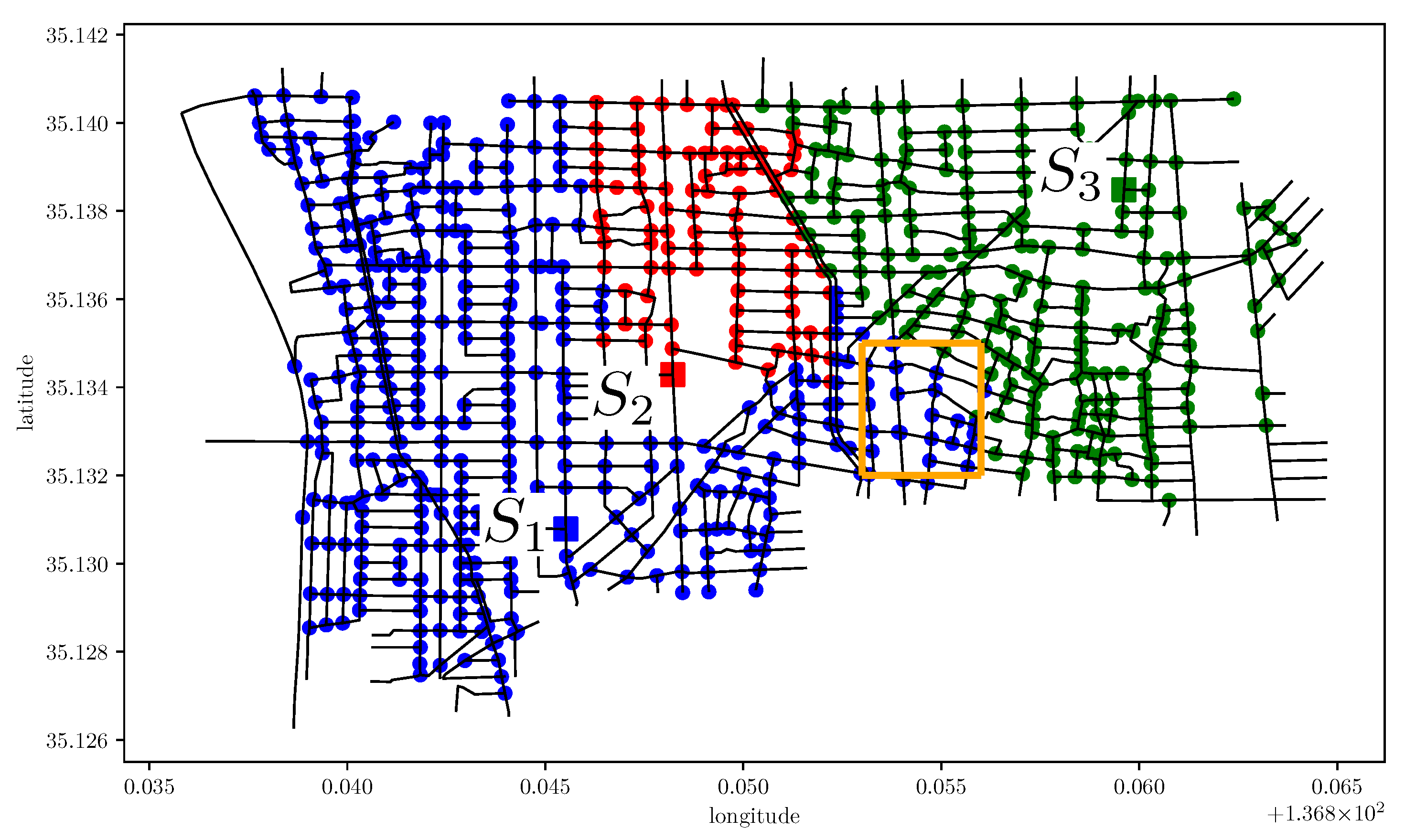
For the evaluation, we select Nagoya city in Japan because it provides us with the risk map where each road is annotated by the road blockage probability [13]. There are 263 school districts, each of which is the unit of evacuation planning [25]. We select Arako district from them by considering the high average road blockage probability. The green area in Figure 2 shows the risk map of $2.7\left[\mathrm{km}\right]\times 1.9\left[\mathrm{km}\right]$ Arako district. This map’s internal graph structure is composed of 801 vertices and 1220 edges.

As for the disaster scenario, Nagoya city provides us with the information of the road blockage probabilities for several classes depending on the degree of damages. In this paper, we use the data of maximum class that consider Nankai megathrust earthquake. Each road in Figure 2 is colored according to the road blockage probability: red (resp. black) means high (resp. low) road blockage probability. The average road blockage probability among all roads is 0.151. The orange area in Figure 2 contains the roads with high road blockage probability, i.e., the average road blockage probability in this area is 0.278. We also show the three actual refuges $D=\{S_1,S_2,S_3\}$ as blue points in Figure 2, according to [26]. The capacity of each refuge is given as $C_{S_1}=$ 11,500, $C_{S_2}=$ 1964, and $C_{S_3}=$ 8000.

There are 23,156 residents in Arako district [27] and the geographical distribution of residents is shown in Figure 3. We confirm that the three refuges cannot accommodate all the residents, i.e., ${\sum }_{j\in \mathcal{D}}{C}_j=$ 21,464 < 23,156.

In what follows, we set $\beta$ to be 0.7 as an example scenario where some of the residents stay their home or workplace even under the emergency.

For comparison purpose, we use the three schemes depending on the combination of the refuge assignment and the route selection, as shown in

Table 2. Schemes for evaluation.

Scheme	Refuge Assignment	Route Selection
Distance-based scheme	${\mathsf{OP}}_{\mathrm{d}}$ without (8)	Shortest path selection
Proposed scheme	${\mathsf{OP}}_{\mathrm{p}}$ and ${\mathsf{OP}}_{\mathrm{d}}$	$\mathsf{speedy}\_\mathsf{reliable}\_\mathsf{path}\left(\right)$
Proposed scheme without capacity constraint	${\mathsf{OP}}_{\mathrm{p}}$ and ${\mathsf{OP}}_{\mathrm{d}}$ without (6)	$\mathsf{speedy}\_\mathsf{reliable}\_\mathsf{path}\left(\right)$

. The distance-based scheme only considers the minimization of the average route length among evacuees, which can be obtained by solving a modified version of ILP ${\mathsf{OP}}_{\mathrm{d}}$ where constraint (8) is removed.

We use two kinds of criteria. The first one is the average route length, ${\overline{f}}_{\mathrm{d}}$, to evaluate the speediness of the evacuation, which corresponds to the objective function (7). The second one is the average route reliability, ${\overline{f}}_{\mathrm{p}}$, which is related to the objective function (3).

$$\begin{array}{c}\hfill {\overline{f}}_{\mathrm{d}}=N^{-1}\sum _{i\in \mathcal{N}}\sum _{j\in \mathcal{D}}{f}_{\mathrm{d}}\left(r_{i,j}\right)x_{i,j},{\overline{f}}_{\mathrm{p}}=N^{-1}\sum _{i\in \mathcal{N}}\sum _{j\in \mathcal{D}}{f}_{\mathrm{p}}\left(r_{i,j}\right)x_{i,j}.\end{array}$$

In what follows, we show the average of ten independent numerical results, each of which has different initial locations of evacuees. Through preliminary experiments, we set the parameters for the route selection as follows: $k_{max}=$ 5000, ${\delta }_{max}=$ 300, and $\eta =$ 0.1.

4.2. Analysis of Trade-Off between Speediness and Safety under Capacity Constraint

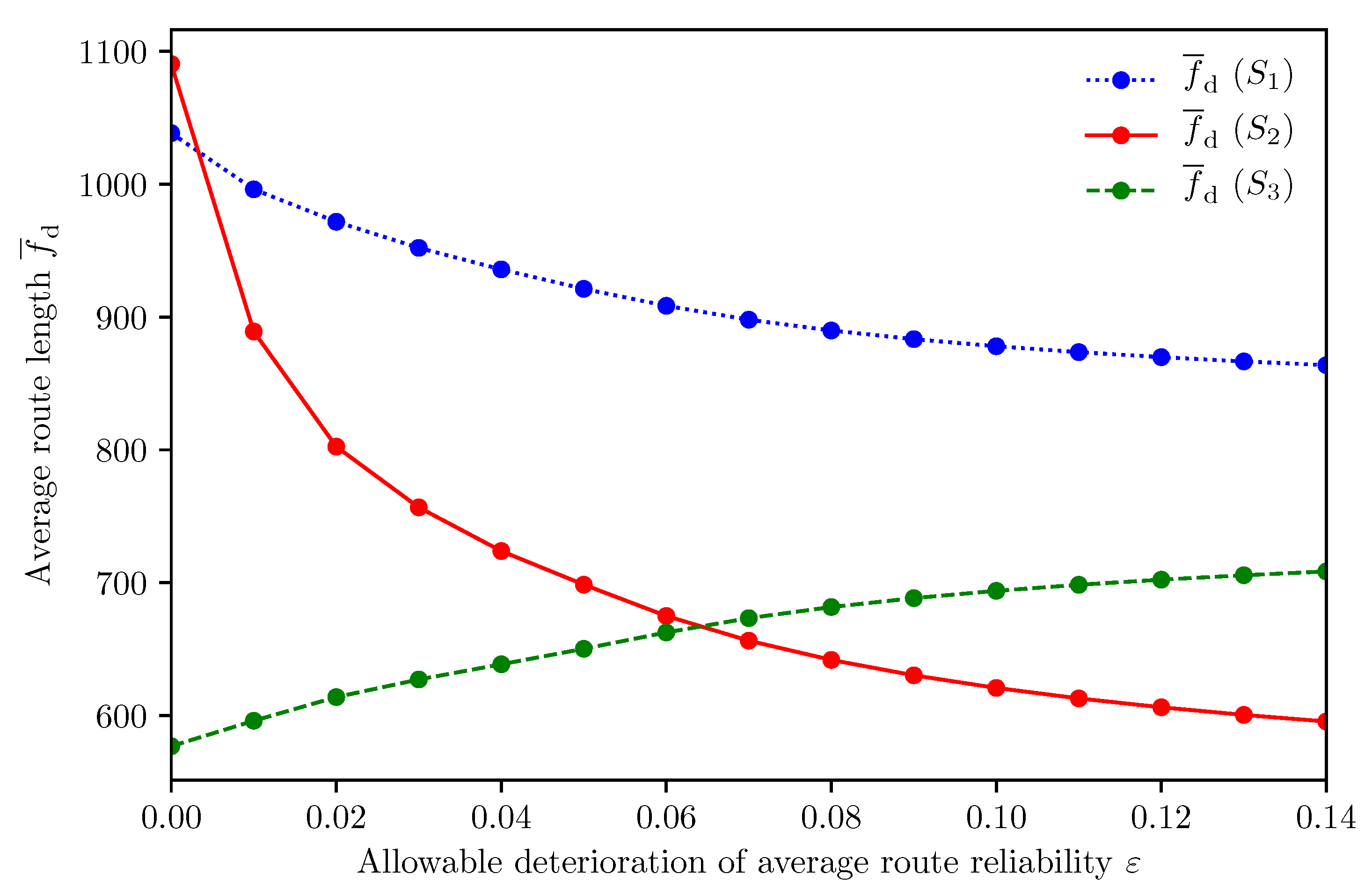
In this subsection, we show the performance of the proposed scheme compared with the distance-based scheme under the capacity constraint. Figure 4 illustrates how the allowable deterioration of average route reliability $\epsilon$ affects the average route length ${\overline{f}}_{\mathrm{d}}$ and average route reliability ${\overline{f}}_{\mathrm{p}}$ in case of relatively large evacuation demand, i.e., $\beta =0.7$. We first focus on the performance of the proposed scheme. Since small (resp. large) $\epsilon$ places emphasis on the average route reliability (resp. average route length), we observe that ${\overline{f}}_{\mathrm{p}}$ and ${\overline{f}}_{\mathrm{d}}$ of the proposed scheme decrease with increase in $\epsilon$. We observe that $\epsilon =0.05$ is one of the appropriate parameter settings in terms of both speedy and reliable evacuation. In particular, the proposed scheme can improve ${\overline{f}}_{\mathrm{p}}$ by 13.6% with 7.3% increase of ${\overline{f}}_{\mathrm{d}}$, compared with the distance-based scheme. In what follows, we set $\epsilon$ to be 0.05. In actual cases, the value of $\epsilon$ may also be affected by other factors, e.g., political judgment.

Next, we focus on the obtained refuge assignment. Figure 5 and Figure 6 illustrate the refuge assignment of the distance-based scheme and that of the proposed scheme, respectively. Recall that the orange area in Figure 2 contains the roads with high road blockage probability, i.e., the average road blockage probability in this area is 0.278. In the orange area of Figure 5, some evacuees assigned to $S_3$ are forced to pass through the area with high road blockage probability. Comparing the orange areas in Figure 5 and Figure 6, we confirm that the proposed scheme can reduce such unsafe evacuation by assigning them to $S_1$.

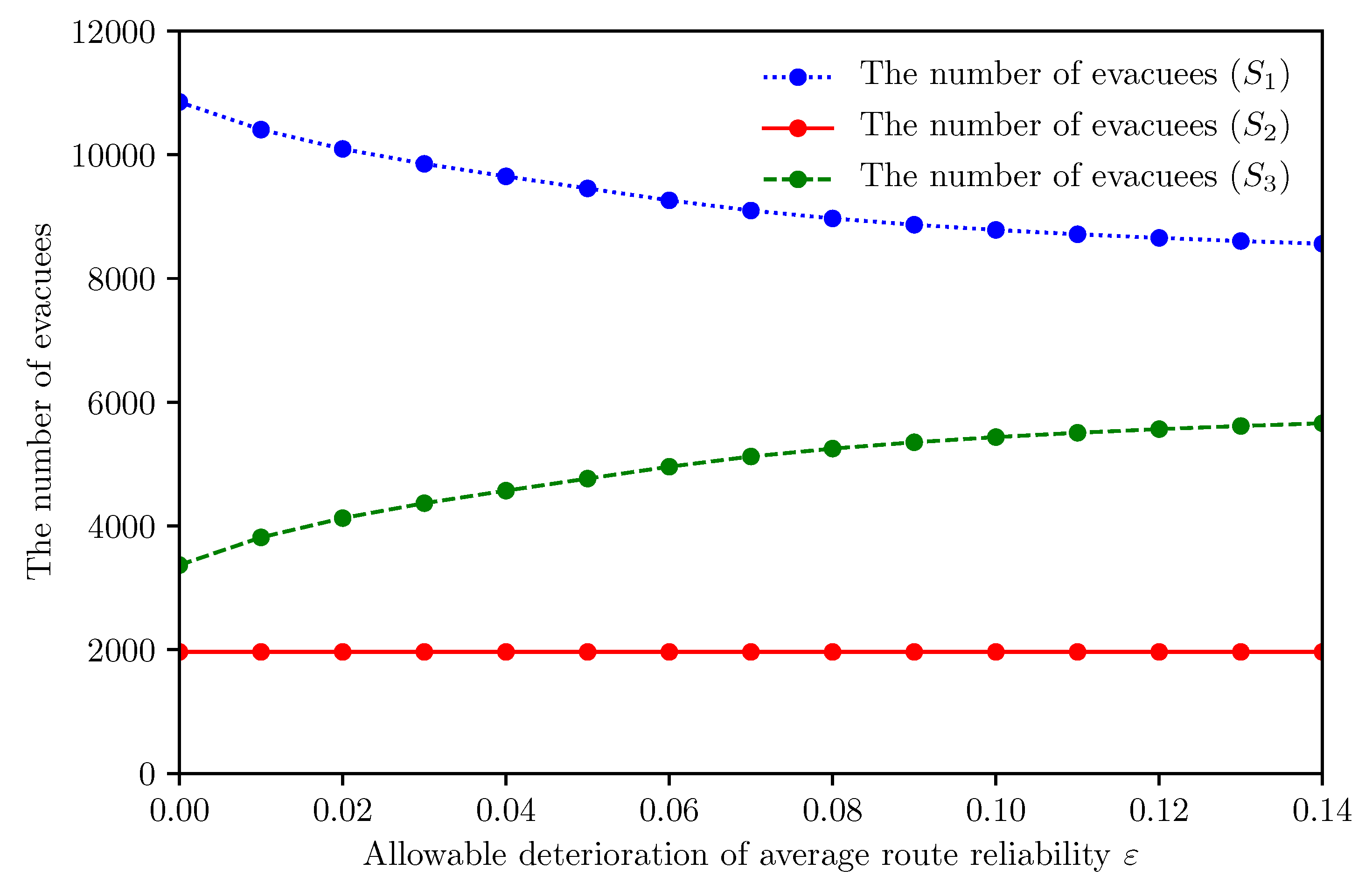
To deeply analyze the characteristics of the proposed scheme, we further show the detailed results per refuge. Figure 7, Figure 8 and Figure 9 illustrate how $\epsilon$ affects the number of allocated evacuees, ${\overline{f}}_{\mathrm{d}}$, and ${\overline{f}}_{\mathrm{p}}$, per refuge, respectively. We first focus on refuge $S_2$. We observe that ${\overline{f}}_{\mathrm{d}}$ decreases with $\epsilon$ while keeping the number of allocated evacuees, due to the capacity limit (6). Specifically, we confirm that ${\overline{f}}_{\mathrm{d}}$ of $S_2$ can improve by 35.9%, i.e., 392.0 [$\mathrm{m}$], by comparing the result of $\epsilon =0$ with that of $\epsilon =0.05$. This result means that evacuees near refuge $S_2$ are assigned to $S_2$ by the relaxation of the constraint (8). On the contrary, we observe that ${\overline{f}}_{\mathrm{p}}$ of $S_2$ increases with $\epsilon$, which indicates that part of evacuees cannot be assigned to their appropriate refuges, due to the capacity limit (6) in case of $\epsilon =0$. We will describe the details of this result in Section 4.3.

Finally, we focus on refuges $S_1$ and $S_3$. We confirm that ${\overline{f}}_{\mathrm{d}}$ of $S_1$ and the number of allocated evacuees of $S_1$ decrease with $\epsilon$. This phenomenon can be explained as follows. At first, evacuees distant from $S_1$ are assigned to $S_1$ in case of $\epsilon =0$, to improve the average route reliability. By increasing $\epsilon$, these evacuees can be assigned to nearer refuges, $S_2$ and $S_3$, but most of them can only be assigned to the refuge $S_3$, due to the limited capacity of $S_2$. As a result, the number of evacuees allocated to $S_3$ increases with $\epsilon$. This forces some of them to pass through the area with high road blockage probability, and thus ${\overline{f}}_{\mathrm{p}}$ of $S_3$ decreases with $\epsilon$.

4.3. Impact of Capacity Limit on Speedy and Reliable Evacuation

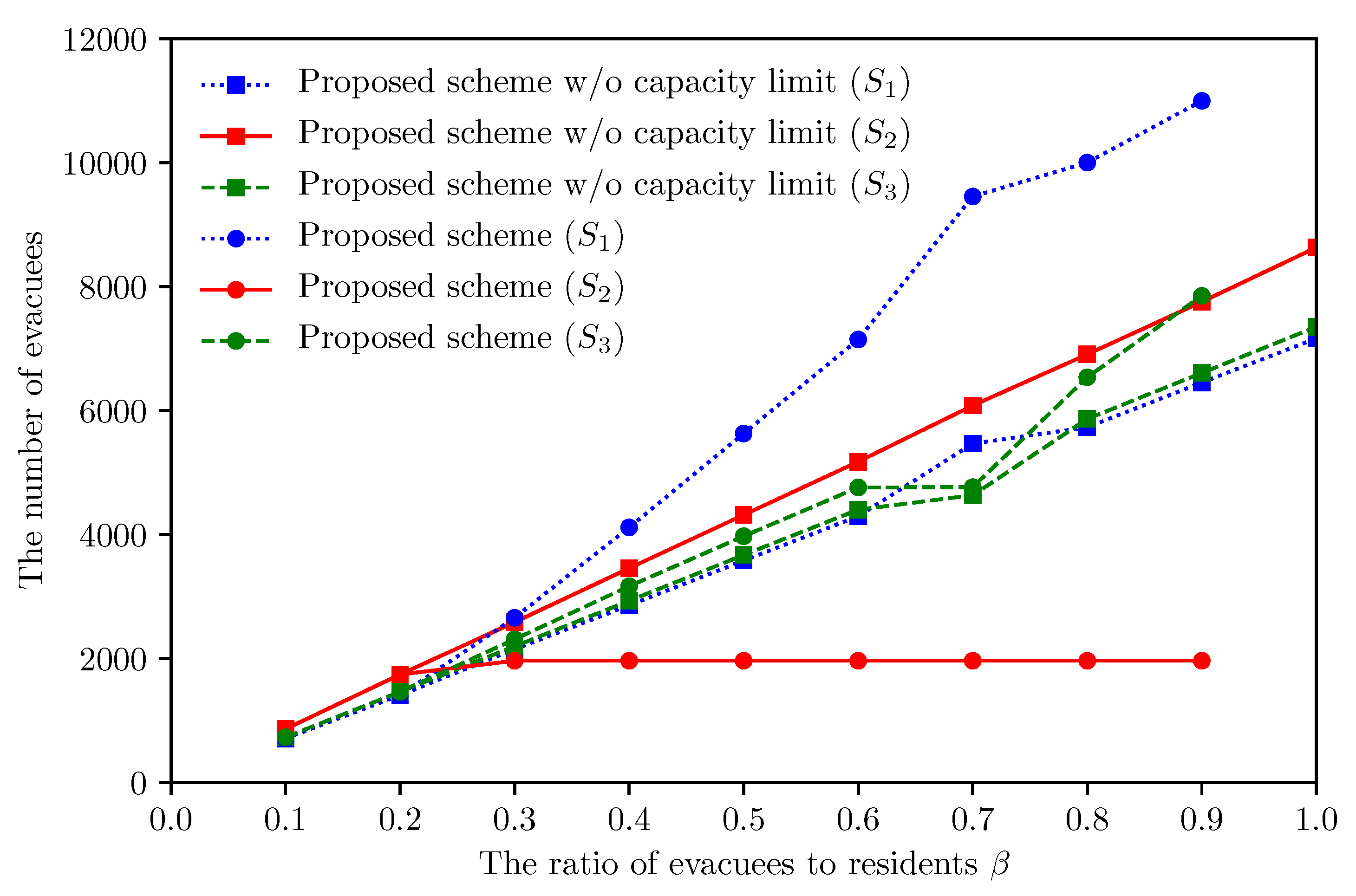
In this subsection, we examine the appropriate design for the refuge capacity by comparing the proposed scheme and that without the capacity constraint, which can be regarded as an ideal case.

Figure 10 presents the refuge assignment of the proposed scheme without the capacity constraint when $\beta =0.7$. Comparing Figure 6 with Figure 10, we first confirm that the proposed scheme without the capacity constraint assigns more evacuees to refuge $S_2$. This result indicates that the demand for the refuge $S_2$ significantly exceeds the current refuge capacity $C_{S_2}$.

Figure 11 illustrates how the impact of $\beta$ on ${\overline{f}}_{\mathrm{d}}$ and ${\overline{f}}_{\mathrm{p}}$ changes between the proposed scheme and that without the capacity constraint. Figure 12 shows the corresponding result per refuge. We observe that the proposed scheme increases ${\overline{f}}_{\mathrm{d}}$ by 6.5% compared with the proposed scheme without (6) when $\beta =0.7$. This is because the capacity of refuge $S_2$ lacks 4118 of the actual demand as shown in Figure 12. In the proposed scheme, the overflow evacuees tend to be assigned to $S_1$, which has sufficient capacity and is located at relatively safe region. In Figure 11, we also confirm that the proposed scheme keeps ${\overline{f}}_{\mathrm{p}}$ regardless of $\beta$, compared with the proposed scheme without the capacity constraint.

These results indicate that the current setting for refuge capacity should be reconsidered especially for refuge $S_2$. In other words, the proposed scheme can be used to a tool to calculate the required capacity of each refuge for speedy and reliable evacuation.

4.4. Discussion

At the last of this section, we briefly discuss the limit of the proposed scheme from the viewpoint of implementation in real-world context. The refuge assignment based on the proposed scheme should be announced/advertised to evacuees before their evacuations. We expect that the cooperation with the mobile-cloud collaborative automatic evacuation guiding system [19] is one possible way. In this system, the mobile application of an evacuee can automatically estimate the actual road state (i.e., passable or blocked) during the evacuation, with the help of the implicit interactions with its owner. The estimated information will be shared with other mobile devices (evacuees) and cloud through the terrestrial communication networks (e.g., cellular networks and Wi-Fi) and/or D2D communication. These dynamically obtained information can be used to update the refuge assignment.

5. Conclusions

When a large-scale disaster occurs, each evacuee should move to an appropriate refuge in a speedy and safe manner. This can be achieved by the combination of both pre-disaster and post-disaster approaches. In this paper, we have considered an earthquake case study and proposed a refuge assignment scheme that can support speedy and reliable evacuation under the refuge capacity constraint. Given route candidates between evacuees and their possible refuges, we have first formulated the refuge assignment problem as the two-step ILP, which minimizes the average route length while guaranteeing a certain level of the average route reliability under the constraint on the refuge capacity. As for the route candidates, we have further proposed a speedy and reliable route selection scheme that generates the input of the two-step ILP, i.e., route candidates between evacuees and their possible refuges.

Through numerical results using the actual data of Arako district of Nagoya city in Japan, representative results have shown that (1) the proposed scheme can control the balance between the evacuation speediness and reliability under the refuge capacity constraint by adjusting a control parameter and (2) the proposed scheme with the appropriate parameter setting can improve the average route reliability by 13.6% while suppressing the increase of the average route length by 7.3%, compared with the distance-based scheme. In addition, we have also revealed that the proposed scheme can be used as a tool to reconsider the current settings for the refuge capacity. In particular, we have demonstrated that the capacity of a certain refuge lacks 4,118 of the actual demands, which increases the average route length by 6.5%.

In future work, we plan to conduct a comprehensive survey of the potential risks in other districts of Nagoya city.