GIS-Based Mapping of Seismic Parameters for the Pyrenees
Abstract
:1. Introduction
2. Study Area
2.1. Geological Settings
- The North Pyrenean Zone (NPZ), which was mainly formed by Mesozoic (Cretaceous) deposits, rides northward over the Aquitaine basin along with the North Pyrenean Frontal Trust (NPFT). The NPZ contains Paleozoic outcrops.
- The Paleozoic Axial Zone, which is located at the central part and presents the highest peaks of the Pyrenees, is composed of Hercynian structures that were reactivated during the Alpine orogeny.
- The South Pyrenean Zone (SPZ), which slid southward down from the Axial zone when it rose, presents Mesozoic (Cretaceous) and Cenozoic (Oligocene) sediments in its composition.
2.2. Seismicity
2.3. Related Works on the Pyrenees Seismicity
3. Data and Methods
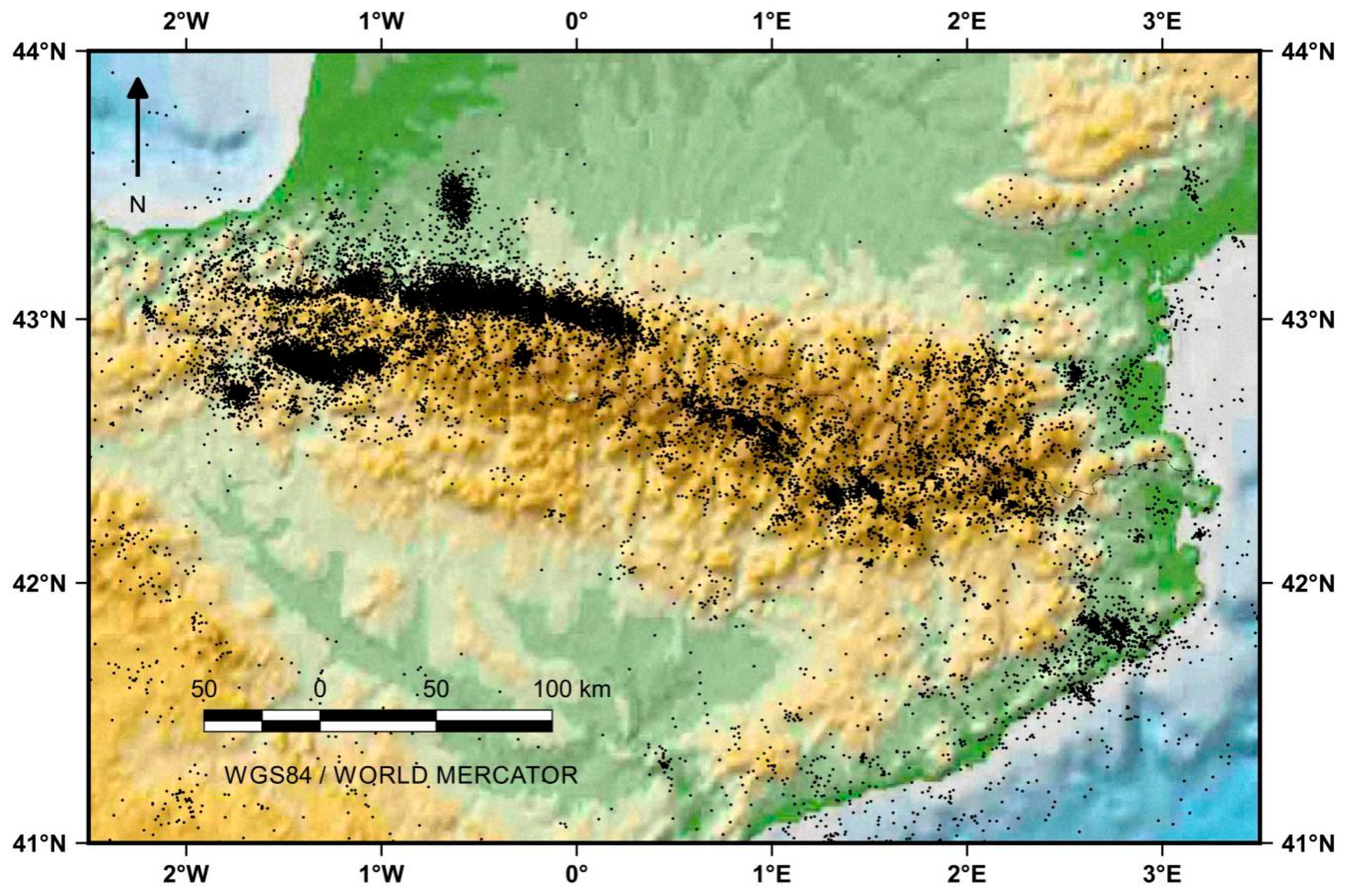
3.1. Catalog generation
3.1.1. The National Geographic Institute of Spain Earthquake Catalog
3.1.2. Review from Other Catalogs and Specific Studies
3.1.3. Magnitude Homogenization and Cut-off Magnitude
- Epicentral or maximum intensity (until 1923) (0.5 ≤ σ ≤ 1.5).
- Pre-instrumental 1924–February 1962: Duration magnitude [68], mD(MMS) (σ = 0.4).
- March 1962–February 1998: Surface–wave magnitude [68], mbLg(MMS) (σ = 0.3) (<1985); (σ = 0.2) (>1985).
- March 1998–2002: Body–wave magnitude [69], mb(VC) (σ = 0.2) and mbLg(MMS) (σ = 0.2).
- March 2002–onward: Surface–wave magnitude [70], mbLg(L) (σ = 0.2) or mb(VC) (σ = 0.2), or, for the most significant events, Mw (σ = 0.1).
3.1.4. Declustering
3.1.5. Year of Completeness
3.1.6. Seismic Catalog of the Work
3.2. Seismic Parameters
3.2.1. The Maximum Magnitude
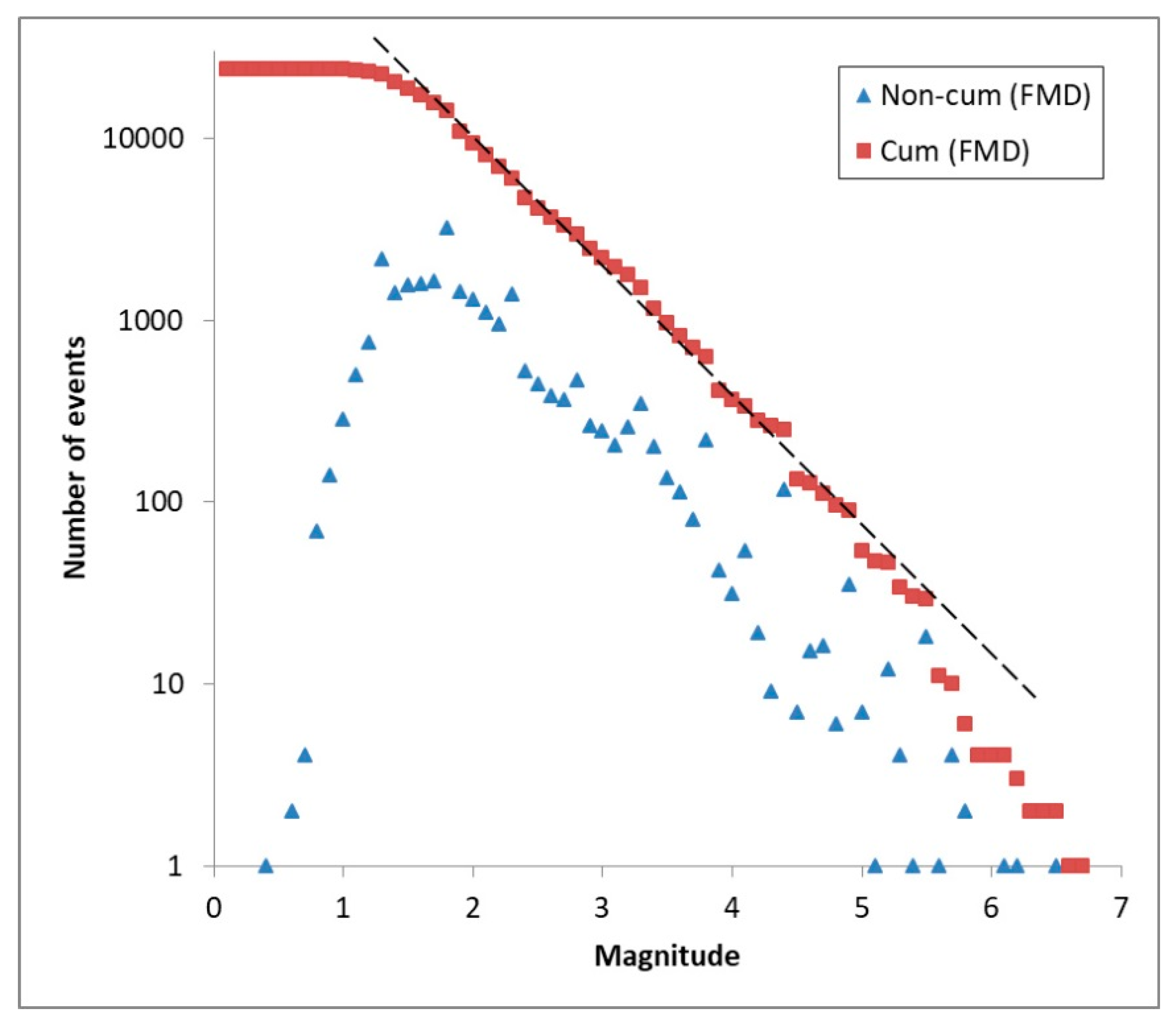
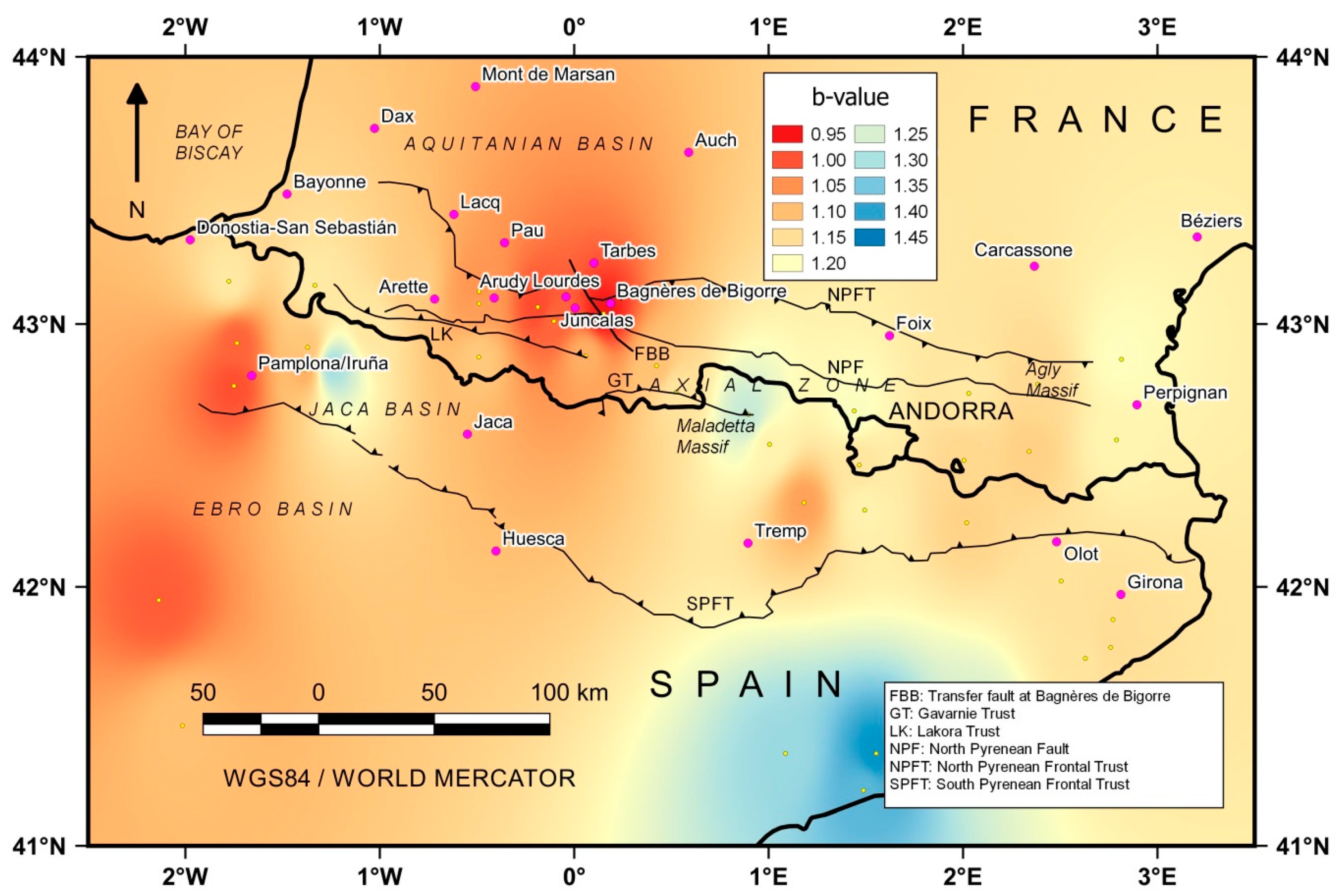
3.2.2. The b-value
3.2.3. The Annual Rate (Normalized)
4. Results and Discussion
4.1. The Maximum Magnitude
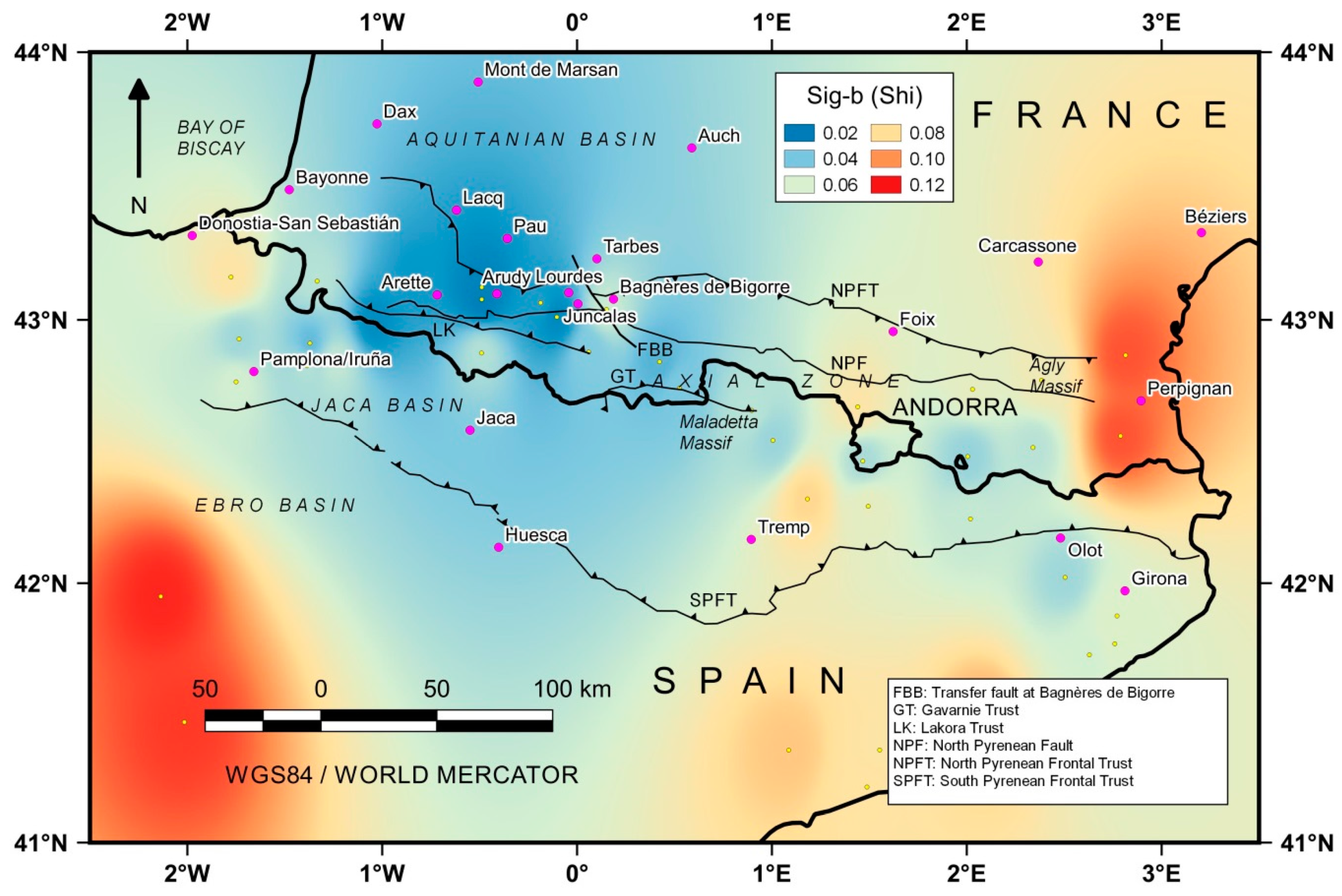
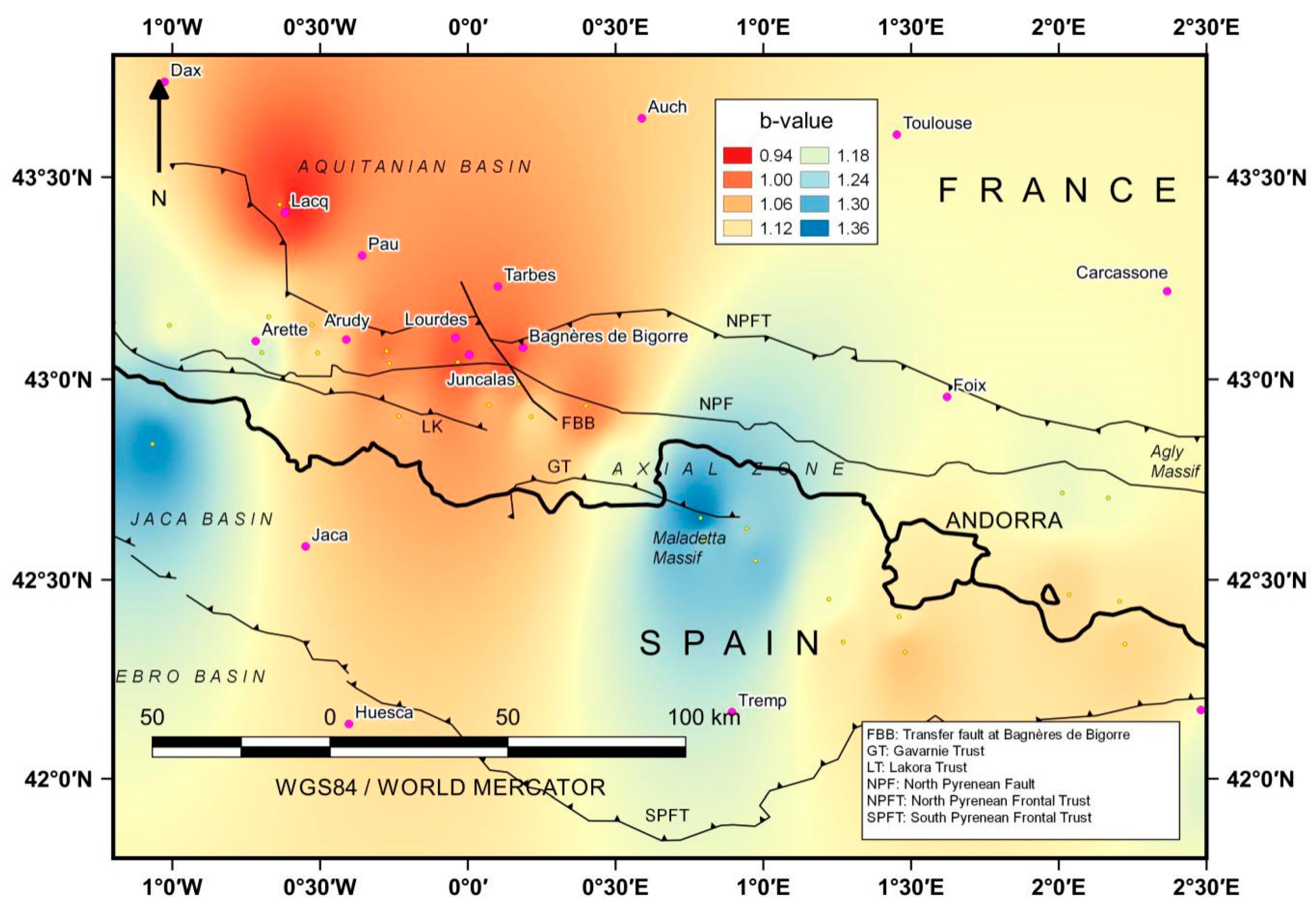
4.2. The b-value
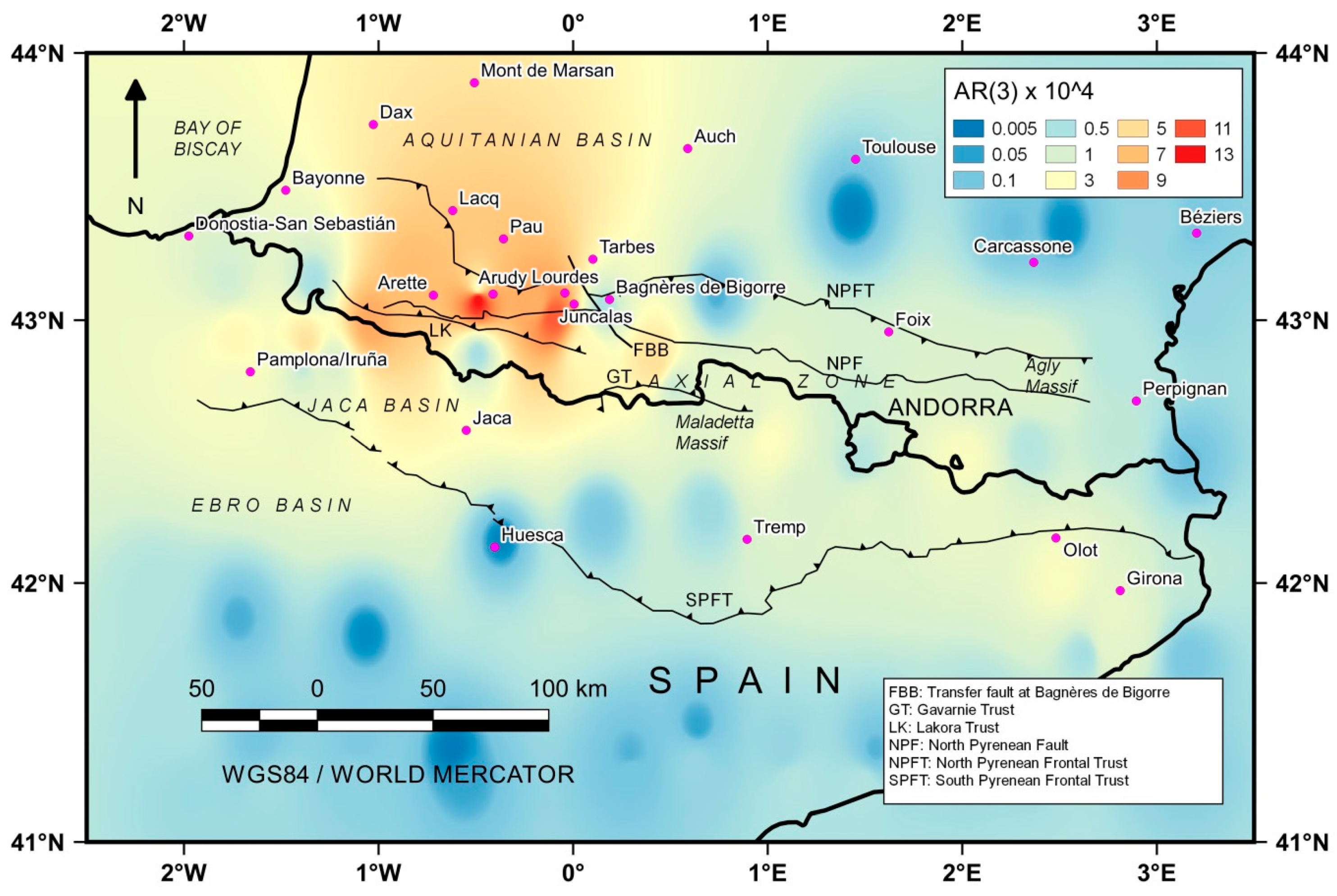
4.3. The Annual Rate (Normalized)
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mezcua, J.; Rueda, J.; García Blanco, R.M. A new probabilistic seismic hazard study of Spain. Nat. Hazards 2011, 59, 1087–1108. [Google Scholar] [CrossRef]
- IGN-UPM-Working Group. Actualización de Mapas de Peligrosidad Sísmica 2012; Instituto Geográfico Nacional: Madrid, Spain, 2013; ISBN 9788441626850.
- Hamdache, M.; Peláez, J.A.; Kijko, A.; Smit, A.; Sawires, R. Seismic Hazard Parameters of Main Seismogenic Source Zone Model in the Algeria-Morocco Region. In Proceedings of the Geo-Risks in the Mediterranean and their Mitigation, Valletta, Malta, 20–21 July 2015; pp. 99–101. [Google Scholar]
- Hamdache, M.; Peláez, J.A.; Kijko, A.; Smit, A. Energetic and spatial characterization of seismicity in the Algeria–Morocco region. Nat. Hazards 2017, 86, 273–293. [Google Scholar] [CrossRef] [Green Version]
- Hong, T.-K.; Park, S.; Lee, J.; Kim, W. Spatiotemporal Seismicity Evolution and Seismic Hazard Potentials in the Western East Sea (Sea of Japan). Pure Appl. Geophys. 2020, 1–14. [Google Scholar] [CrossRef]
- Amaro-Mellado, J.L.; Morales-Esteban, A.; Asencio-Cortés, G.; Martínez-Álvarez, F. Comparing seismic parameters for different source zone models in the Iberian Peninsula. Tectonophysics 2017, 717, 449–472. [Google Scholar] [CrossRef]
- Amaro-Mellado, J.L.; Morales-Esteban, A.; Martínez-Álvarez, F. Mapping of seismic parameters of the Iberian Peninsula by means of a geographic information system. Cent. Eur. J. Oper. Res. 2018, 26, 739–758. [Google Scholar] [CrossRef]
- Hossain, B.; Hossain, S.S. Probabilistic estimation of seismic parameters for Bangladesh. Arab. J. Geosci. 2020, 13. [Google Scholar] [CrossRef]
- Popandopoulos, G.A.; Chatziioannou, E. Gutenberg-Richter Law Parameters Analysis Using the Hellenic Unified Seismic Network Data Through FastBee Technique. Earth Sci. 2014, 3, 122. [Google Scholar] [CrossRef]
- Sawires, R.; Santoyo, M.A.; Peláez, J.A.; Corona Fernández, R.D. An updated and unified earthquake catalog from 1787 to 2018 for seismic hazard assessment studies in Mexico. Sci. data 2019, 6, 241. [Google Scholar] [CrossRef] [Green Version]
- Mousavi, S.M. Mapping seismic moment and b-value within the continental-collision orogenic-belt region of the Iranian Plateau. J. Geodyn. 2017, 103, 26–41. [Google Scholar] [CrossRef]
- Beirlant, J.; Kijko, A.; Reynkens, T.; Einmahl, J.H.J. Estimating the maximum possible earthquake magnitude using extreme value methodology: The Groningen case. Nat. Hazards 2019, 98, 1091–1113. [Google Scholar] [CrossRef] [Green Version]
- Kijko, A.; Smit, A. Extension of the Aki-Utsu b-Value Estimator for Incomplete Catalogs. Bull. Seismol. Soc. Am. 2012, 102, 1283–1287. [Google Scholar] [CrossRef] [Green Version]
- Ghosh, A.; Newman, A.V.; Thomas, A.M.; Farmer, G.T. Interface locking along the subduction megathrust from b-value mapping near Nicoya Peninsula, Costa Rica. Geophys. Res. Lett. 2008, 35, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Mapa_Sismotectónico_WG. Análisis Sismotectónico de la Península Ibérica, Baleares y Canarias; Instituto Geográfico Nacional: Madrid, Spain, 1992; Volume 26.
- Deligiannakis, G.; Papanikolaou, I.D.; Roberts, G. Fault specific GIS based seismic hazard maps for the Attica region, Greece. Geomorphology 2018, 306, 264–282. [Google Scholar] [CrossRef] [Green Version]
- De Donatis, M.; Pappafico, G.; Romeo, R. A Field Data Acquisition Method and Tools for Hazard Evaluation of Earthquake-Induced Landslides with Open Source Mobile GIS. ISPRS Int. J. Geo-Information 2019, 8, 91. [Google Scholar] [CrossRef] [Green Version]
- Tien Bui, D.; Shahabi, H.; Omidvar, E.; Shirzadi, A.; Geertsema, M.; Clague, J.; Khosravi, K.; Pradhan, B.; Pham, B.; Chapi, K.; et al. Shallow Landslide Prediction Using a Novel Hybrid Functional Machine Learning Algorithm. Remote Sens. 2019, 11, 931. [Google Scholar] [CrossRef] [Green Version]
- Naegeli, T.J.; Laura, J. Back-projecting secondary craters using a cone of uncertainty. Comput. Geosci. 2019, 123, 1–9. [Google Scholar] [CrossRef]
- Gutenberg, B.; Richter, C.F. Seismicity of the Earth; Princeton University: Princeton, NJ, USA, 1954. [Google Scholar]
- Udías, A.; Mezcua, J. Fundamentos de Geofísica; Alianza Universidad Textos; Alianza Editorial: Madrid, Spain, 1997. [Google Scholar]
- Hiemer, S.; Woessner, J.; Basili, R.; Danciu, L.; Giardini, D.; Wiemer, S. A smoothed stochastic earthquake rate model considering seismicity and fault moment release for Europe. Geophys. J. Int. 2014, 198, 1159–1172. [Google Scholar] [CrossRef] [Green Version]
- Frohlich, C.; Davis, S.D. Teleseismic b values; Or, much ado about 1.0. J. Geophys. Res. 1993, 98, 631–644. [Google Scholar] [CrossRef]
- Nava, F.A.; Ávila-Barrientos, L.; Márquez-Ramírez, V.H.; Torres, I.; Zúñiga, F.R. Sampling uncertainties and source b likelihood for the Gutenberg-Richter b value from the Aki-Utsu method. J. Seismol. 2018, 22, 315–324. [Google Scholar] [CrossRef]
- Tormann, T.; Wiemer, S.; Mignan, A. Systematic survey of high-resolution b value imaging along Californian faults: Inference on asperities. J. Geophys. Res. Solid Earth 2014, 119, 2029–2054. [Google Scholar] [CrossRef]
- Morales-Esteban, A.; Martínez-Álvarez, F.; Reyes, J. Earthquake prediction in seismogenic areas of the Iberian Peninsula based on computational intelligence. Tectonophysics 2013, 593, 121–134. [Google Scholar] [CrossRef]
- Rigo, A.; Souriau, A.; Sylvander, M. Spatial variations of b-value and crustal stress in the Pyrenees. J. Seismol. 2018, 22, 337–352. [Google Scholar] [CrossRef]
- Amorèse, D.; Grasso, J.R.; Rydelek, P.A. On varying b-values with depth: Results from computer-intensive tests for Southern California. Geophys. J. Int. 2010, 180, 347–360. [Google Scholar] [CrossRef] [Green Version]
- Pandey, A.K.; Chingtham, P.; Roy, P.N.S. Homogeneous earthquake catalogue for Northeast region of India using robust statistical approaches. Geomatics, Nat. Hazards Risk 2017, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Haque, D.M.E.; Chowdhury, S.H.; Khan, N.W. Intensity Attenuation Model Evaluation for Bangladesh with Respect to the Surrounding Potential Seismotectonic Regimes. Pure Appl. Geophys. 2020, 177, 157–179. [Google Scholar] [CrossRef]
- Waseem, M.; Khan, S.; Asif Khan, M. Probabilistic Seismic Hazard Assessment of Pakistan Territory Using an Areal Source Model. Pure Appl. Geophys. 2020. [Google Scholar] [CrossRef]
- Peláez, J.A.; Chourak, M.; Tadili, B.A.; Aït Brahim, L.; Hamdache, M.; López Casado, C.; Martínez Solares, J.M. A catalog of main Moroccan earthquakes from 1045 to 2005. Seismol. Res. Lett. 2007, 78, 614–621. [Google Scholar] [CrossRef]
- Hamdache, M.; Pelaez, J.A.; Talbi, A.; Casado, C.L. A Unified Catalog of Main Earthquakes for Northern Algeria from A.D. 856 to 2008. Seismol. Res. Lett. 2010, 81, 732–739. [Google Scholar] [CrossRef] [Green Version]
- Zare, M.; Amini, H.; Yazdi, P.; Sesetyan, K.; Demircioglu, M.B.; Kalafat, D.; Erdik, M.; Giardini, D.; Khan, M.A.; Tsereteli, N. Recent developments of the Middle East catalog. J. Seismol. 2014, 18, 749–772. [Google Scholar] [CrossRef]
- Das, R.; Sharma, M.L.; Wason, H.R.; Choudhury, D.; Gonzalez, G. A seismic moment magnitude scale. Bull. Seismol. Soc. Am. 2019, 109, 1542–1555. [Google Scholar] [CrossRef]
- Cabañas, L.; Rivas-Medina, A.; Martínez-Solares, J.M.; Gaspar-Escribano, J.M.; Benito, B.; Antón, R.; Ruiz-Barajas, S. Relationships Between M w and Other Earthquake Size Parameters in the Spanish IGN Seismic Catalog. Pure Appl. Geophys. 2015, 172, 2397–2410. [Google Scholar] [CrossRef]
- Scordilis, E.M. Empirical Global Relations Converting MS and mb to Moment Magnitude. J. Seismol. 2006, 10, 225–236. [Google Scholar] [CrossRef]
- Njike-Kassala, J.-D.; Souriau, A.; Gagnepain-Beyneix, J.; Martel, L.; Vadell, M. Frequency-magnitude relationship and Poisson’s ratio in the Pyrenees, in relation to earthquake distribution. Tectonophysics 1992, 215, 363–369. [Google Scholar] [CrossRef]
- Rigo, A.; Pauchet, H.; Souriau, A.; Grésillaud, A.; Nicolas, M.; Olivera, C.; Figueras, S. The February 1996 earthquake sequence in the eastern Pyrenees: First results. J. Seismol. 1997, 1, 3–14. [Google Scholar] [CrossRef]
- Vissers, R.L.M.; Meijer, P.T. Iberian plate kinematics and Alpine collision in the Pyrenees. Earth-Science Rev. 2012, 114, 61–83. [Google Scholar] [CrossRef]
- Lacan, P.; Ortuño, M. Active Tectonics of the Pyrenees: A review. J. Iber. Geol. 2012, 38, 9–30. [Google Scholar] [CrossRef] [Green Version]
- Singh, C. Spatial variation of seismic b-values across the NW Himalaya. Geomat. Nat. Hazards Risk 2016, 7, 522–530. [Google Scholar] [CrossRef]
- Souriau, A.; Rigo, A.; Sylvander, M.; Benahmed, S.; Grimaud, F. Seismicity in central-western Pyrenees (France): A consequence of the subsidence of dense exhumed bodies. Tectonophysics 2014, 621, 123–131. [Google Scholar] [CrossRef]
- Teixell, A.; Labaume, P.; Lagabrielle, Y. The crustal evolution of the west-central Pyrenees revisited: Inferences from a new kinematic scenario. Comptes Rendus-Geosci. 2016, 348, 257–267. [Google Scholar] [CrossRef] [Green Version]
- Roigé, M.; Gómez-Gras, D.; Remacha, E.; Daza, R.; Boya, S. Tectonic control on sediment sources in the Jaca basin (Middle and Upper Eocene of the South-Central Pyrenees). Comptes Rendus-Geosci. 2016, 348, 236–245. [Google Scholar] [CrossRef]
- Baize, S.; Cushing, E.M.; Lemeille, F.; Jomard, H. Updated seismotectonic zoning scheme of Metropolitan France, with reference to geologic and seismotectonic data. Bull. la Soc. Geol. Fr. 2013, 184, 225–259. [Google Scholar] [CrossRef]
- Olivera, C.; Redondo, E.; Lambert, J.; Riera-Melis, A.; Roca, A. Els terratrèmols de segles XIV i XV a Catalunya; Institut Cartogràfic de Catalunya: Barcelona, Spain, 2006; ISBN 8439369611. [Google Scholar]
- Insitituto Geográfico Nacional Terremotos más Importantes. Available online: https://www.ign.es/web/ign/portal/terremotos-importantes (accessed on 29 April 2020).
- Perea, H. The Catalan seismic crisis (1427 and 1428; NE Iberian Peninsula): Geological sources and earthquake triggering. J. Geodyn. 2009, 47, 259–270. [Google Scholar] [CrossRef] [Green Version]
- Honoré, L.; Courboulex, F.; Souriau, A. Ground motion simulations of a major historical earthquake (1660) in the French Pyrenees using recent moderate size earthquakes. Geophys. J. Int. 2011, 187, 1001–1018. [Google Scholar] [CrossRef] [Green Version]
- Cara, M.; Alasset, P.J.; Sira, C. Magnitude of Historical Earthquakes, from Macroseismic Data to Seismic Waveform Modelling: Application to the Pyrenees and a 1905 Earthquake in the Alps. In Historical Seismology. Modern Approaches in Solid Earth Sciences; Fréchet, J., Meghraoui, M., Stucchi, M., Eds.; Springer: Cham, Switzerland, 2008; Volume 2, pp. 369–384. [Google Scholar]
- Rigo, A.; Massonnet, D. Investigating the 1996 Pyrenean Earthquake (France) with SAR interferograms heavily distorted by atmosphere. Geophys. Res. Lett. 1999, 26, 3217–3220. [Google Scholar] [CrossRef]
- Ministerio de Fomento (Gobierno de España). Norma de la Construcción Sismorresistente Española (NCSE-02); Boletín Oficial del Estado: Madrid, Spain, 2002.
- Gallart, J.; Dainières, M.; Banda, E.; Suriñach, E.; Hirn, A. The eastern Pyrenean domain: Lateral variations at crust-mantle level. Ann. Geophys. 1980, 36, 141–158. [Google Scholar]
- Sylvander, M.; Souriau, A.; Rigo, A.; Tocheport, A.; Toutain, J.-P.; Ponsolles, C.; Benahmed, S. The 2006 November, M L = 5.0 earthquake near Lourdes (France): New evidence for NS extension across the Pyrenees. Geophys. J. Int. 2008, 175, 649–664. [Google Scholar] [CrossRef] [Green Version]
- Secanell, R.; Martin, C.; Goula, X.; Susagna, T.; Tapia, M.; Bertil, D. Evaluacion probabilista de la peligrosidad sísmica de la región pirenaica. In 3° Congreso Nacional de Ingeniería Sísmica; Asociación Española de Ingeniería Sísmica: Madrid, Spain, 2007; pp. 1–17. [Google Scholar]
- Secanell, R.; Bertil, D.; Martin, C.; Goula, X.; Susagna, T.; Tapia, M.; Dominique, P.; Carbon, D.; Fleta, J. Probabilistic seismic hazard assessment of the Pyrenean region. J. Seismol. 2008, 12, 323–341. [Google Scholar] [CrossRef]
- Rigo, A.; Vernant, P.; Feigl, K.L.; Goula, X.; Khazaradze, G.; Talaya, J.; Morel, L.; Nicolas, J.; Baize, S.; Chery, J.; et al. Present-day deformation of the Pyrenees revealed by GPS surveying and earthquake focal mechanisms until 2011. Geophys. J. Int. 2015, 201, 947–964. [Google Scholar] [CrossRef] [Green Version]
- Insitituto Geográfico Nacional Catálogo de Terremotos. Available online: http://www.ign.es/web/ign/portal/sis-catalogo-terremotos (accessed on 29 April 2020).
- González, Á. The Spanish National Earthquake Catalogue: Evolution, precision and completeness. J. Seismol. 2017, 21, 435–471. [Google Scholar] [CrossRef]
- Mezcua, J.; Rueda, J.; Blanco, R.M.G. Reevaluation of historic Earthquakes in Spain. Seismol. Res. Lett. 2004, 75, 75–81. [Google Scholar] [CrossRef]
- Martínez-Solares, J.M.; Mezcua, J. Catálogo Sísmico de la Península Ibérica (800 a. C.-1900); Instituto Geográfico Nacional: Madrid, Spain, 2002.
- Susagna, T.; Roca, A.; Goula1, X.; Batlló, J. Analysis of macroseismic and instrumental data for the study of the 19 November 1923 earthquake in the Aran Valley (Central Pyrenees). Nat. Hazards 1994, 10, 7–17. [Google Scholar] [CrossRef]
- Martín, R.; Stich, D.; Morales, J.; Mancilla, F. Moment tensor solutions for the Iberian-Maghreb region during the IberArray deployment (2009–2013). Tectonophysics 2015, 663, 261–274. [Google Scholar] [CrossRef] [Green Version]
- García-Mayordomo, J.; Insua-Arévalo, J.M. Seismic hazard assessment for the Itoiz dam site (Western Pyrenees, Spain). Soil Dyn. Earthq. Eng. 2011, 31, 1051–1063. [Google Scholar] [CrossRef]
- Stich, D.; Ammon, C.J.; Morales, J. Moment tensor solutions for small and moderate earthquakes in the Ibero-Maghreb region. J. Geophys. Res. Solid Earth 2003, 108. [Google Scholar] [CrossRef]
- Stich, D.; Martín, R.; Batlló, J.; Macià, R.; Mancilla, F.d.L.; Morales, J. Normal Faulting in the 1923 Berdún Earthquake and Postorogenic Extension in the Pyrenees. Geophys. Res. Lett. 2018, 45, 3026–3034. [Google Scholar] [CrossRef]
- Mezcua, J.; Martínez-Solares, J.M. Sismicidad del área Íbero-Magrebí; Instituto Geográfico Nacional: Madrid, Spain, 1983; Volume 203.
- Veith, K.F.; Clawson, G.E. Magnitude from short period P-wave data. Bull. Seismol. Soc. Am. 1972, 62, 435–452. [Google Scholar]
- López, C. Nuevas fórmulas de Magnitud para la Península Ibérica y su Entorno; Universidad Complutense de: Madrid, Spain, 2008. [Google Scholar]
- Das, R.; Wason, H.R.; Gonzalez, G.; Sharma, M.L.; Choudhury, D.; Lindholm, C.; Roy, N.; Salazar, P. Earthquake magnitude conversion problem. Bull. Seismol. Soc. Am. 2018, 108, 1995–2007. [Google Scholar] [CrossRef]
- Johnston, A.C. Seismic moment assessment of earthquakes in stable continental regions-I. Instrumental seismicity. Geophys. J. Int. 1996, 124, 381–414. [Google Scholar] [CrossRef]
- Johnston, A.C. Seismic moment assessment of earthquakes in stable continental regions-II. Historical seismicity. Geophys. J. Int. 1996, 125, 639–678. [Google Scholar] [CrossRef] [Green Version]
- Castellaro, S.; Mulargia, F.; Kagan, Y.Y. Regression problems for magnitudes. Geophys. J. Int. 2006, 165, 913–930. [Google Scholar] [CrossRef]
- Mignan, A.; Woessner, J. Estimating the Magnitude of Completeness for Earthquake Catalogs. CORSSA (Community Online Resource for Statistical Seismicity Analysis). 2012, pp. 1–45. Available online: https://tcs.ah-epos.eu/eprints/1587/ (accessed on 29 April 2020).
- Page, M.T.; van der Elst, N.; Hardebeck, J.; Felzer, K.; Michael, A.J. Three Ingredients for Improved Global Aftershock Forecasts: Tectonic Region, Time-Dependent Catalog Incompleteness, and Intersequence Variability. Bull. Seismol. Soc. Am. 2016, 106, 2290–2301. [Google Scholar] [CrossRef]
- Karimzadeh, S.; Matsuoka, M.; Kuang, J.; Ge, L. Spatial prediction of aftershocks triggered by a major earthquake: A binary machine learning perspective. ISPRS Int. J. Geo-Inf. 2019, 8, 462. [Google Scholar] [CrossRef] [Green Version]
- Gardner, J.K.; Knopoff, L. Is the sequence of earthquakes in Southern California, with aftershocks removed, Poissonian? Bull. Seismol. Soc. Am. 1974, 64, 1363–1367. [Google Scholar]
- Reasenberg, P. Second-order moment of Central California Seismicity, 1960–1982. J. Geophys. Res. 1985, 90, 5479–5495. [Google Scholar] [CrossRef]
- Van Stiphout, T.; Zhuang, J.; Marsan, D. Seismicity Declustering, Community Online Resource for Statistical Seismicity Analysis; ETH—Swiss Federal Institute of Technology: Zurich, Switzerland, 2012. [Google Scholar] [CrossRef]
- Khan, M.M.; Munaga, T.; Kiran, D.N.; Kumar, G.K. Seismic hazard curves for Warangal city in Peninsular India. Asian J. Civ. Eng. 2020, 21, 543–554. [Google Scholar] [CrossRef]
- Pandey, A.K.; Chingtham, P.; Prajapati, S.K.; Roy, P.N.S.; Gupta, A.K. Recent seismicity rate forecast for North East India: An approach based on rate state friction law. J. Asian Earth Sci. 2019, 174, 167–176. [Google Scholar] [CrossRef]
- Uhrhammer, R. Characteristics of Northern and Central California Seismicity. Earthq. Notes 1986, 57, 21. [Google Scholar]
- Khan, M.M.; Kalyan Kumar, G. Statistical Completeness Analysis of Seismic Data. J. Geol. Soc. India 2018, 91, 749–753. [Google Scholar] [CrossRef]
- Papadakis, G.; Vallianatos, F.; Sammonds, P. Evidence of Nonextensive Statistical Physics behavior of the Hellenic Subduction Zone seismicity. Tectonophysics 2013, 608, 1037–1048. [Google Scholar] [CrossRef]
- Wiemer, S. A Software Package to Analyze Seismicity: ZMAP. Seismol. Res. Lett. 2001, 72, 373–382. [Google Scholar] [CrossRef]
- Mulargia, F.; Tinti, S. Seismic sample areas defined from incomplete catalogues: An application to the Italian territory. Phys. Earth Planet. Int. 1985, 40, 273–300. [Google Scholar] [CrossRef]
- Tinti, S.; Mulargia, F. Confidence intervals of b values for grouped magnitudes. Bull. Seismol. Soc. Am. 1987, 77, 2125–2134. [Google Scholar]
- Wiemer, S.; Wyss, M. Minimum magnitude of completeness in earthquake catalogs: Examples from Alaska, the Western United States, and Japan. Bull. Seismol. Soc. Am. 2000, 90, 859–869. [Google Scholar] [CrossRef]
- Wesseloo, J. Addressing misconceptions regarding seismic hazard assessment in mines: B-value, Mmax, and space-time normalization. J. South. Afr. Inst. Min. Metall. 2020, 120, 67–80. [Google Scholar] [CrossRef] [Green Version]
- Kijko, A.; Singh, M. Statistical tools for maximum possible earthquake magnitude estimation. Acta Geophys. 2011, 59, 674–700. [Google Scholar] [CrossRef] [Green Version]
- Asim, K.M.; Moustafa, S.S.; Niaz, I.A.; Elawadi, E.A.; Iqbal, T.; Martínez-Álvarez, F. Seismicity analysis and machine learning models for short-term low magnitude seismic activity predictions in Cyprus. Soil Dyn. Earthq. Eng. 2020, 130, 105932. [Google Scholar] [CrossRef]
- Tan, Y.J.; Waldhauser, F.; Tolstoy, M.; Wilcock, W.S.D. Axial Seamount: Periodic tidal loading reveals stress dependence of the earthquake size distribution (b value). Earth Planet. Sci. Lett. 2019, 512, 39–45. [Google Scholar] [CrossRef] [Green Version]
- Arvanitakis, K.; Gounaropoulos, C.; Avlonitis, M. Locating Asperities by Means of Stochastic Analysis of Seismic Catalogs. Bull. Geol. Soc. Greece 2017, 50, 1293. [Google Scholar] [CrossRef] [Green Version]
- Martínez-Álvarez, F.; Reyes, J.; Morales-Esteban, A.; Rubio-Escudero, C. Determining the best set of seismicity indicators to predict earthquakes. Two case studies: Chile and the Iberian Peninsula. Knowl.-Based Syst. 2013, 50, 198–210. [Google Scholar] [CrossRef]
- Weitcher, D.H. Estimation of the earthquake recurrence parameters for unequal observation periods for different magnitudes. Bull. Seismol. Soc. Am. 1980, 70, 1337–1346. [Google Scholar]
- Kamer, Y.; Hiemer, S. Data-driven spatial b value estimation with applications to California seismicity: To b or not to b. J. Geophys. Res. Solid Earth 2015, 120, 5191–5214. [Google Scholar] [CrossRef]
- Bender, B. Maximum likelihood estimation of b values for magnitude grouped data. Bull. Seismol. Soc. Am. 1983, 73, 831–851. [Google Scholar]
- Aki, K. Maximum likelihood estimate of b in the formula logN = a-bM and its confidence limits. Bull. Earthq. Res. Inst. 1965, 43, 237–239. [Google Scholar]
- Utsu, T. A method for determining the value of b in a formula log n = a-bM showing the magnitude-frequency relation for earthquakes. Geophys. Bull. Hokkaido Univ. 1965, 13, 99–103. [Google Scholar]
- Ogata, Y.; Yamashina, K. Unbiased estimate for b-value of magnitude frequency. J. Phys. Earth 1986, 34, 187–194. [Google Scholar] [CrossRef] [Green Version]
- Shi, Y.; Bolt, B.A. The standard error of the magnitude-frequency b value. Bull. Seismol. Soc. Am. 1982, 72, 1677–1687. [Google Scholar]
- Dominique, P.; Andre, E. Probabilistic seismic hazard map on the French national territory. In Proceedings of the 12th World Conference on Earthquake Engineering, Auckland, New Zealand, 30 January–4 February 2000; pp. 1–8. [Google Scholar]
- Skordas, E.; Kulhánek, O. Spatial and temporal variations of Fennoscandian seismicity. Geophys. J. Int. 1992, 111, 577–588. [Google Scholar] [CrossRef] [Green Version]
- Roberts, N.S.; Bell, A.F.; Main, I.G. Are volcanic seismic b-values high, and if so when? J. Volcanol. Geotherm. Res. 2015, 308, 127–141. [Google Scholar] [CrossRef] [Green Version]
- Marzocchi, W.; Spassiani, I.; Stallone, A.; Taroni, M. How to be fooled searching for significant variations of the b-value. Geophys. J. Int. 2020, 220, 1845–1856. [Google Scholar] [CrossRef]
- Wiemer, S.; Wyss, M. Mapping spatial variability of the frequency-magnitude distribution of earthquakes. Adv. Geophys. 2002, 45, 259–302. [Google Scholar] [CrossRef]
- Bardainne, T.; Dubos-Sallée, N.; Sénéchal, G.; Gaillot, P.; Perroud, H. Analysis of the induced seismicity of the Lacq gas field (Southwestern France) and model of deformation. Geophys. J. Int. 2008, 172, 1151–1162. [Google Scholar] [CrossRef] [Green Version]


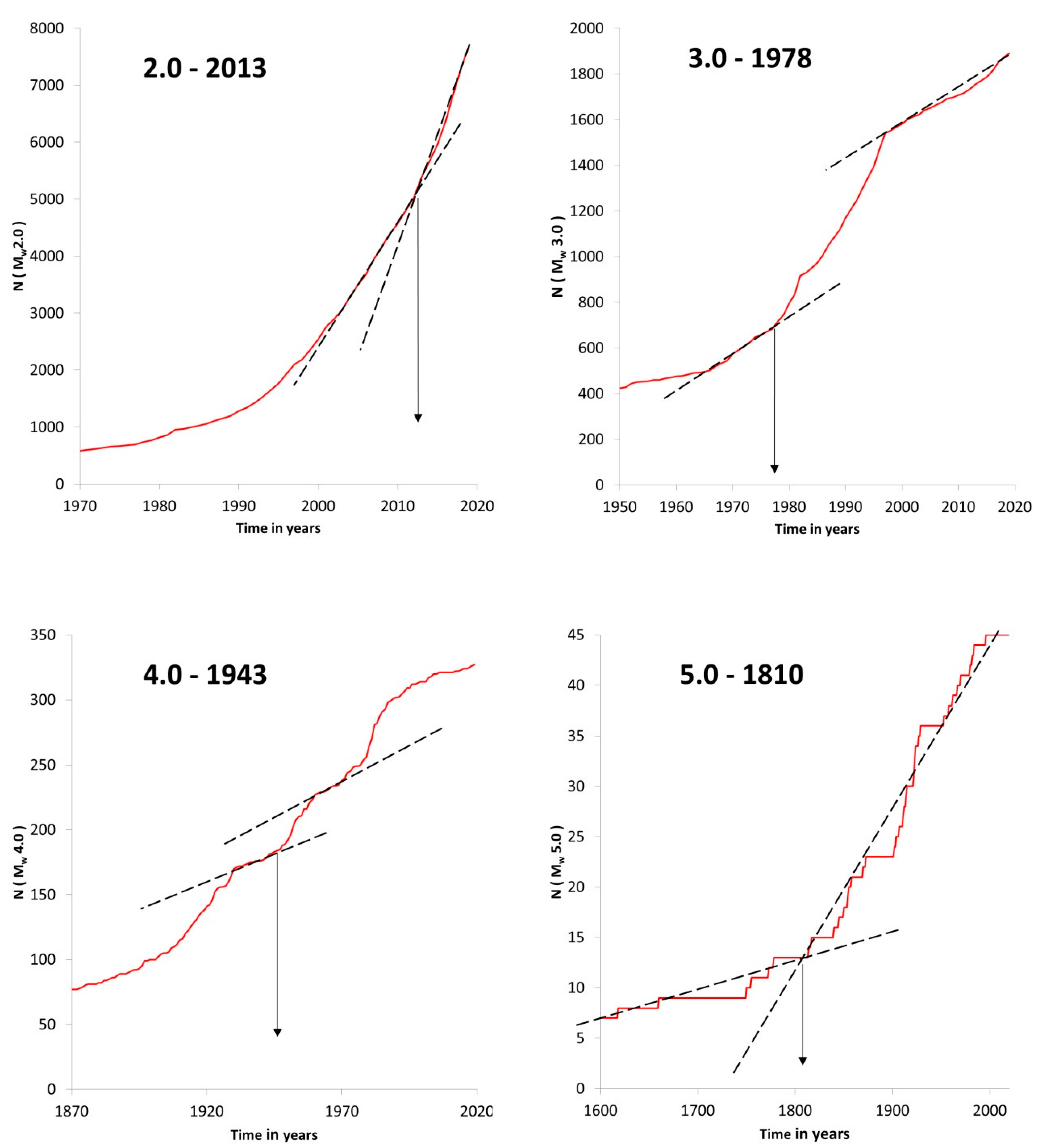


| Magnitude | Year |
|---|---|
| Mw ≥ 2.0 | 2013 |
| Mw ≥ 3.0 | 1978 |
| Mw ≥ 4.0 | 1943 |
| Mw ≥ 5.0 | 1810 |
| Magnitude | Year |
|---|---|
| Mw ≥ 2.0 | 2013–2019 |
| Mw ≥ 3.0 | 1978–2012 |
| Mw ≥ 4.0 | 1943–1977 |
| Mw ≥ 5.0 | 1810–1942 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amaro-Mellado, J.L.; Tien Bui, D. GIS-Based Mapping of Seismic Parameters for the Pyrenees. ISPRS Int. J. Geo-Inf. 2020, 9, 452. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi9070452
Amaro-Mellado JL, Tien Bui D. GIS-Based Mapping of Seismic Parameters for the Pyrenees. ISPRS International Journal of Geo-Information. 2020; 9(7):452. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi9070452
Chicago/Turabian StyleAmaro-Mellado, José Lázaro, and Dieu Tien Bui. 2020. "GIS-Based Mapping of Seismic Parameters for the Pyrenees" ISPRS International Journal of Geo-Information 9, no. 7: 452. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi9070452






