1. Introduction
Urban commutes using automobiles are important daily tasks for most city dwellers. The urban streets system is a vital network that connects places and people within and across urban areas. The urban street system can be effectively modeled as a network using graph theory, and the commutes become network-constrained movements [
1] with each section of the network responsible to move traffic towards the destination. Having information about the elements of the network with particular objectives is very important for planners and engineers. These objectives range from long-distance traveling to serving neighborhood travel to nearby shopping centers. The functional classification of roadways defines the role each element of the roadway network plays to accommodate user needs. The spatial configuration of the street network creates constraints on movement patterns through the network. The effect of the spatial configuration of the street network on traffic flow has been studied by several researchers [
2,
3,
4,
5,
6,
7]. However, in our work, the spatial configuration of the network is used to classify the functionality of individual streets.
The functional classification of streets defines the role each element of the urban street network (USN) plays in the urban transportation network. Streets are usually assigned to a functional class according to their characteristics and the type of service [
8] they provide. Streets help a user to access and egress from their current location toward their destination. Based on the street functionality concepts provided by the U.S. Department of Transportation (USDoT), those streets that provide a high level of mobility are called “Arterial”, those that provide a high level of accessibility are called “Local”, and those that are a balanced in term of mobility and accessibility are called “Collector”. Based on the aforementioned concepts related to street functional classification, the USNs are classified into two main groups of Arterial and Non-Arterial with Principal and Minor as sub-classes of the Arterial group, and Collector and Local street as a subclass of the Non-Arterial group.
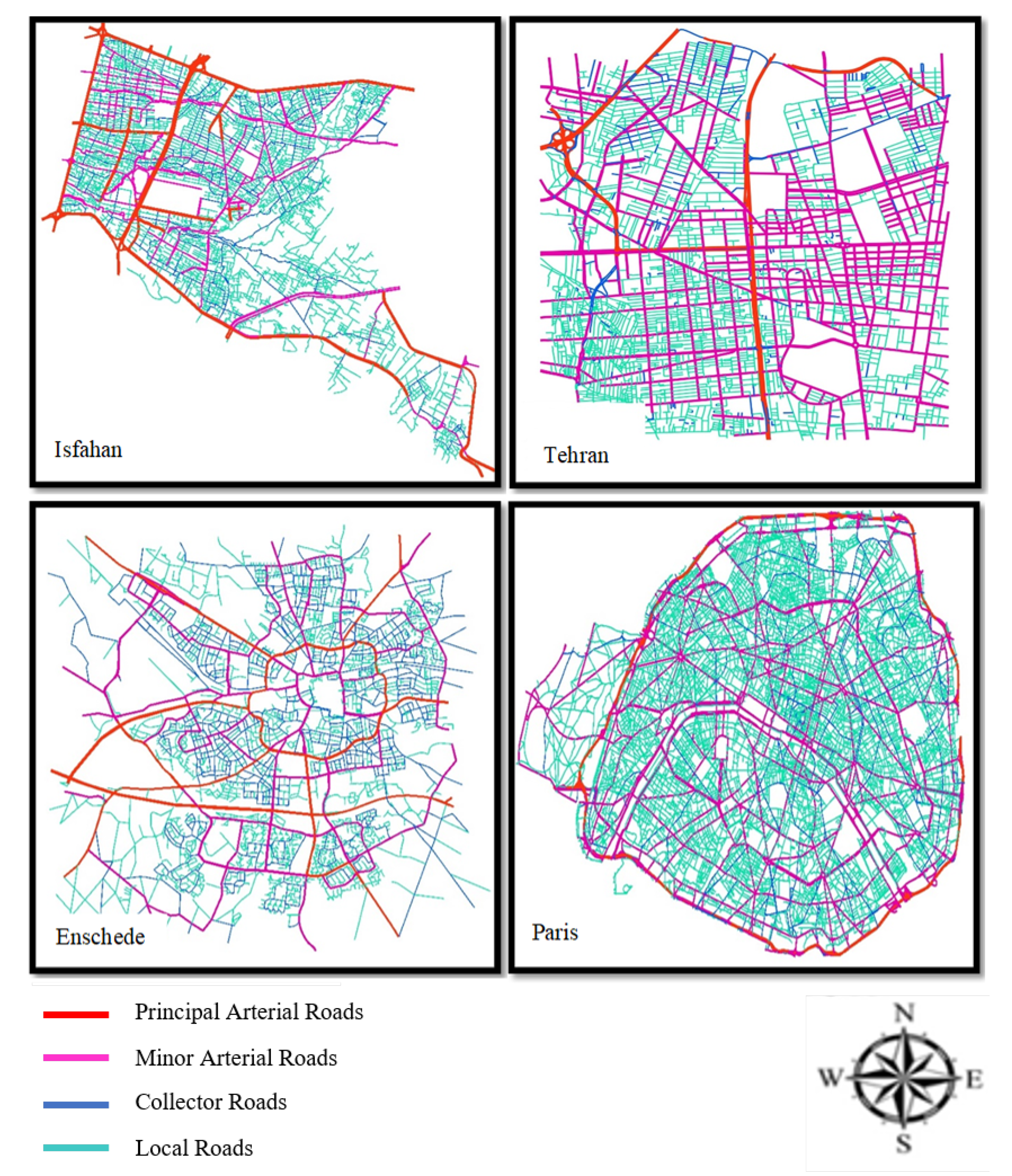
Figure 1 shows examples of several street networks categorized by functionality.
Street Functional Classification (SFC) has received additional significance beyond its purpose as a tool for identifying the particular role of streets in moving vehicles through USN. SFC has been used to describe roadway system performance, benchmarks, and targets by several transportation agencies. Aiming towards having a more performance-based approach for transportation agencies, SFC will be an increasingly important consideration in measuring outcomes mainly for preservation, mobility, and safety. So far, SFC has been achieved according to street rules and classified based on attributes such as mobility, access, trip length, speed limit, volume, annual average daily traffic (AADT), vehicle miles of travel (VMT), etc. However, evidence reveals that classification only based on the discussed elements is not enough, and streets cannot properly be classified. In many cases, assigning a functional class to a street is straightforward. However, deciding between adjacent classification is very challenging. For instance, deciding whether a given street acts as Minor Arterial or Collector can be subject to debate, because a street can be a Minor Arterial according to AADT and a collector based on VMT. Deciding between a Principal Arterial and Minor Arterial assignment can be even more challenging.
We suggest a new strategy for assigning SFC based on the spatial structure of streets and their roles in the network. Our research shows that the role of streets is more than moving the traffic. Streets are the basic skeleton of the transportation network, so describing the role of each street in the network is a significant concept. The spatial structure of streets in the network is a fundamental attribute of the network, but it has not received enough attention. The configuration of USN using semantic attributes has been analyzed [
3,
4,
5], with recent work analyzing USN using topological [
2] and geometrical attributes [
9]. The Functional Classification System (FCS) was developed in the 1970s as a basis for communication between designers and planners [
10,
11]. It is a common framework for classifying roadways based on mobility and access [
12,
13,
14,
15]. The application of the FCS has expanded, and it is now used throughout the entire project development process and influences all transportation project development phases, from programming and planning through design and into maintenance and operation decisions [
16,
17,
18,
19].
Centrality [
2] is one of the most important concepts in social network analysis; it describes spatial structural properties of nodes (streets) in a network. Several measures have been developed such as betweenness, closeness, degree centrality, eigenvector centrality, information centrality, flow betweenness, and the rush index [
2]. Centrality measures have been considered individually [
7,
20], primarily on how they affect traffic flow. Simple statistical regression and traditional machine learning models have been used for SFC, but only based on one or two centrality measures [
7]. Due to the complexity of the spatial structure of USN more parameters and measurements are needed to adequately model SFC. To consider centrality measures in urban networks, patterns of streets and roads are considered based on graph theory, which helps to extract spatial topology attributes of streets. The goal of centrality measurement is finding the most important central places in the network and their attributes that play a pivotal role in monitoring the efficiency and accessibility of transportation networks [
21,
22,
23,
24]. The centralities can help analyzers understand complex networks more effectively. Technically, centrality measurements inspired our work, where they are used to help domain users explore urban transportation data and provide initial important features from road networks to do a higher-level of analysis in the urban transportation network [
25,
26].
Some experimental studies demonstrate the relationship between the spatial configuration of city structure and traffic in city streets [
6,
9,
23,
27,
28,
29]. Along with other studies, a great deal of research has tried to unveil the movement patterns of individuals by examining the structural features of street networks. Many parameters including the network’s geometrical features, driver movement behavior, and the spatial distribution of urban land uses are influential in traffic distribution. Furthermore, research has shown that these parameters are influenced by the network’s spatial structure. For instance, the spatial structure of the urban network has a high influence on human behavior and the demand for making intra-city trips [
6,
30,
31]. The first time a Self-Organizing Map (SOM) neural network was used in city network generalization was by Kohonen [
32]. Kohonen, in his network, considered the topological, geometrical, and semantic features of the streets. Jiang and Harrie [
1] utilized the SOM neural network for clustering the streets based on their features. In 2012, Zhou [
33] applied SOM and Back-Propagation Neural Network (BPNN) for urban network generalization based on the city plan before city design. Their results showed improvement compared to those achieved with SOM alone.
Deep multilayer neural networks have many nonlinear levels of learning allowing them to compactly learn highly nonlinear and highly-varying functions, and have found a lot of attraction in various earth science research areas [
34,
35,
36,
37,
38], particularly in urban planning problem analysis [
17,
39,
40]. Lv et al. [
40] started applying deep neural networks known as a Stacked Autoencoder (SAE) for traffic flow prediction on a big dataset. In their implementation, they achieved over 93% for traffic flow prediction. They compared their model with some traditional techniques such as Support Vector Machine (SVM), Random Forest (RF), and Back-Propagation Neural Network (BPNN), and SAE [
41] achieved better results. In another research, inclement weather condition information in connection to cars is added to input features for a deep learning model for traffic flow prediction [
42]. They were looking for a correlation between weather conditions and traffic flow prediction. The ability of deep learning to process big data [
34,
43,
44], considering more correlation between datasets and solving the complexity and nonlinearity of datasets, inspired us to rethink analyzing the functionality of streets. In our work, due to having a tabular structure in the input data, a greedy layer-wise deep learning model is applied for unsupervised feature learning to understand the nonlinearity of input data and then logistic regression is used as a classifier. The SDAE model, as one of the best greedy layer-wise unsupervised models, was used to solve the problem of training deep networks [
45]. For evaluating model performance, we compare several machine learning models such as logistic regression, Multi-Layer Perceptron (MLP) [
46], SVM [
47], and RF [
48], with SDAE on four cities with different spatial structures. The four cities used are Tehran, Iran; Isfahan, Iran; Enschede, Netherlands; and Paris, France, and
Figure 1 shows their spatial structure.
Our study proposes a method that can investigate the basic concept of a network’s manner, that is, the spatial structure of a street network. First, we prove that we can extract the functionality of a street with the spatial measurement within an acceptable percentage, and then we suggest the proposed classification method for classifying streets that do not belong to a specific functional class. In this work, first, the USN is modeled as a network using graph theory [
1], then the spatial structure of the USN is described using nine centrality measurements to better understand the complexity of the network to SFC. To utilize SFC, the powerful nonlinear learning model called deep learning has been applied to take advantage of its ability to understand the complexity of the USN and street functionality. Our study investigates the structural properties of each functionality class in the real world. The major contributions of this paper are summarized as follows.
Considering the challenge of street functional classification based on the spatial structure of streets, mainly centrality measures.
Developing an unsupervised deep learning model to improve the accuracy of the street functional classification compared to traditional techniques.
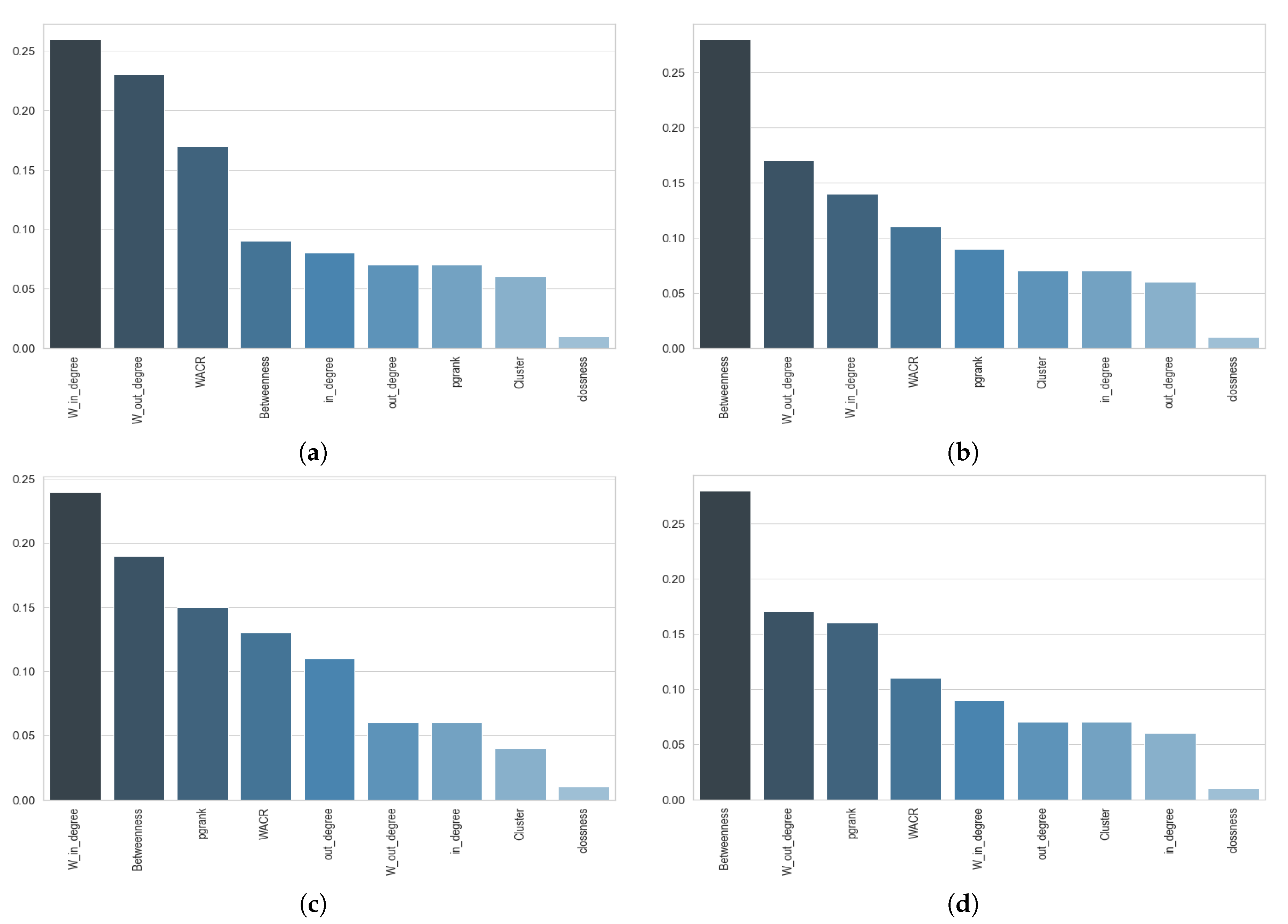
Analyzing the importance of each centrality measure into street functional classification by using random forest technique.
Investigating the impacts of the street network regularity on street functional classification.
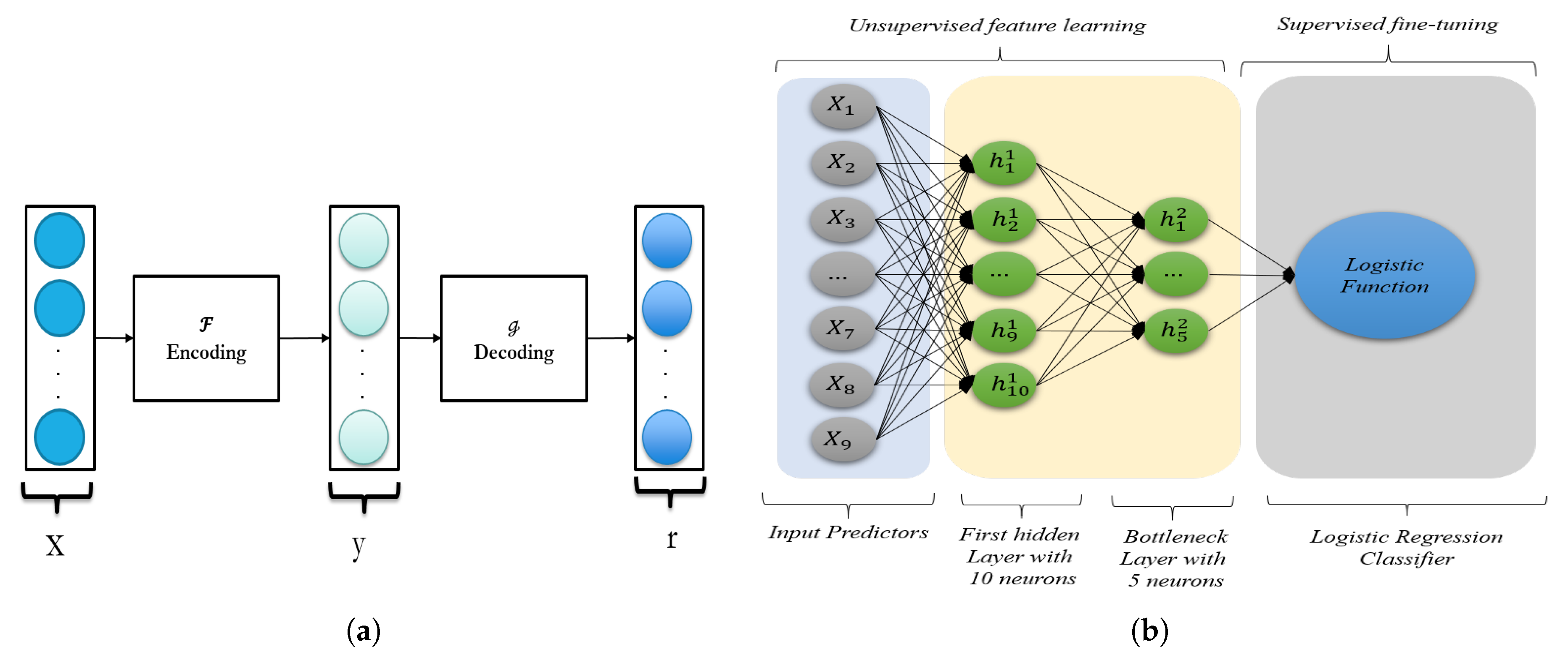
In this study, we choose a Stacked Denoising Autoencoder (SDAE) [
41], as it is one of the best greedy layer-wise, unsupervised learning models [
45,
49]. Although our input data is labeled, we use the SDAE to learn features and weights in an unsupervised, greedy, layer-wise manner, while the supervised fine-tuning is used to further adjust the network’s weights for classification using the labeled data. For fine-tuning classification, we applied logistic regression, but other techniques would work. We compare our deep learning model with four traditional machine learning models.
The rest of the paper describes our work in detail, with
Section 2 explaining SDAE and describing the centrality measures we used.
Section 3 presents the methodology of our evaluation of our implementation using four different data sets. Numerical results from our experiments are discussed in
Section 4, and
Section 5 presents our conclusions.
3. Results
This section describes how we compared the results of our proposed model with four other machine learning models. We describe the datasets we used, the metrics employed, the models we compared with, how we tuned those models, and finally the results of street functionality classification.
3.1. Data Description
To extract the centrality measures, the main axes of all roads are modeled using the street segment method. This means that the road between two consecutive junctions is considered a separate segment in the network. The modeled street segments were used to construct the strokes. These strokes were constructed using the every best fit method. Street directions were also considered in designing the strokes. In this study, the datasets for four different cities are utilized. The streets for each city are grouped into four classes based on the functionalityL Principal Arterial road (PAr), Minor Arterial road (MAr), Collector road (Cr), and Local road (Lr). For each street, nine different centrality features are determined, and the statistical information of all nine centrality measures has been summarized in
Table 1. After preprocessing the data, the structural feature vector is computed for each stroke, then the vectors are normalized to the range of [−1,1]. As a single stroke consists of several street segments with different functionality in the real world, the structural measures of each stroke are assigned to all constituent street segments. Through all of the different machine learning model implementations,
of measures are used for training and
for testing.
3.2. Algorithm Set-Up
We chose four common machine learning models, namely, Logistic Regression (LR), MultiLayer Perceptron (MLP), Support Vector Machines (SVM), and Random Forest (RF), to compare to the proposed SDAE model for use in SFC. Machine learning and deep learning classifiers usually have parameters that need to be set by the user, known as hyperparameters. Hyperparameter tuning involves choosing values for these hyperparameters that result in the optimal performance of a model. The hyperparameters used for each of the traditional machine learning models and our SDAE model are given in
Table 2. The hyperparameter values are selected based on the grid-search technique [
63] with cross-validation [
64]. Each hyperparameter is given a list of discrete values, and for each combination of different hyperparameters, a 5-fold cross-validation training is employed. The data is broken into five equal parts, and each part is used as testing data, while the rest of the data (the other four parts) is used for training, giving 5-fold cross-validation. The set of hyperparameters that achieve the highest classification accuracy are chosen as the hyperparameters to use.
Overfitting is a common problem in all machine learning and deep learning models. Overfitting means the model performed very well on training data but not on test data (unseen data). Regularization is a technique to generalize a model and, in turn, improves the model’s performance on the unseen test data to ameliorate the overfitting problem. Regularization has the same effect on machine learning and deep learning but in different ways. In machine learning, regularization penalizes the coefficients, but in deep learning, it penalizes the weight matrices of the nodes [
45].
To design the architecture of the SDAE model we used, a different number of hidden layers and the number of neurons for each layer were tested. The SDAE is trained based on stochastic gradient descent for of a dataset, and the experiment is repeated 20 times to assess the variability of the process. The trained model is finally evaluated on the test data, the remaining unseen of a dataset. In this experiment, we vary the number of neurons in the hidden layer from 1–20 to determine the optimum number and also vary the number of hidden layers from two to three. Based on the confidence interval and standard error estimation for 20 iterations, we end up with the optimum 10 neurons for the first layer and five neurons for a second or bottleneck layer. Generally, for an SAE model there are three ways to control overfitting: adding a penalty term in the loss function (regularization term) to control the weights, adding noise to the input data to force the SAE model to learn more informative features, and sparse decoding by deactivating some of the nodes in each layer randomly. To avoid overfitting, 0– noise is added to the input data (only the first layer) to satisfy the stacked denoising autoencoder model, and based on the results, was the optimal value. Moreover, for the regularization term, is chosen based on the grid-search technique between the values in the range of 0 to to avoid growing the weights in the deep learning model and overfitting.
LR is a common benchmark machine learning model and is the one simplest used in this work. The regularization term used in the LR model was tested on the range (0.1–10) based on a grid-search strategy to find the optimal value, with 1 chosen. Moreover, to optimize the LR model two different techniques have been tested: SGD and Limited memory Broyden–Fletcher–Goldfarb–Shanno (LBFGS) [
65]; LBFGS was the best optimization technique to use in this work. To configure the MLP model, the number hidden layers, the number of neurons per layer, the type of activation function, the optimization technique, and the learning rate are tested in various combinations to find the best configuration for the MLP model. For the LBFGS optimization technique, three hidden layers and 100 neurons for each of them activated by the ReLU activation function were the best hyperparameters for the MLP model. For SVM, an RBF kernel is tested as one of the best kernel methods in kernel-based machine learning models. The values for C, a regularization term, and Gamma as hyperparameters for the RBF kernel were found based on the grid-search strategy: 1 and 10 for C and Gamma, respectively. In this work, RF as one of the best ensemble models has been applied. In the RF training process, there are a two methods to control overfitting: limit the number of nodes per leaf or limit the depth of trees. Based on a grid-search, the optimal values for both of these two hyperparameters for RF were 5 for maximum depth and 4 for the minimum number of nodes per leaf.
3.3. Experimental Results
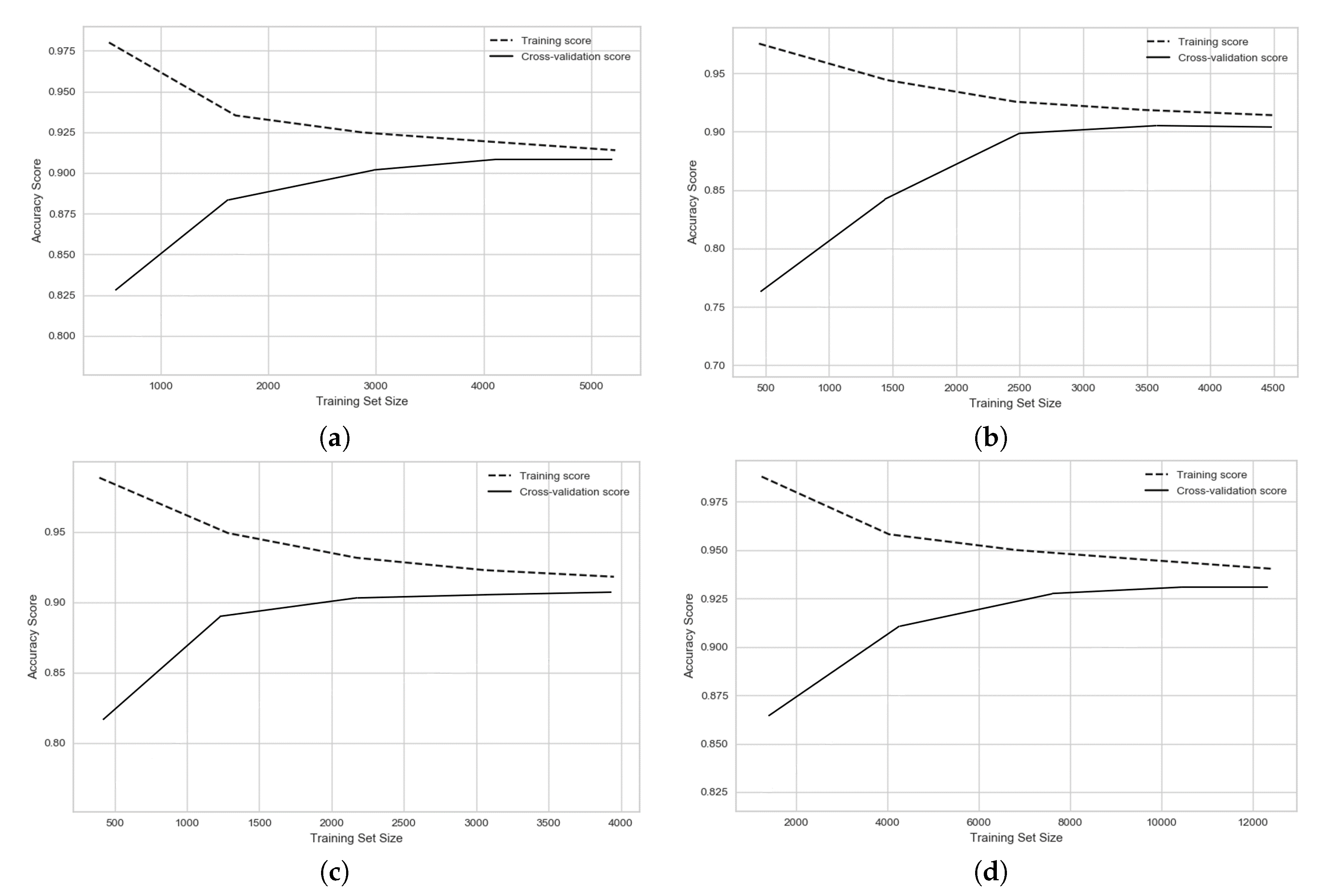
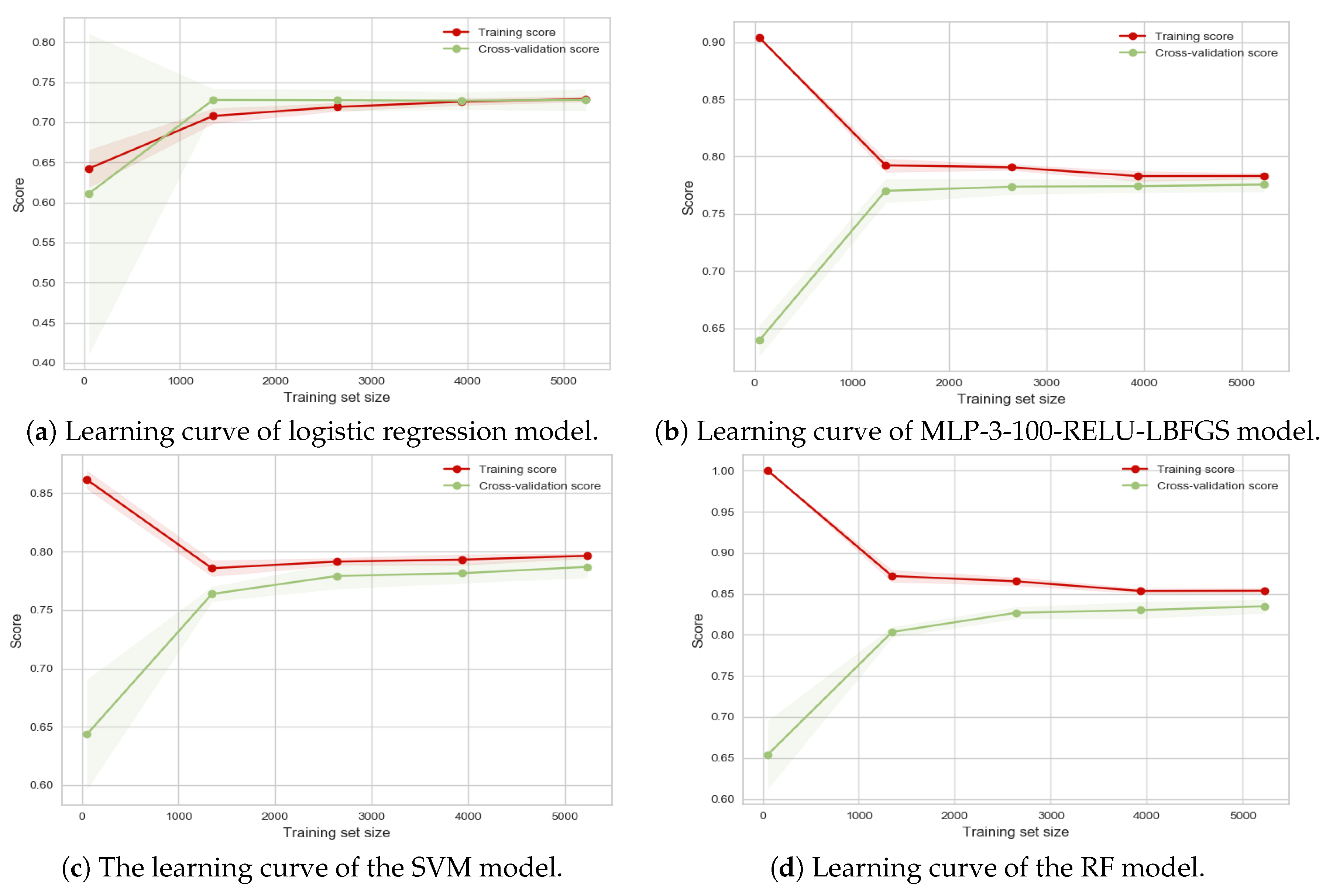
Our proposed SDAE model along with four machine learning models were used to classify the functionality of network streets in four different cities. In this section, the results for all models are shown and discussed. To consider the influence of the amount of input data for different machine learning algorithms and the convergence of the training process, the learning curves for the different models are provided. Each of the input predictors, or the input features, plays a different role and possess a different level of importance on the final performance for a model. In this section, the importance of each input predictor has been considered and discussed. Moreover, the impact of the regularity of the network street and the relationship between regularity of each city on the results of classification is discussed.
Accuracy assessment is an essential step in evaluating the performance and efficiency of different classifiers. In this section, the results of the different implemented models on real data are calculated. To evaluate the performance of the different classifiers, we look at the confusion matrix,
, and Root Mean Squared Error (RMSE). A confusion matrix is a table often used to describe the performance of classification techniques (for more information about the confusion matrix refer to the work in [
66]).
Overall Accuracy (OA) based on this model is the proportion of the total number of correct predictions. The
F-measure metric is based on precision (P) and recall (R) (P is the proportion of the predicted positive cases that were correct and R is the same as true positive), and is calculated as
RMSE [
67] is regularly employed in model evaluation studies. RMSE provides a complete interpretation of the error distribution in the range of
, where values close to zero are better. Moreover, to evaluate the best prediction
is used [
68], the range of this metric is between
, where values close to 1 is better. For the rest of the paper, OA for training data is denoted as “OA-Tr”, and OA for the testing dataset as “OA-Te”. Moreover, the F1 score for PAr, MAr, Cr, and Lr classes is denoted as “F1-PAr”, “F1-MAr”, “F1-Cr”, and “F1-Lr”, respectively.
The classification results of our implementation machine learning and deep learning models are presented in
Table 3,
Table 4,
Table 5 and
Table 6 for four cities. The results for all datasets reveal that machine learning and deep learning can predict and classify the functionality of the street only based on structural properties of streets. As the results are shown in
Table 3,
Table 4,
Table 5 and
Table 6, SDAE has been able to produce more than 90% accuracy of prediction for the training and test sample streets of cities, which are higher than all the proposed models in this experiment.
The overall accuracy for test datasets (OA-Te) is , , , and for Isfahan, Enschede, Tehran, and Paris, respectively. The results help to infer that the spatial structure of streets plays an important role in forming the functionality of urban roads, because the functionality of streets is detectable by only using structural and spatial properties.
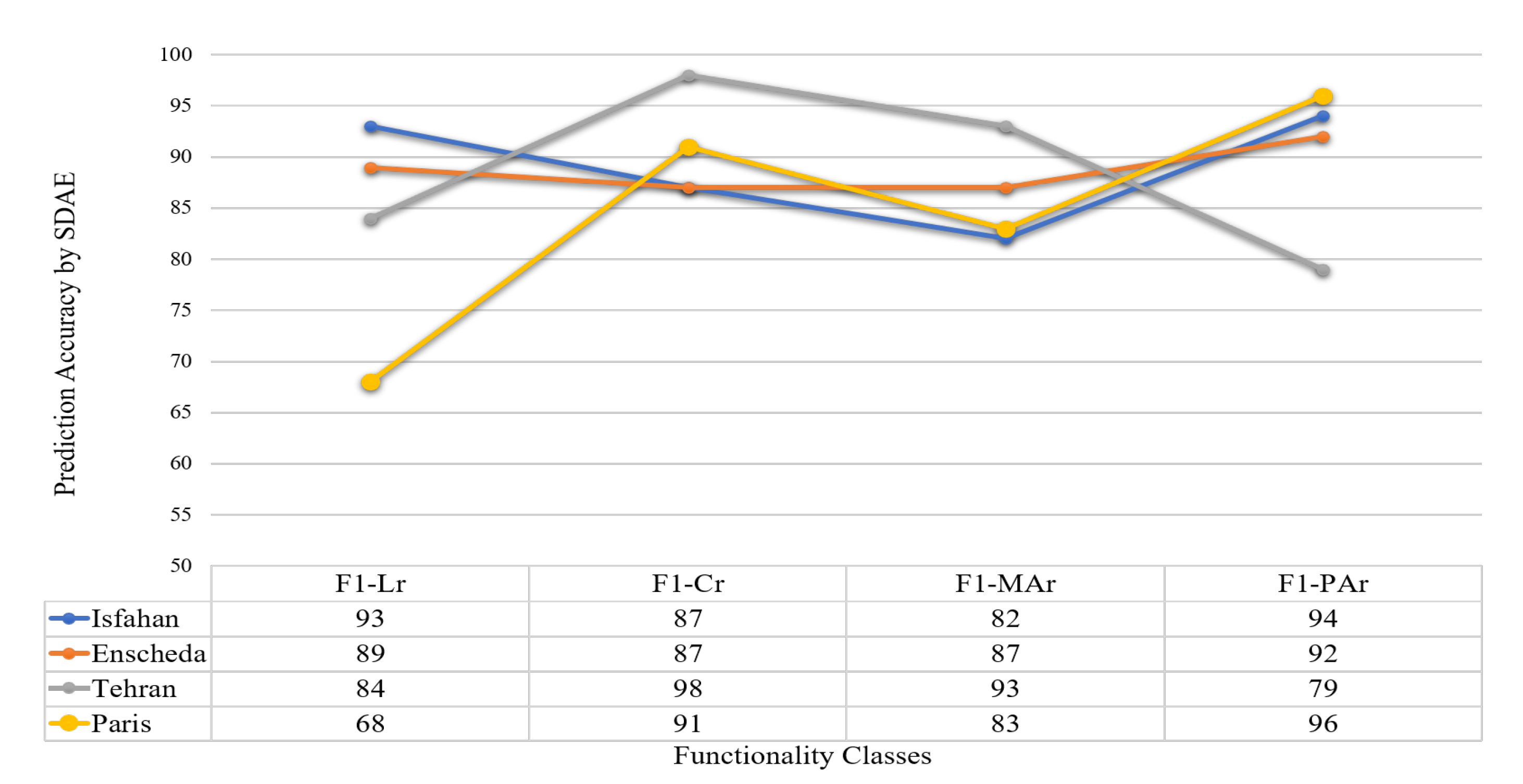
Based on the results of the F1-score proposed for each class of street functionality, it can be stated that every functionality class possessed a specific structural pattern that was distinguishable. The graph depicted in
Figure 5 shows the prediction results of the SDAE model for testing sample datasets of each class of street functionality. As shown in the graph, the majority of errors in functionality classes occurred in the most similar classes. Thus, misclassification mostly happens between classes which are similar, rather than between those structurally completely different. For example, misclassification will happen for Cr as Lr classes are structurally and spatially similar and the same for the two classes of primary roads.
Figure 5 reveals that the accuracy to detect the class of PAr is higher than MAr and more detectable because spatial properties of MAr’s is very close to PAr, and the same analysis for Cr which has received lower accuracy than Lr.
5. Conclusions
There have been many studies conducted on understanding the role of spatial structures in the individual movement pattern. The current study provides two new perspectives on a spatial structural study in urban networks. In this study, nine different structural measures were used to examine the spatial structural effect on forming the functionality of urban roads. Different machine learning techniques, such as logistic regression, MLP, SVM, and random forest, alongside a deep learning model called Stacked Denoising Autoencoder, are applied to reveal the patterns existing in each functionality class of urban roads. To achieve this goal, a training set of street segments, defined by their feature vector and functionality class was fed to the different models.
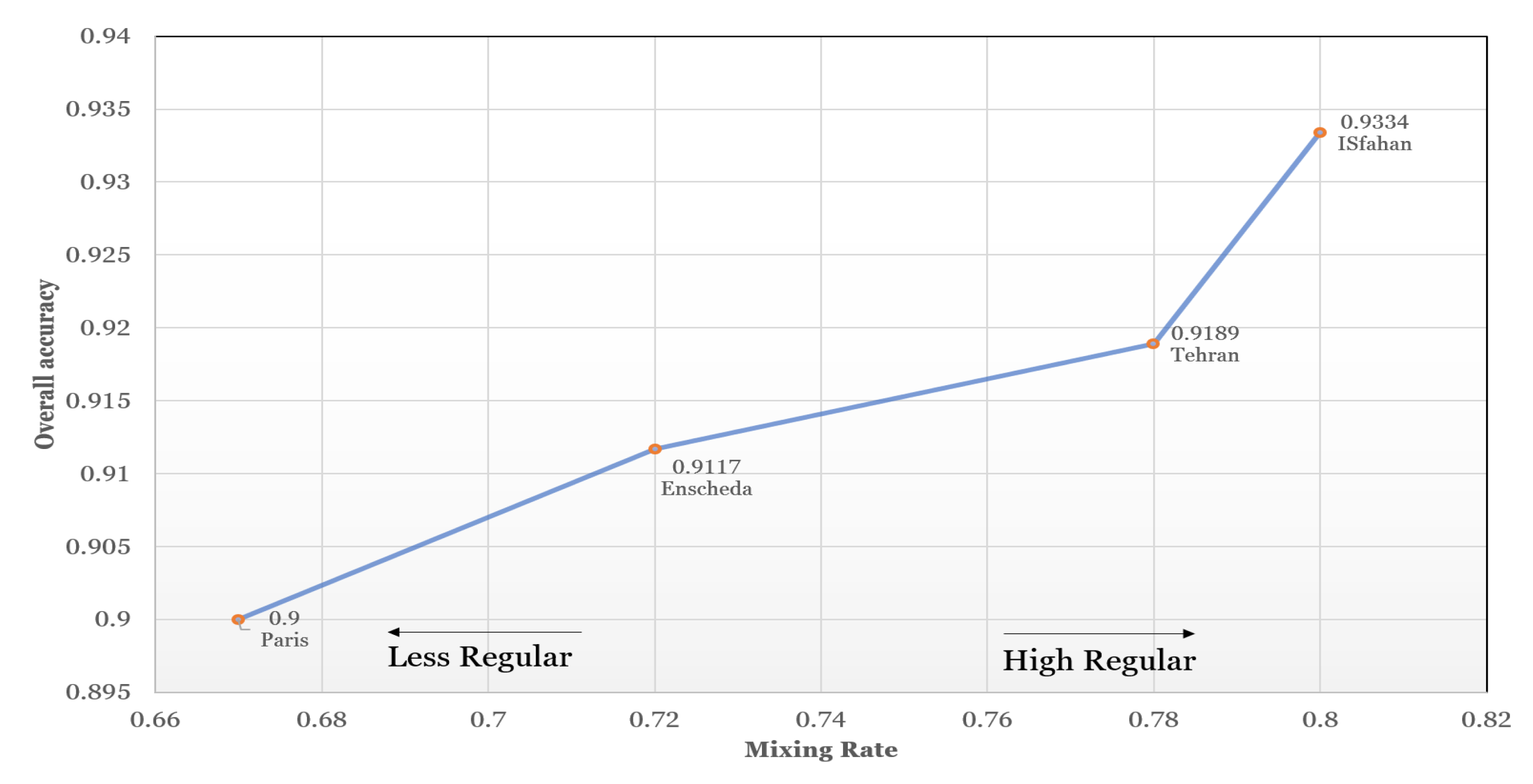
The results show that with an acceptable accuracy provided by SDAE, it is possible to predict the functionality of streets just based on their spatial structural properties. This means that for each real-world functionality class, there exists a specific spatial structural pattern, and the structural properties of streets within a functionality class seem quite similar. It can be concluded that the spatial structure of urban networks is an effective factor in forming the role and importance of each street in the real world. In other words, the structural importance of some urban roads has caused them to be used more frequently than others, which in turn leads to some physical changes in the road’s features to adapt to the high traffic demands. This consequently turns most of these roads to famous roads with high capacity, mostly known as arterial roads. On the other hand, some other roads, because of their spatial positions in city networks, are usually used by fewer passengers; this situation leads to these roads becoming access roads which are known as minor roads.
The classification results also presented a hierarchy that was interestingly similar to the road conceptual hierarchy in the real world. In other words, although this classification was performed by just applying structural properties, its results were arranged exactly in the same way urban roads did. This means that in all functionality classes predicted by machine learning and deep learning models, a majority of errors occurred in the most similar classes. It would be remarkable when we notice that the training dataset did not have any information about the order of functionality classes and the resulted hierarchy in classification has occurred just based on structural properties. Furthermore, the results showed that in regular networks, in which a spatial pattern is repeated in different parts of the city, the deep learning model was able to predict the real-world functionality class more accurately. It implies that in regular networks, there is a prominent spatial structure pattern in each functionality class in comparison with less regular networks. It means that in regular networks, the spatial structures and configurations have a higher impact on forming street roles in the real world. On the other hand, in less regular networks, the significance of spatial structure is reduced in forming street functionality, which in turn produces weak structural patterns in each functionality class in the real world. In conclusion, the level of structural regularity in urban networks is a key factor in forming functionality and the importance of streets in the real world. Furthermore, SDAE demonstrated that for processing big data with nonlinearity and complexity, deep learning models outperform all traditional machine learning and ensemble models.