1. Introduction
The last two decades have brought a huge increase of the scope and complexity of the applications of computational methods and tools developed within the field of geographical information science [
1,
2,
3]. They have become essential components of the information infrastructure of contemporary societies and their institutions. One possibility of increasing the utility of geographical information systems even further is to combine them with artificial intelligence methods for inference, decision making, optimization, and prediction. This work direction has been active for a long time [
4,
5,
6,
7], but the increased available computational power and the onset of more refined and effective algorithms makes it more promising than ever [
8]. In particular, machine learning algorithms may be used to discover and generalize non-trivial relationships between geographical information and other factors or quantities, turning them into reusable predictive models.
One specific important application area where geographical information science meets machine learning is predictive policing [
9]. The capability to predict which areas have particularly high risk of specific types of criminal events may help to effectively allocate law enforcement resources where they are most needed. Crime prediction using analytic algorithms from machine learning and statistics has, therefore, become a popular area of research and practical applications [
10,
11,
12,
13,
14,
15]. The potential contribution of achievements in this direction to the public security provides high motivation for applying a variety of methodologies to various kinds of potentially useful data. Besides police crime records, these may include, e.g., sociodemographic and economic statistics, social media posts, or data from geographical information systems. A widely available and frequently updated type of the latter are point of interest (POI) locations, which may provide a useful characteristic of urban areas.
1.1. Contributions
This work demonstrates how machine learning algorithms can be applied to data from geographical information systems to create crime prediction models. This confirms the high predictive utility potential of geographical information on one hand, and provides practical guidelines on applying machine learning algorithms with geographical data on the other hand. The latter includes a data preparation process with geographical aggregation to grid micro-areas, assigning class labels, deriving geographical attributes, handling class imbalance, dimensionality reduction, and model reuse across different areas.
Crime prediction for urban areas can be considered a classification task where a model is created predicting the risk of particular types of criminal events based on attributes characterizing the properties of particular micro-areas. Creating such a model requires preparing a combined dataset that includes both geographical attributes of micro-areas derived from POI locations and crime risk labels derived from crime records. Classification algorithms make it possible to capture and generalize the relationships between the former and the latter. The resulting models can be applied to predict the crime risk level for arbitrary new micro-areas for which geographical attributes are available, including newly developed or substantially transformed city districts for which previously collected crime records are not available or no longer adequately represent future crime risk.
The assumed model creation and prediction scenario can be summarized as follows:
geographical aggregation: divide the urban area of interest into micro-areas and aggregate crime records and POI counts on the level of micro-areas,
geographical attribute derivation: describe micro-areas by geographical attributes, derived from aggregated POI locations,
hotspot identification: label micro-areas as high/low risk with respect to the number of aggregated historical crime events,
hotspot modeling: create models for predicting high/low risk labels based on geographical attributes using classification algorithms,
hotspot prediction: apply the created models to predict high/low-risk labels for particular micro-areas based on geographical attributes.
The scenario uses historical data to create models capable of predicting future crime risk. It is noteworthy that micro-areas are not represented by identifiers or by coordinates, but rather described exclusively by attributes derived from geographically aggregated POI locations. This makes it possible to capture more general and reusable relationships, independent of a particular city topography.
The experimental procedure used to verify the utility of the proposed approach includes the following additional operations:
predictive power evaluation: assess the quality of obtained crime predictions using the k-fold cross-validation procedure and the ROC analysis,
attribute predictive utility evaluation: rank geographical attributes with respect to their utility for crime risk prediction using the random forest variable importance measure,
dimensionality reduction: verify the possibility of reducing the data dimensionality without degrading model quality by attribute selection and principal component analysis,
model transfer: verify the possibility of applying a model trained on data from one urban area for crime risk prediction in another urban area.
1.2. Related Work
Examining the utility of various available data sources to characterize geographical areas and create crime hotspot prediction models based on these characteristics belong to leading directions of crime prediction research. The literature contains several studies that are partially related to this work. A summary of those of them for which the objectives or methods are the most similar to the objectives or methods adopted in this article is presented in
Table 1.
Each of these related studies combines crime records for a single urban area with some additional spatial data and performs geographical aggregation into micro-areas of different sizes. Then they apply classification or regression algorithms to either predict the crime risk level (after some form of hotspot identification) or the number of crime events. Two partial exceptions of this common pattern that do not create crime prediction models are the works of Traunmueller et al. [
16] and Malleson and Andresen [
17]. The former analyze the correlation between crime counts and the sociodemographic profile of people visiting particular micro-areas, based on footfall counts and customer attributes obtained from a mobile phone provider. The latter look for relationship patterns between population and area characteristics on the one hand, and crime hotspots on the other hand.
Distinguishing features of this work include:
using data from four different urban areas, unaddressed by previous research, rather than a single city,
risk prediction performed separately for several different crime types, with varying occurrence frequency,
fine-grained -meter micro-areas used for geographical aggregation, hotspot labeling, and prediction, instead of much larger LSOA, community, or public statistics dissemination areas,
a broad set of POI categories used to describe micro-areas,
handling class imbalance by appropriate algorithm setup,
systematic comparison of prediction quality using the ROC analysis,
examining the effect of dimensionality reduction by attribute selection and principal component analysis,
examining the possibility of transferring crime prediction models across different urban areas.
It is noteworthy that several prior studies listed in
Table 1 analyze both the spatial and temporal dimensions of crime [
18,
19,
20,
21,
22,
23]. This is achieved either by applying autocorrelation and autoregression analysis of crime event time series, or by adding clock and calendar attributes (such as the hour or hour interval, day of the week, and month) to model inputs. Most of them also combine two or more spatial data sources to derive a more complete and useful micro-area characteristic. It may, therefore, appear to be a limitation of this work that it combines crime data with only one source of spatial data and does not include any temporal factors. While incorporating more sources of spatial and temporal information to crime risk modeling is a natural and promising continuation direction, this research is deliberately focused on POI locations only. This provides a clear picture of the predictive utility of this easily available data source and permits a more systematic and in-depth investigation of the modeling procedure, including the issues of dimensionality reduction and model transfer that received little or no attention so far.
Table 1.
Related work.
| Work | Area | Data Sources | Aggregation Units | Hotspot Identification | Algorithms |
|---|
| traunmueller et al. [16] | London | cellular networks | grid cells a | none | correlation analysis |
| bogomolov et al. [18,19] | London | sociodemography, cellular networks | cellular network cells | comparison to median | random forest |
| Malleson and Andresen [17] | London | sociodemography, cellular networks, social media, POI | LSOA units b | comparison to neighborhood | correlation analysis, descriptive statistics |
| Wang et al. [24] | Chicago | POI, taxi traffic | community areas c | none | linear regression, negative binomial regression |
| Yang et al. [25] | New York | POI, social media | grid cells d | kernel density estimation | logistic regression, naive Bayes classifier, SVM, neural network, decision trees, random forest |
| Lin et al. [20] | Taoyuan | POI | grid cells e | comparison to a threshold | neural networks, kNN, SVM, random forest |
| Dash et al. [21] | Chicago | school, library, and police station locations, library visits, emergency number calls | community areas c | none | polynomial regression, SVM, autoregression |
| Yi et al. [22] | Chicago | sociodemography, POI, taxi trajectories, city hotline requests | community areas c | none | correlation analysis, clustered continuous conditional random field |
| Bappee et al. [23] | Halifax | POI, streetlight infrastructure, social media | dissemination areas f | comparison to a threshold | random forest, gradient boosting |
1.3. Paper Overview
Section 2 presents the datasets used for this work, the data preparation procedure applied to crime and POI data, the algorithms used for creating crime risk prediction models, and the experimental procedure. The results of the experiments are presented in
Section 3. The main findings and future work directions are discussed in
Section 4.
2. Materials and Methods
2.1. Data
The experimental study presented in this article uses two sources of publicly available data: UK Police crime records and OpenStreetMap point of interest locations.
2.1.1. Crime Data
UK Police crime records are available from the
data.police.uk website. For the purpose of this work, crime records were retrieved for the following territorial police forces:
Covering the time span between October 2016 and September 2019. For each crime event the geographical location and crime type information is available.
The four crime datasets were filtered to only include the corresponding biggest urban areas, i.e., respectively, the following UK districts:
Manchester District (referred to as Manchester thereafter),
Liverpool District (referred to as Liverpool thereafter),
Bournemouth, Christchurch and Poole District (referred to as Bournemouth thereafter),
Wakefield District (referred to as Wakefield thereafter).
The filtering was performed using the UK administrative boundaries available from the
ordnancesurvey.co.uk website.
Out of 14 originally included crime types the following subset is used for the experiments:
Anti-social behaviour (referred to as ANTISOCIAL thereafter),
Violence and sexual offences (referred to as VIOLENCE thereafter),
Burglary (referred to as BURGLARY thereafter),
Shoplifting (referred to as SHOPLIFTING thereafter),
Other theft (referred to as THEFT thereafter),
Robbery (referred to as ROBBERY thereafter).
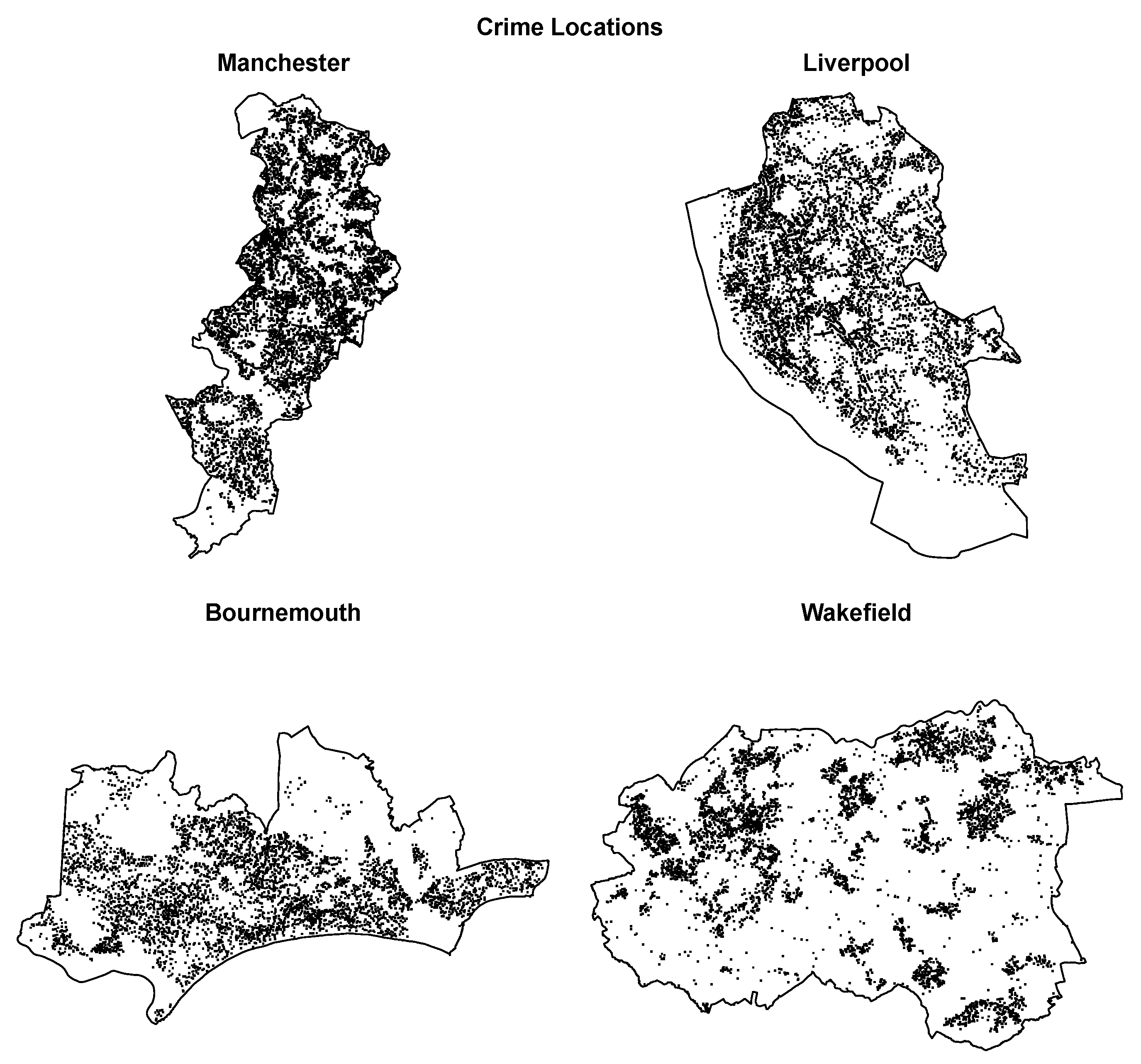
Figure 1 presents crime count barplots for these crime types within each of the urban areas of interest.
Figure 2 illustrates crime locations on the borderline maps of the corresponding areas. The distribution of crime types is similar for each urban area, with the ANTISOCIAL and VIOLENCE types being the most frequent, the BURGLARY, SHOPLIFTING, and THEFT types having a medium frequency, and the ROBBERY type being the least frequent. The frequency and spatial density of crimes are the highest for Manchester and the lowest for Wakefield.
2.1.2. POI Data
The point of interest data were obtained as shapefiles with selected
OpenStreetMap layer extracts, available from
Geofabrik.de [
26]. POI shapefile loading and preprocessing was performed using the
rgdal [
27] and
sp [
28] R packages. The following layers were used:
- pois:
POI objects represented as points,
- pois_a:
POI objects represented as polygons,
- transport:
transport objects represented as points,
- transport_a:
transport objects represented as polygons.
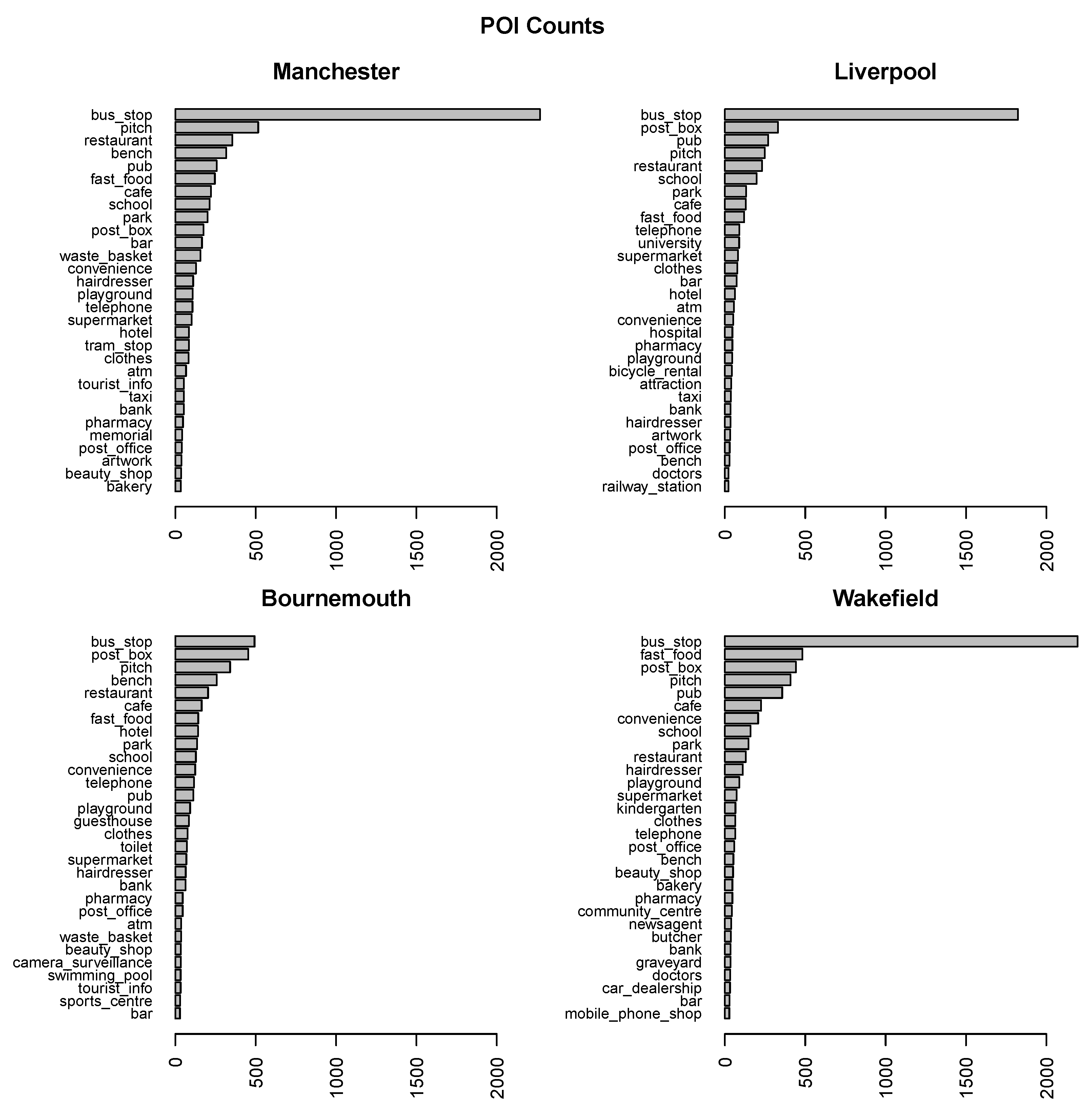
Each POI object is described by geographical coordinates and a category. The number of actually occurring categories differs across areas and ranges from 107 for Liverpool to 122 for Bournemouth. There are 97 common categories occurring in each of the four urban areas and only these are used in the experimental study.
Figure 3 presents POI count barplots for the most frequent 30 categories within each of the urban areas of interest.
Figure 4 illustrates POI locations on the borderline maps of the corresponding areas. The most frequent POI categories are mostly the same for all urban areas. The main difference is that the
bus_stop category, which is always the most frequent, absolutely dominates other categories for Manchester, Liverpool, and Wakefield, whereas it is just slightly above the next category for Bournemouth.
2.1.3. Geographical Aggregation
For the purpose of simple hotspot identification, each urban area was partitioned into a square grid with dimensions of
m, as illustrated in
Figure 5. The POI data were aggregated using the same
grid. POI counts within
grid cells for each of the common POI categories serve as input attributes for prediction.
The applied grid resolution may be considered a reasonable tradeoff between providing crime hotspot predictions at the level of small micro-areas for maximum utility on one hand, and using larger micro-areas for greater prediction reliability on the other hand. A fine-grained grid would make model predictions more useful for law enforcement agencies, making it possible to more precisely allocate prevention resources, but the number of POI objects within grid cells might be too small to permit discovering generalizable patterns with predictive value. A coarse-grained grid would ensure that there are enough data points within grid cells, but the resulting predictions would be of questionable practical utility. The
grid cells are much smaller micro-areas than those used in most previous studies mentioned in
Section 1.2, but still sufficiently large to usually contain several POI objects.
2.1.4. Hotspot Identification
Crime counts for particular crime types within grid cells were converted to binary
high/
low risk labels using the 3rd quartile as the cutoff point (
high risk if the event count is above the 3rd quartile,
low risk otherwise). The resulting binary risk indicators serve as target attributes for prediction. High-risk micro-areas can be considered crime hotspots [
29].
The applied method of hotspot identification is simple and efficient, but clearly imperfect. Arbitrary square grid boundaries and fixed resolution, insensitive to differences in building and population density as well as traffic patterns, are its obvious shortcomings. This approach is adopted for this work, despite its limitations, to focus on the utility of POI data and the level of prediction quality possible to obtain in a most basic setting, and postpone investigating more refined variable-resolution methods to future work.
One possible alternative to a regular fixed-resolution grid could be dividing the urban area along street boundaries [
30]. Since traffic, residential buildings, offices, shops etc. concentrate along streets, determining boundaries based on their layout and connections may identify more homogeneous micro-areas with respect to the risk and type of criminal events. They could be also more useful for planning crime prevention activities.
Geographical aggregation of crime events within micro-areas, even with a variable resolution, implies fixed boundaries and step changes between adjacent micro-areas. Even very close locations belonging to two different micro-areas could be then assigned substantially different risk levels. A more adequate representation of actual risk could be a smoothed risk level, gradually changing with the distance. This can be achieved using
kernel density estimation (KDE) [
31]. In this approach, event locations are used to estimate a probability density function by smoothing, controlled by a bandwidth parameter. This produces a continuous mapping of points from an analyzed area to an event probability density. Micro-areas with the highest probability density, considered hotspots, have no arbitrarily predefined boundaries, but are identified based on event distribution [
32,
33,
34,
35]. Combining crime risk modeling and prediction based on POI attributes with a KDE-based hotspot identification method could be an interesting future work direction.
The idea of crime hotspots can be extended to incorporate crime frequency changes in time, besides their territorial density. Such spatio-temporal hotspots represent combinations of micro-areas and time windows with a high risk of criminal activity [
14,
36]. This study does not incorporate the time dimension into the analysis, though, to entirely focus on the predictive utility of POI data.
2.1.5. Combined Data
Joining the geographically aggregated crime data and POI data by grid cells yields combined datasets for each urban area that are used for model creation and evaluation. Rows of these datasets correspond to grid cells and columns correspond to the risk indicators and POI attributes. Each of these datasets is limited to grid cells that fall within or intersect with the corresponding urban area, according to UK district boundaries.
Table 2 presents the size of each dataset and the hotspot percentage for particular crime types. For the least frequent crime types this percentage is substantially below the expected level of 25%. This occurs when there are less than 25% grid cells with non-zero event counts for the corresponding crime type.
2.2. Algorithms
An arbitrary classification algorithm can be used to predict high/low risk labels based on POI attributes. A selection of the most useful algorithms known from the literature is applied in this work: logistic regression, support vector machines, decision trees, and random forests [
37].
2.2.1. Logistic Regression
Logistic regression is an instantiation of generalized linear models which adopts a composite model representation function, with an inner linear model and an outer logit transformation [
38]. Training a logistic regression model consists in finding model parameters which maximize the log-likelihood of training set classes.
Due to the probabilistic objective function used for parameter estimation, logistic regression can generate well-calibrated probability predictions and is often the classification algorithm of the choice where this is required. It is easy to apply and not overly prone to overfitting unless used for high-dimensional data. In our experiments, logistic regression serves as a natural comparison baseline for the more refined support vector machines algorithm which extends linear classification, achieving better overfitting resistance and permitting nonlinear relationships.
2.2.2. Support Vector Machines
Support Vector Machines (SVM), which often belong to the most effective general-purpose classification algorithms, can be viewed as a considerably strengthened version of a basic linear-threshold classifier with the following enhancements [
39,
40,
41]:
margin maximization: the location of the decision boundary (separating hyperplane) is optimized with respect to the classification margin,
soft margin: incorrectly separated instances are permitted,
kernel trick: complex nonlinear relationships can be represented by representation transformation using kernel functions.
The SVM algorithm assumes a binary classification scenario with two classes. Class predictions are generated using a standard linear-threshold rule. Model parameters are found by solving a quadratic programming problem defined to achieve classification margin maximization, i.e., placing the decision boundary so as to maximize the distance from the closest correctly separated instances, with a penalty for constraint violations controlled by a cost parameter.
Transforming this problem to a dual form by applying Lagrange multipliers provides substantial advantages [
42,
43]. A particularly important property of the dual form is that it only uses attribute value vectors within dot products, both during model creation and during prediction. This makes it possible to apply the kernel trick—an implicit representation transformation. Instead of dot products of original attribute value vectors kernel function values are used, which represent dot products of enhanced attribute value vectors. This achieves the effect of transforming attribute values vectors without actually applying the transformation.
Instead of binary linear-threshold SVM predictions, it may be often more convenient to use probabilistic predictions. This is possible by applying a logistic transformation to the signed distance of classified instances from the decision boundary, with parameters adjusted for maximum likelihood [
44].
A noteworthy property of SVM is the insensitivity of model quality to data dimensionality, which—unlike for many other algorithms—does not increase the risk of overfitting because model complexity is related to the number of instances close to the decision boundary rather than to the number of attributes.
2.2.3. Decision Trees
A decision tree [
45,
46] is a hierarchical structure that represents a classification model. Internal tree nodes represent splits applied to decompose the domain into regions, and terminal nodes assign class labels or probabilities to regions believed to be sufficiently small or sufficiently uniform.
Decision trees are popular in many applications due to their capability of combining reasonably good prediction accuracy with the human readability of models. They may require appropriately tuned stop criteria or pruning to avoid overfitting. In our experiments, decision trees serve as a natural comparison baseline for the more refined random forest algorithm which combines multiple trees to achieve better prediction quality and overfitting resistance.
2.2.4. Random Forest
Random forests belong to the most popular ensemble modeling algorithms [
47], which achieve improved predictive performance by combining multiple diverse models for the same domain. A random forest [
48] is an ensemble model represented by a set of unpruned decision trees, grown based on multiple bootstrap samples drawn with replacement from the training set, with randomized split selection. It can be considered an enhanced form of bagging [
49] that additionally stimulates the diversity of individual models in the ensemble by randomizing the decision tree growing algorithm used to create them.
Random forest growing consists in growing multiple decision trees, each based on a bootstrap sample from the training set (usually of the same size as the original training set), by using an essentially standard decision tree growing algorithm [
45,
46]. Since the expected improvement of the resulting model ensemble over a single model is contingent upon sufficient diversity of the individual models in the ensemble [
47,
49], the following modifications are applied to stimulate the diversity of decision trees that are supposed to constitute a random forest:
large maximally fitted trees are grown (with splitting continued until reaching a uniform class, exhausting the set of instances, or exhausting the set of possible splits),
whenever a split has to be selected for a tree node, a small subset of available attributes is selected randomly and only those attributes are considered for candidate splits.
Random forest prediction is achieved by simple unweighted voting of individual trees from the model. Vote distribution can be also used to obtain class probability predictions. With sufficiently many diversified trees (typically hundreds) this simple voting mechanism usually makes random forests extremely accurate and resistant to overfitting. As a matter of fact, in many cases, they belong to the most accurate classification models that can be achieved.
2.3. Dimensionality Reduction
A large number of attributes may prevent some modeling algorithms, particularly those prone to overfitting, from achieving high quality models. This is because model creation is a search process in the model representation space, the complexity of which usually directly depends on data dimensionality [
50]. This increases the risk of overfitted models with insufficient generalization capabilities. Some of the available attributes may have no real predictive value and exhibit a relationship with class labels only by chance.
The datasets prepared for the analysis as described in
Section 2.1 have 97 input attributes, corresponding to POI categories common for all the four urban areas. This can be considered relatively high dimensionality, particularly given the moderate size of the datasets (between about 1500 and 4000), in which instances correspond to grid cells. It may therefore be interesting to see whether dimensionality reduction techniques can lead to improved prediction quality.
Two types of dimensionality reduction will be considered:
attribute selection, which retains a small subset of the set of original attributes,
representation transformation, which replaces the original attributes with a small subset of new attributes.
2.3.1. Attribute Selection
The purpose of attribute selection is to limit the full set of available attributes to its possibly small subset with the highest predictive utility [
51]. Attribute selection methods include filter approaches that use some measures of predictive utility of individual attributes and attribute subset without assuming any specific target modeling algorithm, and wrapper approaches in which a pre-established target algorithm is used to create models on attribute subset to evaluate their utility [
52]. The latter may have advantages when the most useful attribute for a single algorithm is required, but the former is more convenient when experimenting with multiple algorithms, as in this work.
One type of attribute selection filters that has gained high popularity is based on attribute utility measures that can be calculated as a “side effect” of the random forest algorithm [
48], often referred to as random forest variable importance. One of those measures, called mean decrease accuracy (MDA) and considered the most reliable, is the estimated decrease of prediction accuracy due to a random attribute value permutation [
53]. The higher the decrease, the more useful the attribute appears to be. Unlike simple statistic relationship measures, this type of variable importance is sensitive to the context provided by other available attributes.
There are two inconveniences associated with directly applying random forest variable importance to attribute selection. One is instability, resulting from the algorithm’s randomness, and the other is the lack of automated subset selection mechanism determining how many of the most useful attributes should be used. These inconveniences are overcome by the Boruta [
54] algorithm, which repeatedly applies the random forest to decide which attributes should be retained and which ones can be removed from the subset. This comes at a significant computational expense, though. For the experiments presented in this article, the MDA variable importance is used directly, but the stability is increased by averaging importance values from all models created within a cross-validation procedure. These averaged importance values are then used to select subsets of top attributes of a few arbitrarily pre-determined sizes.
2.3.2. PCA Transformation
An alternative approach to dimensionality reduction consists in transforming data to another representation by applying some algebraic transformation. It generates a new smaller set of attributes, each of which is functionally dependent on some or all of the original attributes. The most common type of such a transformation is principal component analysis (PCA) [
55,
56].
The PCA transformation is performed by identifying new attributes as principal components—uncorrelated linear combinations of the original attributes. Each subsequent principal component is supposed to maximize the variance while preserving orthogonality to the preceding ones. This can be achieved by determining eigenvectors and eigenvalues of the attribute correlation or covariance matrix or by applying the singular value decomposition [
57] to the covariance matrix.
To reduce the original dimensionality n one has to select first principal components. When using the dataset of reduced dimensionality to create predictive models, it is necessary to transform new data at the prediction phase to the same representation as determined based on the training data, by multiplying by the corresponding projection matrix.
2.4. Predictive Performance Evaluation
The most common classification quality measures such as the misclassification error or classification accuracy are not very useful whenever classes are unbalanced or likely to have different predictability. They also do not adequately capture the predictive power of probabilistic models which can be used in various operating points, corresponding to different probability cutoff values. This is why, in the experiments reported in this article, classification quality is visualized using ROC curves, presenting possible tradeoff points between the true positive rate and the false positive rate [
58,
59]. The former is the ratio of the number of all crime hotspots correctly predicted by the model to the number of all actual crime hotspots, and the latter is the ratio of the number of non-hotspot grid cells incorrectly predicted by the model to be hotspots to the number of all non-hotspot grid cells. Model operating points visualized by ROC curves are summarized using the area under the ROC curve (AUC). It serves as an overall measure of predictive power and can be interpreted as the probability of a hotspot grid cell achieving a higher crime risk prediction than a non-hotspot grid cell. It is proportional to the value of the Mann–Whitney
U statistic for testing the hypothesis that hotspots receive higher risk predictions than non-hotspots.
To achieve reliable, low-bias and low-variance predictive performance estimates, the 10-fold cross-validation procedure repeated 10 times is applied [
60]. It makes effective use of the available data for both model creation and evaluation by randomly splitting it into 10 equally sized subsets, each of which serves as a test set for evaluating the model created on the combined remaining subsets, and repeating this process 10 times to further reduce the variance. The true class labels and predictions for all
iterations are then combined to determine ROC curves and AUC values.
2.5. Algorithm Implementations and Setup
The following algorithm implementations are used in the experiments:
logistic regression: the implementation provided by the standard
glm R function [
61],
SVM: the implementation provided by the
e1071 R package [
62],
decision trees: the implementation provided by the
rpart R package [
63].
random forest: the implementation provided by the
randomForest R package [
64].
For the logistic regression and SVM algorithms parameters controlling the underlying optimization process were left at default values. The SVM parameters specifying the optimization problem were set as follows:
the cost of constraint violation (cost): 1,
the kernel type (kernel):radial,
the kernel parameter (gamma): the inverse of the number of attributes (input dimensionality),
class weights in constraint violation penalty (class.weights): 3 for the high risk class, 1 for the low risk class.
For the decision tree algorithm, the default stop criteria were used, including minsplit (the minimum number of instances required for a split) set to 20 and cp (the complexity parameter) set to . This is supposed to prevent overfitting and verify whether the relationships between crime risk and POI attributes are simple enough to enable successful prediction with relatively small trees. Uniform prior probabilities for the two classes were set via the prior parameter.
For the random forest algorithm, the following setup was used:
the number of trees (ntree): 500,
the number of attributes for split selection at each node (mtry): the square root of the total number of available attributes,
the stratified bootstrap sample size (sampsize): the number of instances of the high risk class (the minority class).
It is worthwhile to notice that the parameter setups for the SVM, decision tree, and random forest algorithm include settings responsible for properly handling unbalanced classes (ensuring sufficient sensitivity to the minority class). This is achieved by specifying class weights for SVM (assigning a higher weight to the minority class when calculating the constraint violation penalty term in the optimization objective), setting uniform class priors for decision trees, and specifying stratified bootstrap sample size for the random forest algorithm (drawing the maximum possible number of minority class instances and the same number of the majority class instances). These settings were verified to indeed improve model quality. No form of class rebalancing is necessary for the logistic regression algorithm, since any class weights or priors would only shift the default class probability cutoff point used for predicted class label assignment. This would serve no useful purpose given the fact that the ROC analysis used for predictive performance evaluation is based on predicted class probabilities instead of class labels anyway.
3. Results
The experimental evaluation of the utility of POI data for crime risk prediction is based on the assessment of the quality of classification models which predict risk indicators for the selected crime types based on POI attributes. The experiments are organized into the following three studies:
prediction quality: evaluating the level of crime risk prediction quality achieved by particular algorithms using all POI attributes,
attribute predictive utility: assessing the predictive utility of particular POI attributes,
dimensionality reduction: examining the effects of dimensionality reduction by attribute selection and principal component analysis,
model transfer: verifying the possibility of applying a model trained on data from one urban area to predict crime risk in another urban area.
3.1. Prediction Quality
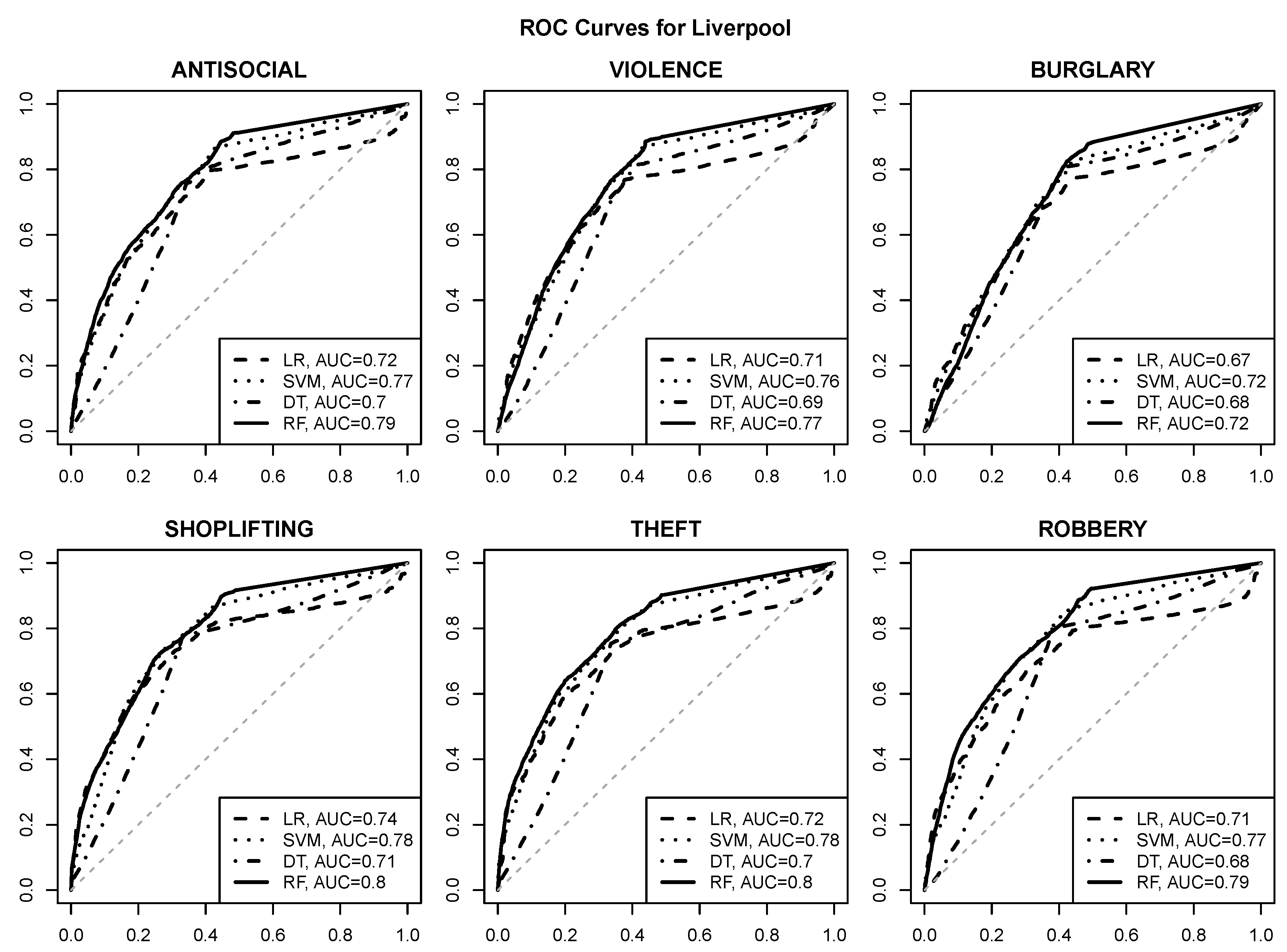
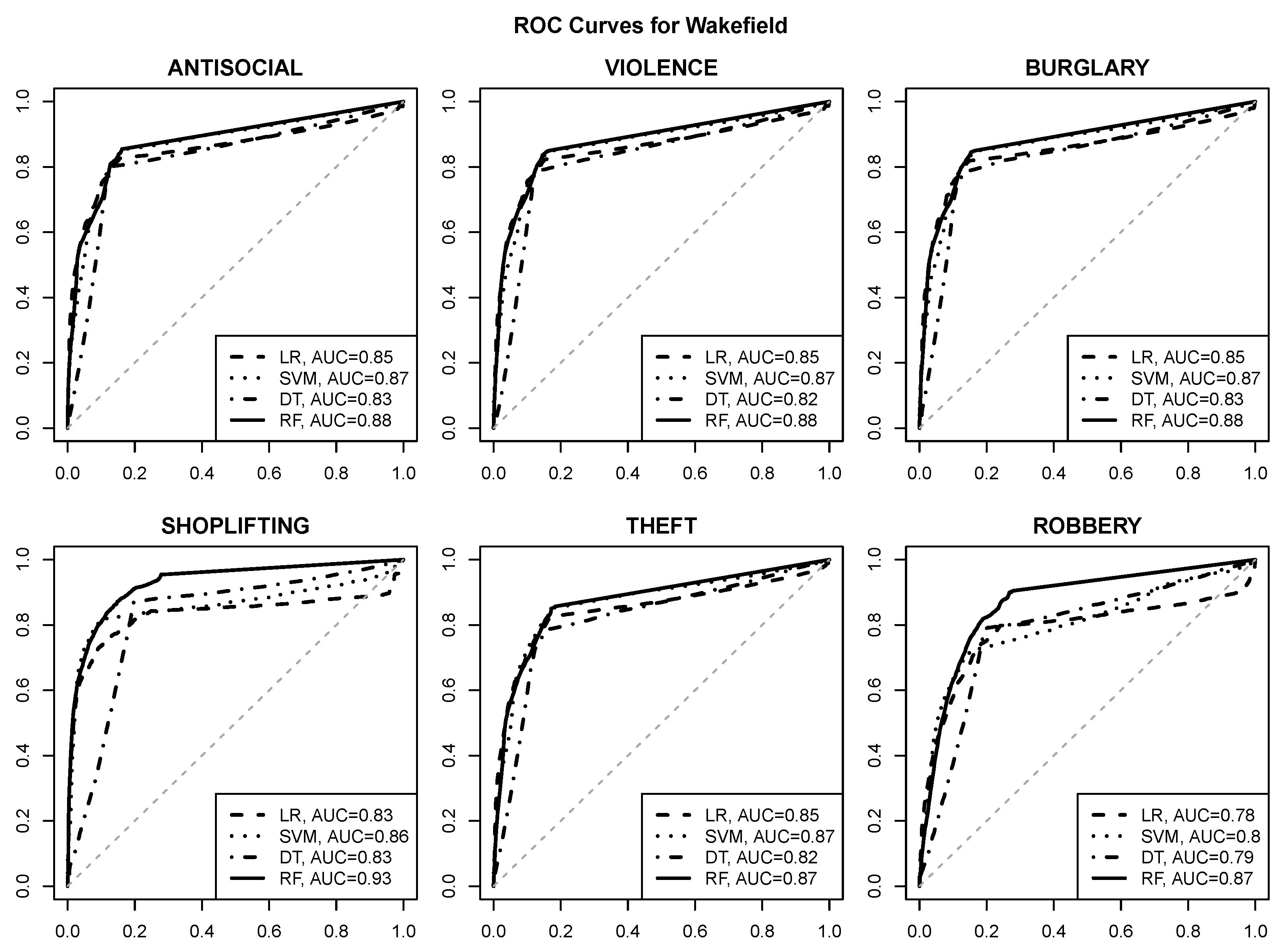
The ROC curves visualizing the prediction quality for logistic regression (LR), SVM, decision tree (DT) and random forest (RF) models are presented in
Figure 6,
Figure 7,
Figure 8 and
Figure 9. The area under curve values are provided in the plot legends. The gray dashed diagonal line represents the random guess performance with an AUC of
.
The following observations can be made:
good quality risk prediction for each of the six selected crime types is possible using POI attributes, with AUC values approaching or exceeding for most urban areas and crime types,
reasonable operating points with a true positive rate of about and a false positive rate of at most are usually achievable (and can be identified, e.g., by selecting class probability cutoff values yielding the maximum true positive rate with the false positive rate not exceeding ),
the random forest algorithm achieves the best predictive performance regardless of the urban area and the crime type,
the SVM algorithm is similarly successful in most cases,
logistic regression and decision tree models give clearly inferior prediction quality, which suggests that the relationship between crime risk and POI attributes may not be simple enough to be adequately represented by a linear function or a small tree,
crime predictability for Wakefield appears to be better than for the other urban areas, with AUC values approaching or exceeding ,
SHOPLIFTING appears to be the best predictable crime type based on POI attributes, which is not surprising given its obvious relationship to store locations.
To verify whether the observed differences in algorithm performance are statistically significant, the nonparametric DeLong test [
65] for AUC comparison was applied. For each of the four urban areas and the six crime types, and for each pair of algorithms, the
p-value was determined for the alternative hypothesis that the AUC value achieved by the first algorithm is greater than the one achieved by the other algorithm.
Table 3 summarizes the obtained test results, by providing for each pair of algorithms
, where
is a table row label and
is a table column label, the number of times (i.e., urban area-crime type pairs) for which
significantly outperformed
at the
level of significance.
It can be immediately seen than the random forest was better than both logistic regression and decision trees in all 24 cases, and better than SVM in 14 out of 24 cases. The latter was always better than logistic regression, and almost always better than decision trees. Logistic regression performed mostly similarly as decision trees, being significantly better in 10 out of 24 cases and significantly worse in 4 out of 24 cases. The decision tree algorithm exhibits the worst overall performance.
3.2. Attribute Predictive Utility
The random forest mean decrease accuracy variable importance measure was used to examine the predictive utility of POI attributes for particular crime types. The corresponding MDA values from the random forest models previously created for prediction quality evaluation were averaged over all cross-validation iterations and over crime types. The results are presented in
Figure 10. In each plot, the top 30 attributes are presented, ranked from the most useful to the least useful.
The rankings of predictive utility do not vary substantially across urban areas. The following are among the most predictively useful categories of POI objects:
bus_stop,
supermarket,
post_box,
pub,
school,
cafe,
convenience,
fast_food,
restaurant,
telephone. While
bus_stop,
post_box,
pub,
cafe and
fast_food belong to the most frequent POI categories (as it can be seen in
Figure 3), this is not quite the case for
supermarket,
convenience, or
telephone. The importance of POI categories cannot be therefore attributed just to their occurrence frequency.
3.3. Dimensionality Reduction
To examine the effect of dimensionality reduction, the experiments from the prediction quality study were repeated in the following two modified variants:
with attribute selection: using 5, 10, and 25 top attributes according to the random forest variable importance ranking,
with PCA: using 5, 10, and 25 first principal components.
To save space, only AUC values, averaged over all crime types, are presented for this dimensionality reduction study: in
Table 4 for attribute selection and in
Table 5 for PCA. For easier comparison with the results obtained using the original dimensionality, for each algorithm there is an additional row corresponding to attribute subset size or the number of principal components equal 97, i.e., the number of all POI attributes used in the previously presented experiments.
The following observations can be made:
dimensionality reduction helps the logistic regression and decision tree algorithms achieve better prediction quality (only PCA gives an improvement for the latter),
the quality of SVM and random forest predictions does not improve due to dimensionality reduction,
dimensionality reduction by PCA is more effective than by attribute selection (the latter gives a smaller improvement for logistic regression and no improvement for decision trees),
the top 25 attributes are usually sufficient to achieve the best possible level of prediction quality,
the first five principal components are usually sufficient to achieve the best possible level of prediction quality.
3.4. Model Transfer
In the model transfer experiments, all pairs of different urban areas were considered. For each pair, the dataset for one urban area was used to create prediction models for all crime types. The obtained models were then applied to generate crime risk predictions for the other urban area. The quality of these predictions was evaluated, as before, using the area under the ROC curve. Notice that, unlike in the previous two studies, the -fold cross-validation procedure was not used. This is because the datasets for model creation and for model evaluation are naturally disjoint, as coming from two different urban areas.
Since input attributes used by the predictive models are POI counts within grid cells of a fixed uniform resolution, they actually represent densities and therefore need no normalization by area to enable model transfer. Other forms of normalization—e.g., by population or by the overall number of POI objects in a given urban area—might be useful to compensate for differences between densely-developed and sparsely-developed urban areas, but examining the impact of such techniques on model transfer performance is postponed for future work.
The AUC values obtained in the model transfer study are presented in
Table 6. A separate section of this table corresponds to each crime type and contains rows and columns corresponding to the four urban areas. Rows correspond to urban areas used for model creation (training) and columns correspond to urban areas used for model application (prediction). Diagonal values, however, are not obtained by training and evaluating on the same dataset. These are the cross-validated AUC obtained in the prediction quality study (
Figure 6,
Figure 7,
Figure 8 and
Figure 9). This makes it possible to compare the prediction quality of models transferred to a different urban area and models used in the same urban area where they were trained (although on previously unseen data).
The observations can be summarized as follows:
model transfer can be generally considered successful, with the difference of AUC values between “foreign” and “native” models not exceeding – in most cases,
the models trained on the Manchester and Liverpool data have better transfer performance than those trained on the Bournemouth and Wakefield data,
when applied for prediction in Bournemouth and Wakefield, “foreign” models are as good as the “native” ones.
4. Discussion
This paper experimentally investigated the utility of point of interest data for crime risk prediction. The study was performed using police crime records for selected UK urban areas
OpenStreetMap POI layers. A simple grid aggregation method for combining geotagged crime events with point-of-interest locations was applied. The results suggest that POI attributes are highly useful for crime prediction, making it possible to accurately discriminate between high-risk and low-risk areas. High-quality models for crime hotspot prediction based on POI attributes may become essential components of predictive policing systems, allowing law enforcement agencies to more effectively prevent crime using constrained resources [
9].
It is worthwhile to underline that crime risk predictions are made using per-category POI counts as the only type of area description, without any area identifiers or coordinates. The created models capture relationships between crime risk and POI density observed in historical data and use them to predict future crime risk, without being tied to a particular city topography.
The patterns of relationship between crime risk and POI attributes are not trivial, though, since logistic regression and decision trees are outperformed by SVM and random forest models by a substantial margin. The superiority of the latter two algorithms, verified to be statistically significant, is not unexpected given the fact that they belong to the most successful classification algorithms. In particular, they are both relatively resistant to overfitting, which turns out to be a significant advantage in this application, with nearly a hundred POI attributes and no more than a few thousand grid cells to learn from. This is also consistent with the observation that their performance did not improve after applying dimensionality reduction, which suggests that they can use use the full set of available attributes without overfitting.
The classification quality achieved by both decision trees and logistic regression improved due to dimensionality reduction by PCA. It turned out more effective than attribute selection: no small subset of POI categories turned out sufficient for high quality crime prediction, but projection into a space of just a few principal components permitted achieving nearly the same predictive performance as the full set of attributes. This confirms that the relationships between crime risk and POI attributes cannot be adequately captured by formulas or attribute-value conditions based on a small number of the most common or most characteristic POI categories.
Further work is needed to verify the usefulness of POI attributes for crime prediction for multiple diverse cities. It would be also interesting to examine the impact of grid resolution on prediction quality and the utility of more refined methods of spatial aggregation and hotspot identification, including variable-resolution grids and kernel density estimation. By comparing crime records and predictions obtained using time-tagged POI data (e.g., from map extracts collected over a period of several months or years) it may be possible to observe how new city district development is reflected by changing POI counts corresponding to emerging new risk areas. More extensive model transfer experiments, enriched by the analysis of urban area differences with respect to population characteristics and the level of development and normalization techniques compensating for these differences, could help identify conditions under which successful model transfer is possible. It may be also interesting and useful to have the detected relationships between specific POI categories and crime types examined by criminology experts.
The promising results obtained with classification models provide an encouragement to consider other types of modeling using crime records and POI attributes, such as regression for crime count prediction or clustering for identifying similarity patterns between micro-areas with respect to POI and crime occurrence. It would be also worthwhile to verify the utility of other data sources from which attributes describing city areas can be derived, such as geotagged social media data and mobile network data.
While this research only considers the relationship of crime risk to area attributes, a natural extension would be to additionally consider attributes describing time. These could include, in particular, hour, day of week, month of year, and a holiday indicator, as well as attributes describing actual or forecasted weather conditions. This work direction could be further extended by adopting some spatio-temporal hotspot identification methods [
14,
36] and appropriate spatio-temporal prediction evaluation procedures [
66].
Data and Code Availability