Index for the Consistent Measurement of Spatial Heterogeneity for Large-Scale Land Cover Datasets
Abstract
:1. Introduction
2. Spatial Heterogeneity of Land Cover: Problems and Solution
2.1. Inconsistency Problems at Large Scales
2.2. Solution: Land Cover Complexity Index (LCCI) Design
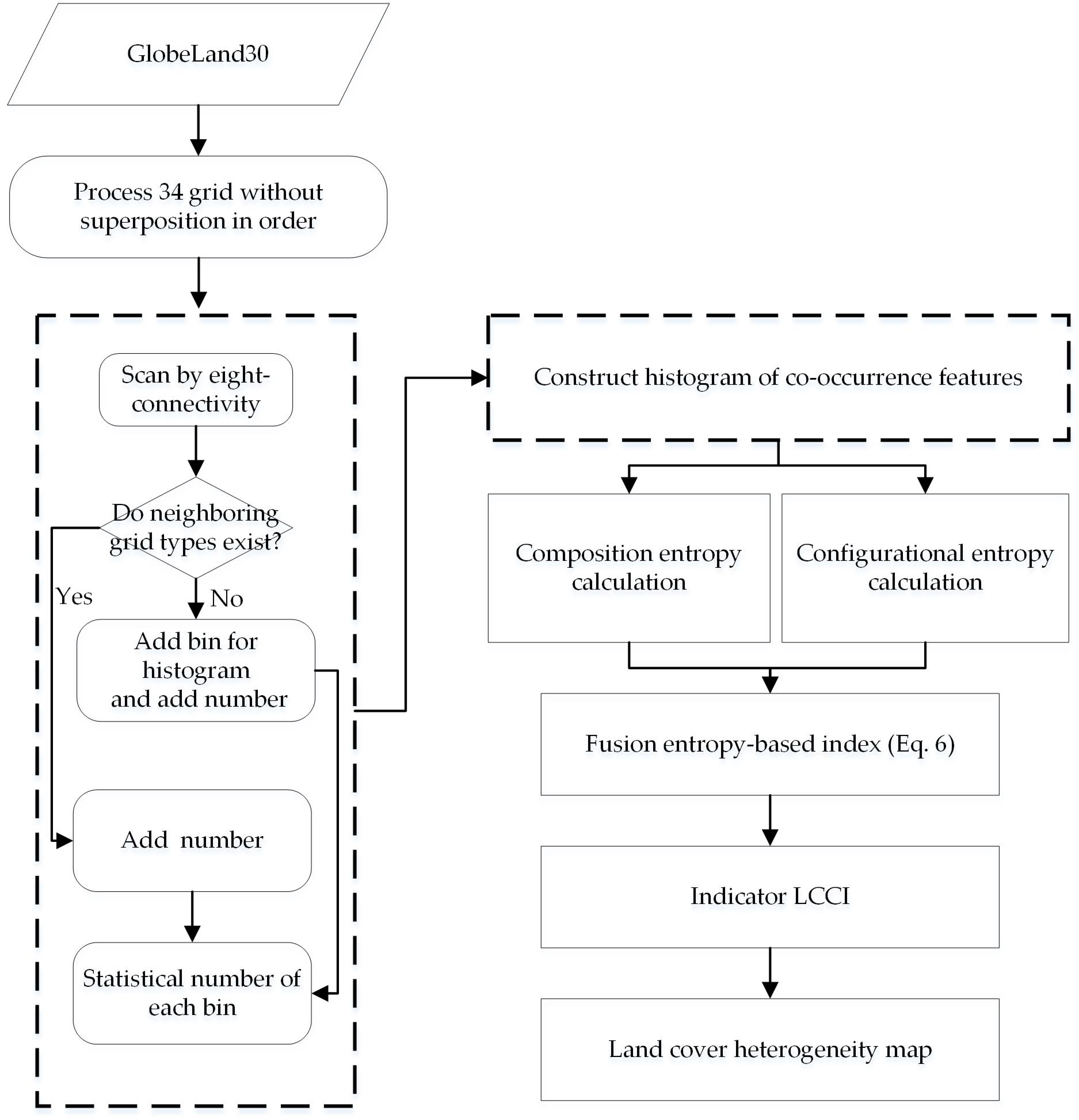
3. Adaptive Method for Index Fusion
3.1. Entropy-Based Fundamental Index of Spatial Heterogeneity Measurements
3.2. Fusion of Entropy-Based Indices
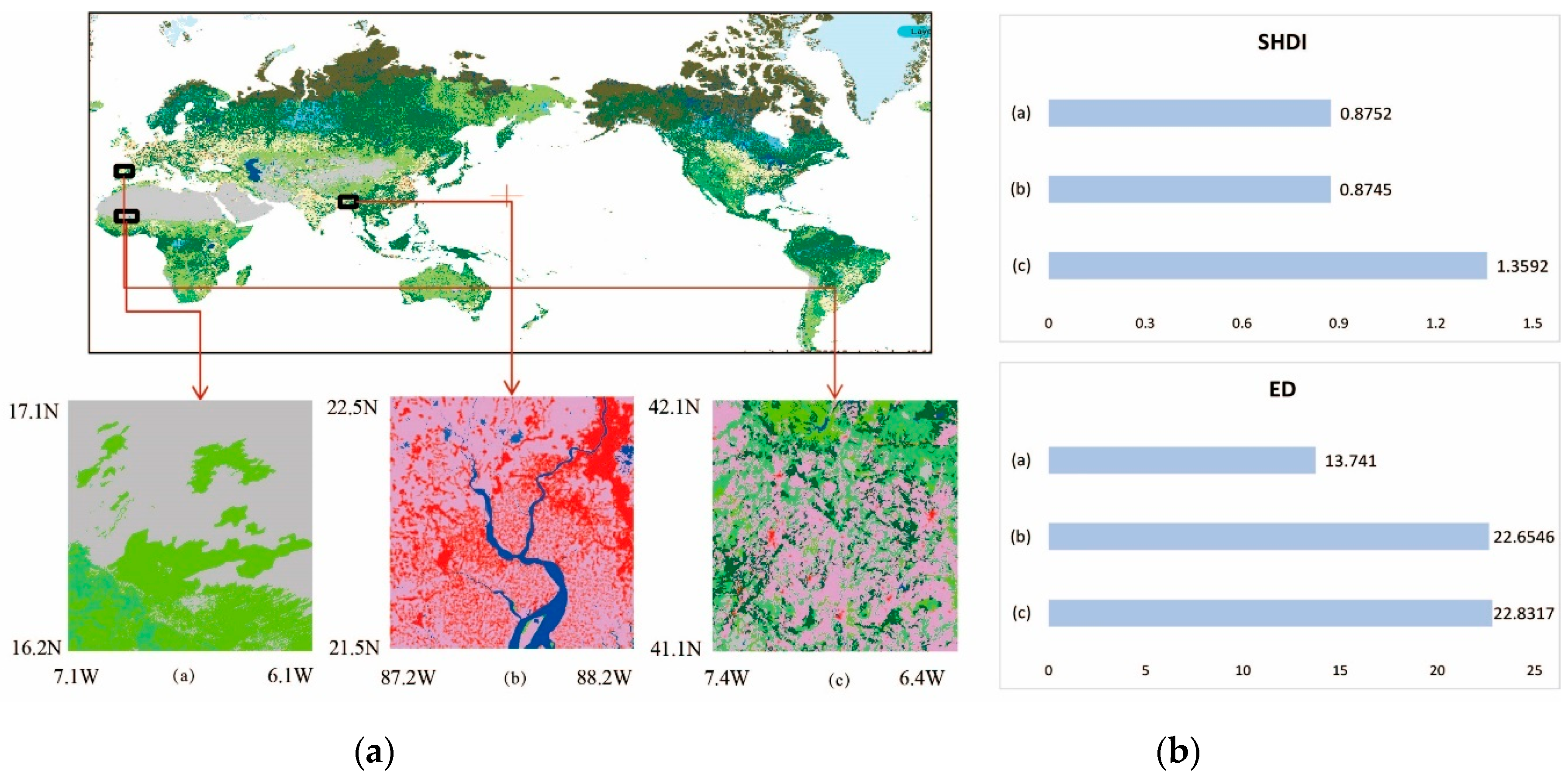
4. Experiment and Analysis
4.1. Datasets and Quantization Scheme
4.2. Validation of LCCI
4.3. Relationships between LCCI and Landscape Metrics
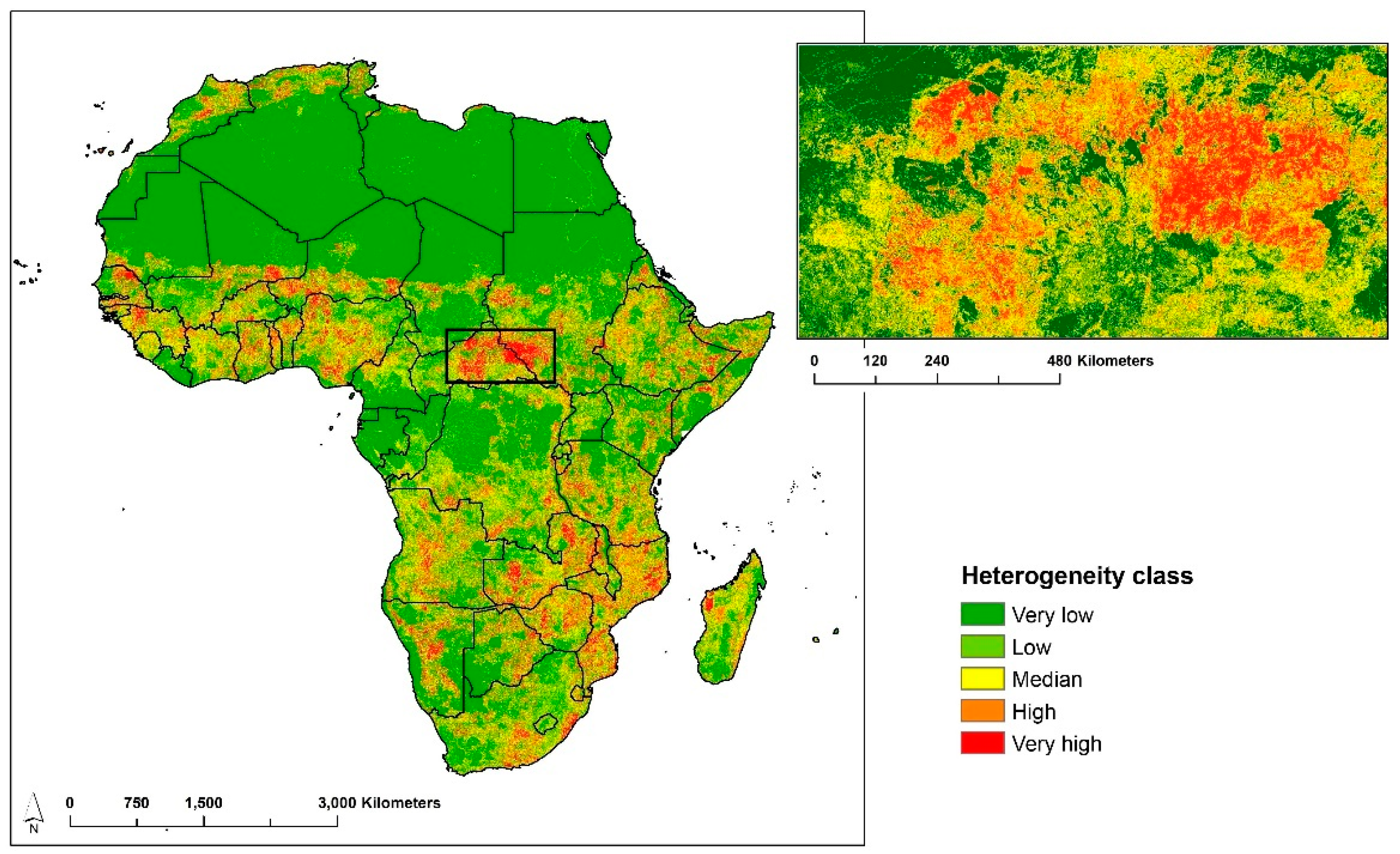
4.4. Large-Scale Application: Example Africa
5. Summary and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Skidmore, A.K.; Pettorelli, N.; Coops, N.C.; Geller, G.N.; Hansen, M.; Lucas, R. Environmental science: Agree on biodiversity metrics to track from space. Nature 2015, 523, 403–405. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tuanmu, M.-N.; Jetz, W.A. Global remote sensing-based characterization of terrestrial habitat heterogeneity for biodiversity and ecosystem modelling. Glob. Ecol. Biogeogr. 2015, 24, 1329–1339. [Google Scholar] [CrossRef]
- Yu, Q.; Hu, Q.; van Vliet, J.; Verburg, P.H.; Wu, W. GlobeLand30 shows little cropland area loss but greater fragmentation in China. Int. J. Appl. Earth Obs. 2018, 66, 37–45. [Google Scholar] [CrossRef]
- Verburg, P.H.; Neumann, K.; Nol, L. Challenges in using land use and land cover data for global change studies. Glob. Chang. Biol. 2011, 17, 974–989. [Google Scholar] [CrossRef] [Green Version]
- Li, S.; Yang, B. Introducing a new method for assessing spatially explicit processes of landscape fragmentation. Ecol. Indic. 2015, 56, 116–124. [Google Scholar] [CrossRef]
- Schindler, S.; von Wehrden, H.; Poirazidis, K.; Hochachka, W.M.; Wrbka, T.; Kati, V. Performance of methods to select landscape metrics for modelling species richness. Ecol. Model. 2015, 295, 107–112. [Google Scholar] [CrossRef]
- Hernández, A.; Miranda, M.; Arellano, E.C.; Saura, S.; Ovalle, C. Landscape dynamics and their effect on the functional connectivity of a Mediterranean landscape in Chile. Ecol. Indic. 2015, 48, 198–206. [Google Scholar] [CrossRef]
- Parrott, L. Measuring ecological complexity. Ecol. Indic. 2010, 10, 1069–1076. [Google Scholar] [CrossRef]
- Chen, F.; Chen, J.; Wu, H.; Hou, D.; Zhang, W.; Zhang, J.; Zhou, X.; Chen, L. A landscape shape index-based sampling approach for land cover accuracy assessment. Sci. China Earth Sci. 2016, 59, 2263–2274. [Google Scholar] [CrossRef]
- Tran, T.; Julian, J.; de Beurs, K. Land cover heterogeneity effects on sub-pixel and per-pixel classifications. ISPRS Int. J. Geo.-Inf. 2014, 3, 540–553. [Google Scholar] [CrossRef] [Green Version]
- Cochran, F.; Daniel, J.; Jackson, L.; Neale, A. Earth observation-based ecosystem services indicators for national and subnational reporting of the sustainable development goals. Remote Sens. Environ. 2020, 244, 111796. [Google Scholar] [CrossRef] [PubMed]
- Gustafson, E.J. Quantifying landscape spatial pattern: What is the state of the art? Ecosystems 1998, 1, 143–156. [Google Scholar] [CrossRef]
- Riitters, K.H. Spatial Patterns of Land Cover in the United States: A Technical Document Supporting the Forest Service 2010 RPA Assessment; Gen. Tech. Rep. SRS–136; Department of Agriculture Forest Service, Southern Research Station: Asheville, NC, USA, 2011; 64p.
- Jaeger, J.A.G.; Madrinan, L.F. Landscape Fragmentation in Europe; Joint EEA-FOEN report; European Environmental Agency, Publications Office of the European Union: Luxembourg, 2011; pp. 20–46. ISSN 1725-9177. [Google Scholar] [CrossRef]
- Dale, V.H.; Kline, K.L. Issues in using landscape indicators to assess land changes. Ecol. Indic. 2013, 28, 91–99. [Google Scholar] [CrossRef]
- Nalewajski, R.F. Elements of Information Theory. In Perspectives in Electronic Structure Theory; Springer: Berlin/Heidelberg, Germany, 2012; pp. 371–395. [Google Scholar] [CrossRef]
- Proulx, R.; Parrott, L. Measures of structural complexity in digital images for monitoring the ecological signature of an old-growth forest ecosystem. Ecol. Indic. 2008, 8, 270–284. [Google Scholar] [CrossRef]
- Vranken, I.; Baudry, J.; Aubinet, M.; Visser, M.; Bogaert, J. A review on the use of entropy in landscape ecology: Heterogeneity, unpredictability, scale dependence and their links with thermodynamics. Landsc. Ecol. 2015, 30, 51–65. [Google Scholar] [CrossRef] [Green Version]
- Andrienko, Y.A.; Brilliantov, N.V.; Kurths, J. Complexity of two-dimensional patterns. Eur. Phys. J. B 2000, 15, 539–546. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Reynolds, J.F. A new contagion index to quantify spatial patterns of landscapes. Landsc. Ecol. 1993, 8, 155–162. [Google Scholar] [CrossRef]
- Bogaert, J.; Farina, A.; Ceulemans, R. Entropy increase of fragmented habitats: A sign of human impact? Ecol. Indic. 2005, 5, 207–212. [Google Scholar] [CrossRef]
- Cousins, S.A.O.; Auffret, A.G.; Lindgren, J.; Trank, L. Regional-scale land-cover change during the 20th century and its consequences for biodiversity. Ambio 2015, 44, S17–S27. [Google Scholar] [CrossRef] [Green Version]
- Chmielewski, S.; Chmielewski, T.J.; Tompalski, P. Land cover and landscape diversity analysis in the West Polesie Biosphere Reserve. Int. Agrophys. 2014, 28, 153–162. [Google Scholar] [CrossRef] [Green Version]
- Gao, P.C.; Li, Z.L. Computation of the Boltzmann entropy of a landscape: A review and a generalization. Landsc. Ecol. 2019, 34, 2183–2196. [Google Scholar] [CrossRef]
- Wang, C.; Zhao, H. Spatial heterogeneity analysis: Introducing a new form of spatial entropy. Entropy 2018, 20, 398. [Google Scholar] [CrossRef] [Green Version]
- Claramunt, C. A Spatial form of Diversity; Springer: Berlin/Heidelberg, Germany, 2005; pp. 218–231. [Google Scholar]
- Li, Z.L.; Huang, P.Z. Quantitative measures for spatial information of maps. Int. J. Geogr. Inf. Sci. 2002, 16, 699–709. [Google Scholar] [CrossRef]
- Altieri, L.; Cocchi, D.; Roli, G. A new approach to spatial entropy measures. Environ. Ecol. Stat. 2018, 25, 95–110. [Google Scholar] [CrossRef]
- Gao, P.C.; Li, Z.L.; Zhang, H. Thermodynamics-Based Evaluation of Various Improved Shannon Entropies for Configurational Information of Gray-Level Images. Entropy 2018, 20, 19. [Google Scholar] [CrossRef] [Green Version]
- Cushman, S.A. Calculation of Configurational Entropy in Complex Landscapes. Entropy 2018, 20, 298. [Google Scholar] [CrossRef] [Green Version]
- Cushman, S.A. Calculating the configurational entropy of a landscape mosaic. Landsc. Ecol. 2015, 31, 481–489. [Google Scholar] [CrossRef]
- Cushman, S.A. Editorial: Entropy in Landscape Ecology. Entropy 2018, 20, 314. [Google Scholar] [CrossRef] [Green Version]
- Gao, P.C.; Zhang, H.; Li, Z.L. An efficient analytical method for computing the Boltzmann entropy of a landscape gradient. Trans. GIS 2018, 22, 1046–1063. [Google Scholar] [CrossRef]
- Gao, P.; Zhang, H.; Li, Z. A hierarchy-based solution to calculate the configurational entropy of landscape gradients. Landsc. Ecol. 2017, 32, 1133–1146. [Google Scholar] [CrossRef]
- Cushman, S.A.; McGarigal, K.; Neel, M.C. Parsimony in landscape metrics: Strength, universality, and consistency. Ecol. Indic. 2008, 8, 691–703. [Google Scholar] [CrossRef]
- Fahrig, L.; Nuttle, W.K. Population Ecology in Spatially Heterogeneous Environments. In Ecosystem Function in Heterogeneous Landscapes; Lovett, G.M., Turner, M.G., Jones, C.G., Weathers, K.C., Eds.; Springer: New York, NY, USA, 2005; pp. 95–118. [Google Scholar] [CrossRef]
- Llausàs, A.; Nogué, J. Indicators of landscape fragmentation: The case for combining ecological indices and the perceptive approach. Ecol. Indic. 2012, 15, 85–91. [Google Scholar] [CrossRef]
- Riitters, K. Pattern metrics for a transdisciplinary landscape ecology. Landsc. Ecol. 2018, 34, 2057–2063. [Google Scholar] [CrossRef] [Green Version]
- Riitters, K.H.; O′Neill, R.V.; Hunsaker, C.T.; Wickham, J.D.; Yankee, D.H.; Timmins, S.P.; Jones, K.B.; Jackson, B.L. A factor analysis of landscape pattern and structure metrics. Landsc. Ecol. 1995, 10, 23–39. [Google Scholar] [CrossRef]
- Nowosad, J.; Stepinski, T.F. Information theory as a consistent framework for quantification and classification of landscape patterns. Landsc. Ecol. 2019, 34, 2091–2101. [Google Scholar] [CrossRef] [Green Version]
- Bordogna, G.; Boschetti, M.; Brivio, P.A.; Carrara, P.; Stroppiana, D.; Weissteiner, C.J. Handling heterogeneous bipolar information for modelling environmental syndromes of global change. Environ. Modell Softw. 2012, 36, 131–147. [Google Scholar] [CrossRef]
- ESRI, R. ArcGIS Desktop: Release 10; Environmental Systems Research Institute: Redlands, CA, USA, 2011. [Google Scholar]
- Niesterowicz, J.; Stepinski, T.F. Regionalization of multi-categorical landscapes using machine vision methods. Appl. Geogr. 2013, 45, 250–258. [Google Scholar] [CrossRef]
- Peng, J.; Wang, Y.; Zhang, Y.; Wu, J.; Li, W.; Li, Y. Evaluating the effectiveness of landscape metrics in quantifying spatial patterns. Ecol. Indic. 2010, 10, 217–223. [Google Scholar] [CrossRef]
- Tian, Y.; Jim, C.Y.; Tao, Y.; Shi, T. Landscape ecological assessment of green space fragmentation in Hong Kong. Urban. For. Urban. Green 2011, 10, 79–86. [Google Scholar] [CrossRef]
- Reddy, C.S.; Sreelekshmi, S.; Jha, C.S.; Dadhwal, V.K. National assessment of forest fragmentation in India: Landscape indices as measures of the effects of fragmentation and forest cover change. Ecol. Eng. 2013, 60, 453–464. [Google Scholar] [CrossRef]
- Thakkar, J.J. Applications of Structural Equation Modelling with AMOS 21, IBM SPSS. In Structural Equation Modelling: Application for Research and Practice (with AMOS and R); Springer: Singapore, 2020; pp. 35–89. [Google Scholar] [CrossRef]
- Mayaux, P.; Eva, H.; Gallego, J.; Strahler, A.H.; Herold, M.; Agrawal, S.; Naumov, S.; De Miranda, E.E.; Di Bella, C.M.; Ordoyne, C.; et al. Validation of the global land cover 2000 map. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1728–1737. [Google Scholar] [CrossRef] [Green Version]
- Zeng, Y.L.; Li, J.; Liu, Q.H.; Li, L.H.; Xu, B.D.; Yin, G.F.; Peng, J.J. A Sampling Strategy for Remotely Sensed LAI Product Validation Over Heterogeneous Land Surfaces. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2014, 7, 3128–3142. [Google Scholar] [CrossRef]
- Wang, S.G.; Li, X.; Ge, Y.; Jin, R.; Ma, M.G.; Liu, Q.H.; Wen, J.G.; Liu, S.M. Validation of Regional-Scale Remote Sensing Products in China: From Site to Network. Remote Sens. 2016, 8, 980. [Google Scholar] [CrossRef] [Green Version]
- Niesterowicz, J.; Stepinski, T.F. On using landscape metrics for landscape similarity search. Ecol. Indic. 2016, 64, 20–30. [Google Scholar] [CrossRef]
- Li, H.; Peng, J.; Yanxu, L.; Yi′na, H. Urbanization impact on landscape patterns in Beijing City, China: A spatial heterogeneity perspective. Ecol. Indic. 2017, 82, 50–60. [Google Scholar] [CrossRef]
- Freedman, D.; Diaconis, P. On the histogram as a density estimator: L 2 theory. Probab. Theory Rel. 1981, 57, 453–476. [Google Scholar]
- Bunce, R.G.H.; Metzger, M.J.; Jongman, R.H.G.; Brandt, J.; de Blust, G.; Elena-Rossello, R.; Groom, G.B.; Halada, L.; Hofer, G.; Howard, D.C.; et al. A standardized procedure for surveillance and monitoring European habitats and provision of spatial data. Landsc. Ecol. 2007, 23, 11–25. [Google Scholar] [CrossRef]
- Wrbka, T.; Schindler, S.; Pollheimer, M.; Schmitzberger, I.; Peterseil, J. Impact of the Austrian agri-environmental scheme on diversity of landscapes, plants and birds. Community Ecol. 2008, 9, 217–227. [Google Scholar] [CrossRef]
- Zheng, Z.; Du, S.; Wang, Y.-C.; Wang, Q. Mining the regularity of landscape-structure heterogeneity to improve urban land-cover mapping. Remote Sens. Environ. 2018, 214, 14–32. [Google Scholar] [CrossRef]




| Path | Correlation | Direct Path Coefficient | Indirect Path Coefficients | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| PD | LPI | ED | COHE | SHDI | AI | FRAC | DIVISI | SPLIT | |||
| PD→LCCI | 0.914 | 0.115 | - | 0.065 | 0.683 | 0.183 | 0.056 | −0.541 | −0.002 | −0.108 | 0.002 |
| LPI→LCCI | −0.755 | −0.122 | −0.061 | - | −0.526 | −0.185 | −0.071 | 0.408 | −0.003 | 0.189 | −0.002 |
| ED→LCCI | 0.948 | 0.734 | 0.107 | 0.087 | - | 0.199 | 0.066 | −0.579 | 0.000 | −0.146 | 0.002 |
| COHE→LCCI | −0.965 | −0.222 | −0.095 | −0.102 | −0.657 | - | −0.071 | 0.514 | −0.001 | 0.158 | −0.003 |
| SHDI→LCCI | 0.87 | 0.08 | 0.081 | 0.108 | 0.607 | 0.197 | - | −0.469 | 0.002 | −0.177 | 0.002 |
| AI→LCCI | −0.942 | 0.58 | −0.107 | −0.086 | −0.733 | −0.197 | −0.065 | - | 0.000 | 0.143 | −0.002 |
| FRAC→LCCI | −0.009 | 0.011 | −0.018 | 0.036 | 0.014 | 0.014 | 0.011 | −0.009 | - | −0.064 | 0.000 |
| DIVISI→LCCI | 0.758 | −0.193 | 0.064 | 0.119 | 0.555 | 0.182 | 0.073 | −0.430 | 0.004 | - | 0.002 |
| SPILT→LCCI | 0.844 | 0.003 | 0.073 | 0.100 | 0.530 | 0.207 | 0.063 | −0.412 | 0.001 | −0.147 | - |
| Name | ED | LCCI | Name | ED | LCCI |
|---|---|---|---|---|---|
| Egypt | 4.911 | 0.017 | Rwanda | 132.235 | 0.436 |
| Libya | 6.174 | 0.021 | Madeira | 132.541 | 0.442 |
| Sao Tome And Principe | 7.506 | 0.026 | South Africa | 141.229 | 0.462 |
| Western Sahara | 11.070 | 0.036 | Somalia | 142.393 | 0.438 |
| Mayotte | 13.440 | 0.056 | Madagascar | 156.256 | 0.509 |
| Equatorial Guinea | 15.247 | 0.056 | Angola | 164.069 | 0.529 |
| Algeria | 23.089 | 0.075 | Tanzania | 171.451 | 0.545 |
| Gabon | 22.555 | 0.077 | Canarias | 167.345 | 0.554 |
| Mauritania | 26.133 | 0.083 | Burundi | 175.094 | 0.555 |
| Seychelles | 33.432 | 0.097 | Ethiopia | 174.560 | 0.555 |
| Mauritius | 33.937 | 0.126 | Cote D’ Ivoire | 170.183 | 0.555 |
| Chad | 43.717 | 0.140 | Burkina Faso | 174.283 | 0.573 |
| Liberia | 41.498 | 0.148 | Reunion | 167.598 | 0.577 |
| Comoros | 45.797 | 0.160 | Malawi | 185.540 | 0.587 |
| Congo | 49.338 | 0.169 | Gambia | 190.583 | 0.595 |
| Mali | 70.920 | 0.227 | Nigeria | 187.229 | 0.610 |
| Niger | 78.068 | 0.242 | Sierra Leone | 185.612 | 0.613 |
| Tunisia | 81.901 | 0.262 | Ghana | 194.802 | 0.630 |
| Cameroon | 87.971 | 0.293 | Senegal | 211.942 | 0.633 |
| Sudan | 94.708 | 0.298 | Benin | 212.662 | 0.654 |
| Djibouti | 98.053 | 0.316 | Guinea-Bissau | 208.493 | 0.656 |
| Uganda | 105.541 | 0.345 | Zambia | 225.873 | 0.701 |
| Congo | 109.305 | 0.358 | Central African | 226.201 | 0.710 |
| Kenya | 115.615 | 0.374 | Zimbabwe | 228.842 | 0.716 |
| Morocco | 117.283 | 0.380 | Swaziland | 222.681 | 0.723 |
| Lesotho | 114.813 | 0.401 | Guinea | 226.978 | 0.736 |
| Eritrea | 127.472 | 0.411 | Togo | 238.801 | 0.770 |
| Botswana | 136.813 | 0.422 | Mozambique | 259.578 | 0.814 |
| Namibia | 133.939 | 0.431 |
| Complexity Index | Heterogeneity Level | Distribution Characteristics |
|---|---|---|
| <0.2 | Very low | Area with dispersed forest and bare land areas. |
| (0.2, 0.6) | low | Mainly in grassland and cropland mixed areas. |
| (0.6, 1) | Median | Natural and semi-natural mixed areas show moderate fragmentation. |
| (1, 1.5) | High | Distributed in grassland and shrub mixed regions, grasslands, and forest mixed regions. |
| >1.5 | Very high | A small number of areas distributed in a natural area with shrubs, grassland, and forest mosaic. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, J.; Peng, S.; Zhang, W.; Kang, S. Index for the Consistent Measurement of Spatial Heterogeneity for Large-Scale Land Cover Datasets. ISPRS Int. J. Geo-Inf. 2020, 9, 483. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi9080483
Yu J, Peng S, Zhang W, Kang S. Index for the Consistent Measurement of Spatial Heterogeneity for Large-Scale Land Cover Datasets. ISPRS International Journal of Geo-Information. 2020; 9(8):483. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi9080483
Chicago/Turabian StyleYu, Jing, Shu Peng, Weiwei Zhang, and Shun Kang. 2020. "Index for the Consistent Measurement of Spatial Heterogeneity for Large-Scale Land Cover Datasets" ISPRS International Journal of Geo-Information 9, no. 8: 483. https://0-doi-org.brum.beds.ac.uk/10.3390/ijgi9080483




