A Semi-Parametric Approach to the Oaxaca–Blinder Decomposition with Continuous Group Variable and Self-Selection
Abstract
:1. Introduction
2. The OB Decomposition with Selection: Basics
3. Generalized Sample Selection
4. Varying Coefficient Models with Endogenous Membership
4.1. Local Kernel Estimators
4.2. Bandwidth and Standard Errors
- Step 1. Obtain a random paired bootstrap sample from the original sample.
- Step 2. Estimate the selection correction term using any of the methods presented in Section 2.
- Step 3. Estimate the coefficient for the outcome models for all points of interest , based on the bootstrap sample , using local kernel regressions, and the global optimal bandwidth.
- Step 4. Estimate the decomposition components for the group(s) of interest.
- Step 5. Repeat Steps 1 to 4, B times to obtain the empirical distributions of the aggregated and detailed decomposition components.
5. Monte-Carlo Simulations
6. Application: Revising the Impact of Obesity on Wages
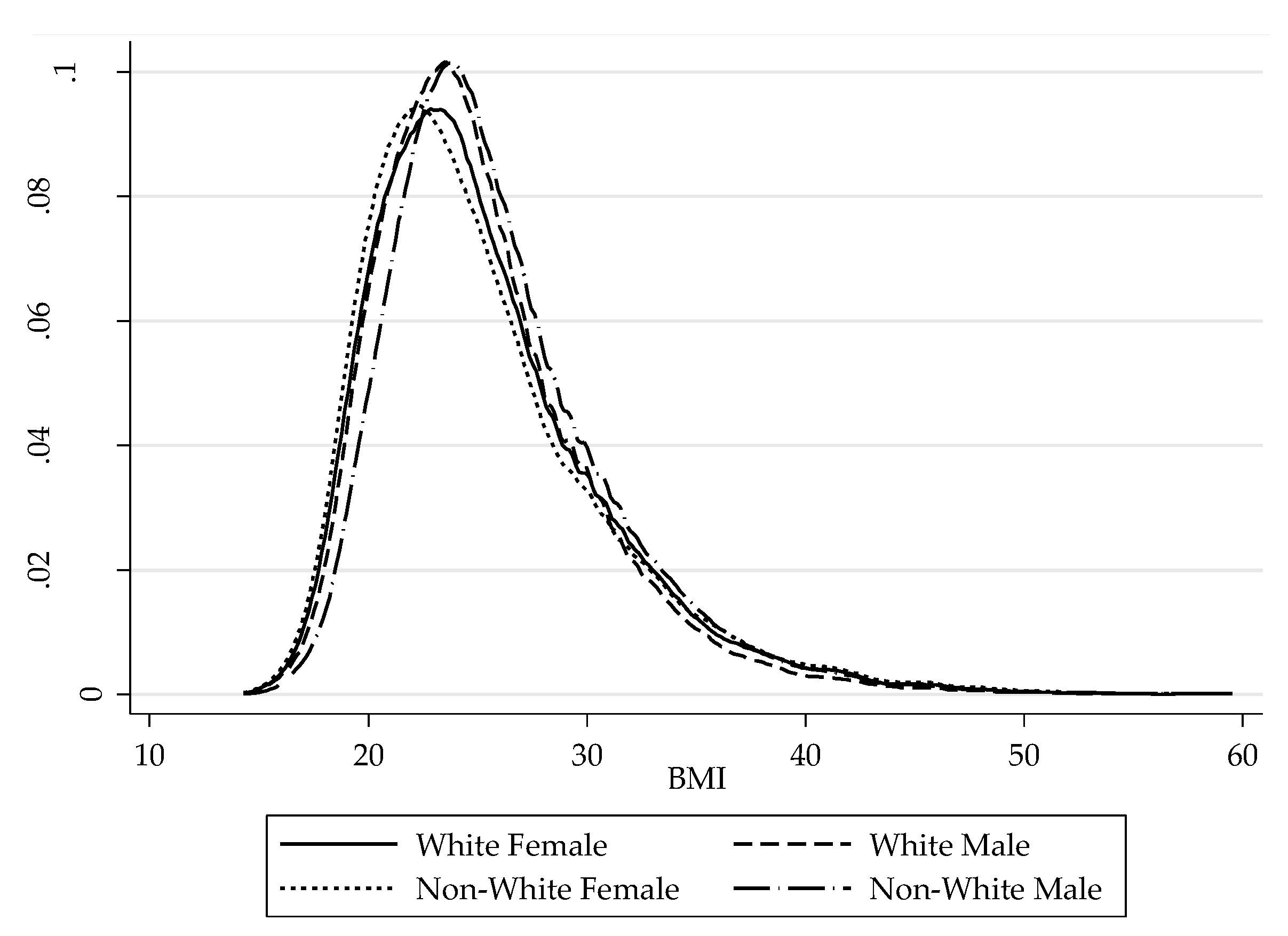
6.1. Replication and Variable Definition Changes
6.2. Semiparametric Oaxaca Decomposition
6.2.1. Oaxaca Decomposition Approach and Implementation
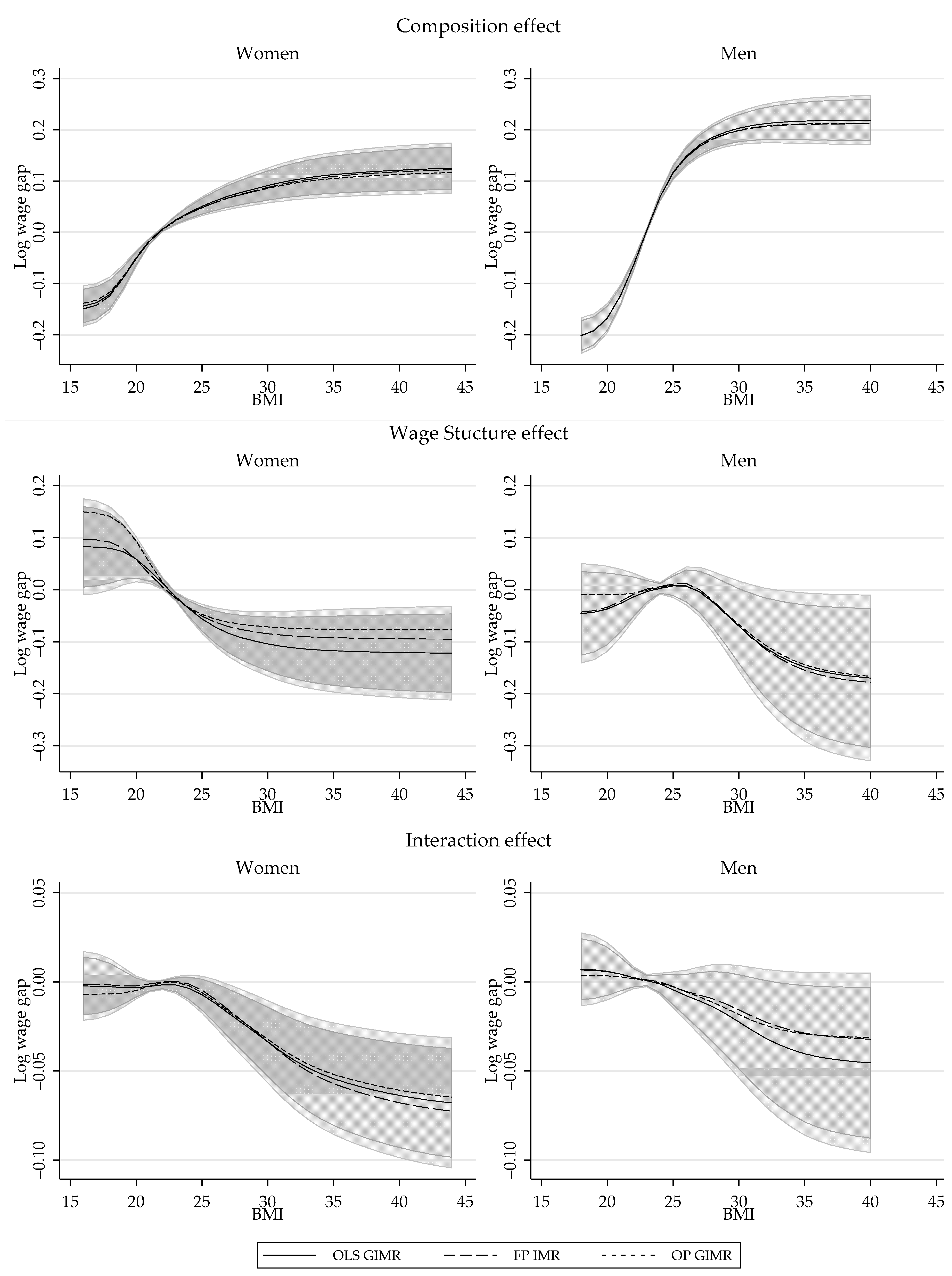
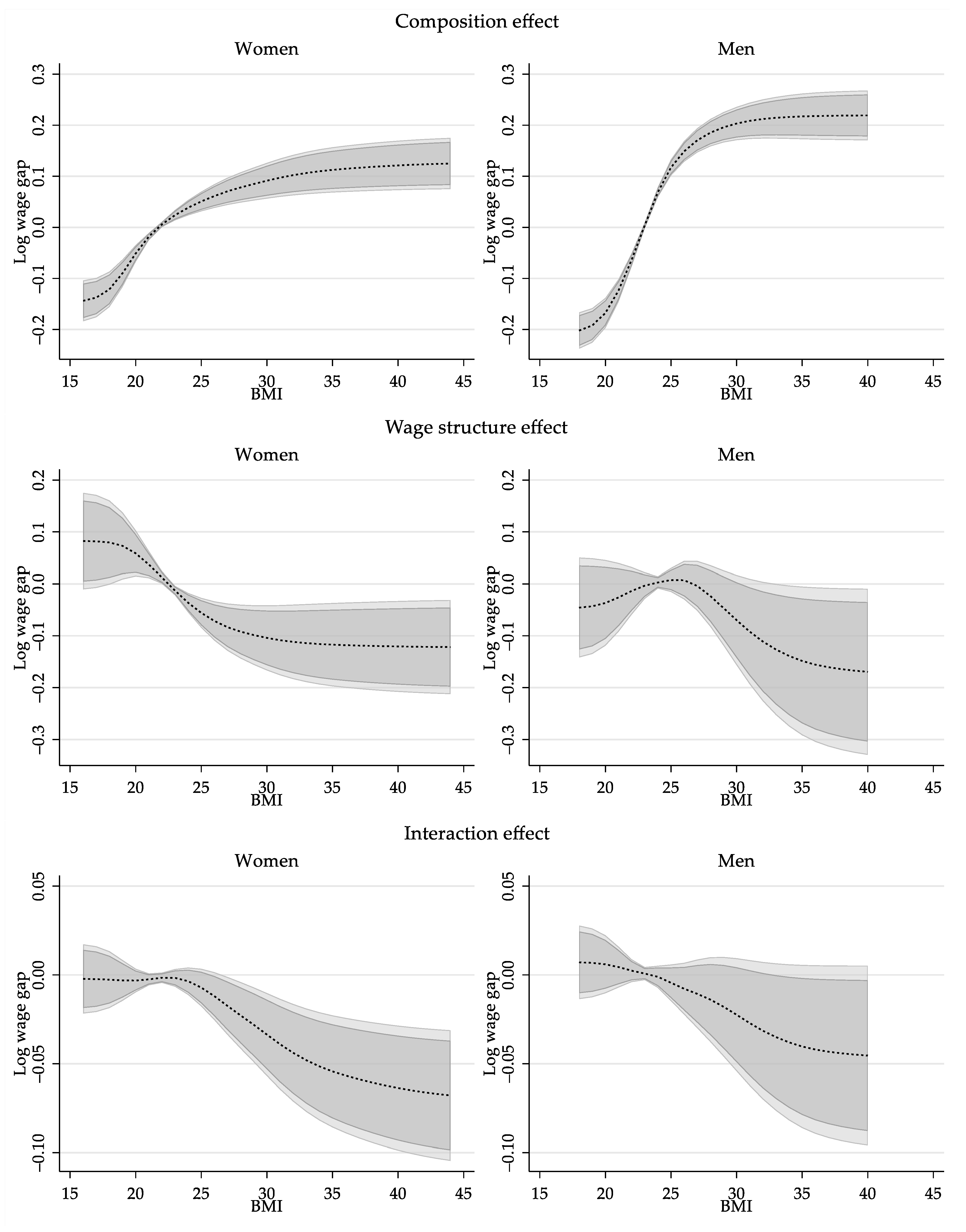
6.2.2. Aggregate Decomposition Results
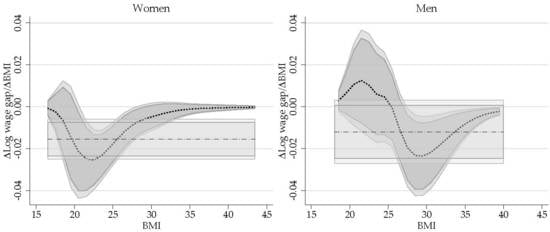
6.2.3. Revisiting the Impact of Obesity on Wages: Partial Effect of BMI
7. Conclusions
Conflicts of Interest
Appendix A. Additional Monte-Carlo Simulations
| True | Bias | 95% | 95% | |||
| Cov. | BC Cov. | |||||
| 0.05 | 0.005 | 0.019 | 0.057 | 0.055 | 93.8% | 94.4% |
| 0.15 | 0.045 | 0.019 | 0.057 | 0.056 | 93.5% | 93.9% |
| 0.25 | 0.125 | 0.019 | 0.059 | 0.056 | 94.2% | 93.7% |
| 0.35 | 0.245 | 0.019 | 0.059 | 0.057 | 93.8% | 93.8% |
| 0.45 | 0.405 | 0.020 | 0.059 | 0.057 | 93.5% | 93.8% |
| 0.55 | 0.605 | 0.019 | 0.059 | 0.058 | 94.8% | 94.7% |
| 0.65 | 0.845 | 0.019 | 0.059 | 0.058 | 94.4% | 95.0% |
| 0.75 | 1.125 | 0.020 | 0.059 | 0.057 | 93.2% | 94.5% |
| 0.85 | 1.445 | 0.020 | 0.059 | 0.057 | 93.5% | 94.1% |
| 0.95 | 1.805 | 0.019 | 0.057 | 0.056 | 93.2% | 94.4% |
| True | Bias | 95% | 95% | |||
| Cov. | BC Cov. | |||||
| 0.05 | 0.156 | 0.000 | 0.026 | 0.026 | 94.7% | 94.8% |
| 0.15 | 0.454 | 0.000 | 0.027 | 0.026 | 95.6% | 95.6% |
| 0.25 | 0.707 | 0.001 | 0.027 | 0.027 | 95.1% | 95.3% |
| 0.35 | 0.891 | 0.000 | 0.028 | 0.027 | 94.7% | 94.8% |
| 0.45 | 0.988 | 0.001 | 0.028 | 0.027 | 94.2% | 94.4% |
| 0.55 | 0.988 | 0.000 | 0.028 | 0.027 | 94.9% | 95.0% |
| 0.65 | 0.891 | 0.000 | 0.027 | 0.027 | 94.8% | 94.8% |
| 0.75 | 0.707 | 0.001 | 0.027 | 0.027 | 94.6% | 94.5% |
| 0.85 | 0.454 | 0.000 | 0.027 | 0.027 | 94.7% | 94.7% |
| 0.95 | 0.156 | 0.000 | 0.026 | 0.026 | 95.2% | 95.3% |
| True | Bias | 95% | 95% | |||
| Cov. | BC Cov. | |||||
| 0.05 | 1.902 | −0.177 | 0.047 | 0.046 | 1.5% | 94.6% |
| 0.15 | 1.721 | −0.256 | 0.044 | 0.043 | 0.0% | 94.7% |
| 0.25 | 1.558 | −0.214 | 0.041 | 0.040 | 0.0% | 94.1% |
| 0.35 | 1.409 | −0.139 | 0.039 | 0.038 | 4.3% | 93.7% |
| 0.45 | 1.275 | −0.053 | 0.036 | 0.036 | 68.6% | 94.0% |
| 0.55 | 1.154 | 0.039 | 0.034 | 0.034 | 77.7% | 94.3% |
| 0.65 | 1.044 | 0.126 | 0.033 | 0.033 | 4.1% | 94.1% |
| 0.75 | 0.945 | 0.200 | 0.033 | 0.033 | 0.0% | 93.9% |
| 0.85 | 0.855 | 0.244 | 0.033 | 0.033 | 0.0% | 94.3% |
| 0.95 | 0.773 | 0.164 | 0.033 | 0.034 | 0.2% | 95.2% |
| True | Bias | 95% | 95% | |||
| Cov. | BC Cov. | |||||
| 0.05 | 0.005 | −0.003 | 0.046 | 0.044 | 94.1% | 94.5% |
| 0.15 | 0.045 | −0.004 | 0.047 | 0.045 | 93.9% | 94.3% |
| 0.25 | 0.125 | −0.003 | 0.047 | 0.045 | 94.2% | 93.8% |
| 0.35 | 0.245 | −0.004 | 0.047 | 0.046 | 94.1% | 94.2% |
| 0.45 | 0.405 | −0.002 | 0.048 | 0.046 | 93.8% | 94.1% |
| 0.55 | 0.605 | −0.003 | 0.047 | 0.046 | 93.6% | 94.2% |
| 0.65 | 0.845 | −0.004 | 0.047 | 0.046 | 94.0% | 94.0% |
| 0.75 | 1.125 | −0.003 | 0.048 | 0.046 | 93.6% | 94.0% |
| 0.85 | 1.445 | −0.003 | 0.047 | 0.046 | 94.1% | 94.3% |
| 0.95 | 1.805 | −0.007 | 0.047 | 0.046 | 93.6% | 94.1% |
| True | Bias | 95% | 95% | |||
| Cov. | BC Cov. | |||||
| 0.05 | 0.156 | 0.000 | 0.022 | 0.022 | 95.5% | 95.5% |
| 0.15 | 0.454 | 0.001 | 0.022 | 0.022 | 95.2% | 95.2% |
| 0.25 | 0.707 | 0.003 | 0.022 | 0.022 | 95.5% | 94.9% |
| 0.35 | 0.891 | 0.004 | 0.022 | 0.023 | 94.9% | 95.2% |
| 0.45 | 0.988 | 0.005 | 0.023 | 0.023 | 94.8% | 95.2% |
| 0.55 | 0.988 | 0.004 | 0.022 | 0.023 | 94.8% | 95.6% |
| 0.65 | 0.891 | 0.003 | 0.023 | 0.023 | 94.8% | 94.9% |
| 0.75 | 0.707 | 0.003 | 0.022 | 0.023 | 94.8% | 95.3% |
| 0.85 | 0.454 | 0.002 | 0.022 | 0.023 | 94.3% | 94.4% |
| 0.95 | 0.156 | 0.000 | 0.022 | 0.023 | 96.0% | 96.0% |
| True | Bias | 95% | 95% | |||
| Cov. | BC Cov. | |||||
| 0.05 | 1.902 | 0.002 | 0.037 | 0.037 | 95.3% | 95.4% |
| 0.15 | 1.721 | 0.001 | 0.034 | 0.033 | 95.5% | 95.5% |
| 0.25 | 1.558 | 0.001 | 0.032 | 0.032 | 94.6% | 94.4% |
| 0.35 | 1.409 | 0.000 | 0.032 | 0.031 | 93.9% | 93.8% |
| 0.45 | 1.275 | 0.000 | 0.031 | 0.030 | 94.4% | 94.4% |
| 0.55 | 1.154 | 0.001 | 0.030 | 0.030 | 94.8% | 95.0% |
| 0.65 | 1.044 | 0.002 | 0.029 | 0.029 | 94.6% | 94.6% |
| 0.75 | 0.945 | 0.001 | 0.029 | 0.029 | 94.6% | 94.7% |
| 0.85 | 0.855 | 0.001 | 0.029 | 0.029 | 94.8% | 94.6% |
| 0.95 | 0.773 | 0.002 | 0.031 | 0.031 | 94.4% | 94.2% |
| True | Bias | 95% | 95% | |||
| Cov. | BC Cov. | |||||
| 0.05 | 0.005 | −0.002 | 0.048 | 0.047 | 94.3% | 94.4% |
| 0.15 | 0.045 | −0.001 | 0.049 | 0.047 | 94.3% | 94.4% |
| 0.25 | 0.125 | −0.001 | 0.050 | 0.048 | 94.6% | 94.3% |
| 0.35 | 0.245 | −0.002 | 0.050 | 0.048 | 93.8% | 93.7% |
| 0.45 | 0.405 | 0.000 | 0.051 | 0.049 | 94.1% | 94.0% |
| 0.55 | 0.605 | −0.002 | 0.050 | 0.050 | 95.7% | 95.5% |
| 0.65 | 0.845 | −0.002 | 0.051 | 0.050 | 94.3% | 94.0% |
| 0.75 | 1.125 | 0.000 | 0.052 | 0.051 | 94.2% | 94.2% |
| 0.85 | 1.445 | −0.001 | 0.052 | 0.051 | 94.6% | 94.9% |
| 0.95 | 1.805 | −0.002 | 0.053 | 0.051 | 94.2% | 94.5% |
| True | Bias | 95% | 95% | |||
| Cov. | BC Cov. | |||||
| 0.05 | 0.156 | 0.000 | 0.023 | 0.023 | 95.3% | 95.1% |
| 0.15 | 0.454 | −0.001 | 0.023 | 0.023 | 94.9% | 95.0% |
| 0.25 | 0.707 | 0.000 | 0.024 | 0.024 | 95.0% | 94.9% |
| 0.35 | 0.891 | 0.000 | 0.024 | 0.024 | 94.5% | 94.6% |
| 0.45 | 0.988 | 0.001 | 0.025 | 0.024 | 95.4% | 95.3% |
| 0.55 | 0.988 | 0.000 | 0.024 | 0.024 | 95.4% | 95.4% |
| 0.65 | 0.891 | 0.000 | 0.025 | 0.025 | 95.8% | 95.8% |
| 0.75 | 0.707 | 0.001 | 0.025 | 0.025 | 94.5% | 94.6% |
| 0.85 | 0.454 | −0.001 | 0.025 | 0.025 | 94.9% | 94.7% |
| 0.95 | 0.156 | −0.001 | 0.025 | 0.025 | 95.2% | 95.1% |
| True | Bias | 95% | 95% | |||
| Cov. | BC Cov. | |||||
| 0.05 | 1.902 | −0.073 | 0.042 | 0.039 | 54.5% | 93.7% |
| 0.15 | 1.721 | −0.037 | 0.038 | 0.034 | 78.9% | 92.4% |
| 0.25 | 1.558 | −0.012 | 0.036 | 0.032 | 90.3% | 90.9% |
| 0.35 | 1.409 | 0.006 | 0.035 | 0.031 | 89.5% | 90.0% |
| 0.45 | 1.275 | 0.022 | 0.035 | 0.030 | 84.2% | 91.3% |
| 0.55 | 1.154 | 0.039 | 0.034 | 0.030 | 71.0% | 90.6% |
| 0.65 | 1.044 | 0.054 | 0.034 | 0.030 | 53.1% | 91.4% |
| 0.75 | 0.945 | 0.067 | 0.034 | 0.029 | 37.9% | 90.9% |
| 0.85 | 0.855 | 0.082 | 0.034 | 0.030 | 22.6% | 90.4% |
| 0.95 | 0.773 | 0.084 | 0.034 | 0.031 | 24.2% | 93.1% |
Appendix B. Sensitivity to Model Specifications and Bandwidth. Illustration
| Replication of Cawley (2004) | ||||||
| White | Black | Hispanic | ||||
| Male | Female | Male | Female | Male | Female | |
| BMI | −0.0131 | −0.0168 * | −0.00258 | −0.00191 | −0.00914 | −0.0124 |
| [0.00831] | [0.00496] | [0.00678] | [0.00600] | [0.00731] | [0.0125] | |
| N | 13,355 | 10,800 | 6811 | 5651 | 4374 | 3035 |
| Pooling Black and Hispanic | ||||||
| White | NonWhite | |||||
| Male | Female | Male | Female | |||
| BMI | −0.0131 | −0.0168 * | −0.00369 | −0.00515 | ||
| [0.00831] | [0.00496] | [0.00508] | [0.00544] | |||
| N | 13,355 | 10,800 | 11,185 | 8686 | ||
| Excluding Sample Weights | ||||||
| White | NonWhite | |||||
| Male | Female | Male | Female | |||
| BMI | −0.0126 | −0.0149 * | −0.00241 | −0.00643 | ||
| [0.00789] | [0.00471] | [0.00472] | [0.00518] | |||
| N | 13,355 | 10,800 | 11,185 | 8686 | ||
| Dropping if Parents education is missing | ||||||
| White | NonWhite | |||||
| Male | Female | Male | Female | |||
| BMI | −0.0118 | −0.0147 * | −0.003 | −0.00634 | ||
| [0.00803] | [0.00480] | [0.00481] | [0.00518] | |||
| N | 12,393 | 10,195 | 10,465 | 8224 | ||
| Modifying model specification | ||||||
| White | NonWhite | |||||
| Male | Female | Male | Female | |||
| BMI | −0.0124 | −0.0155 * | −0.0048 | −0.00673 | ||
| [0.00805] | [0.00487] | [0.00492] | [0.00535] | |||
| N | 12,191 | 10,111 | 9854 | 7963 | ||
| Dropping Extreme BMI values (below 16 and above 60) | ||||||
| White | NonWhite | |||||
| Male | Female | Male | Female | |||
| BMI | −0.0127 | −0.0154 * | −0.00425 | −0.00735 | ||
| [0.00804] | [0.00493] | [0.00504] | [0.00545] | |||
| N | 12,184 | 10,101 | 9844 | 7958 | ||



References
- Averett, Susan L. 2011. Labor market consequences: Employment, wages, disability, and absenteeism. In The Oxford Handbook of the Social Science of Obesity. Edited by J. Cawley. New York: Oxford University Press. [Google Scholar]
- Blinder, Alan S. 1973. Wage Discrimination: Reduced Form and Structural Estimates. The Journal of Human Resources 8: 436–55. [Google Scholar] [CrossRef]
- Cain, Glen G. 1986. The Economic Analysis of Labor Market Discrimination: A Survey. In Handbook of Labor Economics. Edited by Orley Ashenfelter and Richard Layard. Amsterdam: Elsevier Science Publishers, vol. 1. [Google Scholar]
- Cameron, A. Colin, and Pravin K. Trivedi. 2005. Microeconometrics: Methods and Applications. New York: Cambridge University Press. [Google Scholar]
- Cattaneo, Matias, and Michael Jansson. 2018. Kernel-based semiparametric estimators: Small bandwidth asymptotics and bootstrap consistency. Econometrica 86: 955–95. [Google Scholar] [CrossRef]
- Cawley, John. 2004. The Impact of Obesity on Wages. The Journal of Human Resources 39: 451–74. [Google Scholar] [CrossRef]
- Centorrino, Samuele, and Jeffrey S. Racine. 2017. Semiparametric Varying Coefficient Models with Endogenous Covariates. Annals of Economics and Statistics 128: 261–95. [Google Scholar] [CrossRef]
- Chernozhukov, Victor, Iván Fernández-Val, and Blaise Melly. 2013. Inference on Counterfactual Distributions. Econometrica Econometric Society 81: 2205–68. [Google Scholar] [CrossRef]
- Chiburis, Richard, and Michael Lokshin. 2007. Maximum likelihood and two-step estimation of an ordered-probit selection model. Stata Journal 7: 167–82. [Google Scholar] [CrossRef]
- Delgado, Michael S., Deniz Ozabaci, Yiguo Sun, and Subal C. Kumbhakar. 2019. Econometric Reviews, 1–23. [CrossRef]
- Fikkan, Janna L., and Esther D. Rothblum. 2012. Is fat a feminist issue? Exploring the gendered nature of weight bias. Sex Roles 66: 575–92. [Google Scholar] [CrossRef]
- Foresi, Silverio, and Franco Peracchi. 1995. The Conditional Distribution of Excess Returns: An Empirical Analysis. Journal of the American Statistical Association 90: 451–66. [Google Scholar] [CrossRef]
- Fortin, Nicole, Thomas Lemieux, and Sergio Firpo. 2011. Decomposition Methods in Economics. In Handbook of Labor Economics. Edited by Orley Ashenfelter and David Card. Amsterdam: Elsevier, vol. 4, Part A. pp. 1–102. [Google Scholar]
- Hastie, Trevor, and Robert Tibshirani. 1993. Varying-Coefficient Models. Journal of the Royal Statistical Society Series B (Methodological) 55: 757–96. [Google Scholar] [CrossRef]
- Heckman, James. J. 1979. Sample Selection Bias as a Specification Error. Econometrica 47: 53–161. [Google Scholar] [CrossRef]
- Henderson, Daniel J., and Christopher F. Parmeter. 2015. Applied Nonparametric Econometrics. Cambridge: Cambridge University Press. [Google Scholar]
- Horowitz, Joel. L., and Sokbae Lee. 2012. Uniform confidence bands for functions estimated nonparametrically with instrumental variables. Journal of Econometrics 168: 175–88. [Google Scholar] [CrossRef]
- Hotchkiss, Julie L., and Melinda M. Pitts. 2013. Even One Is Too Much: The Economic Consequences of Being a Smoker. Working Paper Series; WP 2013-3. Atlanta: Federal Reserve Bank of Atlanta. [Google Scholar]
- Keele, Luke J. 2008. Semiparametric Regression for the Social Sciences. New York: John Wiley & Sons. [Google Scholar]
- Kluve, Jochen, Hilmar Schneider, Arne Uhlendorff, and Zhong Zhao. 2012. Evaluating continuous training programmes by using the generalized propensity score. Journal of the Royal Statistical Society: Series A (Statistics in Society) 175: 587–617. [Google Scholar] [CrossRef]
- Lee, Lung-Fei. 1978. Unionism and Wage Rates: A Simultaneous Equations Model with Qualitative and Limited Dependent Variables. International Economic Review 19: 415–33. [Google Scholar] [CrossRef]
- Li, Qi, and Jeffrey. S. Racine. 2007. Nonparametric Econometrics: Theory and Practice. Woodstock: Princeton University Press. [Google Scholar]
- Ñopo, Hugo. 2008. An extension of the Blinder–Oaxaca decomposition to a continuum of reference groups. Economics Letters 100: 292–96. [Google Scholar] [CrossRef]
- Oaxaca, Ronald. 1973. Male-Female Wage Differentials in Urban Labor Markets. International Economic Review 14: 693–709. [Google Scholar] [CrossRef]
- Sabia, Joseph J., and Daniel I. Rees. 2012. Body weight and wages: Evidence from Add Health. Economics & Human Biology 10: 14–19. [Google Scholar]
- Terza, Joseph V. 1985. Ordered Probit: A Generalization. Communications in Statistics—A Theory and Methods 14: 1–11. [Google Scholar]
- Ulrick, Shawn W. 2012. The Oaxaca decomposition generalized to a continuous group variable. Economics Letters 115: 35–37. [Google Scholar] [CrossRef]
- Vella, Francis. 1998. Estimating Models with Sample Selection Bias: A Survey. The Journal of Human Resources 33: 127–69. [Google Scholar] [CrossRef]
- Williams, Richard. 2016. Understanding and interpreting generalized ordered logit models. The Journal of Mathematical Sociology 40: 7–20. [Google Scholar] [CrossRef]
- Wooldridge, Jeffrey. M. 2015. Control Function Methods in Applied Econometrics. Journal of Human Resources 50: 420–55. [Google Scholar] [CrossRef]
- Yatchew, Aonis. 2003. Semiparametric Regression for the Applied Econometrician. Cambridge: Cambridge University Press. [Google Scholar]
- Zhang, Wenyang, and Sik-Yum Lee. 2000. Variable bandwidth selection in varying-coefficient models. Journal of Multivariate Analysis 74: 116–34. [Google Scholar] [CrossRef]
| 1 | |
| 2 | This model is also known as smooth coefficient model. |
| 3 | Fortin et al. (2011) provide other scenarios where the conditional independence assumption might be violated. |
| 4 | |
| 5 | While identification of the Heckman selection model can be obtained based on the non-linearity alone, it is recommended to have an instrumental variable for better identification of the model. |
| 6 | For example, assuming counterfactual wages are given by the wage structure observed in Group B, the components of the decomposition would be given by , where can be interpreted as a treatment effect under the conditional independence assumption. |
| 7 | This model is also known as type-3 tobit models, or tobit selection models (Li and Racine 2007, sct. 10.3). |
| 8 | |
| 9 | This can be done, for example, using the kernel cumulative density estimation of . |
| 10 | Notice that does not vary with respect to the point of reference variable , but rather the individual realization . |
| 11 | Since we assume to be continuous, it should have no repeated values. In practice, due to intentional or unintentional measuring strategies continuous variables are available only in discrete form. This is the case for years of education in example used in Centorrino and Racine (2017). |
| 12 | See Cameron and Trivedi (2005), Chapter 9 for details on Kernel regression estimators. |
| 13 | Derivations of the bias and variance for kernel local linear estimators for varying coefficient models are provided in Section 9.3.2. in Li and Racine (2007). |
| 14 | See Section 9.3.2. in Li and Racine (2007) for further details. |
| 15 | This procedure is also followed in Centorrino and Racine (2017) for the construction of their confidence intervals. |
| 16 | Exploring the consequences of bandwidth selection within each bootstrap is beyond the scope of this paper. However, a simple exercise using Stata command npregress suggests that estimating the bandwidth for each bootstrap sample produces larger standard errors compared to using a fixed bandwidth. |
| 17 | Coverage estimates based on percentile confidence intervals show similar levels of coverage, and are not reported here. The simulation files are available upon request. |
| 18 | Appendix A provide additional simulations following the setups from Centorrino and Racine (2017), where d has a bounded distribution between 0 and 1. |
| 19 | |
| 20 | See Cawley (2004, p. 454) for a complete description of the data and model specification. |
| 21 | See Appendix B for complete set of results and intermediate steps for the data and model specification changes. |
| 22 | Control function approach using alternative measures for the GIMR were also estimated and are available upon request. While the results from the alternative specifications are similar to the ones presented here, they are somewhat larger and statistically significant for both white men and white women. |
| 23 | In scenarios like the analysis of wage penalties of smoking behavior, the reference group is clearly identified (non-smokers). In this case, one could argue that the assumption of smooth coefficients is only appropriate for people who smoke, and that coefficients for non-smokers should be estimated separately. |
| 24 | This scenario assumes that BMI has no additional impact on wages within the health group. Alternatively, following the critique raised by Cain (1986) in regards to using pooled data as the reference group, one could also include BMI as control in the pooled regression. For this illustration, such change has no substantial impact on the results. |
| 25 | In principle, this transformation should have no effect on the estimation of the semiparametric model. If , and is a strictly monotone transformation, then . |
| 26 | In practice, the bandwidth selection and estimation of the varying coefficient models are done using a set of commands written for the statistical software Stata. These programs are available upon request. |
| 27 | Figures in Appendix B provide various robustness checks including: Sensitivity to alternative GIMRs, results based on kernel regressions with original BMI distribution, and differences in the bandwidth estimation. |
| 28 | Cawley (2004, p. 465) stated that a two standard-deviation change in weight is associated with a 9 percent change in wages, when in fact this estimate reflects the impact of a one standard-deviation change in weight. |
| 29 | For internal consistency, the instrumental variable estimations include the quadratic terms and interactions as instruments. |


| Sample 500 | Sample 1000 | Sample 2500 | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| True | 95% | 95% BC | 95% | 95% BC | 95% | 95% BC | ||||||||||
| Bias | Cov. | Cov. | Bias | Cov. | Cov. | Bias | Cov. | Cov. | ||||||||
| −3 | −0.600 | 0.178 | 0.326 | 0.299 | 87.0% | 92.6% | 0.110 | 0.232 | 0.223 | 90.3% | 94.2% | 0.056 | 0.157 | 0.154 | 92.4% | 94.6% |
| −2 | −0.393 | 0.145 | 0.224 | 0.205 | 86.4% | 91.9% | 0.096 | 0.159 | 0.152 | 88.4% | 94.3% | 0.052 | 0.107 | 0.105 | 91.7% | 95.8% |
| −1 | −0.119 | 0.130 | 0.185 | 0.178 | 88.2% | 93.0% | 0.094 | 0.139 | 0.132 | 86.0% | 93.7% | 0.059 | 0.094 | 0.090 | 88.7% | 93.7% |
| 0 | 0.363 | 0.007 | 0.185 | 0.182 | 95.2% | 95.4% | 0.005 | 0.135 | 0.134 | 95.4% | 95.4% | 0.004 | 0.093 | 0.092 | 94.5% | 94.5% |
| 1 | 0.798 | −0.143 | 0.218 | 0.204 | 85.4% | 93.0% | −0.113 | 0.158 | 0.152 | 86.8% | 94.0% | −0.077 | 0.106 | 0.104 | 85.2% | 94.1% |
| 2 | 0.763 | −0.050 | 0.243 | 0.238 | 93.0% | 93.6% | −0.025 | 0.174 | 0.179 | 96.2% | 95.7% | −0.007 | 0.126 | 0.124 | 95.3% | 95.5% |
| 3 | 0.681 | 0.009 | 0.292 | 0.285 | 95.2% | 94.7% | 0.028 | 0.206 | 0.218 | 96.6% | 96.1% | 0.032 | 0.156 | 0.151 | 94.2% | 94.6% |
| 4 | 0.807 | −0.065 | 0.391 | 0.357 | 91.7% | 92.8% | −0.020 | 0.278 | 0.274 | 94.3% | 94.5% | −0.002 | 0.202 | 0.191 | 94.3% | 94.3% |
| 5 | 1.000 | −0.144 | 0.528 | 0.494 | 90.8% | 92.3% | −0.075 | 0.384 | 0.371 | 92.8% | 93.5% | −0.041 | 0.258 | 0.258 | 94.4% | 95.3% |
| True | 95% | 95% BC | 95% | 95% BC | 95% | 95% BC | ||||||||||
| Bias | Cov. | Cov. | Bias | Cov. | Cov. | Bias | Cov. | Cov. | ||||||||
| −3 | 0.996 | −0.024 | 0.258 | 0.254 | 94.2% | 94.1% | −0.049 | 0.186 | 0.181 | 92.5% | 92.6% | −0.033 | 0.122 | 0.121 | 94.2% | 94.7% |
| −2 | 0.932 | −0.134 | 0.183 | 0.169 | 83.8% | 92.6% | −0.113 | 0.126 | 0.123 | 83.9% | 94.6% | −0.074 | 0.085 | 0.082 | 83.7% | 94.5% |
| −1 | 0.524 | −0.228 | 0.161 | 0.140 | 61.6% | 91.0% | −0.170 | 0.120 | 0.103 | 57.7% | 90.5% | −0.120 | 0.078 | 0.070 | 56.6% | 92.2% |
| 0 | −0.500 | −0.017 | 0.142 | 0.140 | 95.7% | 95.1% | −0.009 | 0.104 | 0.104 | 94.1% | 94.2% | −0.006 | 0.070 | 0.071 | 95.4% | 94.8% |
| 1 | −1.524 | 0.205 | 0.185 | 0.159 | 66.6% | 90.9% | 0.155 | 0.133 | 0.118 | 69.6% | 91.1% | 0.109 | 0.089 | 0.081 | 67.9% | 92.9% |
| 2 | −1.932 | 0.145 | 0.201 | 0.185 | 82.5% | 92.8% | 0.096 | 0.139 | 0.139 | 88.3% | 94.6% | 0.063 | 0.100 | 0.096 | 87.0% | 93.5% |
| 3 | −1.996 | 0.046 | 0.228 | 0.224 | 93.9% | 94.4% | 0.030 | 0.165 | 0.170 | 95.5% | 95.6% | 0.014 | 0.117 | 0.117 | 94.7% | 95.6% |
| 4 | −2.000 | 0.021 | 0.303 | 0.288 | 93.2% | 93.4% | 0.024 | 0.226 | 0.216 | 94.0% | 94.3% | 0.012 | 0.153 | 0.150 | 95.1% | 95.0% |
| 5 | −2.000 | 0.044 | 0.429 | 0.415 | 93.1% | 92.7% | 0.055 | 0.299 | 0.300 | 93.6% | 94.5% | 0.022 | 0.204 | 0.204 | 94.7% | 95.0% |
| True | 95% | 95% BC | 95% | 95% BC | 95% | 95% BC | ||||||||||
| Bias | Cov. | Cov. | Bias | Cov. | Cov. | Bias | Cov. | Cov. | ||||||||
| −3 | −0.800 | 0.427 | 0.758 | 0.684 | 85.3% | 92.5% | 0.274 | 0.557 | 0.534 | 89.7% | 93.7% | 0.127 | 0.384 | 0.376 | 92.3% | 93.7% |
| −2 | 0.000 | 0.224 | 0.406 | 0.390 | 91.0% | 94.1% | 0.143 | 0.306 | 0.292 | 90.7% | 93.4% | 0.072 | 0.214 | 0.203 | 93.0% | 93.3% |
| −1 | 0.600 | 0.089 | 0.260 | 0.250 | 92.8% | 94.5% | 0.049 | 0.187 | 0.184 | 94.3% | 94.2% | 0.021 | 0.126 | 0.125 | 94.1% | 94.5% |
| 0 | 1.000 | 0.012 | 0.175 | 0.166 | 93.4% | 93.4% | 0.000 | 0.125 | 0.121 | 93.6% | 93.6% | −0.009 | 0.081 | 0.082 | 95.4% | 95.3% |
| 1 | 1.200 | −0.027 | 0.140 | 0.136 | 93.7% | 94.6% | −0.023 | 0.105 | 0.101 | 93.4% | 94.1% | −0.015 | 0.069 | 0.068 | 94.2% | 94.4% |
| 2 | 1.200 | −0.024 | 0.222 | 0.219 | 94.5% | 94.5% | −0.030 | 0.164 | 0.165 | 94.9% | 95.2% | −0.019 | 0.113 | 0.112 | 94.9% | 94.7% |
| 3 | 1.000 | 0.024 | 0.406 | 0.398 | 94.7% | 95.1% | −0.009 | 0.294 | 0.306 | 95.8% | 95.6% | −0.019 | 0.218 | 0.210 | 94.6% | 94.6% |
| 4 | 0.600 | 0.107 | 0.713 | 0.670 | 92.3% | 93.4% | 0.037 | 0.538 | 0.525 | 94.0% | 94.6% | 0.007 | 0.390 | 0.370 | 93.4% | 93.6% |
| 5 | 0.000 | 0.279 | 1.233 | 1.134 | 91.9% | 94.1% | 0.168 | 0.946 | 0.892 | 91.5% | 92.3% | 0.083 | 0.632 | 0.634 | 94.7% | 94.8% |
| Sample 5000 | OLS-GIMR | Oprobit-GIMR | Fprobit-GIMR | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bias | 95% Cov. | 95% BC Cov. | Bias | 95% Cov. | 95% BC Cov. | Bias | 95% Cov. | 95% BC Cov. | ||||||||
| −3 | −0.600 | 0.035 | 0.117 | 0.114 | 92.6% | 93.8% | 0.035 | 0.117 | 0.114 | 92.7% | 93.9% | 0.034 | 0.117 | 0.114 | 92.6% | 93.8% |
| −2 | −0.393 | 0.027 | 0.081 | 0.079 | 93.0% | 93.8% | 0.026 | 0.081 | 0.079 | 93.1% | 93.8% | 0.026 | 0.081 | 0.079 | 93.4% | 93.9% |
| −1 | −0.119 | 0.041 | 0.068 | 0.067 | 90.5% | 94.5% | 0.041 | 0.068 | 0.067 | 90.7% | 94.4% | 0.040 | 0.068 | 0.067 | 90.8% | 94.5% |
| 0 | 0.363 | −0.002 | 0.069 | 0.068 | 94.5% | 94.8% | −0.002 | 0.069 | 0.069 | 94.5% | 94.8% | −0.002 | 0.069 | 0.069 | 94.3% | 94.8% |
| 1 | 0.798 | −0.063 | 0.082 | 0.078 | 86.0% | 94.1% | −0.062 | 0.082 | 0.078 | 86.3% | 94.0% | −0.061 | 0.083 | 0.078 | 86.2% | 94.0% |
| 2 | 0.763 | −0.006 | 0.095 | 0.092 | 93.6% | 93.7% | −0.006 | 0.096 | 0.093 | 93.6% | 93.6% | −0.006 | 0.096 | 0.093 | 93.7% | 93.5% |
| 3 | 0.681 | 0.022 | 0.122 | 0.113 | 93.0% | 92.9% | 0.022 | 0.122 | 0.113 | 93.0% | 92.8% | 0.022 | 0.123 | 0.114 | 93.1% | 92.6% |
| 4 | 0.807 | −0.005 | 0.144 | 0.144 | 94.7% | 94.6% | −0.005 | 0.144 | 0.144 | 94.7% | 94.7% | −0.005 | 0.145 | 0.145 | 95.0% | 94.7% |
| 5 | 1.000 | −0.024 | 0.202 | 0.193 | 93.0% | 92.7% | −0.024 | 0.202 | 0.193 | 92.9% | 93.1% | −0.023 | 0.203 | 0.194 | 92.9% | 93.1% |
| Bias | 95% Cov. | 95% BC Cov. | Bias | 95% Cov. | 95% BC Cov. | Bias | 95% Cov. | 95% BC Cov. | ||||||||
| −3 | 0.996 | −0.025 | 0.091 | 0.090 | 93.7% | 94.8% | −0.025 | 0.091 | 0.090 | 93.7% | 94.7% | −0.024 | 0.091 | 0.090 | 93.6% | 94.7% |
| −2 | 0.932 | −0.050 | 0.064 | 0.062 | 86.8% | 93.5% | −0.050 | 0.064 | 0.062 | 86.8% | 93.5% | −0.049 | 0.064 | 0.063 | 87.2% | 94.0% |
| −1 | 0.524 | −0.089 | 0.057 | 0.052 | 57.6% | 93.3% | −0.089 | 0.057 | 0.052 | 57.8% | 93.4% | −0.088 | 0.057 | 0.052 | 59.3% | 93.3% |
| 0 | −0.500 | −0.002 | 0.054 | 0.053 | 94.7% | 94.3% | −0.002 | 0.054 | 0.053 | 94.6% | 94.3% | −0.002 | 0.054 | 0.053 | 94.5% | 94.3% |
| 1 | −1.524 | 0.083 | 0.066 | 0.060 | 68.6% | 92.2% | 0.083 | 0.067 | 0.060 | 69.1% | 92.2% | 0.081 | 0.067 | 0.061 | 70.0% | 92.1% |
| 2 | −1.932 | 0.045 | 0.072 | 0.072 | 89.0% | 95.5% | 0.045 | 0.072 | 0.072 | 89.2% | 95.6% | 0.044 | 0.072 | 0.072 | 90.0% | 95.3% |
| 3 | −1.996 | 0.011 | 0.086 | 0.088 | 94.6% | 94.6% | 0.011 | 0.087 | 0.088 | 94.6% | 94.6% | 0.011 | 0.087 | 0.088 | 94.6% | 94.8% |
| 4 | −2.000 | 0.009 | 0.111 | 0.112 | 94.9% | 94.9% | 0.009 | 0.111 | 0.112 | 94.9% | 94.9% | 0.009 | 0.111 | 0.113 | 94.8% | 94.8% |
| 5 | −2.000 | 0.012 | 0.154 | 0.152 | 94.7% | 94.6% | 0.012 | 0.154 | 0.152 | 94.8% | 94.6% | 0.012 | 0.155 | 0.153 | 94.4% | 94.5% |
| Bias | 95% Cov. | 95% BC Cov. | Bias | 95% Cov. | 95% BC Cov. | Bias | 95% Cov. | 95% BC Cov. | ||||||||
| −3 | −0.800 | 0.082 | 0.287 | 0.282 | 93.7% | 93.9% | 0.081 | 0.288 | 0.282 | 93.8% | 93.9% | 0.079 | 0.288 | 0.283 | 93.8% | 94.1% |
| −2 | 0.000 | 0.034 | 0.158 | 0.152 | 93.0% | 93.5% | 0.033 | 0.159 | 0.152 | 93.1% | 93.1% | 0.032 | 0.159 | 0.153 | 93.5% | 93.6% |
| −1 | 0.600 | 0.011 | 0.090 | 0.092 | 95.4% | 95.1% | 0.011 | 0.090 | 0.092 | 95.4% | 95.1% | 0.010 | 0.091 | 0.093 | 95.2% | 95.1% |
| 0 | 1.000 | −0.009 | 0.061 | 0.060 | 94.8% | 94.8% | −0.009 | 0.061 | 0.060 | 94.9% | 94.6% | −0.009 | 0.061 | 0.061 | 94.8% | 94.7% |
| 1 | 1.200 | −0.018 | 0.050 | 0.050 | 94.2% | 95.4% | −0.018 | 0.050 | 0.050 | 94.2% | 95.3% | −0.018 | 0.050 | 0.051 | 94.3% | 95.5% |
| 2 | 1.200 | −0.016 | 0.086 | 0.083 | 93.3% | 93.3% | −0.016 | 0.086 | 0.083 | 93.3% | 93.2% | −0.016 | 0.086 | 0.083 | 93.4% | 93.3% |
| 3 | 1.000 | −0.007 | 0.162 | 0.157 | 93.8% | 93.9% | −0.007 | 0.163 | 0.157 | 93.9% | 93.8% | −0.007 | 0.164 | 0.158 | 94.1% | 93.7% |
| 4 | 0.600 | 0.018 | 0.280 | 0.277 | 94.1% | 94.3% | 0.017 | 0.280 | 0.278 | 94.2% | 94.2% | 0.017 | 0.281 | 0.279 | 94.3% | 94.2% |
| 5 | 0.000 | 0.045 | 0.496 | 0.478 | 93.9% | 94.0% | 0.044 | 0.497 | 0.479 | 93.8% | 93.9% | 0.042 | 0.499 | 0.481 | 93.6% | 94.1% |
| Replication of Cawley (2004) | ||||
| Ln (wage per h) | White | Nonwhite | ||
| Male | Female | Male | Female | |
| BMI | −0.0131 | −0.0168 * | −0.00369 | −0.00515 |
| [0.00831] | [0.00496] | [0.00508] | [0.00544] | |
| N | 13,355 | 10,800 | 11,185 | 8686 |
| Replication with changes in model specification and sample | ||||
| Ln (wage per h) | White | Nonwhite | ||
| Male | Female | Male | Female | |
| BMI | −0.0127 | −0.0154 * | −0.00425 | −0.00735 |
| [0.00804] | [0.00493] | [0.00504] | [0.00545] | |
| N | 12,184 | 10,101 | 9844 | 7958 |
| Control Function Approach: Instruments: Siblings BMI, age and sex | ||||
| Ln (wage per h) | White | |||
| Male | Female | |||
| BMI | −0.0127 | −0.0154 * | ||
| [0.00833] | [0.00527] | |||
| N | 12,184 | 10,101 | ||
| Instruments: Siblings BMI, age and sex, including interactions | ||||
| Ln (wage per h) | White | |||
| Male | Female | |||
| BMI | −0.012 | −0.0150 * | ||
| [0.00748] | [0.00530] | |||
| N | 12,184 | 10,101 | ||
| Variable of Reference | Men | CV Criterion | Women | CV Criterion |
|---|---|---|---|---|
| BMI | 3.2900 | −1.40814 | 4.8540 | −1.56378 |
| G(BMI) | 0.1769 | −1.40852 | 0.2241 | −1.54543 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rios-Avila, F. A Semi-Parametric Approach to the Oaxaca–Blinder Decomposition with Continuous Group Variable and Self-Selection. Econometrics 2019, 7, 28. https://0-doi-org.brum.beds.ac.uk/10.3390/econometrics7020028
Rios-Avila F. A Semi-Parametric Approach to the Oaxaca–Blinder Decomposition with Continuous Group Variable and Self-Selection. Econometrics. 2019; 7(2):28. https://0-doi-org.brum.beds.ac.uk/10.3390/econometrics7020028
Chicago/Turabian StyleRios-Avila, Fernando. 2019. "A Semi-Parametric Approach to the Oaxaca–Blinder Decomposition with Continuous Group Variable and Self-Selection" Econometrics 7, no. 2: 28. https://0-doi-org.brum.beds.ac.uk/10.3390/econometrics7020028