The Discovery of Long-Run Causal Order: A Preliminary Investigation †
Abstract
:In the long run, we are all dead.John Maynard KeynesIn the long run, we are simply in another short run.variously attributedContrary to Keynes’ famous dictum in the long run we are all dead,the long run is with us every day of our livesWalt Rostow
1. The Problem of Causal Order in the CVAR
2. Graph-Theoretic Causal Order
2.1. Graphs and Causal Structure
2.2. Graphs and Conditional Independence
3. Where Do Stochastic Trends Come From?7
4. Graphical Analysis of the CVAR
4.1. The Canonical CVAR of a Causally Sufficient, Acyclical Graph
- Each single-variable direct causal pair or each collider is represented by a cointegrating relationship corresponding to a unique row of the β′ matrix where the value of the parameter for the effect is normalized to unity;
- There are as many adjustment parameters in α as there are rows in β′ (at most one per row) with the column of each non-zero parameter in α corresponding to the row of one of the effects (i.e., corresponding to the row in which that variable is normalized to unity) in β′;
- If any variable is a cause, but not an effect with respect to all the other variables, it corresponds to a zero row in α (and, thus, is weakly exogenous).
4.2. Formation and Sharing of Local Trends
4.3. A State-Space Analysis of the CVAR
4.4. Weak Exogeneity and Causal Order
- Case 1.
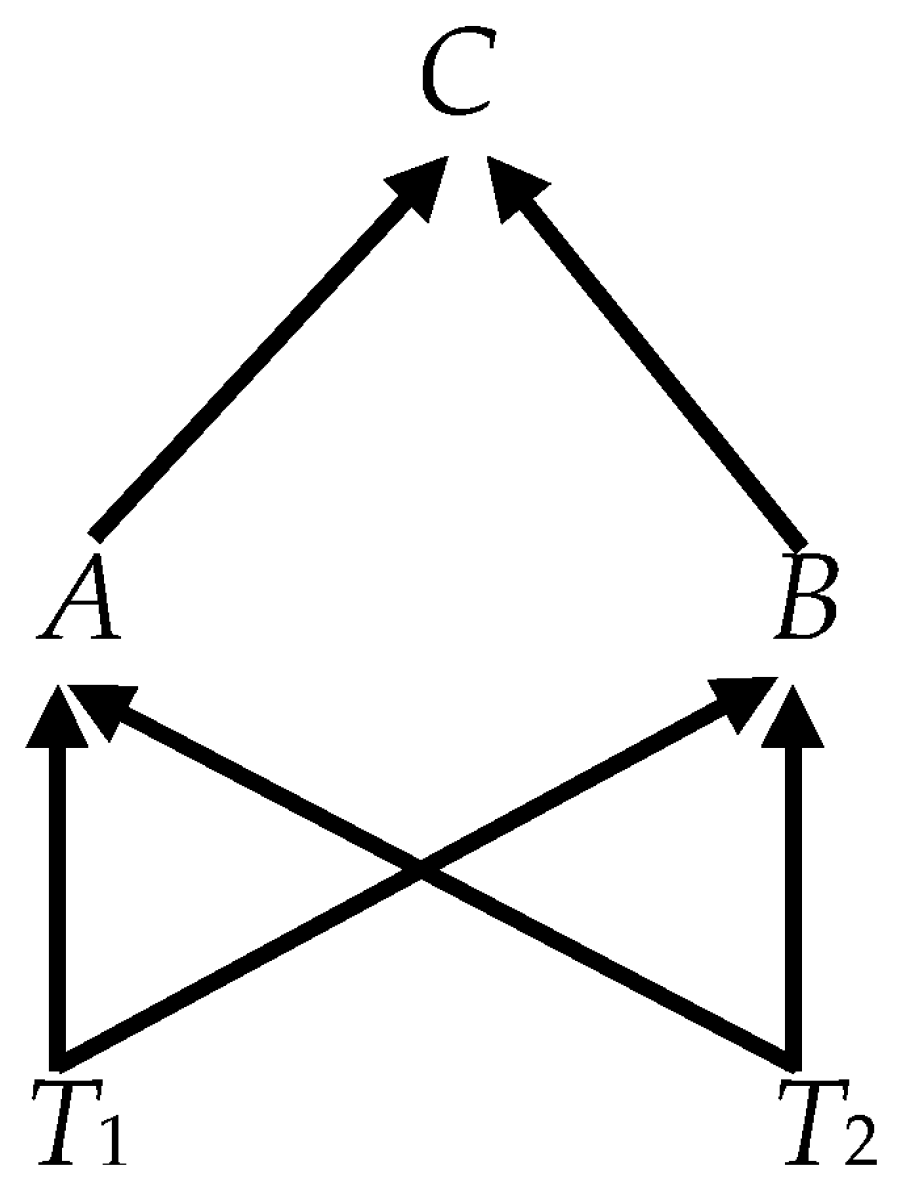
- Consider the causal graph in Figure 3, in which all ordinary variables are observed and only the fundamental trends are unobserved, so that (12), the simpler formula for α, applies. The DGP in Equations (8)–(10) specializes towherewhere ωii = var(εit), i = A, B, C;Thus,where the asterisk (*) indicates a non-zero value.15 The first two rows of α are zero and, therefore, A and B are weakly exogenous for C (i.e., {A, B} ↦ C). Notice that it does not matter, what the causal relations are among the observables, since they are encoded in the M11 matrix, which plays no part in the determination of α in Equation (11). What matters is which variables convey the fundamental trends to the observables.
- Case 2.
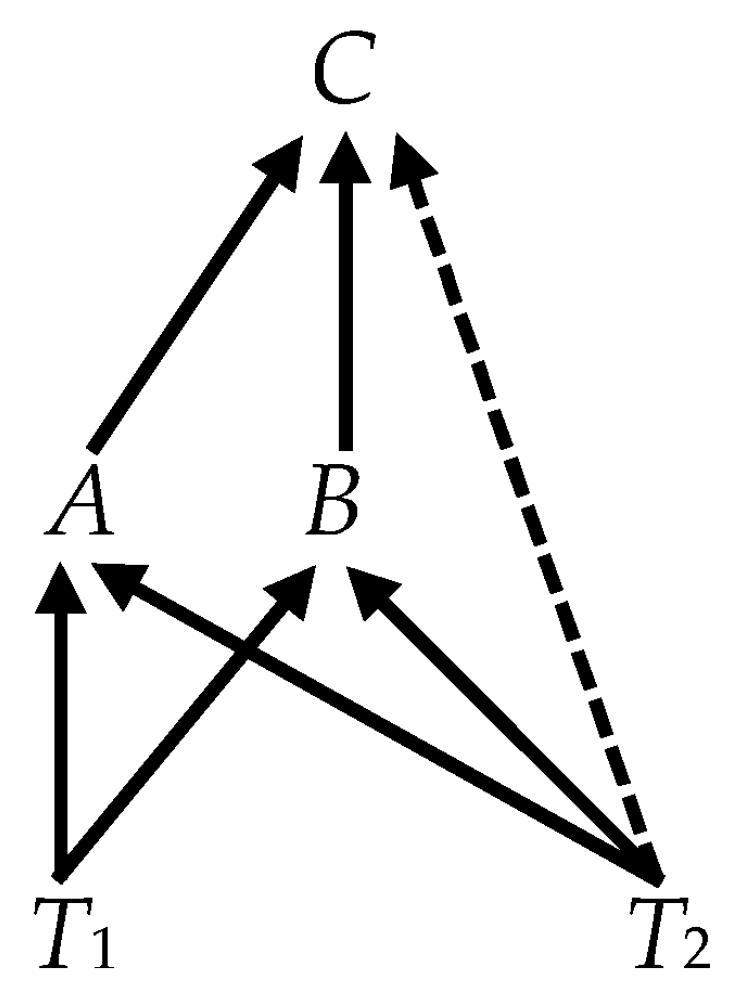
- Unfortunately, the simple mapping between weak exogeneity and causal connection suggested by Case 1 does not hold up. Consider Figure 4, which adds the variable D and edges connecting it to other variables in Figure 3. The analysis proceeds just as in Case 1. Again, since all variables are observable, the simpler formula (12) applies. The other relevant matrices of the state-space formulation are given byThese imply thatwhich has no zero rows; which, in turn, implies that none of the variables is weakly exogenous.16 The variables A, B, C, D are cointegrated (CI({A, B, C, D})); but with two fundamental trends and four variables, every three-member subset of the ordinary variables is also cointegrated, implying not IC({A, B, C, D}). This appears to be a robust finding—the parents in a collider are weakly exogenous only when the colliding set is irreducibly cointegrated.
- Case 3.
- It is tempting to think that we might consider an irreducible subset of the variables in Figure 4, such as {A, B, C} and find the same weak exogeneity relations as we did in Figure 3. That, however, does not work. In analyzing the subset, we are effectively treating D as an unobserved variable; and we must, therefore, apply the more general formula (11), which requires additional information. The critical elements of the state-space representation of this reduced system areand(Note that, although is diagonal by assumption, the off-diagonal elements of VTT here are nonzero. This is the result of D, transmitting T2 to the collider at C. The calculation of V (see Equation (11)) conditions {D, T1, T2} on {A, B, C} and, in effect, conditions the independent (distal) causes T1 and T2 on their common (indirect) effect, which induces probabilistic dependence between them.) The variance of the isandWith no zero rows in α, none of the variables is weakly exogenous. Although D is unobservable in the DGP that actually determines the value of the observable variables, it provides a conduit from the fundamental trends to C that is distinct from the observable conduits, A and B. It is as if the graph of Figure 4 has been transformed into Figure 5, where the dashed arrow indicates a causal connection between T2 and C, mediated by D in the DGP but not observable in the CVAR of the subset {A, B, C}. Unobserved mediating causes, like D, can make an indirect causal connection appear to be direct.
- Case 4.
- In Case 3, weak exogeneity failed to obtain, even though the causal connections were genuine. It can also happen that weak exogeneity does obtain, even when causal connections are missing. Consider Figure 6. The graph shows not (A → C) and not (B → D) and not (B → E), although B does indirectly cause E. Using the same state-space methods, but omitting the details here, we can show that {A, B} ↦ {C, D, E}. And, looking at subsets of variables {A, B} ↦ D. Thus, {A, B, D} have the same apparent pattern of weak exogeneity as found for {A, B, C} in Case 1 (Figure 3); yet these variables do not form a collider group in Figure 6. But notice CI({A, B, D}), but also CI({A, D}). The set {A, B, D}, therefore, is not irreducibly cointegrated. It appears that a mapping between weak exogeneity and causal connections can be established only in irreducibly cointegrated sets.
- Case 5.
- Weak exogeneity may fail to track direct cause. Consider a causal chain:All four observable variables form a single cointegration group, sharing the single fundamental trend. Note that B ↦ C and that {B, C} form a cointegration group. We might be tempted to conclude that these facts would warrant inferring what is, in fact, true that B → C. A similar case shows the problem: A ↦ C and CI({A, C}); but, in fact, it is not true that A → C (A is an indirect, but not a direct, cause of C). It is worth showing why it is the case that A ↦ C, as it highlights a subtle issue. We take {A, C} to be observed and {B, D} to be unobserved. Then the relevant matrices areT → A → B → C → D
- Within a set of variables that form a cointegration group, a particular variable is weakly exogenous for the group if, and only if, it is the sole source of the local trend that cointegrates the group;
- The parents in any set of variables that form a collider group in which two or more local trends are combined are weakly exogenous for the child in the collider group, provided that the number of variables in the group is fewer than one plus the number of fundamental trends carried by those variables;
- If a collider fulfills criterion B, then in any set that replaces one or more weakly exogenous parents with a variable in the same cointegration group as that parent, provided the variable is itself weakly exogenous for the parent, will also be weakly exogenous for the child. (Thus, in Figure 6, in the collider {A, C, E}, {A, C} ↦ E; but in the set in which B replaces C (both in the same collider group), {A, B} ↦ E));
- If a collider fulfills criterion B, then any variable that is weakly exogenous for the child, either as a parent or as a member of the same cointegration group that replaces the parent, will be weakly exogenous for a variable that replaces the child from a cointegration group that includes the child and for which it is weakly exogenous. (Thus, in Figure 2, {T1, T2} ↦ B, but in the set that replaces B with D, which are both in the same cointegration group, {T1, T2} ↦ D.)
5. The Basis for a Long-Run Causal Search Algorithm?
5.1. Long-Run Causal Search in a Causally Sufficient Graph
5.2. Long-Run Causal Search in the Presence of Latent Trends
6. Conclusions
Funding
Conflicts of Interest
References
- Cooley, Thomas F., and Stephen F. LeRoy. 1985. Atheoretical Macroeconomics: A Critique. Journal of Monetary Economics 16: 283–308. [Google Scholar] [CrossRef]
- Cooper, Gregory F. 1999. An Overview of the Representation and Discovery of Causal Relationships using Bayesian Networks. In Computation, Causation, and Discovery. Edited by Clark Glymour and Gregory F. Cooper. Menlo Park: American Association for Artificial Intelligence, Cambridge: MIT Press, pp. 3–64. [Google Scholar]
- Davidson, James, and Stephen Hall. l991. Cointegration in Recursive Systems. Economic Journal 101: 109–251. [Google Scholar] [CrossRef]
- Davidson, James. 1998. Structural Relations, Cointegration and Identification: Som Simple Results and Their Application. Journal of Econometrics 87: 87–113. [Google Scholar] [CrossRef]
- Demiralp, Selva, and Kevin D. Hoover. 2003. Searching for the Causal Structure of a Vector Autoregression. Oxford Bulletin of Economics and Statistics 65: 745–67. [Google Scholar] [CrossRef]
- Demiralp, Selva, Kevin D. Hoover, and Stephen J. Perez. 2008. A Bootstrap Method for Identifying and Evaluating a Structural Vector Autoregression. Oxford Bulletin of Economics and Statistics 70: 509–33. [Google Scholar] [CrossRef] [Green Version]
- Duarte, Pedro Garcia, and Kevin D. Hoover. 2012. Observing Shocks. In Histories of Observation in Economics. (Supplement to History of Political Economy 44). Edited by Harro Maas and Mary Morgan. Durham: Duke University Press, pp. 226–49. [Google Scholar]
- Engle, Robert F., and Clive W. J. Granger. 1987. Cointegration and Error Correction Representation: Estimation and Testing. Econometrica 55: 251–76. [Google Scholar] [CrossRef]
- Engle, Robert F., David F. Hendry, and Jean-François Richard. 1983. Exogeneity. Econometrica 51: 277–304. [Google Scholar] [CrossRef]
- Granger, Clive W. J. 1969. Investigating Causal Relations by Econometric Models and Cross-spectral Methods. Econometrica 37: 424–38. [Google Scholar] [CrossRef]
- Granger, Clive W. J. 1995. Commentary [on Stephen F. LeRoy, Causal Orderings]. In Macroeconometrics: Developments, Tensions, and Prospects. Edited by Kevin D. Hoover. Boston: Kluwer, pp. 229–352. [Google Scholar]
- Haavelmo, Trygve. 1944. The Probability Approach in Econometrics. Econometrica 12: iii–115. [Google Scholar] [CrossRef]
- Hood, William C., and Tjalling Koopmans, eds. 1953. Studies in Econometric Method. (Cowles Commission Monograph vol. 14). New York: Wiley. [Google Scholar]
- Hoover, Kevin D. 1990. The Logic of Causal Inference: Econometrics and the Conditional Analysis of Causation. Economics and Philosophy 6: 207–34. [Google Scholar] [CrossRef] [Green Version]
- Hoover, Kevin D. 2001. Causality in Macroeconomics. Cambridge: Cambridge University Press. [Google Scholar]
- Hoover, Kevin D. 2004. Lost Causes. Journal of the History of Economic Thought 26: 149–64. [Google Scholar] [CrossRef]
- Hoover, Kevin D. 2008. Causality in Economics and Econometrics. In The New Palgrave Dictionary of Economics, 2nd ed. Edited by Steven N. Durlauf and Lawrence E. Blume. London: Palgrave Macmillan. [Google Scholar] [CrossRef] [Green Version]
- Hoover, Kevin D. 2012. Economic Theory and Causal Inference. In Handbook of the Philosophy of Economics. volume 13 of Dov Gabbay, Paul Thagard, and John Woods, general editors. Edited by Uskali Mäki. Amsterdam: Elsevier/North-Holland, pp. 89–113. [Google Scholar]
- Hoover, Kevin D. 2014. On the Reception of Haavelmo’s Econometric Thought. Journal of the History of Economic Thought 36: 45–65. [Google Scholar] [CrossRef] [Green Version]
- Hoover, Kevin D. 2015. The Ontological Status of Shocks and Trends in Macroeconomics. Synthese, 3509–32. [Google Scholar] [CrossRef] [Green Version]
- Hoover, Kevin D., and Katarina Juselius. 2015. Trygve Haavelmo’s Experimental Methodology and Scenario Analysis in a Cointegrated Vector Autoregression. Econometric Theory 31: 249–74. [Google Scholar] [CrossRef] [Green Version]
- Hoover, Kevin D., and Òscar Jordá. 2001. Measuring Systematic Monetary Policy. Federal Reserve Bank of St. Louis Review 83: 113–37. [Google Scholar] [CrossRef] [Green Version]
- Hoover, Kevin D., Søren Johansen, and Katarina Juselius. 2008. Allowing the Data to Speak Freely: The Macroeconometrics of the Cointegrated Vector Autoregression. American Economic Review: Papers and Proceedings 98: 251–55. [Google Scholar] [CrossRef] [Green Version]
- Johansen, Søren, and Katarina Juselius. 2014. An Asymptotic Invariance Property of the Common Trends Under Linear Transformation of the Data. Journal of Econometrics 178: 310–15. [Google Scholar] [CrossRef]
- Johansen, Søren, and Morten Nyboe Tabor. 2017. Cointegration between Trends and Their Estimators in State Space Models and Cointegrated Vector Autoregressive Models. Econometrics 5: 36. [Google Scholar] [CrossRef] [Green Version]
- Johansen, Søren. 1995. Likelihood-based Inference in Cointegrated Vector Autoregressive Models. Oxford: Oxford University Press. [Google Scholar]
- Johansen, Søren. 2019. Cointegration and Adjustment in the CVAR(∞) Representation of Some Partially Observed CVAR(1) Models. Econometrics 7: 2. [Google Scholar] [CrossRef] [Green Version]
- Juselius, Katarina. 2006. The Cointegrated VAR Model. Oxford: Oxford University Press. [Google Scholar]
- Koopmans, Tjalling C., ed. 1950. Statistical Inference in Dynamic Economic Models. (Cowles Commission Monograph 10). New York: Wiley. [Google Scholar]
- LeRoy, Stephen F. 1995. Causal Orderings. In Macroeconometrics: Developments, Tensions, and Prospects. Edited by Kevin D. Hoover. Boston: Kluwer, pp. 235–52. [Google Scholar]
- Liu, Ta-Chung. 1960. Underidentification, Structural Estimation, and Forecasting. Econometrica 28: 855–65. [Google Scholar] [CrossRef]
- Morgan, Mary S. 1990. The History of Econometric Ideas. Cambridge: Cambridge University Press. [Google Scholar]
- Pagan, A. R., and M. Hashem Pesaran. 2008. Econometric analysis of structural systems with permanent and transitory shocks. Journal of Economic Dynamics and Control 32: 3376–95. [Google Scholar] [CrossRef] [Green Version]
- Pearl, Judea. 2009. Causality: Models, Reasoning, and Inference, 2nd ed. Cambridge: Cambridge University Press. [Google Scholar]
- Pesaran, M. Hashem, and Ron P. Smith. 1998. Structural Analysis of Cointegrating VARs. Journal of Economic Surveys 12: 471–506. [Google Scholar] [CrossRef]
- Pesaran, M. Hashem, and Yougcheoi Shin. 2002. Long-run Structural Modelling. Econometric Reviews 21: 49–87. [Google Scholar] [CrossRef]
- Phiromswad, Piyachart, and Kevin D. Hoover. 2013. Selecting Instrumental Variables: A Graph-Theoretic Approach. August 28. Available online: https://ssrn.com/abstract=2318552 (accessed on 28 July 2020).
- Reichenbach, Hans. 1956. The Direction of Time. Berkeley: University of California Press. [Google Scholar]
- Richardson, Thomas. 1996. A Discovery Algorithm for Directed Cyclic Graphs. In Uncertainty in Artificial Intelligence: Proceedings of the Twelfth Conference. Edited by Erich Horvitz and Finn Jensen. San Francisco: Morgan Kaufmann, pp. 454–61. [Google Scholar]
- Simon, Herbert A. 1953. Causal Order and Identifiability. In Hood and Koopmans. New York: Wiley, vol. 14, pp. 49–74. [Google Scholar]
- Sims, Christopher A. 1972. Money, Income and Causality. American Economic Review 62: 540–52. [Google Scholar]
- Sims, Christopher A. 1980. Macroeconomics and Reality. Econometrica 48: 1–48. [Google Scholar] [CrossRef] [Green Version]
- Sims, Christopher A. 1982. Policy Analysis with Econometric Models. Brookings Papers on Economic Activity 13: 107–52. [Google Scholar] [CrossRef] [Green Version]
- Sims, Christopher A. 1986. Are Forecasting Models Usable for Policy Analysis? Federal Reserve Bank of Minneapolis Quarterly Review 10: 2–15. [Google Scholar] [CrossRef]
- Spirtes, Peter, Clark Glymour, and Richard Scheines. 2000. Causation, Prediction, and Search, 2nd ed. Cambridge: MIT Press. [Google Scholar]
- Swanson, Norman R., and Clive W. J. Granger. 1997. Impulse Response Functions Based on a Causal Approach to Residual Orthogonalization in Vector Autoregressions. Journal of the American Statistical Association 92: 357–67. [Google Scholar] [CrossRef]
- White, Halbert, and Davide Pettenuzzo. 2014. Granger-causality, Exogeneity, and Economic Policy Analysis. Journal of Econometrics 178: 316–30. [Google Scholar] [CrossRef] [Green Version]
- White, Halbert, and Karim Chalak. 2009. Settable Systems: An Extension of Pearl’s Causal Model with Optimization, Equilibrium, and Learning. Journal of Machine Learning Research 10: 1759–99. [Google Scholar]
- White, Halbert, and Xun Lu. 2010. Granger-causality and Dynamic Structural Systems. Journal of Financial Econometrics 8: 193–243. [Google Scholar] [CrossRef]
- Wold, Hermann. 1960. A Generalization of Causal Chain Models. Econometrica 28: 277–326. [Google Scholar] [CrossRef]
| 1 | For discussions of various approaches to causality in macroeconomics and macroeconometrics, see (Hoover 2001, 2008, 2012). |
| 2 | See (Hoover 2001, chp. 3). In appealing to an experimental metaphor, Simon followed in the footsteps of Haavelmo (1944), a foundational figure for Cowles Commission econometrics (see Hoover and Juselius 2015; Hoover 2014). |
| 3 | “Graphical” (or “graph-theoretic”) causal modeling should be the preferred term, as the search methods do not require a Bayesian approach to statistics. For compact treatments of the approach and the basic algorithms, see Cooper (1999) and Demiralp and Hoover (2003). |
| 4 | On the general methodology of modeling in relation to the CVAR see Hoover et al. (2008) and Hoover and Juselius (2015). |
| 5 | Hoover (1990; 2001, chps. 2 and 3) provides a detailed account of Simon’s approach and of it generalization to nonlinear systems, including ones with cross-equation restrictions among the parameters. |
| 6 | See Cooper (1999), Spirtes et al. (2000, chps. 5 and 6), and Pearl (2009, chp. 2). The Tetrad software package implements Spirtes et al.’s (2000) algorithms, as well as additional algorithms, and can be downloaded from Carnegie Mellon University’s Tetrad Project website: http://www.phil.cmu.edu/tetrad/. |
| 7 | |
| 8 | In general, calculation of the cointegrating vector is the equivalent of solving out the Ts from the long-run representation of Equation (2) in which we set ΔXt and the error terms to zero; specifically the cointegrating vector is given as The orthogonal complement, indicated by the subscript is defined for a full-rank p × r matrix A, as a p × (p − r) matrix A⊥, such that ; see (Johansen 1995, p. 39). |
| 9 | Row 3 of Π in DGP 2 is simply the first cointegrating relation from the reduced form of DGP 1 when T is latent, while Row 2 is the second. Row 1 is (−0.01) × the first cointegrating relation + (−0.1) × the second. |
| 10 | The eigenvalues of I + Π are 0.70678 ± 0.16146i, and 0.98643. |
| 11 | An analogous case arises in the graph-theoretic search literature in the guise of fragile failures of faithfulness—i.e., failures of the estimated probability distributions to reflect all of the independence relationships implied by the graph of the DGP (Spirtes et al. 2000, p. 41; Pearl 2009, pp. 62–63; Hoover 2001, pp. 45–49, 151–53, 168–69). |
| 12 | The robustness of trend behavior in CVARs driven by exogenous, latent trends would explain why the trends estimated in CVARs are often robust to widening the data set and recommends Juselius’s specific-to-general approach—once the trends can be characterized, then any new variable is either redundant or carries information with respect to a new trend (Juselius 2006, chp. 22; Johansen and Juselius 2014). |
| 13 | ΨXX is assumed to be full rank because, were it reduced rank, then it would itself generate trends in the manner of DGP 2 in Section 3—a case that we have argued is possible, but unlikely, in actual economies and which, therefore, we rule out by assumption in this analysis. |
| 14 | The connection of weak exogeneity to the efficient estimation of β might suggest that our notion approach is similar to LeRoy’s (1995) approach to causality (cf. Hoover 2001, pp. 170–74). An importance difference, however, is that while LeRoy defines causal orderings in terms of efficient estimation, we seek only the implications for a possible of the lack of error correction of a condition that incidentally guarantees efficient estimation. |
| 15 | The orthogonal complement for any matrix is not, in general, unique; but each admissible complement spans the same space and places zero rows in the same positions. |
| 16 | This is, as in similar cases, a generic claim and does not rule out that zero rows in α might occur for carefully chosen coefficients. |
| 17 | The rule refers to the DGP, so that an unobserved intermediate cause would appear to warrant the inference of a direct causal connection when only an indirect connection existed in the DGP. This implies that widening the data set might, in effect, open the “black box” and provide more refined information about causal mechanisms. |





© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hoover, K.D. The Discovery of Long-Run Causal Order: A Preliminary Investigation. Econometrics 2020, 8, 31. https://0-doi-org.brum.beds.ac.uk/10.3390/econometrics8030031
Hoover KD. The Discovery of Long-Run Causal Order: A Preliminary Investigation. Econometrics. 2020; 8(3):31. https://0-doi-org.brum.beds.ac.uk/10.3390/econometrics8030031
Chicago/Turabian StyleHoover, Kevin D. 2020. "The Discovery of Long-Run Causal Order: A Preliminary Investigation" Econometrics 8, no. 3: 31. https://0-doi-org.brum.beds.ac.uk/10.3390/econometrics8030031



