Indirect Inference Estimation of Spatial Autoregressions
Abstract
:1. Introduction
2. Main Results
2.1. The Asymptotic Behavior of the OLS estimator
2.2. The Indirect Inference Estimator
3. The Special Case of Pure SAR
4. Monte Carlo Evidence
5. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Lemmas
Appendix B. Proofs
Appendix B.1. Proof of Theorem 1
Appendix B.2. Proof of Theorem 2
Appendix B.3. Proof of Theorem 3
Appendix B.4. Proof of Theorem 4
Appendix B.5. Proof of Corollary 2
Appendix B.6. The Case of Homoscedastic Error Term
References
- Badinger, Harald, and Peter Egger. 2011. Estimation of higher-order spatial autoregressive cross-section models with heteroscedastic disturbances. Papers in Regional Science 90: 213–35. [Google Scholar] [CrossRef]
- Case, Anne C. 1991. Spatial patterns in household demand. Econometrica 59: 953–65. [Google Scholar] [CrossRef] [Green Version]
- Cheng, Xu, Zhipeng Liao, and Ruoyao Shi. 2019. On uniform asymptotic risk of averaging GMM estimators. Quantitative Economics 3: 931–97. [Google Scholar] [CrossRef]
- Cliff, Andrew David, and J. Keith Ord. 1981. Spatial Processes: Models and Applications. London: Pion Ltd. [Google Scholar]
- Debarsy, Nicolas, Fei Jin, and Lung-Fei Lee. 2015. Large sample properties of the matrix exponential spatial specification with an applicationto FDI. Journal of Econometrics 188: 1–21. [Google Scholar] [CrossRef] [Green Version]
- Gospodinov, Nikolay, Ivana Komunjer, and Serena Ng. 2017. Simulated minimum distance estimation of dynamic models with errors-in-variables. Journal of Econometrics 200: 181–93. [Google Scholar] [CrossRef]
- Gouriéroux, Christian, Alain Monfort, and Eric Renault. 1993. Indirect inference. Journal of Applied Econometrics 8: S85–S118. [Google Scholar] [CrossRef]
- Jin, Fei, and Lung-Fei Lee. 2019. GEL estimation and tests of spatial autoregressive models. Journal of Econometrics 208: 585–612. [Google Scholar] [CrossRef]
- Kelejian, Harry H., and Ingmar R. Prucha. 1999. A generalized moments estimator for the autoregressive parameter in a spatial model. International Economic Review 40: 509–33. [Google Scholar] [CrossRef] [Green Version]
- Kelejian, Harry H., and Ingmar R. Prucha. 2001. On the asymptotic distribution of the Moran I test statistic with applications. Journal of Econometrics 104: 219–57. [Google Scholar] [CrossRef] [Green Version]
- Kelejian, Harry H., and Ingmar R. Prucha. 2010. Specification and estimation of spatial autoregressive models with autoregressive and heteroskedastic disturbances. Journal of Econometrics 157: 53–67. [Google Scholar] [CrossRef] [Green Version]
- Kyriacou, Maria, Peter C. B. Phillips, and Francesca Rossi. 2017. Indirect inference in spatial autoregression. The Econometrics Journal 20: 168–89. [Google Scholar] [CrossRef]
- Lam, Clifford, and Pedro C. L. Souza. 2019. Estimation and selection of spatial weight matrix in a spatial lag model. Journal of Business and Economic Statistics 3: 693–710. [Google Scholar] [CrossRef]
- Lee, Lung-Fei. 2001. Asymptotic Distribution of Quasi-Maximum Likelihood Estimators for Spatial Autoregressive Models I: Spatial Autoregressive Processes. Working Paper. Columbus: Department of Econommics, Ohio State University. [Google Scholar]
- Lee, Lung-Fei. 2002. Consistency and efficiency of least squares estimation for mixed regressive, spatial autoregressive models. Econometric Theory 18: 252–77. [Google Scholar] [CrossRef]
- Lee, Lung-Fei. 2004. Asymptotic distribution of quasi-maximum likelihood estimators for spatial autoregressive models. Econometrica 72: 1899–925. [Google Scholar] [CrossRef]
- Lee, Lung-Fei. 2007. GMM and 2SLS estimation of mixed regressive, spatial autoregressive models. Journal of Econometrics 137: 489–514. [Google Scholar] [CrossRef]
- Lin, Xu, and Lung-Fei Lee. 2010. GMM estimation of spatial autoregressive models with unknown heteroskedasticity. Journal of Econometrics 157: 34–52. [Google Scholar] [CrossRef]
- Liu, Shew Fan, and Zhenlin Yang. 2015. Modified QML estimation of spatial autoregressive models with unknown heteroskedasticity and nonnormality. Regional Science and Urban Economics 52: 50–70. [Google Scholar] [CrossRef]
- Nagar, Anirudh L. 1959. The bias and moment matrix of the general k-class estimators of the parameters in simultaneous equations. Econometrica 27: 575–95. [Google Scholar] [CrossRef]
- Phillips, Peter C. B. 2012. Folklore theorems, implicit maps, and indirect inference. Econometrica 80: 425–54. [Google Scholar]
- Robinson, Peter M. 2008. Correlation testing in time series, spatial and cross-sectional data. Journal of Econometrics 147: 5–16. [Google Scholar] [CrossRef] [Green Version]
- Smith, Anthony A., Jr. 1993. Estimating nonlinear time-series models using simulated vector autoregressions. Journal of Applied Econometrics 8: S63–S84. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Xinyu, and Jihai Yu. 2018. Spatial weights matrix election and model averaging for spatial autoregressive models. Journal of Econometrics 203: 1–18. [Google Scholar] [CrossRef]
| 1. | Recent literature on dealing with heteroscedasticity in the spatial framework includes Kelejian and Prucha (2010), Badinger and Egger (2011), Liu and Yang (2015), Jin and Lee (2019), among others. An essential idea in this strand of literature is to use some moment conditions that are robust to unknown heteroscedasticity. |
| 2. | It should be pointed out when (and , where is the order of magnitude of elements of ), is consistent, as shown in Lee (2002), and thus one may not need to seek a consistent estimator of separately and then use it to construct a consistent estimator of . In practice, one may not know a priori the rate of , but the II estimator to be introduced is always consistent regardless of the rate of . |
| 3. | Multicollinearities can happen, for example, when and is row-normalized. Lee (2004) showed that under homoscedasticity, however, the QML estimator can still be consistent in spite of violation of this condition. Since the II estimator to be discussed in this paper is to correct the possible inconsistency of the OLS estimator, Assumption 5(ii) is maintained. |
| 4. | The asymptotic variances are given by and , respectively, for the (properly recentered) OLS estimator and the resulting II estimator. Their explicit expressions are given respectively in Theorems 1 and 2 to be introduced. Assumption 5(ii) implies that exists and is nonzero. It can be shown (see Appendix A) that , where the covariance term disappears under normality, and . When diverges, is the dominating term in as well as . Then the usual condition that exists and is nonsingular is sufficient for Assumption 6 to hold. When is bounded, a more precise characterization of a sufficient condition is not immediately obvious. Essentially, it requires, in addition to the existence and nonsingularity of , the existence of and , where and . |
| 5. | The use of observed, endogenous but non-simulated, variables within the binding function does not appear to be common. An interesting example is Gospodinov et al. (2017), where the authors used observed data within the binding function to hedge against misspecification bias. In their set-up of the autoregressive distributed lag model with a latent scalar predictor under the presence of measurement error, a similar technical difficulty exists regarding the invertibility condition of their binding function and they resorted to simulations to approximate the binding function and then the invertibility condition is numerically verified based on the approximated binding function. |
| 6. | This follows similarly from the proof of Proposition 2 in Lin and Lee (2010). |
| 7. | Neither Lin and Lee (2010) nor Liu and Yang (2015) reported how the inference procedures based on their estimators would perform in finite samples. |
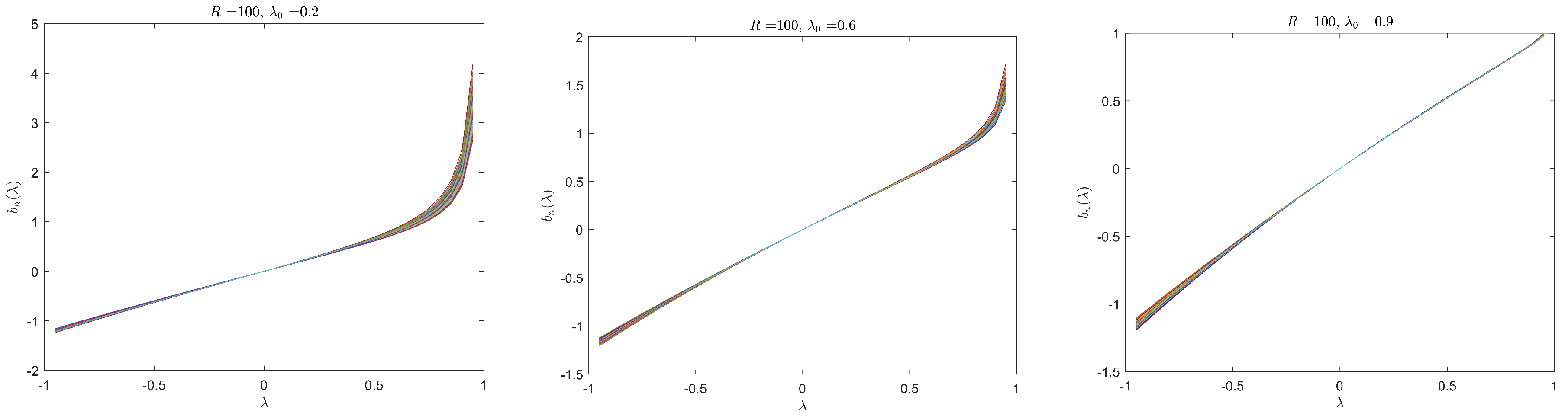
| 8. | Each sub-figure contains 1000 lines, one for each of the simulated data set. |
| 9. | The authors thank a referee for suggesting this comparison. Since one needs to concentrate out the scalar error variance instead of the nuisance matrix , the II procedure needs to be modified, see Appendix B.6. |
| 10. | Very recently, Zhang and Yu (2018) and Lam and Souza (2019) proposed combining spatial weight matrices in recognition of possible misspecification of the weight matrix and Cheng et al. (2019) suggested combining a conservative GMM estimator based on valid moment conditions and an aggressive GMM estimator based on both valid and possibly misspecified moment conditions. |
| MQML | GMM | GMM() | II | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R | Bias | RMSE | Bias | RMSE | Bias | RMSE | Bias | RMSE | |||||||||
| 100 | 0.2 | −0.009 | 0.067 | 3.6% | −0.015 | 0.073 | 5.8% | 0.000 | 0.01 | 4.9% | −0.009 | 0.067 | 3.8% | ||||
| 0.8 | 0.034 | 0.367 | 4.5% | 0.050 | 0.377 | 5.4% | 0.001 | 0.036 | 5.6% | 0.033 | 0.367 | 4.7% | |||||
| 0.2 | −0.002 | 0.099 | 5.0% | −0.002 | 0.099 | 5.1% | 0.000 | 0.008 | 5.5% | −0.002 | 0.099 | 5.0% | |||||
| 1.5 | −0.004 | 0.088 | 4.9% | −0.005 | 0.088 | 5.1% | 0.000 | 0.007 | 4.1% | −0.004 | 0.088 | 4.9% | |||||
| 0.6 | −0.005 | 0.035 | 3.0% | −0.008 | 0.039 | 7.2% | 0.000 | 0.005 | 5.3% | −0.005 | 0.035 | 4.1% | |||||
| 0.8 | 0.032 | 0.366 | 3.8% | 0.047 | 0.378 | 5.9% | 0.001 | 0.037 | 5.6% | 0.031 | 0.367 | 4.7% | |||||
| 0.2 | −0.001 | 0.102 | 5.5% | −0.001 | 0.102 | 5.5% | 0.000 | 0.008 | 5.7% | −0.001 | 0.102 | 5.5% | |||||
| 1.5 | 0.004 | 0.089 | 4.9% | 0.004 | 0.089 | 4.9% | 0.000 | 0.007 | 4.6% | 0.004 | 0.089 | 4.9% | |||||
| 0.9 | −0.001 | 0.009 | 0.3% | −0.002 | 0.01 | 7.7% | 0.000 | 0.001 | 6.1% | −0.001 | 0.009 | 4.3% | |||||
| 0.8 | 0.022 | 0.367 | 4.0% | 0.037 | 0.378 | 6.0% | 0.003 | 0.04 | 6.5% | 0.02 | 0.367 | 5.6% | |||||
| 0.2 | −0.002 | 0.102 | 4.4% | −0.002 | 0.102 | 4.4% | 0.000 | 0.008 | 5.3% | −0.002 | 0.102 | 4.4% | |||||
| 1.5 | 0.000 | 0.093 | 5.9% | 0.000 | 0.094 | 6.0% | 0.000 | 0.007 | 4.7% | 0.00 | 0.094 | 6.1% | |||||
| 200 | 0.2 | 0.000 | 0.047 | 5.6% | −0.003 | 0.051 | 8.0% | 0.000 | 0.007 | 5.3% | 0.000 | 0.047 | 6.1% | ||||
| 0.8 | −0.005 | 0.255 | 5.1% | 0.003 | 0.261 | 5.8% | 0.001 | 0.026 | 6.9% | −0.005 | 0.255 | 5.2% | |||||
| 0.2 | 0.002 | 0.071 | 5.8% | 0.001 | 0.071 | 5.7% | 0.000 | 0.006 | 5.4% | 0.002 | 0.071 | 5.8% | |||||
| 1.5 | 0.003 | 0.061 | 3.3% | 0.002 | 0.061 | 3.4% | 0.000 | 0.005 | 5.4% | 0.003 | 0.061 | 3.3% | |||||
| 0.6 | −0.003 | 0.025 | 2.2% | −0.005 | 0.028 | 8.6% | 0.000 | 0.004 | 5.1% | −0.003 | 0.025 | 5.0% | |||||
| 0.8 | 0.021 | 0.256 | 4.1% | 0.030 | 0.264 | 6.0% | 0.000 | 0.026 | 5.2% | 0.020 | 0.256 | 4.7% | |||||
| 0.2 | −0.001 | 0.069 | 4.5% | −0.001 | 0.069 | 4.6% | 0.000 | 0.006 | 5.7% | −0.001 | 0.069 | 4.5% | |||||
| 1.5 | 0.000 | 0.062 | 4.2% | −0.001 | 0.062 | 4.3% | 0.000 | 0.005 | 4.9% | 0.000 | 0.062 | 4.2% | |||||
| 0.9 | −0.001 | 0.006 | 0.7% | −0.001 | 0.007 | 8.3% | 0.000 | 0.001 | 6.0% | −0.001 | 0.006 | 4.7% | |||||
| 0.8 | 0.022 | 0.262 | 4.2% | 0.030 | 0.269 | 6.7% | 0.000 | 0.026 | 4.5% | 0.021 | 0.262 | 5.7% | |||||
| 0.2 | −0.001 | 0.072 | 5.5% | −0.001 | 0.072 | 5.3% | 0.000 | 0.005 | 4.8% | −0.001 | 0.072 | 5.5% | |||||
| 1.5 | 0.000 | 0.063 | 3.8% | 0.000 | 0.063 | 3.9% | 0.000 | 0.005 | 4.4% | 0.000 | 0.063 | 3.8% | |||||
| MQML | GMM | GMM() | II | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R | Bias | RMSE | Bias | RMSE | Bias | RMSE | Bias | RMSE | |||||||||
| 100 | 0.2 | −0.010 | 0.076 | 5.5% | −0.014 | 0.078 | 5.9% | −0.003 | 0.049 | 5.4% | −0.009 | 0.076 | 5.7% | ||||
| 0.2 | 0.007 | 0.335 | 5.7% | 0.013 | 0.336 | 6.0% | 0.005 | 0.056 | 5.8% | 0.007 | 0.335 | 5.8% | |||||
| 0.2 | 0.001 | 0.102 | 5.7% | 0.001 | 0.102 | 5.7% | −0.001 | 0.008 | 6.3% | 0.001 | 0.102 | 5.7% | |||||
| 0.1 | 0.000 | 0.095 | 5.9% | 0.000 | 0.096 | 5.9% | 0.000 | 0.007 | 6.0% | 0.000 | 0.095 | 5.9% | |||||
| 0.6 | −0.005 | 0.039 | 2.8% | −0.007 | 0.040 | 5.2% | −0.002 | 0.026 | 4.8% | −0.004 | 0.039 | 4.6% | |||||
| 0.2 | −0.004 | 0.330 | 4.1% | 0.002 | 0.331 | 4.3% | 0.005 | 0.058 | 5.3% | −0.004 | 0.330 | 4.2% | |||||
| 0.2 | 0.005 | 0.100 | 4.3% | 0.005 | 0.100 | 4.4% | 0.000 | 0.008 | 6.4% | 0.005 | 0.100 | 4.3% | |||||
| 0.1 | 0.000 | 0.091 | 5.6% | 0.000 | 0.091 | 5.7% | 0.000 | 0.007 | 5.3% | 0.000 | 0.091 | 5.6% | |||||
| 0.9 | −0.001 | 0.010 | 0.9% | −0.002 | 0.010 | 4.6% | 0.000 | 0.006 | 3.9% | −0.001 | 0.010 | 5.0% | |||||
| 0.2 | 0.013 | 0.335 | 5.2% | 0.018 | 0.336 | 6.1% | 0.001 | 0.055 | 4.1% | 0.012 | 0.335 | 5.7% | |||||
| 0.2 | −0.001 | 0.102 | 5.2% | −0.001 | 0.102 | 5.4% | 0.000 | 0.008 | 7.3% | −0.001 | 0.102 | 5.2% | |||||
| 0.1 | 0.002 | 0.089 | 5.1% | 0.002 | 0.089 | 5.1% | 0.000 | 0.007 | 5.9% | 0.002 | 0.089 | 5.1% | |||||
| 200 | 0.2 | −0.007 | 0.054 | 5.4% | −0.009 | 0.055 | 5.9% | −0.005 | 0.034 | 5.6% | −0.007 | 0.054 | 5.9% | ||||
| 0.2 | 0.013 | 0.231 | 4.7% | 0.016 | 0.232 | 4.7% | 0.006 | 0.040 | 6.0% | 0.013 | 0.231 | 4.7% | |||||
| 0.2 | −0.002 | 0.071 | 4.3% | −0.002 | 0.071 | 4.4% | 0.000 | 0.005 | 5.1% | −0.002 | 0.071 | 4.3% | |||||
| 0.1 | 0.000 | 0.064 | 4.7% | 0.000 | 0.064 | 4.7% | 0.000 | 0.005 | 5.1% | 0.000 | 0.064 | 4.7% | |||||
| 0.6 | −0.003 | 0.027 | 2.8% | −0.004 | 0.027 | 5.3% | −0.001 | 0.017 | 4.1% | −0.003 | 0.027 | 4.9% | |||||
| 0.2 | −0.001 | 0.233 | 5.2% | 0.001 | 0.233 | 5.4% | 0.002 | 0.039 | 4.4% | −0.002 | 0.233 | 5.2% | |||||
| 0.2 | 0.003 | 0.071 | 4.7% | 0.003 | 0.071 | 4.7% | 0.000 | 0.005 | 5.1% | 0.003 | 0.071 | 4.7% | |||||
| 0.1 | 0.000 | 0.063 | 5.5% | 0.000 | 0.063 | 5.5% | 0.000 | 0.005 | 5.8% | 0.000 | 0.063 | 5.5% | |||||
| 0.9 | −0.001 | 0.007 | 1.3% | −0.001 | 0.007 | 5.7% | −0.001 | 0.005 | 4.9% | −0.001 | 0.007 | 5.3% | |||||
| 0.2 | 0.012 | 0.232 | 3.4% | 0.015 | 0.233 | 4.2% | 0.004 | 0.039 | 5.0% | 0.012 | 0.232 | 4.1% | |||||
| 0.2 | −0.002 | 0.072 | 5.0% | −0.002 | 0.072 | 5.1% | 0.000 | 0.006 | 5.5% | −0.002 | 0.072 | 5.0% | |||||
| 0.1 | 0.002 | 0.063 | 5.0% | 0.002 | 0.063 | 5.0% | 0.000 | 0.005 | 6.7% | 0.002 | 0.063 | 5.0% | |||||
| MQML | GMM | GMM() | II | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R | Bias | RMSE | Bias | RMSE | Bias | RMSE | Bias | RMSE | |||||||||
| 100 | 0.2 | 0.000 | 0.014 | 4.6% | 0.000 | 0.014 | 5.2% | −0.001 | 0.013 | 4.9% | 0.000 | 0.014 | 5.0% | ||||
| 0.8 | 0.001 | 0.047 | 3.6% | 0.000 | 0.047 | 3.7% | 0.003 | 0.042 | 3.7% | 0.001 | 0.046 | 3.7% | |||||
| 0.2 | 0.000 | 0.008 | 4.1% | 0.000 | 0.008 | 4.1% | 0.000 | 0.008 | 5.1% | 0.000 | 0.008 | 4.2% | |||||
| 1.5 | 0.000 | 0.008 | 5.3% | 0.000 | 0.008 | 5.4% | 0.000 | 0.007 | 4.6% | 0.000 | 0.008 | 5.3% | |||||
| 0.6 | 0.000 | 0.008 | 4.3% | 0.000 | 0.008 | 4.9% | −0.001 | 0.007 | 4.3% | 0.000 | 0.008 | 4.6% | |||||
| 0.8 | 0.001 | 0.049 | 4.5% | 0.002 | 0.049 | 5.7% | 0.002 | 0.043 | 4.3% | 0.001 | 0.049 | 5.5% | |||||
| 0.2 | 0.000 | 0.008 | 5.3% | 0.000 | 0.008 | 5.1% | 0.000 | 0.008 | 4.9% | 0.000 | 0.008 | 5.2% | |||||
| 1.5 | 0.000 | 0.008 | 5.3% | 0.000 | 0.008 | 5.4% | 0.000 | 0.007 | 4.7% | 0.000 | 0.008 | 5.3% | |||||
| 0.9 | 0.000 | 0.002 | 5.1% | 0.000 | 0.002 | 7.8% | 0.000 | 0.002 | 5.9% | 0.000 | 0.002 | 6.8% | |||||
| 0.8 | 0.002 | 0.050 | 4.1% | 0.002 | 0.050 | 5.8% | 0.002 | 0.045 | 4.9% | 0.002 | 0.049 | 4.6% | |||||
| 0.2 | 0.000 | 0.008 | 5.4% | 0.000 | 0.008 | 5.4% | 0.000 | 0.008 | 5.6% | 0.000 | 0.008 | 5.4% | |||||
| 1.5 | 0.000 | 0.008 | 5.2% | 0.000 | 0.008 | 5.2% | 0.000 | 0.007 | 4.7% | 0.000 | 0.008 | 5.0% | |||||
| 200 | 0.2 | 0.000 | 0.010 | 3.8% | 0.000 | 0.010 | 4.7% | 0.000 | 0.009 | 3.8% | 0.000 | 0.010 | 4.4% | ||||
| 0.8 | 0.001 | 0.033 | 4.6% | 0.001 | 0.033 | 4.1% | 0.001 | 0.030 | 2.6% | 0.001 | 0.033 | 4.6% | |||||
| 0.2 | 0.000 | 0.006 | 4.6% | 0.000 | 0.006 | 4.6% | 0.000 | 0.005 | 4.7% | 0.000 | 0.006 | 4.6% | |||||
| 1.5 | 0.000 | 0.005 | 4.9% | 0.000 | 0.005 | 4.6% | 0.000 | 0.005 | 5.5% | 0.000 | 0.005 | 4.9% | |||||
| 0.6 | 0.000 | 0.005 | 3.9% | 0.000 | 0.006 | 5.4% | 0.000 | 0.005 | 4.5% | 0.000 | 0.005 | 4.6% | |||||
| 0.8 | 0.000 | 0.034 | 3.7% | −0.001 | 0.034 | 5.0% | 0.000 | 0.030 | 3.8% | 0.000 | 0.034 | 3.9% | |||||
| 0.2 | 0.000 | 0.006 | 5.9% | 0.000 | 0.006 | 6.1% | 0.000 | 0.006 | 5.1% | 0.000 | 0.006 | 5.9% | |||||
| 1.5 | 0.000 | 0.006 | 5.5% | 0.000 | 0.006 | 5.4% | 0.000 | 0.005 | 4.8% | 0.000 | 0.006 | 5.6% | |||||
| 0.9 | 0.000 | 0.001 | 3.9% | 0.000 | 0.001 | 5.9% | 0.000 | 0.001 | 5.4% | 0.000 | 0.001 | 5.0% | |||||
| 0.8 | −0.001 | 0.035 | 4.3% | −0.002 | 0.035 | 5.4% | 0.000 | 0.031 | 5.8% | −0.001 | 0.034 | 5.0% | |||||
| 0.2 | 0.000 | 0.006 | 3.8% | 0.000 | 0.006 | 3.9% | 0.000 | 0.005 | 4.4% | 0.000 | 0.006 | 3.8% | |||||
| 1.5 | 0.000 | 0.006 | 5.1% | 0.000 | 0.006 | 5.2% | 0.000 | 0.005 | 4.6% | 0.000 | 0.006 | 5.5% | |||||
| MQML | GMM | GMM() | II | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R | Bias | RMSE | Bias | RMSE | Bias | RMSE | Bias | RMSE | |||||||||
| 100 | 0.2 | −0.005 | 0.058 | 5.2% | −0.004 | 0.080 | 19.0% | −0.005 | 0.051 | 6.4% | −0.005 | 0.058 | 5.9% | ||||
| 0.2 | 0.006 | 0.066 | 5.0% | 0.006 | 0.086 | 15.4% | 0.006 | 0.058 | 6.4% | 0.006 | 0.066 | 6.7% | |||||
| 0.2 | 0.000 | 0.008 | 4.8% | 0.000 | 0.008 | 4.9% | 0.000 | 0.008 | 5.2% | 0.000 | 0.008 | 4.8% | |||||
| 0.1 | 0.000 | 0.008 | 4.6% | 0.000 | 0.008 | 4.6% | 0.000 | 0.007 | 4.8% | 0.000 | 0.008 | 4.6% | |||||
| 0.6 | −0.003 | 0.029 | 1.4% | −0.001 | 0.042 | 19.7% | −0.003 | 0.027 | 6.5% | −0.003 | 0.029 | 5.5% | |||||
| 0.2 | 0.007 | 0.067 | 1.5% | 0.003 | 0.091 | 17.9% | 0.007 | 0.061 | 6.2% | 0.006 | 0.067 | 5.2% | |||||
| 0.2 | 0.000 | 0.008 | 3.7% | 0.000 | 0.008 | 3.6% | 0.000 | 0.008 | 4.2% | 0.000 | 0.008 | 3.8% | |||||
| 0.1 | 0.000 | 0.007 | 4.4% | 0.000 | 0.007 | 4.0% | 0.000 | 0.007 | 5.6% | 0.000 | 0.007 | 4.4% | |||||
| 0.9 | −0.001 | 0.008 | 0.4% | −0.001 | 0.011 | 19.2% | −0.001 | 0.007 | 5.4% | −0.001 | 0.007 | 5.8% | |||||
| 0.2 | 0.009 | 0.067 | 0.4% | 0.008 | 0.093 | 17.8% | 0.009 | 0.059 | 4.4% | 0.007 | 0.065 | 5.0% | |||||
| 0.2 | 0.000 | 0.009 | 4.8% | 0.000 | 0.009 | 5.7% | 0.000 | 0.008 | 6.1% | 0.000 | 0.009 | 5.1% | |||||
| 0.1 | 0.000 | 0.008 | 5.5% | 0.000 | 0.008 | 5.7% | 0.000 | 0.007 | 5.6% | 0.000 | 0.008 | 5.6% | |||||
| 200 | 0.2 | −0.003 | 0.039 | 5.4% | −0.004 | 0.058 | 20.1% | −0.004 | 0.035 | 5.9% | −0.003 | 0.039 | 6.0% | ||||
| 0.2 | 0.005 | 0.045 | 4.9% | 0.006 | 0.064 | 17.1% | 0.005 | 0.041 | 6.4% | 0.004 | 0.045 | 5.7% | |||||
| 0.2 | −0.001 | 0.006 | 5.3% | −0.001 | 0.006 | 5.6% | 0.000 | 0.006 | 5.4% | −0.001 | 0.006 | 5.3% | |||||
| 0.1 | 0.000 | 0.005 | 5.8% | 0.000 | 0.005 | 5.7% | 0.000 | 0.005 | 5.3% | 0.000 | 0.005 | 5.8% | |||||
| 0.6 | −0.002 | 0.020 | 0.7% | −0.001 | 0.029 | 16.8% | −0.003 | 0.018 | 4.8% | −0.001 | 0.020 | 4.6% | |||||
| 0.2 | 0.003 | 0.045 | 1.1% | 0.002 | 0.062 | 15.6% | 0.005 | 0.040 | 4.3% | 0.002 | 0.044 | 4.5% | |||||
| 0.2 | 0.000 | 0.006 | 5.0% | 0.000 | 0.006 | 5.0% | 0.000 | 0.005 | 4.9% | 0.000 | 0.006 | 5.0% | |||||
| 0.1 | 0.000 | 0.005 | 5.3% | 0.000 | 0.005 | 5.2% | 0.000 | 0.005 | 5.2% | 0.000 | 0.005 | 5.1% | |||||
| 0.9 | 0.000 | 0.005 | 0.1% | 0.000 | 0.008 | 17.3% | 0.000 | 0.004 | 5.4% | 0.000 | 0.005 | 4.7% | |||||
| 0.2 | 0.002 | 0.045 | 0.2% | 0.002 | 0.064 | 15.9% | 0.003 | 0.039 | 3.7% | 0.002 | 0.044 | 3.9% | |||||
| 0.2 | 0.000 | 0.006 | 4.4% | 0.000 | 0.006 | 5.3% | 0.000 | 0.006 | 4.6% | 0.000 | 0.006 | 4.7% | |||||
| 0.1 | 0.000 | 0.005 | 5.8% | 0.000 | 0.005 | 5.8% | 0.000 | 0.005 | 5.1% | 0.000 | 0.005 | 5.9% | |||||
| QML | GMM | II | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R | Bias | RMSE | Bias | RMSE | Bias | RMSE | |||||||
| 100 | 0.2 | 0.014 | 0.043 | 19.0% | −0.007 | 0.040 | 7.5% | −0.003 | 0.037 | 5.6% | |||
| 0.8 | −0.032 | 0.146 | 18.5% | 0.025 | 0.144 | 6.7% | 0.013 | 0.138 | 6.3% | ||||
| 0.2 | −0.002 | 0.029 | 15.9% | −0.002 | 0.029 | 6.1% | −0.002 | 0.029 | 6.1% | ||||
| 1.5 | −0.001 | 0.026 | 17.7% | −0.002 | 0.026 | 6.1% | −0.001 | 0.026 | 5.9% | ||||
| 0.6 | 0.026 | 0.032 | 34.1% | −0.004 | 0.020 | 5.4% | −0.002 | 0.019 | 5.2% | ||||
| 0.8 | −0.137 | 0.188 | 26.5% | 0.022 | 0.137 | 5.4% | 0.010 | 0.131 | 4.7% | ||||
| 0.2 | −0.001 | 0.029 | 17.3% | −0.001 | 0.029 | 5.1% | 0.000 | 0.029 | 5.1% | ||||
| 1.5 | −0.005 | 0.026 | 15.3% | 0.000 | 0.026 | 4.5% | 0.001 | 0.026 | 4.4% | ||||
| 0.9 | 0.011 | 0.011 | 51.3% | −0.001 | 0.005 | 5.2% | 0.000 | 0.005 | 4.1% | ||||
| 0.8 | −0.213 | 0.248 | 39.9% | 0.022 | 0.140 | 5.5% | 0.009 | 0.134 | 5.0% | ||||
| 0.2 | −0.002 | 0.028 | 14.5% | −0.001 | 0.028 | 4.3% | −0.001 | 0.028 | 3.9% | ||||
| 1.5 | −0.011 | 0.029 | 19.8% | 0.001 | 0.027 | 5.1% | 0.001 | 0.027 | 4.7% | ||||
| 200 | 0.2 | 0.017 | 0.032 | 23.0% | −0.003 | 0.026 | 5.6% | −0.001 | 0.025 | 4.3% | |||
| 0.8 | −0.044 | 0.103 | 18.6% | 0.009 | 0.094 | 5.0% | 0.003 | 0.090 | 3.6% | ||||
| 0.2 | −0.001 | 0.020 | 15.7% | −0.001 | 0.020 | 4.1% | −0.001 | 0.020 | 4.2% | ||||
| 1.5 | 0.001 | 0.017 | 14.1% | 0.001 | 0.017 | 4.6% | 0.001 | 0.017 | 4.9% | ||||
| 0.6 | 0.028 | 0.030 | 62.1% | −0.002 | 0.014 | 5.3% | −0.001 | 0.013 | 4.2% | ||||
| 0.8 | −0.145 | 0.172 | 47.1% | 0.009 | 0.096 | 4.8% | 0.003 | 0.093 | 3.8% | ||||
| 0.2 | 0.000 | 0.021 | 18.4% | 0.000 | 0.021 | 4.5% | 0.000 | 0.021 | 4.5% | ||||
| 1.5 | −0.005 | 0.019 | 18.1% | 0.000 | 0.018 | 5.3% | 0.001 | 0.018 | 4.8% | ||||
| 0.9 | 0.011 | 0.011 | 85.1% | 0.000 | 0.004 | 6.3% | 0.000 | 0.003 | 4.1% | ||||
| 0.8 | −0.220 | 0.237 | 68.7% | 0.009 | 0.097 | 5.9% | 0.004 | 0.093 | 5.0% | ||||
| 0.2 | −0.002 | 0.021 | 17.7% | 0.000 | 0.021 | 4.5% | 0.000 | 0.021 | 4.4% | ||||
| 1.5 | −0.014 | 0.023 | 25.0% | −0.002 | 0.019 | 4.6% | −0.001 | 0.019 | 4.5% | ||||
| QML | GMM | II | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R | Bias | RMSE | Bias | RMSE | Bias | RMSE | |||||||
| 100 | 0.2 | 0.041 | 0.078 | 13.3% | −0.007 | 0.056 | 5.7% | −0.004 | 0.055 | 5.6% | |||
| 0.2 | −0.037 | 0.121 | 14.7% | 0.017 | 0.112 | 5.3% | 0.011 | 0.109 | 5.1% | ||||
| 0.2 | −0.002 | 0.029 | 16.2% | −0.004 | 0.029 | 5.9% | −0.002 | 0.029 | 6.0% | ||||
| 0.1 | 0.000 | 0.026 | 18.0% | −0.001 | 0.026 | 6.6% | 0.000 | 0.026 | 6.4% | ||||
| 0.6 | 0.072 | 0.076 | 29.7% | −0.004 | 0.029 | 4.6% | −0.002 | 0.028 | 4.3% | ||||
| 0.2 | −0.149 | 0.181 | 25.9% | 0.007 | 0.108 | 5.3% | 0.001 | 0.107 | 5.6% | ||||
| 0.2 | −0.001 | 0.029 | 16.4% | −0.001 | 0.029 | 5.2% | 0.001 | 0.029 | 5.2% | ||||
| 0.1 | 0.000 | 0.026 | 18.2% | 0.000 | 0.027 | 6.6% | 0.001 | 0.027 | 6.2% | ||||
| 0.9 | 0.026 | 0.027 | 48.5% | −0.001 | 0.008 | 5.3% | −0.001 | 0.008 | 5.3% | ||||
| 0.2 | −0.214 | 0.235 | 38.4% | 0.010 | 0.110 | 5.3% | 0.004 | 0.109 | 4.9% | ||||
| 0.2 | −0.003 | 0.028 | 15.8% | 0.000 | 0.028 | 4.0% | 0.001 | 0.028 | 4.2% | ||||
| 0.1 | −0.002 | 0.025 | 15.2% | 0.000 | 0.026 | 5.1% | 0.001 | 0.026 | 4.9% | ||||
| 200 | 0.2 | 0.046 | 0.064 | 23.3% | −0.004 | 0.038 | 4.6% | −0.003 | 0.038 | 4.5% | |||
| 0.2 | −0.046 | 0.093 | 18.7% | 0.009 | 0.079 | 5.3% | 0.005 | 0.078 | 4.7% | ||||
| 0.2 | −0.001 | 0.021 | 17.5% | −0.002 | 0.021 | 6.0% | −0.001 | 0.021 | 5.6% | ||||
| 0.1 | 0.000 | 0.018 | 15.8% | 0.000 | 0.018 | 4.3% | 0.000 | 0.018 | 4.0% | ||||
| 0.6 | 0.074 | 0.076 | 70.7% | −0.002 | 0.020 | 4.8% | −0.001 | 0.020 | 4.6% | ||||
| 0.2 | −0.152 | 0.170 | 49.3% | 0.004 | 0.081 | 6.3% | 0.000 | 0.079 | 5.9% | ||||
| 0.2 | −0.002 | 0.021 | 17.6% | −0.001 | 0.021 | 5.0% | 0.001 | 0.021 | 5.0% | ||||
| 0.1 | 0.000 | 0.019 | 17.8% | 0.000 | 0.019 | 6.1% | 0.001 | 0.019 | 6.4% | ||||
| 0.9 | 0.027 | 0.027 | 95.2% | −0.001 | 0.005 | 4.6% | 0.000 | 0.005 | 4.1% | ||||
| 0.2 | −0.218 | 0.229 | 72.6% | 0.005 | 0.081 | 6.0% | 0.001 | 0.079 | 5.2% | ||||
| 0.2 | −0.003 | 0.020 | 15.3% | 0.000 | 0.020 | 4.8% | 0.001 | 0.020 | 4.8% | ||||
| 0.1 | −0.001 | 0.018 | 15.0% | 0.000 | 0.018 | 4.2% | 0.001 | 0.018 | 3.9% | ||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bao, Y.; Liu, X.; Yang, L. Indirect Inference Estimation of Spatial Autoregressions. Econometrics 2020, 8, 34. https://0-doi-org.brum.beds.ac.uk/10.3390/econometrics8030034
Bao Y, Liu X, Yang L. Indirect Inference Estimation of Spatial Autoregressions. Econometrics. 2020; 8(3):34. https://0-doi-org.brum.beds.ac.uk/10.3390/econometrics8030034
Chicago/Turabian StyleBao, Yong, Xiaotian Liu, and Lihong Yang. 2020. "Indirect Inference Estimation of Spatial Autoregressions" Econometrics 8, no. 3: 34. https://0-doi-org.brum.beds.ac.uk/10.3390/econometrics8030034





