An Empirical Model of Medicare Costs: The Role of Health Insurance, Employment, and Delays in Medicare Enrollment
Abstract
:1. Introduction
2. Data and Medicare Delayers
2.1. MCBS Data
2.2. Empirically Identifying Medicare Delayers
3. Medicare Costs: An Empirical Analysis
3.1. Empirical Challenges and Model Specifications
3.2. The Effect of Working and Medicare Secondary Payer on Medicare Costs
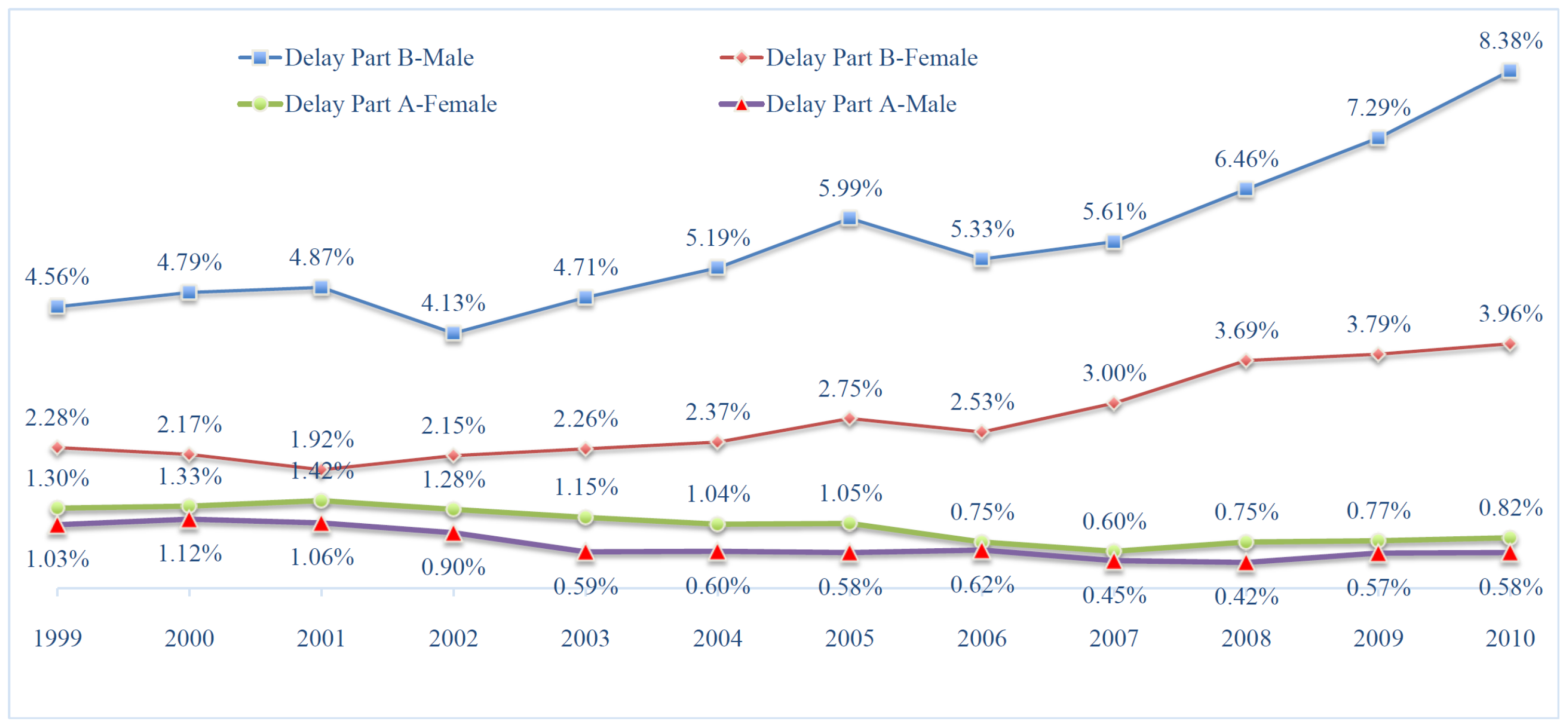
3.3. Delayed Enrollment and Medicare Costs
4. Sensitivity Analysis of the Results
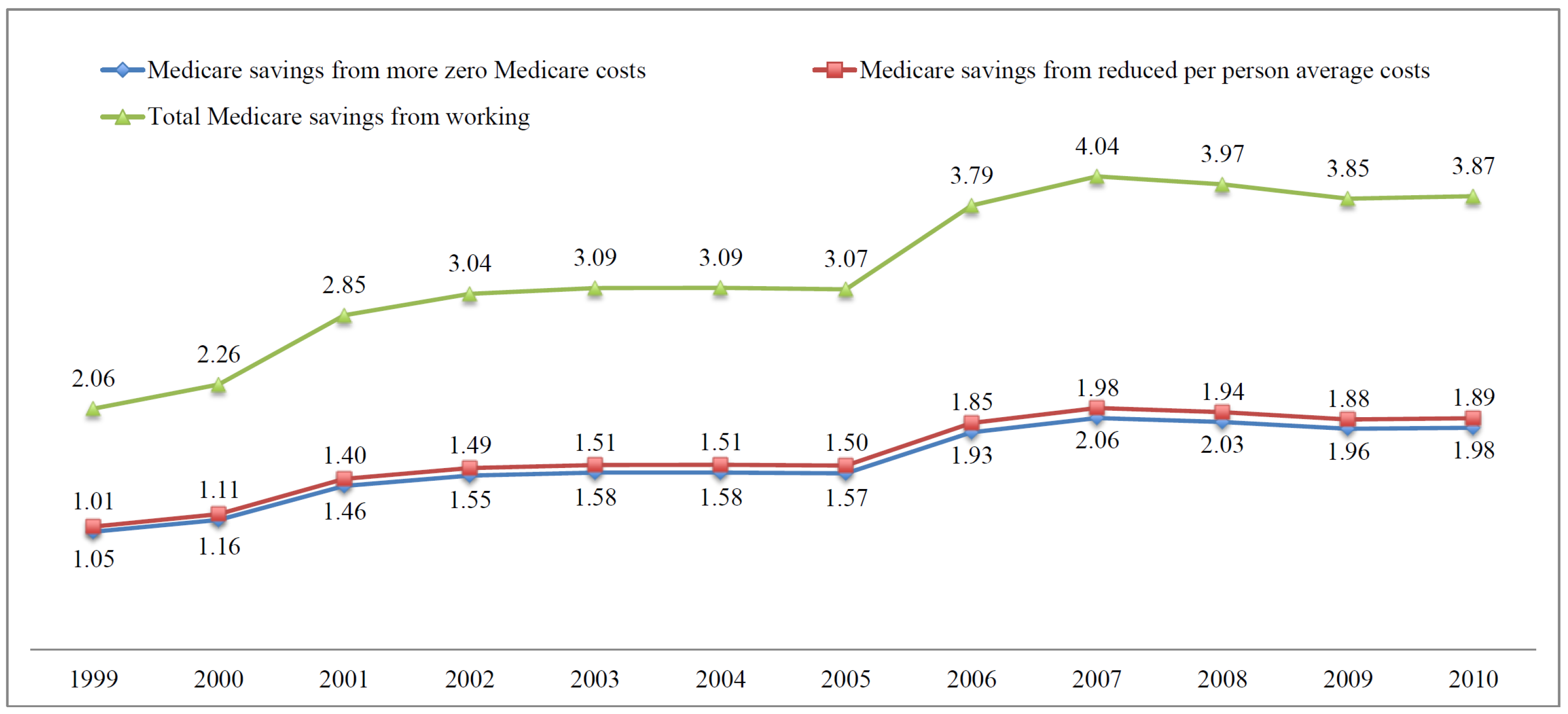
5. Medicare Savings
5.1. Medicare Savings from Work and the Medicare Secondary Payer Effect
5.2. Medicare Savings from Delayed Medicare Enrollment
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MSP | Medicare as secondary payer |
| MCBS | Medicare Current Beneficiary Survey |
| EPHI | Employer-provided health insurance |
| OOP | Out-of-pocket |
| DRC | Delayed retirement credits |
| FRA | Full retirement age |
| CMS | Centers for Medicare & Medicaid Services |
| LFPR | Labor force participation rate |
| IEP | Initial enrollment period |
| SEP | Special enrollment period |
| OLS | Ordinary least squares |
| TPM | Two-part model |
| IV | Instrumental Variable |
| FE | Fixed-Effect |
| NHIS | National Health Interview Survey |
| HRS | Health and Retirement Study |
| CPI | Consumer Price Index |
| MA | Medicare Advantage |
Appendix A
Appendix A.1. Summary Statistics
| Variables | No EPHI | EPHI | All |
|---|---|---|---|
| Age | 75.55 | 70.18 | 75.33 |
| (7.088) | (4.844) | (7.089) | |
| Male | 0.416 | 0.517 | 0.420 |
| (0.493) | (0.500) | (0.494) | |
| Married | 0.554 | 0.751 | 0.562 |
| (0.497) | (0.433) | (0.496) | |
| Black | 0.076 | 0.073 | 0.076 |
| (0.264) | (0.260) | (0.264) | |
| Hispanic | 0.020 | 0.007 | 0.020 |
| (0.141) | (0.083) | (0.139) | |
| High School | 0.300 | 0.242 | 0.297 |
| (0.458) | (0.428) | (0.457) | |
| Some College | 0.252 | 0.286 | 0.254 |
| (0.434) | (0.452) | (0.435) | |
| College | 0.105 | 0.142 | 0.106 |
| (0.306) | (0.350) | (0.309) | |
| Excellent Health | 0.173 | 0.264 | 0.177 |
| (0.379) | (0.441) | (0.382) | |
| Very Good Health | 0.313 | 0.353 | 0.315 |
| (0.464) | (0.478) | (0.465) | |
| Good Health | 0.325 | 0.275 | 0.323 |
| (0.468) | (0.446) | (0.468) | |
| Fair Health | 0.144 | 0.087 | 0.142 |
| (0.352) | (0.283) | (0.349) | |
| Currently Working | 0.129 | 0.652 | 0.151 |
| (0.336) | (0.476) | (0.358) |
| Variables | Female | Male | Total |
|---|---|---|---|
| Premium–A | $3962 | $3954 | $3957 |
| (2011) | (1677) | (1817) | |
| Premium–B | $998 | $1004 | $1001 |
| (234) | (239) | (236) | |
| Medicare Costs | $6782 | $7352 | $7012 |
| (14,309) | (16,407) | (15,193) | |
| Total Health Expenditure | $10,693 | $11,056 | $10,844 |
| (17,465) | (20,026) | (18,576) | |
| OOP Expenditure | $1871 | $1766 | $1827 |
| (4213) | (3895) | (4084) | |
| Income of Respondent | $32,642 | $46,380 | $38,414 |
| (54,373) | (88,417) | (71,027) | |
| Currently Working | 0.114 | 0.202 | 0.151 |
| (0.317) | (0.401) | (0.358) | |
| EPHI among Workers | 0.173 | 0.177 | 0.175 |
| (0.378) | (0.381) | (0.380) | |
| Covered by EPHI | 0.034 | 0.050 | 0.041 |
| (0.181) | (0.218) | (0.197) | |
| Workers among EPHI | 0.583 | 0.717 | 0.652 |
| (0.493) | (0.450) | (0.476) |
Appendix A.2. Additional Estimation Results
| Variables | Medicare Costs | Total Health Exp. | Out-of-Pocket Exp. |
|---|---|---|---|
| Ghost | −0.024 | −0.006 | −0.005 |
| (0.008) | (0.003) | (0.003) | |
| Good Health | 0.019 | 0.007 | 0.010 |
| (0.003) | (0.001) | (0.002) | |
| Fair Health | 0.039 | 0.011 | 0.011 |
| (0.005) | (0.002) | (0.002) | |
| Poor Health | 0.043 | 0.004 | 0.001 |
| (0.009) | (0.005) | (0.004) | |
| Age | 0.126 | 0.008 | 0.014 |
| (0.008) | (0.003) | (0.003) | |
| Age | −0.001 | −0.000 | −0.000 |
| (0.000) | (0.000) | (0.000) | |
| Ever Smoke | −0.001 | 0.000 | 0.002 |
| (0.004) | (0.001) | (0.002) | |
| Smoker | −0.033 | −0.012 | −0.017 |
| (0.005) | (0.002) | (0.002) | |
| No Schooling | 0.021 | −0.009 | −0.022 |
| (0.018) | (0.005) | (0.005) | |
| Less than 8th | −0.019 | −0.007 | −0.012 |
| (0.006) | (0.002) | (0.002) | |
| Some High School | −0.009 | −0.004 | −0.006 |
| (0.006) | (0.002) | (0.002) | |
| Some College | 0.001 | 0.004 | 0.005 |
| (0.005) | (0.002) | (0.002) | |
| College | 0.022 | 0.008 | 0.013 |
| (0.007) | (0.003) | (0.003) | |
| Graduate School | 0.036 | 0.011 | 0.017 |
| (0.007) | (0.003) | (0.004) | |
| Widow | −0.009 | −0.005 | −0.005 |
| (0.004) | (0.002) | (0.002) | |
| Separated | −0.040 | −0.008 | −0.013 |
| (0.016) | (0.005) | (0.005) | |
| Never Married | −0.017 | −0.013 | −0.017 |
| (0.010) | (0.003) | (0.004) | |
| Black | −0.069 | −0.011 | −0.013 |
| (0.006) | (0.002) | (0.002) | |
| Hispanic | −0.056 | −0.000 | −0.023 |
| (0.011) | (0.004) | (0.004) | |
| Other Race | −0.010 | −0.006 | −0.017 |
| (0.011) | (0.003) | (0.004) | |
| Number of Kids | −0.000 | −0.000 | −0.001 |
| (0.001) | (0.000) | (0.000) | |
| Male | −0.043 | −0.013 | −0.016 |
| (0.004) | (0.001) | (0.002) | |
| Income 10 K–15 K | −0.031 | 0.006 | 0.016 |
| (0.006) | (0.002) | (0.002) | |
| Income 15 K–20 K | −0.017 | 0.010 | 0.023 |
| (0.006) | (0.002) | (0.002) | |
| Income 20 K–25 K | −0.009 | 0.012 | 0.029 |
| (0.007) | (0.002) | (0.003) | |
| Income 25 K–30 K | −0.007 | 0.014 | 0.031 |
| (0.007) | (0.002) | (0.003) | |
| Income 30 K–35 K | 0.010 | 0.021 | 0.039 |
| (0.007) | (0.003) | (0.003) | |
| Income 35 K–40 K | 0.019 | 0.020 | 0.038 |
| (0.008) | (0.003) | (0.003) | |
| Income 15 K–20 K | −0.017 | 0.010 | 0.023 |
| (0.006) | (0.002) | (0.002) | |
| Income 20 K–25 K | −0.009 | 0.012 | 0.029 |
| (0.007) | (0.002) | (0.003) | |
| Income 25 K–30 K | −0.007 | 0.014 | 0.031 |
| (0.007) | (0.002) | (0.003) | |
| Income 30 K–35 K | 0.010 | 0.021 | 0.039 |
| (0.007) | (0.003) | (0.003) | |
| Income 35 K–40 K | 0.019 | 0.020 | 0.038 |
| (0.008) | (0.003) | (0.003) | |
| Income 40 K–45 K | 0.028 | 0.024 | 0.048 |
| (0.009) | (0.003) | (0.004) | |
| Income 45 K–50 K | 0.036 | 0.025 | 0.046 |
| (0.009) | (0.003) | (0.004) | |
| Income 50 K+ | 0.030 | 0.031 | 0.052 |
| (0.007) | (0.003) | (0.003) | |
| Mid–West | 0.075 | 0.003 | 0.002 |
| (0.005) | (0.002) | (0.002) | |
| South | 0.065 | 0.000 | −0.001 |
| (0.005) | (0.002) | (0.002) | |
| West | −0.071 | −0.001 | −0.006 |
| (0.005) | (0.002) | (0.002) | |
| had_hbp | 0.045 | 0.022 | 0.029 |
| (0.004) | (0.001) | (0.002) | |
| had_diabts | 0.019 | 0.016 | 0.018 |
| (0.005) | (0.002) | (0.002) | |
| had_emphys | 0.021 | 0.012 | 0.013 |
| (0.005) | (0.002) | (0.003) | |
| had_myocar | 0.013 | 0.006 | 0.008 |
| (0.006) | (0.002) | (0.003) | |
| had_chd | 0.016 | 0.011 | 0.009 |
| (0.006) | (0.003) | (0.003) | |
| had_stroke | 0.008 | 0.008 | 0.008 |
| (0.006) | (0.003) | (0.003) | |
| had_psych | −0.009 | 0.007 | 0.002 |
| (0.007) | (0.004) | (0.004) | |
| had_alzhmr | 0.019 | 0.011 | 0.008 |
| (0.010) | (0.006) | (0.005) | |
| had_brkhip | −0.021 | −0.003 | −0.002 |
| (0.009) | (0.004) | (0.004) | |
| had_arth | 0.030 | 0.013 | 0.014 |
| (0.004) | (0.001) | (0.002) | |
| had_cancer | 0.028 | 0.014 | 0.016 |
| (0.004) | (0.002) | (0.002) | |
| had_ctarac | 0.037 | 0.009 | 0.009 |
| (0.004) | (0.002) | (0.002) | |
| had_hraid | −0.001 | 0.011 | 0.016 |
| (0.006) | (0.003) | (0.003) | |
| diff_walkblks | 0.006 | 0.002 | 0.004 |
| (0.004) | (0.002) | (0.002) | |
| diff_walkblks_nr | −0.014 | 0.016 | 0.014 |
| (0.029) | (0.012) | (0.012) | |
| diff_stoop | 0.017 | 0.002 | 0.005 |
| (0.004) | (0.001) | (0.002) | |
| diff_stoop_nr | 0.129 | 0.000 | 0.018 |
| (0.068) | (.) | (0.033) | |
| diff_reach | 0.019 | −0.000 | 0.003 |
| (0.004) | (0.002) | (0.002) | |
| diff_reach_nr | −0.100 | 0.001 | −0.004 |
| (0.051) | (0.019) | (0.020) | |
| diff_lift | 0.013 | 0.005 | 0.000 |
| (0.004) | (0.002) | (0.002) | |
| diff_lift_nr | 0.035 | −0.029 | −0.026 |
| (0.043) | (0.012) | (0.016) | |
| diff_dres | −0.006 | −0.001 | 0.000 |
| (0.012) | (0.006) | (0.006) | |
| diff_walk | −0.010 | 0.000 | 0.000 |
| (0.005) | (0.002) | (0.002) | |
| diff_bath | −0.002 | 0.001 | 0.003 |
| (0.008) | (0.004) | (0.005) | |
| diff_eat | −0.015 | 0.001 | −0.009 |
| (0.013) | (0.007) | (0.005) | |
| diff_char | −0.000 | −0.003 | −0.004 |
| (0.006) | (0.003) | (0.003) | |
| diff_toil | −0.003 | −0.004 | 0.007 |
| (0.010) | (0.005) | (0.005) | |
| diff_meal | 0.003 | 0.004 | 0.002 |
| (0.007) | (0.003) | (0.003) | |
| diff_shop | 0.002 | −0.004 | −0.007 |
| (0.009) | (0.004) | (0.004) | |
| diff_tele | −0.010 | −0.013 | −0.009 |
| (0.008) | (0.003) | (0.004) | |
| diff_bils | 0.017 | −0.002 | 0.002 |
| (0.009) | (0.004) | (0.004) | |
| help_dres | −0.007 | 0.029 | 0.006 |
| (0.016) | (0.011) | (0.007) | |
| help_walk | −0.007 | 0.004 | −0.000 |
| (0.010) | (0.006) | (0.005) | |
| help_bath | 0.018 | 0.001 | −0.002 |
| (0.012) | (0.006) | (0.006) | |
| help_eat | 0.071 | −0.020 | 0.006 |
| (0.024) | (0.010) | (0.009) | |
| help_chair | 0.013 | 0.012 | 0.004 |
| (0.013) | (0.007) | (0.007) | |
| help_toil | 0.028 | −0.012 | −0.007 |
| (0.018) | (0.008) | (0.008) | |
| help_meal | −0.001 | 0.006 | −0.006 |
| (0.010) | (0.005) | (0.005) | |
| help_shop | −0.004 | −0.002 | 0.001 |
| (0.010) | (0.005) | (0.005) | |
| help_tele | 0.013 | 0.009 | 0.006 |
| (0.012) | (0.005) | (0.005) | |
| help_bills | −0.018 | 0.004 | 0.007 |
| (0.011) | (0.006) | (0.006) | |
| drc35 | 0.075 | 0.008 | 0.011 |
| (0.007) | (0.003) | (0.003) | |
| drc40 | 0.107 | 0.008 | 0.011 |
| (0.008) | (0.003) | (0.003) | |
| drc45 | 0.155 | 0.004 | 0.015 |
| (0.008) | (0.003) | (0.004) | |
| drc50 | 0.188 | 0.009 | 0.023 |
| (0.009) | (0.003) | (0.004) | |
| drc55 | 0.227 | 0.005 | 0.022 |
| (0.009) | (0.003) | (0.004) | |
| drc60 | 0.279 | 0.007 | 0.025 |
| (0.010) | (0.004) | (0.004) | |
| drc65 | 0.314 | 0.007 | 0.025 |
| (0.012) | (0.004) | (0.005) | |
| drc65_fra2 | 0.334 | 0.005 | 0.023 |
| (0.013) | (0.004) | (0.005) | |
| drc70_fra4 | 0.345 | 0.008 | 0.029 |
| (0.013) | (0.004) | (0.005) | |
| drc70_fra6 | 0.342 | 0.011 | 0.031 |
| (0.014) | (0.005) | (0.006) | |
| drc75_fra8 | 0.394 | 0.006 | 0.030 |
| (0.015) | (0.005) | (0.006) | |
| drc75_fra10 | 0.377 | 0.008 | 0.032 |
| (0.017) | (0.006) | (0.007) | |
| drc80_fra66 | 0.361 | 0.000 | 0.021 |
| (0.013) | (0.005) | (0.006) |
| Variables | Medicare Costs | Total Health Exp. | Out-of-Pocket Exp. |
|---|---|---|---|
| Ghost | −0.139 | −0.210 | −0.203 |
| (0.035) | (0.035) | (0.022) | |
| Good Health | 0.314 | 0.233 | 0.161 |
| (0.014) | (0.015) | (0.009) | |
| Fair Health | 0.515 | 0.396 | 0.213 |
| (0.019) | (0.021) | (0.013) | |
| Poor Health | 0.896 | 0.627 | 0.225 |
| (0.031) | (0.034) | (0.021) | |
| Age | 0.193 | 0.178 | 0.124 |
| (0.022) | (0.024) | (0.015) | |
| Age | −0.001 | −0.001 | −0.001 |
| (0.000) | (0.000) | (0.000) | |
| Ever Smoke | 0.072 | 0.046 | 0.016 |
| (0.013) | (0.014) | (0.009) | |
| Smoker | −0.211 | −0.174 | −0.145 |
| (0.022) | (0.023) | (0.015) | |
| No Schooling | −0.072 | −0.084 | −0.586 |
| (0.054) | (0.058) | (0.038) | |
| Less than 8th | −0.088 | −0.133 | −0.228 |
| (0.021) | (0.022) | (0.014) | |
| Some High School | −0.078 | −0.065 | −0.079 |
| (0.019) | (0.020) | (0.012) | |
| Some College | 0.066 | 0.043 | 0.071 |
| (0.016) | (0.017) | (0.011) | |
| College | 0.070 | 0.088 | 0.176 |
| (0.022) | (0.023) | (0.015) | |
| Graduate School | 0.086 | 0.155 | 0.219 |
| (0.025) | (0.026) | (0.017) | |
| Widow | 0.066 | 0.056 | 0.045 |
| (0.015) | (0.016) | (0.010) | |
| Divorced | 0.064 | 0.015 | −0.033 |
| (0.024) | (0.025) | (0.016) | |
| Separated | 0.145 | 0.006 | −0.188 |
| (0.070) | (0.072) | (0.047) | |
| Never Married | −0.037 | −0.023 | −0.102 |
| (0.037) | (0.040) | (0.025) | |
| Black | 0.036 | −0.096 | −0.287 |
| (0.024) | (0.024) | (0.016) | |
| Hispanic | 0.011 | −0.194 | −0.468 |
| (0.043) | (0.044) | (0.029) | |
| Other Race | 0.045 | −0.059 | −0.511 |
| (0.039) | (0.040) | (0.026) | |
| Number of Kids | 0.000 | 0.001 | −0.008 |
| (0.003) | (0.003) | (0.002) | |
| Male | 0.054 | −0.003 | −0.151 |
| (0.014) | (0.015) | (0.010) | |
| Income 10 K–15 K | −0.003 | 0.002 | 0.412 |
| (0.023) | (0.025) | (0.016) | |
| Income 15 K–20 K | 0.012 | 0.051 | 0.579 |
| (0.025) | (0.027) | (0.018) | |
| Income 20 K–25 K | −0.001 | 0.093 | 0.655 |
| (0.026) | (0.028) | (0.019) | |
| Income 25 K–30 K | 0.064 | 0.156 | 0.699 |
| (0.027) | (0.029) | (0.019) | |
| Income 30 K–35 K | 0.020 | 0.127 | 0.691 |
| (0.029) | (0.032) | (0.021) | |
| Income 35 K–40 K | 0.073 | 0.206 | 0.729 |
| (0.030) | (0.032) | (0.021) | |
| Income 40 K–45 K | 0.087 | 0.240 | 0.763 |
| (0.033) | (0.036) | (0.024) | |
| Income 45 K–50 K | 0.090 | 0.265 | 0.790 |
| (0.034) | (0.037) | (0.024) | |
| Income 50 K+ | 0.152 | 0.305 | 0.880 |
| (0.026) | (0.029) | (0.019) | |
| Mid–West | −0.204 | −0.043 | 0.080 |
| (0.019) | (0.019) | (0.012) | |
| South | −0.139 | −0.016 | 0.128 |
| (0.017) | (0.017) | (0.011) | |
| West | −0.101 | −0.217 | −0.056 |
| (0.021) | (0.020) | (0.013) | |
| had_hbp | 0.099 | 0.194 | 0.198 |
| (0.013) | (0.015) | (0.010) | |
| had_diabts | 0.293 | 0.250 | 0.214 |
| (0.015) | (0.016) | (0.010) | |
| had_emphys | 0.275 | 0.251 | 0.142 |
| (0.017) | (0.018) | (0.011) | |
| had_myocar | 0.226 | 0.214 | 0.113 |
| (0.018) | (0.019) | (0.012) | |
| had_chd | 0.260 | 0.213 | 0.135 |
| (0.018) | (0.020) | (0.013) | |
| had_stroke | 0.168 | 0.156 | 0.121 |
| (0.018) | (0.020) | (0.013) | |
| had_psych | 0.137 | 0.147 | 0.184 |
| (0.025) | (0.026) | (0.017) | |
| had_alzhmr | 0.017 | 0.072 | 0.103 |
| (0.032) | (0.035) | (0.022) | |
| had_brkhip | 0.267 | 0.184 | 0.073 |
| (0.030) | (0.032) | (0.020) | |
| had_arth | 0.130 | 0.120 | 0.088 |
| (0.013) | (0.014) | (0.009) | |
| had_cancer | 0.328 | 0.234 | 0.137 |
| (0.012) | (0.013) | (0.008) | |
| had_ctarac | 0.102 | 0.114 | 0.055 |
| (0.013) | (0.014) | (0.009) | |
| had_hraid | 0.096 | 0.174 | 0.283 |
| (0.018) | (0.020) | (0.012) | |
| diff_walkblks | 0.219 | 0.166 | 0.085 |
| (0.016) | (0.017) | (0.011) | |
| diff_walkblks_nr | −0.012 | −0.077 | 0.034 |
| (0.127) | (0.136) | (0.085) | |
| diff_stoop | 0.059 | 0.074 | 0.063 |
| (0.015) | (0.016) | (0.010) | |
| diff_stoop_nr | 0.009 | 0.115 | 0.123 |
| (0.273) | (0.299) | (0.191) | |
| diff_reach | −0.020 | 0.010 | 0.009 |
| (0.015) | (0.016) | (0.010) | |
| diff_reach_nr | 0.478 | −0.006 | −0.198 |
| (0.271) | (0.283) | (0.182) | |
| diff_lift | 0.184 | 0.138 | 0.047 |
| (0.016) | (0.017) | (0.011) | |
| diff_lift_nr | −0.060 | 0.336 | 0.090 |
| (0.177) | (0.195) | (0.124) | |
| diff_dres | −0.008 | −0.012 | −0.021 |
| (0.044) | (0.048) | (0.030) | |
| diff_walk | 0.096 | 0.082 | 0.088 |
| (0.019) | (0.021) | (0.013) | |
| diff_bath | 0.056 | 0.047 | 0.027 |
| (0.032) | (0.035) | (0.022) | |
| diff_eat | −0.035 | −0.007 | 0.062 |
| (0.051) | (0.055) | (0.035) | |
| diff_char | −0.087 | −0.049 | −0.018 |
| (0.025) | (0.027) | (0.017) | |
| diff_toil | 0.003 | 0.064 | 0.100 |
| (0.037) | (0.041) | (0.025) | |
| diff_meal | 0.133 | 0.051 | −0.006 |
| (0.026) | (0.028) | (0.018) | |
| diff_shop | 0.030 | 0.036 | −0.002 |
| (0.036) | (0.040) | (0.025) | |
| diff_tele | −0.210 | −0.101 | −0.025 |
| (0.032) | (0.034) | (0.022) | |
| diff_bils | 0.024 | 0.043 | 0.033 |
| (0.034) | (0.037) | (0.023) | |
| help_dres | 0.037 | 0.017 | 0.054 |
| (0.057) | (0.062) | (0.039) | |
| help_walk | 0.023 | −0.007 | −0.059 |
| (0.037) | (0.041) | (0.026) | |
| help_bath | 0.324 | 0.229 | 0.061 |
| (0.043) | (0.048) | (0.030) | |
| help_eat | 0.120 | 0.224 | 0.033 |
| (0.080) | (0.089) | (0.056) | |
| help_chair | −0.024 | 0.002 | 0.022 |
| (0.049) | (0.054) | (0.034) | |
| help_toil | 0.137 | 0.111 | 0.027 |
| (0.064) | (0.071) | (0.044) | |
| help_meal | 0.053 | 0.049 | −0.000 |
| (0.037) | (0.041) | (0.026) | |
| help_shop | 0.092 | 0.078 | 0.025 |
| (0.040) | (0.044) | (0.028) | |
| help_tele | −0.033 | −0.029 | 0.058 |
| (0.042) | (0.046) | (0.029) | |
| help_bills | −0.059 | −0.058 | −0.005 |
| (0.042) | (0.046) | (0.029) | |
| constant | −0.877 | 0.703 | 0.831 |
| (0.877) | (0.939) | (0.592) |
| (1) With Health Controls | (2) Without Health Controls | |||||
|---|---|---|---|---|---|---|
| Medicare | Total | OOP | Medicare | Total | OOP | |
| Work | −0.030 | 0.002 | 0.001 | −0.033 | 0.001 | 0.001 |
| (0.005) | (0.002) | (0.002) | (0.005) | (0.002) | (0.002) | |
| EPHI | 0.002 | 0.001 | 0.008 | 0.002 | 0.001 | 0.008 |
| (0.014) | (0.006) | (0.008) | (0.014) | (0.006) | (0.008) | |
| wepc | −0.003 | 0.004 | 0.001 | −0.002 | 0.004 | 0.002 |
| (0.017) | (0.007) | (0.009) | (0.017) | (0.007) | (0.009) | |
| Delay–A–current | 0.112 | −0.000 | −0.047 | 0.113 | 0.000 | −0.047 |
| (0.019) | (0.006) | (0.005) | (0.019) | (0.006) | (0.005) | |
| Delay–B–current | −0.460 | −0.017 | −0.019 | −0.460 | −0.017 | −0.019 |
| (0.011) | (0.003) | (0.004) | (0.011) | (0.003) | (0.004) | |
| EPHI–B–current | −0.093 | 0.003 | −0.002 | −0.093 | 0.003 | −0.002 |
| (0.026) | (0.006) | (0.009) | (0.026) | (0.006) | (0.009) | |
| Good Health | 0.020 | 0.007 | 0.010 | |||
| (0.003) | (0.001) | (0.002) | ||||
| Fair Health | 0.037 | 0.011 | 0.011 | |||
| (0.005) | (0.002) | (0.002) | ||||
| Poor Health | 0.039 | 0.004 | 0.002 | |||
| (0.008) | (0.005) | (0.004) | ||||
| Obs. | 95,146 | 95,103 | 95,146 | 95,146 | 95,103 | 95,146 |
| (1) With Health Controls | (2) Without Health Controls | |||||
|---|---|---|---|---|---|---|
| Medicare | Total | OOP | Medicare | Total | OOP | |
| Work | −0.031 | 0.002 | 0.001 | −0.033 | 0.002 | 0.001 |
| (0.005) | (0.002) | (0.002) | (0.005) | (0.002) | (0.002) | |
| EPHI | 0.002 | 0.001 | 0.008 | 0.002 | 0.001 | 0.008 |
| (0.014) | (0.006) | (0.008) | (0.014) | (0.006) | (0.008) | |
| wepc | −0.003 | 0.004 | 0.001 | −0.002 | 0.004 | 0.002 |
| (0.017) | (0.007) | (0.009) | (0.017) | (0.007) | (0.009) | |
| Delay–A–current | 0.114 | −0.001 | −0.048 | 0.115 | −0.000 | −0.048 |
| (0.019) | (0.006) | (0.005) | (0.019) | (0.006) | (0.005) | |
| Delay–B–current | −0.459 | −0.017 | −0.019 | −0.459 | −0.017 | −0.019 |
| (0.011) | (0.003) | (0.004) | (0.011) | (0.003) | (0.004) | |
| EPHI–B–current | −0.093 | 0.003 | −0.002 | −0.093 | 0.003 | −0.002 |
| (0.026) | (0.006) | (0.009) | (0.026) | (0.006) | (0.009) | |
| Delay–past | 0.021 | −0.003 | −0.009 | 0.021 | −0.003 | −0.009 |
| (0.011) | (0.004) | (0.004) | (0.011) | (0.004) | (0.004) | |
| Good Health | 0.019 | 0.007 | 0.010 | |||
| (0.003) | (0.001) | (0.002) | ||||
| Fair Health | 0.037 | 0.011 | 0.011 | |||
| (0.005) | (0.002) | (0.002) | ||||
| Poor Health | 0.039 | 0.004 | 0.002 | |||
| (0.008) | (0.005) | (0.004) | ||||
| Obs. | 95,146 | 95,103 | 95,146 | 95,146 | 95,103 | 95,146 |
Appendix A.3. Medicare Savings
| Year | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 |
|---|---|---|---|---|---|---|---|
| Past Delayers | 0.85 | 0.75 | 0.78 | 0.83 | 0.77 | 0.77 | 0.81 |
| Medicare ≻ 0 | 81.4% | 79.6% | 92.2% | 95.1% | 96.8% | 98.5% | 94.5% |
| Medicare = 0 | 18.6% | 20.4% | 7.8% | 4.9% | 3.2% | 1.5% | 5.5% |
| Prob(Medicare ≻ 0) | 79.3% | 77.5% | 89.8% | 92.6% | 94.3% | 95.9% | 92% |
| Diff. of prob. | 2.11% | 2.06% | 2.39% | 2.46% | 2.51% | 2.55% | 2.45% |
| Avg. Medicare costs | $7291 | $7308 | $7159 | $7253 | $7007 | $6702 | $6673 |
| Current Part A delayers | 0.26 | 0.25 | 0.21 | 0.16 | 0.19 | 0.23 | 0.24 |
| Medicare ≻ 0 | 86.2% | 96.3% | 96.5% | 97.6% | 100% | 94.9% | 95.5% |
| Medicare = 0 | 13.8% | 3.7% | 3.5% | 2.4% | 0.0% | 5.1% | 4.5% |
| Prob(Medicare ≻ 0) | 74.3% | 83% | 83.2% | 84.1% | 86.2% | 81.8% | 82.3% |
| Diff. of prob. | 11.8% | 3.2% | 3.0% | 2.1% | 0.0% | 4.4% | 3.9% |
| Avg. Part A costs | $2873 | $2744 | $2739 | $2765 | $2573 | $2282 | $2195 |
| Current Part B delayers | 1.05 | 1.23 | 1.12 | 1.27 | 1.56 | 1.74 | 1.99 |
| Medicare ≻ 0 | 3.8% | 3.5% | 6.9% | 14.6% | 12.5% | 15.2% | 9.2% |
| Medicare = 0 | 96.2% | 96.5% | 93.1% | 85.4% | 87.5% | 84.8% | 90.8% |
| Prob(Medicare ≻ 0) | 8.7% | 8.1% | 16.0% | 33.8% | 28.9% | 35.1% | 21.3% |
| Diff. of prob. | 4.9% | 4.6% | 9.1% | 19.2% | 16.4% | 19.9% | 12.1% |
| Avg. Part B costs | $2873 | $2978 | $2949 | $2842 | $2736 | $2675 | $2773 |
| Part B delayers & EPHI | 0.37 | 0.45 | 0.37 | 0.39 | 0.50 | 0.50 | 0.76 |
| Medicare ≻ 0 | 2.9% | 0.0% | 2.2% | 11.3% | 10.9% | 10.9% | 1.9% |
| Medicare = 0 | 97.1% | 100% | 97.8% | 88.7% | 89.1% | 89.1% | 98.1% |
| Prob(Medicare ≻ 0) | 3.2% | 0.0% | 2.45% | 12.8% | 12.36% | 12.26% | 2.15% |
| Diff. of prob. | 0.4% | 0.0% | 0.3% | 1.5% | 1.4% | 1.4% | 0.25% |
| Avg. Part B costs | $2873 | $2978 | $2949 | $2842 | $2736 | $2675 | $2773 |
| 1. | |
| 2. | The percentage of workers covered by EPHI and Medicare does not follow a particular trend, and it varies between 13 percent and 20 percent between 1999–2010. The population of employed Medicare beneficiaries covered by EPHI more than doubled from 1999 (0.53 million) to 2010 (1.14 million). |
| 3. | The aggregate statistics from the Bureau of Labor Statistics show that the labor force participation rate (LFPR) of those 65 years and older increased during the 1995–2016 period, from 12 percent to 19 percent. Furthermore, the LFPR among individuals aged 65–69 has been more than 32 percent in recent years, and even for people aged 70–74 the trend is similar. Mastrobuoni (2009) focuses on the labor supply effects of the 1983 reforms to the Social Security System and finds that older workers reacted strongly to the increase in the Normal Retirement Age by increasing their labor supply. Aísa et al. (2012) present evidence of the changes in OECD countries up to 2006, and emphasize the role of raising longevity in increases in participation. Purcell (2016) and Purcell (2020) provide an updated discussion on these increases. |
| 4. | There are a number of reasons why individuals might hold this type of dual insurance coverage. The first has to do with coverage of dependents, especially older children, who might be covered under EPHI but not under Medicare. If the insured individual were to drop their employer-provided coverage, then their dependents would lose their coverage. Second, having MSP might be of value to some individuals, depending on their health care needs, such as (limited) nursing home care or out-of-network care. Third, once an individual receives old-age retirement benefits, they are automatically enrolled in Medicare and the premiums are deducted automatically from their paycheck. While it is possible for someone to drop their Medicare coverage, this requires an active decision, and individuals might be concerned about the future implications of dropping Medicare. |
| 5. | Owing to data limitations, we focus on delay behavior into Medicare Part A and Part B. Individuals with at least 40 quarters (around 10 years) of Medicare-covered employment are eligible for premium-free Part A. People with 30 to 39 quarters (less than 30 quarters) of Medicare-covered employment pay a monthly premium of $240 ($437) in 2019. Part B is not free, and the standard Part B premium was $135.5 per month in 2019. |
| 6. | As of 1985, premium-paying individuals who do not purchase Part A coverage beyond their IEP because of age are subject to a 10 percent premium penalty for each 12 months that they are late in enrolling. The 10 percent premium penalty is limited to twice the number of years enrollment is delayed. Therefore, if enrollment were to be delayed 1 year, the penalty would be carried for 2 years. Individuals who are eligible for premium free Part A can enroll in Part A any time once their IEP starts without paying a Part A late enrollment penalty. The Part B delayed enrollment penalty is an increase of 10 percent in the standard Part B premium for each 12-month period the individual delays enrollment. The individual carries this penalty with their Medicare costs for as long as they have Medicare Part B. Effective November 1984, a Special Enrollment Period (SEP) is available for individuals aged 65 and over who did not enroll in Medicare Part A and/or Part B beyond the IEP: individuals can sign up for Part A and/or Part B any time as long as they are covered by EPHI. They also have an 8-month SEP to sign up for Part A and/or Part B without paying penalties; this period starts the month after their employment ends or the group health plan through current employment ends, whichever happens first. |
| 7. | Total Medicare expenditure for personal health care in 2010 was $493.8 billion dollars, as shown in the Medicare and Medicaid Statistical Supplement (2011). Our calculations of the savings are in real 2009 USD, so, in order to do the percentage calculations, we deflate the Medicare expenditure appropriately. |
| 8. | The COVID-19 crisis is likely to accelerate the solvency crisis of the Medicare system due to the expected drop in payroll taxes linked to the precipitous fall in employment we saw during 2020, likely reigniting, once the health crisis passes, discussions of reforms to a system intimately linked with the labor supply and insurance status of older Americans. |
| 9. | Cutler and Sheiner (1999), Fisher et al. (2003a, 2003b), and Zuckerman et al. (2010) address the existing geographical differences in Medicare spending. In order to take these differences into account, we include regional controls in our analysis, aggregating all the states into four regions. Our finding that the number of older Americans plays a key role in understanding the trend in Medicare cost savings is in line with Lubitz et al. (1995) and Miller (2001), who conclude that compared with the increase in longevity, the increase in the number of aged Medicare enrollees has a more significant effect on Medicare spending. |
| 10. | The Access to Care file contains information on Medicare beneficiaries’ access to health care, satisfaction with care, and usual source of care. |
| 11. | |
| 12. | We classify individuals as in good health if their self-reported health is better than “Poor”. |
| 13. | Among the 19 percent of individuals who have zero Medicare costs, 2.1 percent of them are not generating any expenditure in any given year because they also have zero total health expenditure. |
| 14. | There are weighted 1.99 percent observations in the estimation sample who have health insurance coverage through their spouse’s current employer: 29.18 percent of those are working and the remaining 70.82 percent are not working. |
| 15. | Following Fang et al. (2008), we include self-reported health status; current smoker; ever smoker; diagnoses of arthritis, high blood pressure, diabetes, cancer, lung disease, heart attack, chronic heart problems, stroke, psychiatric illness, Alzheimer’s disease, broken hip; and treatment of cataract surgery or a hearing aid. We also include activities of daily living and instrumental activities of daily living. |
| 16. | We also estimate a Tobit specification using the same sample and the results are very similar to the OLS estimates. In fact, the estimates are slightly larger in absolute value. |
| 17. | We also estimate a random effects panel data specification. The results show coefficients considerably larger than those from the FE estimator for the variables of interest, that is, the effect of , , and their interaction. The estimates are more in line with those from OLS. |
| 18. | If we use the “just parametrically identified” specification, rather than this preferred sample selection corrected specification, the total average yearly savings are slightly higher, at $5.77 billion. |
| 19. | Using the National Health Interview Survey (NHIS), as well as the Health and Retirement Study (HRS), in the 2006–2018 period, we tabulate the percentage of individuals aged 65 and over covered by EPHI alone, as well as those covered by both Medicare and EPHI. The former percentage is on the rise, more clearly in the NHIS and among males, while the latter is on the decline in both surveys. This suggests that the savings coming from delay behavior are likely to have become even larger, while MSP savings are probably getting smaller. |
| 20. | If we were to expand the sample, the analysis would be dominated by the determinants of the costs in those last months of life. As discussed in Hogan et al. (2001) and Riley and Lubitz (2010), expenditure in the last year of life represents more than a quarter of the total Medicare outlays in a given year, and 70 percent of the cost of the last year of life happen in the last six months of life. We will be studying those individuals separately in future research. |
| 21. | Those persons are generating high Medicare costs and deserve a separate analysis. |
References
- Aísa, Rosa, Fernando Pueyo, and Marcos Sanso. 2012. Life Expectancy and Labor Supply of the Elderly. Journal of Population Economics 25: 545–68. [Google Scholar] [CrossRef]
- Cabral, Marika, and Neale Mahoney. 2019. Externalities and taxation of supplemental insurance: A study of medicare and medigap. American Economic Journal: Applied Economics 11: 37–73. [Google Scholar] [CrossRef]
- CMS Fast Facts. 2020. Centers for Medicare and Medicaid Services. Available online: https://www.cms.gov/fastfacts/ (accessed on 14 February 2021).
- CMS Fast Facts. 2021. Centers for Medicare and Medicaid Services. Available online: https://www.cms.gov/Research-Statistics-Data-and-Systems/Statistics-Trends-and-Reports/CMS-Fast-Facts (accessed on 15 May 2021).
- Cutler, David M., and Louise Sheiner. 1999. The geography of medicare. American Economic Review 89: 228–33. [Google Scholar] [CrossRef]
- Duan, Naihua, Willard G. Manning, Carl N. Morris, and Joseph P. Newhouse. 1983. A comparison of alternative models for the demand for medical care. Journal of Business & Economic Statistics 1: 115–26. [Google Scholar]
- Ettner, Susan L. 1997. Adverse Selection and the Purchase of Medigap Insurance by the Elderly. Journal of Health Economics 16: 543–62. [Google Scholar] [CrossRef]
- Fang, Hanming, Michael P. Keane, and Dan Silverman. 2008. Sources of Advantageous Selection: Evidence from the Medigap Insurance Market. Journal of Political Economy 116: 303–50. [Google Scholar] [CrossRef] [Green Version]
- Fisher, Elliott S., David E. Wennberg, Thrse A. Stukel, Daniel J. Gottlieb, F.J. Lucas, and Etoile L. Pinder. 2003a. The implications of regional variations in medicare spending. part 1: The content, quality, and accessibility of care. Annals of Internal Medicine 138: 273–87. [Google Scholar] [CrossRef] [Green Version]
- Fisher, Elliott S., David E. Wennberg, Thrse A. Stukel, Daniel J. Gottlieb, F.J. Lucas, and Etoile L. Pinder. 2003b. The implications of regional variations in medicare spending. part 2: Health outcomes and satisfaction with care. Annals of Internal Medicine 138: 288–98. [Google Scholar] [CrossRef]
- Fronsdal, Toren L., Jay Bhattacharya, and Suzanne Tamang. 2020. Variation in Health Care Prices Across Public and Private Payers. National Bureau of Economic Research (NBER) Working Paper 27490. Cambridge: NBER. [Google Scholar]
- Glied, Sherry, and Mark Stabile. 2001. Avoiding Health Insurance Crowd-Out: Evidence from the Medicare as Secondary Payer Legislation. Journal of Health Economics 20: 239–60. [Google Scholar] [CrossRef] [Green Version]
- Goda, Gopi Shah, John B. Shoven, and Sita Nataraj Slavov. 2007. A Tax on Work for the Elderly: Medicare as a Secondary Payer. National Bureau of Economic Research (NBER) Working Paper 13383. Cambridge: NBER. [Google Scholar]
- Goda, Gopi Shah, John B. Shoven, and Sita Nataraj Slavov. 2011. Implicit Taxes on Work from Social Security and Medicare. Tax Policy and the Economy 25: 69–88. [Google Scholar] [CrossRef]
- Heckman, James J. 1979. Sample Selection Bias as a Specification Error. Econometrica 47: 153–61. [Google Scholar] [CrossRef]
- Hogan, Christopher, June Lunney, Jon Gabel, and Joanne Lynn. 2001. Medicare Beneficiaries’ Costs of Care in the Last Year of Life. Health Affairs 20: 188–95. [Google Scholar] [CrossRef] [Green Version]
- Hurd, Michael D., and Kathleen McGarry. 1997. Medical Insurance and the Use of Health Care Services by the Elderly. Journal of Health Economics 16: 129–54. [Google Scholar] [CrossRef]
- Khandker, Rezaul K., and Lauren A. McCormack. 1999. Medicare Spending by Beneficiaries with Various Types of Supplemental Insurance. Medical Care Research and Review 56: 137–55. [Google Scholar] [CrossRef]
- Lubitz, James, James Beebe, and Colin Baker. 1995. Longevity and Medicare Expenditures. New England Journal of Medicine 332: 999–1003. [Google Scholar] [CrossRef]
- Mastrobuoni, Giovanni. 2009. Labor Supply Effects of the Recent Social Security Benefit Cuts: Empirical Estimates Using Cohort Discontinuities. Journal of Public Economics 93: 1224–33. [Google Scholar] [CrossRef] [Green Version]
- Medicare and Medicaid Statistical Supplement. 2011. Centers for Medicare and Medicaid Services. Available online: https://www.cms.gov/Research-Statistics-Data-and-Systems/Statistics-Trends-and-Reports/Archives/MMSS/2011 (accessed on 14 February 2021).
- Medicare and Medicaid Statistical Supplement. 2012. Centers for Medicare and Medicaid Services. Available online: https://www.cms.gov/Research-Statistics-Data-and-Systems/Statistics-Trends-and-Reports/Archives/MMSS/2012 (accessed on 14 February 2021).
- Miller, Tim. 2001. Increasing Longevity and Medicare Expenditures. Demography 38: 215–26. [Google Scholar] [CrossRef]
- Purcell, Patrick J. 2016. Employment at Older Ages and Social Security Benefit Claiming. Social Security Bulletin 76: 1–17. [Google Scholar] [CrossRef]
- Purcell, Patrick J. 2020. Employment at Older Ages and Social Security Benefit Claiming, 1980–2018. Research and Statistics Notes 2020-01. pp. 1–19. Available online: https://www.ssa.gov/policy/docs/rsnotes/rsn2020-01.html (accessed on 5 June 2021).
- Riley, Gerald F., and James D. Lubitz. 2010. Long-Term Trends in Medicare Payments in the Last Year of Life. Health Services Research 45: 565–76. [Google Scholar] [CrossRef] [Green Version]
- Sloan, Frank A., Kofi F. Acquah, Paul P. Lee, and Devdutta G. Sangvai. 2012. Despite ‘Welcome To Medicare’ Benefit, One In Eight Enrollees Delay First Use Of Part B Services For At Least Two Years. Health Affairs 31: 1260–68. [Google Scholar] [CrossRef] [PubMed]
- Vella, Francis. 1998. Estimating Models with Sample Selection Bias: A Survey. Journal of Human Resources 33: 127–69. [Google Scholar] [CrossRef] [Green Version]
- Zuckerman, Stephen, Timothy Waidmann, Robert Berenson, and Jack Hadley. 2010. Clarifying Sources of Geographic Differences in Medicare Spending. The New England Journal of Medicine 363: 54–62. [Google Scholar] [CrossRef]


| Not Working | Working | ||||
|---|---|---|---|---|---|
| No EPHI | EPHI | No EPHI | EPHI | ||
| Age = 65∼69, Good Health | |||||
| Medicare Costs | Mean | $3555 | $3245 | $3102 | $1404 |
| S.D. | $8766 | $10,481 | $6943 | $3258 | |
| Total Health Expenditure | Mean | $6444 | $6206 | $5285 | $5503 |
| S.D. | $11,551 | $11,925 | $8367 | $9722 | |
| OOP Expenditure | Mean | $1425 | $1157 | $1285 | $1412 |
| S.D. | $3127 | $2049 | $2079 | $2094 | |
| Age = 65∼69, Bad Health | |||||
| Medicare Costs | Mean | $12,504 | $6250 | $8778 | $2598 |
| S.D. | $27,167 | $11,820 | $19,570 | $3240 | |
| Total Health Expenditure | Mean | $17,095 | $12,481 | $11,236 | $12,976 |
| S.D. | $37,580 | $19,018 | $21,540 | $36,894 | |
| OOP Expenditure | Mean | $1939 | $1806 | $2224 | $3048 |
| S.D. | $2987 | $2739 | $5672 | $11,051 | |
| Variables | Medicare Costs | Total Health Expenditure | OOP Expenditure |
|---|---|---|---|
| (1) | (2) | (3) | |
| Work | −0.055 | 0.001 | 0.000 |
| (0.005) | (0.002) | (0.002) | |
| EPHI | −0.075 | −0.001 | 0.004 |
| (0.014) | (0.005) | (0.007) | |
| wepc | −0.080 | 0.001 | −0.002 |
| (0.017) | (0.007) | (0.009) | |
| Pseudo R | 0.146 | 0.243 | 0.212 |
| Obs. | 95,146 | 95,103 | 95,146 |
| Variables | Medicare Costs | Total Health Expenditure | OOP Expenditure |
|---|---|---|---|
| (1) | (2) | (3) | |
| Work | −0.076 | −0.116 | 0.046 |
| (0.021) | (0.021) | (0.013) | |
| EPHI | −0.108 | 0.074 | 0.006 |
| (0.055) | (0.057) | (0.036) | |
| wepc | −0.281 | 0.006 | −0.024 |
| (0.076) | (0.074) | (0.046) | |
| Lambda | −0.806 | −1.871 | −0.364 |
| (0.058) | (0.134) | (0.084) | |
| Wald | 11,934 | 6548 | 7662 |
| p value | 0.000 | 0.000 | 0.000 |
| Obs. | 78,827 | 93,499 | 92,417 |
| (1) With Health Controls | (2) Without Health Controls | |||||
|---|---|---|---|---|---|---|
| Medicare | Total | OOP | Medicare | Total | OOP | |
| Work | −0.102 | −0.106 | 0.051 | −0.146 | −0.135 | 0.035 |
| (0.020) | (0.021) | (0.013) | (0.021) | (0.021) | (0.013) | |
| EPHI | −0.194 | 0.089 | 0.017 | −0.191 | 0.086 | 0.014 |
| (0.055) | (0.056) | (0.036) | (0.055) | (0.059) | (0.036) | |
| wepc | −0.415 | 0.036 | −0.007 | −0.396 | 0.054 | 0.004 |
| (0.076) | (0.073) | (0.047) | (0.076) | (0.077) | (0.047) | |
| Delay–A–current | −0.238 | −0.135 | −1.071 | −0.193 | −0.114 | −1.058 |
| (0.061) | (0.066) | (0.049) | (0.062) | (0.069) | (0.049) | |
| Delay–B–current | 1.144 | −0.369 | −0.285 | 1.108 | −0.366 | −0.286 |
| (0.119) | (0.045) | (0.030) | (0.121) | (0.047) | (0.030) | |
| EPHI–B–current | −0.399 | 0.144 | 0.127 | −0.431 | 0.145 | 0.129 |
| (0.274) | (0.090) | (0.059) | (0.279) | (0.095) | (0.059) | |
| Lambda | −0.722 | −1.813 | −0.378 | −0.664 | −1.895 | −0.378 |
| (0.054) | (0.127) | (0.081) | (0.055) | (0.136) | (0.082) | |
| Wald | 14,235 | 7073 | 8028 | 12,986 | 5966 | 7692 |
| p value | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Obs. | 78,827 | 93,499 | 92,417 | 78,827 | 93,499 | 92,417 |
| (1) With Health Controls | (2) Without Health Controls | |||||
|---|---|---|---|---|---|---|
| Medicare | Total | OOP | Medicare | Total | OOP | |
| Work | −0.102 | −0.106 | 0.057 | −0.146 | −0.135 | 0.042 |
| (0.020) | (0.020) | (0.015) | (0.021) | (0.021) | (0.015) | |
| EPHI | −0.194 | 0.089 | 0.068 | −0.191 | 0.086 | 0.065 |
| (0.055) | (0.056) | (0.041) | (0.055) | (0.059) | (0.042) | |
| wepc | −0.415 | 0.036 | −0.036 | −0.396 | 0.054 | −0.026 |
| (0.076) | (0.073) | (0.054) | (0.076) | (0.077) | (0.054) | |
| Delay–A–current | −0.236 | −0.132 | −1.760 | −0.190 | −0.111 | −1.748 |
| (0.061) | (0.066) | (0.049) | (0.062) | (0.069) | (0.049) | |
| Delay–B–current | 1.145 | −0.368 | −0.218 | 1.110 | −0.365 | −0.215 |
| (0.119) | (0.045) | (0.034) | (0.121) | (0.047) | (0.034) | |
| EPHI–B–current | −0.399 | 0.143 | 0.062 | −0.432 | 0.144 | 0.062 |
| (0.274) | (0.090) | (0.067) | (0.279) | (0.094) | (0.068) | |
| Delay–past | 0.025 | 0.035 | −0.201 | 0.027 | 0.036 | −0.196 |
| (0.036) | (0.039) | (0.029) | (0.037) | (0.040) | (0.029) | |
| Lambda | −0.722 | −1.811 | −1.176 | −0.664 | −1.894 | −1.221 |
| (0.054) | (0.127) | (0.096) | (0.055) | (0.136) | (0.098) | |
| Wald | 14,235 | 7099 | 12,482 | 12,986 | 5981 | 12,064 |
| p value | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Obs. | 78,827 | 93,499 | 93,499 | 78,827 | 93,499 | 93,499 |
| OLS | FE | TPM | Sample Selection | |
|---|---|---|---|---|
| (1) | (2) | (3) | (4) | |
| Work | −0.539 | −0.244 | −0.133 | −0.076 |
| (0.046) | (0.047) | (0.023) | (0.021) | |
| EPHI | −0.735 | −0.176 | −0.189 | −0.108 |
| (0.131) | (0.096) | (0.067) | (0.055) | |
| wepc | −1.153 | 0.081 | −0.419 | −0.281 |
| (0.168) | (0.141) | (0.093) | (0.076) | |
| Lambda | −0.806 | |||
| (0.058) | ||||
| R | 0.217 | 0.061 | 0.195 | |
| Wald | 7662 | |||
| p value | 0.000 | |||
| Obs. | 95,146 | 80,995 | 78,827 | 78,827 |
| IV_1 | IV_2 | IV_3 | IV_4 | IV_5 | |
|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | |
| Work | −1.208 | −1.403 | −1.394 | −0.817 | −0.906 |
| (0.625) | (0.638) | (0.656) | (0.649) | (0.382) | |
| EPHI | −0.905 | −0.819 | −0.786 | −1.034 | 1.579 |
| (0.280) | (0.285) | (0.292) | (0.289) | (2.860) | |
| F Stat. | 126.979 | 123.102 | 119.706 | 120.686 | 22.920 |
| J test | 0.652 | 3.659 | 1.250 | 55.996 | 0.818 |
| p value_J test | 0.419 | 0.055 | 0.264 | 0.000 | 0.366 |
| Hausman test | 1.189 | 1.892 | 1.772 | 0.201 | 1.004 |
| p value_Hausman test | 0.276 | 0.168 | 0.183 | 0.654 | 0.316 |
| Centered R | 0.195 | 0.194 | 0.171 | 0.177 | 0.178 |
| Obs. | 95,146 | 95,146 | 95,146 | 95,146 | 95,146 |
| Year | 2004 | 2006 | 2007 | 2008 | 2009 | 2010 |
|---|---|---|---|---|---|---|
| Workers | 4.48 | 4.67 | 4.82 | 5.03 | 5.22 | 5.61 |
| Medicare ≻ 0 | 63.54% | 76.13% | 77.65% | 75.67% | 73.96% | 69.47% |
| Medicare = 0 | 36.46% | 23.87% | 22.35% | 24.33% | 26.04% | 30.53% |
| Prob(Medicare ≻ 0) | 68.17% | 81.67% | 83.31% | 81.18% | 79.34% | 74.53% |
| Diff of Prob. | 4.63% | 5.55% | 5.66% | 5.51% | 5.39% | 5.06% |
| EPHI | 1.22 | 1.29 | 1.37 | 1.27 | 1.30 | 1.64 |
| Medicare ≻ 0 | 60.06% | 62.26% | 60.95% | 60.51% | 62.00% | 47.85% |
| Medicare = 0 | 39.94% | 37.74% | 39.05% | 39.49% | 38.00% | 52.15% |
| Prob(Medicare ≻ 0) | 66.19% | 68.61% | 67.17% | 66.69% | 68.33% | 52.73% |
| Diff of Prob. | 6.13% | 6.35% | 6.22% | 6.18% | 6.33% | 4.88% |
| Workers with EPHI | 0.79 | 0.87 | 0.91 | 0.89 | 0.88 | 1.14 |
| Medicare ≻ 0 | 46.14% | 55.83% | 51.41% | 51.91% | 52.92% | 38.59% |
| Medicare = 0 | 53.86% | 44.17% | 48.59% | 48.09% | 47.08% | 61.41% |
| Prob(Medicare ≻ 0) | 51.20% | 61.95% | 57.04% | 57.60% | 58.72% | 42.82% |
| Diff of Prob. | 5.06% | 6.12% | 5.64% | 5.69% | 5.80% | 4.23% |
| Avg. Medicare Costs | $7291 | $7159 | $7253 | $7007 | $6702 | $6673 |
| Medicare Beneficiaries | 29.70 | 30.14 | 30.87 | 31.93 | 32.81 | 33.90 |
| Year | Part A | Part B | Part A + B | Total |
|---|---|---|---|---|
| 1999 | 2,508,887,296 | 4,243,138,048 | 4,660,755,456 | 11,412,780,800 |
| 2000 | 2,313,744,384 | 4,583,156,736 | 4,340,261,888 | 11,237,163,008 |
| 2001 | 2,538,497,280 | 4,899,589,120 | 4,858,211,840 | 12,296,298,240 |
| 2002 | 2,320,211,200 | 5,201,255,936 | 4,854,670,848 | 12,376,137,984 |
| 2003 | 1,979,582,976 | 5,410,360,320 | 3,875,293,696 | 11,265,236,992 |
| 2004 | 1,730,988,416 | 5,908,411,392 | 2,985,637,376 | 10,625,037,184 |
| 2005 | 1,316,721,792 | 5,755,548,160 | 1,963,387,648 | 9,035,657,600 |
| 2006 | 1,126,692,480 | 5,247,505,920 | 1,758,030,592 | 8,132,228,992 |
| 2007 | 995,435,840 | 5,421,378,560 | 1,044,982,144 | 7,461,796,544 |
| 2008 | 806,216,000 | 5,601,479,680 | 371,533,472 | 6,779,229,152 |
| 2009 | 488,684,576 | 4,304,261,120 | 184,595,936 | 4,977,541,632 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, Y.; Benítez-Silva, H. An Empirical Model of Medicare Costs: The Role of Health Insurance, Employment, and Delays in Medicare Enrollment. Econometrics 2021, 9, 25. https://0-doi-org.brum.beds.ac.uk/10.3390/econometrics9020025
Deng Y, Benítez-Silva H. An Empirical Model of Medicare Costs: The Role of Health Insurance, Employment, and Delays in Medicare Enrollment. Econometrics. 2021; 9(2):25. https://0-doi-org.brum.beds.ac.uk/10.3390/econometrics9020025
Chicago/Turabian StyleDeng, Yuanyuan, and Hugo Benítez-Silva. 2021. "An Empirical Model of Medicare Costs: The Role of Health Insurance, Employment, and Delays in Medicare Enrollment" Econometrics 9, no. 2: 25. https://0-doi-org.brum.beds.ac.uk/10.3390/econometrics9020025






