1. Introduction
The El Niño Southern Oscillation (ENSO) is an erratic climate phenomenon caused by coupled atmospheric–ocean interactions in the tropical Pacific Ocean. The El Niño phenomenon refers to the prolonged heating of surface temperatures over the eastern and central Pacific Ocean for a half-year period of two to seven years. Different heating positions in the tropical Pacific Ocean have resulted in a wide range of consequences and climate anomalies all across the world. La Niña, on the other hand, is the polar opposite of El Niño and happens when ocean surface temperatures in the central and eastern Pacific Oceans fall below average. It brings in heavy rainfall in some locations, while others experience dry spells. During El Niño, rain tends to decrease throughout the Asian continent and western Pacific regions such as Indonesia, Malaysia, and Australia, which causes long dry spells. In contrast, rainfall increases over the central and eastern tropical Pacific Ocean [
1]. However, during La Niña, rain reduces over the central and eastern tropical Pacific Oceans, whereas rainfall increases over the western Pacific.
The World Meteorological Organization (WMO) recently observed in 2020 that the tropical Pacific had been ENSO neutral since July 2019. However, sea surface temperature (SST) values have decreased marginally below the average since May 2020. Therefore, the WMO predicts that the chance of La Niña in September to November 2020 is about 60 percent, while for ENSO-neutral conditions, it remains at 40 percent. For El Niño, it is close to zero.
It is known that there is a connection between ENSO and climatic and hydrological phenomena across the world. Extreme drought and related food shortages, floods, rainfall, and temperature rises due to ENSO are causing a wide range of health problems, including outbreaks of disease, malnutrition, heat stress, and respiratory diseases. The Malaysian climate is influenced by ENSO, with drier-than-normal conditions during El Niño and wetter-than-normal conditions during La Niña. During the strongest El Niño years, 1997–1998, Malaysia and other Southeast Asian regions such as Thailand, Vietnam, Indonesia, and Singapore experienced dry conditions [
2]. These El Niño episodes brought severe drought conditions, such as prolonged dry spells that negatively impacted Malaysia’s human health and economic activities. Susilo et al. [
3] concluded that El Niño events had a stronger effect on rainfall than La Niña events in Central Kalimantan, Indonesia. They found that the El Niño events were associated with an increase in the number of days with less than 1 mm of rainfall during the dry season. Stanley Raj and Chendhoor [
4] studied the influence of ENSO on the rainfall characteristics of coastal Karnataka, India. Their findings indicated that La Niña brought more rainfall than El Niño to the area.
A different scenario has been observed for other continents. El Niño years have been seen to bring excessive rainfall to South Florida, notably around Lake Okeechobee. The La Niña years, on the other hand, were marked by severe drought. During the 1997 El Niño event, it was difficult to maintain a safe water level in Lake Okeechobee due to limited discharge capacity [
5]. In Peru, the 1997 El Niño event had the most significant impact, especially in the northern coastal region, which experienced heavy rain and severe flooding [
6]. The heavy rains and flooding caused considerable damage to houses, schools, and health institutions. Additionally, increased cases of malaria, diarrhea, and acute respiratory infections were also reported. These effects of the ENSO and the ENSO phenomenon’s abnormality have led many researchers to become interested in its modeling.
Statistical modeling represents a major tool in developing the understanding of the ENSO phenomenon. Several authors have investigated different approaches to model the ENSO. Previous studies have focused on the conventional multivariate statistical techniques using linear and nonlinear time series models. Models such as a nonlinear univariate time series model [
7], parametric seasonal autoregressive integrated moving average (SARIMA) model [
8,
9], and a nonparametric kernel predictor [
10,
11,
12] have been widely used in modeling and forecasting of the data series. The rapid development of new technology such as artificial intelligence (AI), machine learning, and deep learning also provides alternative ways to forecast the ENSO phenomenon [
13,
14,
15,
16].
The Southern Oscillation Index (SOI) is the oldest indicator used to describe the ENSO phenomenon. The SOI is an indicator of the advancement and intensity of El Niño and La Niña in the Pacific Ocean. It serves as a regulated index dependent on the variations in ocean pressure levels between the Eastern Pacific (Tahiti) and the Indian Ocean (Darwin). During El Niño, the pressure drops below average in Tahiti and rises above normal in Darwin, resulting in negative SOI values, whereas during La Niña, the pressure behaves in the opposite manner, resulting in a positive index. Katz [
17] reviewed the history of the SOI’s statistical modeling, while Fedorov et al. [
18] studied the ENSO’s physical predictability. Both concluded that the ENSO might not be predictable by deterministic physical models. They preferred probabilistic forecasts based on ensemble forecasts. Anh and Kim [
7] found that a nonlinear stochastic model was better than a linear stochastic model for modeling the SOI series. They concluded that the autoregressive moving average (ARMA) model was not appropriate for the SOI series because there is no linearity in the time series. Therefore, they suggested using a nonlinear approach, an autoregressive conditional heteroscedasticity model, for the SOI series. Gallo et al. [
19] proposed a different modeling method, namely the Markov approach, to forecast the ENSO pattern. A Markov autoregressive switching model was developed to describe the SOI using two autoregressive processes. Each was associated with a particular ENSO phase: La Niña or El Niño. They then extended the model by adding sinusoidal functions to forecast future SOI values.
Other than the SOI, sea surface temperature (SST) indices including Niño-1+2, Niño-3, Niño-4, and Niño-3.4 have also been used to describe the ENSO phenomenon. Ham et al. [
13] employed a deep-learning approach to forecast the ENSO for lead times of up to one and a half years. They trained a convolutional neural network (CNN) and found that the model was also effective at predicting the detailed zonal distribution of sea surface temperatures. In addition, He et al. [
14] introduced a deep-learning ENSO forecasting model (DLENSO), which is a sequence-to-sequence model consisting of multilayered convolutional long short-term memory (ConvLSTM), to predict ENSO events by predicting the regional SST of Niño-3.4. Hanley et al. [
20] compared several ENSO indices to determine the best index for defining ENSO events. They observed that Niño-4 has a weak relationship with El Niño but a strong response to La Niña, while Niño-1+2 shows the opposite characteristics. Their findings suggested that the choice of index depends on the phase of the corresponding ENSO. Their study concluded that SOI, Niño-3.4, and Niño-4 indices are equally sensitive to El Niño events, but are more sensitive than Niño-1+2 and Niño-3 indices. However, Mazarella et al. [
21,
22] commented that those indices could not represent the coupled ocean–atmosphere phenomena. Hence, they suggested using the multivariate ENSO index (MEI) since it is the most comprehensive index to describe the ENSO.
Nowadays, climate data or earth data are always thought of as continuous data even though they are computed at discrete time intervals such as daily, monthly, or annually. Functional data analysis (FDA) is a new modern statistical method that can express discrete observations arising from time series as functional data representing the entire measured function and a continuum interval, which can be regarded as a single entity, curve, or image. With recent technological advances, the idea of functional data analysis has become more prevalent. The development of FDA in statistical theory provides an alternative approach to the current conventional statistical methods, since it provides additional information on their smoothing curves or functions. Normally, conventional statistical techniques could not possibly generate further details on the data. The FDA can usually provide information on the functions and their derivatives based on the smoothing curves. Statistical frameworks using FDA techniques have been successfully applied in various fields. For example, in hydrology and meteorology studies, researchers such as Alaya et al. [
23], Bonner et al. [
24], Chebana et al. [
25], Hael [
26], Suhaila and Yusop [
27], and Suhaila et al. [
28] have successfully employed several FDA tools in their analyses. The detailed applications of the FDA and its tools have been well reviewed by Wang et al. [
29] and Ullah and Finch [
30].
Functional data visualization and outlier identification have recently become one of the most important statistical approaches used with these new advanced technologies. Therefore, this study investigated the potential of functional data for visualizing the changes in the MEI, which is used to characterize the intensity of ENSO events. The MEI is considered to be the most comprehensive ENSO monitoring index because it incorporates the analysis of various meteorological and oceanographic components into a single index. Here, we applied a modern statistical method to examine the pattern, variation, and shape of the functional MEI and relate it to the El Niño and La Niña events. The concept of functional data allowed us to provide more effective and efficient estimates of the ENSO phenomenon’s risk.
2. Materials and Methods
The multivariate ENSO index is measured as the first principal component of six main variables observed over the tropical Pacific, including sea level pressure, zonal and meridional components of the surface wind, sea surface temperature, surface air temperature, and sky cloudiness. It was developed at the National Oceanic Atmospheric Administration (NOAA) Climatic Diagnostic Center [
31,
32]. A new version of MEI named MEI.v2 was computed using five variables: sea level pressure, sea surface temperature, zonal and meridional components of the surface wind, and outgoing longwave radiation. All variables were interpolated to a standard 2.5° latitude–longitude grid, and standardized anomalies were determined with respect to the 1980–2018 reference period.
MEI.v2 is the leading main principal component time series of the empirical orthogonal function (EOF) standardized anomalies of the above five combined variables over the tropical Pacific during the 1980–2018 period. EOFs were estimated for 12 overlapping bimonthly “seasons” (Dec–Jan, Jan–Feb, Feb–Mar, …, Nov–Dec) to consider ENSO’s seasonality and reduce the impact of high-frequency intraseasonal variability. The detail of the methods is described on the website
https://psl.noaa.gov/enso/mei/ (accessed on 25 June 2020). The data consisting of the monthly values of MEI were taken from this website. The highest MEI values represent the warm ENSO phase (El Niño), while the lowest values represent the cold ENSO phase (La Niña). The MEI values from 1980 to 2019 were considered in this study.
2.1. Functional Data Smoothing
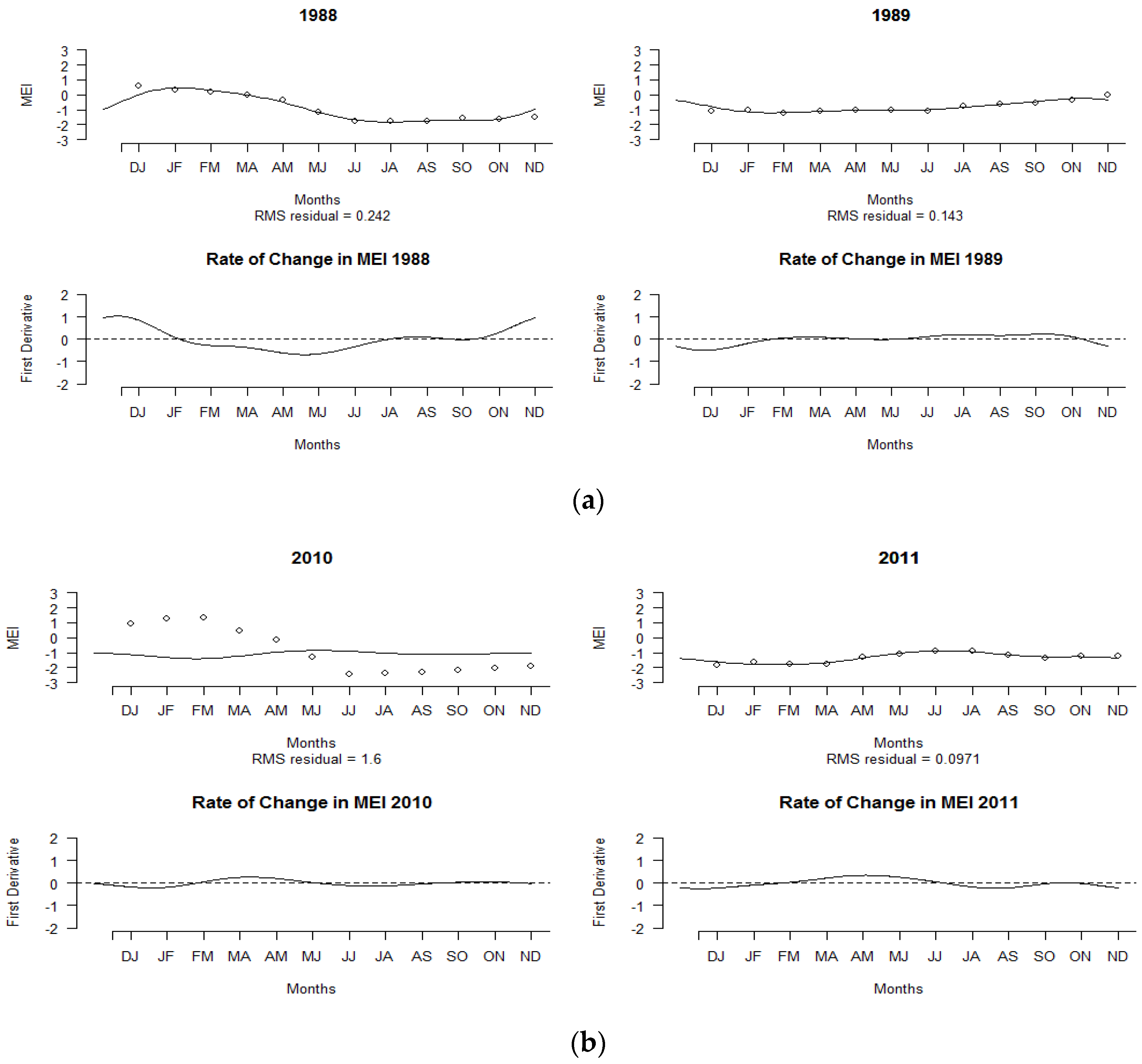
Suppose we have a data set such as where T = 12 months, n is the number of years, and is the MEI measured at the month tj of the i-th year. These discrete observations are transformed into smoothing curves xi(t) as temporal functions with a base period of T = 12 months and a k basis function. Since the MEI data of the entire series had some seasonal variability and periodicity over the annual cycle, Fourier bases were preferred. The value of k can be chosen to capture the variation.
A common statistical approach for smoothing is to use the basis expansion, which is given as
where
refers to the basis coefficient,
is the known basis function, and
K is the size of the maximum basis required. The type and relevance of a dataset are factors in determining the basis. According to Ramsay and Silverman [
33], the properties of the smooth curve play a significant role in making the best decision. There was a clear periodic structure in this situation and the best-known basis function for a periodic set of data is the Fourier series, which can be written as
defined by the basis
with
The constant
is related to the period
T by the relation of
The coefficients of the basis function are solved by minimizing the least-squares criterion, which can be written as
The amount of smoothing is determined by the number of basis functions used. A large number of basis functions usually results in a lower bias than a small number of basis functions; however, the former is often less smooth [
34]. As a result, when creating a smooth curve from discrete data, the roughness penalty approach is suggested. Roughness, as defined by the integrated square of the second derivatives, is penalized. Putting them together will create a penalized residual sum of squares, which is given as
The smoothing parameter λ controls a compromise between the fit to the data and the variability in the function. Large values of λ will increase the amount of smoothing. In choosing the best value of λ, the technique called generalized cross-validation (GCV) was applied in the analysis [
28,
33].
2.2. Summary Statistics of Functional Data
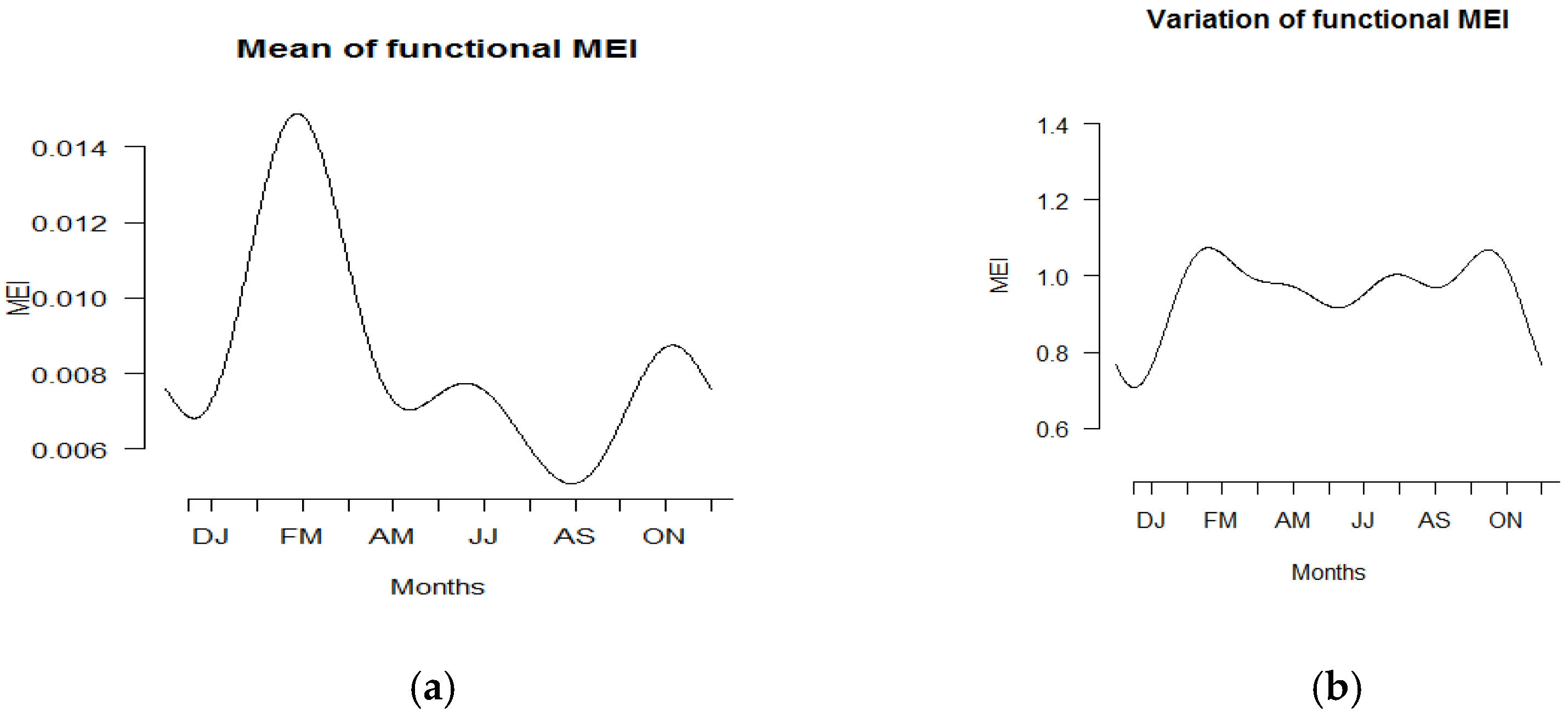
In classical statistics, measures of central tendency such as mean, median, and mode are often used to characterize the middle of the dataset. Dispersion measures such as variance and standard deviation, on the other hand, are used to show the dataset’s variability. Both measurements were used to explain the shape of the curves in this analysis. The mean curve, which is based on the sample curves,
can be defined as
The mean curve is often used to evaluate the centrality of a sample curve; however, if there is a chance of outliers, the mean curve should be scrutinized. The functional framework’s location curves may also be the median and mode, which are based on the statistical notion of a depth function. Fraiman and Muniz [
35] and Febrero et al. [
36] extended the notion of depth to functional data. To obtain a robust location estimator for the distribution centre, they introduced the functional trimmed mean. The trimmed mean is defined as the mean of the most central
curves, where
α is given such that
. The proposed method of depth defined by Fraiman and Muniz [
35] is given in the form
where
represents the univariate depth of
and
refers to the empirical distribution of the sample
Suppose we define the functional depth as
and each curve
corresponds to its functional depth given in Equation (7). The curves
are ranked according to the values
. The functional median is referred to as the deepest function in the sample, which attains the maximum values of functional depth. Another central measure is the modal curve, which represents the densest curve surrounded by the rest of the curves. The functional mode is given in terms of kernel estimator, as defined by Febrero et al. [
36].
On the other hand, scale parameters are used to measure the dispersion of a distribution or a sample. The variability of function samples can be measured using the sample variance functions, which can be defined as
while the covariance function, which is used to summarize the dependence structure between curve values
and
at times
s and
t, respectively, can be written as
The surface of covariance and the contour map are used to plot the variability of the function sample. Another functional method that can also be used to capture the variability of the function samples is through functional principal component analysis (FPCA).
2.3. Functional Principal Component Analysis (FPCA)
Principal component analysis (PCA) is a multivariate statistical method that reduces the number of correlated variables to a smaller number of uncorrelated variables called principal components. After subtracting the mean from each observation, the method is typically used to find the principal modes of variation in the results. To achieve a satisfactory approximation to the original data, the numbers of these principal modes of variations are needed.
The key concept behind the extension of multivariate PCA to functional PCA is the substitution of functions for vectors, matrices for compact linear operators, covariance matrices for covariance operators, and scalar products in vector space for scalar products in
L2 space [
37]. In statistical reviews, there are at least two ways to perform smoothed FPCA. The first approach is to smooth the functional data before applying FPCA. The second method smooths principal components using a roughness penalty term in the sample covariance and optimizes it to ensure that the approximate principal components are sufficiently smooth. FPCA can identify new functions that show the most important type of variation in the curve data after transforming the data into functions. Under orthonormal constraints, the FPCA approach maximizes the sample variance of the scores. The following is a brief description of the FPCA method.
Let be the functional observations obtained by smoothing the discrete observations
Let be the centred functional observations where is the mean function. A FPCA is then applied to , creating a small set of functions, called harmonics, that reveal the most important variations in the data.
The first principal component
describes a weight function for the
that exists over the same range and accounts for the maximum variation. The first principal component yields the maximum variation in the functional principal component scores
subject to the normalization constraint
The next principal components
are obtained by maximizing the variance of the corresponding scores
under the constraints
In a functional context, the interpretation of FPCA is quite complicated, and the best way to consider the plots of the overall mean function and perturbations around the mean is based on
zk. A method known as varimax rotation can be used to enhance interpretability. The details are given in Ramsay and Silverman [
33].
2.4. Visualization and Outlier Detection Using a Functional Concept
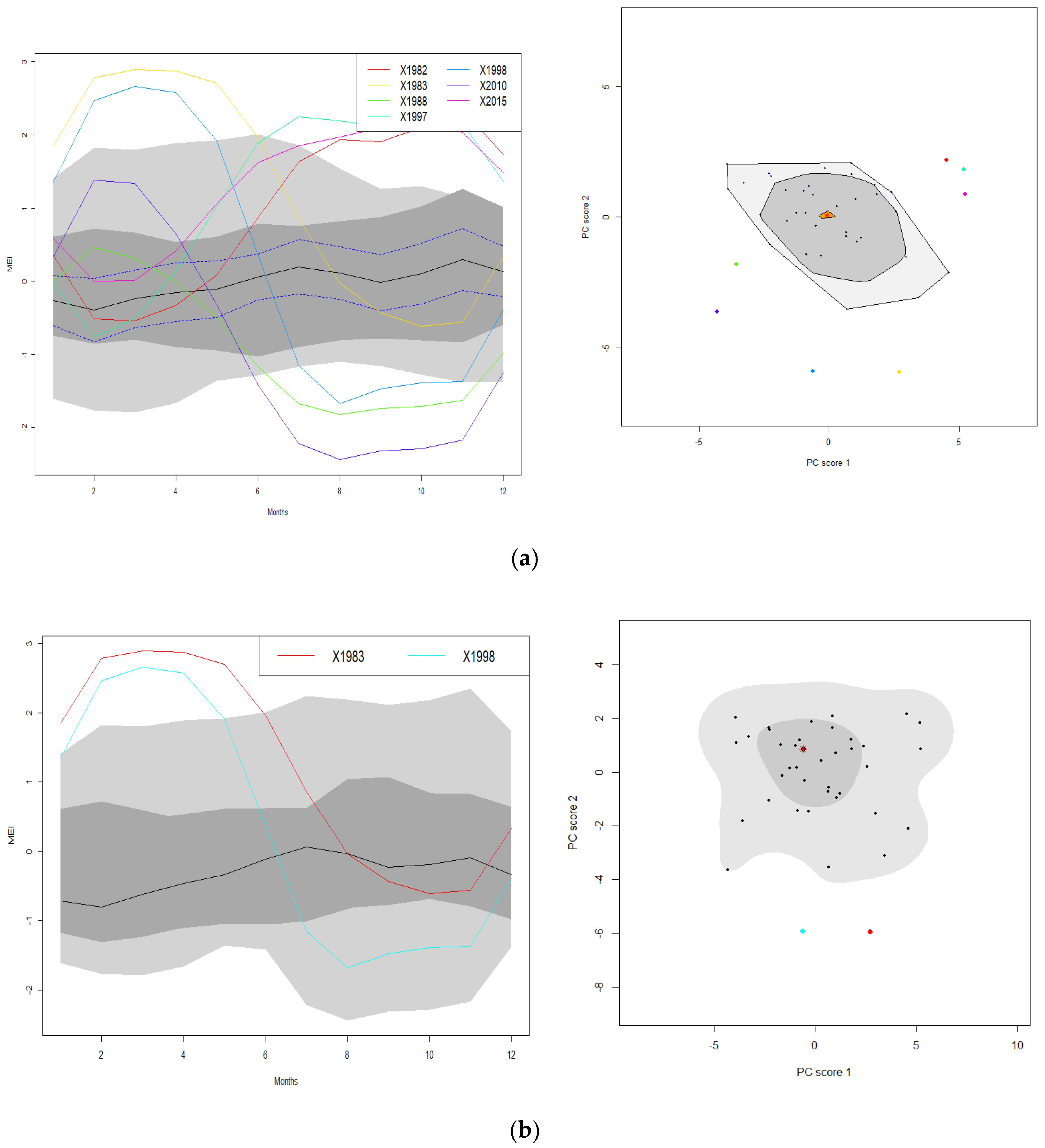
In this study, three graphical methods were used to explore, visualize, and analyze unique features of MEI curves, such as outliers, that cannot be captured using summary statistics. These methods were first suggested by Hyndman and Shang [
38]. A rainbow plot was used to visualize functional data, while outliers were identified using a functional bagplot and a functional high-density region (HDR) boxplot.
2.4.1. Rainbow Plot
A rainbow plot is a simple plot of all the data with the addition of a colour palette depending on the data’s ordering. Orders were focused on bivariate depth or bivariate kernel density in the functional context. The bivariate scores of the first two principal components were used in both methods. Let
and
be the first two vector scores and
be the bivariate score points. The first way of ordering the functional observations was based on Tukey’s half-space location depth of the bivariate principal component scores given by
where
is the half-space depth function introduced by Tukey [
39]. It is defined as the smallest number of data points included in close half space containing
on its boundary. The observations are decreasingly ordered according to their depth values
OTi. The first ordered curve is considered to represent the median curve, while the last curve is considered the outermost curve.
The second method of ordering was based on the bivariate kernel density estimate, which was also computed using the bivariate robust principal component scores given as
where
is the kernel function and
is the bandwidth for the
jth bivariate score points. The functional curves were ordered based on the value of
ODi. The modal curve was the first curve with the highest density, while the most peculiar curve was the last curve with the lowest density. The rainbow colours reflect the order of the curves. The outlying curves with the lowest depth or density are shown in violet, while the curves with the maximum density or depth are shown in red. After that, the plotting curves are sorted by depth and density.
2.4.2. Functional Bagplot
Rousseeuw et al. [
40] introduced the bivariate bagplot based on Tukey’s half-space depth function. The values obtained from the first two principal component scores determine the bivariate bagplot in functional models. The functional bagplot maps the functional curves to the bagplot of the first two robust principal component scores. The median curve and the inner and outer regions are shown in the functional bagplot. The area bounded by all curves corresponding to the points in the bivariate bag, which covers 50% of the curves, is referred to as the inner region. The outer region, on the other hand, is characterized as the area enclosed by all curves that correspond to points in the bivariate fence regions. Outliers are points that are outside of the field. According to Hyndman and Shang [
38], when outliers are far from the median, a functional bagplot is a good outlier-detection tool.
2.4.3. Functional High-Density Region (HDR) Boxplot
The third method, the functional HDR boxplot, was based on the bivariate HDR boxplot, which was constructed using a bivariate kernel density estimate [
41]. This outlier detection was again based on the first two principal component scores. The functional HDR boxplot displays the modal curve and the inner and outer regions. The inner region is defined as the region bounded by all curves corresponding to points inside the 50% bivariate HDR and usually the 99% outer highest-density region. The outer region is similarly defined as the region bounded by all curves corresponding to the points within the outer bivariate HDR. A detailed review of these three methods can be found in [
38].