Does Time Varying Risk Premia Exist in the International Bond Market? An Empirical Evidence from Australian and French Bond Market
Abstract
:1. Introduction
2. Review of Related Literature
- Minimize the variance of portfolio return given expected return, and
- Maximize expected return, given variance.
3. The Data, Models and Methodology
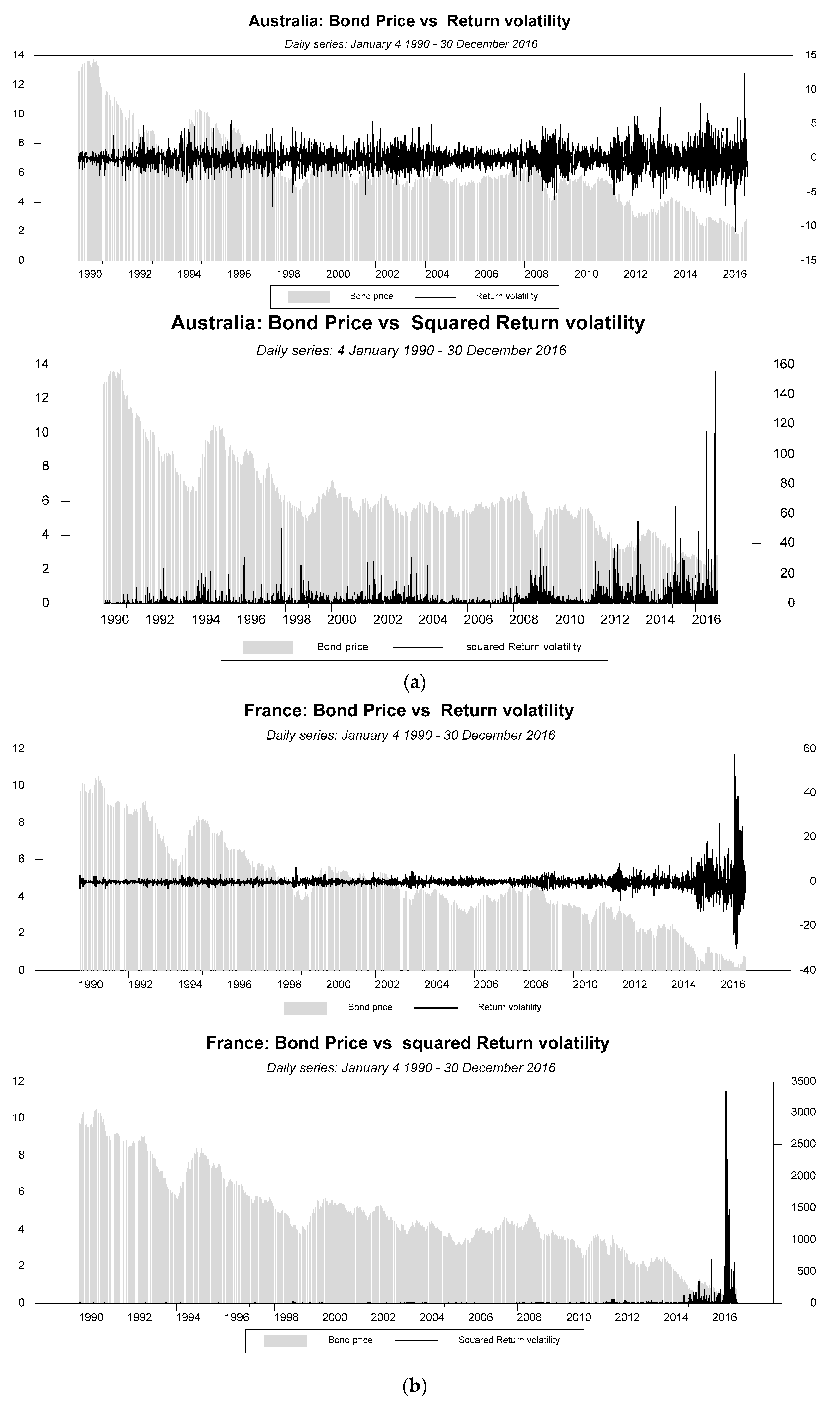
3.1. The Data
3.2. Specification of the Model
3.2.1. Univariate Models for Conditional Mean and Conditional Volatility
3.2.2. Multivariate Models for Conditional Mean and Conditional Volatility
3.2.3. VARMA-DBEKK-AGARCH-in Mean Model
3.3. Estimation
3.4. Co-Volatility Spillovers Effect
4. Empirical Results
4.1. Preliminary Data Analysis
4.2. Empirical Estimation of the Univariate ARMA-AGARCH-M Models
- (a)
- Empirical estimation of risk premium of the Australia bond return having maturity of 10 year:
- (b)
- Empirical estimation of risk premium of the France bond return having maturity of 10 year:
4.3. Empirical Estimation, Causality, and Partial Co-Volatility of the VARMA-DBEKK-AGARCH-M Model
- (a)
- Estimation of the bivariate VARMA-DBEKK-AGARCH model.
- (b)
- Empirical estimation and partial co-volatility of the DBEKK-AGARCH model
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Arshanapalli, Bala, Frank J. Fabozzi, and William Nelson. 2011. Modeling the Time-Varying Risk Premium Using a Mixed GARCH and Jump Diffusion Model. SSRN Electronic Journal. [Google Scholar] [CrossRef]
- Banz, Rolf W. 1981. The Relationship between Return and Market Value of Common Stocks. Journal of Financial Economics. [Google Scholar] [CrossRef] [Green Version]
- Basu, S. 1977. Investment Performance of Common Stocks in Relation to Their Price-Earnings Ratios: A Test of the Efficient Market Hypothesis. The Journal of Finance. [Google Scholar] [CrossRef]
- Basu, Sanjoy. 1983. The Relationship Between Earnings Yeild, Market Value and Retrun for NYSE Common Stocks. Journal of Financial Economics 12: 129–56. [Google Scholar] [CrossRef]
- Bauwens, Luc, Sébastien Laurent, and Jeroen V. K. Rombouts. 2006. Multivariate GARCH Models: A Survey. Journal of Applied Econometrics. [Google Scholar] [CrossRef] [Green Version]
- Beg, A. B. M. Rabiul Alam, and Sajid Anwar. 2014. Detecting Volatility Persistence in GARCH Models in the Presence of the Leverage Effect. Quantitative Finance 14: 2205–13. [Google Scholar] [CrossRef]
- Bera, Anil K., and Matthew L. Higgins. 1993. ARCH MODELS: PROPERTIES, ESTIMATION AND TESTING. Journal of Economic Surveys. [Google Scholar] [CrossRef]
- Bollerslev, Tim. 1986. Generalized Autoregressive Conditional Heteroskedasticity. Journal of Econometrics. [Google Scholar] [CrossRef] [Green Version]
- Bollerslev, Tim. 1987. A Conditionally Heteroskedastic Time Series Model for Speculative Prices and Rates of Return. The Review of Economics and Statistics. [Google Scholar] [CrossRef] [Green Version]
- Bollerslev, Tim, Robert F. Engle, and Jeffrey M. Wooldridge. 1988. A Capital Asset Pricing Model with Time-Varying Covariances. Journal of Political Economy. [Google Scholar] [CrossRef]
- Campbell, John Y. 1986. Bond and Stock Returns in a Simple Exchange Model. Quarterly Journal of Economics. [Google Scholar] [CrossRef] [Green Version]
- Campbell, John Y., Carolin Pflueger, and Luis M. Viceira. 2020. Macroeconomic Drivers of Bond and Equity Risks. Journal of Political Economy. [Google Scholar] [CrossRef] [Green Version]
- Chang, Chia Lin, Michael McAleer, and Guangdong Zuo. 2017. Volatility Spillovers and Causality of Carbon Emissions, Oil and Coal Spot and Futures for the EU and USA. Sustainability (Switzerland). [Google Scholar] [CrossRef] [Green Version]
- Chang, Chia Lin, Michael McAleer, and Yu Ann Wang. 2018. Modelling Volatility Spillovers for Bio-Ethanol, Sugarcane and Corn Spot and Futures Prices. Renewable and Sustainable Energy Reviews. [Google Scholar] [CrossRef] [Green Version]
- Christoffersen, Peter, Kris Jacobs, and Chayawat Ornthanalai. 2012. Dynamic Jump Intensities and Risk Premiums: Evidence from S&P500 Returns and Options. Journal of Financial Economics. [Google Scholar] [CrossRef]
- Cochrane, John H., and Monika Piazzesi. 2005. Bond Risk Premia. American Economic Review. [Google Scholar] [CrossRef]
- Ding, Zhuanxin, Clive W. J. Granger, and Robert F. Engle. 1993. A Long Memory Property of Stock Market Returns and a New Model. Journal of Empirical Finance. [Google Scholar] [CrossRef]
- Domowitz, Ian, and Craig S. Hakkio. 1985. Conditional Variance and the Risk Premium in the Foreign Exchange Market. Journal of International Economics. [Google Scholar] [CrossRef]
- Engle, Robert F. 1982. Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of United Kingdom Inflation. Econometrica. [Google Scholar] [CrossRef]
- Engle, Robert F. 1990. Stock Volatility and the Crash of ’87: Discussion. The Review of Financial Studies 3: 103–6. [Google Scholar] [CrossRef]
- Engle, Robert F., and Kenneth F. Kroner. 1995. Multivariate Simultaneous Generalized Arch. Econometric Theory. [Google Scholar] [CrossRef]
- Engle, Robert F., and Victor K. Ng. 1993. Measuring and Testing the Impact of News on Volatility. The Journal of Finance. [Google Scholar] [CrossRef]
- Engle, Robert F., David M. Lilien, and Russell P. Robins. 1987. Estimating Time Varying Risk Premia in the Term Structure: The Arch-M Model. Econometric. [Google Scholar] [CrossRef]
- Fama, Eugene F., and Kenneth R. French. 1992. The Cross-Section of Expected Stock Returns. The Journal of Finance. [Google Scholar] [CrossRef]
- Fama, Eugene F., and Kenneth R. French. 1996. Multifactor Explanations of Asset Pricing Anomalies. The Journal of Finance. [Google Scholar] [CrossRef]
- Fama, Eugene F., and Kenneth R. French. 2015. A Five-Factor Asset Pricing Model. Journal of Financial Economics. [Google Scholar] [CrossRef] [Green Version]
- Glosten, Lawrence R., Ravi Jagannathan, and David E. Runkle. 1993. On the Relation between the Expected Value and the Volatility of the Nominal Excess Return on Stocks. The Journal of Finance. [Google Scholar] [CrossRef]
- Jagannathan, Ravi, and Zhenyu Wang. 1996. The Conditional CAPM and the Cross-Section of Expected Returns. The Journal of Finance. [Google Scholar] [CrossRef]
- Jarque, Carlos M., and Anil K. Bera. 1987. A Test for Normality of Observations and Regression Residuals. International Statistical Review / Revue Internationale de Statistique. [Google Scholar] [CrossRef]
- Ling, Shiqing, and Michael McAleer. 2003. On Adaptive Estimation in Nonstationary ARMA Models with GARCH Errors. Annals of Statistics. [Google Scholar] [CrossRef]
- Lintner, John. 1965. The Valuation of Risk Assets and the Selection of Risky Investments in Stock Portfolios and Capital Budgets. The Review of Economics and Statistics 47: 13–37. [Google Scholar] [CrossRef]
- Ljung, G. M., and G. E. P. Box. 1978. On a Measure of Lack of Fit in Time Series Models. Biometrika. [Google Scholar] [CrossRef]
- Markowitz, Harry M. 1959. Portfolio Selection. Yale University Press. Available online: http://0-www-jstor-org.brum.beds.ac.uk/stable/j.ctt1bh4c8h (accessed on 24 December 2020).
- McAleer, Michael, Suhejla Hoti, and Felix Chan. 2009. Structure and Asymptotic Theory for Multivariate Asymmetric Conditional Volatility. Econometric Reviews. [Google Scholar] [CrossRef]
- McLeod, Allan I., and William K. Li. 1983. Diagnostic checking ARMA time series models using squared-residual autocorrelations. Journal of Time Series Analysis 4: 269–73. [Google Scholar] [CrossRef]
- Nelson, Daniel B. 1991. Conditional Heteroskedasticity in Asset Returns: A New Approach. Econometrica. [Google Scholar] [CrossRef]
- Rosenberg, Barr, Kenneth Reid, and Ronald Lanstein. 1985. Persuasive Evidence of Market Inefficiency. The Journal of Portfolio Management. [Google Scholar] [CrossRef]
- Sharpe, William F. 1964. Capital Asset Prices: A Theory of Market Equilibrium under Conditions of Risk. The Journal of Finance. [Google Scholar] [CrossRef]
- Shiller, Robert J. 1978. Rational Expectations and the Dynamic Structure of Macroeconomic Models. A Critical Review. Journal of Monetary Economics. [Google Scholar] [CrossRef]
- Shiller, Robert J. 1981. Do Stock Prices Move Too Much to Be Justified by Subsequent Changes in Dividends? American Economic Review 71: 421–36. [Google Scholar]
- Shiller, Robert J., John Y. Campbell, Kermit L. Schoenholtz, and Laurence Weiss. 1983. Forward Rates and Future Policy: Interpreting the Term Structure of Interest Rates. Brookings Papers on Economic Activity. [Google Scholar] [CrossRef] [Green Version]
- Silvennoinen, Annastiina, and Timo Teräsvirta. 2009. Modeling Multivariate Autoregressive Conditional Heteroskedasticity with the Double Smooth Transition Conditional Correlation GARCH Model. Journal of Financial Econometrics. [Google Scholar] [CrossRef]
- Stattman, Devin. 1980. Book Values and Stock Returns. The Chicago MBA: A Journal of Selected Papers 4: 25–45. [Google Scholar]
- Tsay, Ruey S. 1986. Nonlinearity Tests for Time Series. Biometrika. [Google Scholar] [CrossRef]
- Tsay, Ruey S. 1987. Conditional Heteroscedastic Time Series Models. Journal of the American Statistical Association. [Google Scholar] [CrossRef]
- Tsay, Ruey S. 2006. Multivariate Volatility Models. Time Series and Related Topics. [Google Scholar] [CrossRef] [Green Version]
- Tsay, Ruey S. 2010. Analysis of Financial Time Series: Third Edition. Analysis of Financial Time Series. [Google Scholar] [CrossRef]
| Statistics | Australia | France |
|---|---|---|
| Mean | −0.015006 (0.4072) | −0.0031 (0.8938) |
| Standard deviation (st.dev) | 1.4191 | 1.8012 |
| Minimum | −10.7556 | −15.7247 |
| Maximum | 12.9630 | 20.8273 |
| Skewness | 0.295699 (0.0000) | 0.3952 (0.0000) |
| Excess Kurtosis | 5.2828 (0.0000) | 7.5076 (0.0000) |
| Jarque and Bera (JB) | 7232.9308 (0.0000) | 14,586.7843 (0.0000) |
| Sample size | 6144 | 6144 |
| Bond Returns | Type | Null Hypothesis | Alternative Hypothesis | Test Statistic | Critical Value | |
|---|---|---|---|---|---|---|
| (1% Level) | (5% Level) | |||||
| Australia | ADF | Nonstationary | Stationary | −36.5301 *** | −3.435 | −2.863 |
| PP | Nonstationary | Stationary | −84.5055 *** | −3.435 | −2.863 | |
| KPSS | Stationary | Nonstationary | 0.0460 | 0.739 | 0.347 | |
| France | ADF | Nonstationary | Stationary | −37.7938 *** | −3.435 | −2.863 |
| PP | Nonstationary | Stationary | −81.2682 *** | −3.435 | −2.863 | |
| KPSS | Stationary | Nonstationary | 0.0466 | 0.739 | 0.347 | |
| Type | Australia | France |
|---|---|---|
| Ljung–Box | 43.661 (0.000) | 25.704 (0.004) |
| Ljung–Box | 58.920 (0.000) | 37.804 (0.009) |
| Ljung–Box | 669.249 (0.000) | 1133.363 (0.000) |
| Ljung–Box | 1049.775 (0.000) | 2011.404 (0.000) |
| McLeod–Li(10) | 668.992 (0.000) | 1132.953 (0.000) |
| McLeod–Li(20) | 1048.742 (0.000) | 2010.004 (0.000) |
| Tsay Ori_F(10, 6134) lags(4) | 4.362 (0.000) | 3.099 (0.001) |
| ARCH-LM lags(4) | 68.156 (0.000) | 77.092 (0.000) |
| Type | Australia | France |
|---|---|---|
| Log-likelihood | −10,099.3285 | −9976.8864 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aftab, H.; Beg, A.B.M.R.A. Does Time Varying Risk Premia Exist in the International Bond Market? An Empirical Evidence from Australian and French Bond Market. Int. J. Financial Stud. 2021, 9, 3. https://0-doi-org.brum.beds.ac.uk/10.3390/ijfs9010003
Aftab H, Beg ABMRA. Does Time Varying Risk Premia Exist in the International Bond Market? An Empirical Evidence from Australian and French Bond Market. International Journal of Financial Studies. 2021; 9(1):3. https://0-doi-org.brum.beds.ac.uk/10.3390/ijfs9010003
Chicago/Turabian StyleAftab, Hira, and A. B. M. Rabiul Alam Beg. 2021. "Does Time Varying Risk Premia Exist in the International Bond Market? An Empirical Evidence from Australian and French Bond Market" International Journal of Financial Studies 9, no. 1: 3. https://0-doi-org.brum.beds.ac.uk/10.3390/ijfs9010003






