A Novel Kernel-Based Regularization Technique for PET Image Reconstruction
Abstract
:1. Introduction
2. Materials and Methods
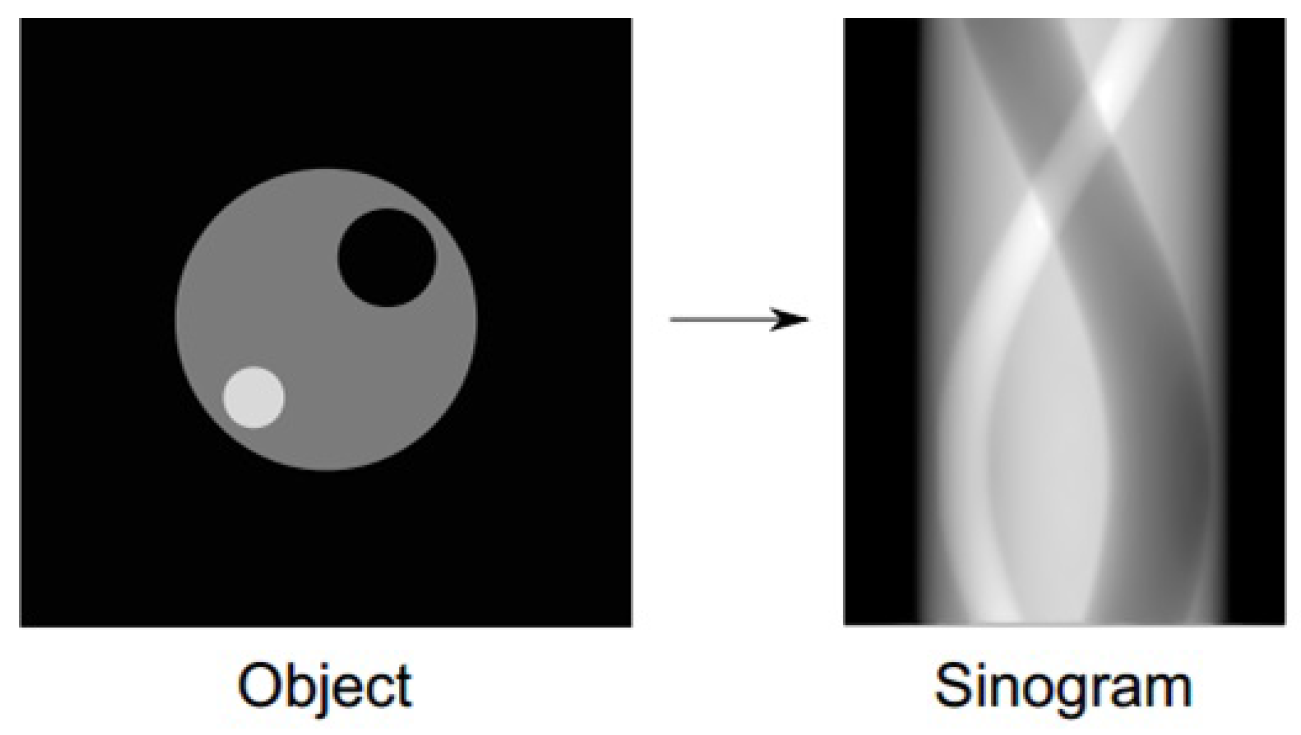
2.1. Data Acquisitions and Sinograms
2.2. PET Data Corrections
2.3. Maximum-Likelihood Expectation-Maximization Algorithm
- Start with an initial estimate satisfying ,
- If denotes the estimate of at the iteration, define a new estimate by using Equation (11),
- If the required accuracy for the numerical convergence has been achieved, then stop.
2.4. Regularization
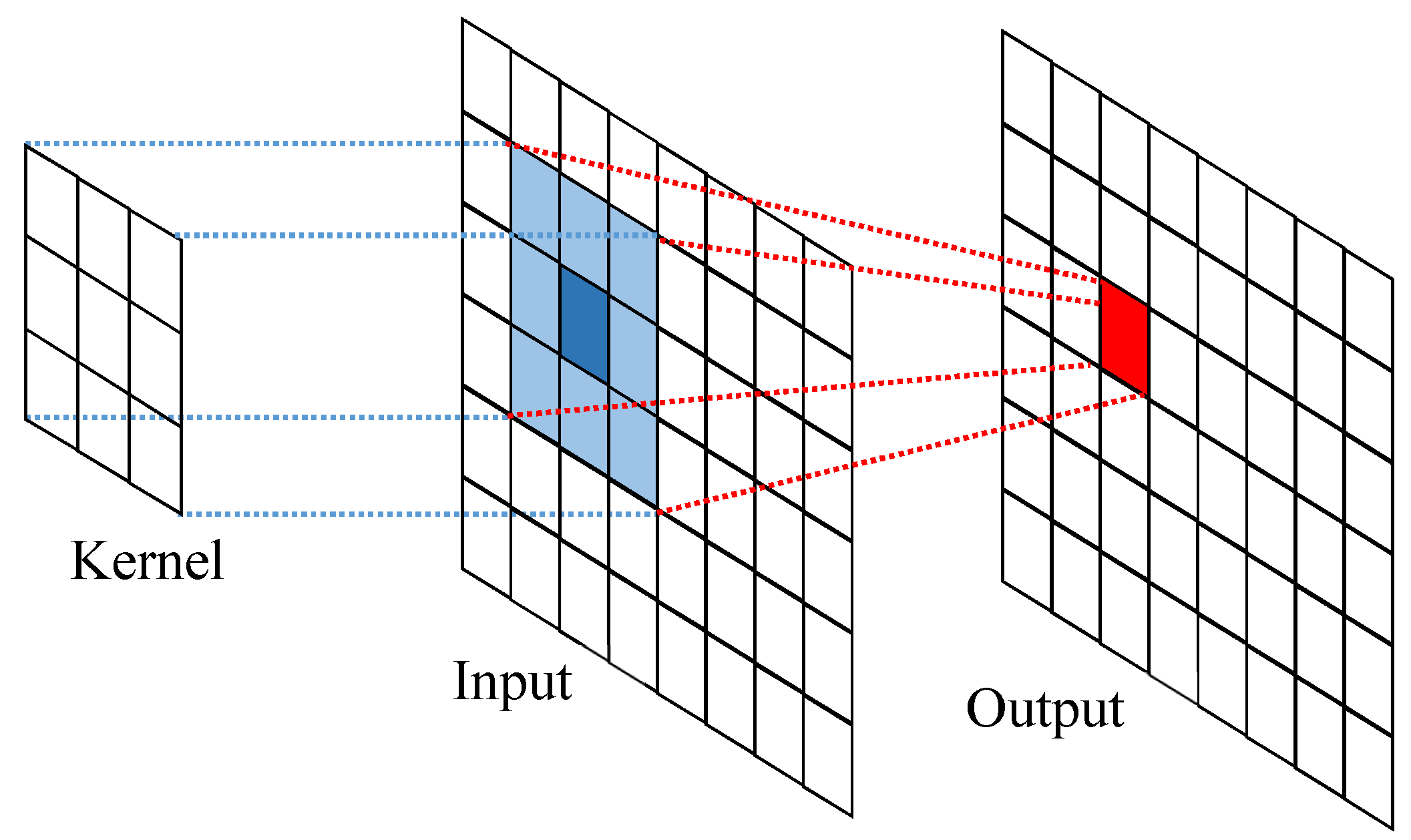
2.4.1. The Non-Local Means Filter
2.4.2. The Anisotropic filtering
2.4.3. Proposed Kernel-Based Exponentially-Modified Gaussian Regularization
3. Computer Simulation
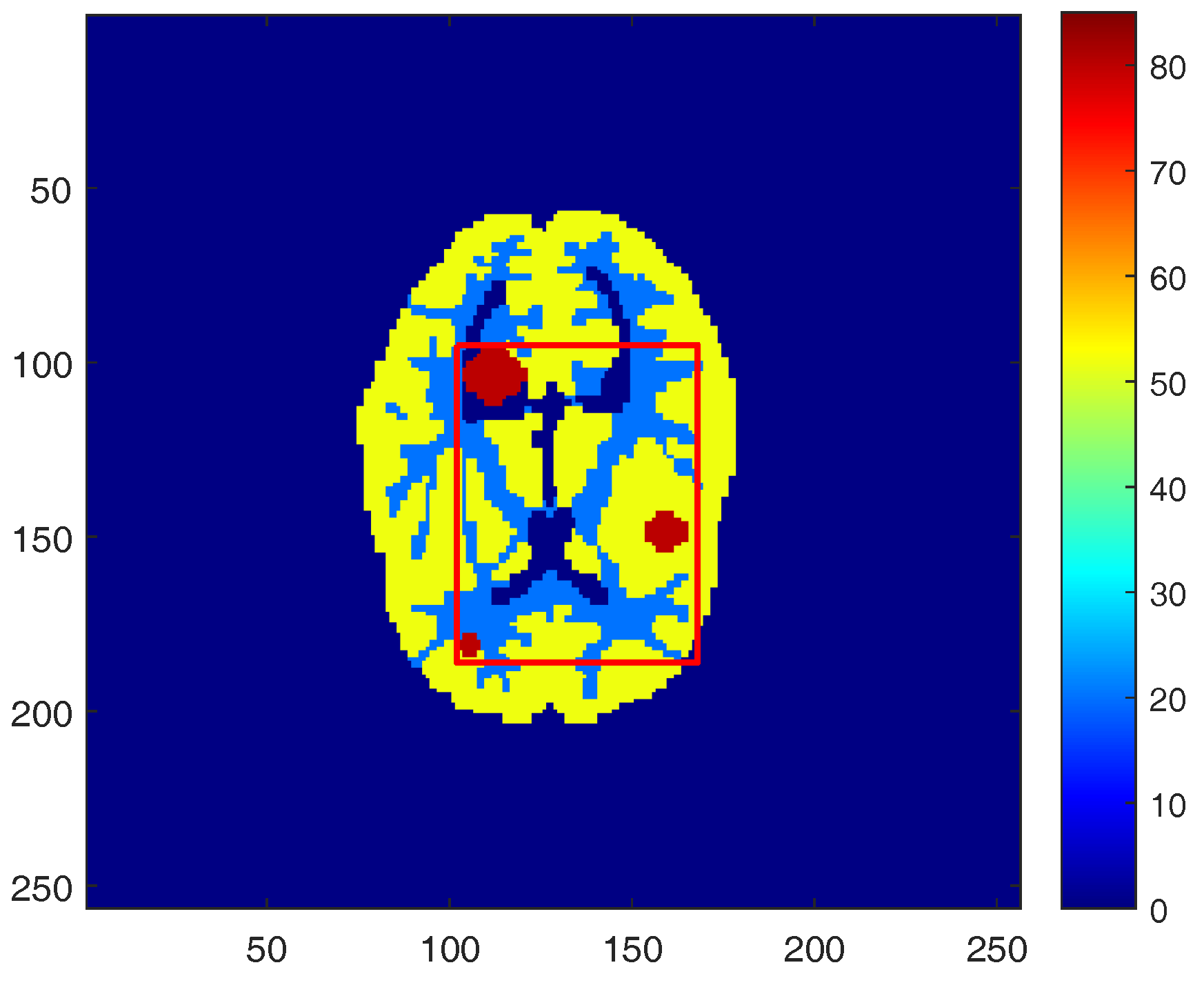
3.1. Simulated PET Data (Setup)
3.2. Quality Evaluation
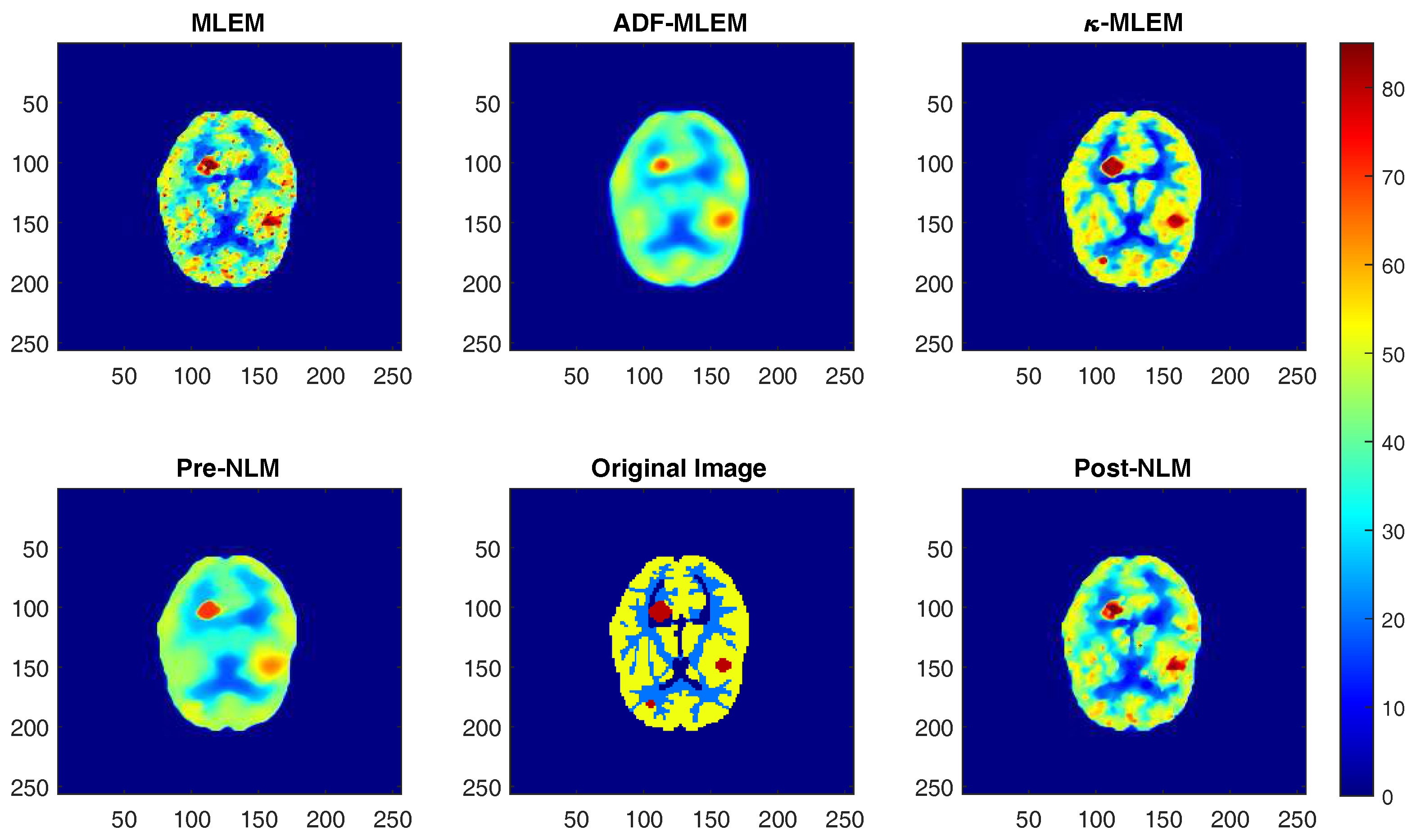
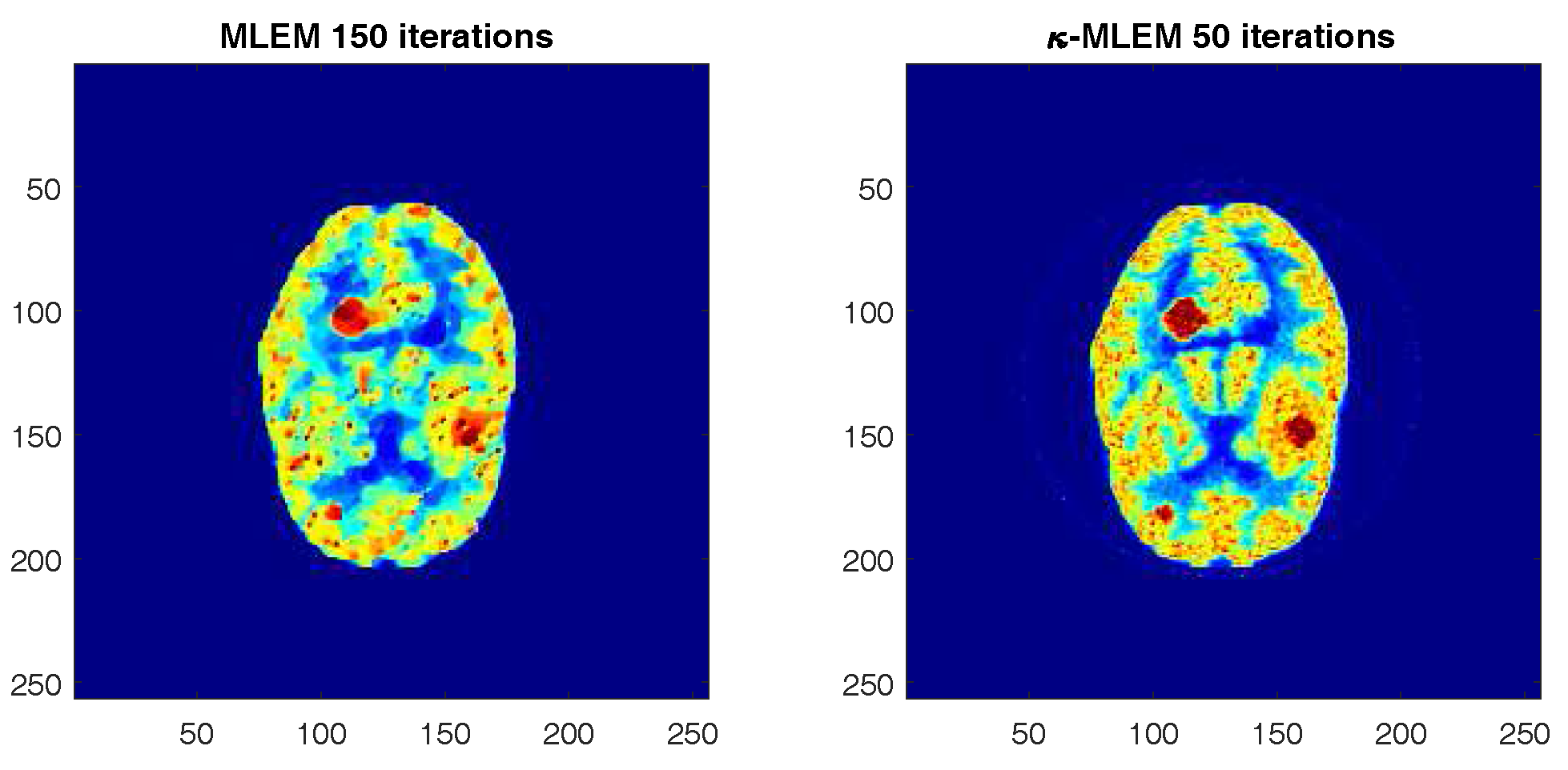
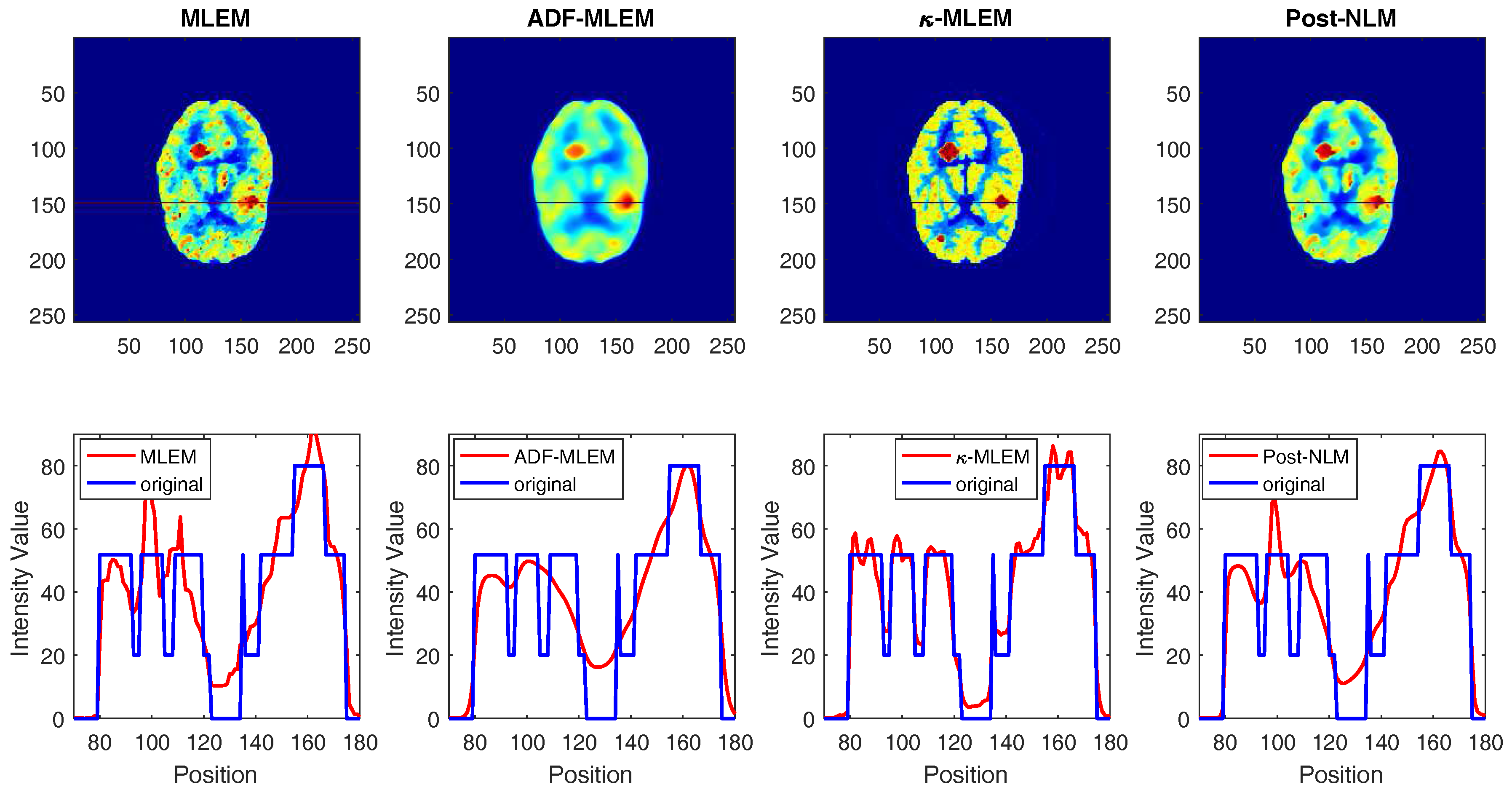
4. Results and Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Turkington, T.G. Introduction to PET instrumentation. J. Nucl. Med. Technol. 2001, 29, 4–11. [Google Scholar] [PubMed]
- Pike, V.W. PET radiotracers: Crossing the blood—Brain barrier and surviving metabolism. Trends Pharmacol. Sci. 2009, 30, 431–440. [Google Scholar] [CrossRef] [PubMed]
- Miele, E.; Spinelli, G.P.; Tomao, F.; Zullo, A.; De Marinis, F.; Pasciuti, G.; Rossi, L.; Zoratto, F.; Tomao, S. Positron Emission Tomography (PET) radiotracers in oncology—Utility of 18F-Fluoro-deoxy-glucose (FDG)-PET in the management of patients with non-small-cell lung cancer (NSCLC). J. Exp. Clin. Cancer Res. 2008, 27, 52. [Google Scholar] [CrossRef] [PubMed]
- Smith, T. The rate-limiting step for tumor [18 F] fluoro-2-deoxy-D-glucose (FDG) incorporation. Nucl. Med. Biol. 2001, 28, 1–4. [Google Scholar] [CrossRef]
- Peller, P.; Subramaniam, R.; Guermazi, A. PET-CT and PET-MRI in Oncology; Springer: Berlin, Germany, 2012. [Google Scholar]
- Machac, J. Cardiac positron emission tomography imaging. Semin. Nucl. Med. 2005, 35, 17–36. [Google Scholar] [CrossRef] [PubMed]
- Gunn, R.N.; Slifstein, M.; Searle, G.E.; Price, J.C. Quantitative imaging of protein targets in the human brain with PET. Phys. Med. Biol. 2015, 60, R363–R411. [Google Scholar] [CrossRef] [PubMed]
- Fodero-Tavoletti, M.T.; Okamura, N.; Furumoto, S.; Mulligan, R.S.; Connor, A.R.; McLean, C.A.; Cao, D.; Rigopoulos, A.; Cartwright, G.A.; O’Keefe, G.; et al. 18F-THK523: A novel in vivo tau imaging ligand for Alzheimer’s disease. Brain 2011, 134, 1089–1100. [Google Scholar] [CrossRef] [PubMed]
- Levin, C.S.; Hoffman, E.J. Calculation of positron range and its effect on the fundamental limit of positron emission tomography system spatial resolution. Phys. Med. Biol. 1999, 44, 781–799. [Google Scholar] [CrossRef] [PubMed]
- Macovski, A. Medical Imaging Systems; Prentice Hall: Upper Saddle River, NJ, USA, 1983. [Google Scholar]
- Demirkaya, O. Anisotropic diffusion filtering of PET attenuation data to improve emission images. Phys. Med. Biol. 2002, 47, N271–N278. [Google Scholar] [CrossRef] [PubMed]
- Li, T.; Li, X.; Wang, J.; Wen, J.; Lu, H.; Hsieh, J.; Liang, Z. Nonlinear sinogram smoothing for low-dose X-ray CT. IEEE Trans. Nucl. Sci. 2004, 51, 2505–2513. [Google Scholar]
- Balda, M.; Hornegger, J.; Heismann, B. Ray contribution masks for structure adaptive sinogram filtering. IEEE Trans. Med. Imaging 2012, 31, 1228–1239. [Google Scholar] [CrossRef] [PubMed]
- Bian, Z.; Ma, J.; Huang, J.; Zhang, H.; Niu, S.; Feng, Q.; Liang, Z.; Chen, W. SR-NLM: A sinogram restoration induced non-local means image filtering for low-dose computed tomography. Comput. Med. Imaging Graph. 2013, 37, 293–303. [Google Scholar] [CrossRef] [PubMed]
- Mokri, S.S.; Saripan, M.; Marhaban, M.; Nordin, A.; Hashim, S. Hybrid registration of PET/CT in thoracic region with pre-filtering PET sinogram. Radiat. Phys. Chem. 2015, 116, 300–304. [Google Scholar] [CrossRef]
- Christian, B.T.; Vandehey, N.T.; Floberg, J.M.; Mistretta, C.A. Dynamic PET denoising with HYPR processing. J. Nucl. Med. 2010, 51, 1147–1154. [Google Scholar] [CrossRef] [PubMed]
- Chan, C.; Meikle, S.; Fulton, R.; Tian, G.J.; Cai, W.; Feng, D.D. A non-local post-filtering algorithm for PET incorporating anatomical knowledge. In Proceedings of the 2009 IEEE Nuclear Science Symposium Conference Record (NSS/MIC), Orlando, FL, USA, 24 October–1 November 2009; pp. 2728–2732. [Google Scholar]
- Kazantsev, D.; Arridge, S.R.; Pedemonte, S.; Bousse, A.; Erlandsson, K.; Hutton, B.F.; Ourselin, S. An anatomically driven anisotropic diffusion filtering method for 3D SPECT reconstruction. Phys. Med. Biol. 2012, 57, 3793–3810. [Google Scholar] [CrossRef] [PubMed]
- Tang, J.; Nett, B.E.; Chen, G.H. Performance comparison between total variation (TV)-based compressed sensing and statistical iterative reconstruction algorithms. Phys. Med. Biol. 2009, 54, 5781–5804. [Google Scholar] [CrossRef] [PubMed]
- Buades, A.; Coll, B.; Morel, J.M. A review of image denoising algorithms, with a new one. Multiscale Model. Simul. 2005, 4, 490–530. [Google Scholar] [CrossRef]
- Chun, S.Y.; Fessler, J.A.; Dewaraja, Y.K. Non-local means methods using CT side information for I-131 SPECT image reconstruction. In Proceedings of the 2012 IEEE Nuclear Science Symposium and Medical Imaging Conference Record (NSS/MIC), Anaheim, CA, USA, 27 October–3 November 2012; pp. 3362–3366. [Google Scholar]
- Shepp, L.A.; Vardi, Y. Maximum likelihood reconstruction for emission tomography. IEEE Trans. Med. Imaging 1982, 1, 113–122. [Google Scholar] [CrossRef] [PubMed]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. Ser. B 1977, 39, 1–38. [Google Scholar]
- Jiao, J.; Markiewicz, P.; Burgos, N.; Atkinson, D.; Hutton, B.; Arridge, S.; Ourselin, S. Detail-preserving pet reconstruction with sparse image representation and anatomical priors. In Proceedings of the International Conference on Information Processing in Medical Imaging, Isle of Skye, UK, 28 June–3 July 2015; pp. 540–551. [Google Scholar]
- Wang, G.; Qi, J. PET image reconstruction using kernel method. IEEE Trans. Med. Imaging 2015, 34, 61–71. [Google Scholar] [CrossRef] [PubMed]
- Jacobs, F.; Matej, S.; Lewitt, R. Image Reconstruction Techniques for PET. ELIS Technical Report R9810, M1PG Technical Report MIPG245. 1998. Available online: https://pdfs.semanticscholar.org/1bbf/ 51088e22255c96eb0678643c404ad29c2061.pdf (accessed on 19 June 2017).
- Chow, P.L.; Rannou, F.R.; Chatziioannou, A.F. Attenuation correction for small animal PET tomographs. Phys. Med. Biol. 2005, 50, 1837–1850. [Google Scholar] [CrossRef] [PubMed]
- Brasse, D.; Kinahan, P.E.; Lartizien, C.; Comtat, C.; Casey, M.; Michel, C. Correction methods for random coincidences in fully 3D whole-body PET: Impact on data and image quality. J. Nucl. Med. 2005, 46, 859–867. [Google Scholar] [PubMed]
- Cherry, S.R.; Sorenson, J.A.; Phelps, M.E. Physics in Nuclear Medicine; Elsevier Health Sciences: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Valk, P.E.; Bailey, D.L.; Townsend, D.W.; Maisey, M.N. Positron Emission Tomography: Basic Science and Clinical Practice; Springer: London, UK, 2003. [Google Scholar]
- Wernick, M.N.; Aarsvold, J.N. Emission Tomography: The Fundamentals of PET and SPECT; Academic Press: Cambridge, MA, USA, 2004. [Google Scholar]
- Perona, P.; Malik, J. Scale-space and edge detection using anisotropic diffusion. IEEE Trans. Pattern Anal. Mach. Intell. 1990, 12, 629–639. [Google Scholar] [CrossRef]
- Golubev, A. Exponentially modified Gaussian (EMG) relevance to distributions related to cell proliferation and differentiation. J. Theor. Biol. 2010, 262, 257–266. [Google Scholar] [CrossRef] [PubMed]
- Leahy, R.; Yan, X. Incorporation of anatomical MR data for improved functional imaging with PET. In Proceedings of the 12th International Conference on Information Processing in Medical Imaging, London, UK, 7–12 July 1991; pp. 105–120. [Google Scholar]
- Hoffman, E.; Cutler, P.; Digby, W.; Mazziotta, J. 3-D phantom to simulate cerebral blood flow and metabolic images for PET. IEEE Trans. Nucl. Sci. 1990, 37, 616–620. [Google Scholar] [CrossRef]
- Wang, C.X.; Snyder, W.E.; Bilbro, G.; Santago, P. Performance evaluation of filtered backprojection reconstruction and iterative reconstruction methods for PET images. Comput. Biol. Med. 1998, 28, 13–25. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Strother, S.; Casey, M.; Hoffman, E. Measuring PET scanner sensitivity: relating countrates to image signal-to-noise ratios using noise equivalents counts. IEEE Trans. Nucl. Sci. 1990, 37, 783–788. [Google Scholar] [CrossRef]
- Eskicioglu, A.M.; Fisher, P.S. Image quality measures and their performance. IEEE Trans. Commun. 1995, 43, 2959–2965. [Google Scholar] [CrossRef]



© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boudjelal, A.; Messali, Z.; Elmoataz, A. A Novel Kernel-Based Regularization Technique for PET Image Reconstruction. Technologies 2017, 5, 37. https://0-doi-org.brum.beds.ac.uk/10.3390/technologies5020037
Boudjelal A, Messali Z, Elmoataz A. A Novel Kernel-Based Regularization Technique for PET Image Reconstruction. Technologies. 2017; 5(2):37. https://0-doi-org.brum.beds.ac.uk/10.3390/technologies5020037
Chicago/Turabian StyleBoudjelal, Abdelwahhab, Zoubeida Messali, and Abderrahim Elmoataz. 2017. "A Novel Kernel-Based Regularization Technique for PET Image Reconstruction" Technologies 5, no. 2: 37. https://0-doi-org.brum.beds.ac.uk/10.3390/technologies5020037



