Rule-Based Production of Mathematical Expressions

Abstract

There are situations in which one needs to write various kinds of mathematical expressions, such as practicing tests and school exams. There is a variety of methods to produce such expressions, but they are usually based on a database. This paper addresses the production of new expressions using the template ones that can be derived from the evaluation process or entered by users. With special limitations on the values of parameters, some templates can be dynamically constructed for the automatic generation of mathematical expressions and represented in the form of classes. For this purpose, a new type of grammar is proposed. This grammar is similar to Context-Free Grammar, but it empowers the producer to gain control over the generation of rules for different expressions. Our work mainly focuses on generating mathematical expressions in a user-oriented way, using a predefined set of templates of production rules. The production of expressions is not completely random, and is based on the defined subject.

1. Introduction

With the development of computer systems and their increasing use, it has been easier to see the effects of technology on several different fields, including education and health. In recent years, there have been many technological changes in educational practices and materials. The technologies that have been used have made significant educational changes for both students and teachers. In this regard, classrooms are equipped with digital learning tools, such as computers and handheld devices. It is possible to take advantage of independent training without the constraints of time and place. This has led to the construction of online platforms for participation and increased motivation for learners. Also, new technologies have provided a new model for communication between students and teachers in order to support the possibility of personalized education in the shadow of this model. Generally, technology changes educational practice, changing the way, time, and place that students learn and empowering them at each stage of education.

Mathematical expressions need to be written for several reasons, such as practicing for school exams and function optimization algorithms. Some systems may use a database of mathematical equations where all expressions are written once and then used many times. Solutions or answers of such equations might be stored in a non-dynamic fashion, which might lead to a lack of variety in types. Also, there are various methods for the random generation of mathematic expressions. Depending on the involved operators, operands, and variables, different types of generators can be implemented.

This paper addresses a grammar-directed approach to automatically generate mathematical expressions. The generation process is closely related to the synthesis of expressions. Synthesis, as opposed to analysis, takes the terms of which an expression is composed, and combines them together, so as to produce that expression. Since both analysis and synthesis involve the description of a language via grammar rules, it is also possible to use analysis grammars for synthesis to some extent. However, these activities exhibit two different kinds of indeterminacy; analysis involves determining which possible representation best fits a particular expression, while synthesis involves determining which possible expression best fits a particular representation. We can see synthesis as just a matter of linearization plus grammatical realization rules. In general, compared to analysis, ambiguity is not a problem in synthesis.

Producing mathematical expressions is an important topic in learning systems. Learners need to practice and solve various mathematical problems to improve their solving skills. This paper proposes a mathematical expression generator based on various types of expressions for topics such as first-degree equations and polynomials.

2. Related Work

In this work, a Context-Free Grammar like (CFG-like grammar) is used to parse and produce mathematical expressions. String inputs are passed to a parser that verifies their syntax. At the same time, an Abstract Syntax Tree (AST), which is a suitable data structure to work with mathematical expressions, is created. This tree serves as the main core part of the proposed approach to apply various enhancement algorithms on the string input. This structure has been used in other applications, such as solving mathematical problems [1].

Different systems are developed for expression generation using templates in Natural Language Generation (NLG). YAG [2] produces Template-Based strings in real time for general purposes. D2S (Data-to-Speech) [3] has been developed for different applications, such as rout description, music, soccer reports, and also for different languages, including English. EXEMPLARS [4] is an object-oriented, rule-based framework that supports dynamic text generation, and is a superset for JAVA, that can be used as templates of HTML/SGML. XtraGen [5] is an XML- and JAVA-based software system for NLG, which can be easily integrated with other applications.

Tillman Bechar [6] presents a generation method for template-based NLG, using TAG. This work focuses on random language generation by integrating Basic Tree Nodes. Of course, random template generation is not limited to random string generation; e.g., Amruth N. Kumar [7] used templates to produce problems and programs. Test case generation is another application of random generation. Takahide Y. et al. [8] designed a tool to generate tests for Just-In-Time (JIT) compilers. The issue of random generation is also presented in designing automatic tests. Various systems are designed to help teachers generate questions [9,10,11]. In [12], Joao et al. generated a system to produce automatic mathematical tests with simple answers in which some structures have been designed to generate tests. In [13], Ana Paula designed a system for the automatic generation of mathematics exercises based on Constraining Logic Programming (CLP). Such systems provide facilities for the automatic generation of tests in environments such as virtual training systems.

Random production is also considered in Natural Language Processing (NLP), resulting in different systems being developed under the title of NLG, such as measures taken by Langkilde [14] using stochastic techniques for NLG. These systems can be divided into two categories: real and template-based. Kees Van Deemter [15] has compared these categories.

The Microsoft MathWorksheet Generator automatically produces mathematical problems. This approach is limited to simpler algebraic domains, such as counting and linear and quadratic equation solving. Also, each domain has its own set of features that needs to be programmed separately.

Most of the studies addressed above refer to the generation of text phrases, particularly offering solutions for producing text using NLP patterns. These studies deal with such issues as finding real-time text structures, creating text and matching it with speech, and constructing test cases for programming languages and other systems. However, they do not have a suitable systematic structure for producing some specific mathematical expressions. Similarly, other research has been done to generate or design expressions using templates created for terms or specific issues. Users cannot use the designed templates to produce some other kinds of expressions. In addition, there are some commercial applications that have been developed to support mathematical requirements. The literature has no information about their underlying algorithms and data structures. They work in a non-user controlled way of automatic expression generation and are only open to evaluations from the perspective of users.

The method presented in this article is grammatically oriented. So, with a change in the rules of the grammar, new patterns can be created as appropriate templates for generating distinct mathematical expressions. This provides a useful way to produce and design any common mathematical expressions or other phrases in various research sciences. Using the proposed method, users can design and tailor grammar for their subject matter and create their own expressions.

3. Traditional Methods for Generating Expression

This section will look at the various ways in which the expressions are produced. One of the important issues in generating mathematical expressions is that the generated phrases should be designed as needed. In this section, the problems that are associated with the production of arbitrary expressions with specific features are examined and evaluated, and the need for a structured method is discussed.

3.1. Iterative Methods

The simple way to produce random math expressions is to use a well-formed generation algorithm in the domain of operators and numbers as shown in Listing 1.

The algorithm generates algebraic expressions by randomly selecting an operator from the set [+, −, *, /] and numeric operands. An example expression would be “23 + 5 × 3 − 2/3 + 10”.

A similar algorithm is given for polynomial expressions in Listing 2. With an initial value of degree n, the algorithm can generate polynomials that can have up to n terms. A typical example is the polynomial “3x⁵ − 8x² + 9”.

Listing 1. An algorithm for the random generation of arithmetic expressions.

Str ← generate a random number while condition    Operator ← select a random operator from {+, -,×, /}    Operand ← generate a random number    Str ← Str.Operator.Operand

Listing 1. An algorithm for the random generation of arithmetic expressions.

Str ← generate a random number while condition    Operator ← select a random operator from {+, -,×, /}    Operand ← generate a random number    Str ← Str.Operator.Operand

These algorithms can be improved by adding other attributes, such as parentheses. However, in this case, the generation process for expressions must be held under control to conduct different kinds of evaluation or interpretation.

Listing 2. An algorithm for the random generation of polynomial expressions.

n ← Number of terms in the polynomial c ← Generate a random number polyExp ← c. ‘xn’ n - - while n > 0    c ← Generate a random number    if c > 0: polyExp ← polyExp. ‘+’. c. ‘xn’    if c == 0;    if c < 0: polyExp ← polyExp. ‘-’. c. ‘xn’    n - -

Listing 2. An algorithm for the random generation of polynomial expressions.

n ← Number of terms in the polynomial c ← Generate a random number polyExp ← c. ‘xn’ n - - while n > 0    c ← Generate a random number    if c > 0: polyExp ← polyExp. ‘+’. c. ‘xn’    if c == 0;    if c < 0: polyExp ← polyExp. ‘-’. c. ‘xn’    n - -

3.2. Rule-Based Methods

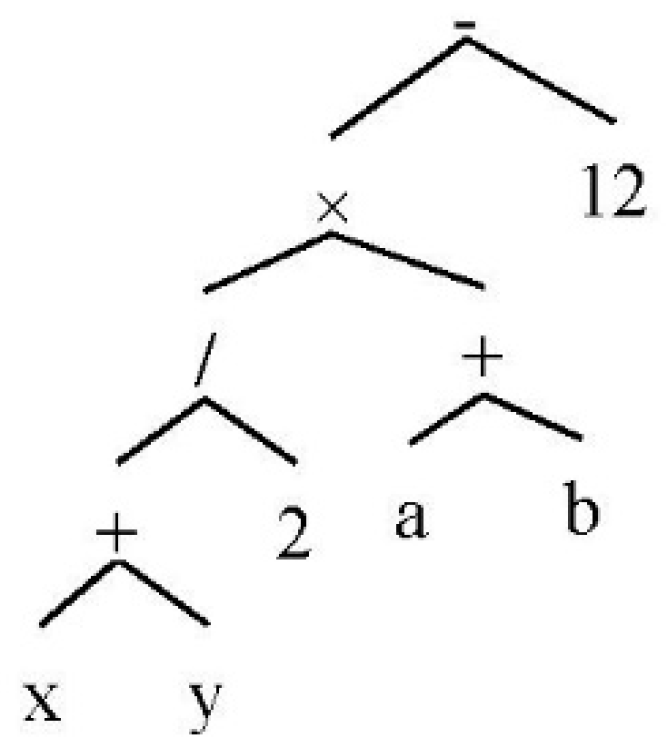
In general, we need a special structure in accordance with the recursive nature of generating expressions. This structure must have all of the properties of binary trees. Figure 1 shows the expression tree of “((x + y)/2) × (a + b) − 12”.

The binary tree is a suitable data structure that supports the inclusion of algebraic operators and single parameter functions. It provides a simple way to represent operator precedence. Besides this, it is easy to convert a tree to other data structures for the requirements of document formatters. Another advantage is that it supports the development of formal grammars, because the evaluation of each tree node resembles a recursive invocation of the head (parent) and body (children) of a grammar rule.

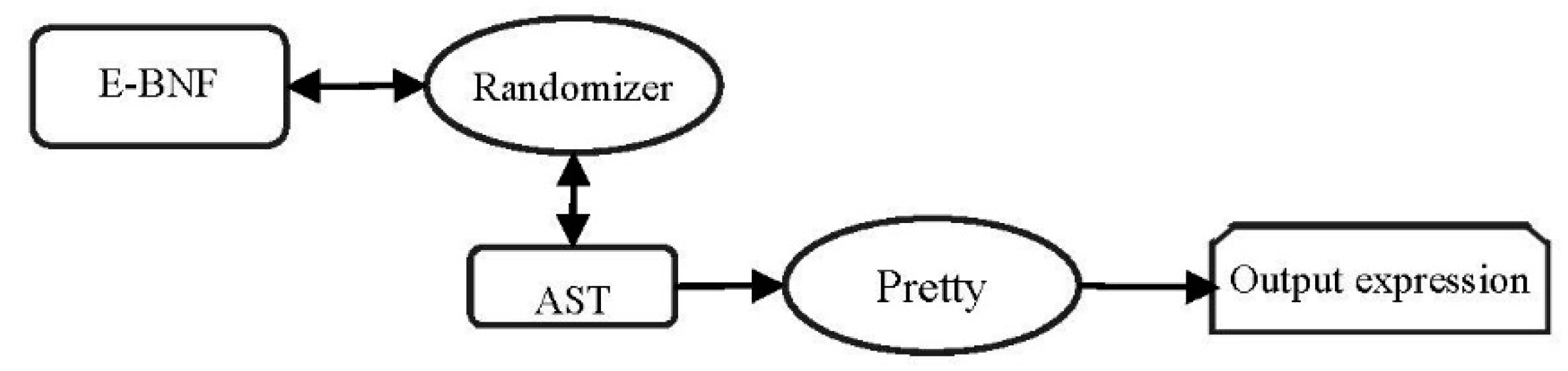
Figure 2 shows a block diagram of the mathematical components that are required to create a random mathematical expression using trees.

In Figure 2, the Randomizer is a rule selector that first places the beginning rule of a grammar into an AST and then recursively expands the non-terminals in that rule, replacing them with the other possible rules until encountering a non-expandable rule.

Table 1. Grammar rules for randomly generating mathematical expressions.

Non-Terminals	Rule
S	E
E	E + E
E	E − E
E	E * E
E	E/E
E	Sin(E)
E	Ln(E)
…
E	D
E	V
…
D	0|1|2|…|9

shows an example of grammar rules that can be placed into an indexed table for easy selection.

Note that the rules presented in Table 1 do not consider the precedence of operators, which will be considered in the evaluation phase. Listing 3 displays the main algorithm used by the Randomizer component in Figure 2.

Listing 3. The random expression generating algorithm.

AST ← Start symbol While a Non-Terminal exists in AST   E   ← Select a non-Terminal in AST   sub  ← Expand E using a random rule   AST ← Replace E with sub in AST In-order traverse the AST and print mathematical expression

Listing 3. The random expression generating algorithm.

AST ← Start symbol While a Non-Terminal exists in AST   E   ← Select a non-Terminal in AST   sub  ← Expand E using a random rule   AST ← Replace E with sub in AST In-order traverse the AST and print mathematical expression

In Listing 3, it is possible to invoke a sequence of the non-terminals; thus, rules S, E, and D in the specified order. For example, a resulting AST and expression would be Num(7) and “7”, respectively.

One problem with the current algorithm is that rules can create an unlimited number of non-terminals, e.g., “S → E → E + E → E + E + E → E + E + E + E…”. Stochastic Grammars [16] can be used to control the status of the invoked rules. Initializing an invocation probability for each rule in the algorithm, controlled through the expression steps, we can restrict the number of non-terminals expanded for an AST to a finite value. Some restrictions can be imposed on the following parameters:

• The length of output expression
• The number of nodes in the AST
• The number of levels in the AST.

These parameters determine the expression level of the AST, generating mathematical expressions of the desired characteristics. Listing 4 shows an improved version of the algorithm presented in Listing 3.

Listing 4. An improved algorithm based on the one in Listing 3.

AST ← Start symbol N  ← Number of maximum nodes  n  ← 0 While a Non-Terminal exists in AST   E   ← Select a non-Terminal in AST   if (n < N) then sub ← Expand E using a random rule   else     sub ← Expand E using a random rule without a non-terminal   AST ← Replace E with sub in AST In-order traverse the AST and print mathematical expression

Listing 4. An improved algorithm based on the one in Listing 3.

AST ← Start symbol N  ← Number of maximum nodes  n  ← 0 While a Non-Terminal exists in AST   E   ← Select a non-Terminal in AST   if (n < N) then sub ← Expand E using a random rule   else     sub ← Expand E using a random rule without a non-terminal   AST ← Replace E with sub in AST In-order traverse the AST and print mathematical expression

3.3. Type-Specific Grammars for Expressions

The generating and evaluating methods of expressions vary widely from one subject of mathematics to another. Therefore, it is clear that a different kind of expression would require a different grammar. In this section, we first focus on the linear (first-degree) and quadratic equations and then introduce a new grammar called a rule-iterated context-free grammar.

3.3.1. Grammars for First-Degree Equations

In a first-degree equation, the degree of the terms on the left- and right-hand sides of the symbol “=“ is 1 for x. A first-degree polynomial can be constructed in a few ways. Listing 5 presents a CFG grammar that considers all possible ways of generating polynomials of degree 1. For example, the expression “(x − 1)/(1 − x) = −1” generated by the grammar would correspond to the first-degree equation “x − 1 = 1 − x”.

Listing 5. A Context-Free grammar for first-degree equations.

G = {N, T, P, S} N = {E, E’, S, var, number, digit}⊆Σ T = {x, +, −, *} ⊆ Σ S   ⟶ E “=“ E|E “/” E “=“ E’ E   ⟶ E “+” E|E “−” E|number|var E   ⟶ E “*” E’|E’ “*” E E’   ⟶ E’ “+” E’|E’ “−” E’|E’ “*” E’|Number Var  ⟶ x Number ⟶ “−”? [digit] + [“.” [digit]+]? digit  ⟶ [“0” − “9”]

Listing 5. A Context-Free grammar for first-degree equations.

G = {N, T, P, S} N = {E, E’, S, var, number, digit}⊆Σ T = {x, +, −, *} ⊆ Σ S   ⟶ E “=“ E|E “/” E “=“ E’ E   ⟶ E “+” E|E “−” E|number|var E   ⟶ E “*” E’|E’ “*” E E’   ⟶ E’ “+” E’|E’ “−” E’|E’ “*” E’|Number Var  ⟶ x Number ⟶ “−”? [digit] + [“.” [digit]+]? digit  ⟶ [“0” − “9”]

3.3.2. Grammars for Quadratic Equations

Note that the alternative production rule of E with the division operator (/) represents an equation with a constant number on the right-hand side. Another grammar is given for quadratic equations in Listing 6.

Listing 6. A CFG grammar for quadratic equations.

G = {N, T, P, S} N = {E, E’, E’’, S, var, number, digit} T = {x, +, −, *, /, ^} S   ⟶E “=“ E E   ⟶E “+” E|E “−” E|number|var|var^2 E   ⟶E’ “*” E’|E “*” E’’|E’’ “*” E E’   ⟶E’ “+” E’ |E’ “−” E’|E’ “*” E’’|E’’ “*” E’|number|var E’’  ⟶E’’ “+” E’’|E’’ “−” E|E’’ “*” E’’|Number var  ⟶x number⟶“−”? (digit)+ [“.” (digit)+]? digit  ⟶[“0”–”9”]

Listing 6. A CFG grammar for quadratic equations.

G = {N, T, P, S} N = {E, E’, E’’, S, var, number, digit} T = {x, +, −, *, /, ^} S   ⟶E “=“ E E   ⟶E “+” E|E “−” E|number|var|var^2 E   ⟶E’ “*” E’|E “*” E’’|E’’ “*” E E’   ⟶E’ “+” E’ |E’ “−” E’|E’ “*” E’’|E’’ “*” E’|number|var E’’  ⟶E’’ “+” E’’|E’’ “−” E|E’’ “*” E’’|Number var  ⟶x number⟶“−”? (digit)+ [“.” (digit)+]? digit  ⟶[“0”–”9”]

Listing 6 explains the grammar for the first degree and quadratic equations, and how the CFG grammar works in generating a polynomial of degree 1.

The equations generated by the grammars in Listings 5 and 6 do not have structural control on either the length of the output expression or the number of the operators. The restrictions that were discussed in the previous section must be considered to hold the expression generation under control.

3.4. Statistical Space Analysis

A mathematical expression that is generated by the discussed grammar can be selected randomly or can be selected from an infinite number of expressions. If we limit the expression-generating space by measurable parameters, such as the maximum number of nodes or levels of the tree, it is possible to convert the infinite space of the problem to a finite one.

Suppose that the limit of producing mathematical expressions is related to the number of nodes. For a tree with n nodes, one of these nodes is the root node, and the rest of the n − 1 internal nodes are children or parents of underlying nodes. Obviously, there is one way to make a binary tree with zero or one node. Equation (1) calculates the number of binary trees with n nodes, shortly called Catalan Numbers [16].

$$S_n=\frac{1}{n+1}.\left(\begin{array}{c}2n\\ n\end{array}\right)=\frac{2n!}{n!\left(n+1\right)!}$$

(1)

The total number of trees, which can contain up to n nodes, is calculated by Equation (2)

$$S_{total}={\displaystyle \sum }_{n=1}^N\frac{2n!}{n!\left(n+1\right)!}$$

(2)

where N denotes the maximum number of nodes. Based on the type and location of operators, operands, and functions in an AST, there can arise various combinations that lead to different mathematical expressions. It is not easy to calculate the variations of an AST using only the number of nodes. We can determine it in terms of the depth of the tree.

The Equation (3) calculates the number of possible ASTs at a single level.

$$S_1=v+d$$

(3)

where v and d are the numbers of variables and integers, respectively, which can construct a single leaf of the AST. Figure 3 shows a possible AST for a maximum of up to two levels.

So, the number of ASTs can be given as Equation (4).

$$S_2=S_1\left(1+F+P\times S_1\right)$$

(4)

where F is the number of functions, such as sin and ln, and P is the number of operators, such as “+” and “*”. Figure 4 demonstrates the ASTs constructed through up to three levels.

The relation in Equation (5) would calculate the number of such ASTs.

$$S_3=S_2\left(1+F+P\times S_2\right)$$

(5)

In general, we can give the following relation for the number of possible ASTs based on up to L levels as Equation (6).

$$S_L=\{\begin{array}{ll}v+d& L=1\\ S_{L-1}\left(1+F+P\times S_{L-1}\right)& L>1\end{array}$$

(6)

Table 2. The numbers of possible ASTs with some different levels.

Level	Number of Trees
1	102
2	52,938
3	14,012,635,662
...
7	6.743220307892116 × 10172
8	2.273551006038432 × 10346

shows the number of the ASTs for some small values of L, assuming that there are P = 5 operators, F = 8 functions, v = 1 variable, and d = 100 digits.

The amount of ASTs that can be created at eight levels is incredibly high. It means that the method can produce many different ASTs. However, some ASTs would contain expressions that are not worth constructing. With this aspect, it uses an algorithm that generates expressions without using ASTs. On the other hand, we need some control rather than the number of nodes or levels in a generated expression. For example, the rule-invoking steps must end in a reasonable amount of time, without waiting for the generation of a particular type of expression. Next, we propose a new method to address these issues. The main purpose is that it explains that the division operator with the sign (/) represents an equation with a number on the right-hand side.

4. Materials and Methods

4.1. Rule-Iterated Context-Free Grammar (RI-CFG)

The grammars in Listings 5 and 6 have the potential to produce an unlimited number of equations. The production process must guarantee to terminate by using a deterministic grammar in terms of rule invocations. The rule-based grammars, such as a CFG, do not have convenient structures to limit the number of rule invocations to some certain value. Such a grammar is given in Listing 7. A comparison with other types of grammars goes outside the scope of the paper.

Listing 7. A sample grammar with no specific control structures.

E → E + E|D D →0|1|...|9

Listing 7. A sample grammar with no specific control structures.

E → E + E|D D →0|1|...|9

Therefore, we propose a rule-iterated context free grammar, shortly called RI-CFG.

An RI-CFG is represented by G = <T, N, P, S>, where T and N are disjoint finite non-empty sets of terminals and non-terminals respectively; S ∈ N is the start symbol; and P is a non-empty finite set of rules. Each set of rules in P has the form of “u → v, n”, where u ∈ N, v ∈ (N ∪ T) *, and n is a positive integer that indicates the number of rule selections in a non-terminal expression. Let n be the number of rule-specific selections. In this case, for n = 1, the system behaves like a CFG. Listing 8 shows a small example of an RI-CFG grammar for addition expressions.

Listing 8. A sample rule-iterated context free (RI-CFG) grammar.

S → DT, 1 T → +D, 2 D → 0|1|...|9, 2

Listing 8. A sample rule-iterated context free (RI-CFG) grammar.

S → DT, 1 T → +D, 2 D → 0|1|...|9, 2

Using the grammar in Listing 8, the expression “12 + 63 + 47” can be derived as seen in

Table 3. A sample derivation with the grammar in Listing 8.

Production	Rule
S	-
DT	S → DT,1
D + D + D	T → +D,2
12 + D + D	D → 0|1|...|9, 2
12 + 63 + D	D → 0|1|...|9, 2
12 + 63 + 47	D → 0|1|...|9, 2

.

The derived expression in Table 3 is demonstrated as a tree in Figure 5.

The use of RI-CFG grammars facilitates the control of the generating process. Through iterations of the rules, it is possible to generate mathematical expressions of desired types. An iterative grammar looks like the step-by-step sequential arrangement of its rules in terms of given iteration numbers. In this way, it requires that CFG grammars must be transformed into an iterative form.

4.1.1. Grammar Manipulation

As with parsing expressions, expression generation must also be controlled via functions that can be individually defined for each non-terminal of a grammar. Each of these functions is typically implemented as a loop with a certain number of iterations. Listing 9 shows a typical implementation of such a function, called repeater(), where a class Rule holds a list of grammar rules.

Listing 9. An implementation for a generating function called repeater().

public Rule[]repeater(Rule r)   out ←[]   for i = 1 to r.n    out.push(r.v)   return out

Listing 9. An implementation for a generating function called repeater().

public Rule[]repeater(Rule r)   out ←[]   for i = 1 to r.n    out.push(r.v)   return out

Expression generation can be customized through the iterations of grammar rules. For example, by assigning different values to x, we can obtain different types of expressions, such as first-degree and quadratic equations. A particular type of expression is represented by a class in which a value is set for the number of iterations of grammar rules. It is possible to define various classes that represent distinct types of expressions. With modified rules of the grammar shown in Listing 10, a new one is given in Listing 4.

Listing 10. An enhanced version of the grammar in Listing 4.

AST ← Start Symbol N  ← Number of maximum nodes n  ← 0 While a Non-Terminal exists in AST   E  ← Select a non-Terminal in AST   if (n < N)    sub ← Expand E using a random rule   else    sub ← Expand E using a random rule without a non-terminal   sub ← repeater(sub, E.n) # Using Listing 9   AST ← Replace E with sub in AST In-order traverse the AST and print mathematical expression

Listing 10. An enhanced version of the grammar in Listing 4.

AST ← Start Symbol N  ← Number of maximum nodes n  ← 0 While a Non-Terminal exists in AST   E  ← Select a non-Terminal in AST   if (n < N)    sub ← Expand E using a random rule   else    sub ← Expand E using a random rule without a non-terminal   sub ← repeater(sub, E.n) # Using Listing 9   AST ← Replace E with sub in AST In-order traverse the AST and print mathematical expression

4.1.2. CFG versus RI-CFG

In this section, we compare CFG and RI-CFG grammars through some particular examples. Even though the RI-CFG grammar is almost identical to CFG for some cases, they have noticeable differences in complex expressions.

Table 4. CFG and RI-CFG grammars for the language aⁿbⁿ.

CFG	RI-CFG
S → aSb	S → aSb, 1
S → λ	S → λ, 1

shows an example of CFG and RI-CFG grammars that produce the sentences of the same language. Note that RI-CFG rules have a controlled number of iterations.

Another comparative example is shown in

Table 5. CFG and RI-CFG grammars for the language a³ⁿb³ⁿ.

CFG	RI-CFG
S → aaaSbbb S → λ	S → ASB, 1 A → a, 3 B → b, 3 S → λ, 1

. Note that, unlike CFG, the RI-CFG grammar contains additional non-terminals, A and B. Although this increases the number of non-terminals, a RI-CFG that accepts the same language as CFG (e.g., as with aⁿb²ⁿ) can easily be derived. Another important point for such grammars is that the number of iterations of a rule can change dynamically at runtime. Thus, an extension of the grammar can always be constructed without changing the existing ones.

A CFG grammar with specific restrictions requires complex structures and various controls over a generated string. However, it is easy to apply such restrictions via the proposed grammar.

Table 6. The grammar of first-degree equations in the CFG and RI-CFG notations.

CFG	RI-CFG
S ⟶ E = E E ⟶ E + E|E − E |Number|Var E ⟶ E * F|F * E F ⟶ F + F|F − F |F * F|Number Var ⟶ x Number ⟶−?[digit]+[.[digit]+]? digit ⟶ [0–9]	S ⟶ TE = TE, 1 E ⟶ [+T|−T], n T ⟶  Number(x)?, 1 Number⟶−?[digit]+[.[digit]+]?,1 digit ⟶ [0–9], 1

shows the grammar of first-degree equations in CFG and RI-CFG notations.

The grammar in Table 6 produces first-degree equations of n terms. As mentioned before, integer n can be entered during the implementation or even at runtime to change the number of terms. Besides, one can select a random integer value for n from n_a to n_b.

By adding, modifying, or replacing some rules, we can easily transform the grammar in Table 6 into another one. For example, the grammar would start to yield quadratic equations with the addition of a rule “T ⟶ Dx²”.

4.2. A Methodology for Expression Generation

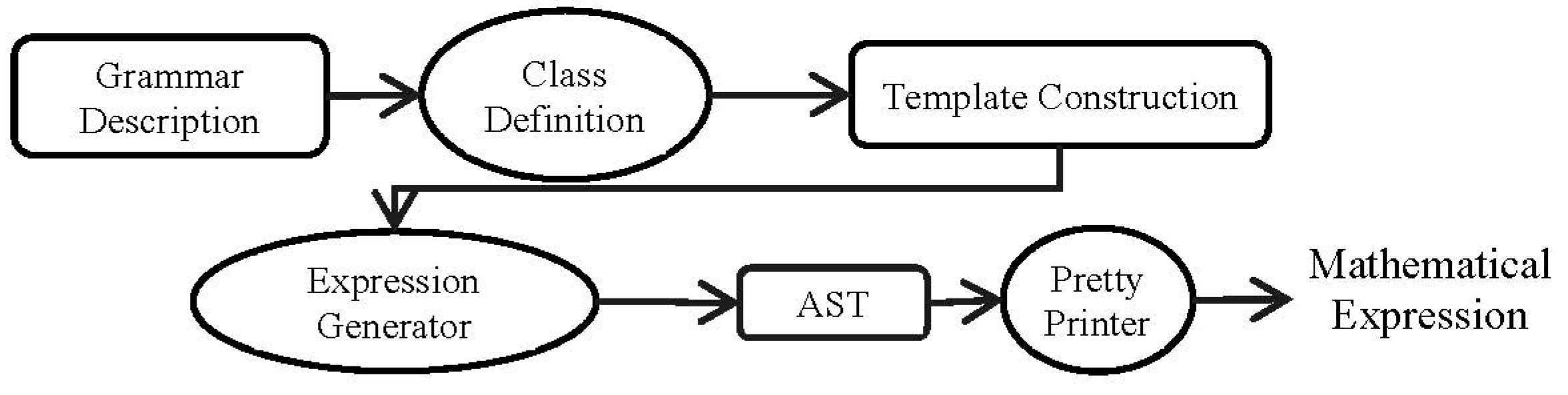
In previous sections, we discussed the importance of generating random mathematical expressions. This section presents a grammar-based approach that uses expression templates to produce different types of expressions.

4.2.1. RI-CFG-Based Production of Expressions

The proposed approach manages the expression generation process via RI-CFG grammars. Using the approach, a considerable number of expression templates can easily be embedded. Figure 6 shows the steps of the approach.

In Figure 6, the grammar pool contains various RI-CFG templates for first-degree equations, quadratic equations, polynomials, trigonometric equations, etc. We have developed a class called RICFG, which has the core implementations of Rule, Grammar, and other classes. This RICFG class is extended by every expression template.

Grammar Development

In this approach, first we develop an RI-CFG grammar specialized for the target mathematical expressions. Listing 11 shows a typical example of such a grammar.

In Listing 11, @n_i is an attribute of the grammar that controls the number of generated terms. This attribute controls the iterations of the related rules for a limited number of times. The other components of the approach shown in Listing 11 are described in the following sections.

Listing 11. An example of an RI-CFG grammar.

S⟶  DT, 1 T⟶  [+D|−D], @n1 D⟶  [0|1|2...|9], @n2

Listing 11. An example of an RI-CFG grammar.

S⟶  DT, 1 T⟶  [+D|−D], @n1 D⟶  [0|1|2...|9], @n2

Class Definition

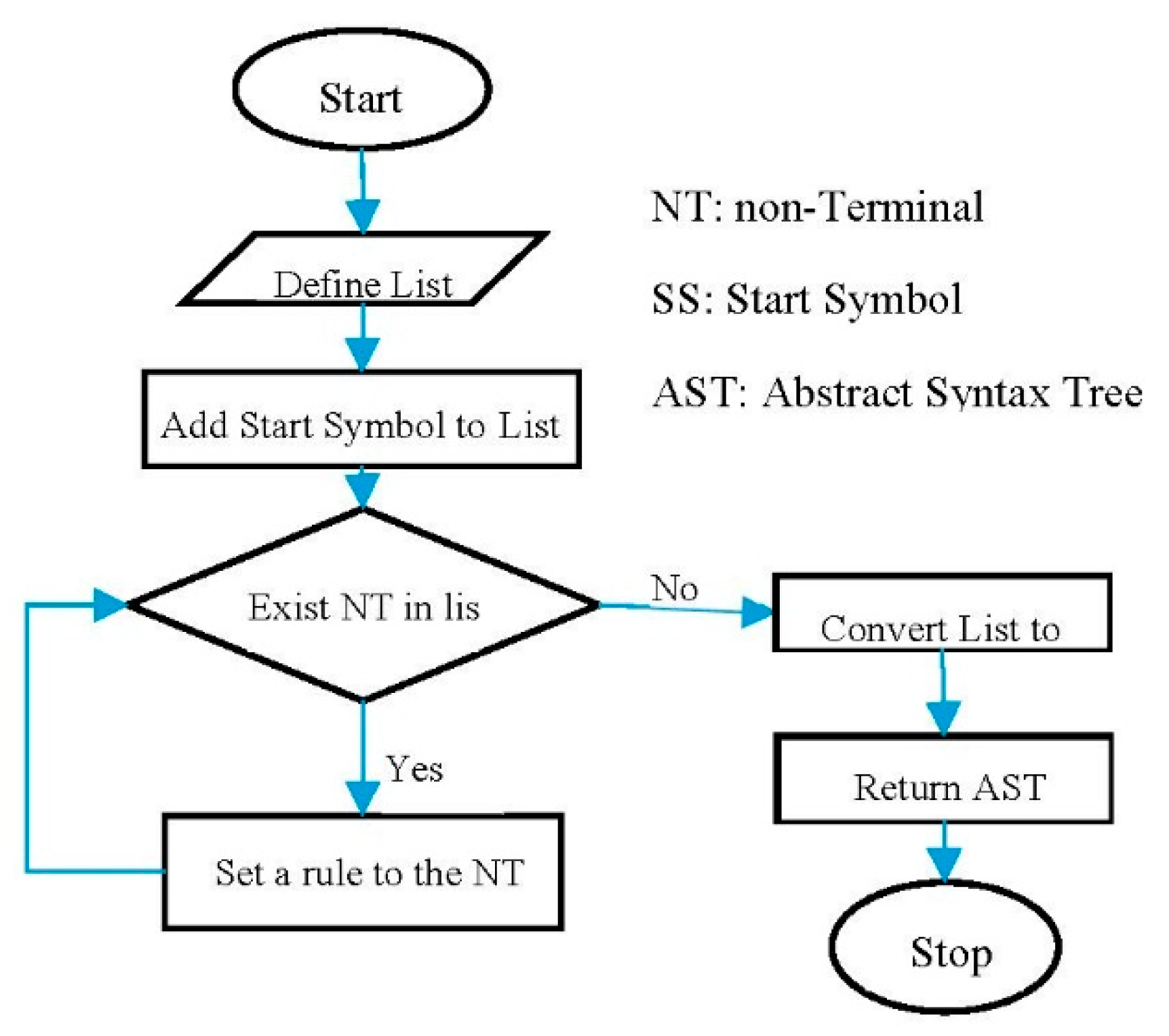
In our analysis of expressions, each grammar rule is represented with a class that can be defined using any object-oriented programming language. We code the rules in the Java language, extending the RI-CFG class. The superclass RI-CFG contains methods such as hasNonTerminal(), SelectRandomRule(), and generate(). Here, we give one of its methods, generate(), in Listing 12.

Listing 12. A method, generate(), of the RICFG class.

public Exp generate(){   ArrayList< Object > list = new ArrayList< > ();   list.add (START);   while(hasNonTerminal (list)){   Rule nt = getFirstNonTerminal(list);    replaceOnce(list, SelectRandomRule(nt).repeat());   }    return getAST(list);  }

Listing 12. A method, generate(), of the RICFG class.

public Exp generate(){   ArrayList< Object > list = new ArrayList< > ();   list.add (START);   while(hasNonTerminal (list)){   Rule nt = getFirstNonTerminal(list);    replaceOnce(list, SelectRandomRule(nt).repeat());   }    return getAST(list);  }

The flowchart corresponding to the method presented in Listing 12 is given in Figure 7.

Given the grammar rules in Listing 12, the non-terminals T and D are represented by the class NonTerminal. The rules, together with their alternatives, are implemented as the objects of the class Rule. Listing 13 demonstrates the class implementations of the rules.

Listing 13. Class definitions of templates.

// S⟶  DT, 1   // T ⟶  [+D|−D], @n1   // D ⟶ [0|1|2...|9], @n2 public class ExampleGrammar extends RICFG {  public void ExampleGrammar (Range n1, Range n2) {   NonTerminal T = NonTerminal.get(“T”);   NonTerminal D = NonTerminal.get(“D”);   pool = new ArrayList< >()   pool.add (new Rule (START, new Object[] {D, T}, 1));   pool.add (new Rule (T, new Object[] {“+”, D}, n1));   pool.add (new Rule (T, new Object[] {“−“, D}, n1));   pool.add (new Rule (D, “0”, n2));   pool.add (new Rule(D, “1”, n2));   pool.add (new Rule(D, “2”, n2));   ...   pool.add (new Rule(D, “9”, n2));  } }

Listing 13. Class definitions of templates.

// S⟶  DT, 1   // T ⟶  [+D|−D], @n1   // D ⟶ [0|1|2...|9], @n2 public class ExampleGrammar extends RICFG {  public void ExampleGrammar (Range n1, Range n2) {   NonTerminal T = NonTerminal.get(“T”);   NonTerminal D = NonTerminal.get(“D”);   pool = new ArrayList< >()   pool.add (new Rule (START, new Object[] {D, T}, 1));   pool.add (new Rule (T, new Object[] {“+”, D}, n1));   pool.add (new Rule (T, new Object[] {“−“, D}, n1));   pool.add (new Rule (D, “0”, n2));   pool.add (new Rule(D, “1”, n2));   pool.add (new Rule(D, “2”, n2));   ...   pool.add (new Rule(D, “9”, n2));  } }

In Listing 13, the class ExampleGrammar can be supported with additional methods for simplicity and customization.

The Listing 14 displays the pseudo code of Listing 13.

Listing 14. The pseudo code for class definitions of templates.

Definition:    Struct Range {      min as double      max as double    } Pseudo code: 1. make a rule list 2. Add each rule into the list 3. Set a range for each rule 4. return list

Listing 14. The pseudo code for class definitions of templates.

Definition:    Struct Range {      min as double      max as double    } Pseudo code: 1. make a rule list 2. Add each rule into the list 3. Set a range for each rule 4. return list

Template Construction

Expression templates are in fact implemented as objects of the related classes of RICFGs in which the attributes are set to proper values. It is adequate to manipulate the object attributes with the aim of generating various forms of expressions. A collection of templates can be packaged as a framework to support various forms of mathematical expressions. Listing 15 displays some expression templates for the rules defined in Listing 13.

The usage of expression templates is a metaprogramming technique that builds structures representing a computation at compile time, where expression is evaluated only as they are needed to produce efficient code for the entire computation. The key idea for the expression is to create reusable and efficient code.

Listing 15. The definitions of some expression templates.

// expressions with two digits ExampleGrammar term 1 = new ExampleGrammar (new Range (1, 5), new Range (2, 2)); // expressions with 3 to 10 terms ExampleGrammar term 2 = new ExampleGrammar (new Range (3, 10), new Range (1, 4));

Listing 15. The definitions of some expression templates.

// expressions with two digits ExampleGrammar term 1 = new ExampleGrammar (new Range (1, 5), new Range (2, 2)); // expressions with 3 to 10 terms ExampleGrammar term 2 = new ExampleGrammar (new Range (3, 10), new Range (1, 4));

Production of Expressions

The method generate() listed in Listing 12 produces an AST. Working with AST is easy as it can provide useful methods to deal with mathematical expressions. For example, we can define specific methods on ASTs to convert their content into human-readable strings in MathMl and LaTex. Listing 16 shows the outputs of the templates given in Listing 15.

Listing 16. The outputs of the templates in Listing 15.

// output of term 1 12 + 49 − 30 51 − 25 // output of term2 782 + 63 + 4 − 5120 + 8 + 1 − 576 + 23 7 + 163 − 2 + 87

Listing 16. The outputs of the templates in Listing 15.

// output of term 1 12 + 49 − 30 51 − 25 // output of term2 782 + 63 + 4 − 5120 + 8 + 1 − 576 + 23 7 + 163 − 2 + 87

4.2.2. Applications

A class that implements a template serves as a generator for a certain type of expression represented by that template. An expression template can use a set of other templates. In this section, we will demonstrate some applications of the methodology for generating polynomials using templates. The Java notation is used for code demonstration.

Polynomials

Polynomials are composed of different terms or monomials added or subtracted from each other. Each monomial has a well-known structure. Polynomial expressions can be defined by the RI-CFG grammar given in Listing 17.

Listing 17. A RI-CFG grammar for polynomial expressions.

S⟶  MT, 1 T ⟶  [+M|−M], @n1 M ⟶ DP, 1 P ⟶ [xR|x], 1 R ⟶ [*x], @n2 D ⟶ [0|1|2...|9], @n2

Listing 17. A RI-CFG grammar for polynomial expressions.

S⟶  MT, 1 T ⟶  [+M|−M], @n1 M ⟶ DP, 1 P ⟶ [xR|x], 1 R ⟶ [*x], @n2 D ⟶ [0|1|2...|9], @n2

In Listing 17, N is the number of monomials, P is the maximum exponential, and C is the range of values for coefficients. These three attributes are used to control the production of polynomial expressions. A class named TPolynomial is defined to implement the grammar of polynomials as seen in Listing 18.

Listing 18. Code implementation of Listing 17.

public class TPolynomial extends RICFG {  public Range count = new Range ();  public Range exponential = new Range ();  public Range coefficient = new Range ();  public Tpolynomial () {   NonTerminal T = NonTerminal.get (“T”);   NonTerminal M = NonTerminal.get (“M”);   NonTerminal P = NonTerminal.get (“P”);   NonTerminal R = NonTerminal.get (“R”);   NonTerminal D = NonTerminal.get (“D”);   pool = new ArrayList< > ()   pool.add (new Rule(START, new Object[]{M, T}, 1));   pool.add (new Rule(T, new Object[] {“+”, M}, n1));   pool.add (new Rule(T, new Object[] {“-“, M}, n1));   pool.add (new Rule(M, new Object[] {D, P}, 1));   pool.add (new Rule(P, new Object[] {“x“, R}, 1));   pool.add (new Rule(P, “x”, 1));   pool.add (new Rule(R, new Object[] {“*“, “x”}, n2));   pool.add (new Rule(D, null, n2));  } }

Listing 18. Code implementation of Listing 17.

public class TPolynomial extends RICFG {  public Range count = new Range ();  public Range exponential = new Range ();  public Range coefficient = new Range ();  public Tpolynomial () {   NonTerminal T = NonTerminal.get (“T”);   NonTerminal M = NonTerminal.get (“M”);   NonTerminal P = NonTerminal.get (“P”);   NonTerminal R = NonTerminal.get (“R”);   NonTerminal D = NonTerminal.get (“D”);   pool = new ArrayList< > ()   pool.add (new Rule(START, new Object[]{M, T}, 1));   pool.add (new Rule(T, new Object[] {“+”, M}, n1));   pool.add (new Rule(T, new Object[] {“-“, M}, n1));   pool.add (new Rule(M, new Object[] {D, P}, 1));   pool.add (new Rule(P, new Object[] {“x“, R}, 1));   pool.add (new Rule(P, “x”, 1));   pool.add (new Rule(R, new Object[] {“*“, “x”}, n2));   pool.add (new Rule(D, null, n2));  } }

For example, let us create a polynomial template with the attributes listed in

Table 7. A sample template for polynomials.

Attribute	Value
Number of monomials (N)	(3, 5)
Exponentials (P)	(2, 6)
Coefficients (C)	(−5, 10)

.

Listing 19 shows a method that produces random polynomial expressions using the attributes in Table 7.

Listing 19. A random polynomial generator using templates.

TPolynomial poly = new TPolynomial (); poly.count.set (3, 5); poly.exponential.set (2, 6); poly.coefficient.set (−5, 10); Exp ast = poly.generate ();

Listing 19. A random polynomial generator using templates.

TPolynomial poly = new TPolynomial (); poly.count.set (3, 5); poly.exponential.set (2, 6); poly.coefficient.set (−5, 10); Exp ast = poly.generate ();

In the template given in Listing 19, the count, exponential, and coefficient values of the class are initialized, and then, by calling the generate function, a random polynomial expression is generated under the desired conditions. We can use this template to generate some mathematical expressions. The examples of re-usability of template classes using Listing 18 are shown below:

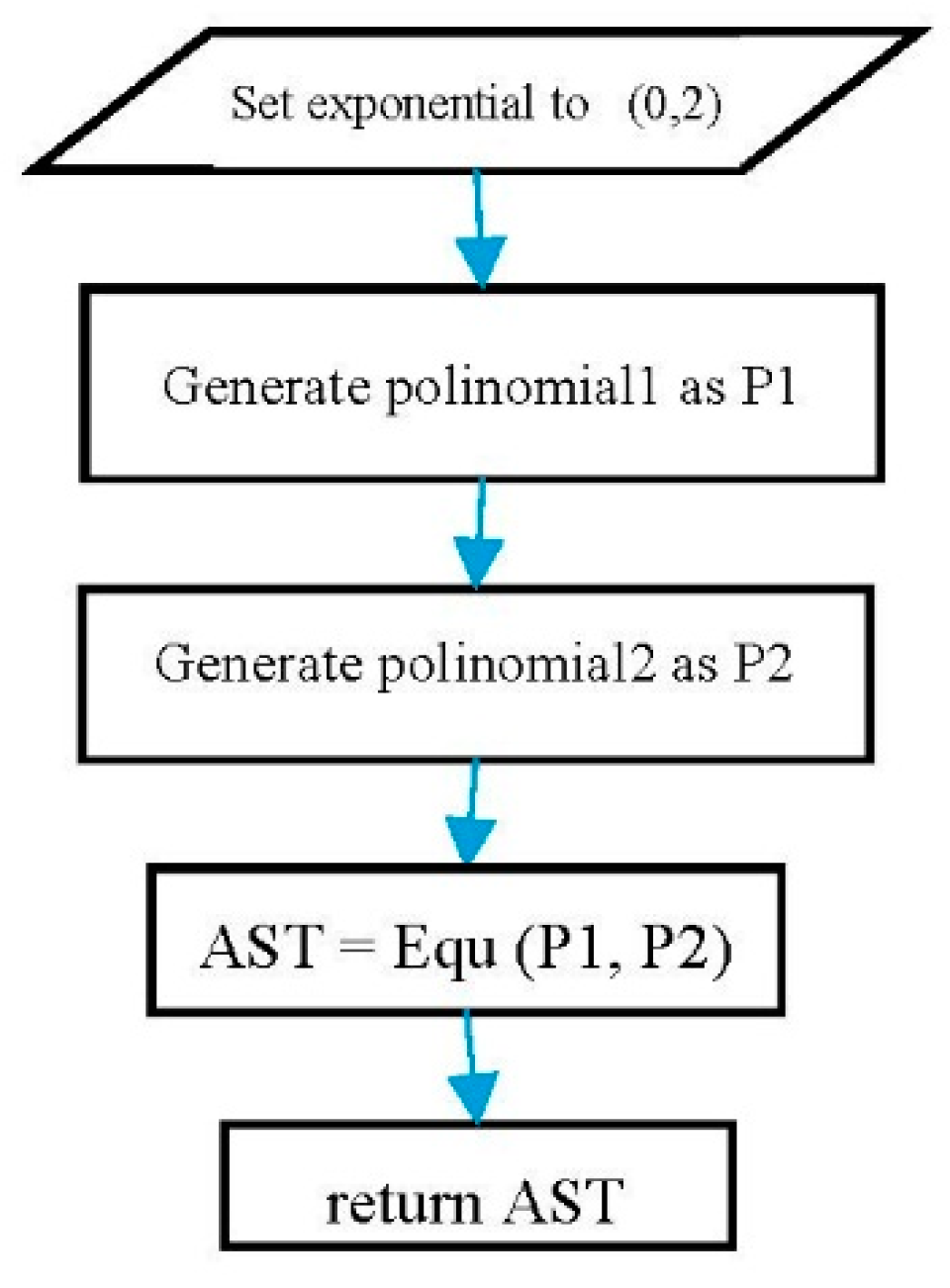
Example 1.

Generate First-Degree and Quadratic Expressions.

To do so, an exponential polynomial has to be set to (0, 2). The related equations must be constructed based on the structure of each equation. Listing 20 shows an example of constructing quadratic equations.

Listing 20. A random quadratic equation using Listing 19.

poly.exponential.set(0, 2); Exp left = poly.generate(); Exp right = poly.generate(); Exp quad = new Equ(left, right);

Listing 20. A random quadratic equation using Listing 19.

poly.exponential.set(0, 2); Exp left = poly.generate(); Exp right = poly.generate(); Exp quad = new Equ(left, right);

Figure 8 show the flowchart of a random quadratic equation using the polynomial template class.

Example 2.

Generate dividable polynomials, such as “P(x)/Q(x)”, where P(x) and Q(x) are polynomials.

Let us consider two polynomials P(x) = a₂x² + a₁x + a₀ and Q(x) = k × b₁x + k × b₀, where P(x) is dividable with “b₁x + b₀” and k is an arbitrary integer. To do so, two polynomials S₁ and S₂ are generated, where deg(S₁) = deg(S₂) = 1. Simplifying S₁ and S₂ will result in S₁= c₁x + c₀ and S₂ = b₁x + b₀. Assuming “P(x) = S₁ × S₂” and “Q = k × S₂” where k = [–7, 7]. Listing 21 shows an implementation of this example.

Listing 21. An example of dividable polynomials using templates.

poly.exponential.set (0, 1); Exp S1 = poly.generate (); Exp S2 = poly.generate (); Exp K = new Rand(−7, 7).get (); Exp P = new Times(S1, S2).Simplify (); Exp Q = new Times(k, S1).Simplify (); Exp div = new Div(P, Q).Simplify ();

Listing 21. An example of dividable polynomials using templates.

poly.exponential.set (0, 1); Exp S1 = poly.generate (); Exp S2 = poly.generate (); Exp K = new Rand(−7, 7).get (); Exp P = new Times(S1, S2).Simplify (); Exp Q = new Times(k, S1).Simplify (); Exp div = new Div(P, Q).Simplify ();

The required polynomials in Listing 21 are of degree 1. Therefore, the exponential field is set to (0, 1) and then two polynomials S₁ and S₂ are generated. Next, an AST is obtained by multiplying the two generated expressions using Times (S₁, S₂) and simplifying it. Similarly, the expression S₂ is multiplied and simplified with a random number in the range of −7 to 7. Finally, the two nodes obtained are divided into a node using Div (P, Q). The resulting AST is a random expression matching the desired attributes.

Example 3.

Generate expressions which “f(x) = a₃k₃x₃ + a₂k₂x₂ + a₁kx + a₀”.

To do so, F(x) and G(x) are generated, where F(x) = a₃x₃ + a₂x₂ + a₁x + a₀, G(x) = kx, and k is an arbitrary integer. Simplifying F(x) and then creating (FoG)(x) will produce expressions with the required patterns. Listing 22 shows an implementation of this example, where k = [7, 7].

Listing 22. An example of polynomials using templates.

Poly.exponential.set (0, 3); Exp F = poly.generate().Simplify (); Exp K = new Rand(−7, 7).get (); Exp G = new Times (K, Var.X ()); Exp div = F.eval (G).Simplify ();

Listing 22. An example of polynomials using templates.

Poly.exponential.set (0, 3); Exp F = poly.generate().Simplify (); Exp K = new Rand(−7, 7).get (); Exp G = new Times (K, Var.X ()); Exp div = F.eval (G).Simplify ();

In the example shown in Listing 22, it first sets up a polynomial, including a term with a maximum power of 3, and then produces polynomials. By multiplying a polynomial in a random number in the range of −7 to 7, a new expression is generated that should be simplified using the Simplify method.

Indeterminate Limits

Expressions such as “lim f(x), x⟶v” can be produced using Exp class, which is discussed in the previous Section, where lim is an extended class of Exp and accepts v and f(x) as parameters. F(x) is generated using other templates that are associated with the kind of expression one may need. Listing 23 shows an implementation of the limit where f(x) is a polynomial expression.

Listing 23. An example of the limit using Listing 22.

Exp F = poly.generate ().Simplify(); Exp v = new Rand (−6, 8).get (); Exp lim = new Limit (v, F); Exp div = F.eval (G).Simplify ();

Listing 23. An example of the limit using Listing 22.

Exp F = poly.generate ().Simplify(); Exp v = new Rand (−6, 8).get (); Exp lim = new Limit (v, F); Exp div = F.eval (G).Simplify ();

In the example of Listing 23, a random polynomial is created and a random number is connected to the Limit node in the range from −6 to 8. Finally, the resulting statement has been simplified.

The common indeterminate forms of limits are denoted 0/0, ∞/∞, 0*∞, 0⁰, and ∞⁰. Of these forms, we will handle the ratio of two functions that both tend to zero in limit, referred to as “the form 0/0”. To generate the expressions of this form, the following steps can be used for the limit of f (x) as x approaches v.

• Define an expression “(x − v)” where v is a number.
• Generate P(x) and Q(x), where P and Q are two polynomials.
• Multiply P(x) and Q(x) by “(x − v)”.
• Replace the resulting P(x) and Q(x) by their simplifications.
• Set f (x) to the ratio of P(x) over Q(x).

Listing 24 shows an implementation of these steps.

Listing 24. An example of an indeterminate limit expression.

Exp T = new Minus (Var.X (), v); Exp P = poly.generate ().Simplify (); Exp Q = poly.generate ().Simplify (); P = new Times (T, P).Simplify (); Q = new Times (T, Q).Simplify (); Exp fx = new Div (P, Q).Simplify ();

Listing 24. An example of an indeterminate limit expression.

Exp T = new Minus (Var.X (), v); Exp P = poly.generate ().Simplify (); Exp Q = poly.generate ().Simplify (); P = new Times (T, P).Simplify (); Q = new Times (T, Q).Simplify (); Exp fx = new Div (P, Q).Simplify ();

5. Evaluation

To investigate the performance of the proposed approach, we generate some mathematical expressions and classify them in terms of some features derived from their graphs in the Cartesian coordinate system. The quality of a polynomial function is assessed through analyzing eight features, namely degree (or type), the number of zeros, end behavior, the number of turning points, increasing, decreasing, concave up, and concave down. The same features are also shared by other kinds of expressions, such as first-degree and quadratic equations and indeterminate limits.

The produced expressions are categorized into four groups (excellent, good, average, and poor quality). Out of the eight features given above, a polynomial with at least six ones is identified as being of excellent quality, and a polynomial with at most three ones is identified as being of poor quality. The results are shown in

Table 8. Evaluation of produced expressions.

Product Type	Total	Excellent	Good	Average	Poor
Polynomial	100	65	25	10	0
First-Degree Equation	100	80	18	2	0
Quadratic Equation	100	73	20	7	0
Indeterminate Limit	100	57	29	11	3

. Note that, for indeterminate limits, there are three expressions that have been identified as poor ones, as a result that the similarity of the numerator and denominator polynomials is also evaluated.

6. Conclusions

In this paper, we propose a grammar-based approach for producing mathematical expressions that can be used to generate exam materials and practicing exercises to improve students’ skills in mathematics. Different forms of mathematical expressions need to have different sets of grammar rules and symbols. First degree and quadratic equations, polynomials, and other mathematical expressions are represented by a formal language that can be modeled by context free grammars (CFG). However, CFGs cannot control the generation process of expressions which meet various requirements in math problems.

The approach imposes some restrictions on the expressions, including the number of terms, the degree of variables, and the range of coefficients. To control these restrictions, we modify the rule structure of CFG grammars, calling it RI-CFG. Unlike CFG grammars, RI-CFGs have an interactive structure where the grammar rules iterate in a way that is directed by the related restrictions during the generation of expressions.

The RI-CFG rules, implemented as classes in the Java programming language, serve as expression templates, for which we can develop new templates, inheriting from the class of an existing one. The behavior of expression templates can be modified by setting the class attributes that are obtained from RI-CFG rules. Each attribute provides a different way of producing random mathematical expressions.

For example, a template of polynomial expressions can be used in various ways as a well-contained one. By limiting the maximum degree of variable x to 1 or 2, first degree or quadratic equations can be generated, respectively. A similar process can also be repeated for other mathematical expressions to produce other RICFG grammars and related templates.