Tree-Based Algorithm for Stable and Efficient Data Clustering
Abstract
:1. Introduction
2. The Kd-Tree and Data Clustering
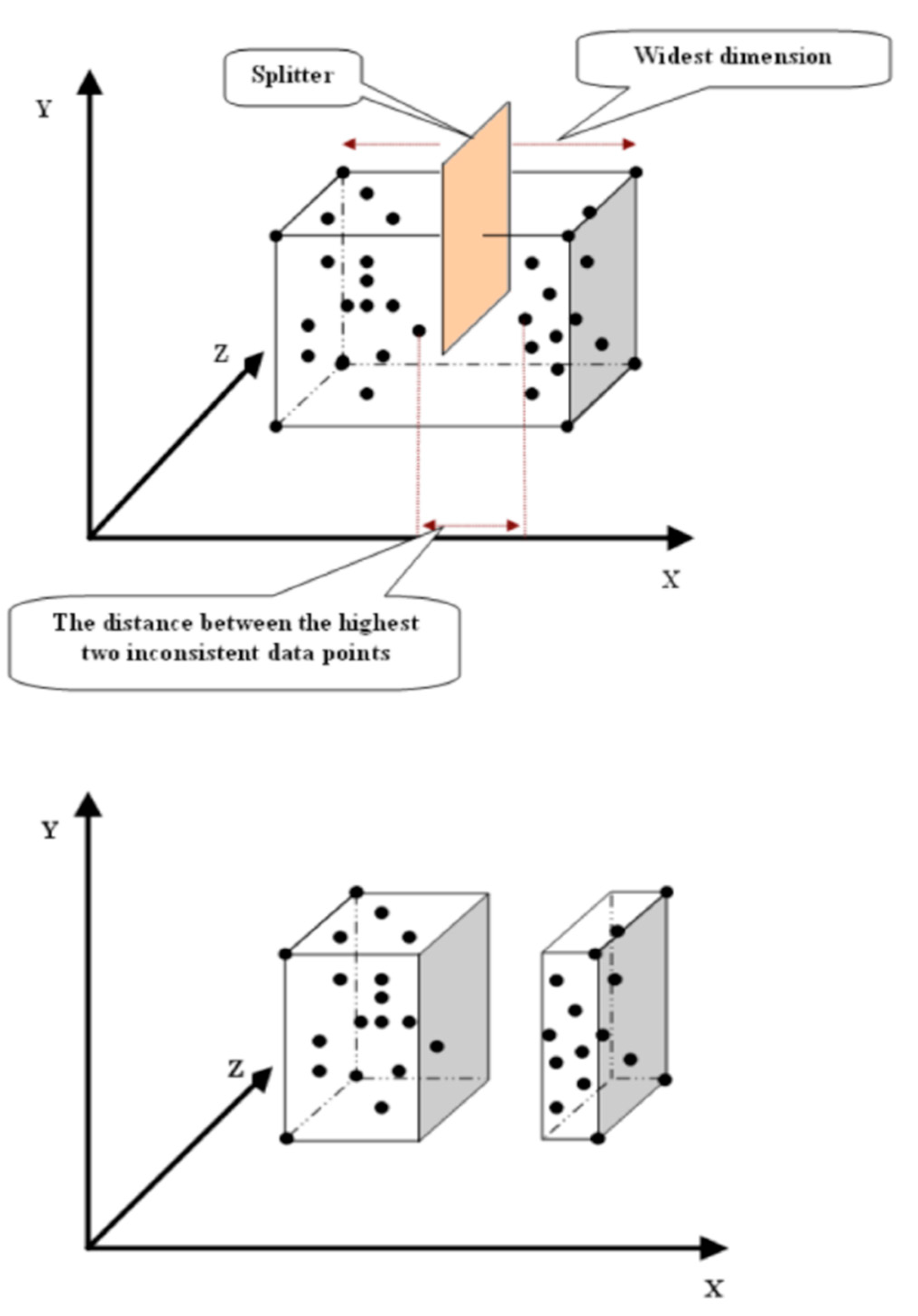
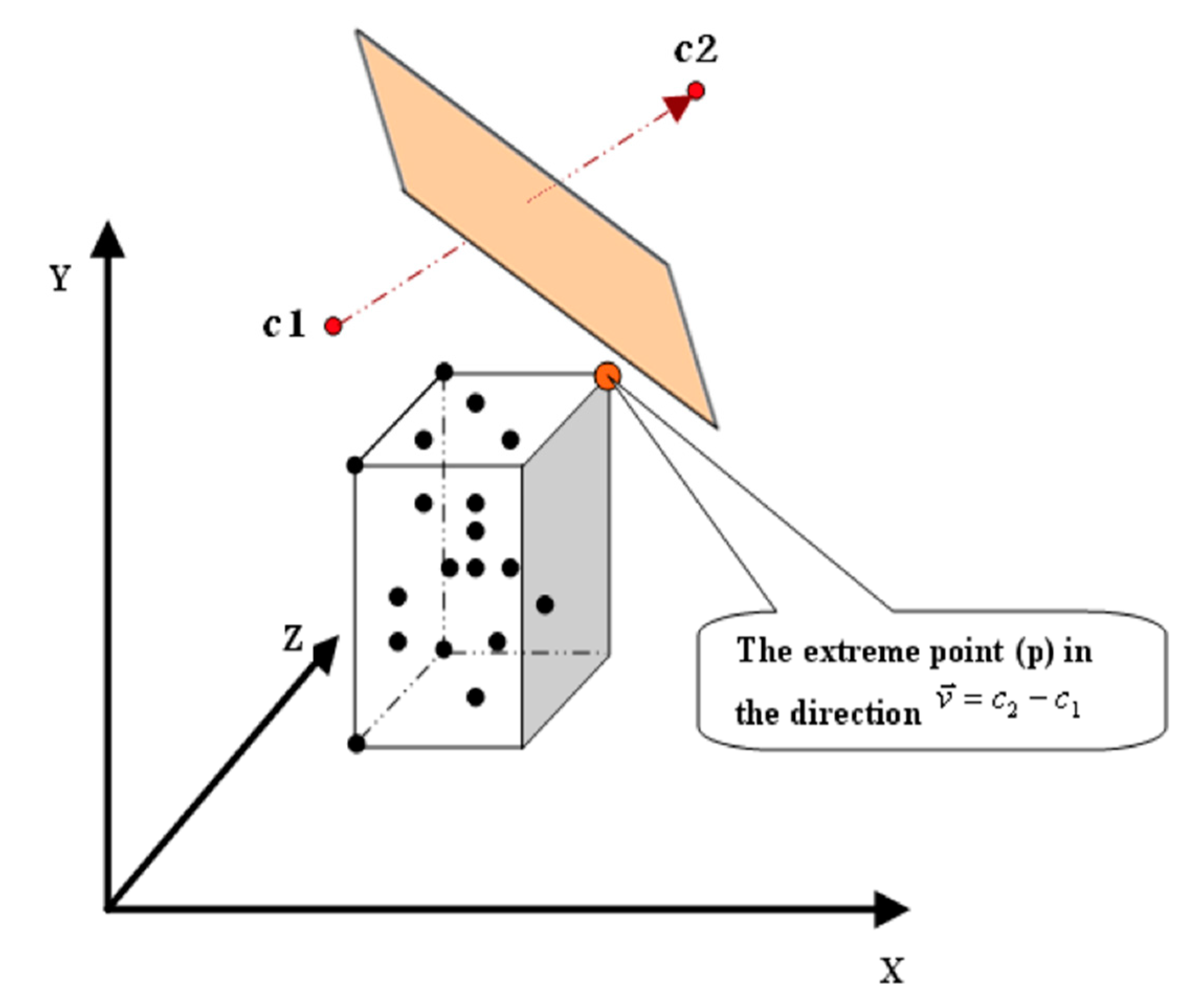
3. The Proposed Algorithm
- p(d): is the coordinate of p in dimension (d).
- c(d): is the coordinate of c in dimension (d).
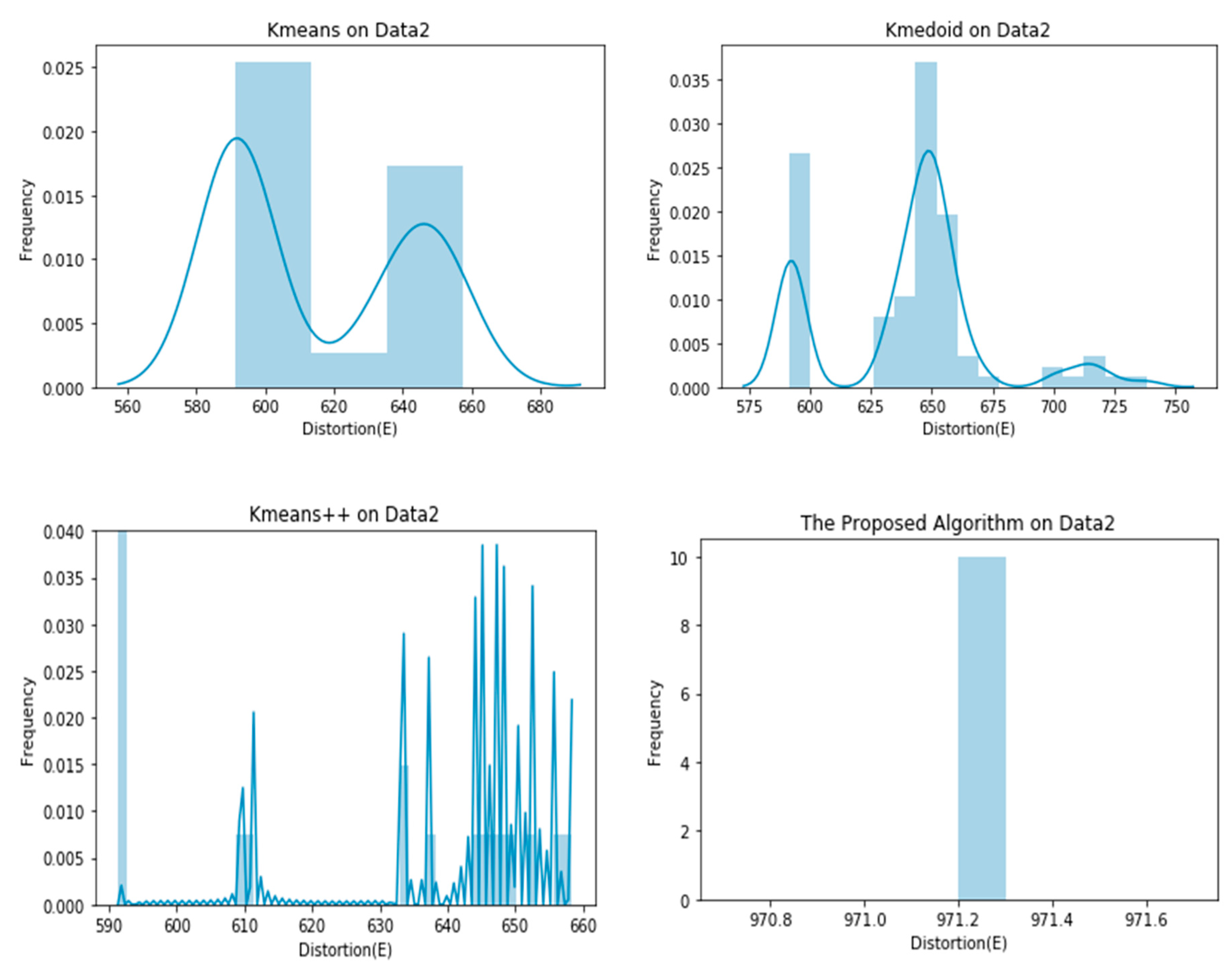
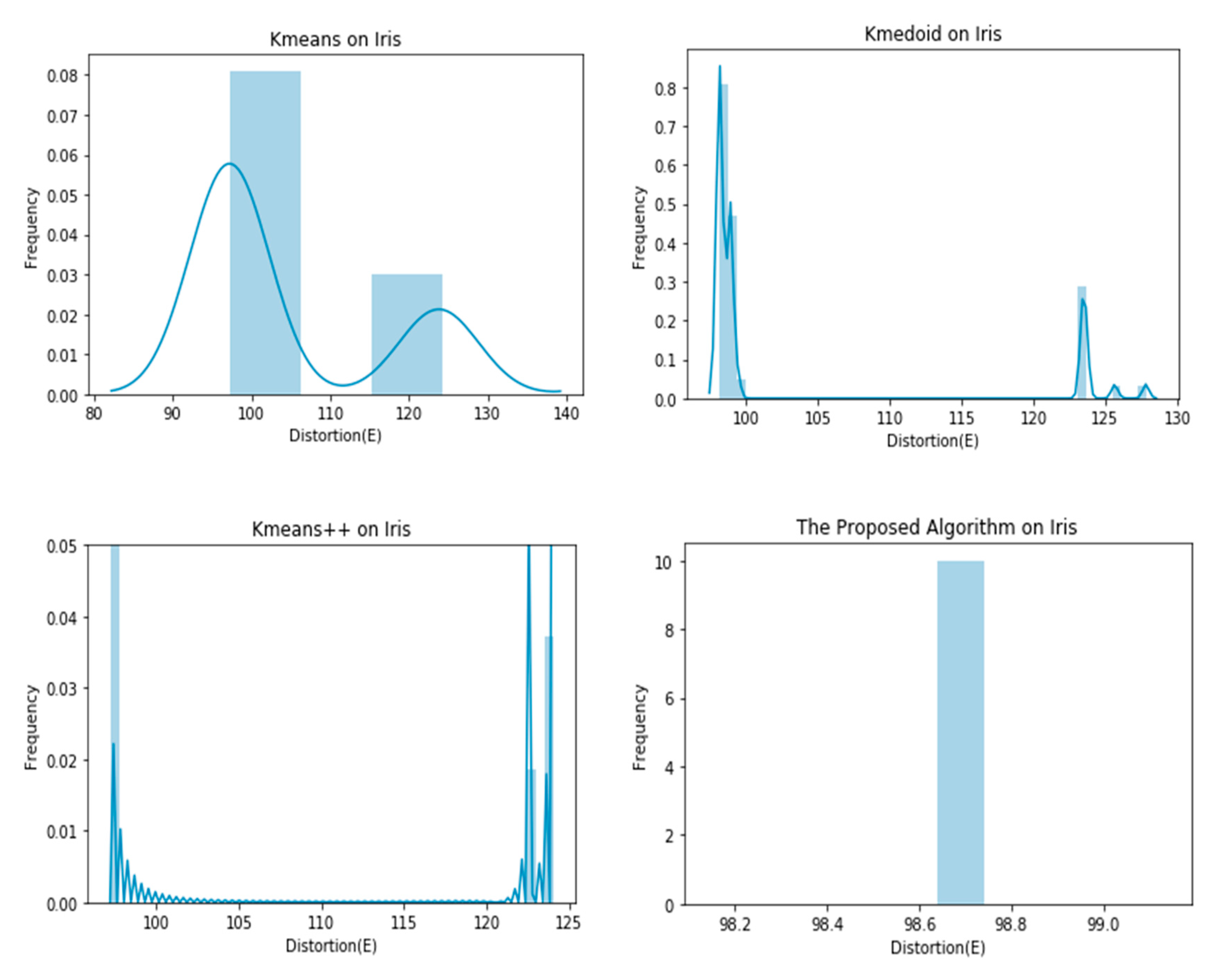
4. Experiments
- is a chosen distance measure between a data point xi(j) in the cluster(j) and the cluster center cj.
- nj is the number of data points in the cluster cj. and k is the number of clusters.
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Berkhin, P. A survey of clustering data mining techniques. In Grouping Multidimensional Data; Springer: Berlin, Germany, 2006; pp. 25–71. [Google Scholar]
- Abdullah, S.S.; Rostamzadeh, N.; Sedig, K.; Garg, A.X.; McArthur, E. Visual Analytics for Dimension Reduction and Cluster Analysis of High Dimensional Electronic Health Records. Informatics 2020, 7, 17. [Google Scholar] [CrossRef]
- Jones, P.J.; James, M.K.; Davies, M.J.; Khunti, K.; Catt, M.; Yates, T.; Rowlands, A.V.; Mirkes, E.M. FilterK: A new outlier detection method for k-means clustering of physical activity. J. Biomed. Inform. 2020, 104, 103397. [Google Scholar] [CrossRef] [PubMed]
- Jain, A.K.; Dubes, R.C. Algorithms for Clustering Data; Prentice Hall: Englewood Cliffs, NJ, USA, 1988; p. 304. [Google Scholar]
- Jain, A.K.; Murty, M.N.; Flynn, P.J. Data Clustering: A Review. ACM Comput. Surv. 1999, 31, 264–323. [Google Scholar] [CrossRef]
- MacQueen, J.B. Some Methods for Classification and Analysis of Multivariate Observations. In 5th Berkeley Symposium on Mathematical Statistics and Probability; University of California Press: Berkeley, CA, USA, 1967; pp. 281–297. [Google Scholar]
- Dobbins, C.; Rawassizadeh, R. Towards Clustering of Mobile and Smartwatch Accelerometer Data for Physical Activity Recognition. Informatics 2018, 5, 29. [Google Scholar] [CrossRef] [Green Version]
- Kuncheva, L.I.; Vetrov, D.P. Evaluation of stability of k-means cluster ensembles with respect to random initialization. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 1798–1808. [Google Scholar] [CrossRef]
- Rakhlin, A.; Caponnetto, A. Stability of K-means clustering. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 4–7 December 2016; City University of Hong Kong: Hong Kong, China, 2007; pp. 1121–1128. [Google Scholar]
- Steinley, D. Stability analysis in K-means clustering. Br. J. Math. Stat. Psychol. 2008, 61, 255–273. [Google Scholar] [CrossRef]
- Steinley, D. K-means Clustering: A Half-Century Synthesis. Br. J. Math. Stat. Psychol. 2007, 59, 1–34. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhao, H.; Ram, S. Clustering Schema Elements for Semantic Integration of Heterogeneous Data Sources. J. Database Manag. 2004, 15, 88–106. [Google Scholar] [CrossRef] [Green Version]
- Zhu, E.; Zhang, Y.; Wen, P.; Liu, F. Fast and stable clustering analysis based on Grid-mapping K-means algorithm and new clustering validity index. Neurocomputing 2019, 363, 149–170. [Google Scholar] [CrossRef]
- Khan, S.S.; Ahmad, A. Cluster Center Initialization Algorithm for K-means Clustering. Pattern Recognit. Lett. 2004, 25, 1293–1302. [Google Scholar] [CrossRef]
- Xu, J.; Xu, B.; Zhang, W.; Zhang, W.; Hou, J. Stable initialization scheme for k-means clustering. Wuhan Univ. J. Nat. Sci. 2009, 14, 24–28. [Google Scholar] [CrossRef]
- Arora, P.; Virmani, D.; Jindal, H.; Sharma, M. Sorted K-means towards the enhancement of K-means to form stable clusters. In Proceedings of the International Conference on Communication and Networks, Ahmedabad, India, 19–20 February 2016; Spring: Singapore, 2017; pp. 479–486. [Google Scholar]
- Bentley, J.L. Multidimensional Divide and Conquer. Commun. ACM 1980, 23, 214–229. [Google Scholar] [CrossRef]
- Friedman, J.H.; Bentley, J.L.; Finkel, R.A. An Algorithm for Finding Best Matches in Logarithmic Expected Time. ACM Trans. Math. Softw. 1977, 2, 209–226. [Google Scholar] [CrossRef]
- Moore, A. Very Fast EM-Based Mixture Model Clustering Using Multiresolution Kd-trees. In Advances in Neural Information Processing Systems II (NIPS); MIT Press: Breckenridge, CO, USA, 1999; pp. 543–549. [Google Scholar]
- Pelleg, D.; Moore, A. Accelerating Exact K-means Algorithms with Geometric Reasoning. In Proceedings of the 5th ACM International Conference of the Special Interest Group on Knowledge Discovery and Data Mining (ACM-SIGKDD-99), San Diego, CA, USA, 15–18 August 1999; pp. 277–281. [Google Scholar]
- Pelleg, D.; Moore, A. Accelerating Exact K-Means Algorithms with Geometric Reasoning-Technical Report; School of Computer Science, Carnegie Mellon University: Pittsburgh, PA, USA, 2000. [Google Scholar]
- Moore, A.; Lee, M.S. Cached Sufficient Statistics for Efficient Machine Learning with Large Datasets. J. Artif. Intell. Res. 1998, 8, 67–91. [Google Scholar] [CrossRef] [Green Version]
- Kanungo, T.; Mount, D.M.; Netanyahu, N.S.; Piatko, C.D.; Silverman, R.; Wu, A.Y. An Efficient K-means Clustering Algorithm: Analysis and Implementation. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 881–892. [Google Scholar] [CrossRef]
- Hussein, N. A Fast Greedy K-Means Algorithm. Master’s Thesis, University of Amsterdam, Amsterdam, The Netherlands, 2002. [Google Scholar]
- Likas, A.; Vlassis, N.; Verbeek, J.J. The Global K-means Clustering Algorithm. Pattern Recognit. 2003, 36, 451–461. [Google Scholar] [CrossRef] [Green Version]
- Redmond, S.J.; Heneghan, C. A Method for Initialising the K-means Clustering Algorithm Using Kd-Trees. Pattern Recognit. Lett. 2007, 28, 965–973. [Google Scholar] [CrossRef]
- Lai, J.Z.; Huang, T.J.; Liaw, Y.C. A fast k-means clustering algorithm using cluster center displacement. Pattern Recognit. 2009, 42, 2551–2556. [Google Scholar] [CrossRef]
- Asuncion, A.; Newman, D.J. UCI Machine Learning Repository. University of California, School of Information and Computer Science. 2007. Available online: http://www.ics.uci.edu/~mlearn/MLRepository.html (accessed on 15 January 2020).
- Johnson, R.A.; Wichern, D.W. Applied Multivariate Statistical Analysis, 5th ed.; Prentice Hall: Englewood Clifs, NJ, USA, 2001; p. 767. [Google Scholar]
- Grabmeier, J.; Rudolph, A. Techniques of Cluster Algorithms in Data Mining. Data Min. Knowl. Discov. 2002, 6, 303–360. [Google Scholar] [CrossRef]





| Dataset | Data1 | Data2 | Data3 | Iris | Crude Oil | Vowel |
|---|---|---|---|---|---|---|
| #Features | 2 | 2 | 10 | 4 | 5 | 3 |
| #Instances | 76 | 900 | 1000 | 150 | 56 | 871 |
| #Classes | 3 | 9 | 2 | 3 | 3 | 6 |
| Data/Algorithm | K-Means | K-Medoids | K-Means++ | Proposed Algorithm |
|---|---|---|---|---|
| Data 1 | 55.1581 ± 6.9611 | 54.3962 ± 6.4543 | 49.1530 ± 4.3717 | 47.6100 ± 0.0000 |
| Data 2 | 615.0904 ± 26.8660 | 640.7589 ± 32.8690 | 597.9887 ± 17.2748 | 971.2000 ± 0.0000 |
| Data 3 | 863.2801 ± 1.5688 | 945.5977 ± 11.2057 | 863.7684 ± 1.4762 | 864.6000 ± 0.0000 |
| Iris | 104.3849 ± 11.7980 | 103.8354 ± 10.4880 | 98.0069 ± 4.4933 | 98.6399 ± 0.0000 |
| Crude oil | 279.6143 ± 0.1867 | 305.8225 ± 22.1917 | 279.5339 ± 0.1989 | 278.9000 ± 0.0000 |
| Vowel | 153,468.1732 ± 4163.8986 | 158,295.8453 ± 8676.5586 | 151,960.0763 ± 3323.1807 | 151,900.0000 ± 0.0000 |
| Data/Algorithm | K-Means | Proposed Algorithm |
|---|---|---|
| Data 1 | 1368 | 228 |
| Data 2 | 24,300 | 9000 |
| Data 3 | 6000 | 2000 |
| Iris | 1800 | 450 |
| Crude oil | 1176 | 168 |
| Vowel | 20,904 | 5226 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aljabbouli, H.; Albizri, A.; Harfouche, A. Tree-Based Algorithm for Stable and Efficient Data Clustering. Informatics 2020, 7, 38. https://0-doi-org.brum.beds.ac.uk/10.3390/informatics7040038
Aljabbouli H, Albizri A, Harfouche A. Tree-Based Algorithm for Stable and Efficient Data Clustering. Informatics. 2020; 7(4):38. https://0-doi-org.brum.beds.ac.uk/10.3390/informatics7040038
Chicago/Turabian StyleAljabbouli, Hasan, Abdullah Albizri, and Antoine Harfouche. 2020. "Tree-Based Algorithm for Stable and Efficient Data Clustering" Informatics 7, no. 4: 38. https://0-doi-org.brum.beds.ac.uk/10.3390/informatics7040038





