Voltage-Based Hybrid Algorithm Using Parameter Variations and Stockwell Transform for Islanding Detection in Utility Grids
Abstract
:1. Introduction
- An islanding detection method (IDM) based on the use of voltage signals is proposed in this paper.
- Features extracted from the voltage signal using the ST and rate of change in RMS voltage are used to define a voltage-based islanding recognition factor (IRFV).
- Islanding events are discriminated from the faulty and operational events using simple decision rules based on the peak magnitude of IRFV.
- Proposed IDM is effective to detect islanding events with minimum NDZ.
- Proposed IDM is more effective compared to the method based on the rate of change in voltage and a discrete wavelet transform (DWT)-based method.
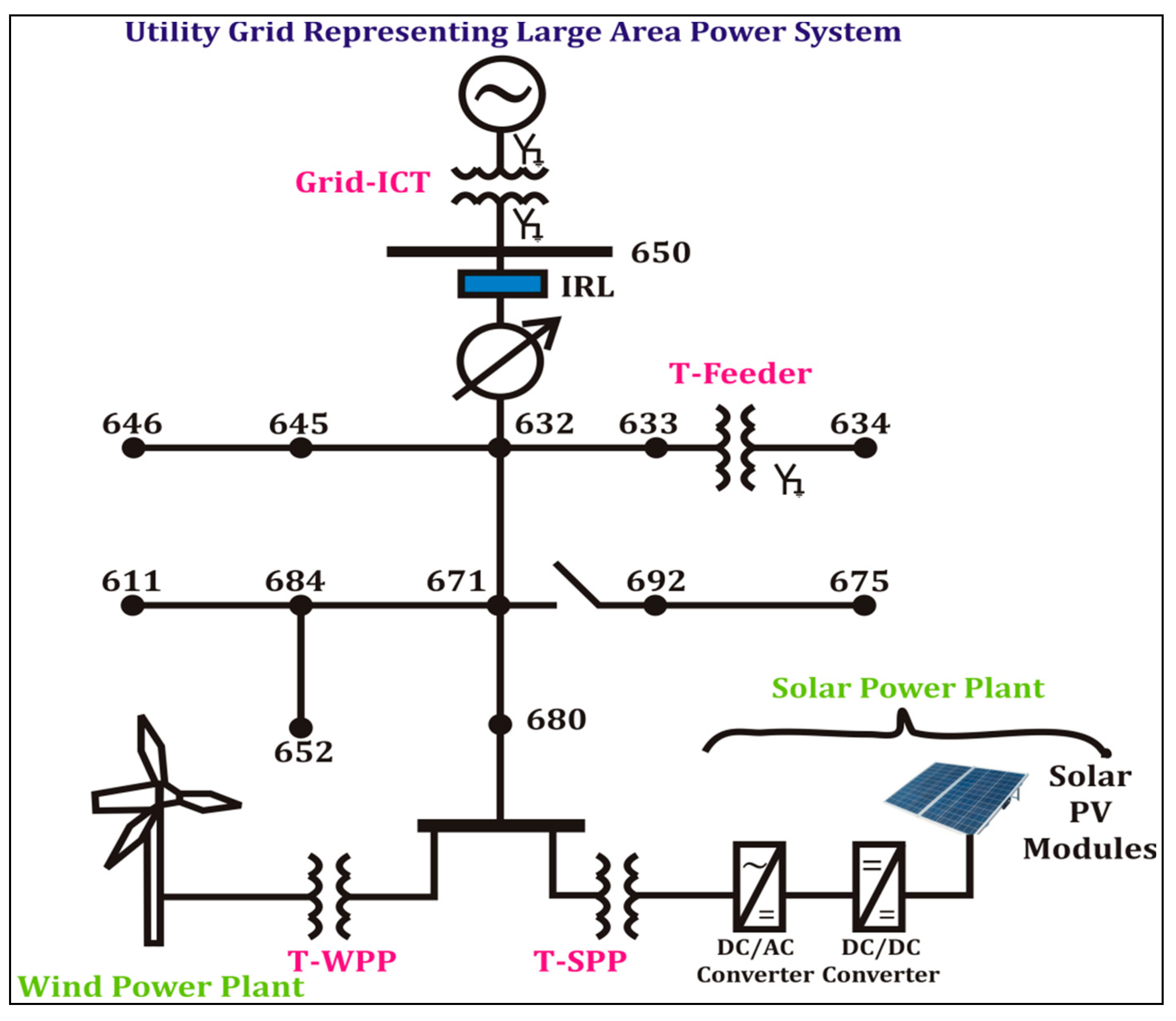
2. Test Grid of IEEE-13 Nodes
2.1. Solar PV System
2.2. Wind Power Plant
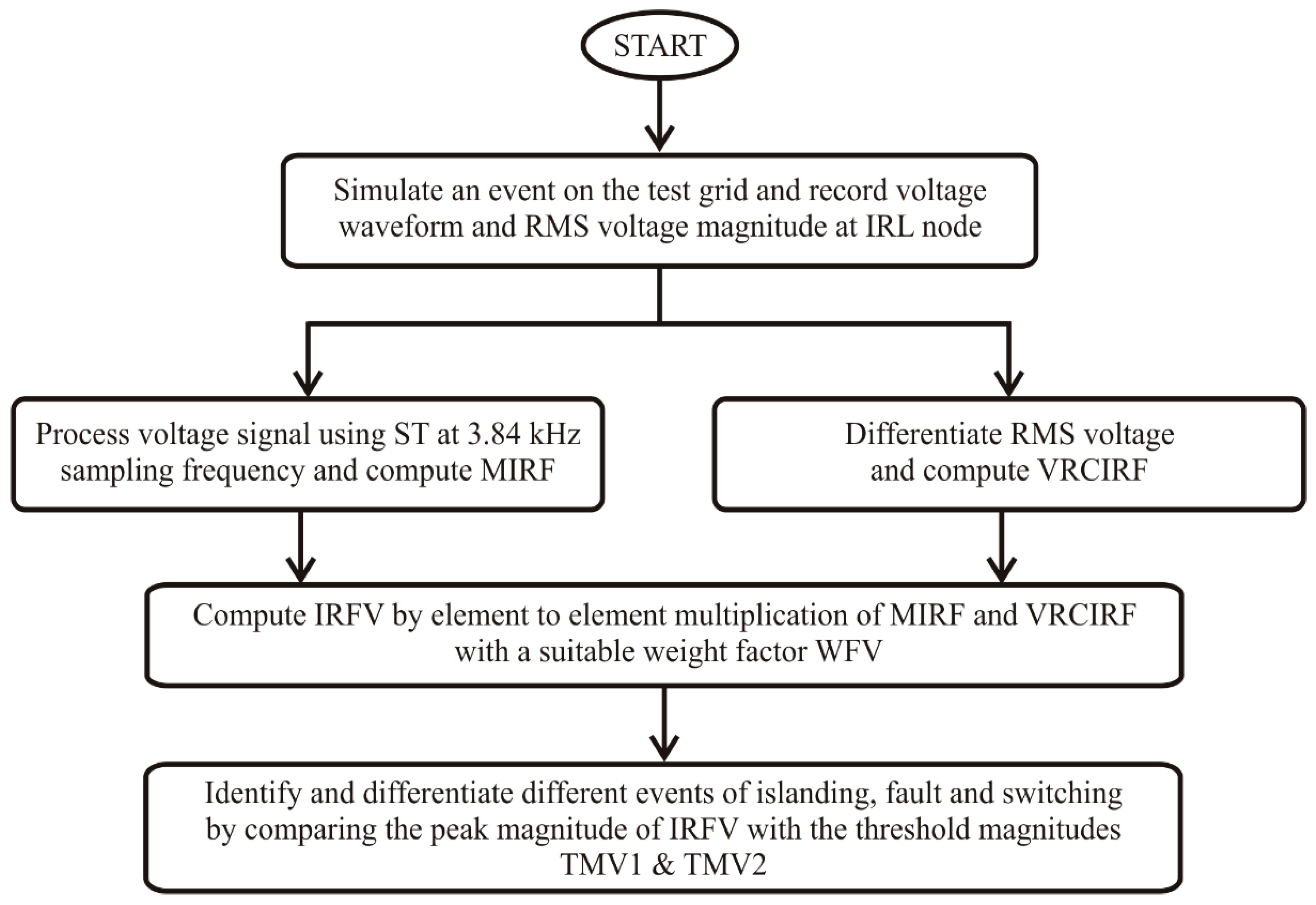
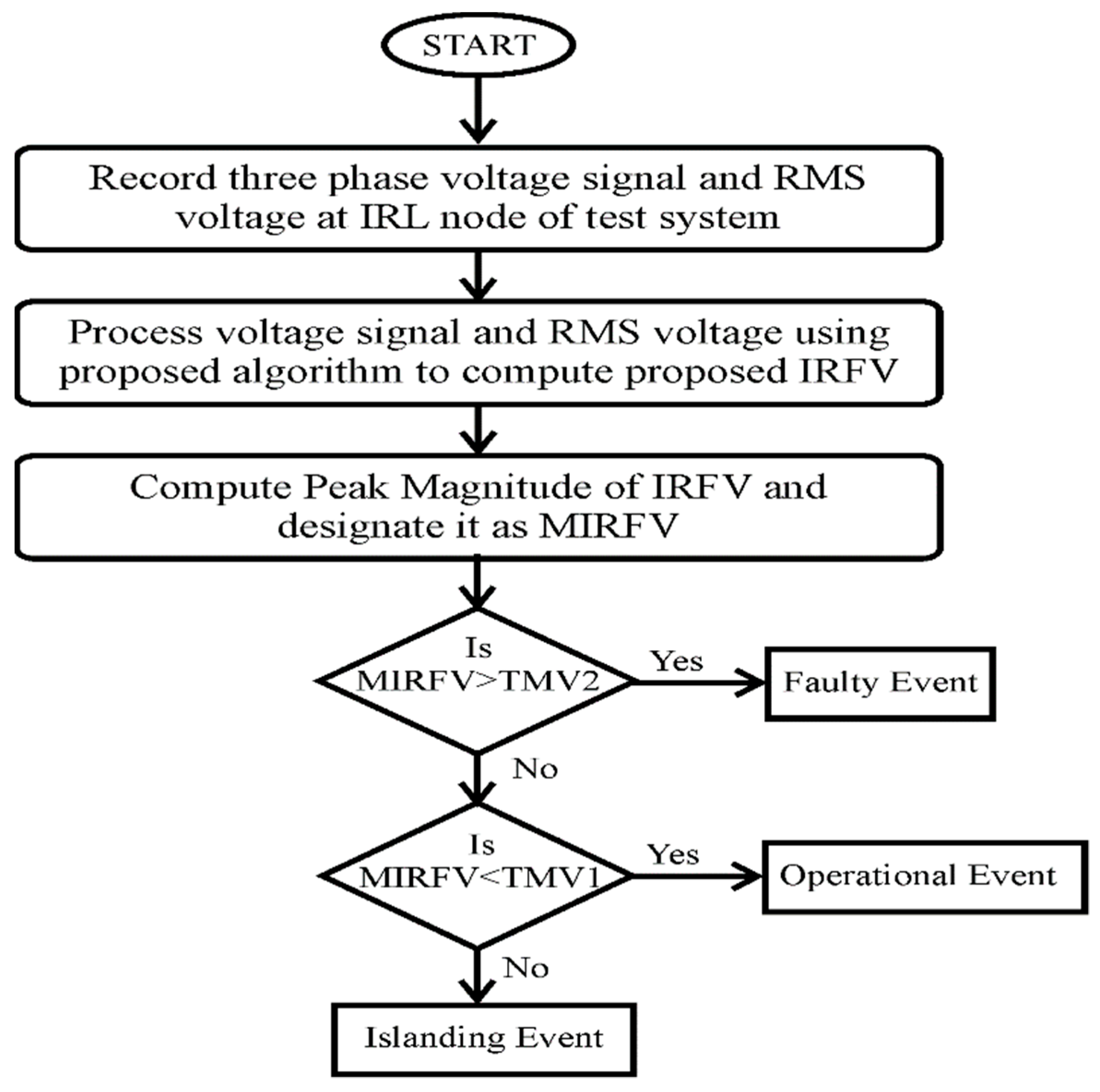
3. Proposed Voltage-Based Algorithm for Identification of Islanding Events
- Record the voltage waveform and root mean square (RMS) values of the voltage (VR) at IRL node.
- Decompose the voltage signal using Stockwell transform at a sampling frequency of 3.84 kHz and designate the output matrix as SV. Equation (7) described in Section 3.1 is used to compute SV. Detailed mathematical formulation of Stockwell transform are reported in [22,23,24].
- Compute the median of the columns of the matrix SV and assigned symbol median-based islanding recognition factor (MIRF), which is defined in the Equation (2).
- Compute the rate of change in RMS voltage (ROCOV) and assign the symbol voltage rate of change in islanding recognition factor (VRCIRF). This is achieved by differentiating the voltage signal with respect to time. VRCIRF is defined in the Equation (3).
- Compute the voltage-based islanding recognition factor (IRFV) by multiplying the MIRF and VRCIRF element to element, as detailed below. Here, WFV is the voltage-based weight factor. WFV is considered equal to the 1000 for this study.
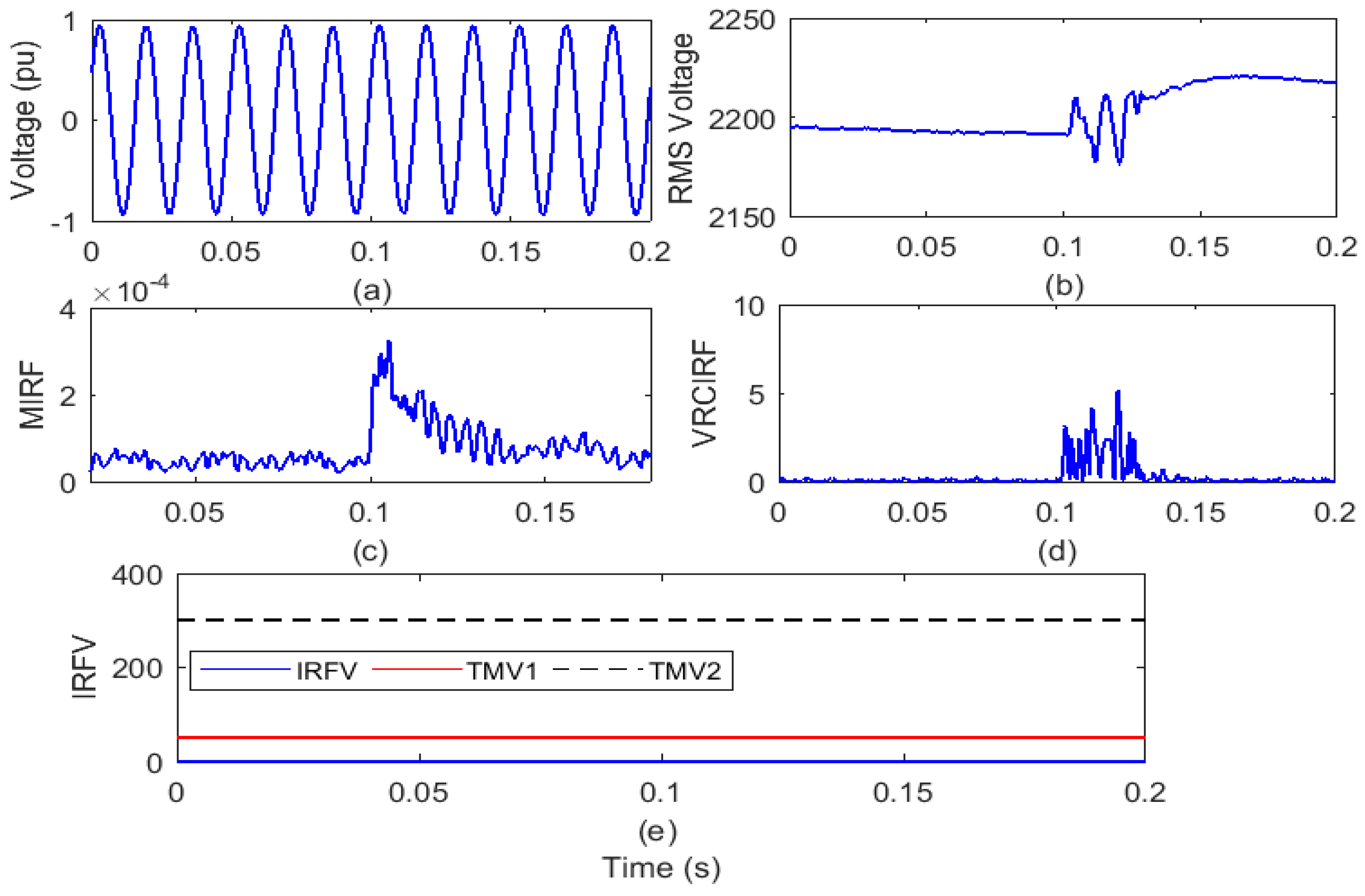
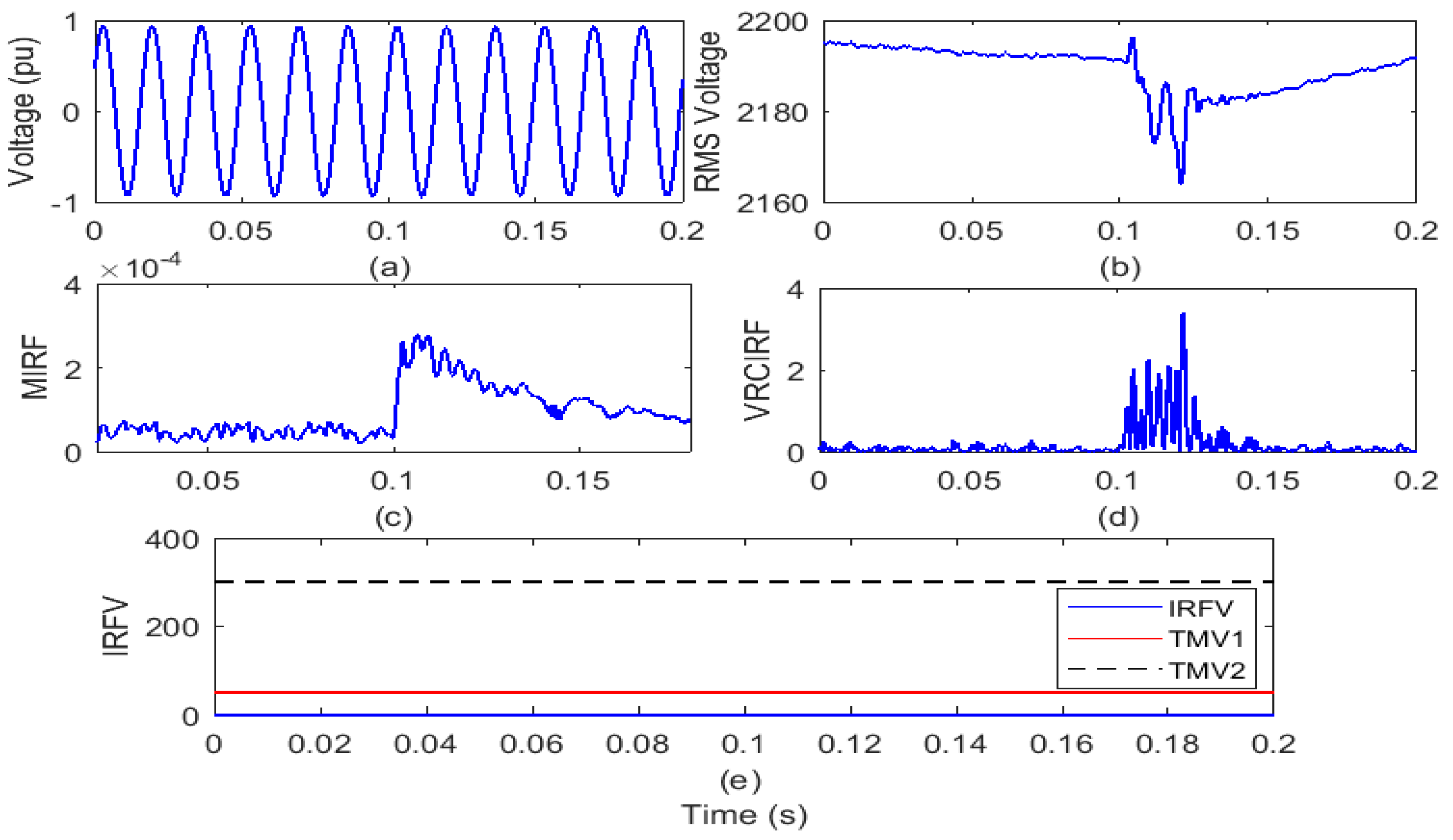
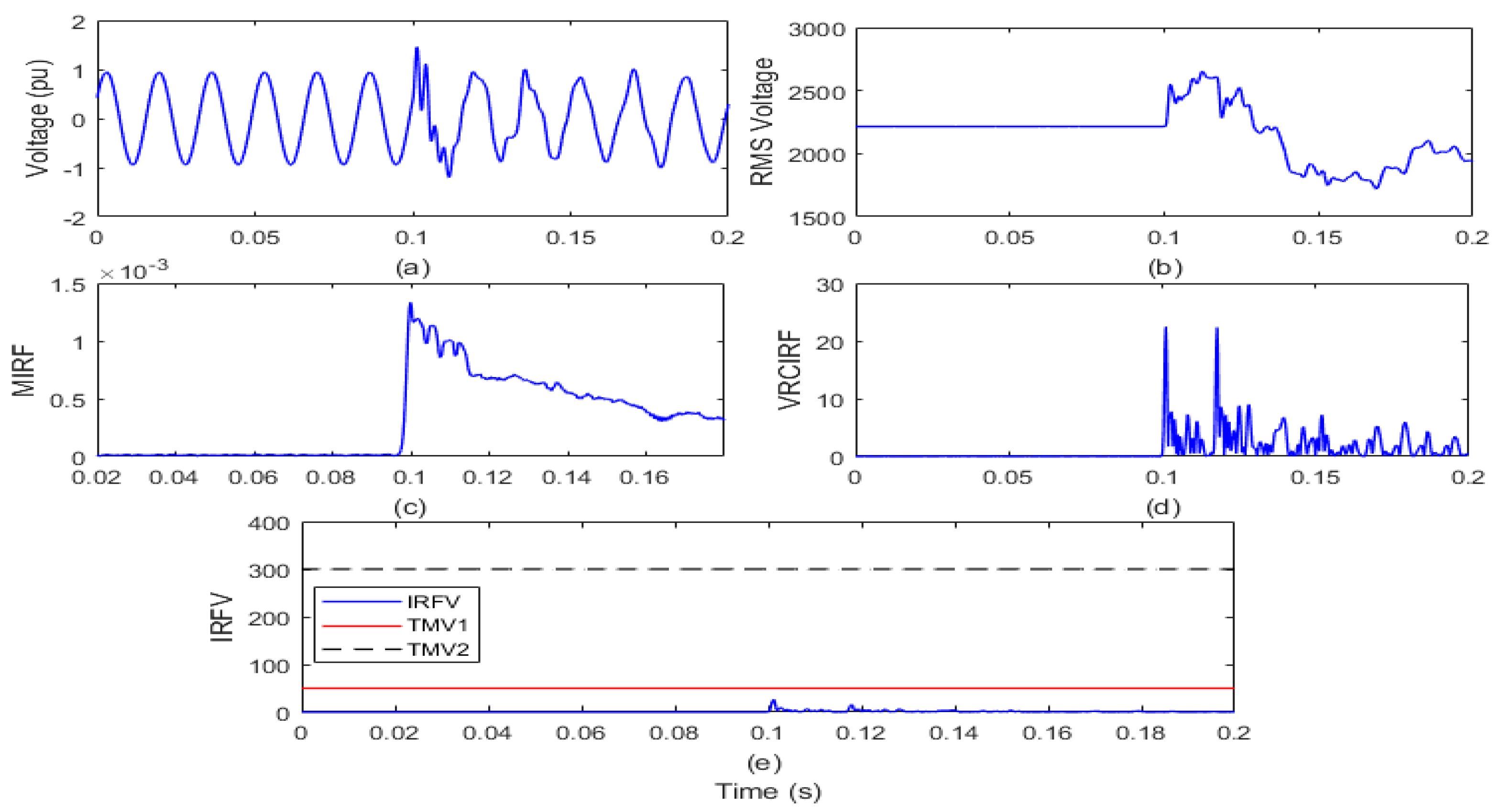
- Set the threshold magnitudes TMV1 and TMV2 equal to 50 and 300, respectively, for the IRFV. If peak magnitude of IRFV is less than TMV1, then the event is an operational event. For peak magnitudes of IRFV between the TMV1 and TMV2, the event is islanding. However, if the peak magnitude of IRFV is greater than the TMV2 then the event is faulty in nature.
3.1. Stockwell Transform
3.2. Decision Tree Rules
4. Results and Discussion
4.1. Healthy Condition without Any Disturbance
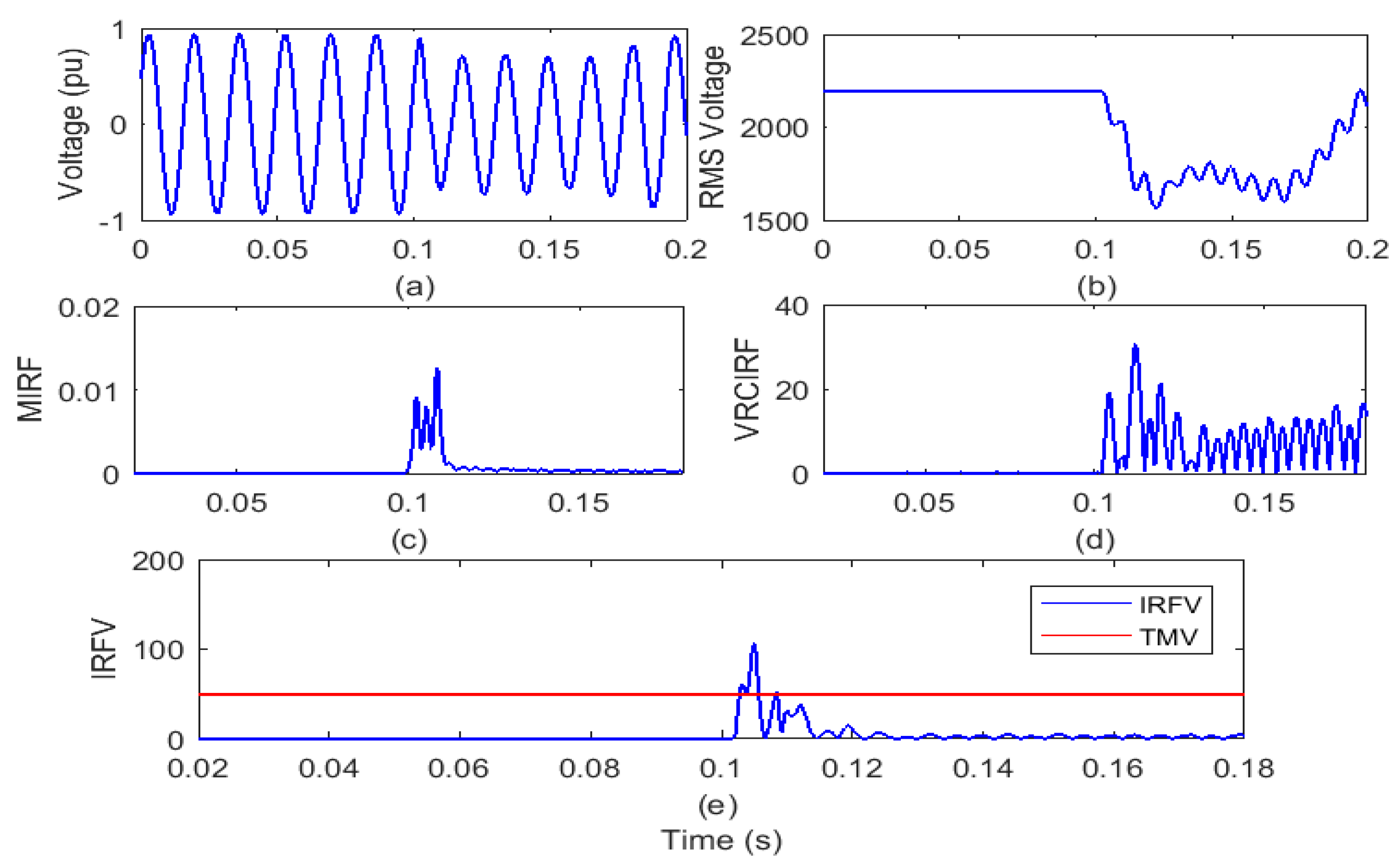
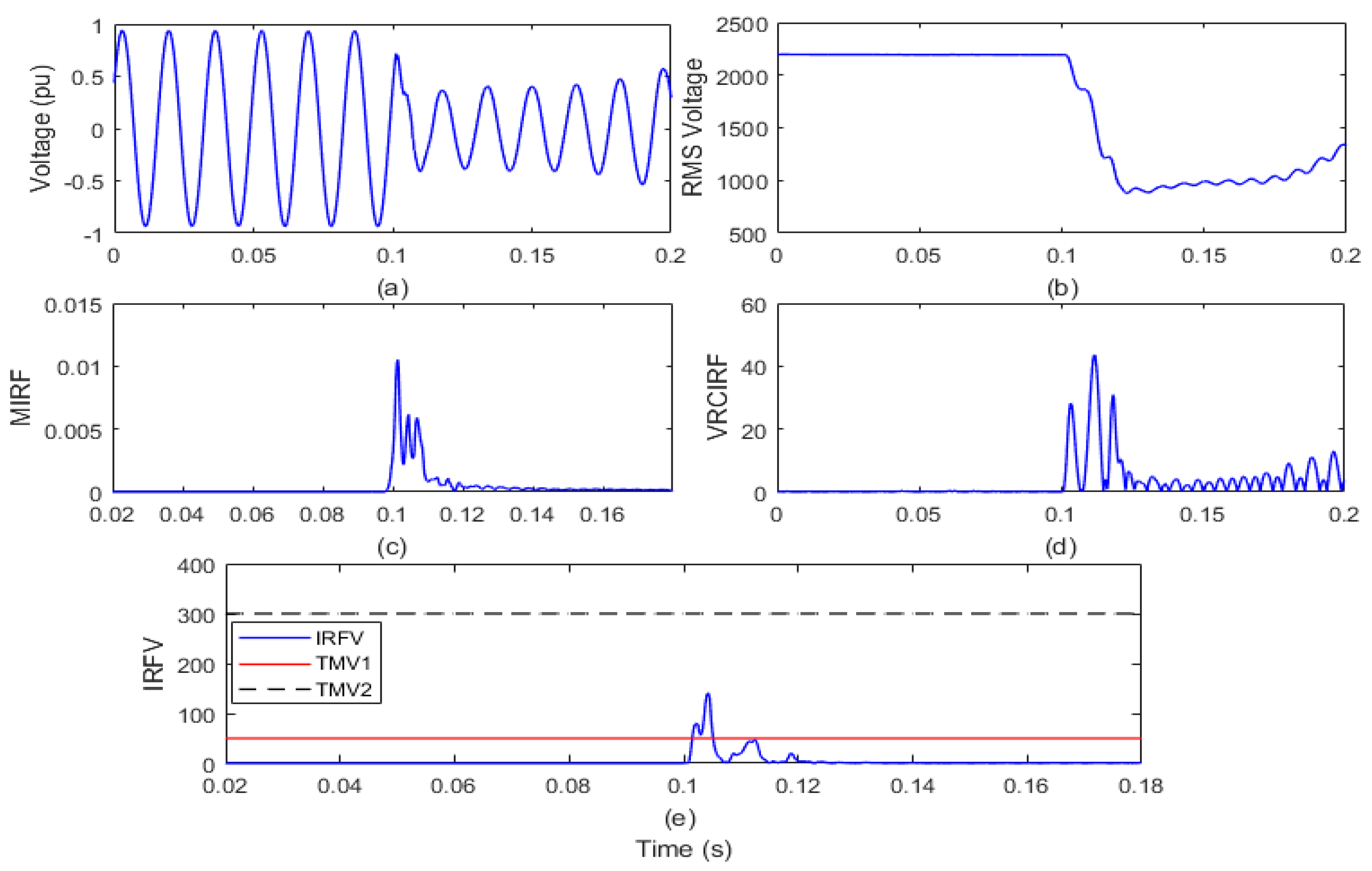
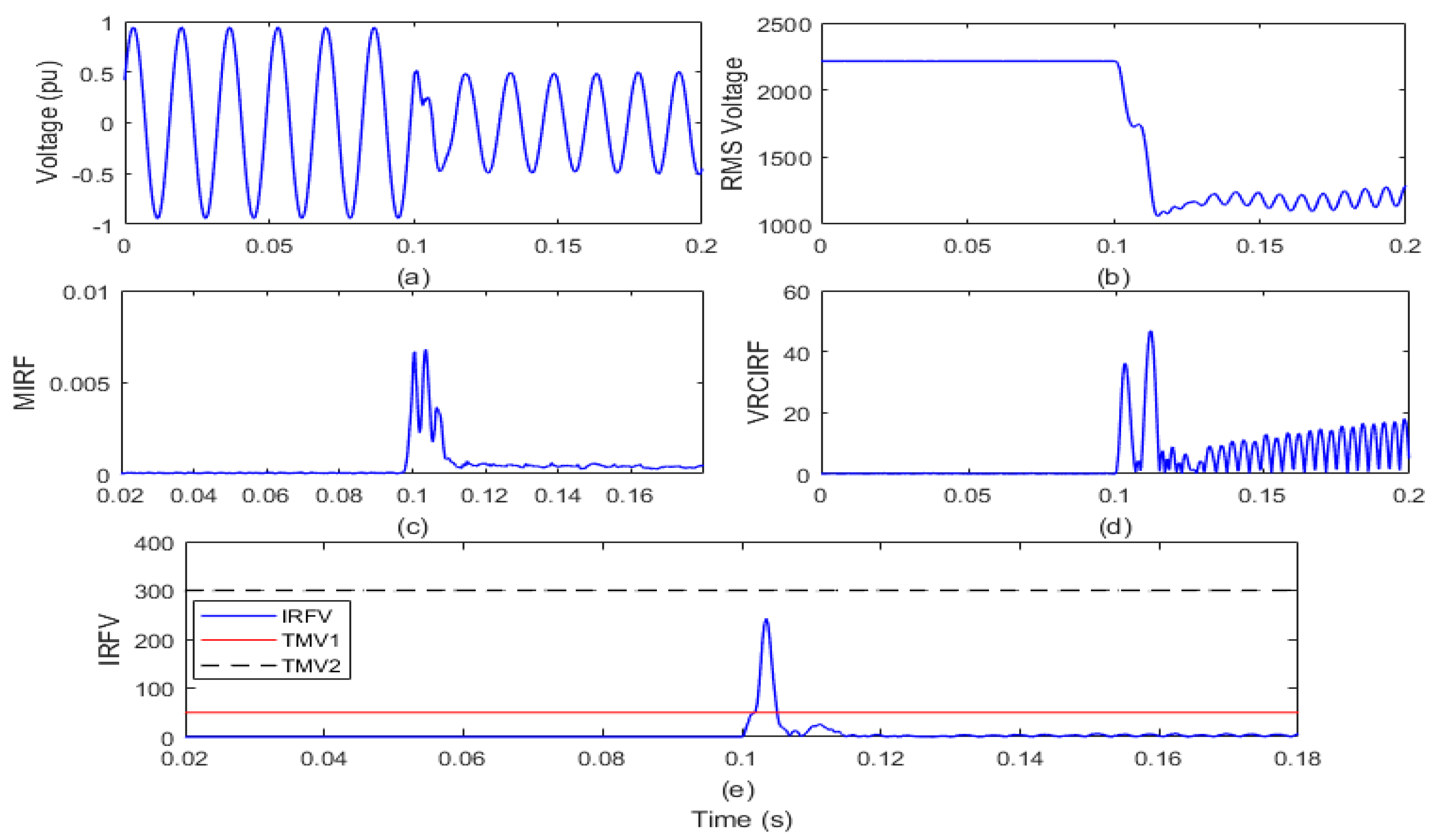
4.2. Recognition of Islanding Events
4.2.1. Islanding with Wind and Solar Energy Production
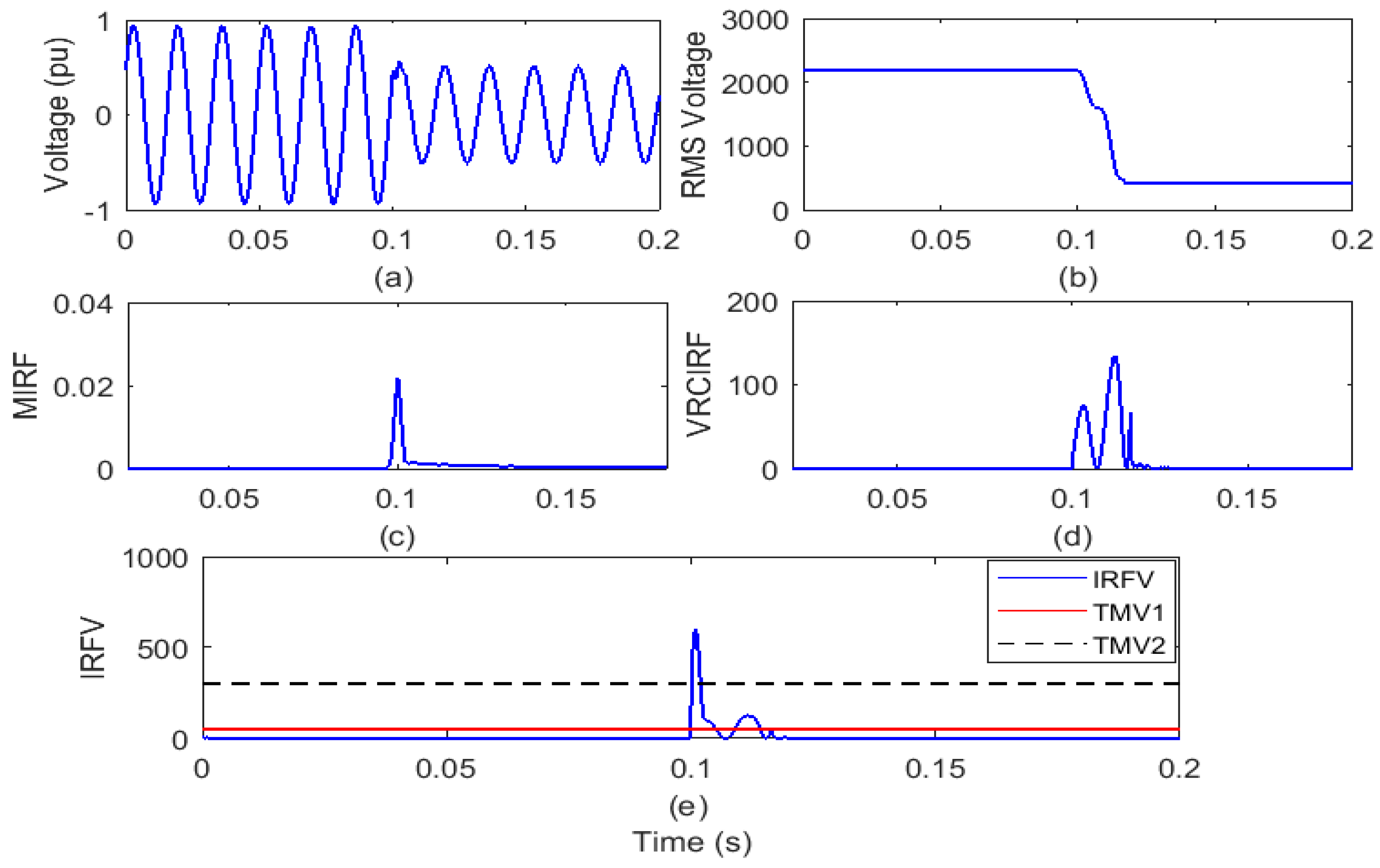
4.2.2. Islanding with Wind Energy Production
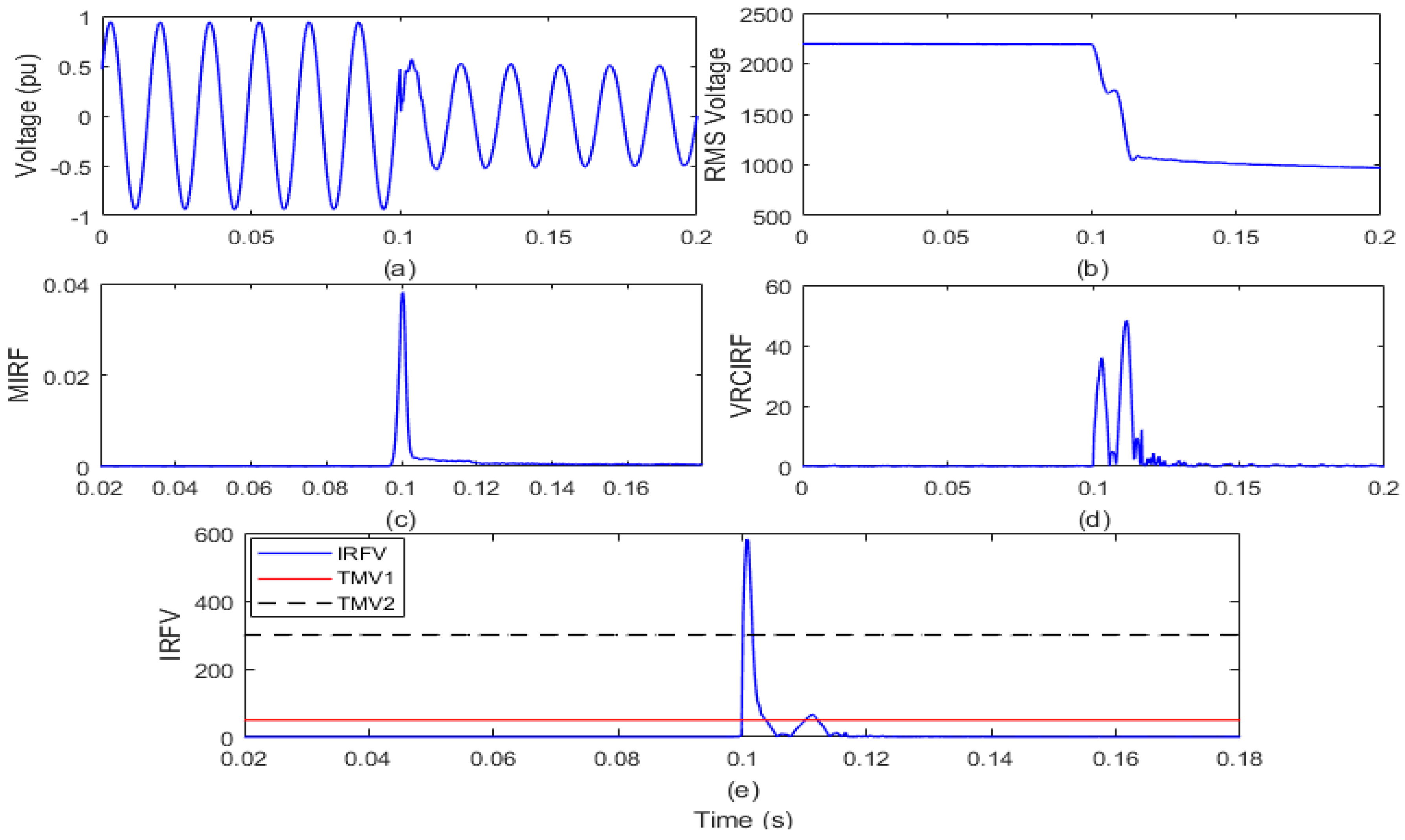
4.2.3. Islanding with Solar Energy Production
4.3. Faulty Events
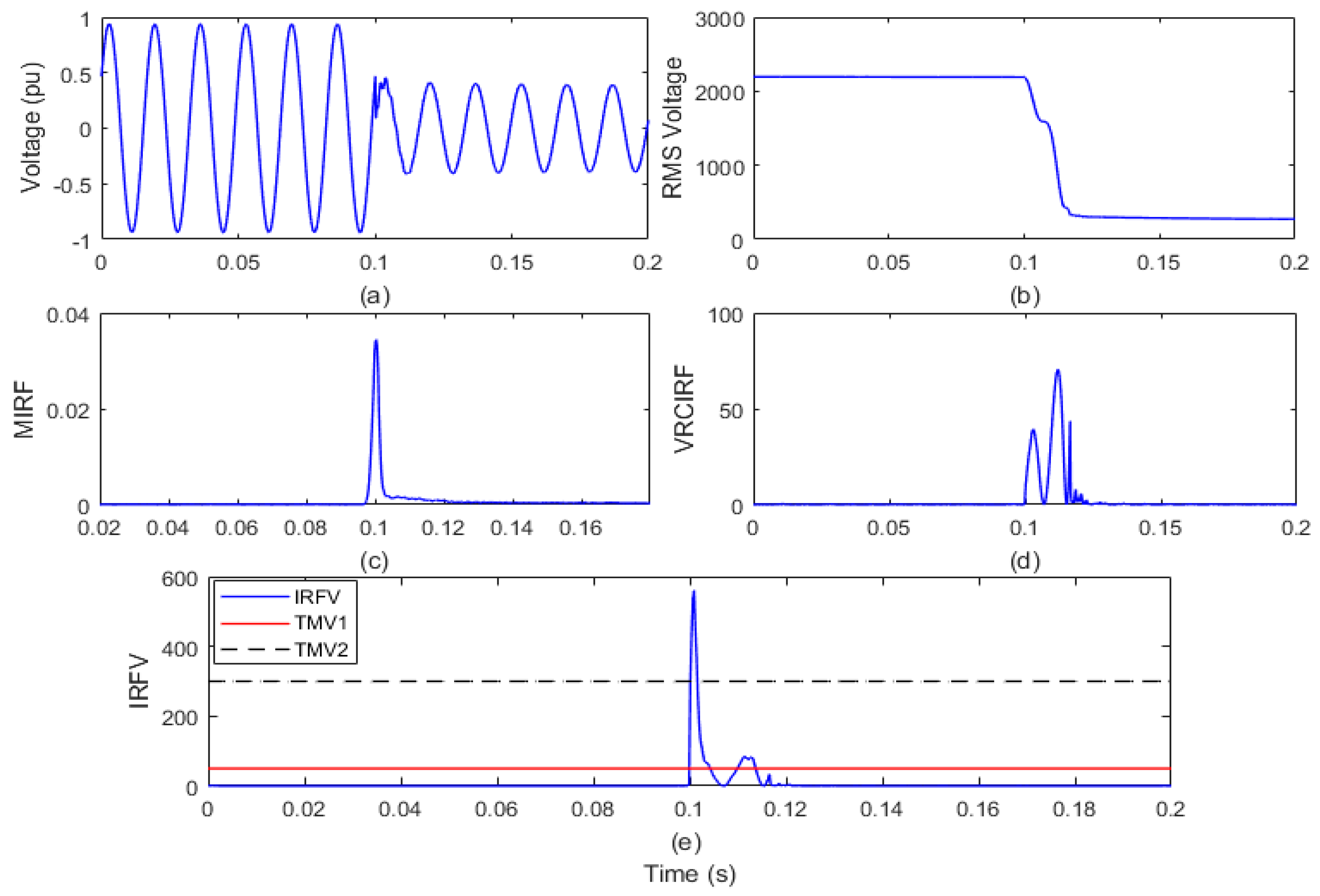
4.3.1. Single-Phase-to-Ground Fault
4.3.2. Two-Phase Fault
4.3.3. Two-Phase-to-Ground Fault
4.3.4. Three-Phase Fault with Ground
4.4. Operational Events
4.4.1. Outage of Wind Power Plant from Test Grid
4.4.2. Outage of Solar Power Plant from Test Grid
4.4.3. Synchronization of SPP to Grid
4.4.4. Synchronization of WPP to Grid
4.4.5. Feeder Operation
4.4.6. Capacitor Switching
4.4.7. Load Switching
5. Identification of Non-Detection Zone
6. Classification of Events
7. Performance Comparison of Algorithm
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xie, X.; Huang, C.; Li, D. A new passive islanding detection approach considering the dynamic behaviour of load in micro-grid. Electr. Power Energy Syst. 2020, 117, 105619. [Google Scholar] [CrossRef]
- Paiva, S.C.; de Araujo Ribeiro, R.L.; Alves, D.K.; Costa, F.B.; Rocha, T.D. A wavelet-based hybrid islanding detection system applied for distributed generators interconnected to AC microgrids. Electr. Power Energy Syst. 2020, 121, 106032. [Google Scholar] [CrossRef]
- Tsang, K.M.; Chan, W.L. Rapid islanding detection using multi-level inverter for grid-interactive PV system. Energy Convers. Manag. 2014, 77, 278–286. [Google Scholar] [CrossRef]
- Kolli, A.T.; Ghaffarzadeh, N. A novel phaselet-based approach for islanding detection in inverter-based distributed generation systems. Electr. Power Syst. Res. 2020, 182, 106226. [Google Scholar] [CrossRef]
- Ahmad, K.N.; Selvaraj, J.; Abd Rahim, N. A review of the islanding detection methods in grid-connected PV inverters. Renew. Sustain. Energy Rev. 2013, 21, 756–766. [Google Scholar] [CrossRef]
- Kaushik, R.; Mahela, O.P.; Bhatt, P.K.; Khan, B.; Garg, A.R.; Alhelou, H.H.; Siano, P. Recognition of Islanding and Operational Events in Power System with Renewable Energy Penetration Using a Stockwell Transform Based Method. IEEE Syst. J. 2020, 1–10. [Google Scholar] [CrossRef]
- Mahela, O.P.; Heydarian-Forushani, E.; Alhelou, H.H.; Khan, B.; Garg, A.R.; Al-Sumaiti, A.S. Combined Stockwell and Hilbert Transforms Based Technique for the Detection of Islanding Events in Hybrid Power System. In Proceedings of the 46th Annual Conference of the IEEE Industrial Electronics Society (IES), IECON 2020, Singapore, 18–21 October 2020. [Google Scholar] [CrossRef]
- Mahela, O.P.; Gupta, R.; Khan, B.; Sanjeevikumar, P.; Leonowicz, Z.; Choudhary, S.; Alhelou, H.H. A Voltage Based Algorithm Using Combined Features of Stockwell Transform and Hilbert Transform for Detection of Islanding Events. In Proceedings of the 2020 IEEE International Conference on Environment and Electrical Engineering, Madrid, Spain, 9–12 June 2020. [Google Scholar]
- Ahmadipour, M.; Hizam, H.; Othman, M.L.; Radzi, M.A.; Chireh, N. A novel islanding detection technique using modified Slantlet transform in multi-distributed generation. Int. J. Electr. Power Energy Syst. 2019, 112, 460–475. [Google Scholar] [CrossRef]
- Ahmadipour, M.; Hizam, H.; Othman, M.L.; Radzi, M.A.; Murthy, A.S. Islanding detection technique using Slantlet Transform and Ridgelet Probabilistic Neural Network in grid-connected photovoltaic system. Appl. Energy 2018, 231, 645–659. [Google Scholar] [CrossRef]
- Admasie, S.; Bukhari, S.B.; Haider, R.; Gush, T.; Kim, C.H. A passive islanding detection scheme using variational mode decomposition based mode singular entropy for integrated microgrids. Electr. Power Syst. Res. 2019, 177, 105983. [Google Scholar] [CrossRef]
- Omar, A.I.; Aleem, S.H.; El-Zahab, E.E.; Algablawy, M.; Ali, Z.M. An improved approach for robust control of dynamic voltage restorer and power quality enhancement using grasshopper optimization algorithm. ISA Trans. 2019, 95, 110–129. [Google Scholar] [CrossRef]
- Gandoman, F.H.; Sharaf, A.M.; Abdel Aleem, S.H.; Jurado, F. Distributed FACTS stabilization scheme for efficient utilization of distributed wind energy systems. Int. Trans. Electr. Energy Syst. 2017, 27, e2391. [Google Scholar] [CrossRef]
- Kulshrestha, A.; Mahela, O.P.; Gupta, M.K.; Gupta, N.; Patel, N.; Senjyu, T.; Danish, M.S.; Khosravy, M. A Hybrid Protection Scheme Using Stockwell Transform and Wigner Distribution Function for Power System Network with Solar Energy Penetration. Energies 2020, 13, 3519. [Google Scholar] [CrossRef]
- Shaik, A.G.; Mahela, O.P. Power quality assessment and event detection in hybrid power system. Electr. Power Syst. Res. 2018, 161, 26–44. [Google Scholar] [CrossRef]
- Mahela, O.P.; Shaik, A.G. Power Quality Improvement in Distribution Network using DSTATCOM with Battery Energy Storage System. Int. J. Electr. Power Energy Syst. 2016, 83, 229–240. [Google Scholar] [CrossRef]
- Mahela, O.P.; Shaik, A.G. Power Quality Recognition in Distribution System with Solar Energy Penetration Using S-Transform and Fuzzy C-Means Clustering. Renew. Energy 2017, 106, 37–51. [Google Scholar] [CrossRef]
- Mahela, O.P.; Shaik, A.G. Comprehensive Overview of Grid Interfaced Solar Photovoltaic Systems. Renew. Sustain. Energy Rev. 2017, 68, 316–332. [Google Scholar] [CrossRef]
- Mahela, O.P.; Shaik, A.G. Detection of power quality disturbances associated with grid integration of 100 kW solar PV plant. In Proceedings of the 1st IEEE Uttar Pradesh Conference-International Conference on Energy Economics and Environment (ICEEE 2015), Galgotia Institute of Engineering and Technology, Noida, India, 27–28 March 2015. [Google Scholar] [CrossRef]
- Mahela, O.P.; Shaik, A.G. Comprehensive Overview of Grid Interfaced Wind Energy Generation Systems. Renew. Sustain. Energy Rev. 2016, 57, 260–281. [Google Scholar] [CrossRef]
- Mahela, O.P.; Shaik, A.G. Power quality detection in distribution system with wind energy penetration using discrete wavelet transform. In Proceedings of the 2nd IEEE International Conference on Advances in Computing and Communication Engineering (ICACCE-2015), Dehradun, India, 1–2 May 2015. [Google Scholar] [CrossRef]
- Mahela, O.P.; Khan, B.; Alhelou, H.H.; Siano, P. Power Quality Assessment and Event Detection in Distribution Network with Wind Energy Penetration Using Stockwell Transform and Fuzzy Clustering. IEEE Trans. Ind. Inform. 2020, 16, 6922–6932. [Google Scholar] [CrossRef]
- Mahela, O.P.; Shaik, A.G.; Khan, B.; Mahla, R.; Alhelou, H.H. Recognition of Complex Power Quality Disturbances Using S-Transform Based Ruled Decision Tree. IEEE Access 2020, 8, 173530–173547. [Google Scholar] [CrossRef]
- Mahela, O.P.; Shaik, A.G. Recognition of Power Quality Disturbances Using S-Transform Based Ruled Decision Tree and Fuzzy C-Means Clustering Classifiers. Appl. Soft Comput. 2017, 59, 243–257. [Google Scholar] [CrossRef]
- Mahela, O.P.; Shaik, A.G.; Gupta, N.; Khosravy, M.; Khan, B.; Alhelou, H.H.; Padmanaban, S. Recognition of the Power Quality Issues Associated with Grid Integrated solar Photovoltaic Plant in Experimental Frame Work. IEEE Syst. J. Early Access 2020, 1–9. [Google Scholar] [CrossRef]
- Mahela, O.P.; Khan, B.; Alhelou, H.H.; Tanwar, S. Assessment of Power Quality in the Utility Grid Integrated with Wind Energy Generation. IET Power Electron. 2020, 13, 2917–2925. [Google Scholar] [CrossRef]
- Samet, H.; Hashemi, F.; Ghanbari, T. Minimum non detection zone for islanding detection using an optimal artificial neural network algorithm based on PSO. Renew. Sustain. Energy Rev. 2015, 52, 1–18. [Google Scholar] [CrossRef]
- Quoc-Tuan, T. New Methods of Islanding Detection for Photovoltaic Inverters. In Proceedings of the 2016 IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT-Europe), Ljubljana, Slovenia, 9–12 October 2016. [Google Scholar]
- Sharma, R.; Singh, P. Islanding Detection and Control in Grid Based System Using Wavelet Transform. In Proceedings of the 2012 IEEE Fifth Power India Conference, Murthal, India, 19–22 December 2012. [Google Scholar]






| Nodes of Test Distribution Grid | Load Connected at Various Nodes of Test Distribution Grid | Capacitor Banks at Various Nodes of Test Distribution Grid (kVAr) | |
|---|---|---|---|
| kW | kVAr | ||
| 634 | 400 | 290 | |
| 645 | 170 | 125 | |
| 646 | 230 | 132 | |
| 652 | 128 | 86 | |
| 671 | 1155 | 660 | |
| 675 | 843 | 462 | 600 |
| 692 | 170 | 151 | |
| 611 | 170 | 80 | 100 |
| 632–671 | 200 | 116 | |
| 680 | |||
| 650 | |||
| Transformer | Transformer MVA Rating | kV-HV Winding Transformer | kV-LV Winding Transformer | HV Winding | LV Winding | ||
|---|---|---|---|---|---|---|---|
| R (Ω) | X (Ω) | R (Ω) | X (Ω) | ||||
| Grid-ICT | 10 | 115 | 4.16 | 29.095 | 211.60 | 0.1142 | 0.8306 |
| T-Feeder | 5 | 4.16 | 0.48 | 0.011 | 3.0159 | 0.011 | 3.0159 |
| T-WPP | 5 | 4.16 | 0.575 | 0.3807 | 2.7688 | 0.0510 | 0.0042 |
| T-SPP | 5 | 4.16 | 0.260 | 0.001 | 1.1310 | 0.001 | 1.1310 |
| ΔP (kW) | Voltage (pu) | |||||||
|---|---|---|---|---|---|---|---|---|
| 0.88 | 0.90 | 0.92 | 0.94 | 0.96 | 0.98 | 1.0 | 1.1 | |
| −10 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| −8 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| −6 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 |
| −4 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| −2 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 4 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| 6 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 |
| 8 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 10 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 12 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| S. No. | Type of Event | Peak Magnitude of IRFV |
|---|---|---|
| 1 | Healthy condition without any disturbance. | 0.03 |
| 2 | Islanding event in the presence of both wind and solar power generation. | 105.04 |
| 3 | Islanding event in the presence of wind power generation. | 141.63 |
| 4 | Islanding event in the presence of solar power generation. | 242.60 |
| 5 | Single-phase-to-ground fault. | 598.12 |
| 6 | Two-phase fault. | 587.70 |
| 7 | Two-phase-to-ground fault. | 561.05 |
| 8 | Three-phase fault with ground. | 399.40 |
| 9 | Outage of wind power plant. | 2.09 |
| 10 | Outage of solar power plant. | 3.14 |
| 11 | Synchronization of SPP. | 32.81 |
| 12 | Synchronization of WPP. | 26.49 |
| 13 | Feeder operation. | 23.15 |
| 14 | Capacitor switching. | 33.25 |
| 15 | Load switching. | 0.351 |
| S. No. | Attribute | Reference [24] | Reference [25] | Proposed IDM |
|---|---|---|---|---|
| 1 | Islanding detection time. | SI | SI | SI |
| 2 | Non-detection zone. | SI | SNI | SI |
| 3 | Effect of noise. | SNI | SNI | SI |
| 4 | Differentiation of islanding events from faulty conditions. | SNI | SNI | SI |
| 5 | Differentiation of islanding events from switching events. | SNI | SNI | SI |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahela, O.P.; Sharma, Y.; Ali, S.; Khan, B.; Garg, A.R. Voltage-Based Hybrid Algorithm Using Parameter Variations and Stockwell Transform for Islanding Detection in Utility Grids. Informatics 2021, 8, 21. https://0-doi-org.brum.beds.ac.uk/10.3390/informatics8020021
Mahela OP, Sharma Y, Ali S, Khan B, Garg AR. Voltage-Based Hybrid Algorithm Using Parameter Variations and Stockwell Transform for Islanding Detection in Utility Grids. Informatics. 2021; 8(2):21. https://0-doi-org.brum.beds.ac.uk/10.3390/informatics8020021
Chicago/Turabian StyleMahela, Om Prakash, Yagya Sharma, Shoyab Ali, Baseem Khan, and Akhil Ranjan Garg. 2021. "Voltage-Based Hybrid Algorithm Using Parameter Variations and Stockwell Transform for Islanding Detection in Utility Grids" Informatics 8, no. 2: 21. https://0-doi-org.brum.beds.ac.uk/10.3390/informatics8020021







