Multiphase Open Phase Processes Differential Equations
Abstract
:1. Introduction
- -
- To test corresponding experimental data, concerning phase equilibrium diagrams and open phase processes diagrams; and
- -
- To predict phase equilibrium diagrams and open phase processes diagrams in multicomponent systems, using modeling parameters of non-ideality, determined later from available experimental data in binary and rarely in ternary subsystems.
- -
- Generalized differential equation of phase equilibrium shifts (van der Waals Equation in Vector-Matrix Form) in the metrics of Gibbs and incomplete Gibbs potentials;
- -
- Differential equations of the open phase processes for two phase and multiphase equilibrium;
- -
- Differential equations of open phase processes in isothermal, isobaric and isothermo-isobaric conditions;
- -
- Non-extreme properties of the driving force parameters in the open phase processes; and
- -
- Some examples of thermodynamic semi-empirical modeling, based on the numerical integration of differential equations of open phase processes in multicomponent semiconductor A3-B5 and water–salt systems.
2. Generalized Differential Equation of Phase Equilibrium Shifts (Van Der Waals Equation in Vector-Matrix Form)
2.1. Metric of Gibbs Potential
2.2. Metric of Incomplete Gibbs Potential (Korjinskiy Potential)
2.3. Multiphase Equilibria
3. Differential Equations of the Open Phase Processes
3.1. Two-Phase Processes
3.2. Multiphase Processes
4. Hybrid Differential Equations for Open Phase Processes
4.1. Two-Phase Systems
4.2. Multiphase Systems
5. Open Phase Processes in Isothermal, Isobaric and Isothermo-Isobaric Conditions
5.1. Isobaric Conditions
5.2. Isothermal Conditions
5.3. Isothermo-Isobaric Conditions
5.4. Properties of the Driving Force Parameters in the Open Phase Processes
6. Examples of Thermodynamic Modeling
- -
- -
- -
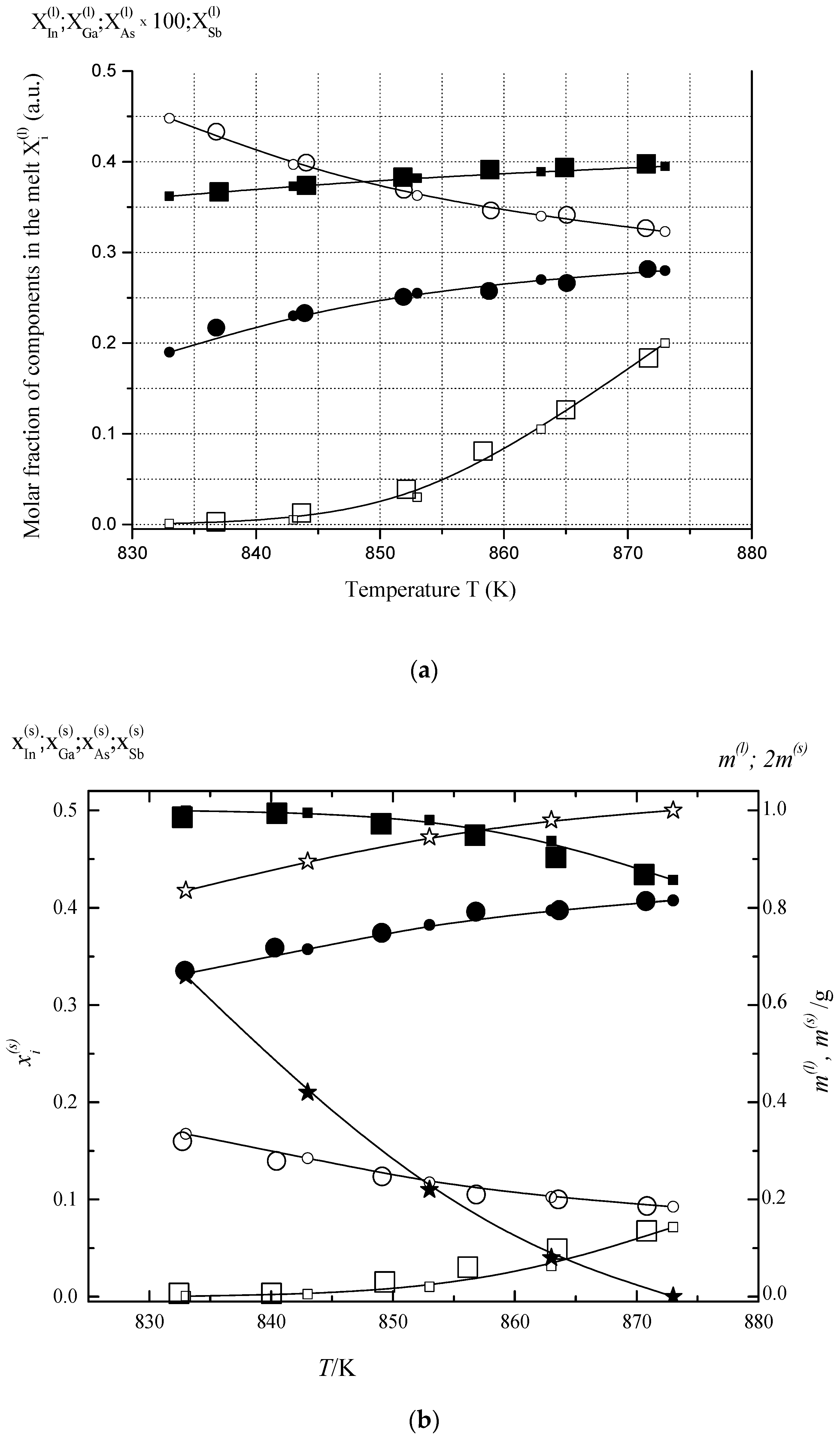
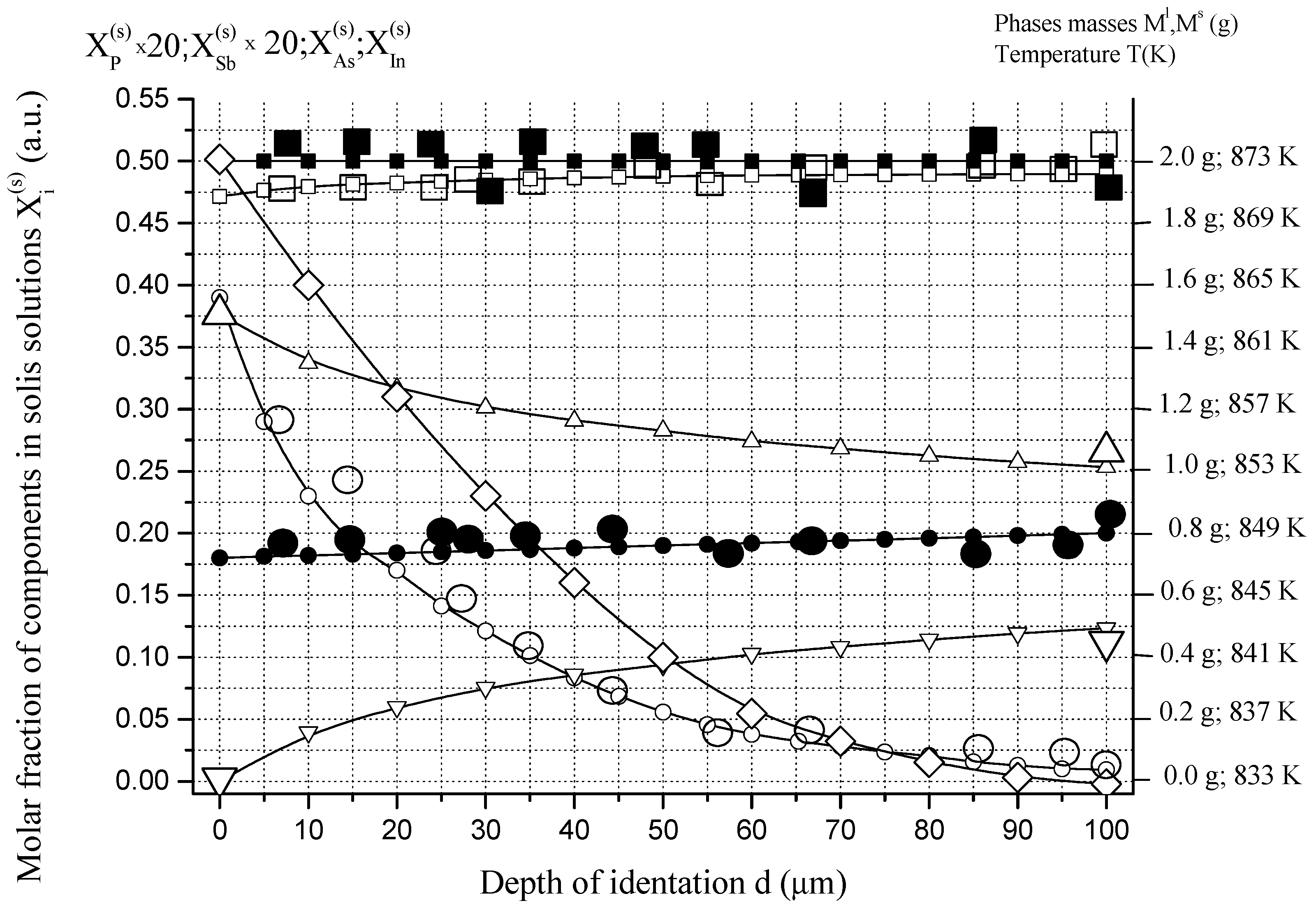
6.1. Two-Phase Open Crystallization in the In-Ga-As-Sb and In-P-As-Sb Systems at Temperature Decrease
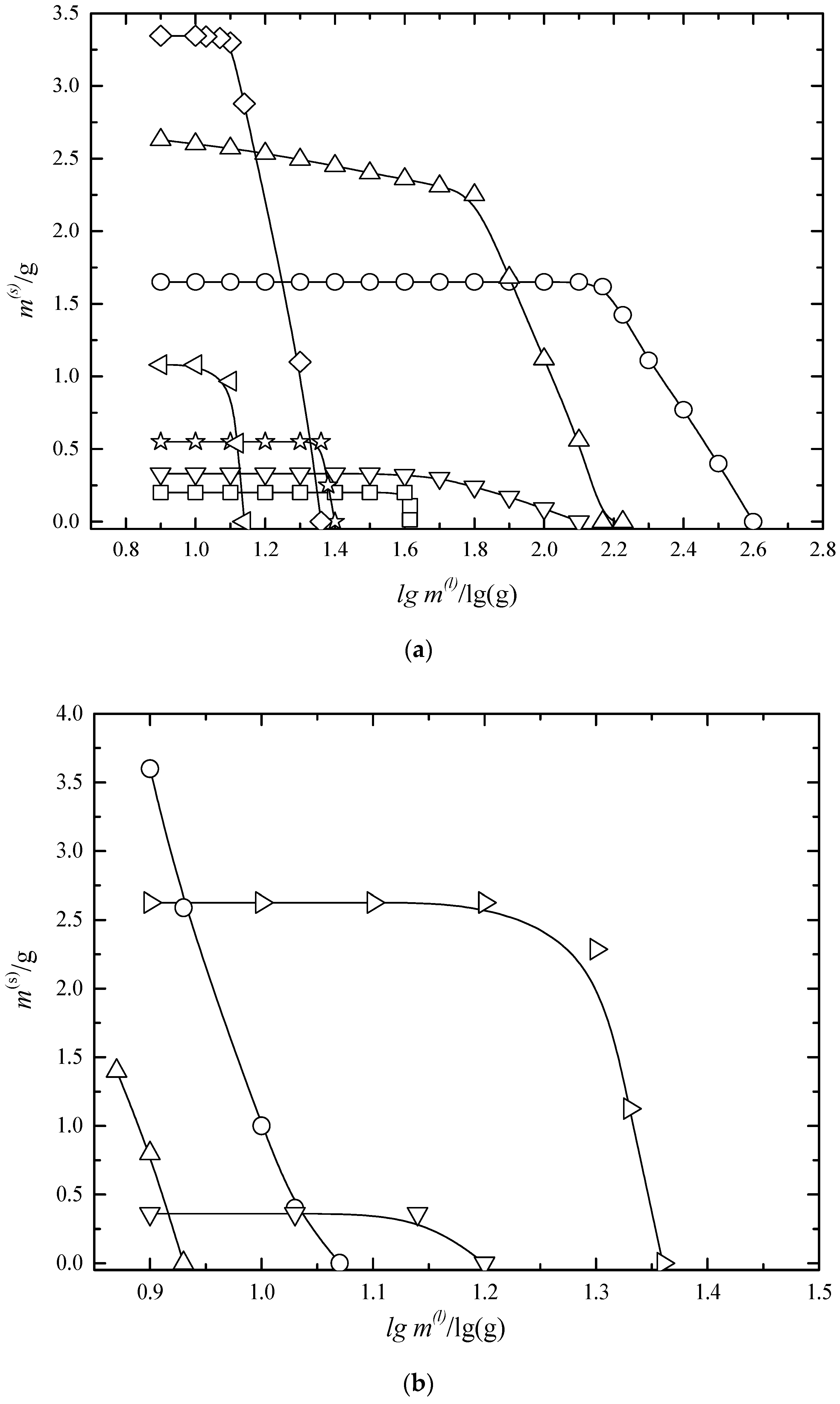
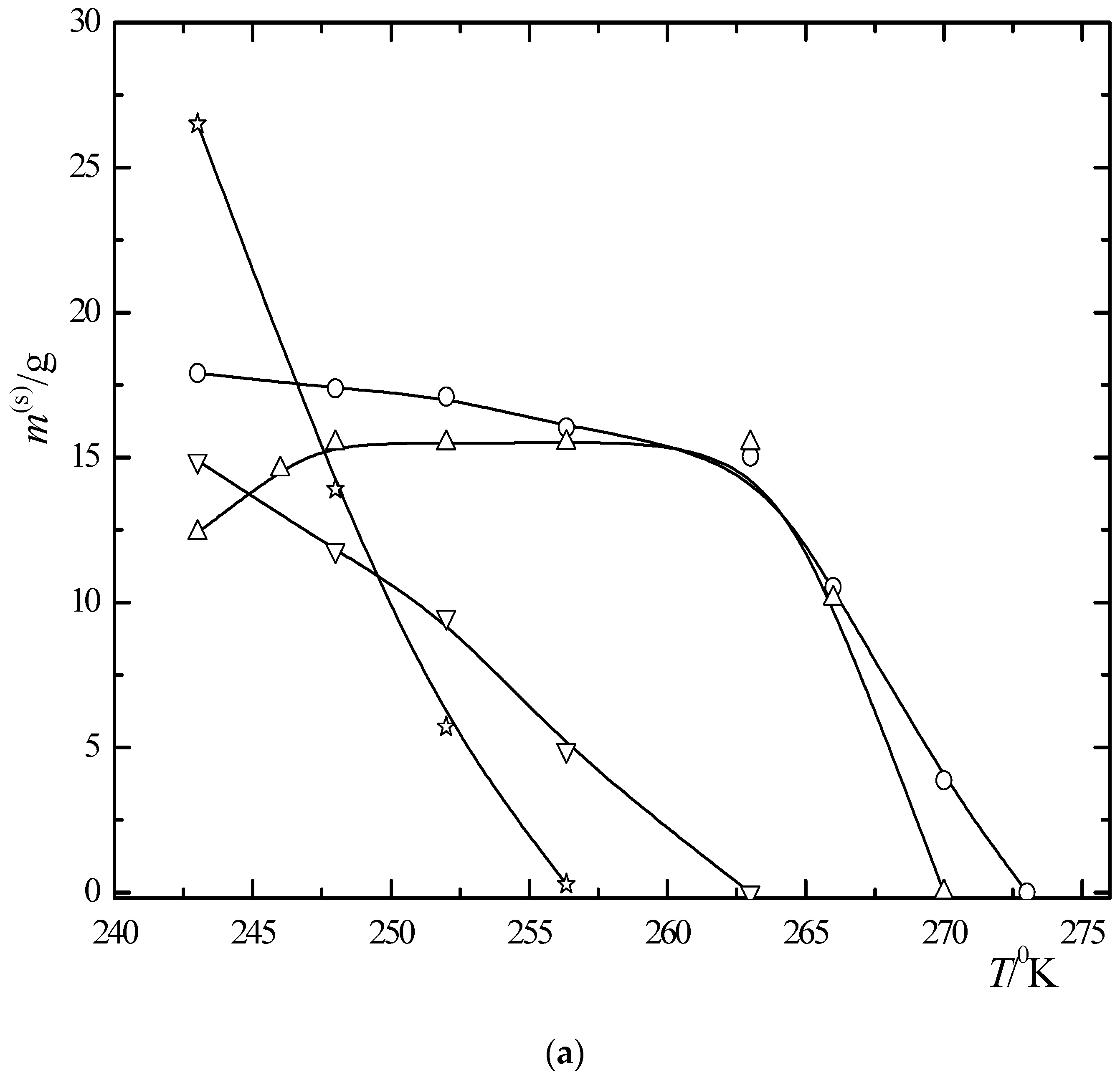
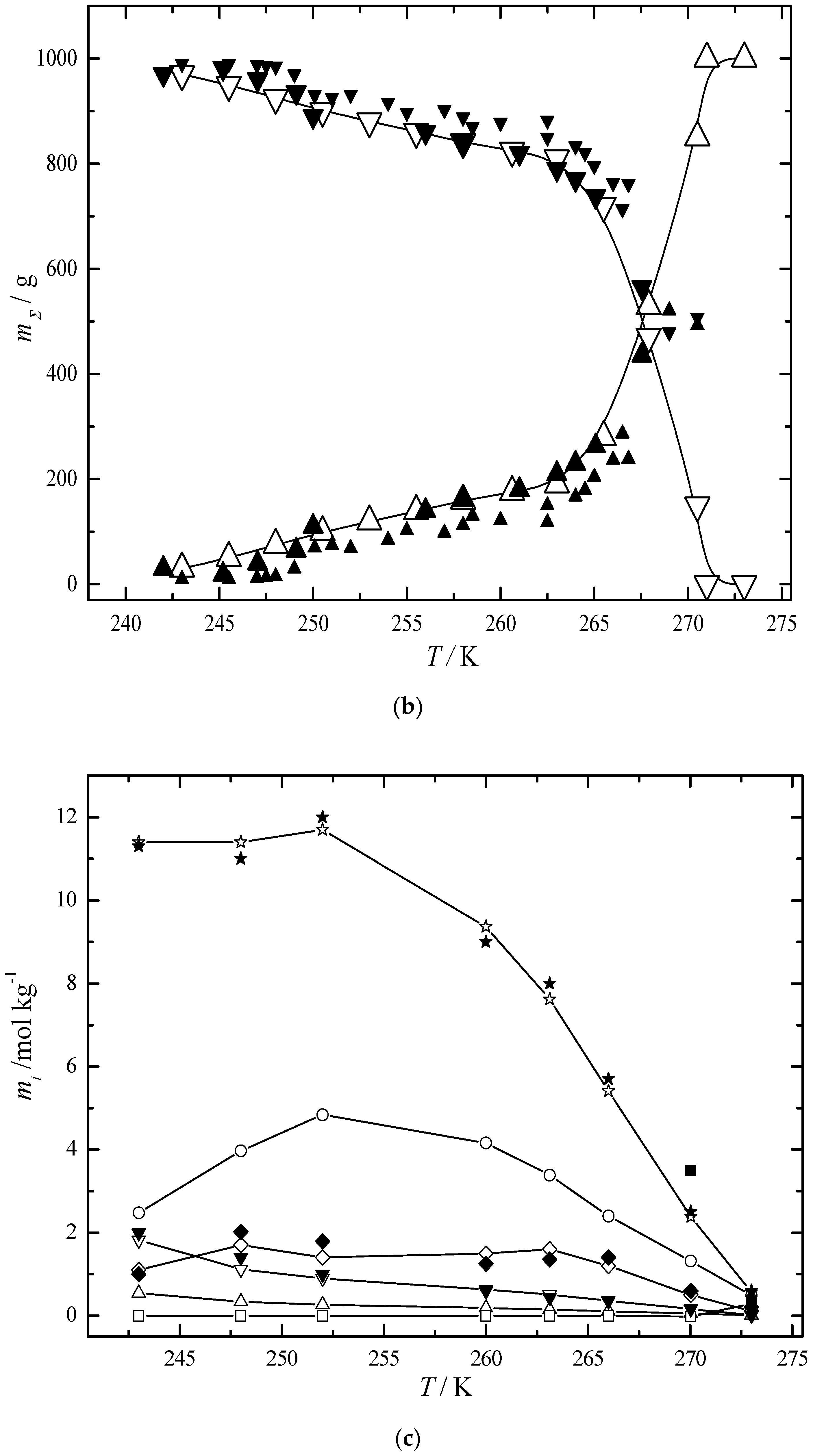
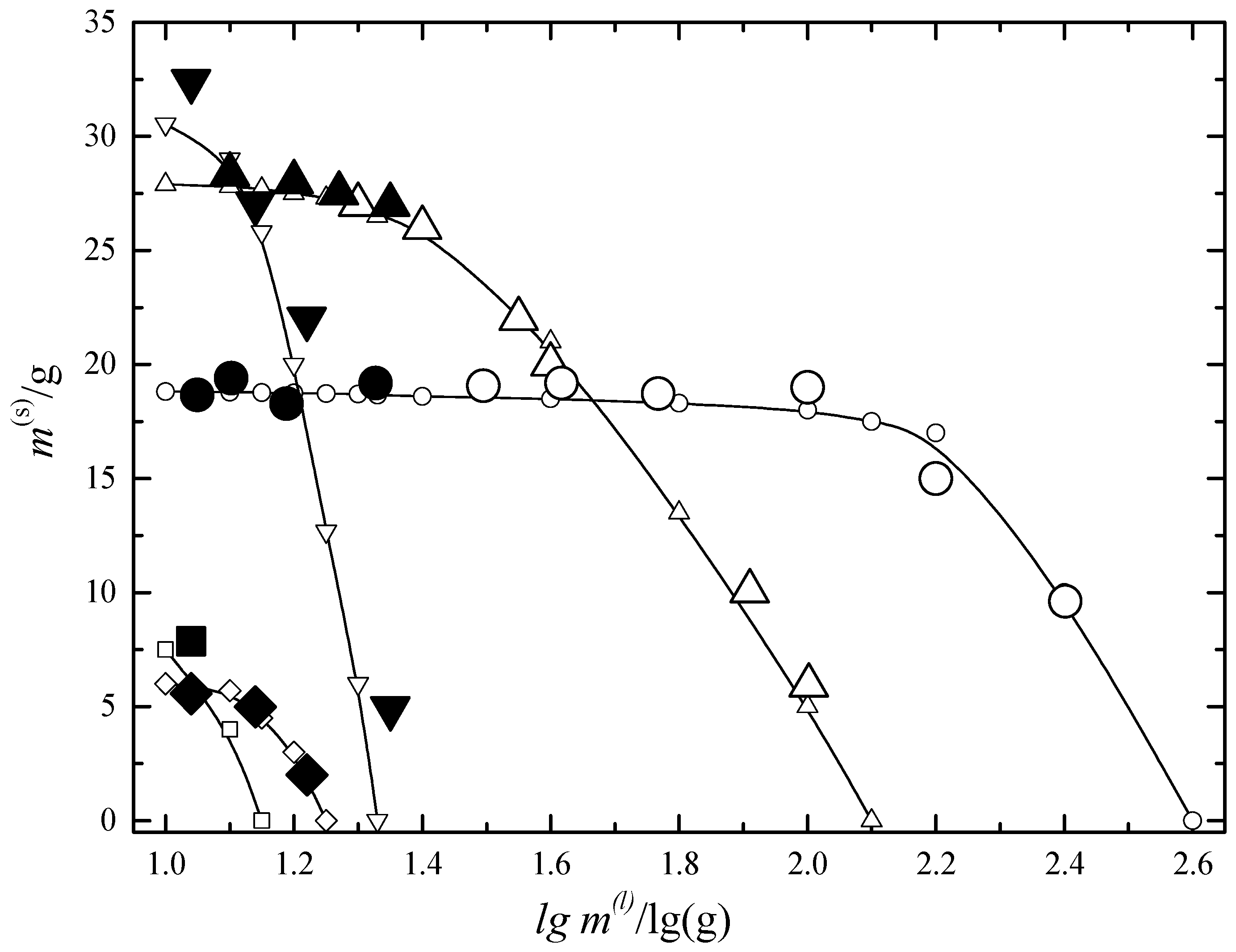
6.2. Multiphase Open Crystallization in the Na+, K+, Mg2+, Ca2+//Cl−, SO42−-H2O System at Water Chemical Potential Decrease (Water Evaporation)
6.3. Multiphase Open Crystallization in the Na+, K+, Mg2+, Ca2+//Cl−, SO42−-H2O System at Temperature Decrease
7. Conclusions
- -
- It is most common and does not depend of the type of phase process or components number.
- -
- It is not recursive and gives unidirectional motion in the direction of action of thermodynamic forces of phase process.
- -
- The algorithm is easy to program, because, in the region of diffusional stability, we are always dealing with convex functions and positively determined (according to Sylvester’s theorem) bilinear forms in our differential equations. The vector-matrix form of writing equations in this case is, in our opinion, the most compact and convenient for the calculation and analysis.
- -
- The main novelty of this work is the following not very obvious result: in the opinion of the authors, for the first time, the equations systems of phase processes have been deduced, where masses of phases are natural parameters of state, absolutely the same as classical parameters: temperature, pressure, components molar numbers, etc.
Author Contributions
Funding
Conflicts of Interest
References
- Gibbs, J.W. The Scientific Papers of J.W. Gibbs; Longmans Green: London, UK, 1906. [Google Scholar]
- Waals, J.D.; Kohnstamm, P. Lehrbuch der Thermostatik das heisst des thermischen Gleichgewichtes materieller Systeme. I Th Allgemeine Thermostatik, zuglesch dritte Auflage des Lehrbuch der Thermodynamik derselben Verfasser; Verlag J. A. Barth: Leipzig, Germany, 1927. [Google Scholar]
- Storonkin, A.V. Thermodynamic of Heterogeneous Systems; LGU: Leningrad, Russia, 1967. (In Russian) [Google Scholar]
- Filippov, V.K. Metrics of Gibbs potential and theory on nonvariant equilibrium. In Thermodynamics of Heterogeneous Systems and Theory of Surface Phenomena; LGU: Leningrad, Russia, 1973; Volume 2, pp. 20–35. (In Russian) [Google Scholar]
- Filippov, V.K.; Sokolov, V.A. Metrics of incomplete Gibbs potentials. In Thermodynamics of Heterogeneous Systems and Theory of Surface Phenomena; LGU: Leningrad, Russia, 1988; Volume 8, pp. 3–34. (In Russian) [Google Scholar]
- Korjinskiy, A.D. Theoretical Basis of the Analysis of Minerals Paragenesis; Nauka: Moscow, Russia, 1973. (In Russian) [Google Scholar]
- Charykova, M.V.; Charykov, N.A. Thermodynamic Modeling of the Processes of Evaporate Sedimentation; Nauka: Saint-Petersberg, Russia, 2003. (In Russian) [Google Scholar]
- Charykov, N.A.; Shakhmatkin, B.A.; Charykova, M.V.; Schultz, M.M. Open multiphase isobaric crystallization from the melts in the conditions of polyvariant equilibrium. Russ. Acad. Sci. Ser. Phys.-Chem. 1999, 368, 260–263. [Google Scholar]
- Charykov, N.A.; Shakhmatkin, B.A.; Charykova, M.V. Crystallization from the melts in the conditions of polyvariant equilibrium. Russ. J. Phys. Chem. 2000, 74, 360–1365. [Google Scholar]
- Jarikov, V.A. Basis of Physical-Chemical Petrology; MGU: Moscow, Russia, 1976. (In Russian) [Google Scholar]
- Sharipov, R.A. Course of Linear Algebra and Multidimensional Geometry; Bashk.GU: Ufa, Russia, 1996. (In Russian) [Google Scholar]
- Charykov, N.A.; Litvak, A.M.; Mikhailova, M.P.; Moiseev, K.D.; Yakovlev, Y.P. Solid solution InxGa1−xAs ySbzP1−y−z. New material ofIR optoelectronics.I. Thermodynamic analysis of production conditions for solid solutions, isoperiodicto the substrates InAs and GaSb, by liquid phase epitaxy method. Russ. Phys. Tech. Semicond. 1997, 31, 410–415. [Google Scholar]
- Litvak, A.M.; Charykov, N.A. New thermodynamic method of calculation of meltsolidphase equilibria (for the example of A3B5 systems). Russ. J. Phys. Chem. 1990, 64, 2331–2335. [Google Scholar]
- Litvak, A.M.; Charykov, N.A. Melt-solid phase equilibria in the system Pb-InAs-InSb. Russ. J. Inorg. Chem. 1990, 35, 3059–3062. [Google Scholar]
- Litvak, A.M.; Charykov, N.A. Application of EF-LCP Method to the Calculation of epitaxial crystal Growth in A3B5 Semiconductor Systems In-Ga-As-Sb, In-As-Sb-P. In Epitaxial Crystal Growth: Proceedings of the 1st International Conference on Epitaxial Crystal Growth, Budapest, Hungary, April 1–7, 1990; Lendvay, E., Ed.; Trans Tech Publications: Aedermannsdorf, Switzerland, 1991; Volume 31, pp. 392–394. [Google Scholar]
- Pitzer, K.S. Thermodynamics of electrolytes. I. Theoretical basis and general equations. J. Phys. Chem. 1973, 77, 268–277. [Google Scholar] [CrossRef]
- Pitzer, K.S.; Kim, J.J. Thermodynamics of electrolytes. IV. Activity and osmotic coefficients for mixed electrolytes. J. Am. Chem. Soc. 1974, 96, 5701–5707. [Google Scholar] [CrossRef] [Green Version]
- Charykov, N.A. Thermodynamic Modeling of Phase Equilibrium and Open Phase Processes on the Basis of Virial Decomposition of Gibbs Potentials of Condensed Phases. Ph.D.Thesis, St-Petersburg State Technological Institute (Technical University), St-Petersburg, Russian, 1993. [Google Scholar]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Charykov, N.A.; Charykova, M.V.; Semenov, K.N.; Keskinov, V.A.; Kurilenko, A.V.; Shaimardanov, Z.K.; Shaimardanova, B.K. Multiphase Open Phase Processes Differential Equations. Processes 2019, 7, 148. https://0-doi-org.brum.beds.ac.uk/10.3390/pr7030148
Charykov NA, Charykova MV, Semenov KN, Keskinov VA, Kurilenko AV, Shaimardanov ZK, Shaimardanova BK. Multiphase Open Phase Processes Differential Equations. Processes. 2019; 7(3):148. https://0-doi-org.brum.beds.ac.uk/10.3390/pr7030148
Chicago/Turabian StyleCharykov, Nikolay A., Marina V. Charykova, Konstantin N. Semenov, Victor A. Keskinov, Alexey V. Kurilenko, Zhassulan K. Shaimardanov, and Botagoz K. Shaimardanova. 2019. "Multiphase Open Phase Processes Differential Equations" Processes 7, no. 3: 148. https://0-doi-org.brum.beds.ac.uk/10.3390/pr7030148





