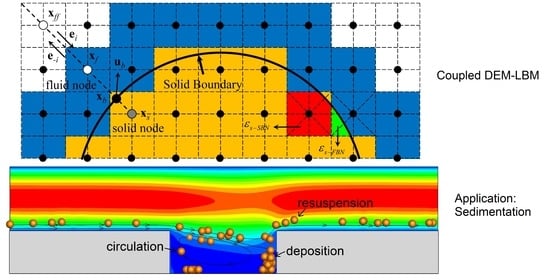
Modelling Complex Particle–Fluid Flow with a Discrete Element Method Coupled with Lattice Boltzmann Methods (DEM-LBM)
Abstract
:1. Introduction
2. Discrete Element Method (DEM)
2.1. Normal Contact Force
2.2. Sliding, Rolling and Twisting Resistance
3. Lattice Boltzmann Method (LBM)
3.1. Lattice Boltzmann Equation
3.1.1. Single-Relaxation-Time Model
3.1.2. Multi-Relaxation-Time Model
3.2. Boundary Conditions
3.3. Unit Conversion in LBM
4. LBM-DEM Coupling
4.1. Modified Bounce-Back Scheme
4.2. Interpolated Bounce-Back Scheme
4.3. Immersed Moving Boundary Method
4.4. Time Steps in the LBM-DEM Coupling
5. Validation
5.1. Poiseuille Flow
5.2. Gravitational Settling of a Particle
5.3. Drag Force on a Stationary Particle
6. LBM-DEM Applications
6.1. Inertial Migration of Dense Particle Suspensions
6.2. Agglomeration of Adhesive Particles in Channel Flow
6.3. Sedimentation of Particle Suspensions in Cavity Flow
7. Summary
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhu, H.; Zhou, Z.; Yang, R.; Yu, A. Discrete particle simulation of particulate systems: Theoretical developments. Chem. Eng. Sci. 2007, 62, 3378–3396. [Google Scholar] [CrossRef]
- Zhu, H.; Zhou, Z.; Yang, R.; Yu, A. Discrete particle simulation of particulate systems: A review of major applications and findings. Chem. Eng. Sci. 2008, 63, 5728–5770. [Google Scholar] [CrossRef]
- Li, S.; Marshall, J.S.; Liu, G.; Yao, Q. Adhesive particulate flow: The discrete-element method and its application in energy and environmental engineering. Prog. Energy Combust. Sci. 2011, 37, 633–668. [Google Scholar] [CrossRef]
- Hounslow, M.; Ryall, R.L.; Marshall, V.R. A discretized population balance for nucleation, growth, and aggregation. AIChE J. 1988, 34, 1821–1832. [Google Scholar] [CrossRef]
- Lister, J.D.; Smit, D.J.; Hounslow, M. Adjustable discretized population balance for growth and aggregation. AIChE J. 1995, 41, 591–603. [Google Scholar] [CrossRef]
- Gidaspow, D. Multiphase Flow and Fluidization; Elsevier: Amsterdam, The Netherlands, 1994. [Google Scholar]
- Zhu, R.; Zhu, W.; Xing, L.; Sun, Q. DEM simulation on particle mixing in dry and wet particles spouted bed. Powder Technol. 2011, 210, 73–81. [Google Scholar] [CrossRef]
- Liu, G.; Li, S.; Yao, Q. A JKR-based dynamic model for the impact of micro-particle with a flat surface. Powder Technol. 2011, 207, 215–223. [Google Scholar] [CrossRef]
- Yang, M.; Li, S.; Yao, Q. Mechanistic studies of initial deposition of fine adhesive particles on a fiber using discrete-element methods. Powder Technol. 2013, 248, 44–53. [Google Scholar] [CrossRef]
- Chen, S.; Li, S.; Yang, M. Sticking/rebound criterion for collisions of small adhesive particles: Effects of impact parameter and particle size. Powder Technol. 2015, 274, 431–440. [Google Scholar] [CrossRef]
- Liu, W.; Li, S.; Baule, A.; Makse, H.A. Adhesive loose packings of small dry particles. Soft Matter 2015, 11, 6492–6498. [Google Scholar] [CrossRef] [Green Version]
- Liu, W.; Li, S.; Chen, S. Computer simulation of random loose packings of micro-particles in presence of adhesion and friction. Powder Technol. 2016, 302, 414–422. [Google Scholar] [CrossRef] [Green Version]
- Liu, W.; Jin, Y.; Li, S.; Chen, S.; Makse, H.A. Equation of state for random sphere packing with arbitrary adhesion and friction. Soft Matter 2017, 13, 421–427. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, W.; Chen, S.; Li, S. Random adhesive loose packings of micron-sized particles under a uniform flow field. Powder Technol. 2018, 335, 70–76. [Google Scholar] [CrossRef]
- Chen, S.; Liu, W.; Li, S. A fast adhesive discrete element method for random packings of fine particles. Chem. Eng. Sci. 2019, 193, 336–345. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Sharma, G.; Wang, Y.; Li, S.; Biswas, P. Numerical modeling of the performance of high flow DMAs to classify sub-2 nm particles. Aerosol Sci. Technol. 2018, 53, 106–118. [Google Scholar] [CrossRef]
- Dong, M.; Li, J.; Shang, Y.; Li, S. Numerical investigation on deposition process of submicron particles in collision with a single cylindrical fiber. J. Aerosol Sci. 2019, 129, 1–15. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Géotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Chen, S.; Doolen, G.D. Lattice boltzmann method for fluid flows. Annu. Rev. Fluid Mech. 1998, 30, 329–364. [Google Scholar] [CrossRef] [Green Version]
- Aidun, C.K.; Clausen, J.R. Lattice-Boltzmann Method for Complex Flows. Annu. Rev. Fluid Mech. 2010, 42, 439–472. [Google Scholar] [CrossRef]
- Krüger, T.; Kusumaatmaja, H.; Kuzmin, A.; Shardt, O.; Silva, G.; Viggen, E.M. The Lattice Boltzmann Method; Springer Science and Business Media: Berlin, Germany, 2017; Volume 10, pp. 4–15. [Google Scholar]
- Moin, P.; Mahesh, K. Direct Numerical Simulation: A Tool in Turbulence Research. Annu. Rev. Fluid Mech. 1998, 30, 539–578. [Google Scholar] [CrossRef] [Green Version]
- Sagaut, P. Large Eddy Simulation for Incompressible Flows; Springer Science and Business Media: Berlin, Germany, 2006. [Google Scholar]
- Ishii, M.; Mishima, K. Two-fluid model and hydrodynamic constitutive relations. Nucl. Eng. Des. 1984, 82, 107–126. [Google Scholar] [CrossRef]
- Tsuji, Y.; Kawaguchi, T.; Tanaka, T. Discrete particle simulation of two-dimensional fluidized bed. Powder Technol. 1993, 77, 79–87. [Google Scholar] [CrossRef]
- Kuipers, J.; Van Duin, K.; Van Beckum, F.; Van Swaaij, W. A numerical model of gas-fluidized beds. Chem. Eng. Sci. 1992, 47, 1913–1924. [Google Scholar] [CrossRef] [Green Version]
- Kafui, K.; Thornton, C.; Adams, M. Discrete particle-continuum fluid modelling of gas-solid fluidised beds. Chem. Eng. Sci. 2002, 57, 2395–2410. [Google Scholar] [CrossRef]
- Guo, Y.; Kafui, K.D.; Wu, C.-Y.; Thornton, C.; Seville, J.P.K. A coupled DEM/CFD analysis of the effect of air on powder flow during die filling. AIChE J. 2009, 55, 49–62. [Google Scholar] [CrossRef]
- Guo, Y.; Wu, C.-Y.; Kafui, K.; Thornton, C. 3D DEM/CFD analysis of size-induced segregation during die filling. Powder Technol. 2011, 206, 177–188. [Google Scholar] [CrossRef]
- Guo, Y.; Wu, C.-Y.; Thornton, C. Modeling gas-particle two-phase flows with complex and moving boundaries using DEM-CFD with an immersed boundary method. AIChE J. 2012, 59, 1075–1087. [Google Scholar] [CrossRef]
- Feng, Y.T.; Han, K.; Owen, D.R.J. Coupled lattice Boltzmann method and discrete element modelling of particle transport in turbulent fluid flows: Computational issues. Int. J. Numer. Methods Eng. 2007, 72, 1111–1134. [Google Scholar] [CrossRef]
- Strack, O.E.; Cook, B.K. Three-dimensional immersed boundary conditions for moving solids in the lattice-Boltzmann method. Int. J. Numer. Methods Fluids 2007, 55, 103–125. [Google Scholar] [CrossRef]
- van der Hoef, M.A.; Annaland, M.V.S.; Deen, N.; Kuipers, H. Numerical Simulation of Dense Gas-Solid Fluidized Beds: A Multiscale Modeling Strategy. Annu. Rev. Fluid Mech. 2008, 40, 47–70. [Google Scholar] [CrossRef]
- Van Wachem, B.; Schouten, J.C.; Bleek, C.M.V.D.; Krishna, R.; Sinclair, J.L. Comparative analysis of CFD models of dense gas–solid systems. AIChE J. 2001, 47, 1035–1051. [Google Scholar] [CrossRef]
- Ladd, A.J.C.; Verberg, R. Lattice-Boltzmann Simulations of Particle-Fluid Suspensions. J. Stat. Phys. 2001, 104, 1191–1251. [Google Scholar] [CrossRef]
- Nguyen, N.-Q.; Ladd, A.J.C. Lubrication corrections for lattice-Boltzmann simulations of particle suspensions. Phys. Rev. E 2002, 66, 046708. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, W. Analysis of inertial migration of neutrally buoyant particle suspensions in a planar Poiseuille flow with a coupled lattice Boltzmann method-discrete element method. Phys. Fluids 2019, 31, 063301. [Google Scholar] [CrossRef]
- Liu, W.; Wu, C.-Y. Migration and agglomeration of adhesive microparticle suspensions in a pressure-driven duct flow. AIChE J. 2020, 66, 16974. [Google Scholar] [CrossRef]
- Maier, R.S.; Kroll, D.M.; Kutsovsky, Y.E.; Davis, H.T.; Bernard, R.S. Simulation of flow through bead packs using the lattice Boltzmann method. Phys. Fluids 1998, 10, 60–74. [Google Scholar] [CrossRef]
- Guo, Z.; Zhao, T. Lattice Boltzmann model for incompressible flows through porous media. Phys. Rev. E 2002, 66, 036304. [Google Scholar] [CrossRef] [PubMed]
- Inamuro, T.; Ogata, T.; Tajima, S.; Konishi, N. A lattice Boltzmann method for incompressible two-phase flows with large density differences. J. Comput. Phys. 2004, 198, 628–644. [Google Scholar] [CrossRef]
- Li, Q.; Luo, K.H.; Kang, Q.; He, Y.; Chen, Q.; Liu, Q. Lattice Boltzmann methods for multiphase flow and phase-change heat transfer. Prog. Energy Combust. Sci. 2016, 52, 62–105. [Google Scholar] [CrossRef] [Green Version]
- Han, Y.; Cundall, P.A. LBM-DEM modeling of fluid-solid interaction in porous media. Int. J. Numer. Anal. Methods Geomech. 2012, 37, 1391–1407. [Google Scholar] [CrossRef]
- Peng, C.; Ayala, O.M.; Wang, L.-P. A direct numerical investigation of two-way interactions in a particle-laden turbulent channel flow. J. Fluid Mech. 2019, 875, 1096–1144. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.; Chen, H.; Martnez, D.; Matthaeus, W. Lattice Boltzmann model for simulation of magnetohydrodynamics. Phys. Rev. Lett. 1991, 67, 3776–3779. [Google Scholar] [CrossRef] [PubMed]
- Pei, C.; Wu, C.-Y.; England, D.; Byard, S.; Berchtold, H.; Adams, M. DEM-CFD modeling of particle systems with long-range electrostatic interactions. AIChE J. 2015, 61, 1792–1803. [Google Scholar] [CrossRef]
- Pei, C.; Wu, C.-Y.; Adams, M.; England, D.; Byard, S.; Berchtold, H. Contact electrification and charge distribution on elongated particles in a vibrating container. Chem. Eng. Sci. 2015, 125, 238–247. [Google Scholar] [CrossRef] [Green Version]
- Pei, C.; Wu, C.-Y.; Adams, M. Numerical analysis of contact electrification of non-spherical particles in a rotating drum. Powder Technol. 2015, 285, 110–122. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.; Li, S.; Liu, W.; Makse, H.A. Effect of long-range repulsive Coulomb interactions on packing structure of adhesive particles. Soft Matter 2016, 12, 1836–1846. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.; Liu, W.; Li, S. Effect of long-range electrostatic repulsion on pore clogging during microfiltration. Phys. Rev. E 2016, 94, 063108. [Google Scholar] [CrossRef]
- Chen, S.; Liu, W.; Li, S. Scaling laws for migrating cloud of low-Reynolds-number particles with Coulomb repulsion. J. Fluid Mech. 2017, 835, 880–897. [Google Scholar] [CrossRef]
- Zhu, R.; Li, S.; Yao, Q. Effects of cohesion on the flow patterns of granular materials in spouted beds. Phys. Rev. E 2013, 87, 022206. [Google Scholar] [CrossRef]
- Zhang, H.; Li, S. DEM simulation of wet granular-fluid flows in spouted beds: Numerical studies and experimental verifications. Powder Technol. 2017, 318, 337–349. [Google Scholar] [CrossRef]
- Chen, H.; Liu, W.; Li, S. Deposition of wet microparticles on a fiber: Effects of impact velocity and initial spin. Powder Technol. 2019, 357, 83–96. [Google Scholar] [CrossRef]
- Hertz, H. Ueber die Berührung fester elastischer Körper. J. für die reine und angewandte Mathematik (Crelles J.) 1882, 1882, 156–171. [Google Scholar] [CrossRef]
- Johnson, K.L.; Kendall, K.; Roberts, A.D. Surface energy and the contact of elastic solids. Proc. R. Soc. London. Ser. A Math. Phys. Sci. 1971, 324, 301–313. [Google Scholar] [CrossRef] [Green Version]
- Derjaguin, B.; Muller, V.; Toporov, Y. Effect of contact deformations on the adhesion of particles. J. Colloid Interface Sci. 1975, 53, 314–326. [Google Scholar] [CrossRef]
- Marshall, J.S.; Li, S. Adhesive Particle Flows; Cambridge University Press (CUP): Cambridge, UK, 2014. [Google Scholar]
- Bhatnagar, P.L.; Gross, E.P.; Krook, M. A Model for Collision Processes in Gases. I. Small Amplitude Processes in Charged and Neutral One-Component Systems. Phys. Rev. 1954, 94, 511–525. [Google Scholar] [CrossRef]
- Chen, H.; Chen, S.; Matthaeus, W.H. Recovery of the Navier-Stokes equations using a lattice-gas Boltzmann method. Phys. Rev. A 1992, 45, R5339–R5342. [Google Scholar] [CrossRef] [PubMed]
- Qian, Y.H.; D’Humières, D.; Lallemand, P. Lattice BGK Models for Navier-Stokes Equation. EPL (Europhysics Lett.) 1992, 17, 479–484. [Google Scholar] [CrossRef]
- Wolf-Gladrow, D.A. Lattice-Gas Cellular Automata and Lattice Boltzmann Models: An Introduction; Springer: New York, NY, USA, 2004. [Google Scholar]
- Guo, Z.; Zheng, C.; Shi, B. Discrete lattice effects on the forcing term in the lattice Boltzmann method. Phys. Rev. E 2002, 65, 046308. [Google Scholar] [CrossRef]
- Lallemand, P.; Luo, L.-S. Theory of the lattice Boltzmann method: Dispersion, dissipation, isotropy, Galilean invariance, and stability. Phys. Rev. E 2000, 61, 6546–6562. [Google Scholar] [CrossRef] [Green Version]
- Ladd, A.J.C. Numerical simulations of particulate suspensions via a discretized Boltzmann equation. Part 1. Theoretical foundation. J. Fluid Mech. 1994, 271, 285. [Google Scholar] [CrossRef] [Green Version]
- Ladd, A.J.C. Numerical simulations of particulate suspensions via a discretized Boltzmann equation. Part 2. Numerical results. J. Fluid Mech. 1994, 271, 311. [Google Scholar] [CrossRef] [Green Version]
- Bouzidi, M.; Firdaouss, M.; Lallemand, P. Momentum transfer of a Boltzmann-lattice fluid with boundaries. Phys. Fluids 2001, 13, 3452–3459. [Google Scholar] [CrossRef]
- Filippova, O.; Hänel, D. Grid Refinement for Lattice-BGK Models. J. Comput. Phys. 1998, 147, 219–228. [Google Scholar] [CrossRef]
- Mei, R.; Luo, L.-S.; Shyy, W. An Accurate Curved Boundary Treatment in the Lattice Boltzmann Method. J. Comput. Phys. 1999, 155, 307–330. [Google Scholar] [CrossRef]
- Mei, R.; Shyy, W.; Yu, D.; Luo, L.-S. Lattice Boltzmann Method for 3-D Flows with Curved Boundary. J. Comput. Phys. 2000, 161, 680–699. [Google Scholar] [CrossRef] [Green Version]
- Yu, D.; Mei, R.; Luo, L.-S.; Shyy, W. Viscous flow computations with the method of lattice Boltzmann equation. Prog. Aerosp. Sci. 2003, 39, 329–367. [Google Scholar] [CrossRef]
- Peng, C.; Teng, Y.; Hwang, B.; Guo, Z.; Wang, L.-P. Implementation issues and benchmarking of lattice Boltzmann method for moving rigid particle simulations in a viscous flow. Comput. Math. Appl. 2016, 72, 349–374. [Google Scholar] [CrossRef] [Green Version]
- Peskin, C.S. Numerical analysis of blood flow in the heart. J. Comput. Phys. 1977, 25, 220–252. [Google Scholar] [CrossRef]
- Peskin, C.S. The immersed boundary method. Acta Numer. 2002, 11, 479–517. [Google Scholar] [CrossRef] [Green Version]
- Feng, Z.-G.; Michaelides, E.E. The immersed boundary-lattice Boltzmann method for solving fluid–particles interaction problems. J. Comput. Phys. 2004, 195, 602–628. [Google Scholar] [CrossRef]
- Uhlmann, M. An immersed boundary method with direct forcing for the simulation of particulate flows. J. Comput. Phys. 2005, 209, 448–476. [Google Scholar] [CrossRef] [Green Version]
- Breugem, W.-P. A second-order accurate immersed boundary method for fully resolved simulations of particle-laden flows. J. Comput. Phys. 2012, 231, 4469–4498. [Google Scholar] [CrossRef]
- Favier, J.; Revell, A.; Pinelli, A. A Lattice Boltzmann–Immersed Boundary method to simulate the fluid interaction with moving and slender flexible objects. J. Comput. Phys. 2014, 261, 145–161. [Google Scholar] [CrossRef] [Green Version]
- Valero-Lara, P.; Igual, F.D.; Prieto, M.; Pinelli, A.; Favier, J. Accelerating fluid–solid simulations (Lattice-Boltzmann & Immersed-Boundary) on heterogeneous architectures. J. Comput. Sci. 2015, 10, 249–261. [Google Scholar] [CrossRef] [Green Version]
- Valero-Lara, P.; Pinelli, A.; Prieto, M. Accelerating Solid-fluid Interaction using Lattice-boltzmann and Immersed Boundary Coupled Simulations on Heterogeneous Platforms. Procedia Comput. Sci. 2014, 29, 50–61. [Google Scholar] [CrossRef] [Green Version]
- Noble, D.R.; Torczynski, J.R. A Lattice-Boltzmann Method for Partially Saturated Computational Cells. Int. J. Mod. Phys. C 1998, 9, 1189–1201. [Google Scholar] [CrossRef]
- Owen, D.R.J.; Leonardi, C.R.; Feng, Y. An efficient framework for fluid-structure interaction using the lattice Boltzmann method and immersed moving boundaries. Int. J. Numer. Methods Eng. 2010, 87, 66–95. [Google Scholar] [CrossRef]
- Jones, B.D.; Williams, J.R. Fast computation of accurate sphere-cube intersection volume. Eng. Comput. 2017, 34, 1204–1216. [Google Scholar] [CrossRef]
- Sutera, S.P.; Skalak, R. The history of Poiseuille’s law. Annu. Rev. Fluid Mechan. 1993, 25, 1–20. [Google Scholar] [CrossRef]
- Wen, B.; Zhang, C.; Tu, Y.; Wang, C.; Fang, H. Galilean invariant fluid–solid interfacial dynamics in lattice Boltzmann simulations. J. Comput. Phys. 2014, 266, 161–170. [Google Scholar] [CrossRef] [Green Version]
- Cate, A.T.; Nieuwstad, C.H.; Derksen, J.J.; Akker, H.V.D. Particle imaging velocimetry experiments and lattice-Boltzmann simulations on a single sphere settling under gravity. Phys. Fluids 2002, 14, 4012–4025. [Google Scholar] [CrossRef]
- Tritton, D.J. Experiments on the flow past a circular cylinder at low Reynolds numbers. J. Fluid Mech. 1959, 6, 547. [Google Scholar] [CrossRef]
- Schiller, L.; Naumann, A. A drag coefficient correlation. Z. des Ver. Deutsch. Ing. 1935, 77, 318–320. [Google Scholar]
- Segre, G.; Silberberg, A. Behaviour of macroscopic rigid spheres in Poiseuille flow Part 1. Determination of local concentration by statistical analysis of particle passages through crossed light beams. J. Fluid Mech. 1962, 14, 115–135. [Google Scholar] [CrossRef]
- Segre, G.; Silberberg, A. Behaviour of macroscopic rigid spheres in Poiseuille flow Part 2. Experimental results and interpretation. J. Fluid Mech. 1962, 14, 136–157. [Google Scholar] [CrossRef]
- Han, M.; Kim, C.; Kim, M.; Lee, S. Particle migration in tube flow of suspensions. J. Rheol. 1999, 43, 1157–1174. [Google Scholar] [CrossRef]
- Matas, J.-P.; Morris, J.F.; Guazzelli, É. Inertial migration of rigid spherical particles in Poiseuille flow. J. Fluid Mech. 2004, 515, 171–195. [Google Scholar] [CrossRef] [Green Version]
- Di Carlo, D.; Irimia, D.; Tompkins, R.G.; Toner, M. Continuous inertial focusing, ordering, and separation of particles in microchannels. Proc. Natl. Acad. Sci. USA 2007, 104, 18892–18897. [Google Scholar] [CrossRef] [Green Version]
- Choi, Y.-S.; Seo, K.W.; Lee, S.J. Lateral and cross-lateral focusing of spherical particles in a square microchannel. Lab. Chip 2011, 11, 460–465. [Google Scholar] [CrossRef] [Green Version]
- Seo, K.W.; Kang, Y.J.; Lee, S.J. Lateral migration and focusing of microspheres in a microchannel flow of viscoelastic fluids. Phys. Fluids 2014, 26, 063301. [Google Scholar] [CrossRef] [Green Version]
- Ho, B.P.; Leal, L.G. Inertial migration of rigid spheres in two-dimensional unidirectional flows. J. Fluid Mech. 1974, 65, 365–400. [Google Scholar] [CrossRef]
- Schonberg, J.A.; Hinch, E.J. Inertial migration of a sphere in Poiseuille flow. J. Fluid Mech. 1989, 203, 517. [Google Scholar] [CrossRef] [Green Version]
- Asmolov, E.S. The inertial lift on a spherical particle in a plane Poiseuille flow at large channel Reynolds number. J. Fluid Mech. 1999, 381, 63–87. [Google Scholar] [CrossRef]
- Matas, J.-P.; Morris, J.F.; Guazzelli, É. Lateral force on a rigid sphere in large-inertia laminar pipe flow. J. Fluid Mech. 2009, 621, 59. [Google Scholar] [CrossRef]
- Feng, J.J.; Hu, H.H.; Joseph, D.D. Direct simulation of initial value problems for the motion of solid bodies in a Newtonian fluid. Part 2. Couette and Poiseuille flows. J. Fluid Mech. 1994, 277, 271. [Google Scholar] [CrossRef] [Green Version]
- Yang, B.H.; Wang, J.; Joseph, D.D.; Hu, H.H.; Pan, T.-W.; Glowinski, R. Migration of a sphere in tube flow. J. Fluid Mech. 2005, 540, 109. [Google Scholar] [CrossRef] [Green Version]
- Shao, X.; Yu, Z.; Sun, B. Inertial migration of spherical particles in circular Poiseuille flow at moderately high Reynolds numbers. Phys. Fluids 2008, 20, 103307. [Google Scholar] [CrossRef] [Green Version]
- Inamuro, T.; Maeba, K.; Ogino, F. Flow between parallel walls containing the lines of neutrally buoyant circular cylinders. Int. J. Multiph. Flow 2000, 26, 1981–2004. [Google Scholar] [CrossRef]
- Chun, B.; Ladd, A.J.C. Inertial migration of neutrally buoyant particles in a square duct: An investigation of multiple equilibrium positions. Phys. Fluids 2006, 18, 31704. [Google Scholar] [CrossRef] [Green Version]
- Sun, D.-K.; Bo, Z. Numerical simulation of hydrodynamic focusing of particles in straight channel flows with the immersed boundary-lattice Boltzmann method. Int. J. Heat Mass Transf. 2015, 80, 139–149. [Google Scholar] [CrossRef]
- Hu, J.; Guo, Z. A numerical study on the migration of a neutrally buoyant particle in a Poiseuille flow with thermal convection. Int. J. Heat Mass Transf. 2017, 108, 2158–2168. [Google Scholar] [CrossRef]
- Ookawara, S.; Agrawal, M.; Street, D.; Ogawa, K. Quasi-direct numerical simulation of lift force-induced particle separation in a curved microchannel by use of a macroscopic particle model. Chem. Eng. Sci. 2007, 62, 2454–2465. [Google Scholar] [CrossRef]
- Di Carlo, D. Inertial microfluidics. Lab Chip 2009, 9, 3038. [Google Scholar] [CrossRef] [PubMed]
- Ahn, S.W.; Lee, S.S.; Lee, S.J.; Kim, J.M. Microfluidic particle separator utilizing sheathless elasto-inertial focusing. Chem. Eng. Sci. 2015, 126, 237–243. [Google Scholar] [CrossRef]
- Eskin, D.; Ratulowski, J.; Akbarzadeh, K.; Pan, S. Modelling asphaltene deposition in turbulent pipeline flows. Can. J. Chem. Eng. 2011, 89, 421–441. [Google Scholar] [CrossRef]
- Balakin, B.V.; Hoffmann, A.; Kosinski, P. Experimental study and computational fluid dynamics modeling of deposition of hydrate particles in a pipeline with turbulent water flow. Chem. Eng. Sci. 2011, 66, 755–765. [Google Scholar] [CrossRef]
- Bernate, J.A.; Liu, C.; Lagae, L.; Konstantopoulos, K.; Drazer, G. Vector separation of particles and cells using an array of slanted open cavities. Lab Chip 2013, 13, 1086–1092. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Davis, R.H.; Acrivos, A. Sedimentation of noncolloidal particles at low Reynolds numbers. Annu. Rev. Fluid Mechan. 1985, 17, 91–118. [Google Scholar] [CrossRef]
- Mahmoud, M.; Tawfik, A.; El-Gohary, F. Use of down-flow hanging sponge (DHS) reactor as a promising post-treatment system for municipal wastewater. Chem. Eng. J. 2011, 168, 535–543. [Google Scholar] [CrossRef]
- Al-Sammarraee, M.; Chan, A.; Salim, S.M.; Mahabaleswar, U.S. Large-eddy simulations of particle sedimentation in a longitudinal sedimentation basin of a water treatment plant. Part I: Particle settling performance. Chem. Eng. J. 2009, 152, 307–314. [Google Scholar] [CrossRef]
- Samaras, K.; Zouboulis, A.; Karapantsios, T.; Kostoglou, M. A CFD-based simulation study of a large scale flocculation tank for potable water treatment. Chem. Eng. J. 2010, 162, 208–216. [Google Scholar] [CrossRef]
- Black, K.S.; Tolhurst, T.J.; Paterson, D.M.; Hagerthey, S.E. Working with Natural Cohesive Sediments. J. Hydraul. Eng. 2002, 128, 2–8. [Google Scholar] [CrossRef]
- Vignati, D.A.L.; Pardos, M.; Diserens, J.; Ugazio, G.; Thomas, R.; Dominik, J. Characterisation of bed sediments and suspension of the river Po (Italy) during normal and high flow conditions. Water Res. 2003, 37, 2847–2864. [Google Scholar] [CrossRef]
- Walker, S.; Narbaitz, R.M. Hollow fiber ultrafiltration of Ottawa River water: Floatation versus sedimentation pre-treatment. Chem. Eng. J. 2016, 288, 228–237. [Google Scholar] [CrossRef]
- Su, S.; Xiao, R.; Mi, X.; Xu, X.; Zhang, Z.; Wu, J. Spatial determinants of hazardous chemicals in surface water of Qiantang River, China. Ecol. Indic. 2013, 24, 375–381. [Google Scholar] [CrossRef]


























| Physical Parameters | Unit | Real Value | Lattice Value | Conversion Coefficient |
|---|---|---|---|---|
| Pipe length (L) | m | 0.008 | 100 | 8.0 × 10−5 |
| Pipe diameter (D) | m | 0.004 | 50 | 8.0 × 10−5 |
| Fluid density (ρf) | kg/m3 | 1000 | 1 | 1000 |
| Fluid kinematic viscosity (νf) | m2/s | 1.0 × 10−6 | 0.05 | 2.0 × 10−5 |
| Average fluid velocity (V) | m/s | 0.0125 | 0.05 | 0.025 |
| Pressure drop (ΔP) | Pa | 0.2 | 3.2 × 10−3 | 62.5 |
| Time step (Δt) | s | 3.2 × 10−4 | 1 | 3.2 × 10−4 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, W.; Wu, C.-Y. Modelling Complex Particle–Fluid Flow with a Discrete Element Method Coupled with Lattice Boltzmann Methods (DEM-LBM). ChemEngineering 2020, 4, 55. https://0-doi-org.brum.beds.ac.uk/10.3390/chemengineering4040055
Liu W, Wu C-Y. Modelling Complex Particle–Fluid Flow with a Discrete Element Method Coupled with Lattice Boltzmann Methods (DEM-LBM). ChemEngineering. 2020; 4(4):55. https://0-doi-org.brum.beds.ac.uk/10.3390/chemengineering4040055
Chicago/Turabian StyleLiu, Wenwei, and Chuan-Yu Wu. 2020. "Modelling Complex Particle–Fluid Flow with a Discrete Element Method Coupled with Lattice Boltzmann Methods (DEM-LBM)" ChemEngineering 4, no. 4: 55. https://0-doi-org.brum.beds.ac.uk/10.3390/chemengineering4040055