2.1. Free Electron Theory
Ohm’s law of electric conduction and Fourier’s law of heat conduction can be derived from the free electron theory. The range of electrical resistivity of materials varies by 30 orders of magnitude. The range of thermal conductivity of materials varies by five orders of magnitude. No one theory can predict the thermal and electrical conductivity of materials. The free electron model is used. The outermost electrons of the atom are assumed to take part in the conduction process. These electrons are not bound to the atom but are free to move through the entire solid. These electrons have been called the free electron cloud, free electron gas, or Fermi gas. A potential field due to the ion cores is assumed to be uniform throughout the solid. The free electrons possess the same free energy everywhere in the solid. Because of the electrostatic attraction between a free electron and the ion core, this potential energy will be a finite negative value.
Only energy differences are important and the constant potential can be taken to be zero. Then the only energy that has to be considered is the kinetic energy. The kinetic energy is substantially lower than that of the bound electrons in an isolated atom as the field of motion for the free electron is considerably enlarged in the solid as compared to the field around an isolated atom. The free electron theory can be used to better understand electrical conduction.
By the Lorenz analogy [
37], the heat conduction can also be predicted in a similar manner. The independent electron assumption was developed by Drude [
38]. Some of the assumptions in the free electron theory claim that electrons are responsible for all of the conduction. The electrons behave like an ideal gas, occupy negligible volume, undergo collisions, and are perfectly elastic. Electrons are free to move in a constrained flat bottom well. The electron distribution of energy is a continuum.
2.2. Derivation of Alternate Non-Fourier Conduction Equation
Let the number of electrons per unit volume be given by
n. This is the electron density in the material during the conduction process. From the Boltzmann equipartition energy theorem [
39] the microscopic temperature,
T, in (°K) can be given by;
where k
B is the Boltzmann constant, m is the mass of the electron in (kg) and
ve is the velocity of the free electron in (m s
−1). The heat flux,
qz, in (W m
−2) is the rate of energy transfer across a cross-sectional area of the heat conduction path. The heat flux in terms of the properties of the moving electron can be written as follows:
Equation (2) is the product of Equation (1) and (nve). Currently, the rate of energy transfer across surfaces is estimated this way. This is sort of the momentum flux of the electrons as well. The applied temperature gradient acts as a driving force for the motion of the electron. Let the collision time of the electron be given by τ in units of seconds. The applied force and frictional force can be written from the free electron theory as follows:
An earlier study, the
acceleration of the spinless electron, is also taken into account. The derivations in the literature for Fourier’s law of heat conduction from free electron theory assume that the electron has attained a steady drift velocity. This assumption may be reasonable at steady state. However, in transient applications, immediately after the application of the temperature gradient, the electron would be in acceleration. This phase of motion of the electron has not been well studied in the literature. In this study, this is taken into account.
Newton’s second law of motion may be applied to the moving electron(s) as follows:
Eliminating the velocity of the electron in Equation (5) by using Equation (2) and taking the derivative of the velocity of electron as the time derivative of heat flux leads to the damped wave conduction and relaxation equation as shown earlier (Sharma [
40,
41]). By the equi-partitition energy theorem given in Equation (1), the velocity of the electron can be written as follows:
Differentiating Equation (6) with respect to time, and multiplying with the mass of the electron,
m, Equation (6) can be seen to be:
Eliminating the acceleration of the electron term between Equations (5) and (7) and plugging Equation (2) for heat flux in place of the velocity of the electron:
Multiplying Equation (8) by
:
Equation (10) is Fourier’s law of heat conduction. The expression for thermal conductivity of the material from Equation (10) can be seen to be:
The coefficient to the rate of temperature variation with the time term in Equation (9) can be simplified as follows. The rate of temperature variation with time can be called the
ballistic term. This term is unique to the acceleration of the electron and is expected to become significant in transient applications. The term “ballistic” can be used to denote acceleration effects. In an earlier study (Sharma [
41]), the collision time of the electron was shown to be 3τ
r where τ
r is the relaxation time of the materials as defined by Cattaneo [
25] and Vernotte [
26].
Substituting Equation (11) in Equation (9), Equation (9) becomes:
In terms of properties of moving electrons, Equation (12) can be rewritten as follows. Heat capacity at constant volume,
Cv, by definition is the energy needed to raise one mole of a substance by 1° K. For one molecule this would be (1.5 k
B) as a corollary of the equi-partition energy theorem (Equation (1)). The electron cloud is assumed to be ideal gas. It can be shown that for an ideal gas (Sharma [
31]):
Equation (13) is for one mole of the material. For one molecule of the material, Equation (13) can be written as follows:
Plugging Equation (15) into Equation (12), Equation (12) becomes:
It can be realized from Equation (16) that when the relaxation time of the material of heat propagation τ
r is 0.3 τ, where τ is the collision time of the electron, Equation (16) becomes:
Sharma [
41] showed that the relaxation time was found to be a third of the collision time of the electron with the obstacle when the Cattaneo-Vernotte-Maxwell equation of heat conduction was derived from free electron theory including the acceleration effects. Here the relaxation time is of one-third of the collision time of the electron and obstacle.
Further, it can be seen that the velocity of the electron,
ve, is approximately equal to the 95% of the velocity of heat,
vh. The velocity of heat is given in terms of the thermophysical properties of materials as given in Equation (17). The coefficient to the ballistic term in Equation (9) may be simplified as:
Plugging Equation (18) into Equation (9), Equation (9) becomes:
Equations (18)–(20) comprise an alternate non-Fourier heat conduction equation compared with that postulated by Cattaneo [
25] and Vernotte [
26] and Maxwell [
27]. Equation (19) for heat flux comprises two parts: (i) one part is the “Fourier part” which gives the spatial gradient of the temperature, both transient and steady states; and (ii) the second part is the “ballistic part” which gives the contribution of the acceleration motion effects of the electron. In the asymptotic limit of the infinite speed of heat,
vh, Equation (20) reverts to Fourier’s law of heat conduction. In the asymptotic limit of the null transfer of heat, Equation (20) indicates a jump in temperature after an elapsed time at a considered point in the medium. This is at zero drag. This may not be achievable in practical applications.
Another way of viewing the “ballistic term” is in terms of the accumulation effects in time of the energy at the interfacial area through which the heat is traveling. In the kinetic representation of temperature in terms of the square of the velocity of the molecules as given by Equation (1), the heat flux across an interfacial area is defined as the energy of the molecules leaving the surface less the energy of the molecules that enter the surface per unit time. Accumulation of energy during said time at the interfacial surface was neglected in the Fourier representation of heat flux with the spatial temperature gradient in Sharma [
10]. Here the accumulation of energy at the surface is also taken into account in the heat flux expression. This added term can also be viewed as a place to capture the acceleration effects of the moving electron under an applied temperature gradient/force. The postulated non-Fourier equation of Cattaneo [
25] and Vernotte [
26] and Maxwell [
27] is restated as:
2.3. Entropy Production Term
Jou [
1] wrote the entropy production term in terms of the entropic flux and accumulation as follows:
The combined statement of the first and second law of thermodynamics at constant pressure can be written as follows:
Applying Equation (24) to Equation (22), the entropy production term becomes:
For Fourier’s law of heat conduction, the entropy production can be seen to be always positive and in obeyance of the second law of thermodynamics. Equation (23) can be written as follows:
where the finite speed of heat
vh can be seen as:
Eliminating ∇T between Equation (26) and (25), the entropy production can be seen to be:
The entropy production can be seen to be positive for real heat events. The first term in right hand side (RHS) is always positive. The second term can give rise to a negative contribution only when the heat flux, q, and temperature accumulation have opposite signs. This would be a violation of an alternate statement of the second law of thermodynamics.
When the heat flux locally is positive, the accumulation in temperature at that point in that medium is also positive, i.e., the temperature increases with time at that point. It means that the heat is received at that point. Heat flux cannot be negative locally as well as the temperature rises locally at the same time. During cooling, the heat flux is negative locally and the temperature accumulation term is negative. In this case, heat is given out. The heat flux is negative as heat is taken away from that point. The temperature accumulation is also negative.
Polymer liquids are solutions of polymers and polymer in molten form. They behave in a different manner compared with the Newtonian fluids (Bird
et al. [
42]). The viscosity is no longer independent of the velocity gradient, causing the momentum transfer and flow of fluid when subjected to sufficient shear force. Polymers are macromolecules with higher molecular weight compared to small molecules. Staudinger defined when a molecule can be considered a macromolecule. These molecules are now believed to have many internal degrees of freedom. Pronounced “elastic effects” have been seen when practitioners worked with these fluids. Normal stresses such as τ
xx are needed in addition to the applied wall shear stress, τ
xy, in order to completely describe and characterize the flow of these fluids. The viscosity changes exponentially with change in the volume fraction of the polymer in the solution. The change of viscosity with temperature is exponential as well. Master curves have been developed by industrial technologists and rheologists and used in the industry.
Rheology is the study of deformation and flow of non-Hookean solids and non-Newtonian liquids. The Newton Law of Viscosity can be written as follows:
where τ
xy is the tangential shear stress and µ is the viscosity of the liquid and
vy is the velocity of the fluid in the
y direction. The gradient of the velocity is in the
x direction.
A flat plate atop a stationary fluid when pulled with a constant force will result in flow of fluid along the direction of the plate. After steady state is reached, the velocity profile in the fluid can be seen to be steady. The layers of fluid close to the plate reach speeds close to the speed of the plate. The fluid further away from the plate is unaffected and there is no motion of the fluid. The shear stress resulting from the tangential force causes the momentum direction in the azimuthal
x direction. The momentum transfer is in the direction of the azimuthal
x direction. The relation between the shear stress and shear rate is linear at steady state and is given by Equation (29). Before attaining steady state, the momentum transfer is not Newtonian. Other models such as the Maxwell model and Jeffrey model have been reported in the literature. The Maxwell viscoelastic model (Sharma [
10]) can be written as:
The term τ
mom is the relaxation time of the momentum. Sharma [
9] has shown in analogous heat transfer problems that this parameter is a measure of the acceleration time of the free electron that can be used to describe Fourier conduction before it reaches steady state. It was found to be about one-third of the collision time of the free electron and an obstacle. Equation (30) has been used to characterize viscoelastic fluids where µ is the zero shear viscosity. The effects of Equation (30) exist for all transient flows, Newtonian or otherwise. However, these effects are only seen in a pronounced manner in some materials. For instance, “silly putty” is considered viscoelastic. The material flows readily when squeezed slowly using the palms of one’s hands and may be considered to be in the viscous Newtonian state. The material can be rolled into a ball and the ball will rebound when dropped onto a hard surface. It can be expected that the stresses change rapidly and the material can be seen to behave analogous to an elastic solid. In some cases, Equation (30) is simplified to include only the shear rate term and the accumulation of the momentum term. This may be applicable when the changes are rapid. Sharma [
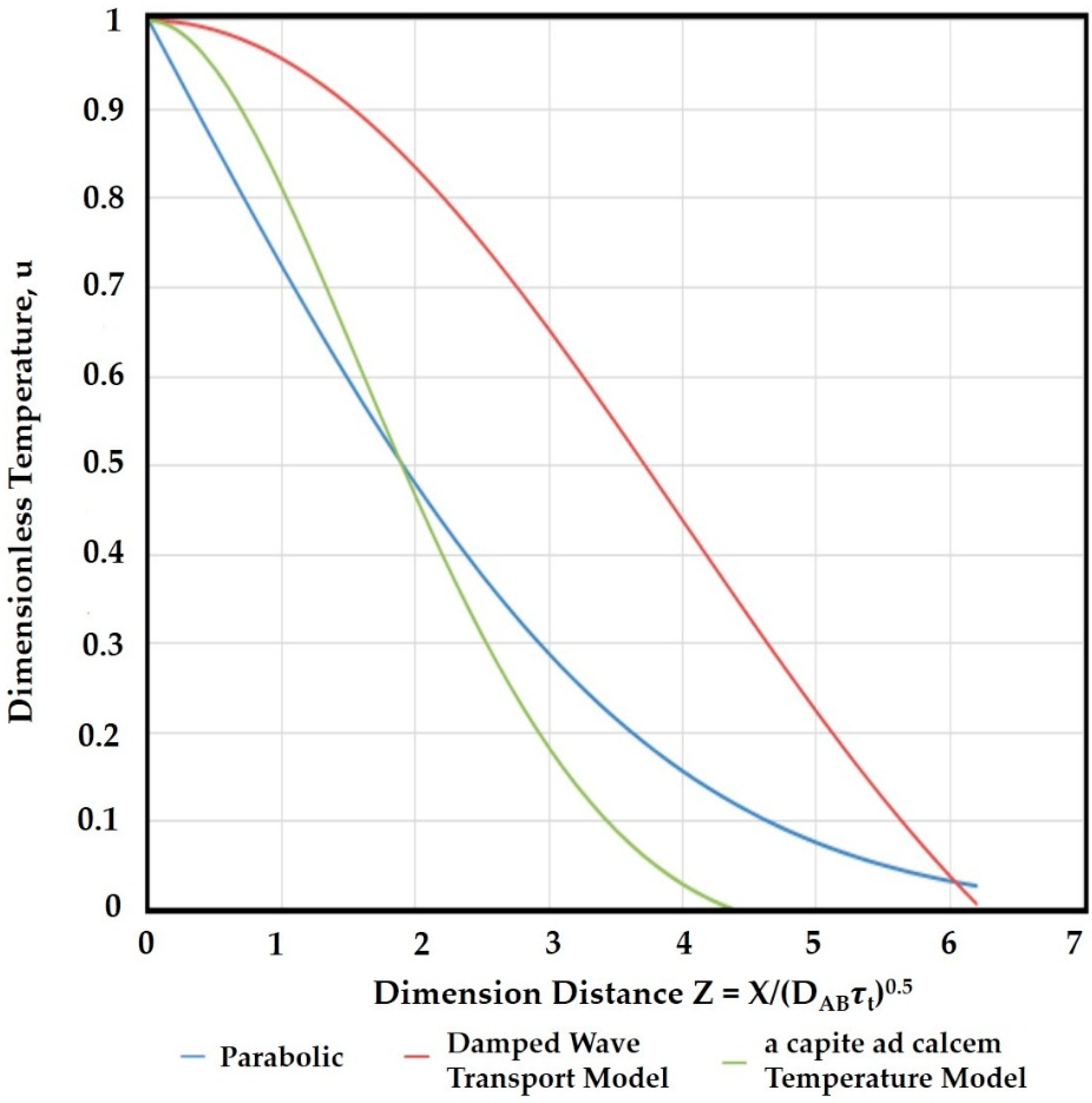
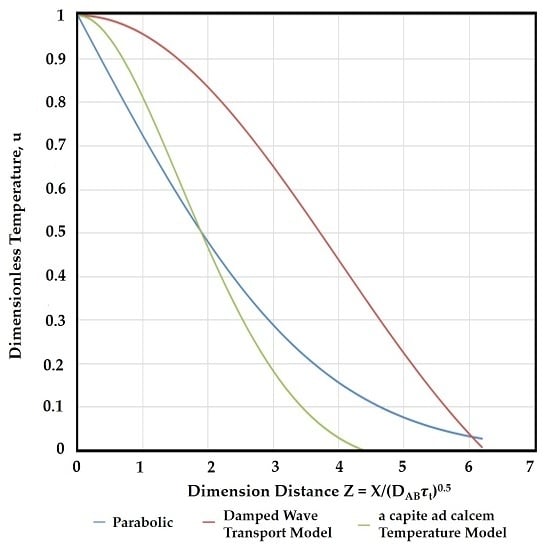
9] discussed how poor use of the initial conditions can result in model solutions that may be in dissonance with the second law of thermodynamics using Equation (30). Damped wave transport and relaxation were studied. The results from an in-depth study of the Cattaneo and Vernotte non-Fourier heat conduction answered a few questions. One issue is that the entropy production becomes negative when the momentum flux is high and the momentum rate is in the opposite direction. This can lead to a violation of the second law of thermodynamics locally. The “overshoot” phenomena were shown to be a mathematical artifact and, when physically reasonable, the final time condition or the higher accumulation of the temperature condition is used and the overshoot was found to disappear. An equation to describe real mass diffusion is derived from Gibbs’ chemical potential formulation for a non-relativistic solute particle. The acceleration term eliminated between the equation of motion for the spinless particle and the accumulation of chemical potential formulation leads to an equation for mass diffusion that is
a capite ad calcem in concentration (Equation (39)). This entropy production for this term can be seen to be positive for real mass transfer events. The d
C/d
t, the time derivative of concentration and mass flux, can either be “both positive” and “both negative” but never one positive and one negative for spontaneous mass diffusion events. So for all
extemporaneous and practical purposes, the second law of thermodynamics is obeyed.
The Nobel Prize in 1991 was obtained by P. G. de Gennes. He discussed in his Nobel lecture what are called “complex fluids”. Natural rubber, enzymes, hydrophobic/hydrophilic surfactants, nematic crystals, ferroelectric smectics, and Ferro fluids made of magnetic particles are examples of complex fluids. He looked at the trajectories of non-relativistic particles and applied the Schrodinger wave equation to explain Raleigh Bernard instability. The behavior changes completely upon “cross-link” formation in the rubber. The relaxation time can be expected to be high for the cross-linked systems. When the rubber chains are elongated or present in chain-extended configuration, the relaxation time can be expected to be short.
Chrysler has introduced electrorheological fluids in the automatic transmission systems. The viscosity of the fluid changes by an order of magnitude upon application of an electrical field. The Fahreus Lindquist effect has been seen during blood flow through narrow capillaries. The viscosity of the fluid appeared to change with the diameter of the capillary. Some of these experimental observations can be explained using the viscoelastic nature of transient flow.
The Jeffrey model (Sharma, [
43]) can be seen to be:
where λ
2 can is a retardation time.
Polymeric liquids were seen (Bird
et al. [
42]) to exhibit constrained recoil after the cessation of flow in a circular fluid in contrast to Newtonian fluid. The polymeric liquid was supposed to have “fading memory”. The Weissenberg rod-climbing effect is when the polymer liquid forms a convex meniscus or moves up a rotating rod in a beaker of fluid.
Au contraire, the Newtonian fluid forms a concave meniscus and forms a trough around the rotating rod in the beaker of fluid. Secondary flows have been observed in polymeric fluids when a disk is rotated in the fluid. The Weissenberg rod-climbing effect can be used in a tubeless siphon when the polymeric fluid is extruded. Near a laterally oscillating rod, the induced secondary flows in polymeric fluid are in the opposite direction of the induced secondary flow in Newtonian fluid.
2.4. Transport Parameters
The motion of oligonucleotide fragments in different gels is a vast subject. There are different regimes of transport where some considerations are more important than other considerations. Calibration is used in the inference of sizes in chromatographic and electrophoretic migrations. Diffusion of oligonucleotides is a phenomenon that is not well characterized under transient conditions. The critical events are the migration of molecular fragments over varying distances depending on their molecular sizes. Calibration is used in order to convert the raw measurements to sequence information. It is not clear why mathematical models are not used for interpretation of the electrophoretic pattern or the paper chromatographic pattern. It is being realized increasingly among investigators that at short time scales, Fick’s description of transient diffusion is not an adequate representation of all the events. Molecular diffusion principles are revisited with particular attention to the derivation of Fick’s laws of diffusion from chemical potential formulation. A generalized Fick’s law of diffusion is used to account for all the transient time events that occur during a real process. The implications on the electrophoretic techniques and sequence errors and shotgun sequencing may be important. The mathematical framework to describe molecular diffusion needs to accommodate terms for the acceleration of the solute in motion. The Newtonian acceleration of a spinless solute without the Brownian dynamics, when accounted for, can lead to spatio-temporal concentration profiles that can be drawn without violating the second law of thermodynamics. Sharma [
8] has listed seven reasons from the works of Nobel laureates Onsager, Landau, Nernst for the non-universality of Fick’s law of diffusion. Fick’s law of diffusion can be written as follows:
where
J is the molar flux with units of (mole m
−2),
DAB is the binary diffusivity,
CA is the concentration of the diffusing solute and
z is the spatial direction of the solute transfer. The solute transfer is considered to be one-dimensional. When motion in other dimensions becomes important, terms can be added for each ordinate. The diffusion coefficient
DAB is obtained from the Stokes–Einstein formulation as follows:
where k
B is the Boltzmann constant with units of J molec
−1K
−1, T is the absolute temperature,
f is the molecular drag coefficient, µ is the viscosity of the surrounding medium, and
R0 is the radius of the solute molecule. Rigid spheres are assumed. Equations (32) and (33) are derived as follows. The chemical potential of an ideal solution of solute A in solvent B can be written as:
The mole fraction
xA can be approximated for dilute solutions as
. At steady state, when the solute is in motion caused by the chemical potential gradient, the driving force and drag forces will be equal to each other and:
The molar flux
J″ =
is given by
CAvA and:
The Stokes drag is
f = 6 µπ
R0. The diffusion coefficient recovered from Equation (36) by comparing Equation (36) and Equation (32) can be seen to be the same as given for the diffusion coefficient in Equation (33). Equation (36) is at
steady state. Often times, during the electrophoretic measurements there exists a time period between the start of the experiment to the time when the fragment motion can be considered to be at steady state. During this transient regime the solute molecules can be expected to undergo
translational acceleration. The Newtonian acceleration effects are not accounted for in Fick’s law of diffusion. The use of the Cattaneo and Vernotte equation in order to account for transient diffusion effects was discussed in Sharma [
41]. The acceleration motion of the diffusing solute may be modeled by looking at the accumulation of the chemical potential. Thus, Equation (35) can be written including the accelerating term and:
After realizing that the velocity of molecule
vm can be taken as the velocity of mass
vmass, (Sharma [
34]) it is characterized by a relaxation time τ
mr such that:
Equation (37) can be seen to be:
where τ
mr is the mass relaxation time. It is a characteristic measure of the acceleration time of the solute from the instant of application of the driving force which causes the flow to the steady state regime. It can be seen to be:
where
N is the molecular weight of the oligonucleotide. The velocity of mass from the Maxwell speed distribution of molecules for ideal gases can be written as in Sharma [
44]: