1. Introduction
Electrification of the global transport sector is expected to be rapidly increasing in the coming decade. The global electric vehicle (EV) stock is predicted to reach 140–245 million by 2030, which is about more than 30 times of today’s amount. The increase of EV demands concurrent increase of production of automotive batteries, where global EV battery capacity is predicted to be increased from today’s value of around 170 GWh per year to 1.5–3 TWh per year in 2030. This drives a remarkable cost reduction in batteries together with increased use of improved technologies. Although there exists novel advanced battery technologies, lithium-ion batteries are the most likely to dominate the EV battery market in the recent future [
1]. With the existing and upcoming lithium-ion battery technologies, the cost reduction in battery production is to be achieved with high quality standards, automation, improved manufacturing technologies, and maximum energy and resource efficiency [
2].
On the other hand, the increasing use of EV batteries in the world creates a significant impact on both the society and the environment as it demands policy changes related with electrification, resource and money allocation, and the production of green energy. Therefore, there is a need for the availability of transparent information especially on cost and energy requirements in battery production. Battery manufacturing process details in this regard is available in the industry, but quite rare in the scientific community or the public. Furthermore, different battery manufacturing process steps have different energy and material demands and will thus result in different global warming potential (GWP) emission values, when expressed using life-cycle assessment (LCA) studies. The existing GWP emission data for automotive lithium-ion battery production is in the range of 1.1–424
CO
2-eq. per 1 kWh of battery pack capacity [
3,
4,
5,
6], while the existing energy usage (energy for production per energy storage capacity) data is in the range of 28–740 Wh for producing 1 Wh of stored cell energy [
7,
8,
9]. The source of the high variance in the data is from the use of generalized data for inherently different battery production systems. Most of these data are based on estimations or old plant data which cannot be applicable to today’s plants of much higher capacity, and with technologies and materials that are different to each other. The production systems and their energy demands vary with the factory capacity, location of the factory, type, energy and chemistry of the battery cell that is being produced, and the specific technologies that are used [
10], as illustrated in
Figure 1. A general trend in here is that the energy demand for production is reduced when the size of the factory (capacity) is increased significantly.
A process model of a general battery cell manufacturing plant which is flexible to the key factors such as plant capacity, cell chemistry, cell type and process technologies, can cater these variations due to its physics-based design nature. Furthermore, it could provide a benchmark for the battery production energy values. An added advantage would be the ability to incorporate in to LCA models to provide specific material and energy values for their respective LCA studies. Once established for known cell chemistries, such a model can compare different cell material and chemistry options as well as different technologies and energy minimization options. A cell manufacturing model that can compare different options can be well used in LCA studies as well as in plant design and technology developments.
Therefore, the main aim of this study is to develop a generalized, industrial scale, lithium-ion battery cell manufacturing model for calculation of energy and material demands for different production volumes, process steps, cell types, and chemistries.
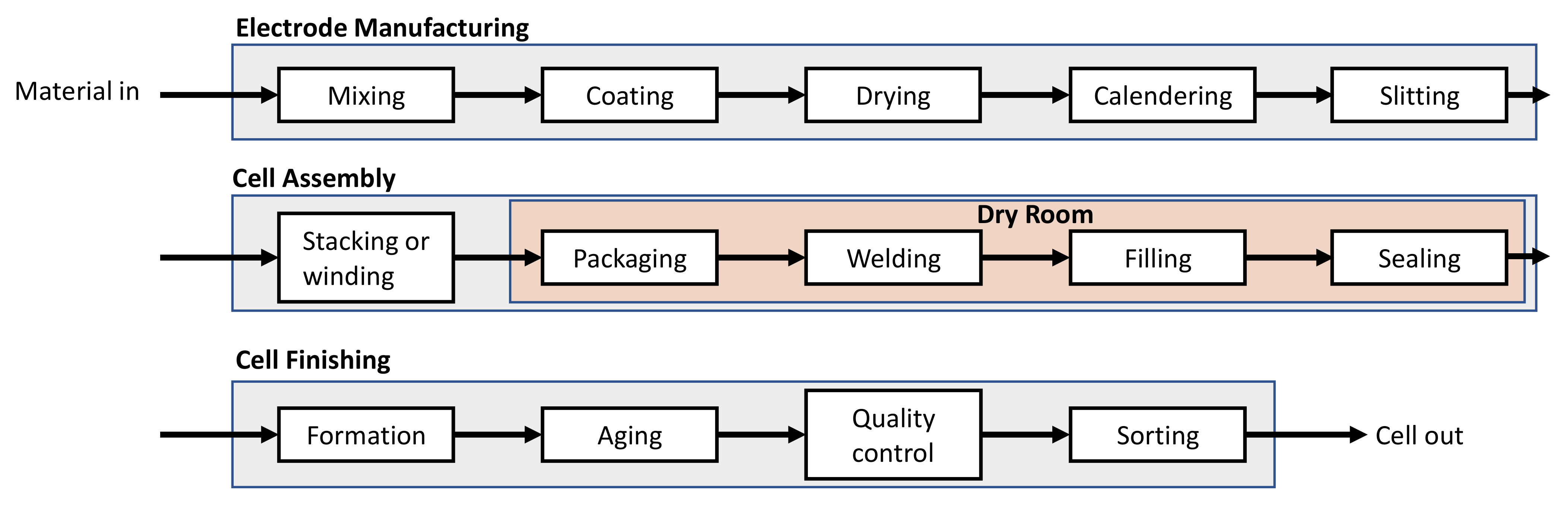
For the modeling of this process, a thorough understanding of each process step is needed. Most of the knowledge in this regard is available on the experimental level and pilot scale plant level. Out of these, many experimental studies have done on different cell manufacturing process steps [
15,
16,
17]; however, only a limited number of modeling studies have been undertaken.
These models are developed for individual process steps of the cell manufacturing process, which are mostly focused on the quality and performance of the product. For the calendering process, a Heckel-based model is developed for the lowest achievable coating porosity by Meyer et al. [
18], which also can find the influence of different active materials on the compaction behavior during calendering. The model by Schreiner et al. [
19] determines the output porosity after calendering based on the input parameters such as roll temperature, velocity, coating thickness, adhesion strength, and machine behavior parameters. Similarly, for mixing, Mayer et al. [
20] have used a model to investigate the dispersion process and breakage of carbon aggregates. Furthermore, Cunha et al. [
21] have used several machine-learning techniques to model the interdependecies between the parameters of slurry mixing and the electrode properties. Similarly, Thiede et al. [
22] have used multivariate regression-based models to relate the intermediate product parameters and cell performance parameters, while Komas et al. [
23] have used data and expert driven models to find the cause-effect relationships in cell manufacturing process chain.
Moreover, Chouchane et al. [
24] have developed a model to find out the electrochemical performance of a battery for different material compositions. Similarly, Schneider et al. [
25] have developed a pseudo-2D electrochemical model which can calculate the electrochemical performance for various geometries of lithium-ion batteries. There are also a few studies on process operation-oriented modeling done by Ahmed et al. [
26], Oppegård et al. [
27] on electrode drying process, where the parts of these models are used in this study and discussed in detail in
Section 2.1 where the model is described.
On the structuring of the process model, a good candidate structure can be adapted from various model structures of material and energy flow modeling of general manufacturing process systems. Some of these structures are holistic hierarchical bottom-up structured models which starts from machine level, and goes up to unit level, process chain level to pilot scale factory level [
28,
29,
30]. These are usually data-based models which depend on real-time data acquisitions systems. These models are good for individual plants where it is specialized in energy optimization for the specific plant; however, these are difficult to use for general cases as it is based on specific stochastic systems, and often not open to integrate with other models such as ecological/LCA models.
However, there is a study on cell manufacturing process model, where Thomitzek et al. [
31] introduced a conceptual multilevel modeling approach which links a process chain model that consists of a set of deterministic process models and an electrochemical cell model together. This model approach is expected to predict the performance of the cell based on the initial raw material characteristics and various process parameters. Using this concept, they have analyzed different model uncertainties and how these uncertainties propagate through the process. The results of a case study have shown that out of the uncertainties of coating, drying and calendering, the coating uncertainties (which propagate to thickness and mass loading) have the most impact on the cell performance in four different scenarios [
32].
The same model structure with slight changes is adapted in this study to develop the industrial scale process model (
Section 2). A case study is presented, and the model results are tuned to a similar industrial case, analyzed and compared with the available literature values (
Section 3). Furthermore, a sensitivity analysis is performed for analyzing the effect of different cell chemistries and process parameters on the model results. Finally, it is concluded that the flexible model can provide a theoretical benchmark energy value with low variance for various cell types, chemistries, process technologies and plant capacities (
Section 4).
3. Results and Discussion
The results from the selected case study are presented here. A prismatic cell of a cathode chemistry of NMC333 and an anode chemistry of graphite (NMC333-G) is selected with a 2 production capacity per year. The intensive mixing and convection air drying is selected from the available technologies of the model.
3.1. A Typical Material Flow for the Cell Production
The material flow for the selected throughput is calculated for each battery material component, which are active material, carbon, binder, solvent, current collector, separator, and electrolyte. The amount of scrap material is predefined as a percentage of 5–8% of the cell material [
13]. The total material flow through each process step is illustrated in
Figure 4. As the solvent recovery unit is not included in the model, the evaporated solvent is categorized as solvent waste. The composition of one cell of
of material weight is listed in
Table 1. The active material, carbon and binder mass ratio were referred from the BatPac model by Nelson et al. [
36], which for the anode is 95:0:5 and for cathode is 96:2:2, respectively. The difference between the anode and cathode total mass and the amount of solvent can be seen both from
Figure 4 and
Table 1.
3.2. A Typical Energy Flow for the Cell Production
The tuning parameters of the model described in Equation (
21) are tuned to industrial data of a similar capacity, and same prismatic NMC333-G cell production facility published by Dai et al. [
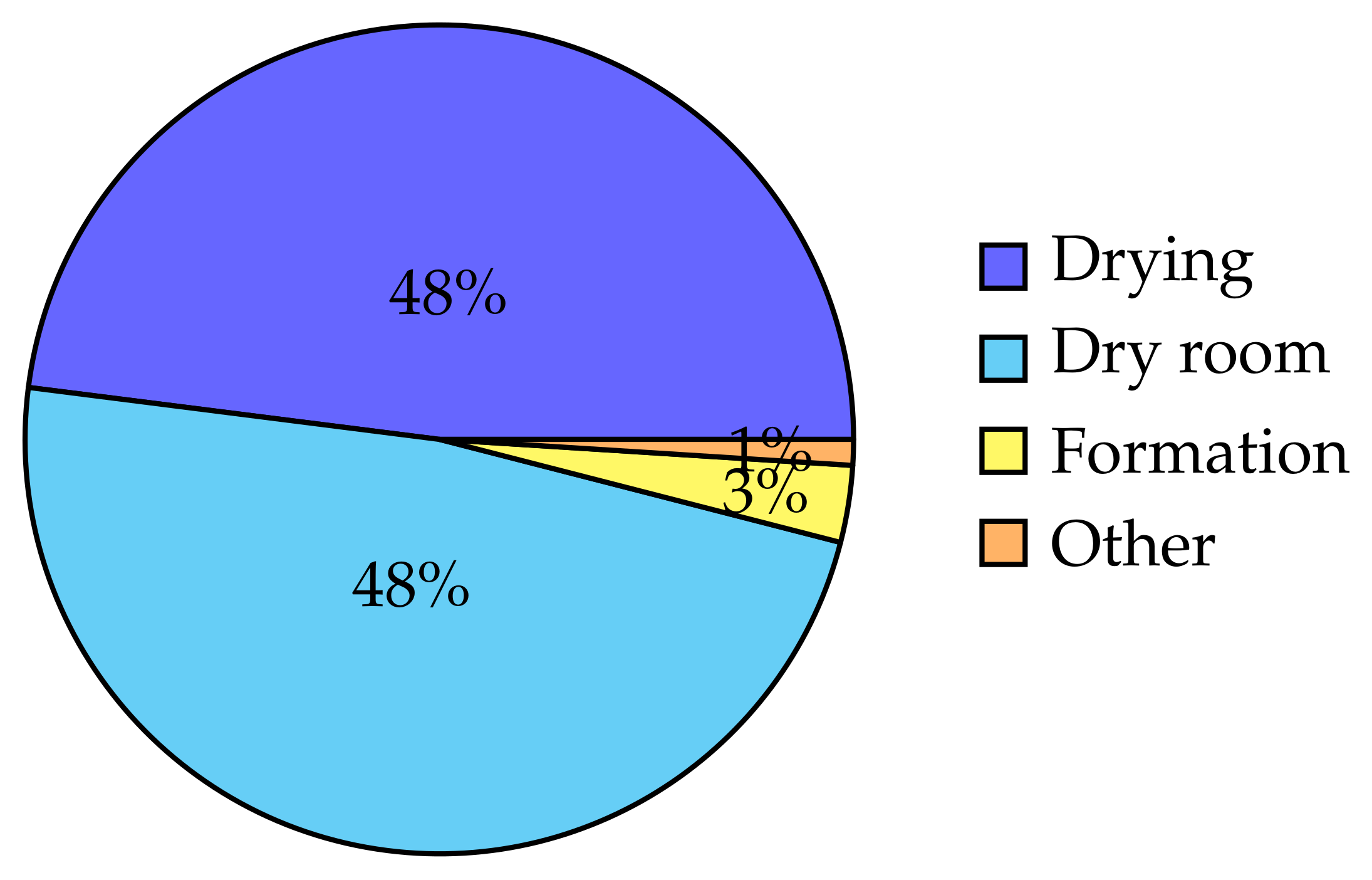
11]. The energy breakdown for the case study is shown in the pie chart in
Figure 5. Both the drying energy and dry room energy dominate than the other process steps. All the energy values are presented as electricity values, although it includes air heating and cooling energy. This is because the energy sources for the air heating and cooling are not decided in the model, hence lack the conversion factors. The energy values for each process step in detail is listed in
Table 2 in terms of
for
of the produced cell. The total energy requirement is
.
It is clearly seen that for mixing and drying, the cathode needs more energy than the anode. Cathode active material mass is higher than the anode active material mass, for this specific battery composition. Accordingly, the slurry mass is higher for cathode; thus, the mixing energy is also higher than the anode. For drying, the drying rate is slower for the cathode due to the NMP being the solvent that is evaporated as opposed to water evaporation rate of anode. The combined effect of the lower drying rate and the higher solvent mass that is being evaporated, resulted in the higher energy usage for cathode than anode drying. The high dry room energy requirement is mainly due to the environmental conditions of the ambient air, and the air flow rate that is needed to be circulated, which is based on the capacity of the plant. The formation step represents the energy for formation, which usually takes a long time compared to the other processes.
3.3. Comparison of the Case Study Results with the Available Literature Values
The availability of energy and material data on lithium-ion cell production is limited. Most of the data are from different LCA studies. Some of the most recent LCA and other studies on lithium-ion battery production is listed in
Table 3 together with the type of the battery that is studied and the source of production data that is used for the calculation. The values indicate a high variance throughout the studies (1–846
, although the LCA inventory values are based on the same set of base studies. Most of these studies do not include the plant capacity, type of the cell, and also these do not include different techniques or the individual process steps, which could have contributed to the high variance indirectly.
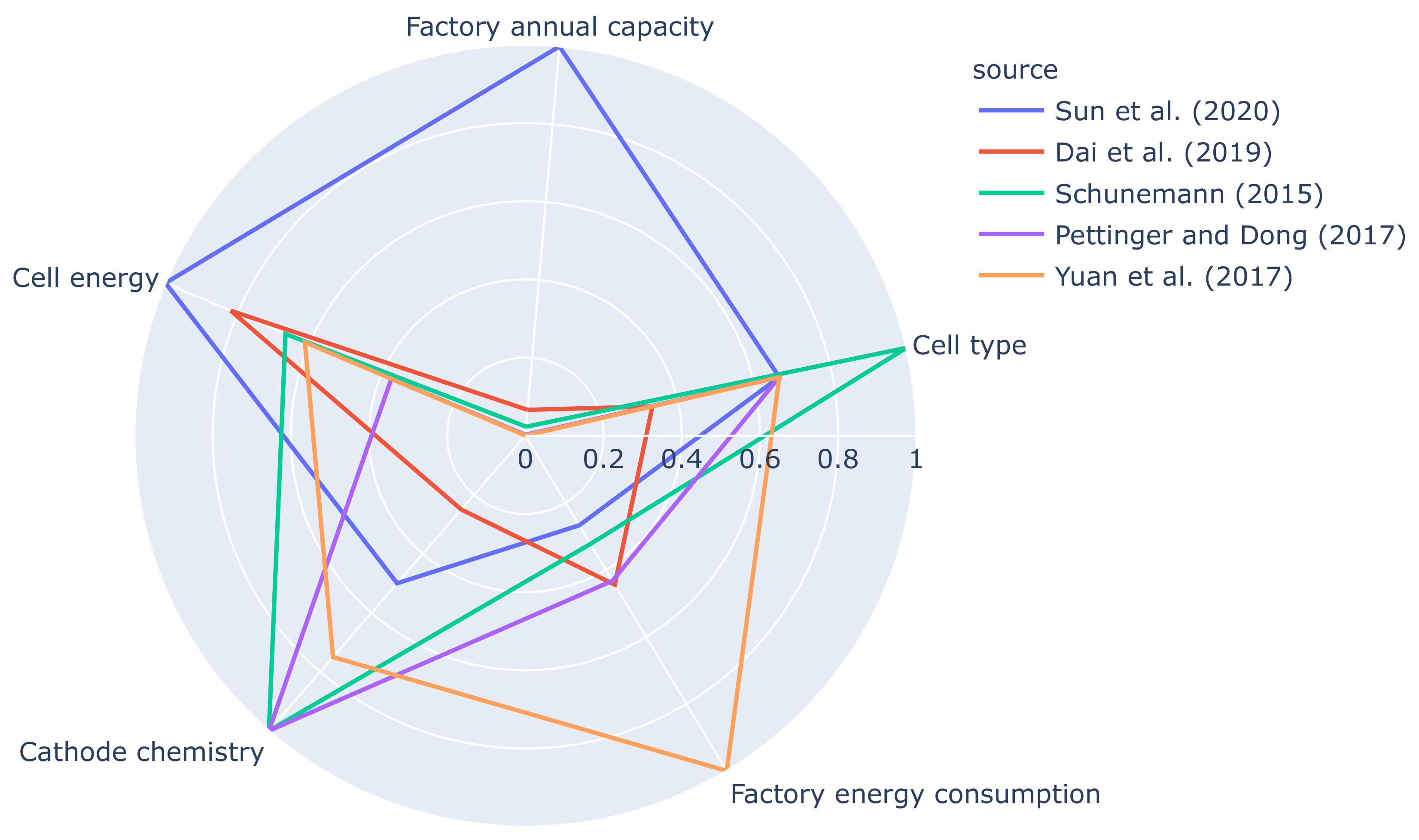
However, there exist a few studies where the calculations are based on actual plant data of various annual production capacities. The energy breakdown of these data into each process step and their plant capacities, cell energy, cell chemistry and cell type are listed in
Table 4. The general trend of these data is that the energy usage reduces when the annual capacity increases, probably due to the fact that mass production plants are designed for optimum profit and energy with various energy recovery methods in place. In contrast, most pilot scale plant facilities are designed for research purposes, where the main focus is for optimum product quality than the energy usage.
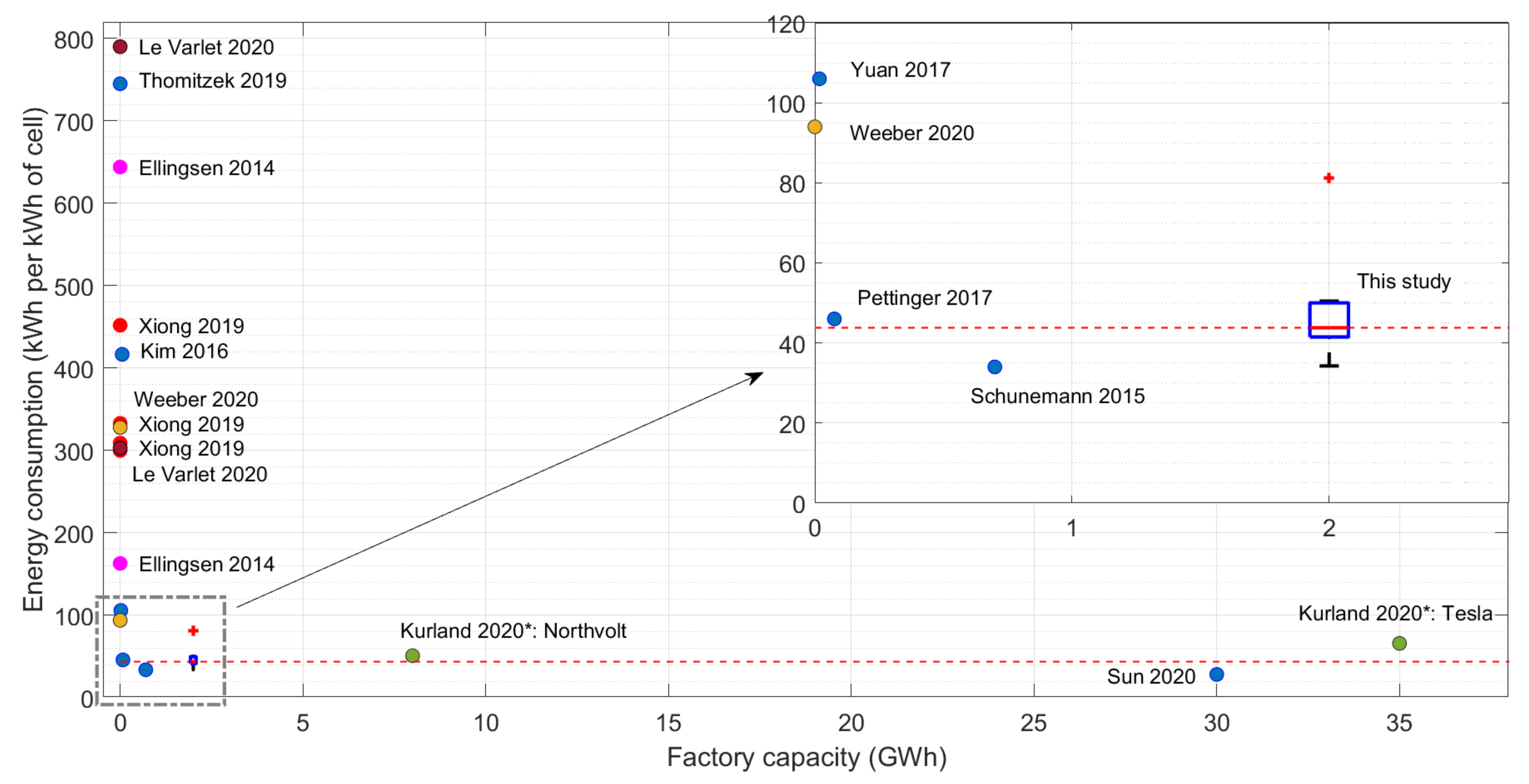
The cell type, chemistry and the plant capacity of the case study is selected to match the study by Dai et al. [
11]. The parameters are tuned to match the average value of the data range. The existing literature data against the plant capacity is plotted in
Figure 6, along with the model results that were tuned to data by Dai et al. [
11]. Whenever the studies have not specified the plant capacities for their data, it is assumed to be zero and plotted along the y-axis. Furthermore, the entire distribution of energy values from the case study without changing the tuning parameters or the process parameters are plotted here.
Considering the giga-scale industrial plant data, the model results for the same battery chemistry as the 30 GWh plant data by Sun et al. [
7] are slightly higher than the literature value, which is expected due to the capacity difference of the model and the plant. Furthermore, the model results are in the same range of 8 and 35 GWh plants estimated by Kurland [
9]. The estimated data are only for the electricity consumption thus can assume to have underestimated. However, the 8 GWh factory is still under construction and the 35 GWh factory is recently built in 2017, thus the potential use of heat could be marginal.
The model results are comparable with most of the giga-scale factories, and it also shows that with the increase of capacity more than 2 GWh, the change of energy usage is very small. However, the data by Sun et al. [
7] suggest that the energy usage can be further reduced, thus energy optimization methods need to be included in the model in the future for better results.
3.4. Sensitivity Analysis
A sensitivity analysis is done to find out the influence of various process parameters and the battery chemistry on the energy consumption of the production process.
3.4.1. Influence of Cell Chemistry on the Energy Usage
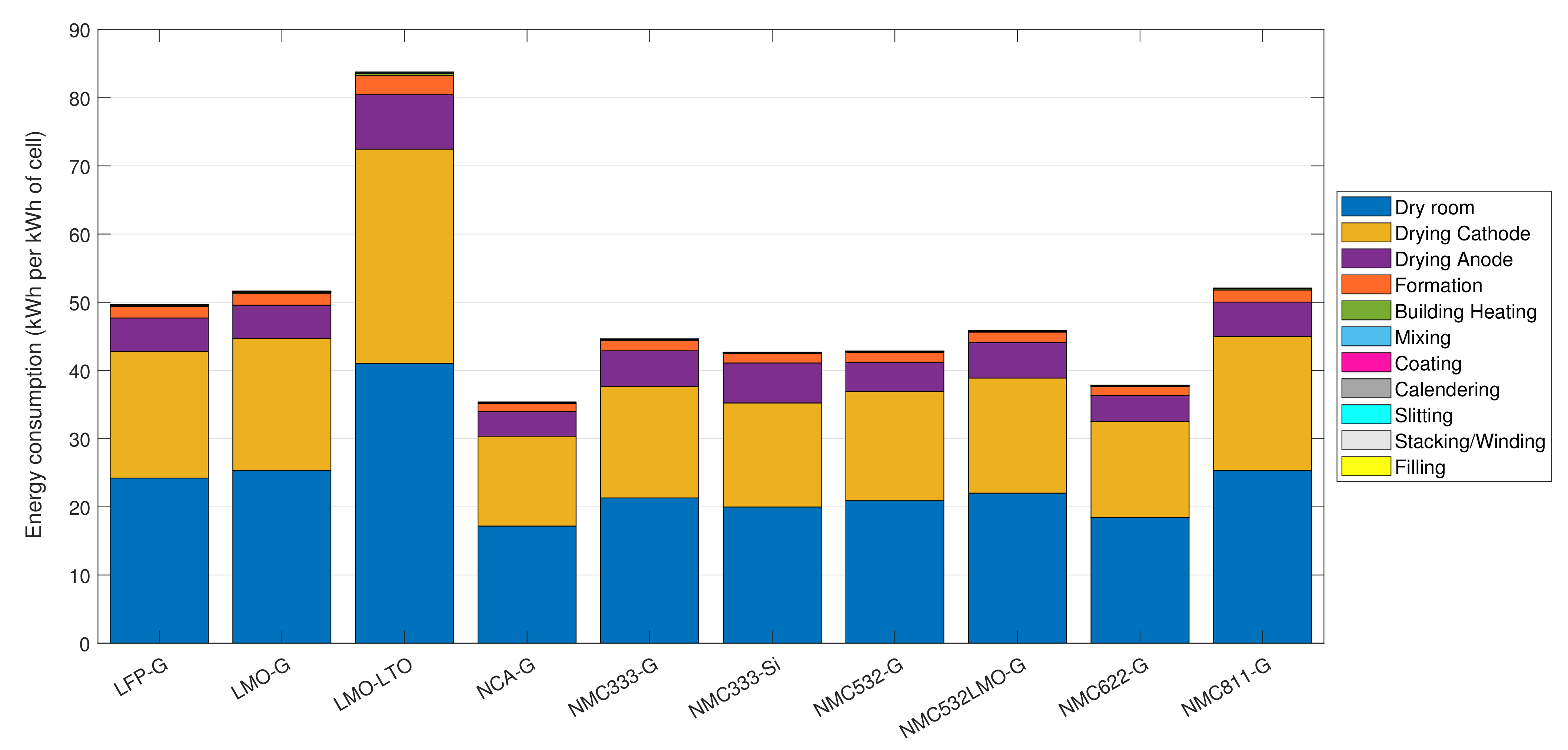
The total energy usage and their breakdown into each process step for various types of cell chemistries are shown in
Figure 7. The process parameters were kept the same as what is used in the case study. The energy values show a high variance in the figure as the cell energy changes with the cell chemistry (
). However, the mean and standard deviation of energy usage per mass is
. LMO-LTO cell has LTO as the anode, and therefore having NMP as the anode solvent. Furthermore, it also has the highest mass for 1 cell, which in combination have resulted a considerably higher energy usage than the other cells. NCA-G cell has the lowest energy usage, while most of the NMC-G cells have a similar energy usage except NMC811-G, which is slightly higher than the rest of NMC cells. The NMC333-Si has a slightly lower energy usage than the NMC333-G cell, although the Si anode cell has the highest energy density among the selected cells. Although the total energy usage varies, the percentage energy breakdowns for each process step do not have a significant variation.
3.4.2. Influence of the Process Parameters on the Energy Usage
The process parameters of each process step are crucial for the final quality and performance of the cell. For example at the wet mixing step, the homogeneity of the slurry, particle size, viscosity and purity are the most important parameters and thus affect the quality of the electrodes [
2,
16,
41,
42]. Different drying and coating product parameters such as the homogeneity, thickness of the coat, mass loading, porosity, conductivity, adhesion and cohesion during the drying, residual humidity of electrode and surface finish influence the final cell performance. Similarly, the process parameters such as the drying temperature, evaporation rate, and speed of air flow affect the physical qualities of the electrode and the electrochemical performance [
34,
41,
42,
55]. The parameters in the formation process such as the internal resistance of the cell, formation and stability of the SEI are the most important quality parameters as these influence the cell performance [
45].
Furthermore, these process steps are interdependent, and their process parameters influences the optimum performance characteristics of the produced cell. Moreover, the process technologies, process parameters, and the quality of the produced cell highly depends on the manufacturer, the type of battery being produced, and the battery materials. This makes optimization of the process as well as generalized modeling difficult. Furthermore, the machinery for each process step is usually provided by different machinery and plant manufacturers who specialize in each step, which becomes a challenge to integrate, automate and optimize into a technologically balanced process [
2].
In the simplified model, the process quality inter-dependencies are not modeled. The process parameters are selected to be optimum values from the available literature; therefore, each process unit is isolated in terms of quality of the final cell. This is mainly because the model does not include a cell model for determining the electrochemical performance based on the components. Hence, it is important to see how a certain deviation of these process parameters will affect the final energy consumption through a sensitivity analysis.
Each process parameter is considered to be a distribution of 2000 samples that are taken from a pool of a normal distribution with a mean of the optimized value and a standard deviation where at least 99% of the normal distribution is included in the sample distribution. Then a random combination of each process parameter for the selected process is simulated and the resulting total energy usage distribution is taken for analysis. Only the mixing, drying, formation and dry room are selected for the analysis as these are the model units that contain process parameters. The process parameters that are used in the sensitivity analysis is listed in
Table 5 with their mean values and the standard deviations. The means and standard deviations of the resultant energy usage distributions (in
) are also shown in
Table 5 while the entire distributions are shown in
Figure 8.
The mixing and formation parameters have less influence on the total energy as the contribution to the total is low. In contrast, the drying and dry room have the biggest contributions to the total energy, and the parameters have a larger influence on the total energy. However, the parameters of dry room, such as the air flow rate, air temperature, humidity, and dew point of the dry air affect to the total energy more than the drying parameters such as drying temperature and rate. The clear separation of all the distributions at the high energy values are the corresponding values from the LMO-LTO cells, where the total energy demand is considerably higher than other cell chemistries. The means and standard deviations of the energy distributions are , , , (), for mixing, drying, formation and dry room, respectively. This shows that the drying and dry room parameters have a high impact on the energy consumption of the model.
3.5. Limitations
The model consists only the most energy intensive process units in detail, and the models are simplified. Cell performance and process parameters are not interconnected as it should be, therefore needs inclusion of these for a better model result. Most of the additional units, such as solvent recovery unit and desiccant regeneration unit, and some of the utilities such as water distribution systems, lighting systems, and ventilation systems are not included due to the complexity. Therefore, the resolution of the existing model is quite low, thus these units should be included in the model for a better resolution and accuracy. To overcome some of these limitations the model is tuned using tuning parameters; however, it is not always possible when the necessary data is not available. Furthermore, the model is validated with existing literature values and further validation using industrial data would enhance the accuracy of the model.
Apart from benchmarking, the model can also be beneficial in identifying different strategies for minimizing energy usage, either by optimizing the process parameters or by recognizing energy intensive process steps. Although this is limited in the current model, this can also be improved by the inclusion of additional utility units to identify different energy reduction strategies within the process, and/or by inclusion of cell performance relationships to process parameters as discussed above.