Key Figure Based Incoming Inspection of Lithium-Ion Battery Cells
Abstract
:1. Introduction
2. Materials and Methods
2.1. Cells and the Professional Test Environment
2.2. Test Scheme of the Incoming Inspection
2.3. Parameter Determination and Evaluation
3. Results
3.1. Correlation of Parameters
3.2. Key Figure Based Performance Assessment
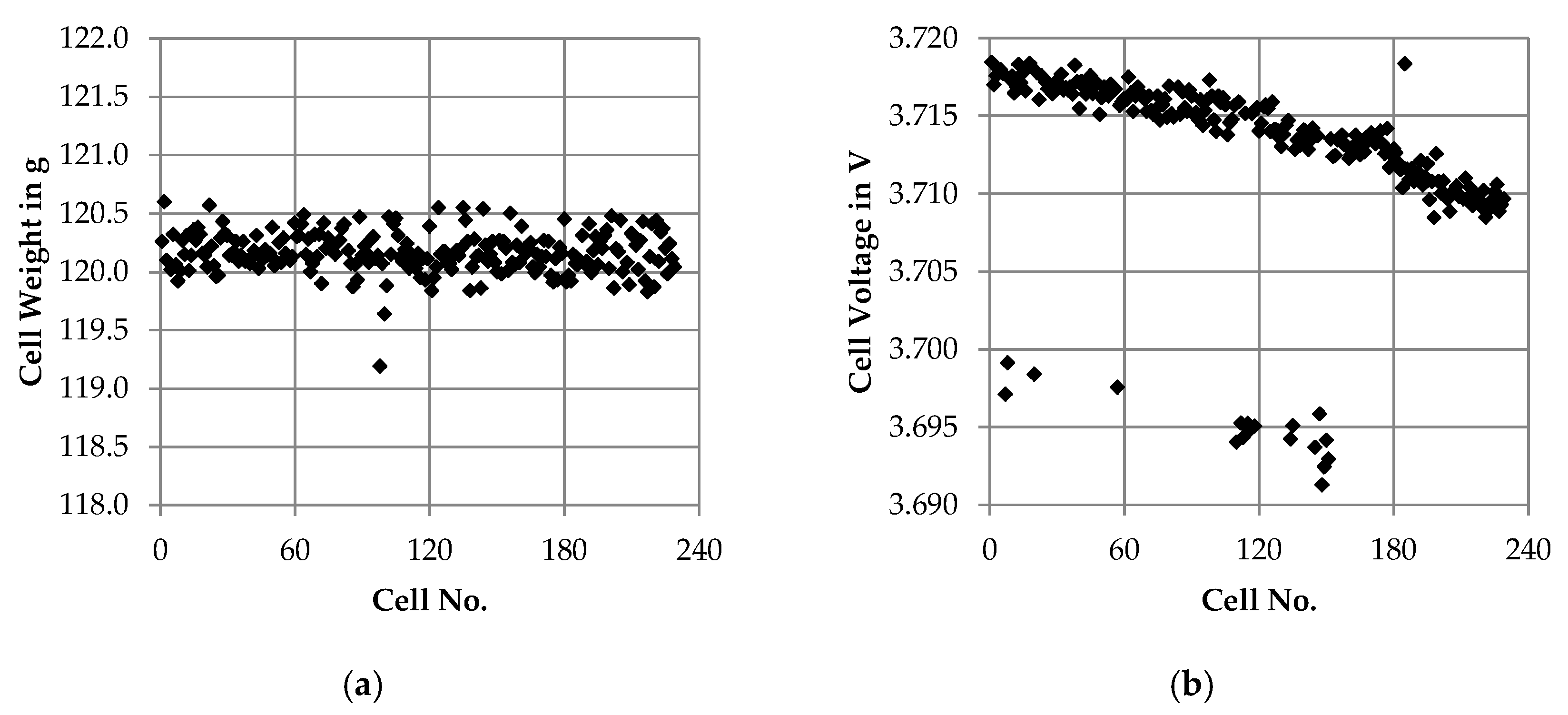
3.2.1. Receiving Inspection
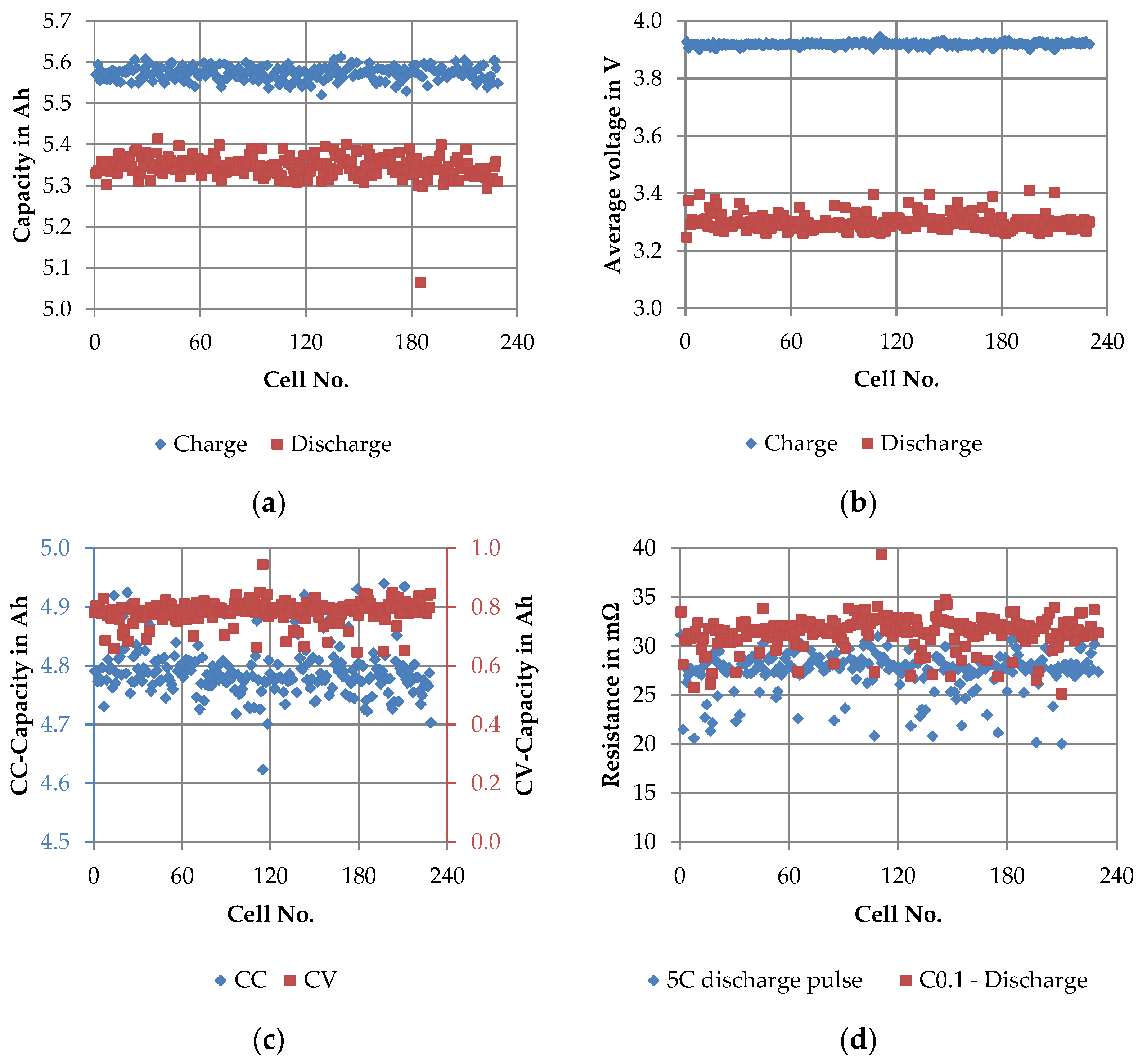
3.2.2. SQT—Short Quality Test
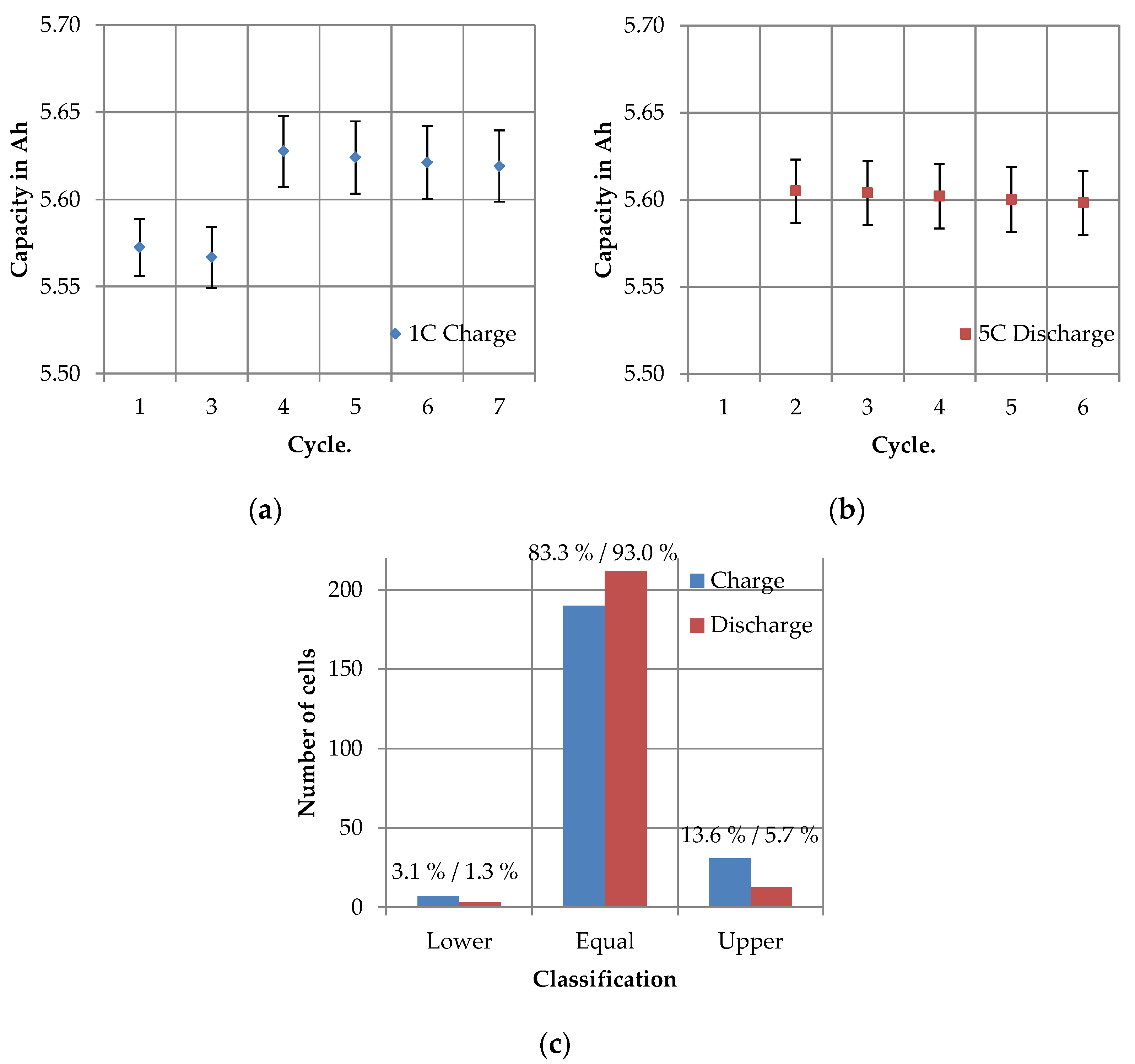
3.2.3. LQT—Long Quality Test
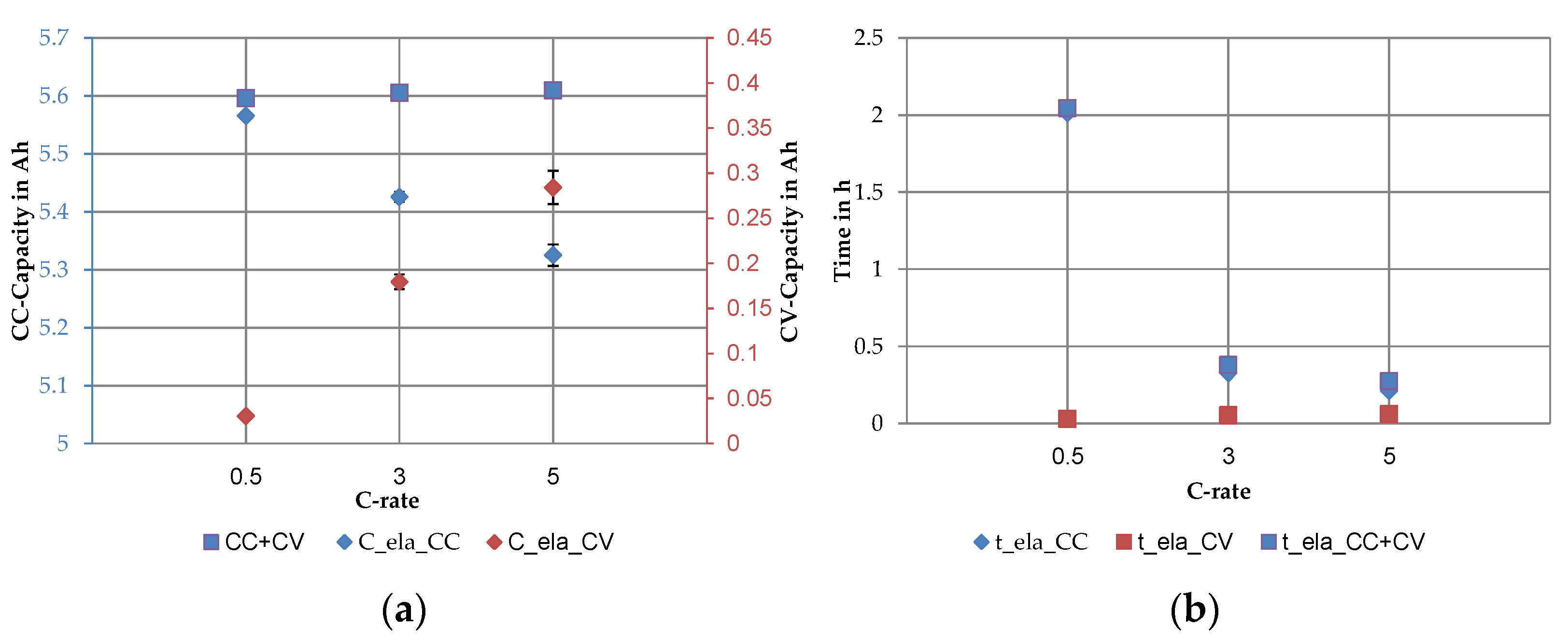
3.3. Key Figures of SQT and LQT in Comparison
4. Discussion
4.1. Correlation of Parameters
4.2. Performance Assessment
4.2.1. Receiving Inspection
4.2.2. Short Quality Test
4.2.3. Long Quality Test
4.3. Key Figures of SQT and LQT in Comparison
4.4. Recommendations for the Design of Test Procedures in the Incoming Inspection
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Leuthner, S.; Korthauer, R. Handbuch Lithium-Ionen-Batterien; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Placke, T.; Kloepsch, R.; Dühnen, S.; Winter, M. Lithium ion, lithium metal, and alternative rechargeable battery technologies: The odyssey for high energy density. J. Solid State Electrochem. 2017, 21, 1939–1964. [Google Scholar] [CrossRef]
- Winter, M.; Barnett, B.; Xu, R. Before Li Ion Batteries. Chem. Rev. 2018, 118, 11433–11456. [Google Scholar] [CrossRef] [PubMed]
- Schmuch, R.; Wagner, R.; Hörpel, G.; Placke, T.; Winter, M. Performance and cost of materials for lithium-based rechargeable automotive batteries. Nat. Energy 2018, 3, 267–278. [Google Scholar] [CrossRef]
- Wagner, R.; Preschitschek, N.; Passerini, S.; Leker, J.; Winter, M. Current research trends and prospects among the various materials and designs used in lithium-based batteries. J. Appl. Electrochem. 2013, 43, 481–496. [Google Scholar] [CrossRef]
- Lu, L.; Han, X.; Li, J.; Hua, J.; Ouyang, M. A review on the key issues for lithium-ion battery management in electric vehicles. J. Power Sources 2013, 226, 272–288. [Google Scholar] [CrossRef]
- Thielmann, A.; Sauer, A.; Isenmann, R.; Wietschel, M.; Plötz, P. Produkt-Roadmap Lithium-Ionen-Batterien 2030; Fraunhofer ISI: Karlsruhe, Germany, 2012. [Google Scholar]
- Michaelis, S. Roadmap Batterie-Produktionsmittel 2030; VDMA Batterieproduktion: Frankfurt am Main, Germany, 2016. [Google Scholar]
- Nationale Plattform Elektromobilität (NPE). Forschungsbericht 2018—Markthochlaufphase; Gemeinsame Geschäftsstelle Elektromobilität der Bundesregierung: Berlin, Germany, 2018. [Google Scholar]
- Campestrini, C.; Keil, P.; Schuster, S.F.; Jossen, A. Ageing of lithium-ion battery modules with dissipative balancing compared with single-cell ageing. J. Energy Storage 2016, 6, 142–152. [Google Scholar] [CrossRef]
- Jossen, A.; Weydanz, W. Moderne Akkumulatoren Richtig Einsetzen; Reichardt Verlag: Untermeitingen, Germany, 2006; pp. 221–230. [Google Scholar]
- Meuser, C. Physikalische und chemische Charakterisierung von Lithiumionenzellen. Ph.D. Dissertation, Technische Universität Dresden, Dresden, Germany, 2011. [Google Scholar]
- Petzl, M. Zerstörungsfreie Charakterisierung von Lithium-Plating in Lithium-Ionen-Batterien. Ph.D. Dissertation, Ulm University, Ulm, Germany, 2015. [Google Scholar]
- Westerhoff, U. Klassifizierung von Lithium-Ionen-Batteriezellen mittels kenngrößenbasierter Methoden. Ph.D. Dissertation, Technischen Universität Carolo-Wilhelmina zu Braunschweig, Braunschweig, Germany, 2018. [Google Scholar]
- Schmidt, J.P. Verfahren zur Charakterisierung und Modellierung von Lithium-Ionen Zellen. Ph.D. Dissertation, Karlsruher Institut für Technologie, Karlsruhe, Germany, 2013. [Google Scholar]
- Bloom, I.; Jansen, A.N.; Abraham, D.P.; Knuth, J.; Jones, S.A.; Battaglia, V.S.; Henriksen, G.L. Differential voltage analyses of high-power, lithium-ion cells. 1. Technique and application. J. Power Sources 2005, 139, 295–303. [Google Scholar] [CrossRef]
- Pastor-Fernández, C.; Uddin, K.; Chouchelamane, G.H.; Widanage, W.D.; Marco, J. A Comparison between Electrochemical Impedance Spectroscopy and Incremental Capacity-Differential Voltage as Li-ion Diagnostic Techniques to Identify and Quantify the Effects of Degradation Modes within Battery Management Systems. J. Power Sources 2017, 360, 301–318. [Google Scholar] [CrossRef]
- Liao, Q.; Mu, M.; Zhao, S.; Zhang, L.; Jiang, T.; Ye, J.; Shen, X.; Zhou, G. Performance assessment and classification of retired lithium ion battery from electric vehicles for energy storage. Int. J. Hydrogen Energy 2017, 42, 18817–18823. [Google Scholar] [CrossRef]
- Wolter, M.; Fauser, G.; Bretthauer, C.; Roscher, M.A. End-of-Line Testing and Formation Process in Li-Ion Battery Assembly Lines. In Proceedings of the 9th International Multi-Conference on Systems, Signals and Devices, Chemnitz, Germany, 20–23 March 2012. [Google Scholar]
- KOKAM Li-ion/Polymer Cell. Available online: https://kokam.com/wp-content/uploads/2016/03/SLPB-Cell-Brochure.pdf (accessed on 13 January 2021).
- Kurzweil, P.; Dietlmeier, O.K. Elekotrochemische Speicher—Superkondensatoren, Batterien, Elektrolyse-Wasserstoff, Rechtliche Rahmenbedingungen; Springer: Wiesbaden, Germany, 2018; pp. 29–30, 233–235. [Google Scholar]
- Wenzl, H. Batteries—Capacity. In Encyclopedia of Electrochemical Power Sources 2009; Garche, J., Ed.; Elsevier Science: Amsterdam, The Netherlands, 2009; pp. 395–400. [Google Scholar]
- Keil, P.; Jossen, A. Charging protocols for lithium-ion batteries and their impact on cycle life—An experimental study with different 18650 high-power cells. J. Energy Storage 2016, 6, 125–141. [Google Scholar] [CrossRef]
- Winter, M.; Besenhard, J.O.; Spahr, M.E.; Novak, P. Insertion Electrode Materials for Rechargeable Lithium Batteries. Adv. Mater. 1998, 10, 725–763. [Google Scholar] [CrossRef]
- Dubarry, M.; Truchot, C.; Liaw, B.Y. Synthesize battery degradation modes via a diagnostic and prognostic model. J. Power Sources 2012, 219, 204–216. [Google Scholar] [CrossRef]
- Barai, A.; Uddin, K.; Widanage, W.D.; McGordon, A.; Jennings, P. A study of the influence of measurement timescale on internal resistance characterisation methodologies for lithium-ion cells. Sci. Rep. 2018, 21, 8. [Google Scholar] [CrossRef] [PubMed]
- Piller, S.; Perrin, M.; Jossen, A. Methods for state-of-charge determination and their applications. J. Power Sources 2001, 96, 113–120. [Google Scholar] [CrossRef]
- Ratnakumar, B.V.; Smart, M.C.; Whitcanack, L.D.; Ewell, R.C. The impedance characteristics of Mars Exploration Rover Li-ion batteries. J. Power Sources 2006, 159, 1428–1439. [Google Scholar] [CrossRef]







| Cycle | Step | C-Rate | Cond. | Rep. | Explanation |
|---|---|---|---|---|---|
| Discharge pulse, 10 s; followed by 5 min break | 5C | - | 1 | Internal resistance | |
| C0.1 | Discharge | 1C | CC | 1 | Presetting for subsequent cycle |
| C1 | Charge/Discharge | 1C/5C | CC-CV/CC | 1 | Capacity test |
| C0.2 | Charge | 1C | CC-CV | 1 | Set original SOC |
| Cycle | Step | C-Rate | Cond. | Rep. | Explanation |
|---|---|---|---|---|---|
| C2 | Discharge | 1C | CC | 1 | Presetting for subsequent cycle |
| C3–C7 | Charge/Discharge | 1C/1C | CC-CV/CC-CV | 5 | Capacity test |
| C8 | Charge/Discharge | 0.1C/0.1C | CC-CV/CC-CV | 1 | Pseudo-OCV measurement |
| C9–C11 | Charge/Discharge | 1C/0.5C 1C/3C 1C/5C | CC-CV/CC-CV | 1 | Current rate dependent performance |
| C12 | Charge | 1C | CC | 9 | Set SoC in 10% steps |
| Charge/Discharge pulse, 30 s; each followed by 4 min break | 0.5C/0.5C 1C/1C 3C/3C 5C/5C | - | Current rate dependent internal resistance (SoC 10–90%) | ||
| Charge/Discharge | 1C/1C | CC-CV/CC | 1 | Presetting for subsequent cycle | |
| C13 | Charge | 1C | CC-CV | 1 | Set original SoC |
| Parameter | Symbol | Equation | Ideal Level | |
|---|---|---|---|---|
| Average Voltage | Ua | Ua = ECC/CCC | C: ↓, D: ↑ | |
| Capacity | Total | Ct | Ct = CCC + CCV | ↑ |
| CC | CCC | ↑ | ||
| CV | CCV | ↓ | ||
| Energy | Total | Et | Et = ECC + ECV | ↑ |
| CC | ECC | ↑ | ||
| CV | ECV | ↓ | ||
| Time | Total | tt | - | ↑ |
| CC | tCC | - | ↑ | |
| CV | tCV | - | ↓ | |
| Efficiency | Voltage | ηU | ηU = Ua_D/Ua_C | ↑ |
| Capacity | ηC | ηC = Ct_D/Ct_C | ↑ | |
| Energy | ηE | ηE = Et_D/Et_C | ↑ | |
| Parameter | Symbol | Equation | Ideal Level |
|---|---|---|---|
| Internal Resistance | Ri | Ri = ∆U/∆I | ↓ |
| Internal Resistance/mΩ | ||||
|---|---|---|---|---|
| Pulse Duration | 0.5C | 1C | 3C | 5C |
| 1 s | 27.325 ± 0.691 | 26.364 ± 0.602 | 22.137 ± 0.547 | 19.950 ± 0.592 |
| 10 s | 20.476 ± 0.663 | 20.120 ± 0.661 | 19.051 ± 0.596 | 18.502 ± 0.678 |
| 18 s | 21.832 ± 0.654 | 21.330 ± 0.662 | 20.024 ± 0.589 | 19.539 ± 0.687 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ryll, K.; Hoffmann, L.; Landrath, O.; Lienesch, F.; Kurrat, M. Key Figure Based Incoming Inspection of Lithium-Ion Battery Cells. Batteries 2021, 7, 9. https://0-doi-org.brum.beds.ac.uk/10.3390/batteries7010009
Ryll K, Hoffmann L, Landrath O, Lienesch F, Kurrat M. Key Figure Based Incoming Inspection of Lithium-Ion Battery Cells. Batteries. 2021; 7(1):9. https://0-doi-org.brum.beds.ac.uk/10.3390/batteries7010009
Chicago/Turabian StyleRyll, Kerstin, Louisa Hoffmann, Oliver Landrath, Frank Lienesch, and Michael Kurrat. 2021. "Key Figure Based Incoming Inspection of Lithium-Ion Battery Cells" Batteries 7, no. 1: 9. https://0-doi-org.brum.beds.ac.uk/10.3390/batteries7010009





