Use of Very High Spatial Resolution Commercial Satellite Imagery and Deep Learning to Automatically Map Ice-Wedge Polygons across Tundra Vegetation Types
Abstract
:1. Introduction
2. Study Area and Data
3. Mapping Application for Permafrost Land Environment
3.1. Mapping Workflow, Training and Validation Experiment
3.2. Accuracy Estimates
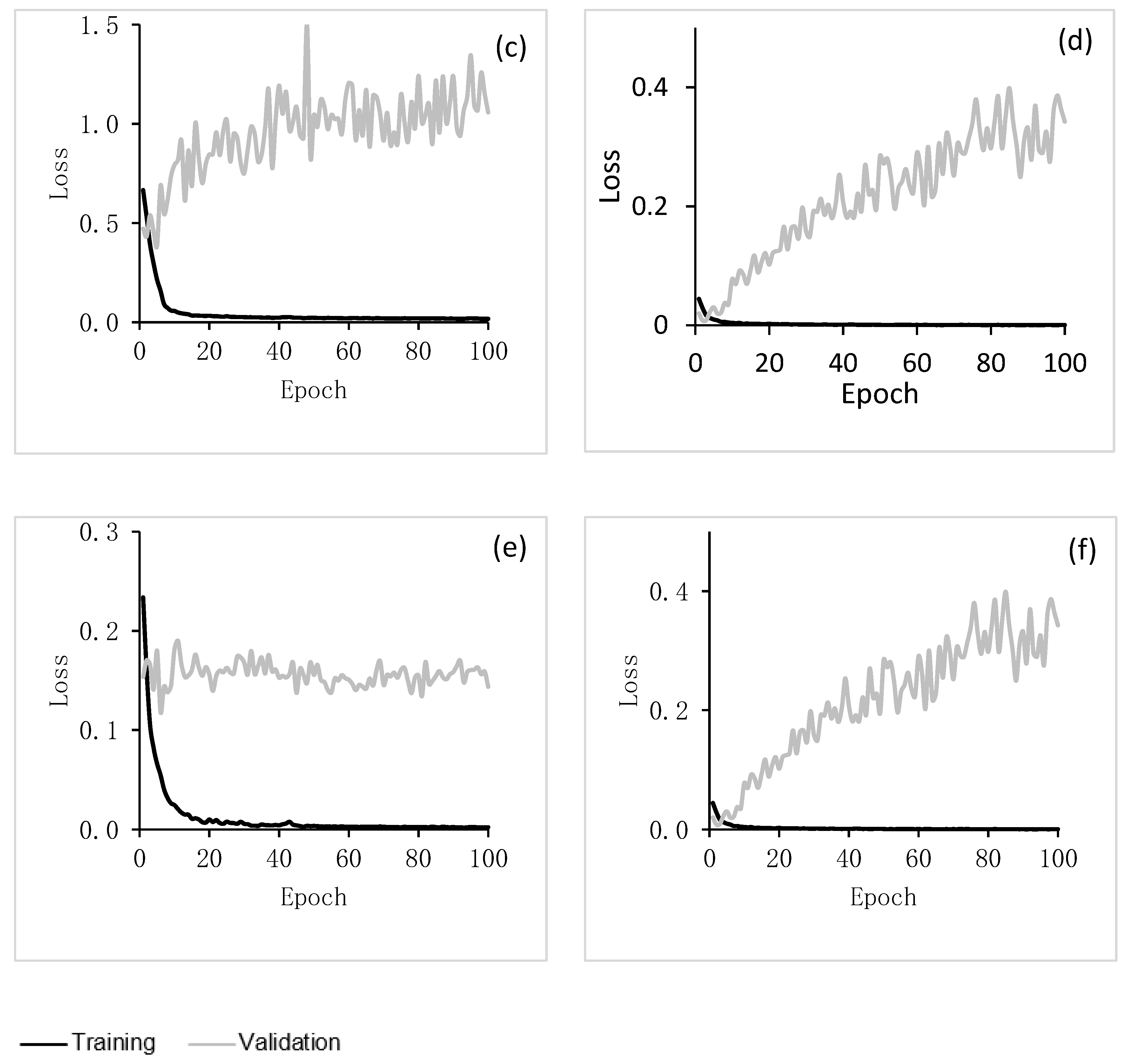
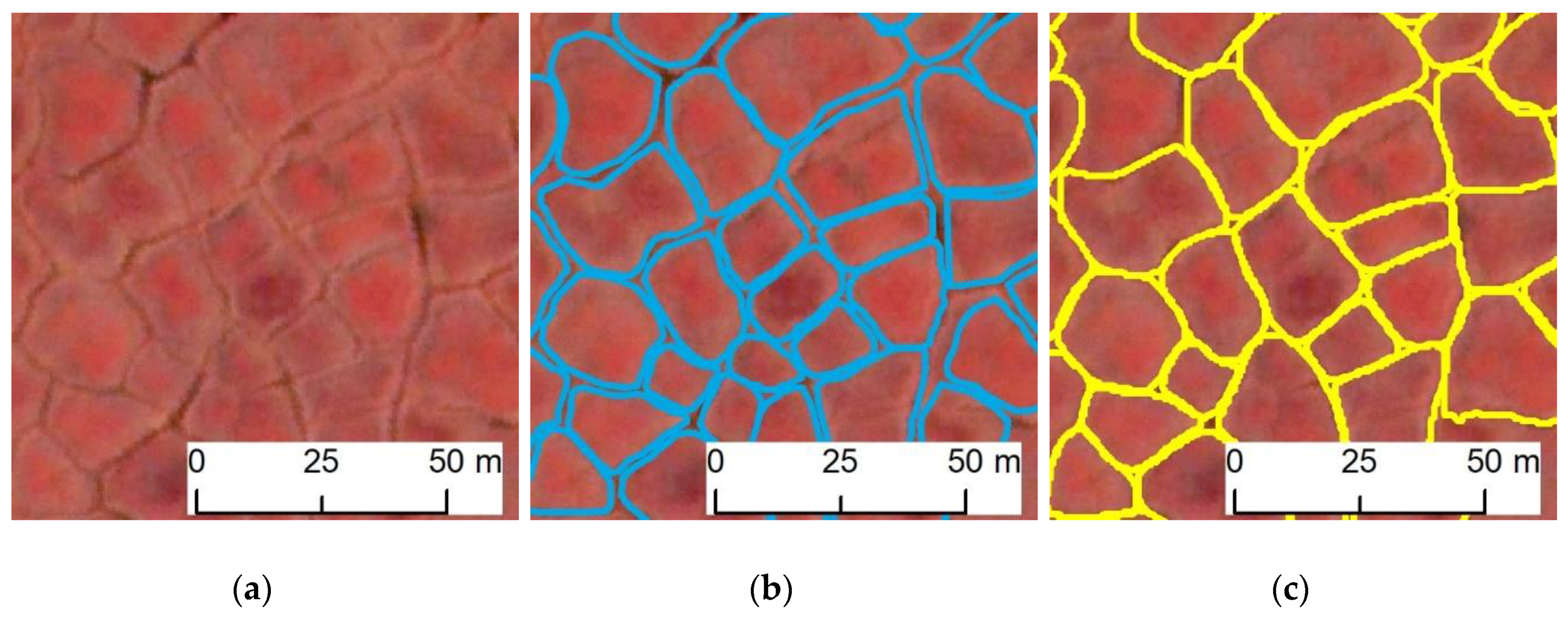
4. Model Evaluation Results and Discussions
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Black, R.F. Permafrost: A review. Geol. Soc. Am. Bull. 1954, 65, 839–856. [Google Scholar] [CrossRef]
- Steedman, A.E.; Lantz, T.C.; Kokelj, S.V. Spatio-temporal variation in high-centre polygons and ice-wedge melt ponds, Tuktoyaktuk coastlands, Northwest Territories. Permafr. Periglac. Process. 2017, 28, 66–78. [Google Scholar] [CrossRef]
- Lachenbruch, A.H. Mechanics of Thermal Contraction Cracks and Ice-Wedge Polygons in Permafrost; Geological Society of America: Boulder, CO, USA, 1962; Volume 70. [Google Scholar]
- Dostovalov, B.N.; Popov, A.I. Polygonal systems of ice-wedges and conditions of their development. In Proceedings of the Permafrost International Conference, Lafayette, IN, USA, 11–15 November 1963. [Google Scholar]
- Liljedahl, A.K.; Boike, J.; Daanen, R.P.; Fedorov, A.N.; Frost, G.V.; Grosse, G.; Hinzman, L.D.; Iijma, Y.; Jorgenson, J.C.; Matveyeva, N.; et al. Pan-Arctic ice-wedge degradation in warming permafrost and its influence on tundra hydrology. Nat. Geosci. 2016, 9, 312. [Google Scholar] [CrossRef]
- Witharana, C.; Bhuiyan, M.A.E.; Liljedahl, A.K. Big Imagery and high-performance computing as resources to understand changing Arctic polygonal tundra. Int. Arch. Photogramm. 2020, 44, 111–116. [Google Scholar]
- Witharana, C.; Bhuiyan, M.A.E.; Liljedahl, A.K.; Kanevskiy, M.; Epstein, H.E.; Jones, B.M.; Daanen, R.; Griffin, C.G.; Kent, K.; Jones, M.K.W. Understanding the synergies of deep learning and data fusion of multispectral and panchromatic high resolution commercial satellite imagery for automated ice-wedge polygon detection. ISPRS J. Photogramm. Remote Sens. 2020, 170, 174–191. [Google Scholar] [CrossRef]
- Lousada, M.; Pina, P.; Vieira, G.; Bandeira, L.; Mora, C. Evaluation of the use of very high resolution aerial imagery for accurate ice-wedge polygon mapping (Adventdalen, Svalbard). Sci. Total Environ. 2018, 615, 1574–1583. [Google Scholar] [CrossRef]
- Mahmoudi, F.T.; Samadzadegan, F.; Reinartz, P. Object recognition based on the context aware decision-level fusion in multiviews imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 8, 812–822. [Google Scholar]
- Zhang, W.; Witharana, C.; Liljedahl, A.K.; Kanevskiy, M. Deep Convolutional Neural Networks for Automated Characterization of Arctic Ice-Wedge Polygons in Very High Spatial Resolution Aerial Imagery. Remote Sens. 2018, 10, 1487. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Liljedahl, A.K.; Kanevskiy, M.; Epstein, H.E.; Jones, B.M.; Jorgenson, M.T.; Kent, K. Transferability of the Deep Learning Mask R-CNN Model for Automated Mapping of Ice-Wedge Polygons in High-Resolution Satellite and UAV Images. Remote Sens. 2020, 12, 1085. [Google Scholar] [CrossRef] [Green Version]
- Bhuiyan, M.A.E.; Witharana, C.; Liljedahl, A.K. Harnessing Commercial Satellite Imagery, Artificial Intelligence, and High Performance Computing to Characterize Ice-wedge Polygonal Tundra. In Proceedings of the AGU Fall Meeting 2020, San Francisco, CA, USA, 1–17 December 2020. [Google Scholar]
- Witharana, C.; Bhuiyan, M.A.E.; Liljedahl, A.K.; Kanevskiy, M.Z.; Jorgenson, T.; Jones, B.M.; Daanen, R.P.; Epstein, H.E.; Griffin, C.G.; Kent, K.; et al. Automated Mapping of Ice-wedge Polygon Troughs in the Continuous Permafrost Zone using Commercial Satellite Imagery. In Proceedings of the AGU Fall Meeting 2020, San Francisco, CA, USA, 1–17 December 2020. [Google Scholar]
- Blaschke, T.; Hay, G.J.; Kelly, M.; Lang, S.; Hofmann, P.; Addink, E.; Feitosa, R.Q.; Van der Meer, F.; Van der Werff, H.; Van Coillie, F.; et al. Geographic object-based image analysis–towards a new paradigm. ISPRS J. Photogramm. Remote Sens. 2014, 87, 180–191. [Google Scholar] [CrossRef] [Green Version]
- Laliberte, A.; Rango, A.; Havstad, K.; Paris, J.; Beck, R.; McNeely, R.; Gonzalez, A. Object-oriented image analysis for mapping shrub encroachment from 1937 to 2003 in southern New Mexico. Remote Sens. Environ. 2004, 93, 198–210. [Google Scholar] [CrossRef]
- Jones, M.K.W.; Pollard, W.H.; Jones, B.M. Rapid initialization of retrogressive thaw slumps in the Canadian high Arctic and their response to climate and terrain factors. Environ. Res. Lett. 2019, 14, 055006. [Google Scholar] [CrossRef]
- Muster, S.; Heim, B.; Abnizova, A.; Boike, J. Water body distributions across scales: A remote sensing based comparison of three arctic tundra wetlands. Remote Sens. 2013, 5, 1498–1523. [Google Scholar] [CrossRef] [Green Version]
- Skurikhin, A.N.; Wilson, C.J.; Liljedahl, A.; Rowland, J.C. Recursive active contours for hierarchical segmentation of wetlands in high-resolution satellite imagery of arctic landscapes. In Proceedings of the Southwest Symposium on Image Analysis and Interpretation, San Diego, CA, USA, 6–8 April 2014; pp. 137–140. [Google Scholar]
- Ulrich, M.; Grosse, G.; Strauss, J.; Schirrmeister, L. Quantifying wedge-ice volumes in Yedoma and thermokarst basin deposits. Permafr. Periglac. Process. 2014, 25, 151–161. [Google Scholar] [CrossRef] [Green Version]
- Wallach, I.; Dzamba, M.; Heifets, A. AtomNet: A deep convolutional neural network for bioactivity prediction in structure-based drug discovery. arXiv 2015, arXiv:1510.02855. [Google Scholar]
- Unterthiner, T.; Mayr, A.; Klambauer, G.; Hochreiter, S. Toxicity Prediction Using Deep Learning. arXiv 2015, arXiv:1503.01445. Available online: https://arxiv.org/abs/1503.01445 (accessed on 11 December 2020).
- Benoit, B.A. Lambert3-D deep learning approach for remote sensing image classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4420–4434. [Google Scholar]
- Wei, X.; Fu, K.; Gao, X.; Yan, M.; Sun, X.; Chen, K.; Sun, H. Semantic pixel labelling in remote sensing images using a deep convolutional encoder-decoder model. Remote Sens. Lett. 2018, 9, 199–208. [Google Scholar] [CrossRef]
- Yang, J.; Zhu, Y.; Jiang, B.; Gao, L.; Xiao, L.; Zheng, Z. Aircraft detection in remote sensing images based on a deep residual network and super-vector coding. Remote Sens. Lett. 2018, 9, 228–236. [Google Scholar] [CrossRef]
- Hinton, G.; Deng, L.; Yu, D.; Dahl, G.; Mohamed, A.; Jaitly, N.; Kingsbury, B. Deep neural networks for acoustic modeling in speech recognition: The shared views of four research groups. IEEE Signal Process Mag. 2012, 29, 82–97. [Google Scholar] [CrossRef]
- Litjens, G.; Kooi, T.; Bejnordi, B.E.; Setio, A.A.A.; Ciompi, F.; Ghafoorian, M.; Sanchez, C.I. A survey on deep learning in medical image analysis. Med. Image Anal. 2017, 42, 60–88. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xing, F.; Xie, Y.; Su, H.; Liu, F.; Yang, L. Deep learning in microscopy image analysis: A survey. IEEE Trans. Neural Netw. Learn. Syst. 2017, 29, 4550–4568. [Google Scholar] [CrossRef] [PubMed]
- Jia, Y.; Shelhamer, E.; Donahue, J.; Karayev, S.; Long, J.; Girshick, R.; Guadarrama, S.; Darrell, T. Caffe: Convolutional architecture for fast feature embedding. arXiv 2014, arXiv:1408.5093, 2014. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition; CoRR: Ithaca, NY, USA, 2015. [Google Scholar]
- Cheng, G.; Yang, C.; Yao, X.; Guo, L.; Han, J. When deep learning meets metric learning: Remote sensing image scene classification via learning discriminative CNNs. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2811–2821. [Google Scholar] [CrossRef]
- Han, W.; Feng, R.; Wang, L.; Cheng, Y. A semi-supervised generative framework with deep learning features for high-resolution remote sensing image scene classification. ISPRS J. Photogramm. Remote Sens. 2017, 145, 23–43. [Google Scholar] [CrossRef]
- Xu, X.; Li, W.; Ran, Q.; Du, Q.; Gao, L.; Zhang, B. Multisource remote sensing data classification based on convolutional neural network. IEEE Trans. Geosci. Remote Sens. 2018, 56, 937–949. [Google Scholar] [CrossRef]
- Ma, L.; Liu, Y.; Zhang, X.; Ye, Y.; Yin, G.; Johnson, B.A. Deep learning in remote sensing applications: A meta-analysis and review. ISPRS J. Photogramm. Remote Sens. 2019, 152, 166–177. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, X.; Wang, Z.; Wang, Z.J.; Ward, R.K.; Wang, X. Deep learning for pixel-level image fusion: Recent advances and future prospects. Inf. Fusion 2018, 42, 158–173. [Google Scholar] [CrossRef]
- Shao, Z.; Cai, J. Remote sensing image fusion with deep convolutional neural network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1656–1669. [Google Scholar] [CrossRef]
- Liu, Y.; Minh, D.; Deligiannis, N.; Ding, W. A MunteanuHourglass-shapenetwork based semantic segmentation for high resolution aerial imagery. Remote Sens. 2017, 9, 522. [Google Scholar] [CrossRef] [Green Version]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE International Conference Computer Vision and Pattern Recognition CVPR, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Zitova, B.; Flusser, J. Image registration methods: A survey. Image Vis. Comput. 2003, 21, 977–1000. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.; Quan, D.; Liang, X.; Ning, M.; Guo, Y.; Jiao, L. A deep learning framework for remote sensing image registration. Isprs J. Photogramm. Remote Sens. 2018, 145, 48–164. [Google Scholar] [CrossRef]
- Gkioxari, G.; Girshick, R.; Malik, J. Actions and attributes from wholes and parts. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 2470–2478. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster r-cnn: Towards real-time object detection with region proposal networks. In Proceedings of the Advances in Neural Information Processing Systems, Montréal, QC, Canada, 7–12 December 2015; pp. 91–99. [Google Scholar]
- Lin, T.Y.; Goyal, P.; Girshick, R.; He, K.; Dollár, P. Focal loss for dense object detection. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2980–2988. [Google Scholar]
- Dai, J.; Li, Y.; He, K.; Sun, J. R-fcn: Object detection via region-based fully convolutional networks. In Proceedings of the Advances in Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 379–387. [Google Scholar]
- He, K.; Gkioxari, G.; Dollár, P.; Girshick, R. Mask RCNN. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2961–2969. [Google Scholar]
- Abdulla, W. Mask R-Cnn for Object Detection and Instance Segmentation on Keras and Tensorflow. GitHub. Repos. 2017. Available online: https://github.com/matterport/Mask_RCNN (accessed on 10 December 2020).
- Vuola, A.O.; Akram, S.U.; Kannala, J. Mask-RCNN and U-net ensembled for nuclei segmentation. In Proceedings of the 2019 IEEE 16th International Symposium on Biomedical Imaging, Venice, Italy, 8–11 April 2019; pp. 208–212. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; Navab, N., Hornegger, J., Wells, W.M., Frangi, A.F., Eds.; Springer: Berlin, Germany; Volume 9351, pp. 234–241. [Google Scholar] [CrossRef]
- Lin, T.Y.; Maire, M.; Belongie, S.; Hays, J.; Perona, P.; Ramanan, D.; Dollár, P.; Zitnick, C.L. Microsoft Coco: Common Objects in Context. In European Conference on Computer Vision; Springer: Cham, Switzerland, 2014; pp. 740–755. [Google Scholar]
- Burnett, C.; Blaschke, T. A multi-scale segmentation/object relationship modeling methodology for landscape analysis. Ecol. Model. 2003, 168, 233–249. [Google Scholar] [CrossRef]
- Hay, G.J. Visualizing ScaleDomain Manifolds: A Multiscale GeoObjectBased Approach. In Scale Issues in Remote Sensing; Wiley: Hoboken, NJ, USA, 2014; pp. 139–169. [Google Scholar]
- Lara, M.J.; Nitze, I.; Grosse, G.; McGuire, A.D. Tundra landform and vegetation productivity trend maps for the Arctic Coastal Plain of northern Alaska. Sci. Data 2018, 5, 180058. [Google Scholar] [CrossRef] [PubMed]
- Greaves, H.E.; Eitel, J.U.; Vierling, L.A.; Boelman, N.T.; Griffin, K.L.; Magney, T.S.; Prager, C.M. 20 cm resolution mapping of tundra vegetation communities provides an ecological baseline for important research areas in a changing Arctic environment. Environ. Res. Commun. 2019, 10, 105004. [Google Scholar] [CrossRef] [Green Version]
- Walker, D.A.F.J.A.; Daniëls, N.V.; Matveyeva, J.; Šibík, M.D.; Walker, A.L.; Breen, L.A.; Druckenmiller, M.K.; Raynolds, H.; Bültmann, S.; Hennekens, M.; et al. Wirth Circumpolar arctic vegetation classification. Phytocoenologia 2018, 48, 181–201. [Google Scholar] [CrossRef]
- Raynolds, M.K.; Walker, D.A.; Balser, A.; Bay, C.; Campbell, M.; Cherosov, M.M.; Daniëls, F.J.; Eidesen, P.B.; Ermokhina, K.A.; Frost, G.V.; et al. A raster version of the Circumpolar Arctic Vegetation Map (CAVM). Remote Sens. Environ. 2019, 232, 111297. [Google Scholar] [CrossRef]
- Walker, D.A.; Raynolds, M.K.; Daniëls, F.J.; Einarsson, E.; Elvebakk, A.; Gould, W.A.; Katenin, A.E.; Kholod, S.S.; Markon, C.J.; Melnikov, E.S.; et al. The circumpolar Arctic vegetation map. J. Veg. Sci. 2005, 16, 267–282. [Google Scholar] [CrossRef]
- Shur, Y.; Kanevskiy, M.; Jorgenson, T.; Dillon, M.; Stephani, E.; Bray, M. Permafrost degradation and thaw settlement under lakes in yedoma environment. In Proceedings of the Tenth International Conference on Permafrost, Salekhard, Russia, 25–29 June 2012; Hinkel, K.M., Ed.; The Northern Publisher: Salekhard, Russia, 2012. [Google Scholar]
- Quezel, P. Les grandes structures de végétation en région méditerranéenne: Facteurs déterminants dans leur mise en place post-glaciaire. Geobios 1999, 32, 19–32. [Google Scholar] [CrossRef]
- Hellesen, T.; Matikainen, L. An object-based approach for mapping shrub and tree cover on grassland habitats by use of LiDAR and CIR orthoimages. Remote Sens. 2013, 5, 558–583. [Google Scholar] [CrossRef] [Green Version]
- Bhuiyan, M.A.E.; Witharana, C.; Liljedahl, A.K.; Jones, B.M.; Daanen, R.; Epstein, H.E.; Kent, K.; Griffin, C.G.; Agnew, A. Understanding the Effects of Optimal Combination of Spectral Bands on Deep Learning Model Predictions: A Case Study Based on Permafrost Tundra Landform Mapping Using High Resolution Multispectral Satellite Imagery. J. Imaging 2020, 6, 97. [Google Scholar] [CrossRef]
- Walker, D.A. Toward a new circumpolar arctic vegetation map. Arct. Alp. Res. 1995, 31, 169–178. [Google Scholar]
- Davidson, S.J.; Santos, M.J.; Sloan, V.L.; Watts, J.D.; Phoenix, G.K.; Oechel, W.C.; Zona, D. Mapping Arctic tundra vegetation communities using field spectroscopy and multispectral satellite data in North Alaska, USA. Remote Sens. 2016, 8, 978. [Google Scholar] [CrossRef] [Green Version]
- Galleguillos, C.; Belongie, S. Context based object categorization: A critical survey. Comput. Vis. Image Underst. 2010, 114, 712–722. [Google Scholar] [CrossRef] [Green Version]
- Guo, J.; Zhou, H.; Zhu, C. Cascaded classification of high resolution remote sensing images using multiple contexts. Inf. Sci. 2013, 221, 84–97. [Google Scholar] [CrossRef]
- Chuvieco, E. Fundamentals of Satellite Remote Sensing: An Environmental Approach; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Bovolo, F.; Bruzzone, L. A detail-preserving scale-driven approach to change detection in multitemporal SAR images. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2963–2972. [Google Scholar] [CrossRef]
- Inamdar, S.; Bovolo, F.; Bruzzone, L.; Chaudhuri, S. Multidimensional probability density function matching for preprocessing of multitemporal remote sensing images. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1243–1252. [Google Scholar] [CrossRef]
- Pitié, F.; Kokaram, A.; Dahyot, R. N-dimensional probability function transfer and its application to color transfer. In Proceedings of the EEE International Conference on Computer Vision (ICCV’05), Beijing, China, 17–21 October 2005; Volume 2, pp. 1434–1439. [Google Scholar]
- Pitié, F.; Kokaram, A.; Dahyot, R. Automated colour grading using colour distribution transfer. Comput. Vis. Image Underst. 2007, 107, 123–137. [Google Scholar] [CrossRef]
- Jhan, J.P.; Rau, J.Y. A normalized surf for multispectral image matching and band co-registration. In International Archives of the Photogrammetry; Remote Sensing & Spatial Information Sciences: Enschede, The Netherlands, 2019. [Google Scholar]
- Gidaris, S. Effective and Annotation Efficient Deep Learning for Image Understanding. Ph.D. Thesis, Université Paris-Est, Marne-la-Vallée, France, 2018. [Google Scholar]
- Bhuiyan, M.A.; Nikolopoulos, E.I.; Anagnostou, E.N. Machine Learning–Based Blending of Satellite and Reanalysis Precipitation Datasets: A Multiregional Tropical Complex Terrain Evaluation. J. Hydrometeor. 2019, 20, 2147–2161. [Google Scholar] [CrossRef]
- Bhuiyan, M.A.; Begum, F.; Ilham, S.J.; Khan, R.S. Advanced wind speed prediction using convective weather variables through machine learning application. Appl. Comput. Geosci. 2019, 1, 100002. [Google Scholar]
- Diamond, S.; Sitzmann, V.; Boyd, S.; Wetzstein, G.; Heide, F. Dirty pixels: Optimizing image classification architectures for raw sensor data. arXiv 2017, arXiv:1701.06487. [Google Scholar]
- Borkar, T.S.; Karam, L.J. DeepCorrect: Correcting DNN models against image distortions. IEEE Trans. Image Process. 2019, 28, 6022–6034. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ghosh, S.; Shet, R.; Amon, P.; Hutter, A.; Kaup, A. Robustness of Deep Convolutional Neural Networks for Image Degradations. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018; pp. 2916–2920. [Google Scholar]
- Buchhorn, M.; Walker, D.A.; Heim, B.; Raynolds, M.K.; Epstein, H.E.; Schwieder, M. Ground-based hyperspectral characterization of Alaska tundra vegetation along environmental gradients. Remote Sens. 2013, 5, 3971–4005. [Google Scholar] [CrossRef] [Green Version]
- Bratsch, S.N.; Epstein, E.; Bucchorn, M.; Walker, D.A. Differentiating among four Arctic tundra plant communities at Ivotuk, Alaska using field spectroscopy. Remote Sens. 2016, 8, 51. [Google Scholar] [CrossRef] [Green Version]




| Site | Sensor | Acquisition Date | Image Off Nadir | Sun Elevation | Azimuth |
|---|---|---|---|---|---|
| V1 | WorldView2 | 07/29/2010 | 38.6° | 35.8° | 135.5° |
| V2 | WorldView2 | 07/04/2012 | 27.2° | 42.2° | 47.6° |
| V3 | WorldView2 | 07/05/2015 | 15.4° | 42.4° | 203.8° |
| V4 | WorldView2 | 09/03/2016 | 25.9° | 27.8° | 207.6° |
| Dataset | Study Sites | Dominant Tundra | |
|---|---|---|---|
| Training | Russia | T1 | G1-Rush/grass, forb, cryptogam tundra G2-Graminoid, prostrate dwarf-shrub, forb tundra P1: Prostrate dwarf-shrub, herb, lichen tundra P2: Prostrate/Hemiprostrate dwarf-shrub |
| Alaska | T2 | G4 Tussock-sedge, dwarf-shrub, moss tundra | |
| Canada | T3 | G4:Tussock-sedge, dwarf-shrub, moss tundra G3:Non-tussock sedge, dwarf-shrub, moss tundra W2:Sedge-wetland complexes | |
| Validation | Alaska | V1 | G3:Non-tussock sedge, dwarf-shrub, moss tundra W2:Sedge-wetland complexes |
| V2 | G3:Non-tussock sedge, dwarf-shrub, moss tundra W2:Sedge-wetland complexes | ||
| V3 | W2:Sedge-wetland complexes | ||
| V4 | G4:Tussock-sedge, dwarf-shrub, moss tundra | ||
| Validation Sites | mIoU |
|---|---|
| V1 | 0.91 |
| V2 | 0.87 |
| V3 | 0.86 |
| V4 | 0.85 |
| Validation Sites | Number of Reference Polygons | Correctness | Completeness | F1 Score |
|---|---|---|---|---|
| V1 | 582 | 0.99 | 89% | 0.96 |
| V2 | 567 | 1 | 85% | 0.94 |
| V3 | 579 | 1 | 83% | 0.92 |
| V4 | 573 | 1 | 81% | 0.89 |
| Validation Sites | Number of Reference Polygons | Correctness | Completeness | F1 Score |
|---|---|---|---|---|
| V1 | 582 | 0.98 | 99% | 0.97 |
| V2 | 567 | 0.99 | 96% | 0.95 |
| V3 | 579 | 0.98 | 97% | 0.96 |
| V4 | 573 | 0.99 | 95% | 0.94 |
| Validation Sites | AMRE |
|---|---|
| V1 | 0.17 |
| V2 | 0.18 |
| V3 | 0.21 |
| V4 | 0.23 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhuiyan, M.A.E.; Witharana, C.; Liljedahl, A.K. Use of Very High Spatial Resolution Commercial Satellite Imagery and Deep Learning to Automatically Map Ice-Wedge Polygons across Tundra Vegetation Types. J. Imaging 2020, 6, 137. https://0-doi-org.brum.beds.ac.uk/10.3390/jimaging6120137
Bhuiyan MAE, Witharana C, Liljedahl AK. Use of Very High Spatial Resolution Commercial Satellite Imagery and Deep Learning to Automatically Map Ice-Wedge Polygons across Tundra Vegetation Types. Journal of Imaging. 2020; 6(12):137. https://0-doi-org.brum.beds.ac.uk/10.3390/jimaging6120137
Chicago/Turabian StyleBhuiyan, Md Abul Ehsan, Chandi Witharana, and Anna K. Liljedahl. 2020. "Use of Very High Spatial Resolution Commercial Satellite Imagery and Deep Learning to Automatically Map Ice-Wedge Polygons across Tundra Vegetation Types" Journal of Imaging 6, no. 12: 137. https://0-doi-org.brum.beds.ac.uk/10.3390/jimaging6120137





