Using Observed Residual Error Structure Yields the Best Estimates of Individual Growth Parameters

Abstract

Obtaining the best possible estimates of individual growth parameters is essential in studies of physiology, fisheries management, and conservation of natural resources since growth is a key component of population dynamics. In the present work, we use data of an endangered fish species to demonstrate the importance of selecting the right data error structure when fitting growth models in multimodel inference. The totoaba (Totoaba macdonaldi) is a fish species endemic to the Gulf of California increasingly studied in recent times due to a perceived threat of extinction. Previous works estimated individual growth using the von Bertalanffy model assuming a constant variance of length-at-age. Here, we reanalyze the same data under five different variance assumptions to fit the von Bertalanffy and Gompertz models. We found consistent significant differences between the constant and nonconstant error structure scenarios and provide an example of the consequences using the growth performance index ϕ′ to show how using the wrong error structure can produce growth parameter values that can lead to biased conclusions. Based on these results, for totoaba and other related species, we recommend using the observed error structure to obtain the individual growth parameters.

1. Introduction

Accurate estimation of individual growth parameters is crucial for population dynamic studies since growth is among the most important aspects in demographic analyses. Stock biomass is related to individual growth, and fish grow in response to seasonal and local environmental conditions in timing or location [1,2]. The importance is reflected in the large amount of scientific literature on individual growth in fisheries, aquaculture, and ecological studies [3,4,5,6].

The von Bertalanffy (vB) growth equation has been widely used to predict size as a function of age since its introduction for fished stock assessments [7] (pp. 218–219). This equation defines the growth by balancing negative and positive (anabolic and catabolic) processes within individuals [8]. Before and after von Bertalanffy published his equation, other models, or extensions of it were made available (for example, the Gompertz, Verhults, and Pütters models) [9,10]. Amongst these, the Gompertz model has also found broad use in growth analyses [10,11]. Unlike the vB, the Gompertz [12] growth function has an inflexion point. Both models have three parameters: Asymptotic length (${\mathrm{L}}_{\infty }$), instantaneous growth coefficient (k), “age” at zero length (t₀) in the case of vB and at the inflexion (t₁) in the Gompertz model [13] (pp. 231–232).

The common question is what kind of growth is anticipated by each mathematical function: Asymptotic, sigmoid, power, oscillating, or linear. Biologists can use their criteria to decide a priori a model to fit the data. Recently, a multi-model approach (MMA) [14,15] has been increasingly used. In MMA, one or several goodness of fit criteria are used to select the most plausible model in terms of fit and parsimony of a set of competing models conditional on the available data. In a previous work, [16] six different tests were analyzed concluding that the Bayesian information criterion (BIC) and Akaike information criterion (AIC) are common choices. These two indices are based on the likelihood or log-likelihood analysis, and likelihood itself is related to error or residual probability density functions [17]. Here, we use BIC as the best fit index since it has been demonstrated that it is asymptotically optimal and more parsimonious than AIC [18,19].

Residual analysis is important to parameterize the mathematical models chosen to describe the growth of species under study. The growth model has unknown parameters that must be solved through an objective function which can be the log-likelihood where the residuals are determined based on the variability around the curve that fits the observed length-at-age data. In growth models, one commonly refers to variability of length at a given age. Alternatively, variability is considered as a function of length itself [20] (pp. 12–15). Here, we use the former notion. Variability of length-at-age has been widely documented and studied, e.g., [21,22,23]. Among the hypotheses proposed to explain this phenomenon are differences in birth dates, genetic makeup, food availability, food assimilation differences, and intra- or interspecies competition [24].

Many studies focus on how this variability can be utilized to parameterize growth models. Once the researcher decides on a model or set of models (often based on exploratory plots or analyses), she/he fits them according to the behavior of the size at age data and the shape of the variance or errors of length-at-age in a diagnostic plot. Therefore, a distribution of residuals can be assumed: (a) Additive: Variance of length does not change with age [13] (pp. 86–87), (b) Multiplicative: Variance increases/decreases with length [20] (pp. 86–86), (c) Depensatory: Variance grows with length and reaches an asymptote [25,26], (d) Compensatory: Variance decreases asymptotically with length [27], and (e) Observed variance: the variance structure used is obtained from the original data [20]. Based on the assumed variance structure, the adequate method can be selected, for example, log-likelihood. Rather than emphasizing the importance of MMA or information theory to select models, this study focuses on selecting the error structure to fit the most plausible model using the vB and the Gompertz growth functions to analyze their robustness.

The totoaba, Totoaba macdonaldi [28], is the largest fish of the Sciaenidae family (drums, croakers, and sea basses). It can reach a total length of 2 m, weight of 100 kg, and has a life span of 27 years [29]. The totoaba is endemic to the Gulf of California, its commercial fishing was banned in 1975 and since 1976 has been classified as Critically Endangered in the Mexican list of species of special interest [30]. After over 45 years of ban, recent research suggests that the population of totoaba recovered [31,32,33]. On the other hand, poaching for the trade of its swim bladder (crop) has recently (in the last 11 years) become a significant threat for the species. Totoaba are vulnerable to poaching because from February to April they congregate to spawn in the shallow, highly variable waters of the upper Gulf of California [33,34]. This has generated renewed interest on the current status and population dynamics of totoaba [34]. The objective of this study is to compare the previously used hypothesis of constant, multiplicative, depensatory, and compensatory variability against the observed variance to parameterize growth models using length-age data for T. macdonaldi as a practical example. Then, we use our results to explore how the estimated growth parameters values can influence the growth performance index ϕ′ [35]. Beyond the scope of the present work, we caution that potential errors in assigning ages were not considered.

2. Materials and Methods

A literature review focused on the growth of totoaba (T. macdonaldi) was conducted, which allowed us to use the maximum amount possible of length-at-age data. The first statistical study of the totoaba dates back to the early 20th century [36]. Growth was reanalyzed using original data [37] for the first estimate of the von Bertalanffy (vB) individual growth parameters (k and ${\mathrm{L}}_{\infty }$). Several other workers did the same (see [34] for a summary of such studies). As a result, the data sets used for the present study were furnished from the following publications: [29,34,38]. Total length (mm) vs. age (years) data were taken from the figures described in the first two publications using digitization techniques, whereas the third data sets were provided by one of the coauthors (M.A.C.-M.). The observed variance of the data was analyzed and, under the premise that most growth analyses consider residuals with constant variance, the vB and Gompertz growth models were evaluated with different error structures. It is important to remember that ${\mathrm{L}}_{\infty }$ is the average length that individuals of a population would reach if they were to grow indefinitely. Being an average, it should not come as a surprise that in many instances some or several sampled individuals are larger than this theoretical asymptotic length e.g., [13,38].

2.1. Modelling

The vB and Gompertz growth models were adjusted using log-likelihood considering five different error structures. The vB model is: L_t = ${\mathrm{L}}_{\infty }$ [1-exp(-k(t-t₀))] and the Gompertz model is: L_t = ${\mathrm{L}}_{\infty }$exp[-exp(−k_g(t−t₁)], where ${\mathrm{L}}_{\infty }$ is the asymptotic length, k_g is the instantaneous growth coefficient at t₁, t₀ is the age at null length, and t₁ is the inflexion point of the Gompertz curve [39].

For each error structure, the expressions for the estimated standard deviations were [13]:

(a)

Additive: ${\hat{\mathsf{\sigma }}}_{\mathrm{a}}=\sqrt{\sum {\left(\mathrm{Y}\mathrm{o}-\mathrm{Y}\mathrm{e}\right)}^2/\mathrm{n}}$

(b)

Multiplicative: ${\hat{\mathsf{\sigma }}}_{\mathrm{m}}=\sqrt{\sum {\left[\mathrm{l}\mathrm{n}\left(\mathrm{Y}\mathrm{o}\right)-\mathrm{l}\mathrm{n}\left(\mathrm{Y}\mathrm{e}\right)\right]}^2/\mathrm{n}}$

where Yo and Ye are, respectively, the observed and expected value of mean length-at-age.

The objective functions for these two models were, respectively [13]: $\mathrm{LL}=-\mathrm{n}\left[\mathrm{Ln}\left(2\mathsf{\pi }\right)+2\mathrm{Ln}\left(\mathsf{\sigma }^\right)+1\right]/2$, and $\mathrm{LL}=-\mathrm{n}\left[\mathrm{Ln}\left(2\mathsf{\pi }\right)+2\mathrm{Ln}\left(\mathsf{\sigma }^\right)+1\right]/2-\sum _{0=1}^{\mathrm{n}}\mathrm{Ln}\left(\mathrm{Yo}\right)$, where n is the number of observed pairs of age-length data.

(c)

Depensatory [26]: ${\hat{\mathsf{\sigma }}}_{\mathrm{d}}^2={\mathsf{\sigma }}_{\mathsf{\infty }}^2{\left[\exp \left(-\exp \left(-\mathrm{K}(\mathrm{t}-\mathrm{T})\right)\right)\right]}^2$

(d)

Compensatory [39]: ${\hat{\mathsf{\sigma }}}_{\mathrm{c}}^2={\mathsf{\sigma }}_{\mathsf{\infty }}^2{\left[\exp \left(-\exp \left(-\mathrm{K}(\mathrm{t}-\mathrm{T})\right)\right)\right]}^{-2}$

where K and T are, respectively, the optimized k or k_g, and t₀ or t₁ values of both growth functions; and

(e)

Observed [20]: ${\hat{\mathsf{\sigma }}}_{\mathrm{o}}=\sqrt{\sum {\left(\mathrm{Y}\mathrm{o}-\mathrm{Y}\mathrm{e}\right)}^2/(\mathrm{n}{\hat{\mathsf{\sigma }}}_{\mathrm{i}})}$

In this case, ${\hat{\mathsf{\sigma }}}_{\mathrm{i}}$ is the observed standard deviation of length-at-age for age group i. ${\mathsf{\sigma }}_{\infty }^2$ is the asymptotic variance (for the oldest individuals). In all cases, n is the number of couples of ages and their corresponding lengths.

In the last three cases the objective function was [26]:

$$-\mathrm{LL}=\sum [0.5\ln (2\mathsf{\pi })+0.5\ln (\hat{\mathsf{\sigma }})+{(\mathrm{Yo}-\mathrm{Ye})}^2/({2\hat{\mathsf{\sigma }}}^2)]$$

The expected variances at-age were computed as follows. In the additive case, it was the square of ${\widehat{\mathsf{\sigma }}}_{\mathrm{a}}$ [13] and in the multiplicative [40] (p. 625): ${\hat{\mathsf{\sigma }}}_{\mathrm{m}}^2\left(\mathrm{t}\right)={\left[\mathrm{f}\left({\mathrm{L}}_{\infty ,}\mathrm{K},\mathrm{T}\right)\right]}^2\left[\exp \left({\mathsf{\sigma }}^2\right)\left(\exp \left({\mathsf{\sigma }}^2\right)-1\right)\right]$ for each age class t, where f(β) refers to either the vB or Gompertz growth functions. For the depensatory and compensatory assumptions, variance models were fitted during the same optimization process to find the growth parameters, using, respectively, ${\widehat{\mathsf{\sigma }}}_{\mathrm{d}}^2$ and ${\widehat{\mathsf{\sigma }}}_{\mathrm{c}}^2$ computed for each age class.

2.2. Criterion to Select the Best Error Structure

The criterion to determine the model that best fits the observed data was the BIC [14]:

BIC = –2LL + ln(n)θ_j, where LL is the maximum log-likelihood, θ_j is the number of parameters in each model, and n is the number of observations. The model with the lowest BIC was chosen as the most plausible. Differences in BIC values (Δ_j = BIC_j−BIC_min) where BIC_min is the minimum BIC of all five j models, were estimated between all the model variances tested. The BIC weight (W_j) was estimated as [14]: ${\mathrm{W}}_{\mathrm{j}}={\mathrm{e}}^{-0.5{\Delta }_{\mathrm{j}}}/\sum _{\mathrm{j}=1}^5{\mathrm{e}}^{-0.5{\Delta }_{\mathrm{j}}}$.

For the additive and multiplicative cases, three parameters of the vB and σ were estimated for a total of four parameters. For the depensatory and compensatory models, four parameters were also estimated, three of the vB model and ${\mathsf{\sigma }}_{\infty }^2$. The number of parameters estimated in the observed variance case was 29; 26 for each age group and one for each of the three vB or Gompertz parameters. In this case, n decreased to 256 since σ² could not be estimated for 13 cases of single length-at-age data pairs.

2.3. Confidence Intervals for Parameters

Ninety-five percent confidence intervals for each growth parameter were calculated using the maximum likelihood and Chi-square profiles [41]. The confidence interval was defined as all the values of θ that satisfy the following inequality: $2\left(\mathrm{LL}\left(\mathrm{Y}|\mathsf{\theta }\right)-\mathrm{L}\left[\mathrm{Y}|{\mathsf{\theta }}_{\mathrm{best}}\right]\right)<{{\mathrm{x}}^2}_{1,1-\propto }$, where $\mathrm{L}\left[\mathrm{Y}|{\mathsf{\theta }}_{\mathrm{best}}\right]$ = maximum likelihood of the most probable value of θ and ${{\mathsf{\chi }}^2}_{1,1-\propto }$ is the Chi-square value with one degree of freedom at the 1-α = 0.95 confidence level. Thus, the 95% confidence interval of θ encompasses all values of θ that are twice the difference between the maximum likelihood of a given θ and the maximum likelihood of the best estimate of being less than 3.84 [13].

2.4. Growth Performance (Phi Prime) ϕ′

The growth performance of totoaba was compared with previous estimates by calculating the phi prime index (ϕ′) using the empirical formula [35]: ${\mathsf{\varphi }}^{\prime }={\log }_{10}\left(\mathrm{k}\right)+2{\log }_{10}\left({\mathrm{L}}_{\infty }\right)$, where k (y⁻¹) and ${\mathrm{L}}_{\infty }$ (in mm) are parameters of the vB and Gompertz growth functions. An anomaly of ϕ′ was then computed as the difference between the value for each model and the maximum value of ϕ′. This metric reflects the relative growth of a fish per unit length and can be used to compare growth performance among different species or the same species in different years and zones [42].

3. Results

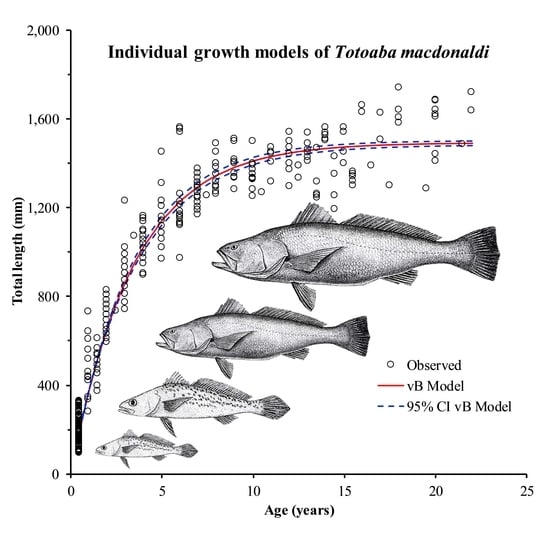
3.1. Observed Variability of Length-Age Data

The five variance-at-length structures used in fitting the five vB and Gompertz models are presented in Figure 1. For the additive and multiplicative error structure cases, the expected variances are similar in both models and differ widely when using depensatory and compensatory error structures.

3.2. Error Structure Used in Both Growth Models

For the observed data, 26 variances were estimated for the same number of age classes, from 0.5 to 22 years and each was considered as a parameter to be included in the information criterion analysis. For all models, the number of age-length-pairs was constrained by the possibility of estimating the 26 possible variances, in this case 256 variances were the sample size. Despite the large number of parameters used in the model fit, the BIC values indicated that the most plausible model was obtained using the observed variance structure of the original length-age data (

Table 1. Results of comparing variance of length-at-age. θj is the number of parameters in each model, n is the sample size or the number of age-length pairs, Wj is the weight of the model, and j refers to the number of parameters in each model.

Case	n	θj	BIC	Wj
von Bertalanffy model
Additive	256	4	3136	0
Multiplicative	256	4	3298	0
Depensatory	256	4	3141	0
Compensatory	256	4	3217	0
Observed	256	29	2393	1.00
Gompertz model
Additive	256	4	3178	0
Multiplicative	256	4	3325	0
Depensatory	256	4	3320	0
Compensatory	256	4	3317	0
Observed	256	29	2479	0

). In this particular case, the vB was selected as the most plausible model. Results should be interpreted as follows: The relative weight of the model using the observed variance indicates that the other four variance structures do not provide additional explanation for the relationship of length versus age notwithstanding the model used (vB or Gompertz).

3.3. Estimated Parameter Values for Different Error Structures

No significant differences for K and ${\mathrm{L}}_{\infty }$ values were found between models, judging by the overlap of their confidence intervals (

Table 2. Mean and 95% confidence intervals for the parameters using five error structures for the two growth models tested. t₀ corresponds to the age at zero length of von Bertalanffy and t₁ to the inflexion point of the Gompertz model. ${\mathrm{L}}_{\infty }$ is the asymptotic total length. For the von Bertalanffy model, k is the growth or Brody coefficient. For the Gompertz model, k_g is the instantaneous growth rate at age t₁.

Error Structure	${\mathbf{L}}_{\mathit{\infty }}$ (mm)	k/kg (year−1)	to/t1 (years)
von Bertalanffy model
Additive	(1466, 1484, 1502)	(0.29, 0.30, 0.31)	(−0.08, 0.0, 0.03)
Multiplicative	(1416, 1451, 1488)	(0.32, 0.33, 0.34)	(0.06, 0.07, 0.09)
Depensatory	(1450, 1470, 1489)	(0.30, 0.31, 0.33)	(−0.04, 0.0, 0.04)
Compensatory	(1488, 1499, 1515)	(0.27, 0.27, 0.29)	(−0.26, −0.17, −0.08)
Observed	(1482, 1492, 1502)	(0.28, 0.29, 0.30)	(− 0.06, 0.0, 0.03)
Gompertz model
Additive	(1420, 1439, 1456)	(0.46, 0.49, 0.52)	(1.58, 1.66, 1.75)
Multiplicative	(1340, 1373, 1409)	(0.66, 0.68, 0.70)	(1.44, 1.48, 1.51)
Depensatory	(1303, 1327, 1369)	(0.64, 0.67, 0.70)	(1.36, 1.40, 1.43)
Compensatory	(1461, 1477, 1494)	(0.33, 0.35, 0.37)	(1.07, 1.21, 1.35)
Observed	(1455, 1464, 1473)	(0.45, 0.47, 0.49)	(1.75, 1.81, 1.87)

). For t₀ and t₁, the meaning is different, hence the difference in the magnitude of the estimated values.

The observed length-at-age data suggest that size reaches an asymptote between years 15 and 22 (Figure 2). The most plausible model (vB with observed errors) included most of the variability in the range of 4 to 12 years but performed poorly for older ages.

3.4. Computed ϕ′ Values

The resulting ϕ′ and their anomalies for the vB parameters obtained in the present study as compared with parameters reported in seven previous studies are indicative of possible errors committed when the wrong set of growth parameters are estimated (

Table 3. The von Bertalanffy parameters k (y⁻¹), ${\mathrm{L}}_{\infty }$ (total length), growth performance ϕ′ values, and their anomalies, from previous investigations and the present study; N: Sample size; R: Size range. For ease of interpretation, the vB growth parameters are also provided.

Sampling Period	N	R	K (year−1)	${\mathbf{L}}_{\infty }$ (mm)	ϕ′	ϕ′ Anomaly	Source
1962	68	565–1586	0.17	1730	3.707	−0.151	[44]
1985	244	1300–1930	0.12	2030	3.694	−0.164	[45]
1986–1991	101	1000–1850	0.23	1290	3.583	−0.275	[38]
1916–1994	1549	76–1540	0.15	1670	3.622	−0.236	[46]
1983–1993	811	700–1890	0.17	2060	3.858	0.000	[43]
2010–2011	235	280–1860	0.22	1430	3.653	−0.205	[29]
2010–2011	360	280–1860	0.13	1800	3.624	−0.234	[31]
2010–2019	256	93–1685	0.29	1492	3.795	−0.048	This study’s best-fit (vB)

). The smallest value resulted from using the parameters reported by [38], and the reference (best growth performance) was obtained using values estimated in [43]. With the parameters of this study, the growth of totoaba is 4.8% less efficient than the reference value. The worst performance results using the vB growth parameters were estimated in the period 1986–1991 by [38]. An exploratory analysis shows that k and ${\mathrm{L}}_{\infty }$ have a significant inverese relationship (r = −0.73, P = 0.034), as expected in the vB model [13].

4. Discussion

The size range and sample size in different studies used in the present work may have affected the results. The different ageing methods and criteria may also affect the original results of each original work. Since fishing often first removes faster-growing individuals, the assumption that samples used to construct individual growth models are well represented in the fishing gear does not hold. In the case of totoaba, poaching targets the largest individuals [34] which might explain why the most plausible estimate of ${\mathrm{L}}_{\infty }$ is smaller than several of the individuals in the sample. On the other hand, an overrepresentation of young totoaba in the sample might have influenced the estimates to yield a rather small ${\mathrm{L}}_{\infty }$.

However, unpublished, ongoing work by the third author indicates that sampling only the younger individuals in a stock produces the largest bias in ${\mathrm{L}}_{\infty }$, and the bias decreases sharply when only the oldest individuals are sampled. Hence, further studies are needed to understand the influence of sampling in the estimates of growth parameters. The rather large variability of length-at-age for the younger fish might reflect the high natural environment variability and possibly food competition in the rather reduced spawning ground of totoaba [30,33,34], and continues to be large as fish age although they migrate to unknown sites [46]. Both sexes were included to parameterize the models, which might also increase the variability of size-at-age [47].

Previous studies on growth analysis of totoaba assumed a constant variance, but when using a multi-criteria approach, the observed variance was the most appropriate based on the BIC. As far as we know, the approach taken in the present study of using the observed variance is novel in the literature of fish growth analysis. A “fat-tail” criterion had been proposed [48] using a combination of two or more probability distributions functions (pdfs) whereby a random variable is derived from a set of different pdfs (e.g., a normal distribution, and a t-distribution). This two-component of combined pdfs, with a probability density function of the fat-tailed distribution required a parameter named “g”, used to adjust the dispersion of data [48]. An increase in g tends to increase the thickness of the tails, thus increasing the probability of having extreme values far from the mean value. For the proposed two-component mixture distribution, reference [48] also used a parameter “p” that represents the “problem” observations (outliers). Despite the novelty of this method, it has a caveat: It works with constant variance.

Individual variability-at-age is real and irrefutable. It has been considered and formulated since the 1980s [22] in two ways: “Growth compensation” (variability tends to decrease with age) and “growth depensation” (variability increases with age). If younger fish were considered to experience high variability in growth, then older fish tend to reach a limiting size [22]. This peculiarity was called “growth compensation” [39]. However, it was also suggested [22] that “many factors may contribute to size variation among fish of one age”, and it is also feasible that individual variability increases with age. This type of individual variability was named “growth depensation” [25,26]. The problem was originally tackled [25] for the vB growth model developing an equation that solved the growth depensation which was later extended to six asymptotic models [26]. On the other hand, equations were developed to compute the growth compensation in five asymptotic models [39].

A novel challenge in parameterizing growth models is to consider the real variability-at-age. The innovation proposed in the present study was using the observed variance, which was compared with the constant, compensatory, and depensatory variance. In this study, the equation for compensatory variance was used based on the lower BIC values compared to the depensatory variance. They can be used in other studies if the depensatory variance is observed.

Computing values of σ²_i through optimization of σ²_∞ led to a better interpretation of the length-at-age. This cannot be observed if variance is assumed constant with either the conventional method or the fat-tail approach. In the present study, a narrow variability of length-at-age for older individuals was captured by the BIC value. The observed variance has the advantage of demonstrating intrinsic variability of length-at-age that cannot be observed if the objective function is solved (as traditionally occurs) based on the conventional constant-variance or the monotonically increasing/decreasing approach.

From the variance of the raw data (cf. Figure 1), the model can be expected to have a constant variance (stable over time). However, it was interesting to observe the differences between this and the models that assumed n variances. No differences are clearly observed in the estimated parameters of the model (cf. Table 2) unless a selection criterion is used. In this case, the BIC made the differences evident. In other words, relying on the confidence intervals for the model parameters could lead to misinterpretation by concluding that the error structure is not important since the growth curves are similar. However, fitting two of the most common growth models in the scientific literature allowed us to show here that the approach of using the observed variance yields robust results, i.e., the observed variance produced the most plausible fits.

Although the objective of the present work was not to select the best model using an MMA but to test differences in the hypothesized variance structure, it turned out that the vB model using the observed length-age dispersion was the most plausible model. This is even more relevant given that the number of parameters in this case was much higher since the observed variances were estimated from the data, and thus should be considered as model parameters in the BIC [14].

The vB function with the observed variance was selected as the best overall alternative considering all data. This model yielded the third smallest value of ${\mathrm{L}}_{\infty }$ and the second highest value of k. On the other hand, analyzing only the results of the present study, for each model the lowest ${\mathrm{L}}_{\infty }$ and second highest k values were the result of using growing variances (multiplicative and compensatory structures). These results are consistent with the inverse correlation expected between ${\mathrm{L}}_{\infty }$ and k [13,49].

The index ϕ´ is used to compare the growth performance of a species in different areas or time periods [42]. The comparison should be based on parameters obtained with the same method. It could be argued that the time period when the totoaba had a more efficient growth was 1983–1993 (cf. Table 3). In the present study, we used maximum log-likelihood, while [43] used the Bhattacharya method. Therefore, the conclusion drawn from this comparison is that results of the present study are appropriate for the species. Aside from the clear caveat that most growth parameters and hence ϕ′ were estimated mixing data from different years, there are at least two explanations for the different values of ϕ′ obtained for totoaba in the present work which can serve as a benchmark for similar studies. The variable productivity and its effect of food availability might affect growth parameters and thus ϕ′ values in different time periods. The variability of primary productivity in the study area has been proposed as a hypothesis [50].

Two results are important in this regard. First, the highest estimate of asymptotic length corresponded to the 1983–1993 period. From 1983 to 1987, a warmer sea surface temperature related to a strong El Niño event [50] resulted in high nutrient input by rain runoff, likely increasing the primary productivity and food for totoaba. Second, the period 2010–2011 was analyzed using the constant variance [29,31] and with the observed variance (present study). Using growth parameters in published studies resulted in a negative anomaly of ϕ′, whereas using the parameter values estimated in the present study resulted in a larger ϕ′. These arguments led to the alternative conclusion: ϕ′ depends not only on primary productivity but on the appropriate estimation of growth parameters. Consequently, we believe that using the adequate error structure in estimating k and ${\mathrm{L}}_{\infty }$ can increase the likelihood of accurately evaluating growth performance of totoaba and other species.

5. Conclusions

Using the observed variance in the present study was the best way to parameterize two commonly used individual growth models (von Betalanffy and Gompertz) with age and length-data for totoaba (Totoaba macdonaldi) as a case study. Even when variances were estimated for the 26-age-group, they were considered as model parameters in the Bayesian information criterion, indicating that the observed error structure yielded the most plausible models. Therefore, whenever it is possible to apply the same approach, the observed error should be used to conduct robust estimates of individual growth. Moreover, this procedure can reduce the chances of incorrectly estimating indicators derived from the growth parameters, as was tested here with the growth performance index.