Effect of Cross-Frames on Load Distribution of Steel Bridges with Fractured Girder
Abstract
:1. Introduction
2. Finite-Element Analysis and Overview of Study
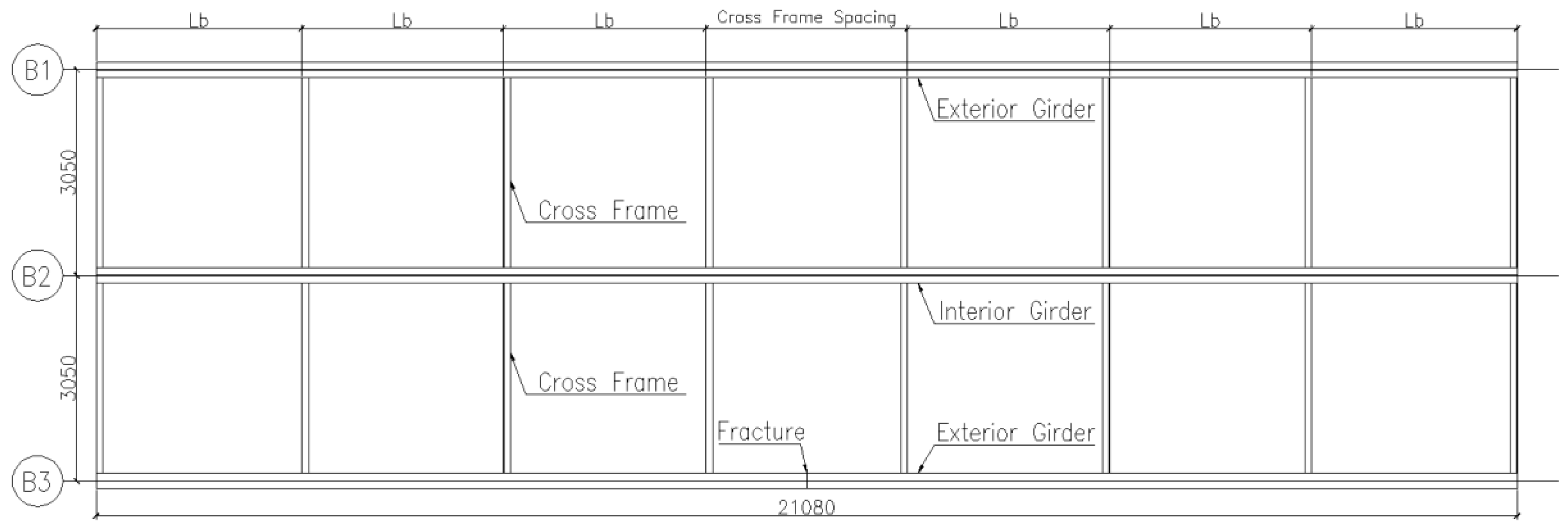
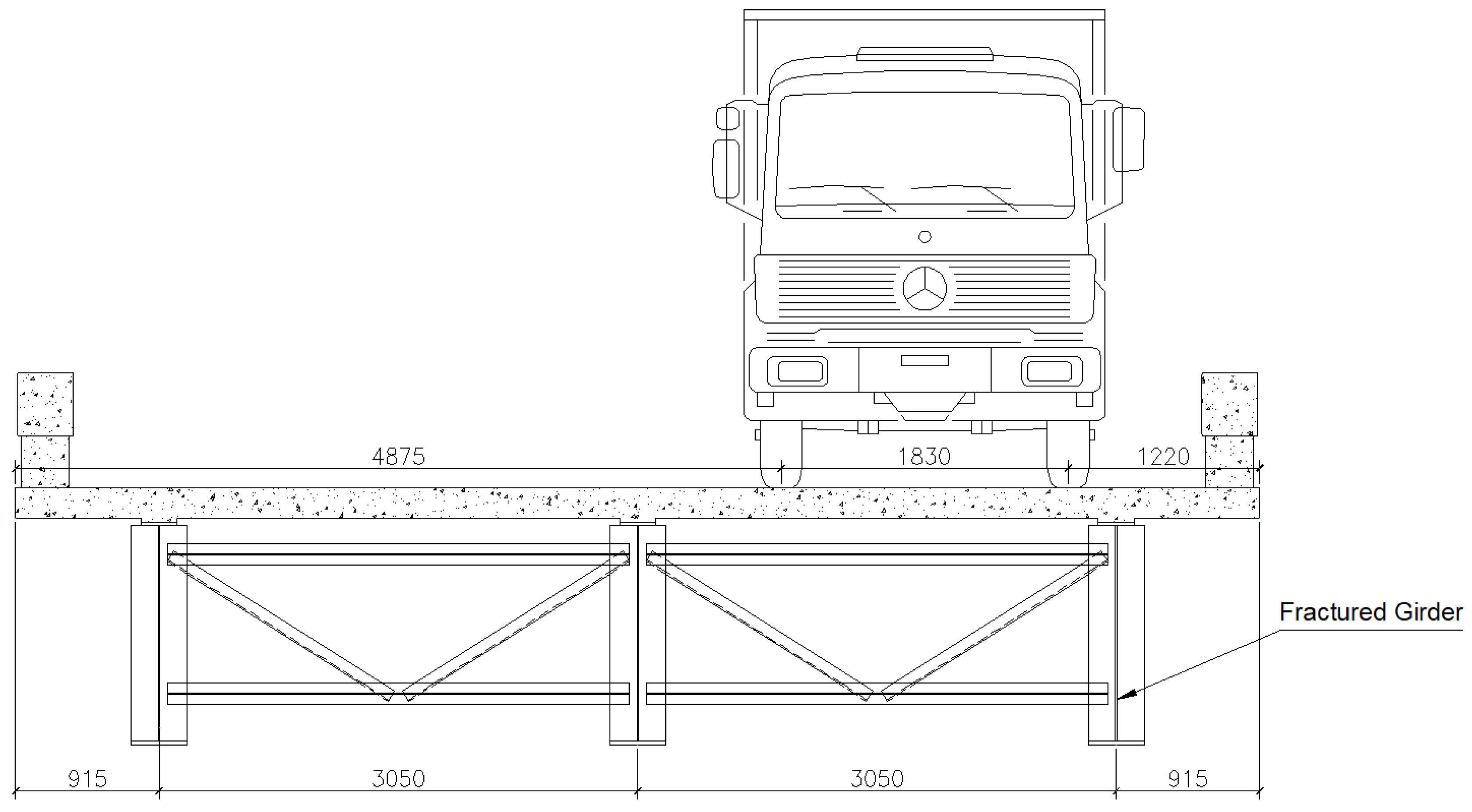
3. Finite Element Model
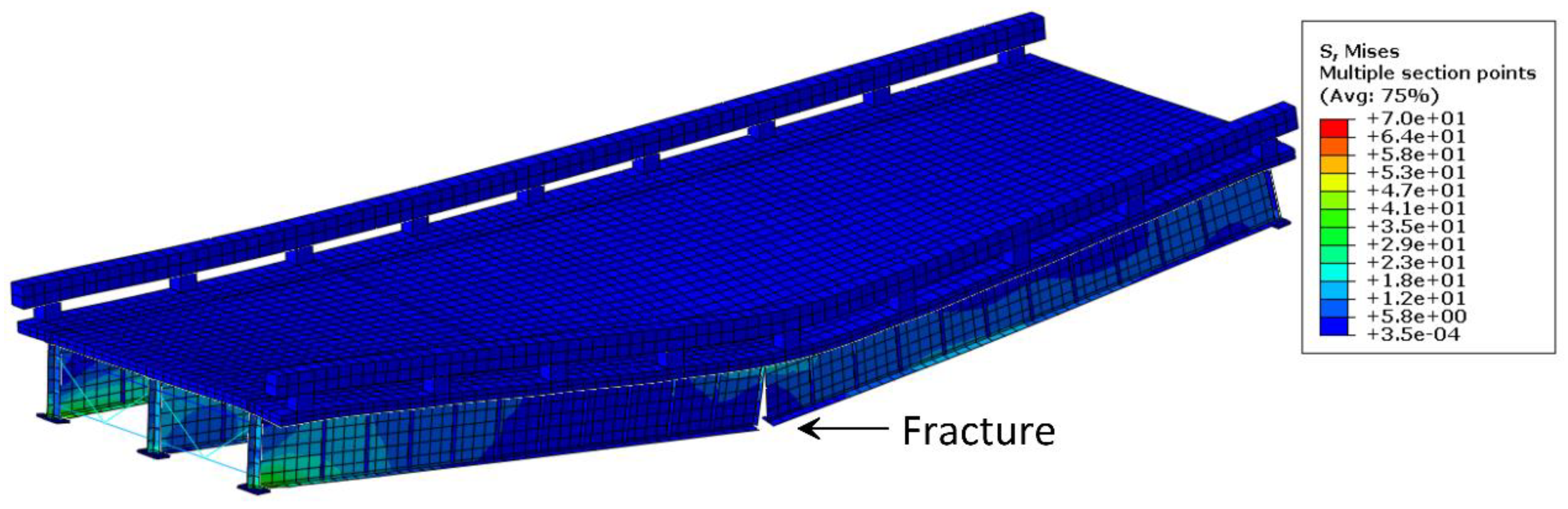
4. Finite Element Validation
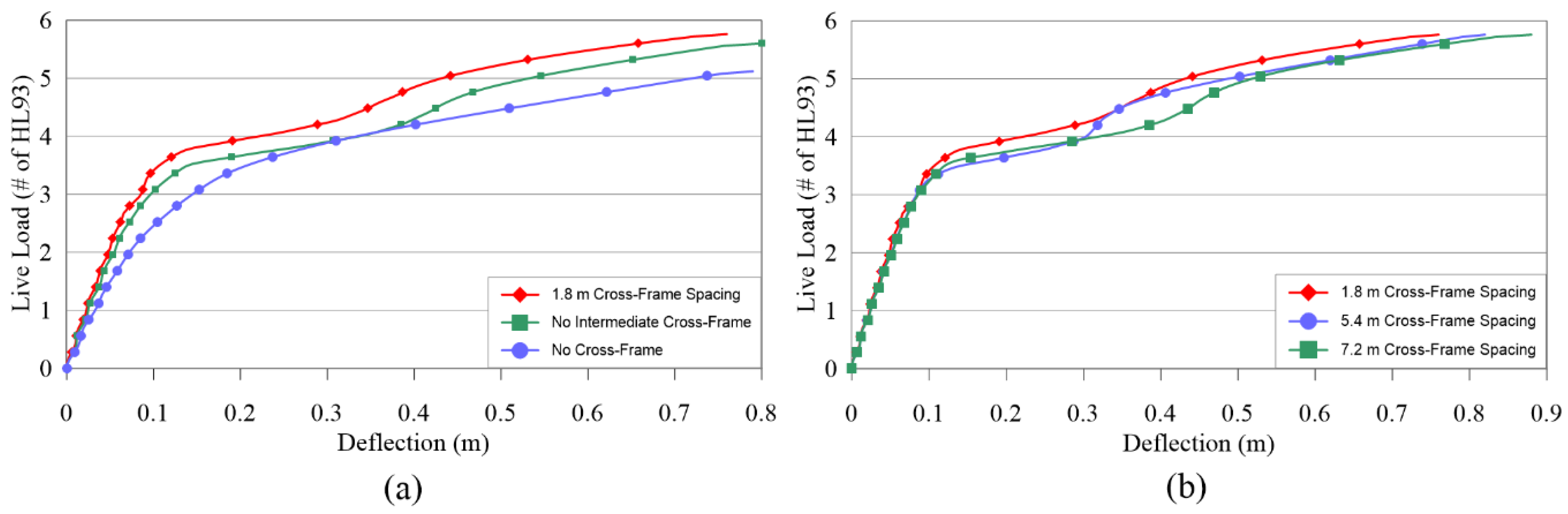
5. Results and Discussion
6. Conclusions
- An adequate cross-frame spacing, and stiffness could decrease the bridge excessive deformation after a sudden fracture e in one girder and has the potential to enhance the bridge redundancy.
- The cross-frames increase the bridge torsional stiffness after fracture of one girder and enable the bridge to deflect more uniformly by transferring the vertical loads from the fractured girder to the intact girders.
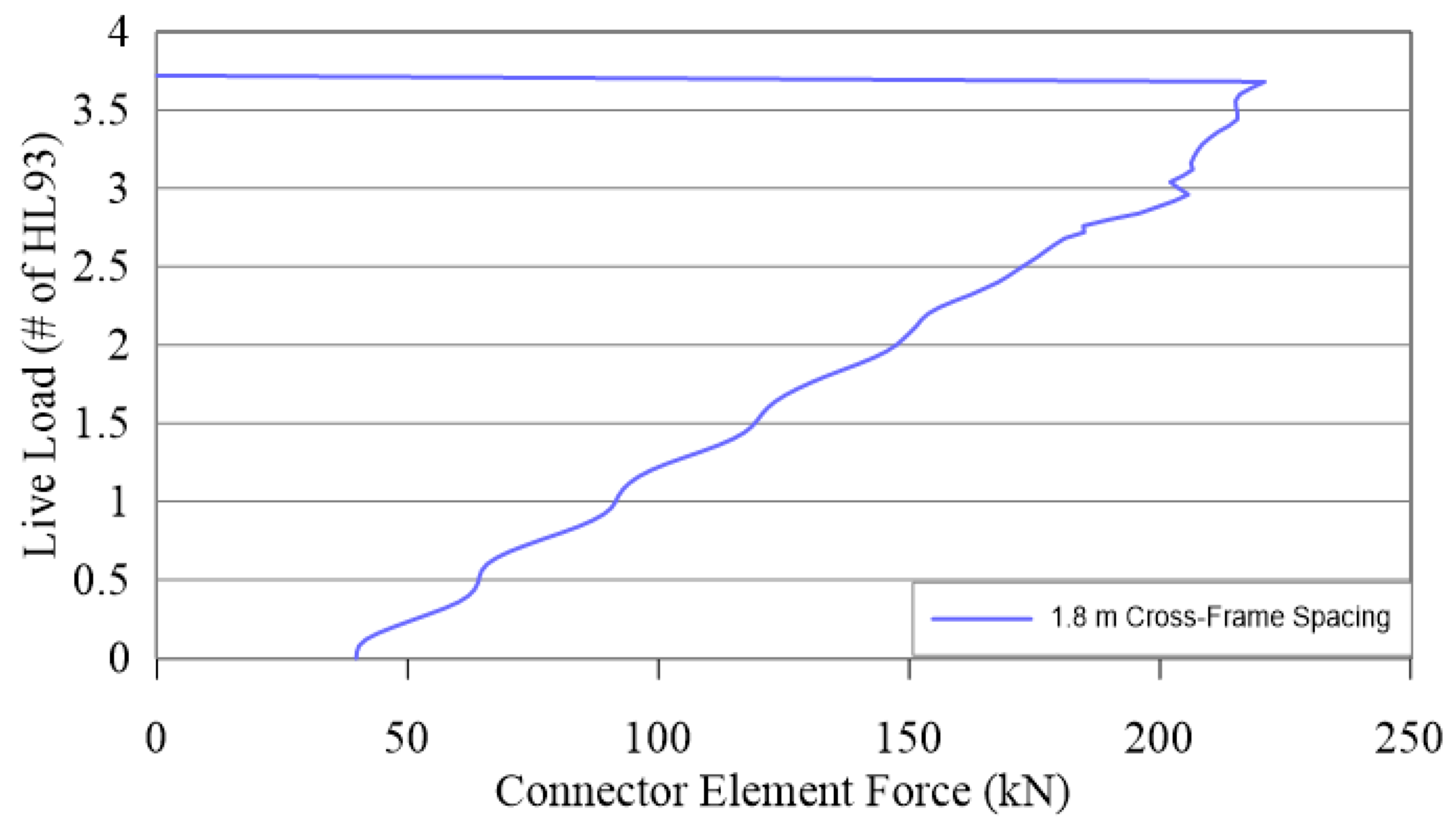
- The typical cross-frame used in this study has enough stiffness to be considered as an alternative load path after a sudden fracture. This was verified for live loading of up to 3.6 times HL90 loading for 1.8 m spacing of the cross-frames in the three I-girder bridge.
- In three I-girder bridges, after a fracture in one of the girders, two remaining intact girders with the cross-frames between demonstrate behavior similar to a box girder with a higher torsional stiffness than two single girders without the cross-frames. This allows for a better distribution of the torsional forces from the eccentric loading and less displacement than the case of two I-girder bridges.
- In the twin I-girder bridge, fracture in one girder results in significantly larger displacements in the fractured and intact girders compared to the three I-girder bridges. The effect of cross-frames however is more pronounced in twin I-girder bridges. The elements of the cross frames in the twin I-girder bridge carry smaller forces than those in the three I-girder bridge because of larger rotation of the intact girder. A large portion of the loads for twin I-girder bridge after fracture of one girder seems to be transferred longitudinally to the support after excessive deflection, however, in the three I-girder bridge because of the high torsional stiffness cross-frames carry the loads from the fractured girder to the intact girders transversely and then to the supports.
- A very important conclusion is that the end cross-frames can play an important role in the fractured scenario and to be effective for the case of fractured girder, they will need to be designed for carrying the torsional forces created by the dead and live loads after the fracture.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yu, J.; Ziehl, P.; Zrate, B.; Caicedo, J. Prediction of fatigue crack growth in steel bridge components using acoustic emission. J. Constr. Steel Res. 2011, 67, 1254–1260. [Google Scholar] [CrossRef]
- Garber, D.; Shahrokhinasab, E. Performance Comparison of In-Service, Full-Depth Precast Concrete Deck Panels to Cast-in-Place Decks; Accelerated Bridge Construction University Transportation Center (ABC-UTC): Miami, FL, USA, 2019. [Google Scholar]
- Abedin, M.; Mehrabi, A.B. Novel Approaches for Fracture Detection in Steel Girder Bridges. Infrastructures 2019, 4, 42. [Google Scholar] [CrossRef] [Green Version]
- Valikhani, A.; Azizinamini, A. Experimental Investigation of High Performing Protective Shell Used for Retrofitting Bridge Elements; Accelerated Bridge Construction University Transportation Center (ABC-UTC): Miami, FL, USA, 2018. [Google Scholar]
- Valikhani, A.; Jahromi, A.J.; Mantawy, I.M.; Azizinamini, A. Experimental evaluation of concrete-to-UHPC bond strength with correlation to surface roughness for repair application. Constr. Build. Mater. 2020, 238, 117753. [Google Scholar] [CrossRef]
- Carden, L.P.; Itani, A.M.; Buckle, I.G. Seismic Performance of Steel Girder Bridges with Ductile Cross Frames Using Single Angle X Braces. J. Struct. Eng. 2006, 132, 329–337. [Google Scholar] [CrossRef]
- Itani, A.M.; Bruneau, M.; Carden, L.; Buckle, I.G. Seismic Behavior of Steel Girder Bridge Superstructures. J. Bridg. Eng. 2004, 9, 243–249. [Google Scholar] [CrossRef] [Green Version]
- Lindquist, W.; Ibrahim, A.; Tung, Y.; Motaleb, M.; Tobias, D.; Hindi, R. Distortion-Induced Fatigue Cracking in a Seismically Retrofitted Steel Bridge. J. Perform. Constr. Facil. 2016, 30, 04015068. [Google Scholar] [CrossRef]
- Dolati, A.; Maleki, S. Ductile behavior of existing internal end diaphragms in steel tub girder bridges. J. Constr. Steel Res. 2019, 153, 356–371. [Google Scholar] [CrossRef]
- Hassel, H.L.; Bennett, C.R.; Matamoros, A.B.; Rolfe, S.T. Parametric Analysis of Cross-Frame Layout on Distortion-Induced Fatigue in Skewed Steel Bridges. J. Bridg. Eng. 2013, 18, 601–611. [Google Scholar] [CrossRef]
- Sharafbayani, M.; Linzell, D.G. Optimizing Horizontally Curved, Steel Bridge, Cross-Frame Arrangements to Enhance Construction Performance. J. Bridg. Eng. 2014, 19, 04014021. [Google Scholar] [CrossRef]
- Egilmez, O.O.; Helwig, T.A.; Herman, R. Buckling Behavior of Steel Bridge I-Girders Braced by Permanent Metal Deck Forms. J. Bridg. Eng. 2012, 17, 624–633. [Google Scholar] [CrossRef] [Green Version]
- Idriss, R.L.; White, R.K. Secondary Load Paths in Bridge Systems. Ph.D. Thesis, New Mexico State University, Las Cruces, NM, USA, 1991. [Google Scholar]
- Idriss, R.L.; White, K.R.; Woodward, C.B.; Jauregui, D.V. After-fracture redundancy of two-girder bridge: Testing I-40 bridges over Rio Grande. In Proceedings of the Fourth International Bridge Engineering Conference, San Francisco, CA, USA, 28–30 August 1995; pp. 316–326. [Google Scholar]
- Park, Y.; Joe, W.; Park, J.; Hwang, M.; Choi, B.H. An experimental study on after-fracture redundancy of continuous span two-girder bridges. Int. J. Steel Struct. 2012, 12, 1–13. [Google Scholar] [CrossRef]
- Connor, R.J.; Martín, F.J.B.; Varma, A.; Lai, Z.; Korkmaz, C. Fracture-Critical System Analysis for Steel Bridges; Transportation Research Board: Washington, DC, USA, 2018; ISBN 0309390540. [Google Scholar]
- Neuman, B.J. Evaluating the Redundancy of Steel Bridges: Full-Scale Destructive Testing of a Fracture Critical Twin Box-Girder Steel Bridge. Ph.D. Thesis, University of Texas at Austin, Austin, TX, USA, 2009. [Google Scholar]
- Irfaee, M.; Mahmoud, H. Mixed-Mode Fatigue and Fracture Assessment of a Steel Twin Box-Girder Bridge. J. Bridg. Eng. 2019, 24, 4019056. [Google Scholar] [CrossRef]
- Hovell, C.G. Evaluation of Redundancy in Trapezoidal Box-Girder Bridges Using Finite Element Analysis. Ph.D. Thesis, University of Texas at Austin, Austin, TX, USA, 2007. [Google Scholar]
- Samaras, V.A.; Sutton, J.P.; Williamson, E.B.; Frank, K.H. Simplified method for evaluating the redundancy of twin steel box-girder bridges. J. Bridg. Eng. 2012, 17, 470–480. [Google Scholar] [CrossRef]
- Kim, J.; Williamson, E.B. Finite-element modeling of twin steel box-girder bridges for redundancy evaluation. J. Bridg. Eng. 2015, 20. [Google Scholar] [CrossRef] [Green Version]
- Lin, W.; Yoda, T.; Kumagai, Y.; Saigyo, T. Numerical study on post-fracture redundancy of the two-girder steel-concrete composite highway bridges. Int. J. Steel Struct. 2013, 13, 671–681. [Google Scholar] [CrossRef]
- Lin, W.; Yoda, T.; Taniguchi, N.; Lam, H.; Nakabayashi, K. Post-Fracture redundancy evaluation of a twin box-girder shinkansen bridge in Japan. In Proceedings of the IABSE Conference, Guangzhou 2016: Bridges and Structures Sustainability - Seeking Intelligent Solutions - Report; International Association for Bridge and Structural Engineering: Guangzhou, China, 2016; Volume 106, pp. 675–682. [Google Scholar]
- Lin, W.; Lam, H.; Yoda, T. Experimental Study on Steel–Concrete Composite Twin I-Girder Bridges. J. Bridg. Eng. 2020, 25. [Google Scholar] [CrossRef]
- Pham, H.V. Evaluation of Redundancy of Twin Steel Box-Girder Bridges. Ph.D. Thesis, Florida International University, Miami, FL, USA, 2016. [Google Scholar]
- Conner, R.J.; Dexter, R.J.; Mahmoud, H. Inspection and Management of Bridges with Fracture-critical Details: A Synthesis of Highway Practice; Transportation Research Board: Washington, DC, USA, 2005; Volume 354, ISBN 0309097614. [Google Scholar]
- Abedin, M.; Maleki, S.; Kiani, N.; Shahrokhinasab, E. Shear lag effects in angles welded at both legs. Adv. Civ. Eng. 2019, 2019. [Google Scholar] [CrossRef]
- Takahashi, S.; Tachibana, Y.; Shimura, T.; Morishita, H.; Ito, H.; Miki, C. Structural details of connection of diaphragm for rationalized plate girder bridges. Doboku Gakkai Ronbunshu 1997, 1997, 107–118. [Google Scholar] [CrossRef] [Green Version]
- Kozy, B.; Tunstall, S. Stability analysis and bracing for system buckling in twin I-girder bridges. Bridg. Struct. 2007, 3, 149–163. [Google Scholar] [CrossRef]
- Ma, H.; Shi, X. Parametric study on behaviour twin-I girder bridge systems with cross-beams. In Proceedings of the Proc. 2016 Structural Congress (Structures 2016), Seoul: Korea Federation of Science and Technology Societies, Jeju Convention Visitors’ Bureau, and Korea Tourism Organization, Jeju Island, Korea, 28 August–1 September 2016. [Google Scholar]
- AASHTO. AASHTO LRFD Bridge Design Specifications, 8th ed.; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2017. [Google Scholar]
- Kathol, S.; Azizinamini, A.; Luedke, J. Strength Capacity of Steel Girder Bridges. Final Report; Transportation Research Board: Washington, DC, USA, 1995. [Google Scholar]
- Abedin, M.; Farhangdoust, S.; Mehrabi, A.B. Fracture detection in steel girder bridges using self-powered wireless sensors. In Proceedings of the In Risk-Based Bridge Engineering: Proceedings of the 10th New York City Bridge Conference, August 26-27, 2019; CRC Press: New York City, NY, USA, 2019; p. 216. [Google Scholar]
- Lonetti, P.; Pascuzzo, A. Vulnerability and failure analysis of hybrid cable-stayed suspension bridges subjected to damage mechanisms. Eng. Fail. Anal. 2014, 45, 470–495. [Google Scholar] [CrossRef]
- Lonetti, P.; Pascuzzo, A. A numerical study on the structural integrity of self-anchored cable-stayed suspension bridges. Frat. ed Integrita Strutt. 2016, 10, 359–376. [Google Scholar] [CrossRef] [Green Version]
- Greco, F.; Lonetti, P.; Pascuzzo, A. A moving mesh FE methodology for vehicle–bridge interaction modeling. Mech. Adv. Mater. Struct. 2018. [Google Scholar] [CrossRef]
- Ghaffary, A.; Karami Mohammadi, R. Framework for virtual hybrid simulation of TADAS frames using opensees and abaqus. J. Vib. Control 2018, 24, 2165–2179. [Google Scholar] [CrossRef]
- Izadpanahi, E.; Moshtaghzadeh, M.; Radnezhad, H.R.; Mardanpour, P. Constructal approach to design of wing cross-section for better flow of stresses. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; p. 275. [Google Scholar]
- Documentation, D.A. ABAQUS/CAE Doc; Simulia: Providence, RI, USA, 2016. [Google Scholar]
- Rahimi, E.; Shamshiripour, A.; Shabanpour, R.; Mohammadian, A.; Auld, J. Analysis of transit users’ waiting tolerance in response to unplanned service disruptions. Transp. Res. Part D Transp. Environ. 2019. [Google Scholar] [CrossRef]
- Rahimi, E.; Shamshiripour, A.; Shabanpour, R.; Mohammadian, A.; Auld, J. Analysis of Transit Users’ Response Behavior in Case of Unplanned Service Disruptions. Transp. Res. Rec. 2020, 0361198120911921. [Google Scholar] [CrossRef]
- Rahimi, E.; Shamshiripour, A.; Samimi, A.; Mohammadian, A. (Kouros) Investigating the injury severity of single-vehicle truck crashes in a developing country. Accid. Anal. Prev. 2020, 137. [Google Scholar] [CrossRef]
- Lubliner, J.; Oliver, J.; Oller, S.; Onate, E. A plastic-damage model for concrete. Int. J. Solids Struct. 1989, 25, 299–326. [Google Scholar] [CrossRef]
- ACI Committee 318. Building Code Requirements for Structural Concrete (ACI 318–14) and Commentary (ACI 318R–14); American Concrete Institute: Hills, MI, USA, 2014; p. 519. [Google Scholar]
- Topkaya, C.; Williamson, E.B.; Frank, K.H. Behavior of curved steel trapezoidal box-girders during construction. Eng. Struct. 2004, 26, 721–733. [Google Scholar] [CrossRef] [Green Version]
- Mouras, J.M.; Sutton, J.P.; Frank, K.H.; Williamson, E.B. The Tensile Capacity of Welded Shear Studs; Transportation Research Board: Washington, DC, USA, 2008; ISBN 9780874216561. [Google Scholar]



| Dead Load + Live Load (2 × HL93) | ||||||||
|---|---|---|---|---|---|---|---|---|
| Girder | Intermediate Cross-Frame Spacing (m) | No Cross-Frame | No Intermediate Cross-frame | |||||
| 1.8 | 3.6 | 5.4 | 7.2 | 9 | ||||
| Ext. Girder (Fractured) | Deflection (mm) | 74.8 | 76.4 | 77.9 | 79.6 | 79.6 | 102.6 | 80.9 |
| Ratio (%) | 7.50 | 5.54 | 3.66 | 1.55 | 1.54 | −26.82 | - | |
| Int. Girder | Deflection (mm) | 37.3 | 36.7 | 36.4 | 36.3 | 36 | 39.2 | 35.5 |
| Ratio (%) | −4.92 | −3.26 | −2.60 | −2.29 | −1.36 | −10.38 | - | |
| Ext. Girder | Deflection (mm) | 16.3 | 16.8 | 17.2 | 17.4 | 17.7 | 13.6 | 18.2 |
| Ratio (%) | 10.10 | 7.31 | 5.32 | 4.23 | 2.60 | 25.19 | - | |
| Spacing (m) | Chord | End Cross-Frame | Intermediate Cross-Frame No. | End Cross-Frame | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |||||
| FAxial Force in the Cross-Frame (kN) | 1.8 | Top | 147.3 | 9.3 | 8.0 | 0.4 | 1.8 | 5.8 | 10.2 | 2.2 | 1.3 | 2.7 | 26.3 | 138.8 |
| Bottom | 147.7 | 10.2 | 2.7 | 20.5 | 36.0 | 49.4 | 40.1 | 36.0 | 9.8 | 16.0 | 12.5 | 136.2 | ||
| 3.6 | Top | 146.9 | 20.5 | 3.6 | 8.5 | 7.1 | 2.2 | 25.4 | - | - | - | - | 131.7 | |
| Bottom | 146.9 | 9.3 | 12.9 | 83.2 | 85.4 | 2.2 | 32.0 | - | - | - | - | 134.4 | ||
| 5.4 | Top | 143.7 | 9.8 | 8.9 | 10.2 | 9.8 | - | - | - | - | - | - | 150.0 | |
| Bottom | 149.1 | 5.8 | 61.0 | 60.5 | 0.4 | - | - | - | - | - | - | 147.7 | ||
| 7.2 | Top | 155.3 | 9.8 | 9.8 | - | - | - | - | - | - | - | - | 149.5 | |
| Bottom | 156.2 | 69.9 | 55.2 | - | - | - | - | - | - | - | - | 146.9 | ||
| 9 | Top | 155.8 | 8.0 | 8.0 | - | - | - | - | - | - | - | - | 145.5 | |
| Bottom | 151.3 | 44.9 | 40.9 | - | - | - | - | - | - | - | - | 148.2 | ||
| No-Int. | Top | 157.1 | - | - | - | - | - | - | - | - | - | - | 147.7 | |
| Bottom | 155.3 | - | - | - | - | - | - | - | - | - | - | 150.4 | ||
| Live Load Distribution (HL93) | |||||||
|---|---|---|---|---|---|---|---|
| Girder | Intermediate Cross-Frame Spacing (m) | No Cross-Frame | No Intermediate Cross-frame | ||||
| 1.8 | 3.6 | 5.4 | 7.2 | 9 | |||
| Ext. Girder (Fractured) | 0.94 | 0.94 | 0.94 | 0.94 | 0.94 | 0.92 | 0.96 |
| Int. Girder | 1.26 | 1.26 | 1.26 | 1.28 | 1.28 | 1.32 | 1.20 |
| Ext. Girder | −0.20 | −0.20 | −0.20 | −0.18 | −0.18 | −0.24 | −0.16 |
| Cross-Frame Type | Dead Load + Live Load (2 × HL93) | |||
|---|---|---|---|---|
| Cross-Frame Spacing | Exterior Girder (fractured) | Interior Girder | Exterior Girder | |
| K-Bracing | 5.4 | 77.9 | 36.4 | 17.2 |
| X-Bracing | 5.4 | 77.6 | 36.2 | 17.1 |
| No Cross-Frame | 5.4 | 102.6 | 39.2 | 13.6 |
| Girder | Dead Load + Live Load (2 × HL93) | |||||||
|---|---|---|---|---|---|---|---|---|
| Intermediate Cross-Frame Spacing (m) | No Cross-Frame | No Intermediate Cross-frame | ||||||
| 1.8 | 3.6 | 5.4 | 7.2 | 9 | ||||
| Right Girder (Fractured) | Deflection (mm) | 159.8 | 162.8 | 163.8 | 164.6 | 165.5 | 220.4 | 176.7 |
| Ratio (%) | 9.5 | 7.8 | 7.3 | 6.8 | 6.3 | −24.7 | - | |
| Left Girder | Deflection (mm) | 47.0 | 47.4 | 46.9 | 45.7 | 46.2 | 48.7 | 44.6 |
| Ratio (%) | −5.4 | −6.3 | −5.1 | −2.4 | −3.6 | −9.0 | - | |
| Spacing (m) | Chord | End Cross-Frame | Intermediate Cross-Frame No. | End Cross-Frame | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |||||
| Axial Force in the Cross-Frame (kN) | 1.8 | Top | 117.9 | 6.2 | 2.8 | 6.2 | 12.0 | 25.1 | 21.1 | 11.3 | 3.5 | 1.3 | 12.6 | 121.5 |
| Bottom | 123.7 | 8.3 | 0.1 | 11.6 | 18.7 | 40.0 | 37.6 | 4.8 | 3.4 | 1.5 | 21.8 | 121.9 | ||
| 3.6 | Top | 115.3 | 12.0 | 2.4 | 10.2 | 9.8 | 5.3 | 23.6 | - | - | - | - | 115.3 | |
| Bottom | 121.5 | 15.1 | 12.5 | 40.9 | 34.3 | 0.8 | 27.6 | - | - | - | - | 113.5 | ||
| 5.4 | Top | 118.1 | 0.1 | 0.3 | 3.8 | 14.2 | - | - | - | - | - | - | 120.6 | |
| Bottom | 123.7 | 4.5 | 32.0 | 19.1 | 24.0 | - | - | - | - | - | - | 120.6 | ||
| 7.2 | Top | 119.7 | 4.4 | 1.9 | - | - | - | - | - | - | - | - | 127.7 | |
| Bottom | 125.9 | 32.9 | 10.7 | - | - | - | - | - | - | - | - | 128.6 | ||
| 9 | Top | 120.2 | 8.0 | 4.9 | - | - | - | - | - | - | - | - | 129.0 | |
| Bottom | 126.4 | 19.1 | 4.9 | - | - | - | - | - | - | - | - | 129.9 | ||
| No-Int. | Top | 119.3 | - | - | - | - | - | - | - | - | - | - | 130.4 | |
| Bottom | 125.5 | - | - | - | - | - | - | - | - | - | - | 131.5 | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abedin, M.; Mehrabi, A.B. Effect of Cross-Frames on Load Distribution of Steel Bridges with Fractured Girder. Infrastructures 2020, 5, 32. https://0-doi-org.brum.beds.ac.uk/10.3390/infrastructures5040032
Abedin M, Mehrabi AB. Effect of Cross-Frames on Load Distribution of Steel Bridges with Fractured Girder. Infrastructures. 2020; 5(4):32. https://0-doi-org.brum.beds.ac.uk/10.3390/infrastructures5040032
Chicago/Turabian StyleAbedin, Mohammad, and Armin B. Mehrabi. 2020. "Effect of Cross-Frames on Load Distribution of Steel Bridges with Fractured Girder" Infrastructures 5, no. 4: 32. https://0-doi-org.brum.beds.ac.uk/10.3390/infrastructures5040032





