1. Introduction
The World Health Organization (WHO) [
1] indicates that approximately 1.35 million people die in road crashes each year, which is the main cause of death among those aged 15–29 years. WHO also predicts road traffic injuries to become the seventh leading cause of death by 2030. To understand crash occurrences and develop effective countermeasures, crash data has been historically analyzed with classic statistical techniques. However, given the complexity of crash mechanisms and the multitude of factors involved, the classic statistical methods, which often impose strong model structure assumptions and frequently fail when dealing with complex and highly nonlinear data (the curse of dimensionality) [
2], may not be adequate for effective crash analysis and modeling. As an increasing number of digital data sources become available, modern machine learning appears to be a well-suited approach for crash analysis. For example, the tree-based ensemble model, eXtreme Gradient Boosting (XGBoost), which uses parallel tree boosting, can solve many data science problems in a fast and accurate way. By leveraging major distributed environments, it can solve problems beyond billions of examples [
3]. The primary difference in practice between classic statistical methods and machine learning methods is that machine learning applications are more “result-driven” and focus on prediction accuracy, while statistical methods are often implemented for interpretation or inference about the relationship between explanatory variables and the response variable. This contrast can be seen in extremely powerful prediction models that offer very limited interpretability, such as neural networks. However, machine learning is a rapidly evolving field and new methods of interpreting complex models have been and continued to be developed. Besides developing machine learning models for crash classification, this study also explores model interpretation techniques that bridge the gap between complex modeling and feature inference. For clarity of presentation, the paper is organized into seven sections.
Section 2 reviews the literature relevant to the subject of the study.
Section 3 describes the data collection and reduction. Our research approach is introduced in
Section 4, followed by data analysis and results in
Section 5.
Section 6 provides a discussion, shedding light on the limitations of the current study and future research directions. Finally, the conclusions are drawn in
Section 7.
2. Literature Review
This review is not intended to be exhaustive, but rather focuses on the studies related to the analysis of crash types. In a recent study, Razi-Ardakani et al. [
4] estimated a nested logit model to determine the primary factors that resulted in two types of crashes, single vehicle and two vehicles. Single-vehicle crashes include collision with a pedestrian or animal, run-off-road, and collision with fixed objects (e.g., parked vehicles). Two-vehicle crashes were divided into five types: rear-end crashes, head-on crashes, angular crashes, sideswipe crashes in opposite directions, and sideswipe crashes in the same direction. The study focused on what distraction-related factors led to these types of crashes. Distraction factors were classified into five categories: cell-phone usage, cognitive distractions, passengers distracting the driver, outside events attracting the driver’s attention, and in-vehicle activities. The study showed that run-off-road crashes were caused primarily by drivers’ distraction. Driver distraction occurs often on dark roads with low traffic where the driver becomes disengaged with the task of driving and is likely to be distracted. It suggested that increased lighting potentially reduces the probability of run-off-road crashes.
Another study that was able to connect crash types with particular modes of distraction was conducted by Neyens et al. [
5]. This study focused on three major crash types: rear-end, angular, and collision with fixed objects. In particular, four modes of distraction were examined, including the presence of passengers, distractions from cell phones, distractions due to in-vehicle activities, and cognitive distractions. One major aspect that differs this research from the work done by Razi-Ardakani et al. [
4] is that it was focused on only teenage drivers. The study concluded that teen drivers were more likely to be involved in rear-end or angular collisions at intersections. However, collisions with fixed objects occurred more frequently with the presence of within-vehicle distractions. Lastly, driver distraction with cell-phone use increases the likelihood of rear-end collision.
Besides the effect of distraction, there is a wide array of factors that could potentially lead to different collision types. For example, the weather has a major impact on vehicle performance and driver behaviors. Research conducted by Faouzi et al. [
6], Daniel et al. [
7], and Khattak et al. [
8] investigated the connection between weather and traffic safety. Kim et al. [
9] looked into the connection between weather/surface and modes of collision and found that at intersections clear weather is associated with an increased number of angular and sideswipe collisions and a decreased number of rear-end collisions. Additionally, the surface of the road had a major effect on collision modes. Dry road surface conditions have a higher probability of angular and rear-end collisions, while wet road surface conditions have a higher probability of side-swipe collisions.
In terms of modeling frameworks, mixed logit models, which can approximate any random utility models [
10], have been applied in analyzing data associated crash types [
11,
12]. The study conducted by Alice Ai-Ichi Chu [
11] used the General Estimates System (GES) data collected from 2011 and 2013, which includes eight different modes of collision: collision with a stationary object, collision with a parked vehicle, collision with a pedestrian, collision with a bicyclist, head-on collision, angle collision, rear-end collision, and rear-to-side collision. Additionally, the study considered three vehicle categories: light vehicles, heavy vehicles, and motorcycles. Including vehicle types adds information that was unaddressed by previously mentioned studies. Vehicle size is important in evaluating crash modes on interstates where there is a large number of trucks (e.g., single- and multi-trailers) that impose sight occlusion and have quite a different vehicle performance and dynamics as compared to other vehicles. This study concluded that Interstate entrance ramps have a major effect on both manner and frequency of collision. Additionally, rear-end collisions have a higher propensity at both entrance and exit ramps, especially for semi-trucks.
Dong et al. [
13] also employed a mixed logit model to investigate the differences in single and multi-vehicle collisions. It was found that factors consequential to both single- and multi-vehicle crashes include the length of the segment, speed gap, and wet road surface while most other features were only cogent to the multi-vehicle mode of collision. Research conducted by McCartt et al. [
14] focused on the effect of entrance and exit ramps on collision modes. It showed that rear-end collisions occur most frequently on entrance ramps, commonly caused by following too closely during periods of congestion.
More recently, discrete mixture models have been attempted for crash analysis. For example, Hong et al. [
15] applied a double hurdle model to study the significant risk factors of multi-vehicle collisions, where a binary logistic regression model was used at the first stage of the double hurdle model to determine the variables that are likely to cause a particular type of crash (i.e., multi-vehicle crashes versus single-vehicle crashes). In the second stage, a truncated regression model was used to estimate the number of vehicles involved in the multi-vehicle collision. Factors considered in this study included time/day/month of crashes, location of crashes, drivers’ violations and characteristics, vehicle malfunctions, roadway geometry, surface, and weather conditions.
Although the nested/mixed logit models and discrete mixture models have been used for crash analysis, the common linear-in-parameter assumption limits their prowess in effectively exploring high dimensional feature space. In contrast, decision tree models are nonlinear and can effectively partition feature space in a much more flexible fashion. Machine learning and statistical learning models have been compared by Karlaftis and Vlahogianni [
2] and Abdel-Aty and Abdelwahab [
16]. It was pointed out that neural networks would generate more accurate models when fitted to complex data structures. However, the elevated accuracy came at the cost of model interpretability and neural network models are often considered as black boxes. It should be noted that techniques focusing on interpreting complex models, such as neural networks, are being developed. Drawing meaningful inferences is the key to crash analysis and mitigation. However, it turns out that decision tree models often outperform statistical methods when tasked to classify data (e.g., crashes) that is not linearly separable, without the loss of interpretability induced by complex model structures, such as neural network models. For instance, Ramani and Shanthi [
17] compared different decision tree models in classifying collision patterns using twenty-four features. In their study, seven classification algorithms were applied, including C4.5, ID3, C&RT, CS-MC4, Decision List, Naïve Bayes, and Random Tree. It was found that the Random Tree algorithm outperformed all others. In another study, López et al. [
18] used the CART decision tree method to analyze accident data, in which seventeen explanatory variables were used, including characteristics of the accidents, weather information, driver, and road characteristics.
As a rapidly evolving field, recent advancement in machine learning offers a collection of versatile tools for crash analysis and modeling. In this study, we explored two modern machine learning techniques, Linear Discriminant Analysis (LDA) and XGBoost, to analyze a unique data set, which is discussed in the following section.
3. Data Collection and Reduction
The objective of this study was to investigate and understand the roadway, traffic, weather, and environmental features, as well as driver-related factors, underlying different crash types, specifically the three common crash types on freeways: (1) rear-end collision, (2) same-direction sideswipe collision, and (3) angle collision. For this study, we compiled a comprehensive data set by fusing data from four major sources, including the traditional crash data, real-time traffic data feeds from the Georgia Department of Transportation (GDOT) Navigator system, highway geometries (e.g., GIS shape files), and weather data from Weather Underground [
19]. Eight months of concurrent data, from October 10, 2017 to June 26, 2018, were acquired from the aforementioned sources on the I-285, approximately 64-mile long interstate loop in Georgia. Specifically, traffic data were gathered in 5-min intervals, including traffic count, speed, occupancy from the GDOT navigator’s video detection system (VDS), which is the primary source of real-time traveler information in Georgia. The VDS stations were installed approximately at one-third mile spacing along major interstates around Atlanta. This granular traffic data allowed us to capture the impact of traffic dynamics coupled with specific geometric features, which is lacking in existing crash models that often consider the daily or hourly traffic volume as an exposure measure [
4,
8].
Roadway, traffic, weather, and environmental (RTWE) factors are commonly treated as exogenous variables for crash modeling and analysis, which has been extensively studied in the literature [
13,
15]. While driver-related factors are often considered as endogenous to crash occurrence and driver-level data are commonly obtained through police reports after the crash event. As such, traditional crash prediction models generally do not include driver-related factors. From an engineering and predictive modeling perspective, our focus is on studying how the RTWE variables impact the modes or types of multi-vehicle collisions. However, given the fact that driver factors are the critical reasons for over 94 percent of crashes [
20], we will also examine the police-reported driver factors separately on their effects on multi-vehicle collision types. Therefore, we divide those factors (“features” in the machine learning context) into two groups. The resultant comprehensive data set included 3721 multi-vehicle crashes. The RTWE features and driver-related features are summarized in
Table 1 and
Table 2, respectively.
Table 3 and
Table 4 present the statistics of feature values for each feature set.
As shown in
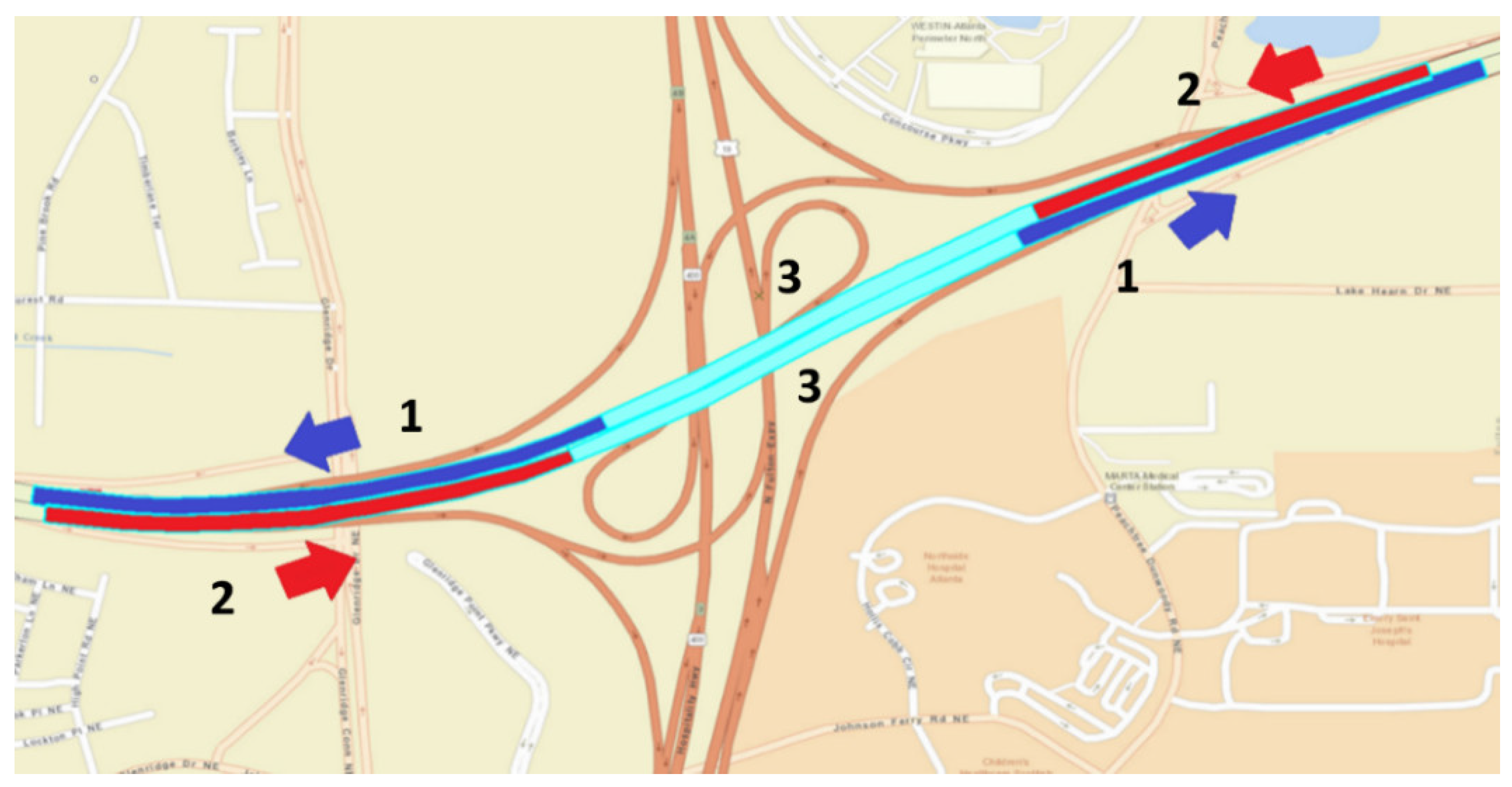
Table 1, RTWE features include road geometry, road composition, traffic conditions, and environmental factors such as weather and lighting conditions. Features of this data set included numerical variables, such as vehicle speed, wind speed, vehicle count, and occupancy, as well as categorical variables that were one-hot-encoded for modeling purposes. For example, road segments relative to an interchange were classified into three sub-features: Merging, Diverging, and Within based on their relative locations to the interchange ramps, as depicted in
Figure 1.
Table 1 also includes weather data that was obtained from Weather Underground [
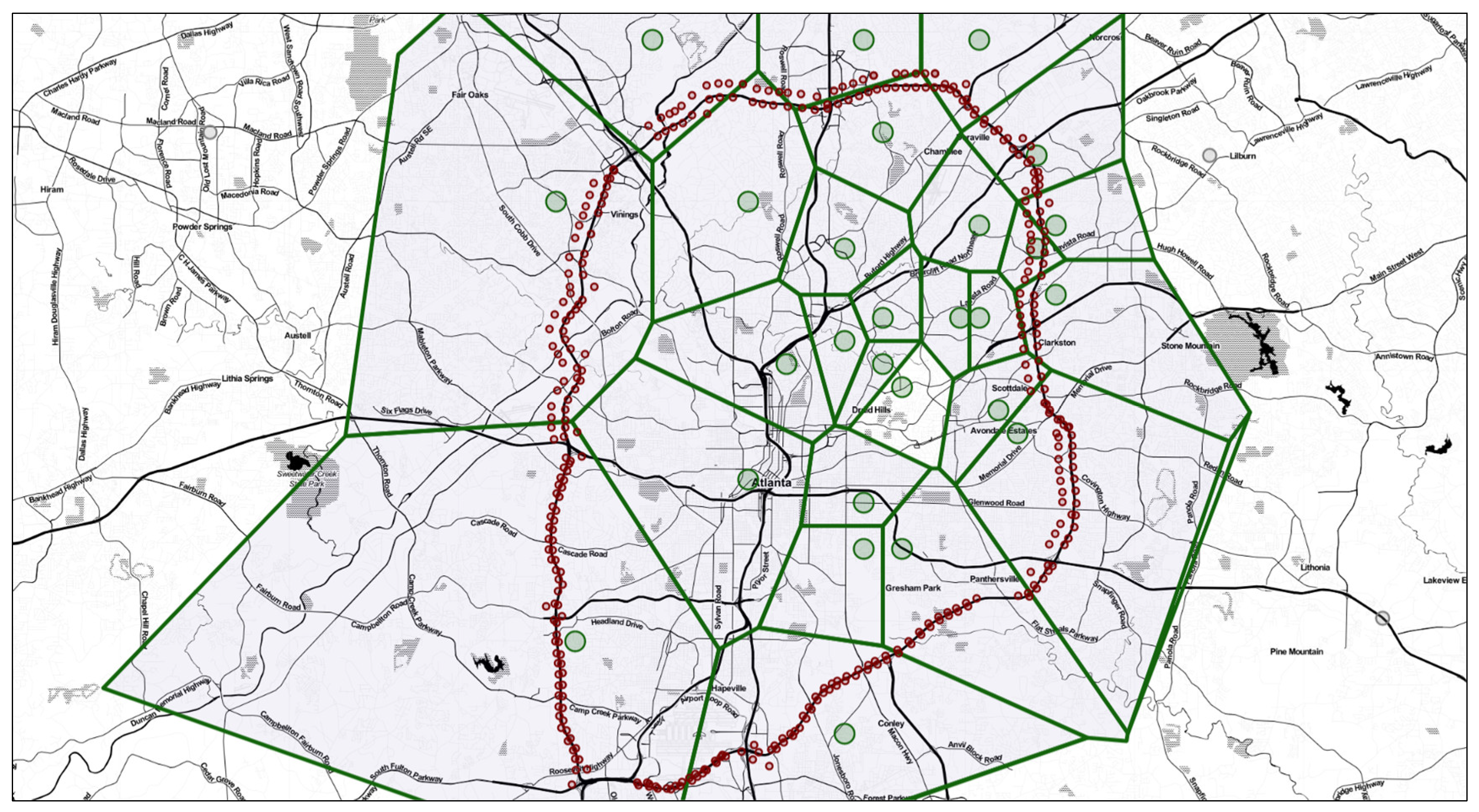
19]. The four major features of weather data collected are precipitation rate, precipitation accumulation, gust, and wind speed. The Weather Underground contains tabulated datasets of weather taken from localized weather stations at varying rates, these intervals range from five to fifteen minutes. Data from all weather stations surrounding I-285 were obtained over the same eight-month study period. The weather data was matched with crash both temporally and spatially. Specifically, weather stations were spatially paired with crashes through the implementation of a Voronoi diagram in
Figure 2.
As shown in
Figure 2, the weather stations are depicted in larger green circle and the traffic cameras in smaller red circle. The Voronoi diagram was constructed around the weather stations to ensure that each crash was geographically assigned to the nearest weather station for obtaining concurrent weather information.
The driver-related factors or features are shown in
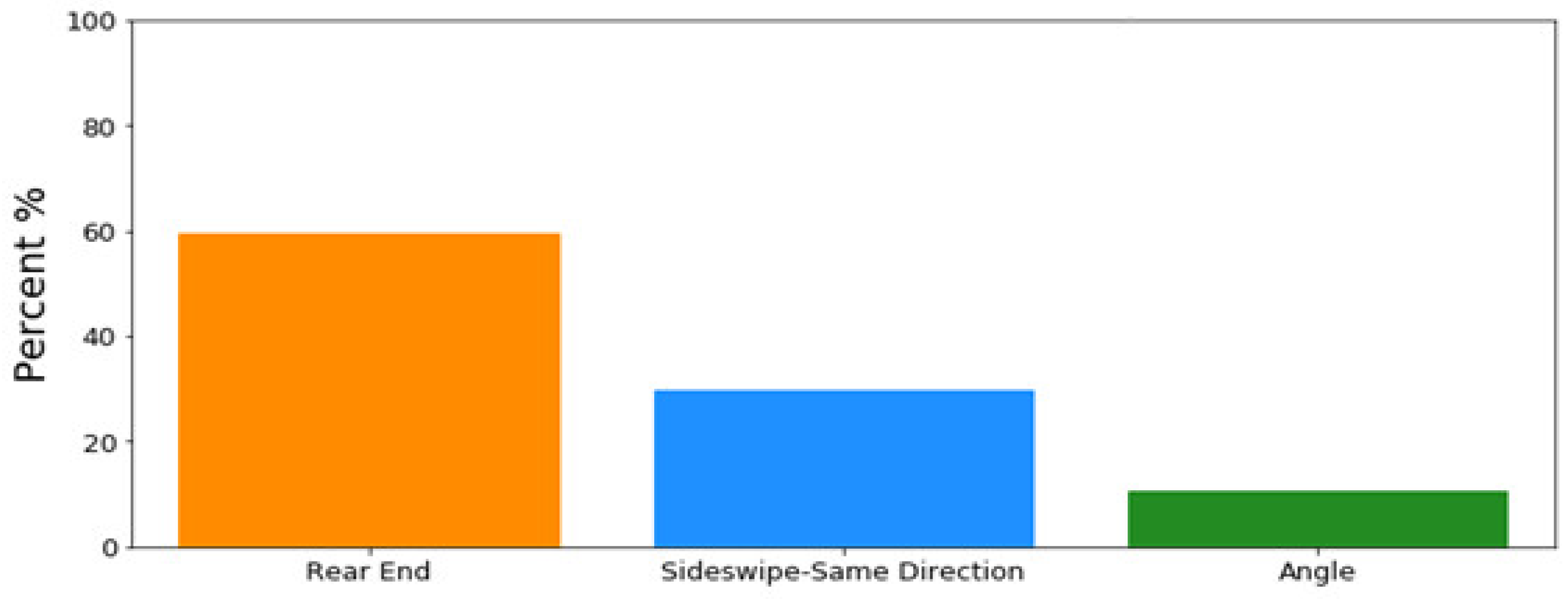
Table 2, including the age of the driver at fault and one-hot-encoded categorical variables, such as reckless driving, driving under the influence and following too closely, as reported by the responding police officer for each accident. Finally, the distribution of multi-vehicle crash types is shown in
Figure 3. As expected, rear-end collision is the dominating crash type on the interstate, followed by same-direction sideswipe and angle.
To gain an understanding of how the features correlate with one another, correlation matrices were generated with correlation coefficients shown in
Figure 4 and
Figure 5, respectively for RTWE features and driver-related features. The correlations among the features in each feature set are relatively low.
4. Research Approach
Different from conventional statistical approaches, we studied the multi-vehicle crash types as a classification problem and explored two modern machine learning techniques, specifically Linear Discriminant Analysis (LDA) and eXtreme Gradient Boosting (XGBoost), which are the state-of-the-art classification algorithms under supervised learning. The main reason for picking LDA, a linear classifier, is for comparison with XGBoost. The classes or labels in this setting are three major multi-vehicle crash types on freeways, i.e., rear end, same-direction sideswipe, and angle. As described in
Section 3, we have two feature sets. One includes road, traffic, weather, and environmental features (
Table 1). The other includes driver-related features (
Table 2). By applying the LDA, we sought to find hyperplanes or linear combinations of factors in lower-dimensional feature space to separate the three crash types. In comparison, XGBoost is a nonlinear tree-based ensemble method, which has proven to be an extremely effective algorithm and won many machine learning competitions. For example, Maksims Volkovs, Guangwei Yu, and Tomi Poutanen implemented gradient boosting models and won the first place of the 2017 ACM RecSys challenge [
21]. Vlad Sandulescu and Mihai Chiru also implemented an XGBoost model that won the 2016 KDD Cup competition [
22], which outperformed the statistical mixed model on the same set of features. Both LDA and XGBoost are introduced subsequently, followed by our data analysis results in the following section.
4.1. Linear Discriminant Analysis
LDA is a supervised machine learning technique that assumes Gaussian distribution and the same variance–covariance matrix (i.e., homoscedasticity) across classes. Modern LDA emerged from Fisher’s work published in 1936 [
23]. The primary focus of LDA is to find k-1 projections or corresponding hyperplanes to separate k classes. In practice, LDA is commonly employed to reduce the dimensionality of large feature spaces.
4.2. Decision Tree Analysis
Decision trees are popular supervised methods in machine learning. Construction of decision trees involves guided decisions on answering sequential questions, such as which feature to split and at what value to split at each decision step to minimize regression error (regression trees) or classification error (classification trees). By making such decisions, tree-based models essentially partition the feature space in a nonlinear fashion into relatively homogenous regions for targeted outcomes. The major advantages of tree-based methods lie in their computational efficiency and flexibility in handling various types of features (e.g., numeric, ordinal, categorical, etc.). However, rudimentary decision trees suffer from high variance. In other words, small changes in data would result in different sequences of splits. In addressing this issue, bagging has been used that takes the average of predictions from many trees estimated with bootstrapped samples. This technique allows us to grow deep trees with high variance and low bias, and then averaging these trees to reduce variance. Bagging also provides a side benefit for free since each bagged tree makes use of about two-thirds of the data, leaving the remaining one-third of the data, referred to as out of the bag (OOB), for model validation. Although bagging has proved itself as a powerful technique for improving model accuracy, bootstrapping from the same training data set would likely result in similar or correlated trees. Random forests rise as an improvement over bagged trees by imposing a small tweak on selecting split features. For each split, instead of picking a predictor from the entire set of features, a random sample of features is considered as split candidates. This added randomness helps to decorrelate the trees and averaging of these decorrelated trees results in more reliable predictions. Random forests can be considered as a generalization of bagging. When the choice set of the split features is the same as the entire feature set, random forests reduce to bagging. Both bagging and random forests are ensemble methods since they take advantage of aggregating many tree models. With bootstrap sampling, these trees are constructed independently in parallel. Thus, bagging and random forests are considered as parallel ensemble methods. In contrast, boosting trees do not involve bootstrap sampling and are constructed sequentially, i.e., each tree is grown using information from previously grown trees. This sequential ensemble method permits the addition of new trees that correct the errors made by the trees previously constructed. In recent years, gradient boosting decision trees have emerged to dominance among machine learning competitions, as previously noted. By leveraging the distributed computing environments, XGBoost is an optimized distributed gradient boosting library designed to be highly efficient, flexible, and portable [
3]. Specifically, XGBoost has a natural way to handle missing data and is well suited for analyzing crash-related features that are inherently heterogeneous. In this study, we used the open-source package, XGBoost, for model estimation. Different from conventional first-order tree-based methods, XGBoost is a second-order method with an objective function expressed in Equation (1), where the first term represents the second-order approximation of loss after removing the constant term, and the second and third terms are regularization terms to control the tree complexity.
where gamma (γ) represents the regularization on the number of nodes (T) and λ is the regularization on the sum square of leaf scores or weights. Both terms control the penalty imposed on tree complexity.
is the weight or score for leaf j and
represents the partitioning or node assignment function. Lastly,
and
are the first-order and second-order gradient statistics on the loss function, defined in Equations (2) and (3), where
is the prediction for
i-th instance at (t − 1) iteration and
is the corresponding label.
The weight for each leaf is calculated using Equation (4). Where
is the set of indices of data points assigned to the j-th leaf.
XGBoost recursively chooses a feature split that maximizes the gain (or reduction in loss). The detailed derivation of XGBoost can be found in [
3]. For a better interpretation of XGBoost results, we implemented the Shapley Additive Explanation (SHAP) package [
24]. Lundberg et al. [
25] showed how SHAP values can be efficiently computed for tree-based ensemble models. Specifically, the SHAP value for each feature represents the feature’s contribution to the final model prediction, weighed against all other feature contributions, and can be computed from Equation (5).
where
M is the number of features,
x is the original feature space.
denotes the set of observed features.
is the expected value of the model prediction conditional on the set of features (S) being examined.
is the expected value of model prediction in the absence of feature
i. For the nonlinear models, such as XGBoost, the order in which features are introduced matters.
is the Shapley Additive Explanation (SHAP) for feature
i averaged across all possible feature orderings of the model.
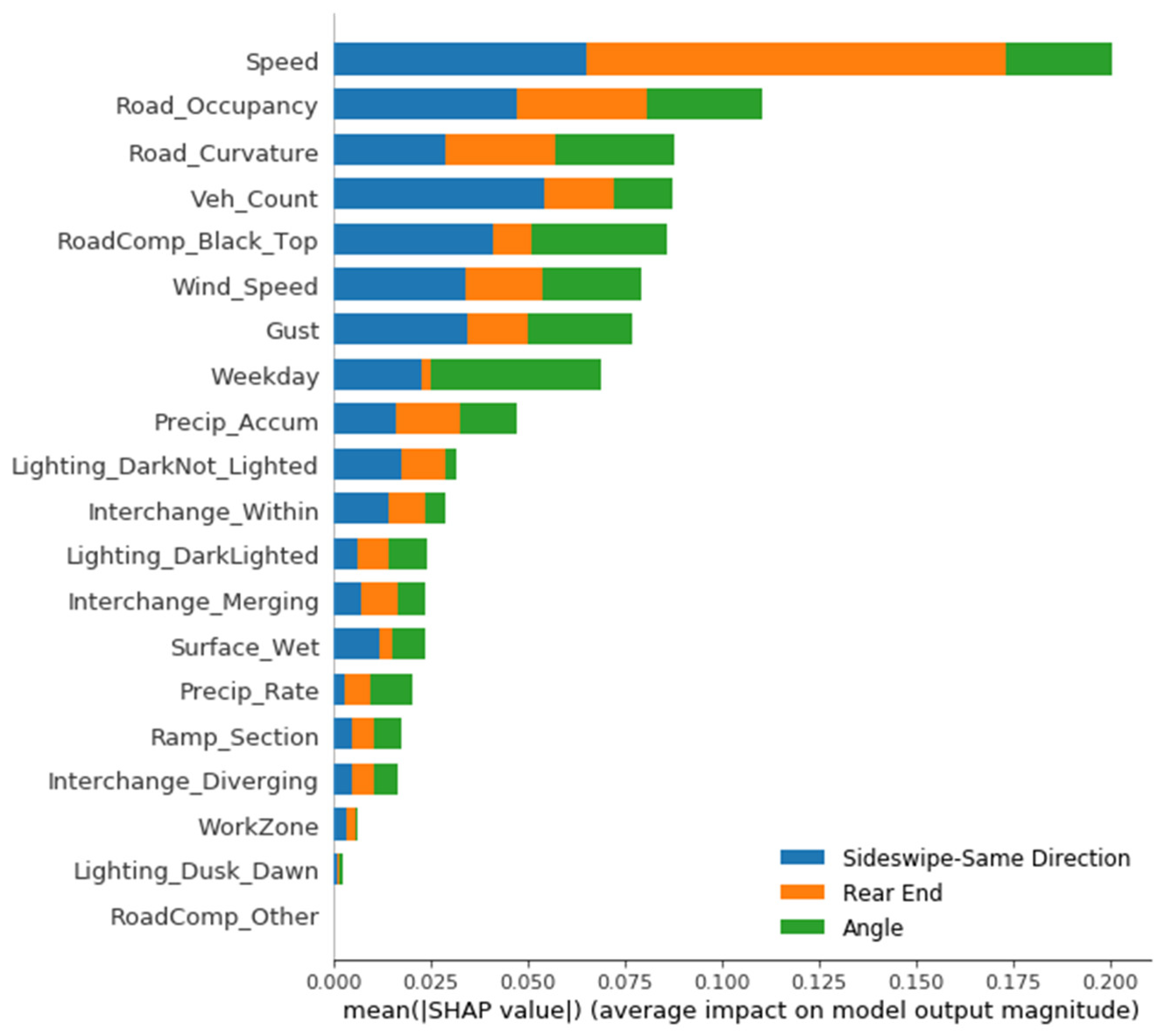
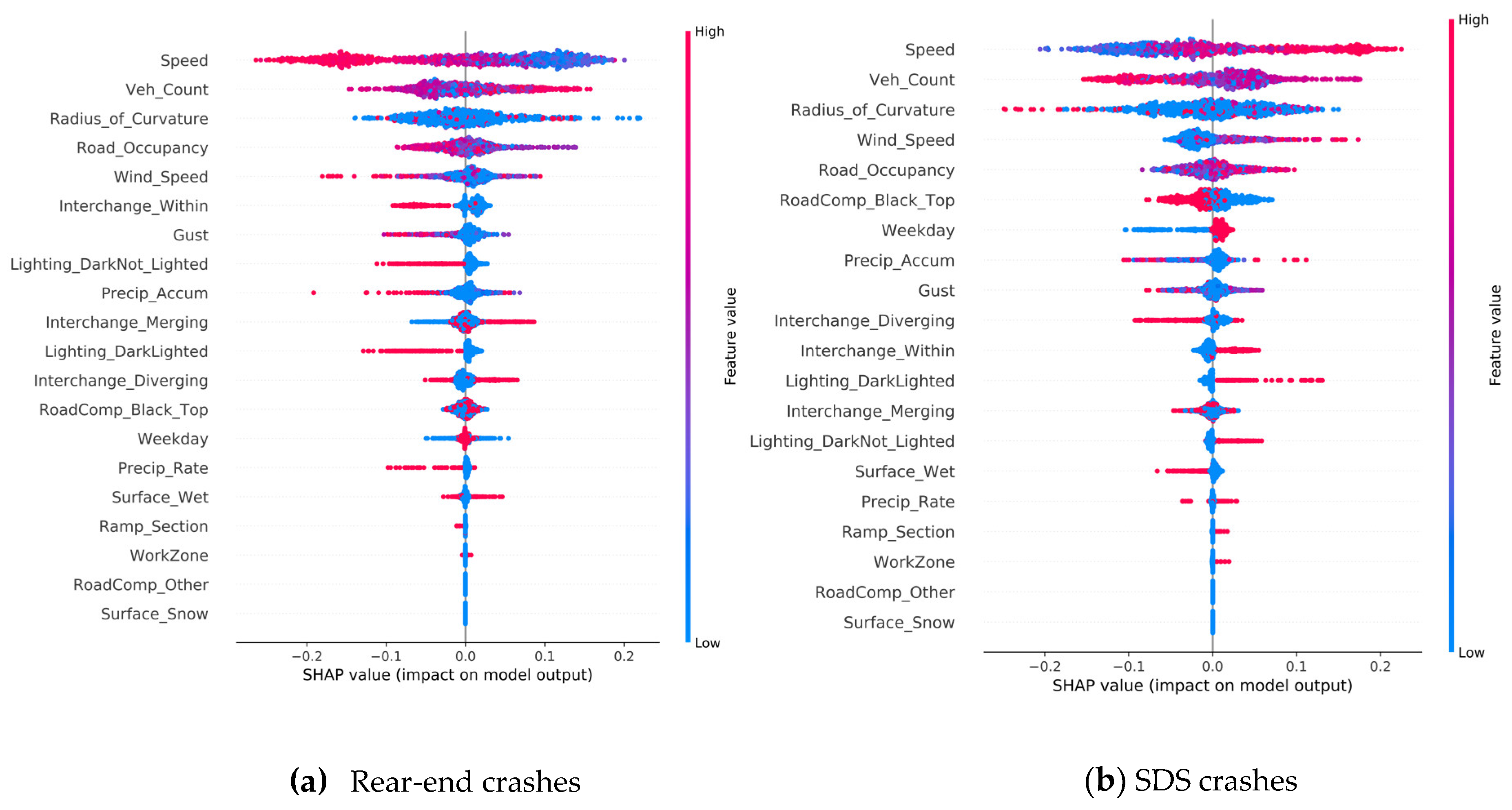
The application of the SHAP values allows us to evaluate the influence of each feature value consistently and explicitly with the complex XGBoost model structure. The impact of each feature value over the multitude of decision trees was summed to ascertain the overall effect on ensembled model prediction. Therefore, the effect of each feature value could potentially be associated with an increased/decreased likelihood of a particular class prediction. Understanding such directional influence of each feature is pertinent to a better interpretation of tree-based ensemble models.
6. Discussion
Crash data has traditionally been analyzed using classic statistical models, such as nested logit, mixed logit, and discrete mixture models. The statistical models often impose strong assumptions on error distribution and correlation and are suitable for data sets with limited features. In this study, we demonstrated the utility of modern machine learning techniques with a fused data set that contains a relatively large number of features. Two sets of features, i.e., RTWE features and driver-related features, were investigated to gain a deeper understanding of how these features potentially related to a particular type of crash, which is a classification problem in a machine learning context. Specifically, two modern machine learning techniques (i.e., LDA and XGboost) were explored to mine a comprehensive data set fused from four distinct data sources. As a result, LDA has limited capacity in classifying the crash types due to its restrictive assumptions. XGBoost models, on the other hand, are nonlinear and able to classify the crash types in a reasonably accurate manner. The XGBoost models were able to achieve the test accuracy levels of 68.4% and 80.2% with the RTWE features and driver-related features, respectively. A potential drawback of XGBoost models is their lack of interpretability. This issue was mitigated by implementing Shapley Additive Explanation (SHAP) value [
23]. Additionally, compared to the classic statistical methods, the tree-based ensemble methods require additional efforts on hyperparameter fine-tuning.
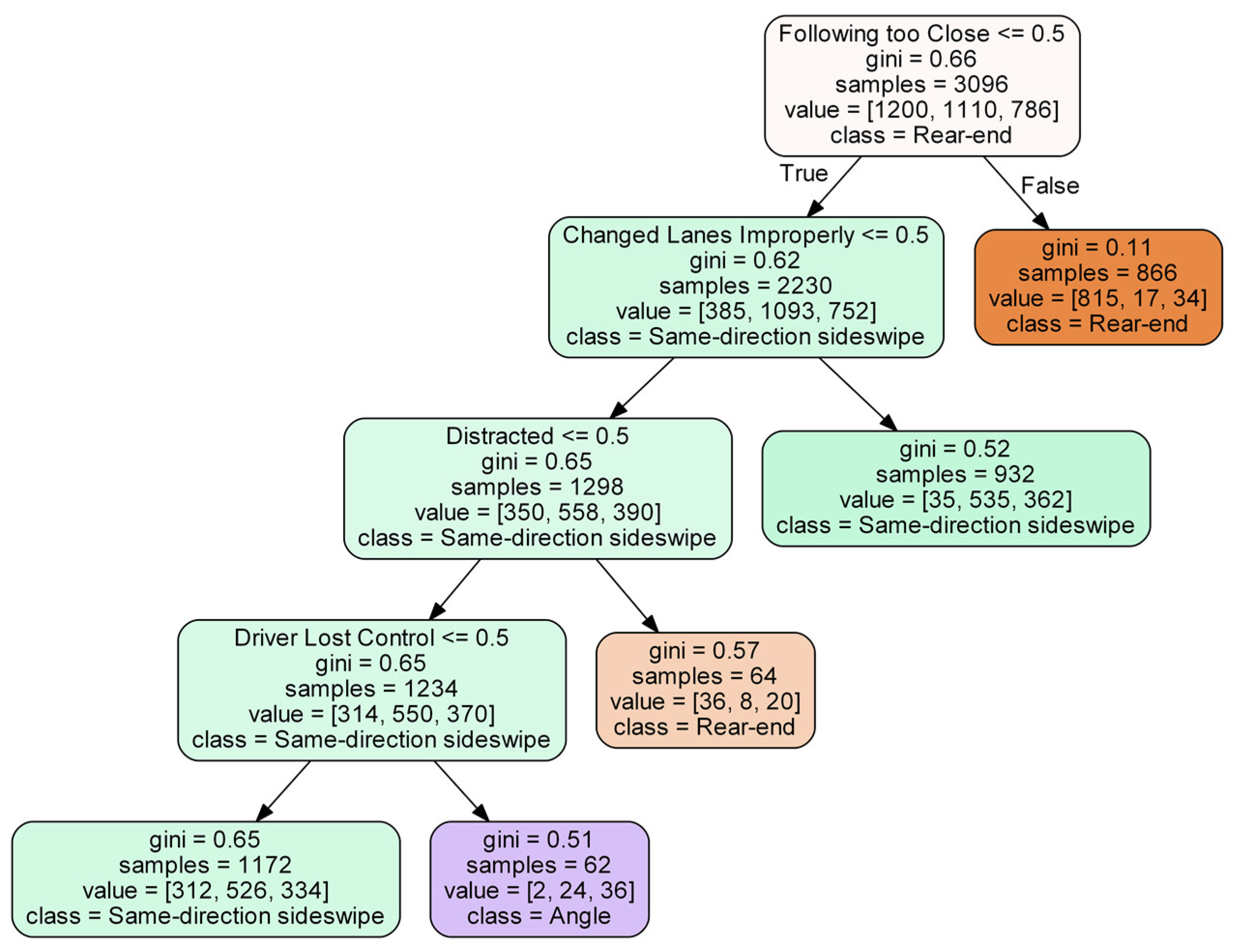
Based on the XGBoost model developed using the RTWE features, it was found that within-interchange locations have a lower chance of rear-end crashes, but a higher propensity for SDS and angle crashes. Merging locations correlate positively with rear-end crashes. Ramp section was positively correlated with both angle and SDS crashes. Angle crashes displayed a higher reactivity to adverse weather conditions, such as precipitation and wet surface. Higher wind speed appears to increase the chance of SDS crashes. Additionally, angle crashes occurred more frequently on weekends, likely due to more aggressive driving. SDS and angle crashes happened more often in dark and low light conditions, likely due to low visibility. Workzone is mainly associated with SDS crashes. Compared to RTWE features, a better classification result was obtained using driver-related features, which is expected because driver-related features, especially driver faults, have a direct impact on crash types. As a result, rear-end crashes were commonly caused by following too close and distracted driving, while angle and SDS crashes were typically related to improperly changing lanes, losing control, misjudged clearance, and failing to yield. In particular, driving under the influence (DUI) is a salient feature for angle crashes, which often occurred on weekend. Additionally, older drivers are more likely to be involved in rear-end crashes, while younger drivers had a relatively higher representation in angle and SDS crashes.
Besides the inspiring results from this study, we would like to point out some limitations that could be addressed by future studies. Given the data-driven nature of machine learning methods, the quality of data is essential to and governs the quality of the resulting models. Although four different sources of data have been fused and used for this study. The data set is still quite limited and localized. The expansion of the geographical coverage of the data set would be desirable. In addition, the data set can be further augmented by including other newly available data sources, such as real-time road conditions and vehicle operating data. Given the various sensors being deployed along with the transportation infrastructure (e.g., intelligent transportation systems and road weather information systems) and within vehicles (e.g., connected and automated vehicles), collecting and fusing these high-resolution real-time data sources become practically possible. These additional data sources can certainly be utilized to construct even more powerful machine learning models to better understand crash patterns and mechanisms. For this study, we focused on understanding the various features underlying different crash patterns or types. As such, only crash-related data were mined. The results of this study cannot be used to directly infer the likelihood of crashes and corresponding attributing factors. Future studies that consider sampling non-crash conditions are necessary to construct predictive models for crash occurrence and frequency. Again, leveraging the modern machine learning methods and increasingly available high-resolution data sources for predicting crashes is a promising area and expected to produce much more accurate and reliable results than the existing models based on conventional regression methods (e.g., zero-inflated Poisson models, negative binomial models, etc.). Additionally, to estimate the probability of crash occurrence as well as crash types, a more generic hierarchical model structure could be adopted to estimate crash probability at a higher level and then model crash types and/or severities at a lower level.
7. Conclusions
Traditionally, crash data has been studied with classic statistical methods as opposed to machine learning techniques. Crash data is often analyzed to engender inferences about the underlying mechanism or relationship. This inference can be used to create countermeasures to mitigate or reduce the risk of collisions. Historically, it has been thought that machine learning techniques should be implemented when the prediction is more important than interpretation. However, new methods, such as the Shapley Additive Explanation [
24], have demonstrated that complex machine learning models, such as gradient boosting decision trees, can be properly interpreted, making it a more versatile technique within various modeling communities. Additionally, machine learning methods are more adept at managing diverse and elaborate data sets. Crash data contains a vast quantity of various features, which are well suited for and potentially better analyzed by modern machine learning techniques as compared to traditional statistical methods.
In this study, we explored and contrasted two modern machine learning techniques (i.e., LDA and XGBoost) by mining a uniquely comprehensive data set fused from four distinct data sources. The objective of the study is two-fold: (1) demonstrate the utility and versatility of the modern machine learning methods, and (2) better understand the effects and intricate relationships of both RTWE features and driver-related features underlying three common freeway collision types: (1) rear-end collision, (2) same-direction sideswipe collision, and (3) angle collision. As a result, many feature effects agree well with those found from previous studies. The high model accuracies with the test data sets are particularly interesting and inspiring, and underscore the superiority and high potential of the XGBoost method in the context of crash analysis and modeling.