Sensitivity Assessment of the Seismic Response of a Masonry Palace via Non-Linear Static Analysis: A Case Study in L’Aquila (Italy)

Abstract

The city of L’Aquila (Italy) includes a significant amount of masonry palaces erected from the middle of the 13th century up to the first half of the 20th century. This paper focuses on the seismic response of a masonry palace built during the first half of the 20th century and characterized by regularity in plan and elevation. The authors investigate the seismic response by varying a suite of modelling parameters that express the actual scatter of the mechanical properties typical of the masonry palaces erected in L’Aquila. The authors discuss the seismic performance exhibited by this building during the 2009 earthquake. Then, they assess the sensitivity of the selected building’s seismic performance via non-linear static analysis to the mechanical properties of masonry, the in-plane stiffness of the floors, and the mechanical resistance of the spandrels. The parametric analysis shows that the three variables markedly affect the shear resistance, the ultimate displacement, and the behavior factors. The fragility functions were then estimated from the results of non-linear static analysis. A significant scatter of the probability of collapse for the considered limit states reveals the limitations of typological approaches for masonry palaces.

1. Introduction

A significant part of the scientific literature about the seismic response of masonry buildings focuses on evaluating synthetic parameters, expressing the seismic vulnerability from visual inspections [1,2,3]. Furthermore, several masonry facilities reveal similar structural responses after a seismic event, which leads to classifying the buildings based on typological characteristics [4,5,6,7,8,9]. This typological and synthetic approach descends from the fact that, despite the intrinsic differences between masonry buildings, a limited set of structural parameters affect the seismic response the most. Among them, masonry’s mechanical properties, the resistance of masonry spandrels, and the in-plane stiffness and resistance of the floors play a crucial role in both the in-plane and out-of-plane seismic response [10,11]. The mechanical properties of masonry markedly affect the damage and the failure of buildings subjected to gravity loads and earthquake actions. The spandrels’ properties affect the strength degradation and the walls’ lateral resistance, influencing the masonry piers’ coupling effect [12]. The in-plane stiffness and resistance of the floors affect the horizontal force’s distribution between the walls and the occurrence of possible out-of-plane phenomena [13]. Careful consideration of these variables is a prerequisite for a reliable prediction of a masonry building’s seismic performance. Most of the masonry buildings belong to architectural heritage. Each construction is a stand-alone case with scattered structural characteristics. The discussion of these buildings’ seismic response deserves a dedicated research effort due to randomness of the structural parameters and the complexity of their seismic behavior, sometimes exasperated by the sensitivity of numerical tools to the input variables [14]. Nevertheless, masonry palaces express their singularity more clearly than other building types. The current research focuses on the seismic response of a masonry palace located in L’Aquila’s historical center (Italy). Yet, to the authors’ knowledge, the seismic response of historical buildings in L’Aquila received interest also from other authors [15,16,17,18,19,20,21,22,23]. The historical masonry constructions located in L’Aquila, but even in different zones, descend from the centuries’ stratification and seldom remain unchanged from their original configuration. Frequently, the modification occurred during the centuries includes structural transformations, embedding also portions of neighboring buildings, leading to a masonry building aggregate composed of structural units with different height, several stories, structural types and materials [24]. The spatial distribution of the structure appears articulated. Figure 1 shows a photo of a masonry historical aggregate, called “Palitti” Palace, located in “Poggio di Roio”, a municipality 10 km North-West of L’Aquila center, built as a residential dwelling of a wealthy family. Figure 2 reports the palace’s prospect, highlighting the different heights of the structural units, which can be identified by visual inspection.

In some cases, the refurbishments after the earthquakes caused significant alterations of the urban layout. For example, during the reconstruction after the earthquakes occurred in 1315 and 1350, a tower of the city wall became the St. Silvestro church’s chapel, a masterpiece of the local monumental heritage [25]. After the restoration carried out in the 16th century, a monastery, called “St. Teresa”, see Figure 3a, arose from the fusion of several dwelling units. The repair works incorporated a neighboring church wall, called St. Domenico, in the St. Teresa building’s body. A historical map, depicted in Figure 3b [26], confirms that the two buildings were isolated before the 16th century.

The palaces built and rebuilt between the 16th and 18th century in the city’s historical center highlight recurrent constructive features and less scattered mechanical properties. Typical features include a hollow rectangular shape in the plan, due to interior courtyards, with a more regular aspect and facades sumptuously embellished. Two masonry palaces, “Pica Alfieri”, see Figure 4, and “Burri Gatti” Palaces, see Figure 5, clearly express the architectural style of the time [27].

Due to the reasons above, the attempt to classify and organize the results of seismic vulnerability assessments of historical masonry buildings is challenging and hardly possible. Each building expresses a singularity, intrinsic geometries, variabilities, alternation of materials, molded by the time. Historical monumental buildings are unique and cannot be reduced to any standard structural scheme [28]. Still, the assessment of the structural archetype’s structural response, or more simple building, may be of great help for the understanding of the role played by the most significant parameters. The authors performed a seismic assessment of a masonry building characterized by a simple plan and elevation configuration. A suite of modelling parameters was selected according to the variability observed among masonry palaces in L’Aquila.

This paper descends from an abstraction. The authors chose to model an existing regular building and varied the modelling parameters according to the scatter observed in the population of masonry palaces in L’Aquila. The authors described five buildings in Figure 6a,b to prove the physical variability of the modelling parameters. Still, the analysis focuses on the modelling of a single existing regular building.

This building will act as a structural archetype, due to the regularity of its geometry. The authors varied its properties to assess their effect on the in-plane seismic performance.

This paper is organized as follows. The first section describes the building and reports the results of the seismic analysis. The second part focuses on the effect of the structural parameters on the outcomes of non-linear static analyses. A parametric study attempts to highlight the role of the masonry characteristics, the resistance of the spandrels, and the floors’ in-plane stiffness in the building’s in-plane seismic response.

The non-linear static analyses’ outcomes are then used to derive fragility curves as a function of the spectral demand displacement.

2. Research Significance

Despite numerous research studies focused on historical buildings’ seismic response, a prediction of their seismic behavior remains challenging. Recurring earthquakes confirm the high vulnerabilities of masonry palaces and the urgent need for seismic mitigation measures. A prerequisite of the seismic analysis is an in-depth knowledge of the monumental buildings [29], often affected by the lack of information and the difficulty in performing invasive diagnostic campaigns.

The current research investigates a masonry palace’s seismic performance attempting to mirror an entire class representative of L’Aquila city’s built-up. Some research activities deepened the seismic response of masonry palaces in L’Aquila, analyzing the damage after the 2009 earthquake [15,16,20]. Other authors investigated a single case study’s seismic performance through numerical analysis [17,18,19]. The authors concentrated on parametric non-linear static analyses of a single masonry palace. The investigation originates from an in-depth knowledge of the case study and the other four buildings, which provided the scatter of the mechanical parameters varied during the analysis.

The authors varied the mechanical parameters that are influential on the seismic performance: the masonry characteristics, the resistance of the spandrels, and the floors’ in-plane stiffness.

Moreover, the undertaken approach gives valuable information for predicting seismic behavior and decision-making after seismic events [30]. The results highlight the three variables’ influence on the shear resistance, the ultimate displacement, and the behavior factors [31,32,33]. The proposed approach supports several research activities focused on masonry palaces’ seismic performance to develop reliable typological approaches for seismic assessment.

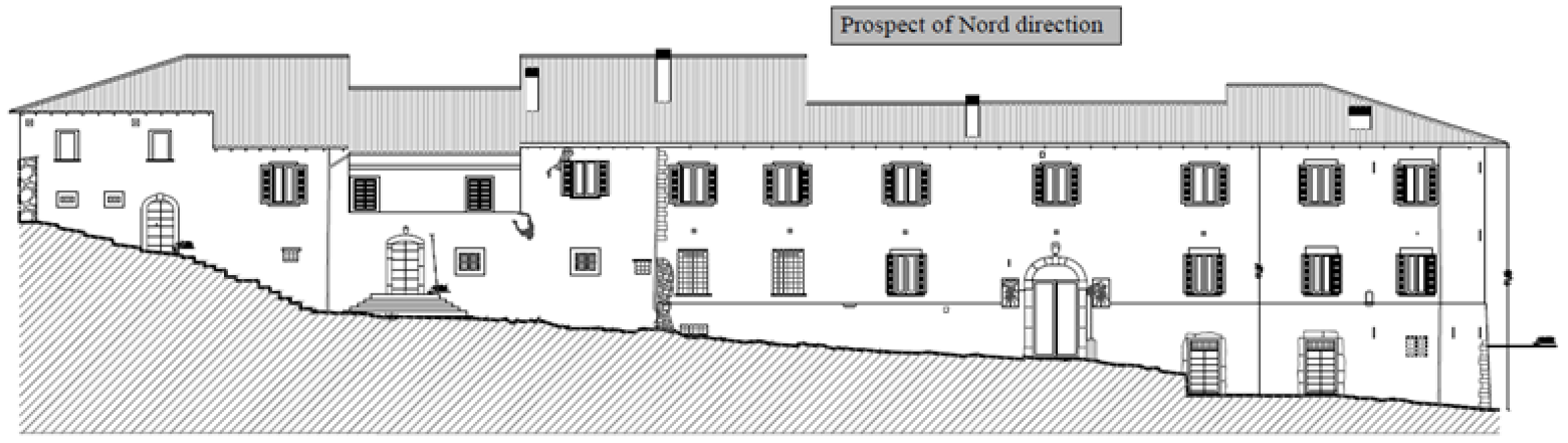
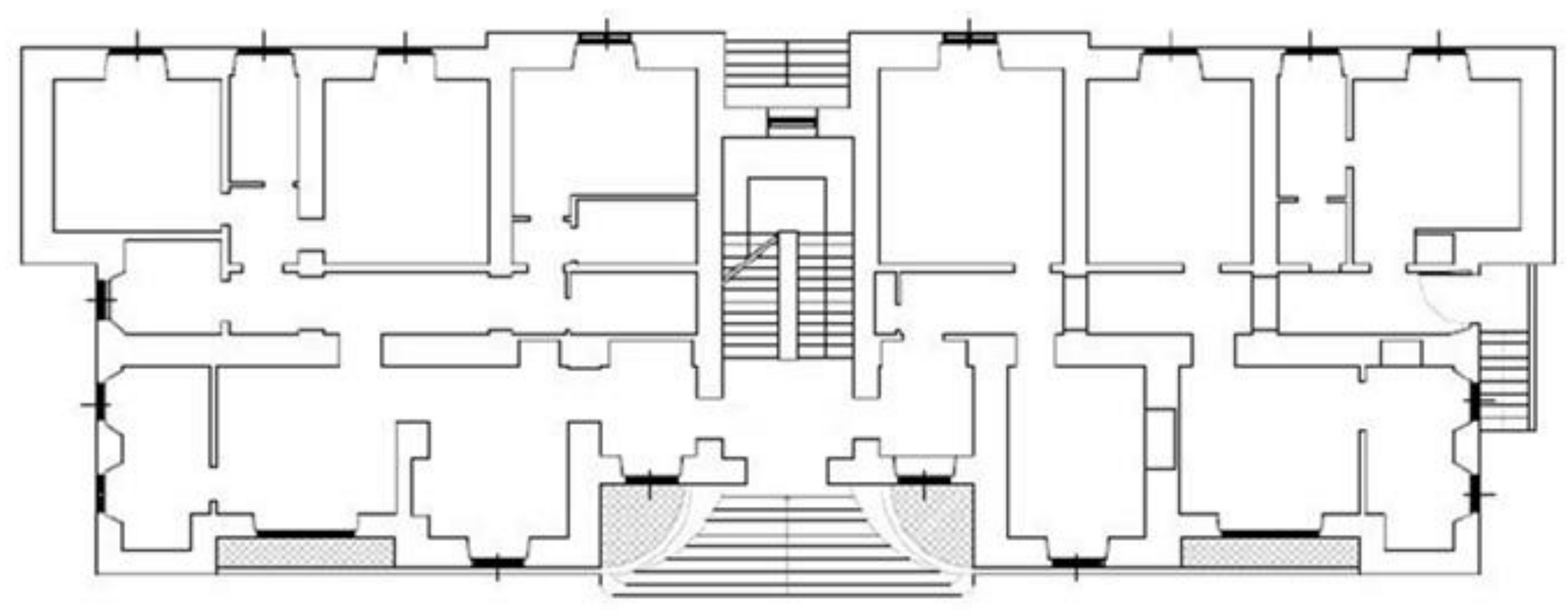
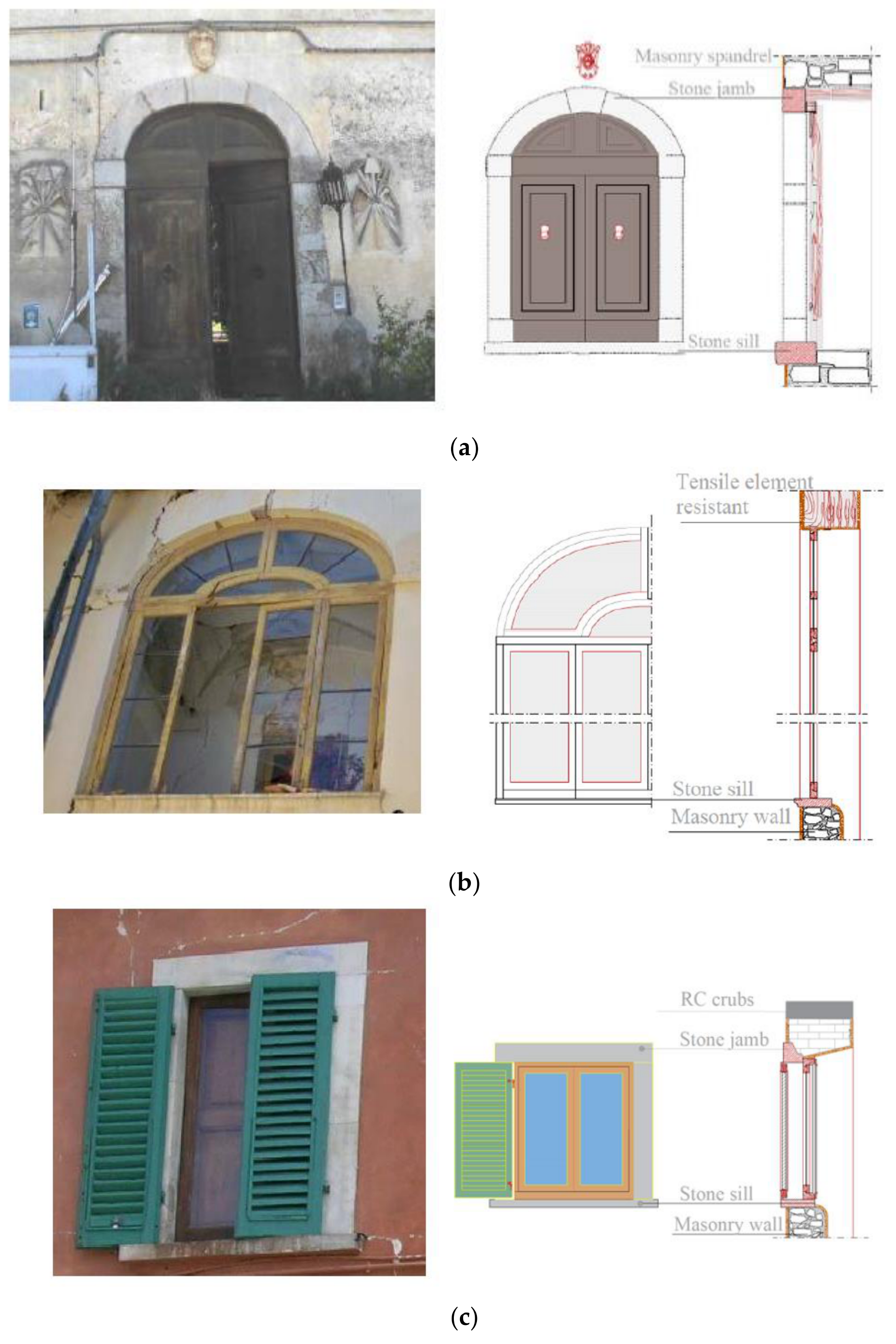
3. The Case Study: Palace 2

The selected masonry palace has a nearly rectangular shape, see Figure 7, 37 m long and 13 m wide, and consists of three stories, approximately 3.4 m high. The openings are aligned and characterized by a considerable height, 1.95 m—the standard windows and 2.45—the French ones. The main entrance has a large door embellished by a white stone frame. The supporting structure consists of stone masonry with lime mortar, and clay bricks layer every 60 cm; three alignments of resistant walls in the longitudinal direction and eight in the transverse one. The thickness of the walls decreases in elevation, from 100 cm at the foundation to 60 cm at the last level. The floors are made of a 15 cm thick reinforced concrete slab, connected to the walls by a 30 cm deep Reinforced Concrete, RC, ring beams. The depth of the foundations is nearly 1 m.

Seismic Response after the 2009 Earthquake in L’Aquila

The building showed extensive damage after the 2009 earthquake, with a prevalent in-plane response due to the RC ring beams’ retaining action and the significant in-plane stiffness and resistance of the RC floors. Specifically, the walls manifested typical x-like cracks, extended to the entire wall thickness, typical of the shear failure mode. The spandrels were heavily damaged and markedly affected the supporting walls by causing a notable coupling between the vertical walls due to their significant strength. The transverse walls exhibited a damage pattern similar to the longitudinal ones, characterized again by x-like cracks through the entire wall thickness. There is no sign of out-of-plane mechanisms: this evidence recurs in all buildings of the 19th architecture and older palaces provided with anti-seismic devices that prevented the trigger of local mechanisms.

4. Numerical Analyses

The numerical analyses of this building were carried out by varying the mechanical properties of masonry (representative of the Vertical Structures, VS), stiffness of the floors (representative of the Horizontal Structures, HS), and stiffness of the spandrel beams (indicated as SP).

The three selected parameters are among the most influential ones regarding building palaces’ seismic performance.

The authors considered five values of the mechanical parameters, in

Table 1. Mechanical properties of the five masonry typologies.

Masonry Typology (VS)	Compressive Strength fm (MPa)	Shear Strength τ0 (MPa)	Young Modulus E (MPa)	Shear Modulus G (MPa)	Specific Weight γ (kN/m3)
VS1	1.00	0.018	870	290	19
VS2	1.30	0.023	870	290	19
VS3	2.00	0.035	1230	410	20
VS4	2.40	0.042	1230	410	20
VS5	3.38	0.073	2262	754	21

, representative of five different qualities of masonry detected in L’Aquila according to the Italian Standard Code [34,35]: (VS1) semi-regular stone arrangements, the so-called “Apparecchio Aquilano” [36] in Figure 8a; (VS2) irregular stone units with scattered clay units in Figure 8b; (VS 3) semi-squared stone units in Figure 8c; (VS4) semi-squared stone units with interspersed clay bricks in Figure 8d; (VS5) split stone masonry with good texture and good quality of the mortar in Figure 8e.

Six values were selected for the stiffness of floors: (HS1) wooden floors, in Figure 9c, with joists and flooring made of one layer of timber planks, with a shear modulus G of 10 MPa; (HS2) wooden floors with joists and flooring made of two layers of perpendicular timber planks, with a shear modulus G of 1000 MPa; (HS3) brick vaults on the ground floor with G equal to 100 MPa, and deformable (wood or steel) floors on the upper floors, in Figure 9a, with G equal to 10 MPa (HS4) floors made of steel joists and brick vaults, with G equal to 8700 MPa; (HS5) floors made of steel joists and brick tiles, see Figure 9b, with G equal to 10,000 MPa; (HS6) RC monolithic floors, with G equal to 14,500 MPa.

The strengths of the spandrels correspond to three cases: (SP1) lack of tension-resistant elements and brittle masonry, see Figure 10a; (SP2) presence of either a lintel due to a good layout of masonry or tension-resistant element, see Figure 10b; (SP3) presence of RC or steel ring beams, see Figure 10c.

A multivariate sensitivity analysis would have caused unbearable computational effort and onerous simulations [37]. Thus, the authors varied a single parameter similar to what was done by several other authors [38,39]. The variation of one of the three selected parameters (vertical structures, horizontal structures and masonry spandrels) in the fixed range values, was carried out by keeping the others two structural parameters constant and equal to their average values.

Fourteen different Finite Element models (FEs), which differed in the mechanical parameters listed before, were implemented in the software package 3Muri^® [40]. The masonry elements are represented using a continuum homogenized model with the finite element method [41]. In this software, the equivalent frame modelling approach is followed: the masonry panels, namely, the piers (the vertical elements) and spandrels (the horizontal elements), are modelled as non-linear beams [42,43] connected to each other by rigid links [44]. The masonry portions confined between piers and spandrels are modelled as rigid nodes.

The masonry piers may exhibit in-plane failure for bending-rocking and shear sliding mechanisms. The strength criteria follow the Eurocode 8, EC8-1 [45], and the Italian Design Code [34,35].

The resistant mechanism of the spandrels is not considered if the openings have not resistant structural elements. The chosen software allows the user to consider the horizontal structures’ stiffness modelled as orthotropic membrane finite elements. The reliability of the adopted modelling approach was confirmed by several authors, also in the case of historical structures [46,47].

Moreover, the Confidence Factor, FC, equal to 1.35, corresponding to a limited knowledge level, LC1, was assigned to penalize the compressive and shear strength of masonry, as prescribed by the Italian Standard Code [34,35].

The seismic action corresponds to the design response spectrum, according to the Italian Seismic Code, defined through the spectral parameter ag (max acceleration value), F0 (max value of the amplification factor for the horizontal acceleration response spectrum) and Tc* (period of the horizontal onset for constant velocity), reported in the Italian Design Code [34] based on the site geographic coordinates of the building site. Taking into account the soil and the topographic category of the site [48], the response spectrum is defined for a return period, TR, of 30 years, for Operational Limit State, LS1; 50 years, for Damage Limit State, LS2; 475 years, for Significant Damage Limit State, LS3; 975 years, for Collapse Limit State, LS4 [34], see

Table 2. Spectral parameters of the selected site.

Limit State	ag (m/sec2)	F0	Tc (sec)
LS1	0.77	2.40	0.27
LS2	1.02	2.33	0.28
LS3	2.56	2.36	0.35
LS4	3.28	2.40	0.36

.

The authors carried out non-linear static analyses along the longitudinal and transversal direction, in Figure 11, by applying two different seismic loads: (i) proportional to the mass distribution; (ii) proportional to the first vibration mode of the structure. According to the Italian Design Code [34], an accidental eccentricity between the mass centroid and the stiffness centroid is considered. Therefore, twenty-four pushover curves were performed from each of the fourteen models, yielding 336 analysis. The Acceleration Displacement Response Spectrum, ADRS [49], was assumed to evaluate the seismic capacity and demand of the structure.

5. Parametric Study

Figure 12a–c illustrates the push-over curves with the lowest safety level, referred to the LS4 case, for each seismic action direction. They display the base shear force (V_b) as a function of the control node’s average displacement (d). The non-linear static analyses were stopped in correspondence of a 20% decay of the maximum base shear force according to the EC8 and Italian Code regulations [34,35,45]. The x and y directions denote the longitudinal and transverse direction of the building, respectively. As expected, the two directions’ capacities are different due to the higher resistant area of load-bearing walls in the longitudinal direction. However, the ultimate displacements in the x-direction are higher than those in the y-direction. Specifically, Figure 12a shows that masonry typology VS5 causes notable increments of the ultimate resistance, while the other typologies yield results similar to each other. The variation of the floors’ in-plane stiffness causes an evident scatter of the results, see Figure 12b. Conversely, modelling the spandrels as stiff leads to a distinct behavior in the x-direction corresponding to the presence of ring beams that causes a remarkable enhancement of the seismic response, see Figure 12c, while there is no substantial distinction between the other two cases.

Table 3. Properties of the capacity curves.

Analysis	X-Direction				Y-Direction
	Fy (kN)	dy (mm)	du (mm)	T (sec)	Fy (kN)	dy (mm)	du (mm)	T (sec)
VS1	2287.29	0.51	5.37	0.36	3498.54	0.74	1.88	0.36
VS2	2330.65	0.51	3.37	0.36	2845.3	0.87	1.90	0.43
VS3	2656.49	0.45	3.27	0.32	3363.95	0.82	1.70	0.32
VS4	2794.00	0.48	3.11	0.32	3582.58	0.88	1.65	0.39
VS5	3814.00	0.43	2.37	0.26	4335.00	0.67	1.58	0.32
HS1	2108.60	1.3	4.39	0.57	2224.60	1.67	1.97	0.61
HS2	2207.50	0.79	2.36	0.42	2617.30	0.82	1.59	0.40
HS3	2097.30	1.21	3.93	0.54	2165.30	1.49	1.85	0.59
HS4	1563.80	0.93	4.79	0.56	3289.60	0.65	1.34	0.33
HS5	2326.61	0.67	2.08	0.39	2887.16	0.85	1.63	0.40
HS6	2757.77	0.47	3.65	0.33	3272.90	0.82	1.71	0.40
SP1	2185.15	0.73	3.46	0.43	2931.84	0.91	1.88	0.43
SP2	2302.11	0.80	3.23	0.44	3008.04	0.96	1.88	0.43
SP3	3403.50	0.63	2.50	0.32	3366.30	0.79	1.64	0.37

reports the main outputs of the pushover analysis with the lowest safety level, for each model: the yielding force F_y, the yielding and ultimate displacements, d_y and d_u, and the vibration period T the of the equivalent Single Degree-of-Freedom (SDOF) system. The displacement demand, d_max, was then used in the estimation of the fragility curves.

The histograms in Figure 13 plot the average response of the 336 non-linear static analyses. These histograms manifest the scatters around the resistance’s average value, ultimate displacement and reduction factors referred to the limit state LS3. The behavior factor, q^*, is calculated as the ratio between the acceleration in the structure with unlimited elastic behavior S_e (T) and with limited strength F_y / m.

The main results can be summarized in the following:

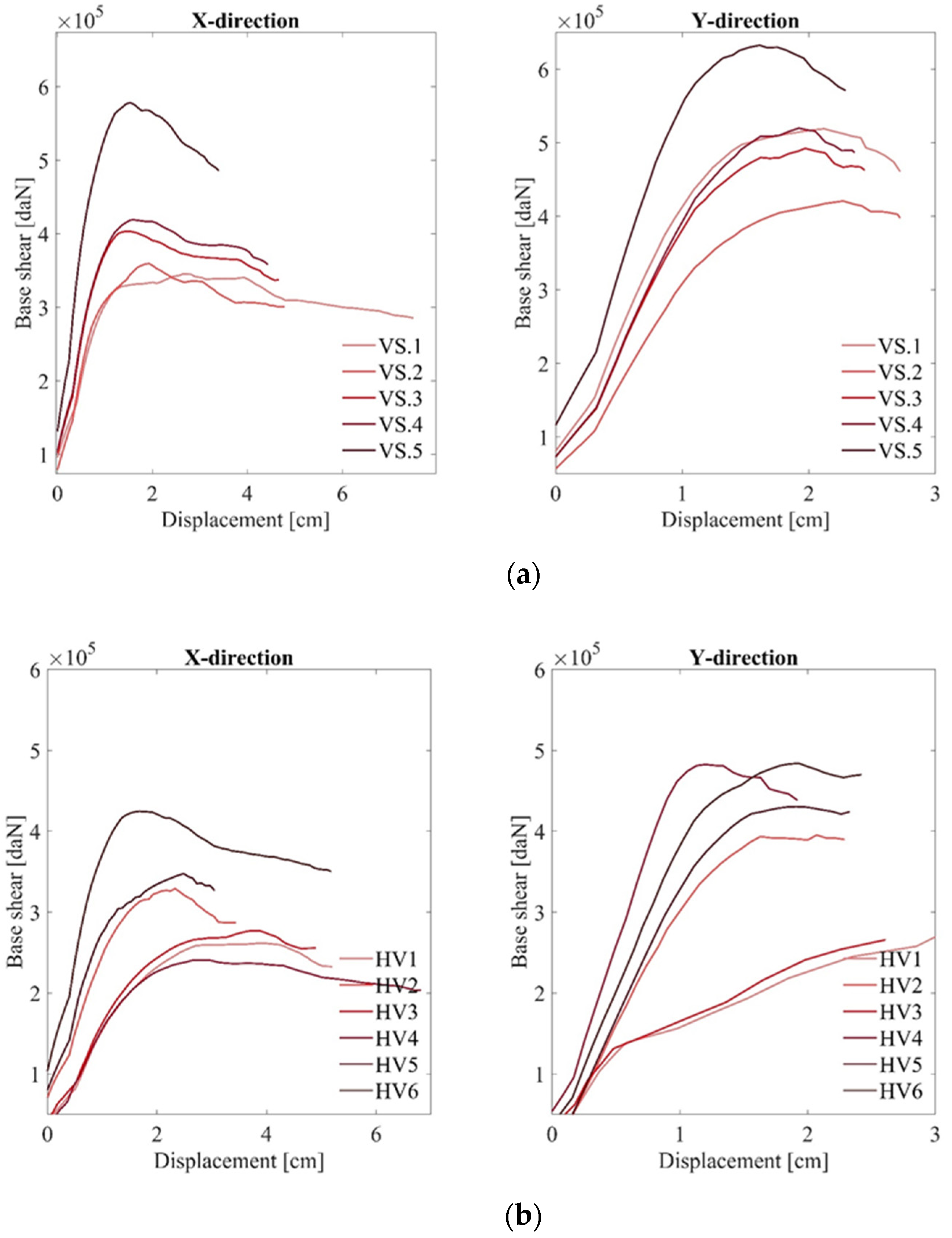
• The variation in the floor structure’s mechanical properties does not cause a manifest variation of the behavior factors. Conversely, the behavior factors are more sensitive to the masonry’s mechanical properties: increasing values of strength reduce the behavior factors, which attain the value of 3 in the case with the most considerable compression strength. Likewise, the behavior factors are not markedly affected by the spandrel properties. However, ring beams cause a notable reduction in the behavior factor, whose value nearly attains 3.
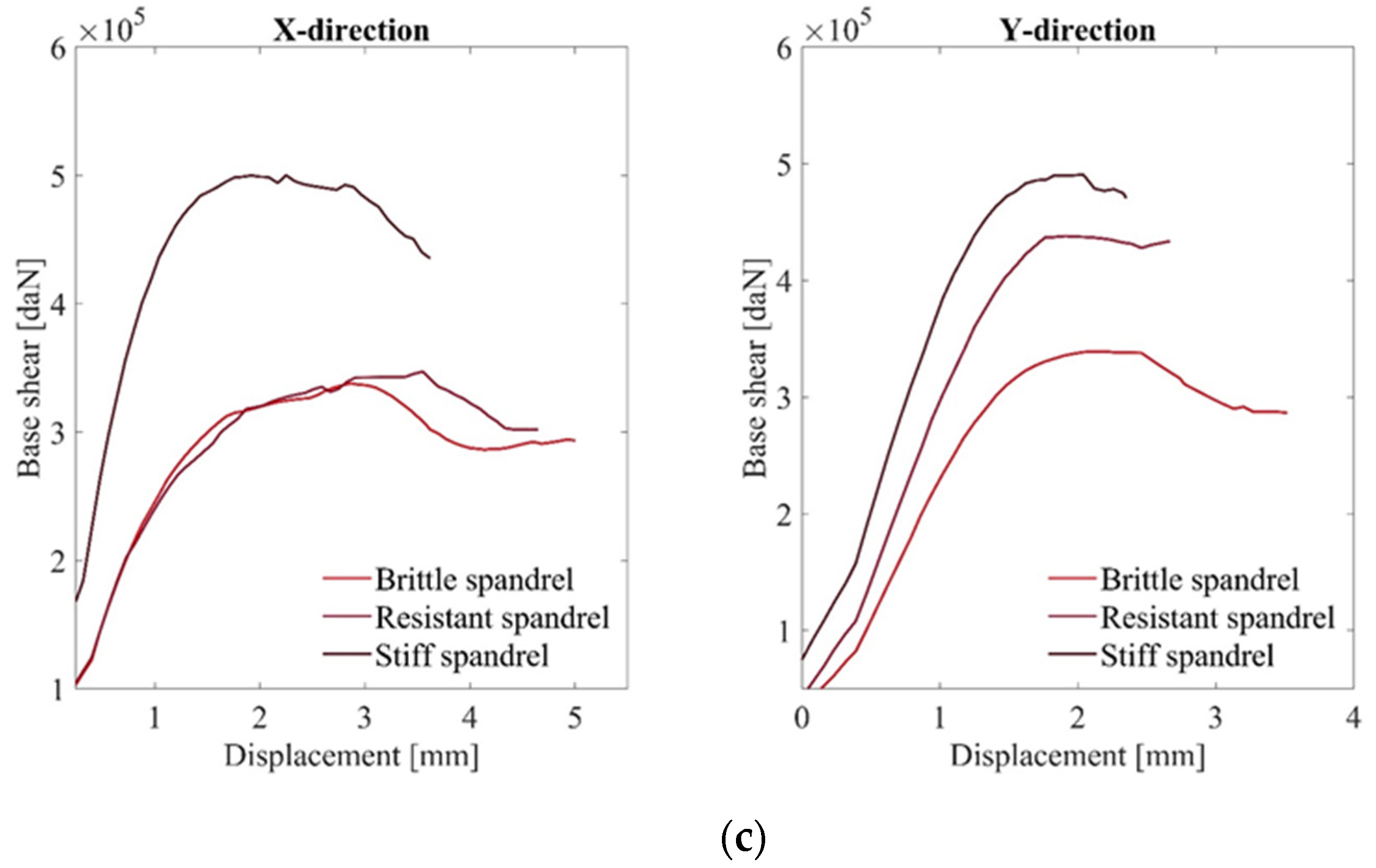
• The ultimate displacement capacity is hardly sensitive to the floors’ in-plane stiffness, ranging between 5 and 4 cm in the x-direction, and approaching 3 cm in the y-direction. Accordingly, the masonry compression strength does not cause significant effects on the ultimate displacement, except for the case with lower resistance, which attains values higher than 9 and 4 cm in the x- and y-direction, respectively. The spandrels’ properties significantly affect the structural response in the last case, as it maximizes the coupling between the supporting walls. The ultimate displacement almost attains the value of 3—the more robust the spandrels, the lower the ultimate displacement capacity.
• The blue sets of histograms illustrate the structural parameters’ impact on the ultimate strength capacity. The stiffer and more resistant are the floors, the larger the shear capacity. Similarly, effective spandrels and more resistant supporting walls cause an increment in the base shear forces.

Better masonry properties, higher in-plane stiffness of the floors, and stronger spandrels lead to increasing shear resistance and decreasing the ultimate displacements and behavior factors.

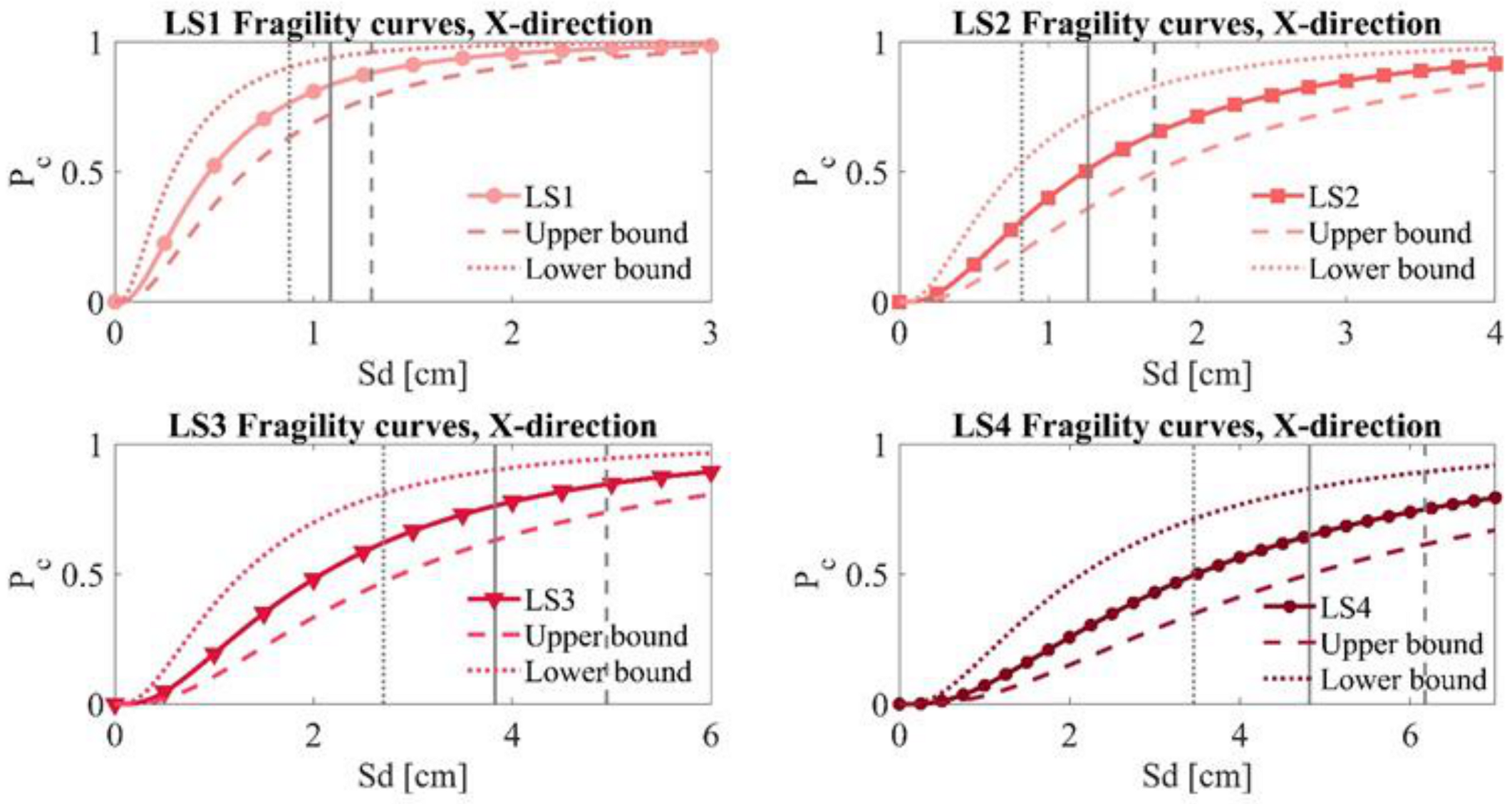
6. Derivation of the Fragility Curves

The estimation of the fragility functions in the considered cases may lead to the possibility of considering the fourteen models as representative of a homogeneous class of buildings, rather than stand-alone cases which always deserve ad-hoc investigations. The probability of collapse, P_c, descends from the estimation of the standard normal cumulative distribution function Φ, as expressed in Equation (1):

$$P\left[d_s|S_d\right]=\varnothing \left[\frac{1}{{\beta }_s}\ln \left(\frac{S_d}{\overline{S_{ds}}}\right)\right]$$

(1)

where d_s is the displacement at the threshold of a certain damage limit state, S_ds is the median value of spectral displacement at d_s, β_ds is the standard deviation of the natural logarithm of spectral displacement at a certain damage state d_s. The definition of the limit damage states d_s (LS1, LS2, LS3 and LS4) follows the formulations by Lagomarsino and Giovinazzi [50], see Equations (2)–(5):

(LS1) S_d1= 0.7·d_y,

(2)

(LS2) S_d2= 0.8·d_y + 0.2 d_u

(3)

(LS3) S_d3= 0.5· (d_y+ d_u)

(4)

(LS4) S_d3= d_u

(5)

where d_y is the yielding displacement and d_u is the ultimate displacement of the equivalent Single Degree-of-Freedom (SDOF) system, determined by push-over analyses.

Both the capacity and the seismic demand are assessed from the equivalent Single Degree-of-Freedom (SDOF) capacity curve in terms of displacement.

Figure 14 and Figure 15 depict fourteen fragility curves representative of the cases with the lowest safety level, for each model, corresponding to the four considered limit states.

Figure 16 and Figure 17 provide a better insight by depicting the average curve, in each limit state and the confidence bounds associated with an estimated variance of the ultimate displacement capacity. The yielding and ultimate displacement adopted to derive the fragility curves of the class correspond to the average of the 336 displacements values, 168 in the x- and y-direction, respectively. The vertical lines indicate the adopted values of the seismic demand and the associated confidence values.

In a complementary way, Figure 18 shows the reliability index as a function of the intensity measure [51], evaluated by the inverse of Equation (6), according to the formulation provided by EN1990 [52].

$$P_c=\varnothing \left(-\beta \right),$$

(6)

The confidence bounds of the fragility curves increase significantly as the severity of the limit state increases.

The failure resistance values may be regarded as too scattered to consider each model as representative of a unique typological class of buildings. Thus, the current research results show that a typological approach could be useful to support seismic risk preliminary studies, but an accurate prediction of the seismic response requires the consideration of each masonry palaces’ uniqueness. Additionally, a classification of the palaces based on their construction time cannot fully represent the typological class’ seismic performance under investigation.

7. Conclusions

The current paper discusses a historical masonry building’s seismic performance, recently damaged by the 2009 earthquake in L’Aquila, Italy.

This paper descends from an abstraction. The authors chose to model an existing regular building and varied the modelling parameters according to the scatter observed in the population of masonry palaces in L’Aquila.

This building acted as a structural archetype, due to the regularity of its geometry. Most of the masonry buildings in L’Aquila exhibited, during the 2009 earthquake event, an in-plane seismic response. However, they might display a significant scatter in masonry’s quality, the resistance of the spandrels, and the floors’ in-plane stiffness. Therefore, an extensive numerical investigation assessed this building’s sensitivity to the three variables (masonry’s quality, the resistance of the spandrels, and the floors’ in-plane stiffness) by estimating the behavior factor, ultimate displacement and strength capacity. The analyses showed that, despite the typological similarities, the structural parameters’ variation yields significant scatter in the seismic performance. The fragility curves highlight the notable dispersion of the probability of collapse in the considered limit states.

Therefore, typological approaches may lead to inaccurate results, as demonstrated by the outcomes of 336 numerical analyses. Therefore, each of these building should be considered a stand-alone case, which always deserves dedicated investigation.