1. Introduction
Many of the recent research efforts in structural dynamics and earthquake engineering focus on predicting the inelastic response of real structures [
1] or structural archetypes [
2,
3,
4]. However, the analyses of rather elementary structures may require significant computational efforts. Consequently, the nonlinear dynamic analyses of more complicated systems are not feasible unless simplified methods are adopted. Among them, the use of empirical hysteresis models can significantly reduce the computational costs of nonlinear dynamic analysis. Empirical hysteresis models aim at reproducing the experimental response of the structural system without concern on the mechanics of materials: The model is empirical, i.e., it blindly matches the experimental data.
In timber structures, the structural dissipation is mainly localised in the connections. The empirical modelling of each connection using empirical hysteresis formulations rather than the Finite Element (FE) modelling of the connector can significantly ease the numerical simulations of complicated structural arrangements. In the scientific literature, there is a variety of empirical hysteresis models, and many models attempt to reproduce the complex phenomena of timber connections: pinching, strength degradation and stiffness degradation. The need to account for these phenomena entails more complex mathematical formulations.
There are two main categories of hysteresis models in structural engineering applications: differential and non-differential [
5]. Differential models originate from Volterra’s pioneering studies at the beginning of the 20th century. Still, the history of hysteresis (i.e., rate-independent memory) is relatively short: Mathematical developments lag behind those of physicists and engineers. It was only in 1966 that hysteresis was first given a functional approach by Bouc, who introduced a differential hysteresis model later extended by Yi-Kwei Wen, Baber and Noori [
6]. The Bouc–Wen–Baber–Noori BWBN model of hysteresis is one of the most used hysteretic models used to describe nonlinear hysteretic systems. This model can follow a wide range of hysteretic shapes. Foliente [
7] modified the BWBN and applied the model to wood structures. Although the Bouc–Wen class models are the most used in structural engineering [
8,
9,
10,
11,
12,
13,
14,
15], the Bouc–Wen class models do not encompass all possible differential models. Mathematicians introduced the notion of hysteresis operator, which aims to unify all mathematical formulations possibly valid for an ample variety of hysteresis phenomena. The scientific literature is abundant of hysteresis models striving for generality and versatility [
16]. However, most of the research in structural engineering, chiefly directed towards applications, does not deal with differential hysteresis models more evolved than the Bouc–Wen class ones and focalizes on non-differential formulations due to flaws and challenges in using these models. The Bouc–Wen class model, for instance, suffers from some shortcomings and require a consistent definition of the parameters to obtain upper-bounded results [
17]. Additionally, the exact modelling of pinching, characterized by a notable boost in stiffness, may cause several convergence problems. Besides, the digital era’s ascension has lessened the energies of structural engineers devoted to the study of analytical models and praised more elementary approaches based on the use of piece-wise functions. Therefore, many scholars dedicated their research to algebraic or transcendental hysteresis models, which may have some stability advantages to the differential ones: They are generally faster and less computationally demanding. Algebraic hysteresis models refer to the formulations based on polynomial expressions, while transcendental ones originate from transcendental functions. Algebraic and transcendental models are non-differential models, compared to the well-known Bouc–Wen which is defined as a first ordinary differential equation.
In the field of timber engineering, a few scholars presented algebraic empirical hysteresis model, and most of them descend from the piece-wise definition of linear functions, like the models by Polensek and Laursen [
18], the trilinear model by Rinaldin et al. [
19] and the SAWS Material Model (OpenSees) [
20]. Conversely, the CUREE model [
21], the evolutionary parameter hysteretic model (EPHM) [
22] and others [
23,
24] present nonlinear branches. Dolan [
25] developed a transcendental hysteresis model based on four exponential functions that define the hysteretic curves. Moreover, [
26] observed the significant stability of piece-wise definitions of the hysteresis models.
The current paper focuses on a Bouc–Wen class hysteresis model, proposed by [
27], applied to the simulation of the lateral response of Cross-Laminated Timber (CLT) panels. The model originates from the hysteresis model by [
28]. CLT is gaining popularity in residential and non-residential applications in Europe [
29,
30]. The novelty as well as the complexity of the seismic behaviour of CLT wall panels fed important experimental research activities [
31,
32,
33,
34]. Among the others, the most relevant were part of the SOFIE Project [
35].
From the pioneering work of Foliente [
7], the Bouc–Wen class hysteresis models have provided reliable tools in predicting the seismic behaviour of timber structural elements [
8,
9,
10,
11,
12,
13,
36,
37].
This paper converges on the Extended Energy-dependent Generalized Bouc–Wen model, initially presented by [
27]. The research has three main objectives:
Estimate the sensitivity of the quadratic error between simulated and experimental data to the EEGBW model’s parameters;
Prove the model versatility in fitting the experimental cyclic response of CLT panels;
Show the performance of the EEGBW model and the results of time integration given a seismic input.
The EEGBW model presents all drawbacks of differential hysteresis models in terms of stability. The reduced computational costs make it a valid alternative for the hysteresis modelling of connections and complex structural arrangements. The EEGBW model’s strength should derive from the interaction between the computational advantages of empirical hysteresis models and the versatility of FE analysis. The paper has the following organization. The second section presents the EEGBW model; the third section focuses on the modelling choices of a CLT panel as a single-degeree-of-freedom oscillator. The fourth and fifth sections present the experimental data and the result of the sensitivity analysis. The sixth and seventh sections present the results and conclusions.
2. Analytical Prediction Model
Theoretically, the response of a structural system may be formalized as follows:
| = Resisting force at a certain point of the wall panel; |
| = The motion of all points of the all body (Panel); |
| t | = Time. |
The constitutive law takes the form of a functional of the function; in short, not just the displacement of all points , but the entire history of displacements of all points () determines the resisting force at a certain time t. This is due to pinching and degradation phenomena.
The resisting force explicitly depends on as the mechanical properties are not uniform, being the structural system a peculiar assemble of timber and metal connectors. The resisting force depends on the motion of all points , not just on the ones nearby .
In particular, a Bouc–Wen hysteresis model is considered, given that empirical hysteresis laws are proved to be quite reliable tools in predicting the seismic behaviour of structural systems [
8], under certain restrictions [
14]. The EEGBW model provides an empirical representation of highly complex constitutive laws, in particular that of a CLT wall panel, where the coexistence of different resisting mechanisms makes a direct FEM approach a quite complex task. This paper focuses on the application of the EEGBW model to simulate the hysteretic response of CLT panels. Several scholars developed a more rigorous method in modelling the lateral response of Cross-Laminated Timber panels. In particular, the a few of them [
38,
39,
40] followed an analytical approach based on the assumption of a suitable kinematic model. Still, the main drawback is the focus on the monotonic pseudo-static response by neglecting the hysteresis contribution. Given the complexity of a rigorous approach in describing the CLT system’s constitutive behaviour, an empirical hysteresis model may be preferable when dealing with nonlinear dynamic analyses. For an inelastic SDOF system with the Generalized Bouc–Wen model, the equation of motion can be expressed as
| m | = Mass; |
| x | = Displacement; |
| = Double derivative of x with respect to time; |
| = Derivative of x with respect to time; |
| = Resisting inelastic force; |
| z | = Auxiliary variable that represents the inelastic behaviour. |
For a structural element described by a Bouc–Wen class model, the resisting force is written as
| = Post-to preyield stiffness ratio; |
| = Initial stiffness. |
The evolution of
z is determined by an auxiliary ordinary differential equation, which can be written in the form
| = Derivative of z with respect to time; |
| A | = Parameter controlling the scale of the hysteresis loops; |
| n | = Parameter controlling the sharpness of the hysteresis loops; |
| = Nonlinear function controlling other shape features of the hysteresis loop. |
The functions for a Generalized Bouc–Wen model, reported in the scientific literature, are
The EEGBW hysteresis model possesses all the important features observed in real structures, which include strength and stiffness degradation and pinching of the successive hysteresis loops.
3. Analytical Modelling of CLT Wall
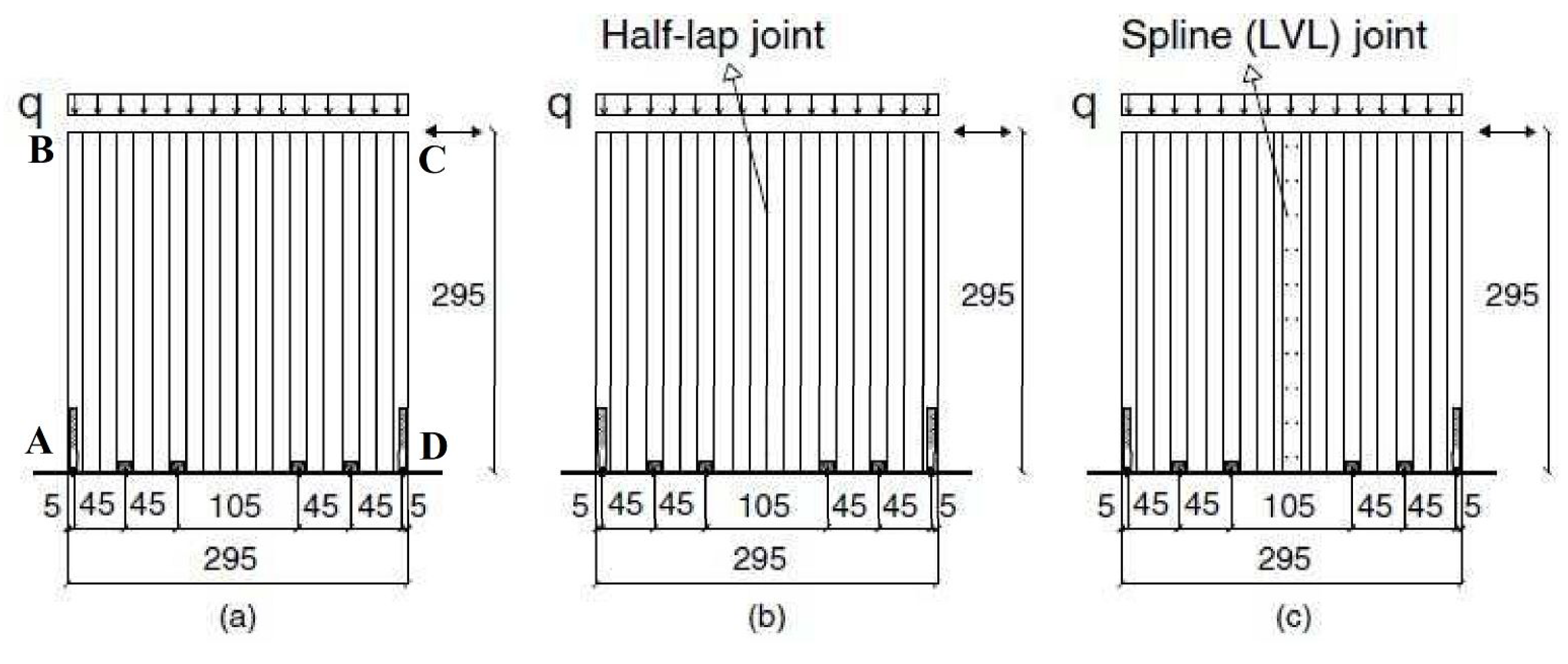
The authors adopted the archetype in
Figure 1, as representative of the simplest structural unit in CLT buildings.
The CLT wall panel (A-B-C-D) is anchored to the foundation (A-D) with hold-downs and angle brackets. A static vertical load is applied on the wall, while a mass
m stands on the top of the wall, as shown in
Figure 1. The specimen in
Figure 1 represents a standard structural configuration in CLT structure: a single panel anchored to the foundation by hold-downs and angle brackets. Reference [
41] tested this sort of panels, depicted in
Figure 2. Therefore, the model in
Figure 1 is the idealization of the panel tested by [
41], whose cyclic response is used to calibrate the EEGBW parameters in the current research. Considering the SDOF hysteretic system in
Figure 1, the equation of motion coincides with the (
2). All the information about the wall is expressed by the
term, the wall configuration, the vertical connections, the static load, etc. The sole explicit terms in the (
2) are the mass
m and the coefficient of dynamic viscosity
c. A global model of the wall is obtained, representative of the particular configuration under test.
5. Parameter Estimation and Sensitivity Analysis
The EEGBW model parameters are estimated by means of an OLS linear regression algorithm [
42].
In particular, the n exponent, the parameters along with the coefficients are identified, for . The value of n, which minimizes the mean square error, is the same for all samples, equal to 0.9, while the and do show significant dispersion.
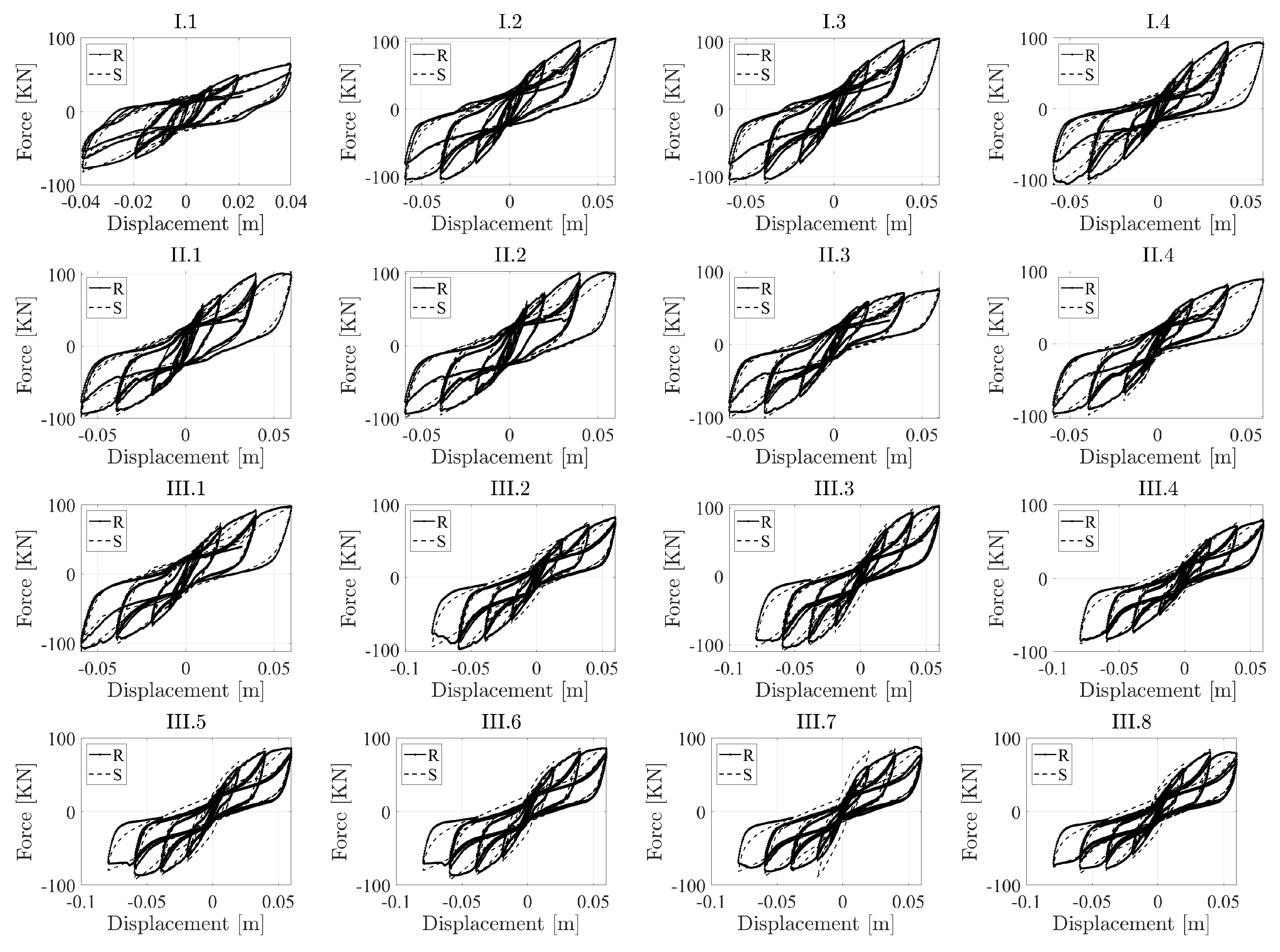
The EEGBW model faithfully describes the experimental data, as shown in
Figure 5.
Despite the similarities exhibited by the different hysteresis loops, the identified parameters show a considerable dispersion.
A confirmation of the observed dispersion is drawn from a Variance-based Sensitivity Analysis [
43]. A sensitivity index is in fact a number that gives quantitative information about the relative sensitivity of the model with respect to a selected set of parameters. A set of powerful global sensitivity indices is the group of Sobol indices [
44].
Both the Sobol index and the total sensitivity index are computed in this paper. While measures the impact of varying a single parameter alone, measures the participation to the output variance of the selected parameter, including all variance caused by its interactions.
In short, the more different is the ranking generated by the two indexes, the more elaborate is the interaction between the parameters [
45]. Information on parameter sensitivity is precious in system identification and system optimization. In the current paper, the sensitivity analysis function is the quadratic error function, that is, the quadratic error measured between the experimental data and the EEGBW parametric model of the first set of data.
The ranking generated by the Sobol indices
does not match that by the total sensitivity indices
;
Table 2. This might suggest that the interactions among the various parameters are very significant over the range specified (The specified ranges of the parameters are
,
and
. Their choice is dictated by the variance exhibited by the parametric identification). As confirmed by
Table 2, great variance of the EEGBW model parameters is expected. The EEGBW parameters, in fact, do not possess a full physical meaning. From their interactions, in fact, a wide range of possible hysteresis shapes is generated; Even the more insignificant variation of the experimental data does affect all the EEGBW parameters.
6. Results
The 16 configurations of single and coupled cross-laminated wall panels, investigated by means of cyclic tests [
41], are represented by the analytical EEGBW model and subjected to a series of 7 selected ground motion earthquakes
Table 3. The mass
m at the head of the panel is assumed equal to 8 KN, ie a fraction of the vertical load applied in quasi-static tests. The viscosity coefficient of timber structures is approximately 2%, as found by [
1,
46]. However, identifying the viscosity coefficient in operational conditions generally underestimates the actual viscosity coefficient at more significant displacements. Therefore, the authors adopted a 5% value, despite the results do not significantly depend on the viscosity coefficient due to the predominant contribution of hysteresis in energy dissipation. The second order non linear differential Equation (
2) is integrated by means of the Runge-Kutta algorithm [
47],
Figure 6.
The CLT wall panels’ dissipative capacity is evaluated in terms of the maximum dissipated hysteretic energy. Thus the seismic performance of the different wall’s configurations (different anchoring systems, single and coupled walls, and different types and number of screws to connect the panels) is assessed.
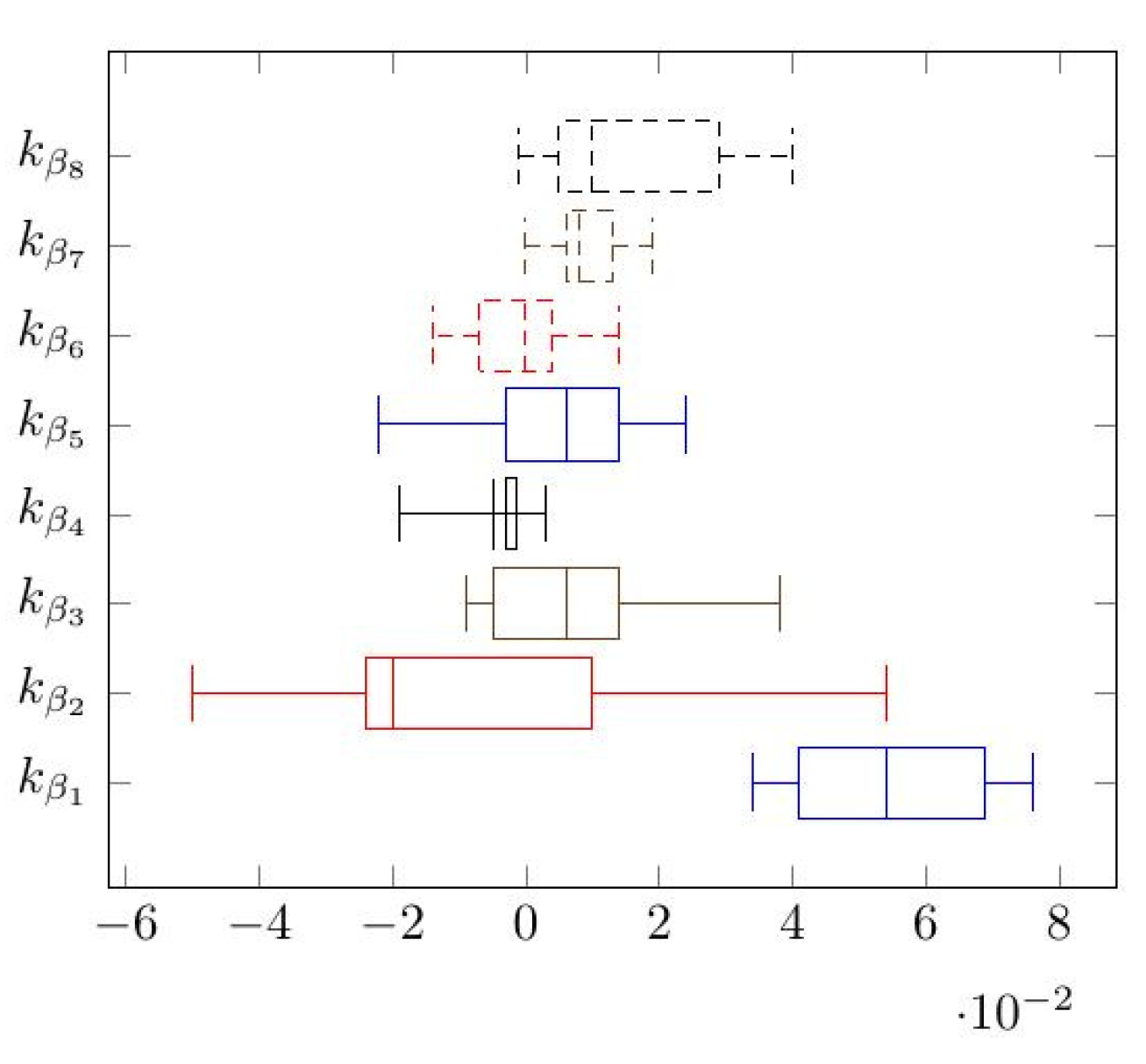
The layout and design of the joints is critical for the overall seismic behaviour of the structural system. In
Figure 7, the box plot of the dissipated hysteresis energy is shown for the 16 different wall configurations.
The outcomes of nonlinear dynamic analyses prove the model stability during numerical integration of Equation (
2). The dissipated hysteretic energy values in
Figure 7 are consistent with the values of ductility estimated from pseudo-static load tests. The parameters of the EEGBW model lack physical meaning. This fact represents an obstacle in extending the model to structural arrangements different from those used in model calibration. However, the model’s primary usefulness stands in the simulation of experimental cyclic response, which is difficult to reproduce with FE modelling. The EEGBW parameters are not related to the panel’s geometric features neither the mechanical parameters of timber: Empirical hysteresis models blindly match cyclic responses. Still, if empirical hysteresis models and FE are used together, the scholar can model the hysteretic response of more realistic structural arrangements with great accuracy and reduced computational costs. In timber structures, the dissipation capacity is localised by the connections. Therefore, the EEGBW model could be used to simulate the hysteretic response of the single connection via a nonlinear user-defined spring, while the panel via the Finite Element Method. In this case, the empirical hysteresis model can manifest its full potential, assisting direct FE modelling where hysteresis is localised in nonlinear springs, representing the structural connections. The authors developed the current research in Matlab. However, they are implementing the model in an Abaqus subroutine for more in-depth model validation.
7. Conclusions
The authors applied the EEGBW model to simulate the experimental cyclic response of Cross-Laminated Timber (CLT) panels tested. Accurately, they estimated the EEGBW parameters of sixteen structural configurations made by single and coupled cross-laminated wall panels. The estimation of the parameters originates from an Ordinary Least Squares (OLS) algorithm presented. Despite the similarities between the experimental data, the estimated parameters exhibited a significant dispersion. A variance-based sensitivity analysis based on Sobol indexes assessed each parameter’s effect on the quadratic error between experimental and numerical data. In a second step, the authors modelled the CLT panel as a single-degree-of-freedom system, whose resisting force is represented by the EEGBW model. They assessed the response of the sixteen-panel idealizations under a set of seven earthquakes using the Runge–Kutta algorithm. The hysteresis loops obtained from seismic excitation confirmed features reproduced in pseudo-static tests, pinching and degradation phenomena. In terms of the maximum dissipated hysteretic energy, the dissipative capacity is evaluated for the different CLT wall configurations. Interestingly, the vertical joint strongly affects the wall’s dissipative capacity; particularly, the half-lap joint determines a significant increase in the maximum dissipated energy. The Laminated Veneer Lumber (LVL) spline joint does not show a substantial difference compared to the configuration without the vertical joint. It could be believed that the presence of a vertical joint, favouring the sliding between the two panels, may increase ductility and energy dissipation. However, the sliding capacity and the type of strength and stiffness degradation of the particular vertical joint drive a CLT wall panel’s dissipative capacity. The EEGBW model is a so-called empirical model. Therefore, its significance and applicability are limited to the experimental data used for calibration. However, the model versatility could serve FE modelling of complex structural arrangements where the dissipative capacity is localised in the connection or structural nodes. These elements could be described by user-defined nonlinear spring in terms of the EEGBW model. The full model potential should emerge from the synergy between empirical hysteresis and FE modelling. Future research efforts will focus on implementing the EEGBW model as a new user-defined element in Abaqus to simulate the nonlinear dynamic response of more complicated structural arrangements.