A Pulse-Multiplication Proposal for MIRACLES, the Neutron TOF-Backscattering Instrument at the European Spallation Source
Abstract
:1. Introduction
2. Materials and Methods
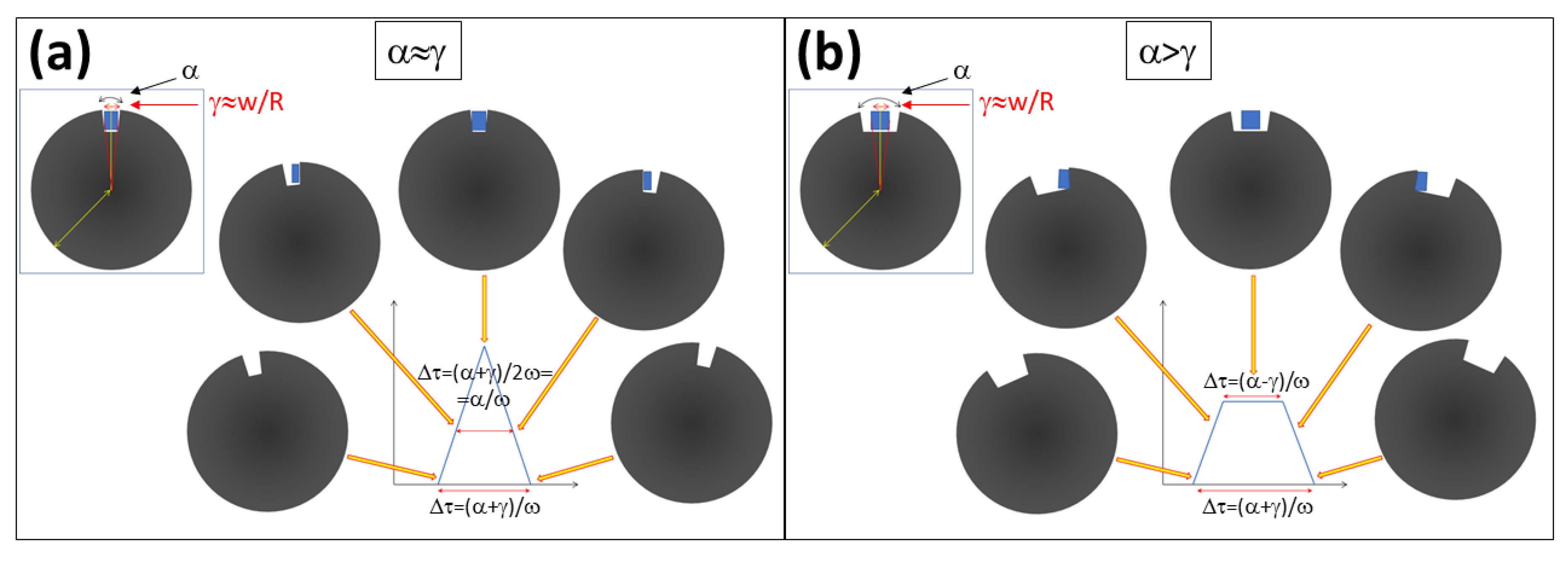
- Pulse shape: Triangular (where the chopper slit opening angle, α, is of the same dimensions as the guide opening angle, γ; thus, α = γ) and trapezoidal (where α > γ) pulse shapes were considered in the calculations; see Figure 2. We note that in the latter case, the chopper must run faster to keep the same full width at half-maximum (FWHM) of the pulse and reduce its rise/decay time.
- Guide opening angle: the angular projection of the guide with respect to the center of the choppers in the straight section (downstream from the curve) ranges from γ = 17° (in the position of the BW/FO chopper) to γ = 21° (in the 90-m straight section before the focusing guide).
- Single chopper opening times: For single disks, the total opening time is given by Δτtot = , while for trapezoidal pulses, the rise/decay time is: ΔτR/D = .
- Double chopper configuration opening times: For counter-rotating double disk choppers, the energy resolution is determined by the FWHM opening times ΔτFWHM = , where angular velocity, in rad/s, and f is in Hz.
- Energy resolution: In a neutron TOF-backscattering spectrometer, the contributions to the final energy resolution from the primary spectrometer, δEP, are mostly determined by the beam divergence, yielding a distribution of flight pathway lengths, ΔL, and a pulse size of Δτ: [22,23]where E is the energy selected, L is the length of the primary spectrometer from source to sample, and τ is its neutron flight time.
3. Results and Discussion
3.1. First Step: Propagating the Neutron Elastic Band
3.2. Second Step: Rationale for Pulse Multiplication
- (a)
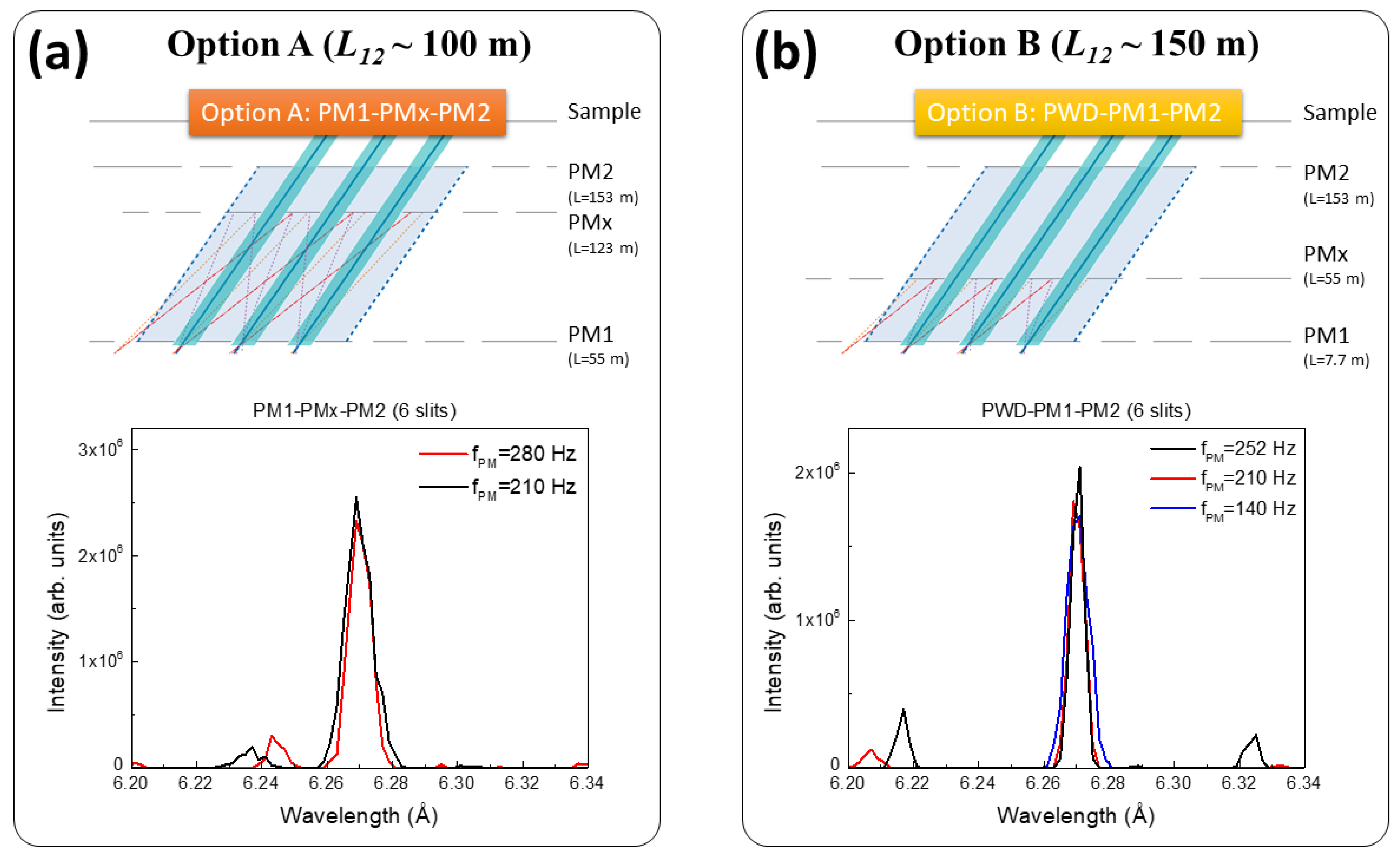
- Option A: LPM1a = 55 m and L12 ~ 100 m, with the PWD pulse shaping chopper working as a bandwidth chopper and running as mentioned above (one disk parked, the other at f = 14 Hz, thus Δτ ~ 2.4 ms), PM1 was placed after the MC1 chopper. This was the most feasible option, since the MIRACLES current chopper cascade would not be modified, and installation of the PM1 chopper would take place outside the ESS bunker.
- (b)
- Option B: LPM1b ≡ LPWD = 7.7 m and L12 ~ 150 m) consisted of rendering the largest possible distance between the fast choppers, using the PWD pulse shaping chopper as the first pulse multiplication chopper (PWD≡PM1). This solution implies exchanging the single-slit PWD chopper for a multislit chopper within the bunker, resulting in pulse multiplication from the pulse shaping.
3.3. Third Step: Multislit Approach with Five Pulses
3.4. Fourth Step: Multislit Approach with Three Pulses
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Telling, M.T.F. A Practical Guide to Quasi-Elastic Neutron Scattering; The Royal Society of Chemistry: London, UK, 2020; p. 157. ISBN 978-1-78801-262-1. [Google Scholar]
- Gates, W.P.; Seydel, T.; Bordallo, H.N. Layer charge effects on anisotropy of interlayer water and structural OH dynamics in clay minerals probed by high-resolution neutron spectroscopy. Appl. Clay Sci. 2020, 201, 105928. [Google Scholar] [CrossRef]
- Khodadadi, S.; Sokolov, A.P. Protein dynamics: From rattling in a cage to structural relaxation. Soft Matter 2015, 11, 4984–4998. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Martins, M.L.; Eckert, J.; Jacobsen, H.; Santos, É.C.d.; Ignazzi, R.; de Araujo, D.R.; Bellissent-Funel, M.-C.; Natali, F.; Koza, M.M.; Matic, A.; et al. Probing the dynamics of complexed local anesthetics via neutron scattering spectroscopy and DFT calculations. Int. J. Pharm. 2017, 524, 397–406. [Google Scholar] [CrossRef] [PubMed]
- Dubey, P.S.; Srinivasan, H.; Sharma, V.K.; Mitra, S.; Sakai, V.G.; Mukhopadhyay, R. Dynamical Transitions and Diffusion Mechanism in DODAB Bilayer. Sci. Rep. 2018, 8, 1862. [Google Scholar] [CrossRef] [PubMed]
- Burankova, T.; Duchêne, L.; Łodziana, Z.; Frick, B.; Yan, Y.; Kühnel, R.-S.; Hagemann, H.; Remhof, A.; Embs, J.P. Reorientational Hydrogen Dynamics in Complex Hydrides with Enhanced Li+ Conduction. J. Phys. Chem. C 2017, 121, 17693–17702. [Google Scholar] [CrossRef]
- Busch, M.; Hofmann, T.; Frick, B.; Embs, J.P.; Dyatkin, B.; Huber, P. Ionic liquid dynamics in nanoporous carbon: A pore-size- and temperature-dependent neutron spectroscopy study on supercapacitor materials. Phys. Rev. Mater. 2020, 4, 055401. [Google Scholar] [CrossRef]
- Frick, B.; Combet, J.; van Eijck, L. Subsurface density mapping of the earth with cosmic ray muons. Nucl. Instrum. Meth. A 2012, 669, 7–13. [Google Scholar] [CrossRef]
- Hansen, H.W.; Frick, B.; Hecksher, T.; Dyre, J.C.; Niss, K. Connection between fragility, mean-squared displacement, and shear modulus in two van der Waals bonded glass-forming liquids. Phys. Rev. B 2017, 95, 104202. [Google Scholar] [CrossRef] [Green Version]
- Gates, W.P.; Bordallo, H.N.; Aldridge, L.P.; Seydel, T.; Jacobsen, H.; Marry, V.; Churchman, G.J. Neutron Time-of-Flight Quantification of Water Desorption Isotherms of Montmorillonite. J. Phys. Chem. C 2012, 116, 5558–5570. [Google Scholar] [CrossRef]
- O’Neill, H.; Pingali, S.V.; Petridis, L.; He, J.; Mamontov, E.; Hong, L.; Urban, V.; Evans, B.; Langan, P.; Smith, J.C.; et al. Dynamics of water bound to crystalline cellulose. Sci. Rep. 2017, 7, 11840. [Google Scholar] [CrossRef] [Green Version]
- Rasmussen, M.K.; Pereira, J.E.M.; Berg, M.C.; Iles, G.N.; de Souza, N.R.; Jalarvo, N.H.; Botosso, V.F.; Sant’Anna, O.A.; Fantini, M.C.A.; Bordallo, H.N. Dynamics of encapsulated hepatitis B surface antigen. Eur. Phys. J. Spec. Top. 2019, 227, 2393–2399. [Google Scholar] [CrossRef]
- Andersen, K.H.; Argyriou, D.N.; Jackson, A.J.; Houston, J.; Henry, P.F.; Deen, P.P.; Toft-Petersen, R.; Beran, P.; Strobl, M.; Arnold, T.; et al. The instrument suite of the european spallation source. Instrum. Meth. A 2020, 957, 163402. [Google Scholar] [CrossRef]
- Luna, P.; Bordallo, H.N.; Tsapatsaris, N.; Andersen, K.H.; Herranz, I.; Sordo, F.; Villacorta, F.J. Tailoring the energy resolution of MIRACLES, the time-of-flight—backscattering spectrometer at the ESS: An updated proposal for the chopper cascade. Phys. B 2019, 564, 64–68. [Google Scholar] [CrossRef]
- Tsapatsaris, N.; Lechner, R.E.; Marko, M.; Bordallo, H.N. Conceptual design of the time-of-flight backscattering spectrometer, MIRACLES, at the European Spallation Source. Rev. Sci. Instrum. 2016, 87, 085118. [Google Scholar] [CrossRef] [PubMed]
- Tsapatsaris, N.; Willendrup, P.K.; Lechner, R.E.; Bordallo, H.N. From BASIS to MIRACLES: Benchmarking and perspectives for high-resolution neutron spectroscopy at the ESS. EPJ Web Conf. 2015, 83, 03015. [Google Scholar] [CrossRef] [Green Version]
- Arai, M.; Zanini, L.; Andersen, K.H.; Klinkby, E.; Villacorta, F.J.; Shibata, K.; Nakajima, K.; Harada, M. The performance of ESS spectrometers in comparison with instruments at a short-pulse source. J. Neutron Res. 2020, 22, 71–85. [Google Scholar] [CrossRef]
- Takahashi, N.; Shibata, K.; Kawakita, Y.; Nakajima, K.; Inamura, Y.; Nakatani, T.; Nakagawa, H.; Fujiwara, S.; Sato, T.J.; Tsukushi, I.; et al. Repetition Rate Multiplication: RRM, an Advanced Measuring Method Planed for the Backscattering Instrument, DNA at the MLF, J-PARC. J. Phys. Soc. Jpn. 2011, 80, SB007. [Google Scholar] [CrossRef] [Green Version]
- Birk, J.O. New Techniques in Neutron Scattering. Ph.D. Thesis, Niels Bohr Institute, University of Copenhagen, Copenhagen, Denmark, 2014. [Google Scholar]
- Willendrup, P.; Farhi, E.; Lefmann, K. McStas 1.7 a new version of the ... Carlo neutron scattering package. Phys. B 2004, 350, 735. [Google Scholar] [CrossRef]
- Zanini, L.; Andersen, K.H.; Batkov, K.; Klinkby, E.B.; Mezei, F.; Schönfeldtab, T.; Takibayev, T.S.A. Design of the cold and thermal neutron moderators for the European Spallation Source. Nuclear Inst. Methods Phys. Res. A 2019, 925, 33–52. [Google Scholar] [CrossRef]
- Mamontov, E.; Herwig, K.W. A time-of-flight backscattering spectrometer at the Spallation Neutron Source, BASIS. Rev. Sci. Instrum. 2011, 82, 085109. [Google Scholar] [CrossRef]
- Shibata, K.; Takahashi, N.; Kawakita, Y.; Matsuura, M.; Yamada, T.; Tominaga, T.; Kambara, W.; Kobayashi, M.; Inamura, Y.; Nakatani, T.; et al. The Performance of TOF near Backscattering Spectrometer DNA in MLF, J-PARC. JPS Conf. Proc. 2015, 8, 036022. [Google Scholar]
- Lechner, R.E. Proceedings of the 11th Meeting of the International Collaboration on Advanced Neutron Sources (ICANS-XI), Tsukuba, Japan, 22–26 October 1990; p. 717. Available online: https://inis.iaea.org/search/search.aspx?orig_q=RN:22090885 (accessed on 22 October 1990).
- Lechner, R.E. Quasielastic high-resolution time-of-flight spectrometers employing multi-disk chopper cascades for spallation sources. In Proceedings of the 15th Meeting of the International Collaboration on Advanced Neutron Sources (ICANS-XV), Tsukuba, Japan, 6–9 November 2000; p. 357. [Google Scholar]
- Lechner, R.E. Optimization of the chopper system for the cold-neutron time-of-flight spectrometer NEAT at the HMI, Berlin. Phys. B 1992, 180–181, 973–977. [Google Scholar] [CrossRef]
- Voigt, J.; Violini, N.; Brückel, T. Chopper layout for spectrometers at long pulse neutron sources. Nucl. Instrum. Meth. A 2014, 741, 28–32. [Google Scholar]
- Lechner, R.E. Advanced Neutron Sources; Journal of Physics: Conference Series No. 97; Hyer, D.K., Ed.; IOP Publishing Ltd.: Bristol, UK; New York, NY, USA, 1989; p. 843. [Google Scholar]
- Bewley, R.I.; Taylor, J.W.; Bennington, S.M. LET, a cold neutron multi-disk chopper spectrometer at ISIS. Nucl. Instrum. Meth. A 2011, 637, 128–134. [Google Scholar] [CrossRef]
- Pérez, M.; Sordo, F.; Bustinduy, I.; Muñoz, J.L.; Villacorta, F.J. ARGITU compact accelerator neutron source: A unique infrastructure fostering R&D ecosystem in Euskadi. Neutron News 2020, 31, 19–25. [Google Scholar]
- Voigt, J.; Böhm, S.; Dabruck, J.P.; Rücker, U.; Gutberlet, T.; Brückel, T. Spectrometers for compact neutron sources. Nucl. Instrum. Meth. A 2018, 884, 59–63. [Google Scholar] [CrossRef]





| Option A (L12 ~ 100 m) | |||||||
|---|---|---|---|---|---|---|---|
| PWD | PS | BW/FO | MC1 | PM1 | MC2 | PM2 | |
| L (m) | 7.7 | 8.3 | 54.5 | 54.9 | 55 | 145 | 153 |
| α (°) | 12 | 15 | 110 | 45 | 27 | 45 | 27 |
| f (Hz) | 0–14 | 14 | 70 | 70 | 280 | 70 | 280 |
| CR/SD | CR | SD | SD | SD | CR | SD | CR |
| Option B (L12 ~ 150 m) | |||||||
| PWD≡PM1 | PS | BW/FO | MC1 | MC2 | PM2 | ||
| L (m) | 7.7 | 8.3 | 54.5 | 54.9 | 145 | 153 | |
| α (°) | 12 | 15 | 110 | 45 | 45 | 27 | |
| f (Hz) | 252 | 14 | 70 | 70 | 70 | 252 | |
| CR/SD | CR | SD | SD | SD | SD | CR | |
| Option A (L12 ~ 100 m) | ||||||||
|---|---|---|---|---|---|---|---|---|
| PWD | PS | BW/FO | MC1 | PM1 | PMx | MC2 | PM2 | |
| L (m) | 7.7 | 8.3 | 54.5 | 54.9 | 55 | 123 | 145 | 153 |
| α (°) | 12 | 15 | 110 | 45 | 27 | 27 | 45 | 27 |
| f (Hz) | 0–14 | 14 | 70 | 70 | 280 | 280 | 70 | 280 |
| CR/SD | CR | SD | SD | SD | CR | CR | SD | CR |
| Option B (L12 ~ 150 m) | ||||||||
| PWD≡PM1 | PS | BW/FO | MC1 | PMx | MC2 | PM2 | ||
| L (m) | 7.7 | 8.3 | 54.5 | 54.9 | 55 | 145 | 153 | |
| α (°) | 12 | 15 | 110 | 45 | 27 | 45 | 27 | |
| f (Hz) | 252 | 14 | 70–112 | 70 | 252 | 70 | 252 | |
| CR/SD | CR | SD | SD | SD | CR | SD | CR | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Villacorta, F.J.; Bordallo, H.N.; Arai, M. A Pulse-Multiplication Proposal for MIRACLES, the Neutron TOF-Backscattering Instrument at the European Spallation Source. Quantum Beam Sci. 2021, 5, 2. https://0-doi-org.brum.beds.ac.uk/10.3390/qubs5010002
Villacorta FJ, Bordallo HN, Arai M. A Pulse-Multiplication Proposal for MIRACLES, the Neutron TOF-Backscattering Instrument at the European Spallation Source. Quantum Beam Science. 2021; 5(1):2. https://0-doi-org.brum.beds.ac.uk/10.3390/qubs5010002
Chicago/Turabian StyleVillacorta, Félix J., Heloisa N. Bordallo, and Masatoshi Arai. 2021. "A Pulse-Multiplication Proposal for MIRACLES, the Neutron TOF-Backscattering Instrument at the European Spallation Source" Quantum Beam Science 5, no. 1: 2. https://0-doi-org.brum.beds.ac.uk/10.3390/qubs5010002





