Extraction Complex Properties of the Nonlinear Modified Alpha Equation
Abstract
:1. Introduction
2. Fundamental Facts of BSEFM
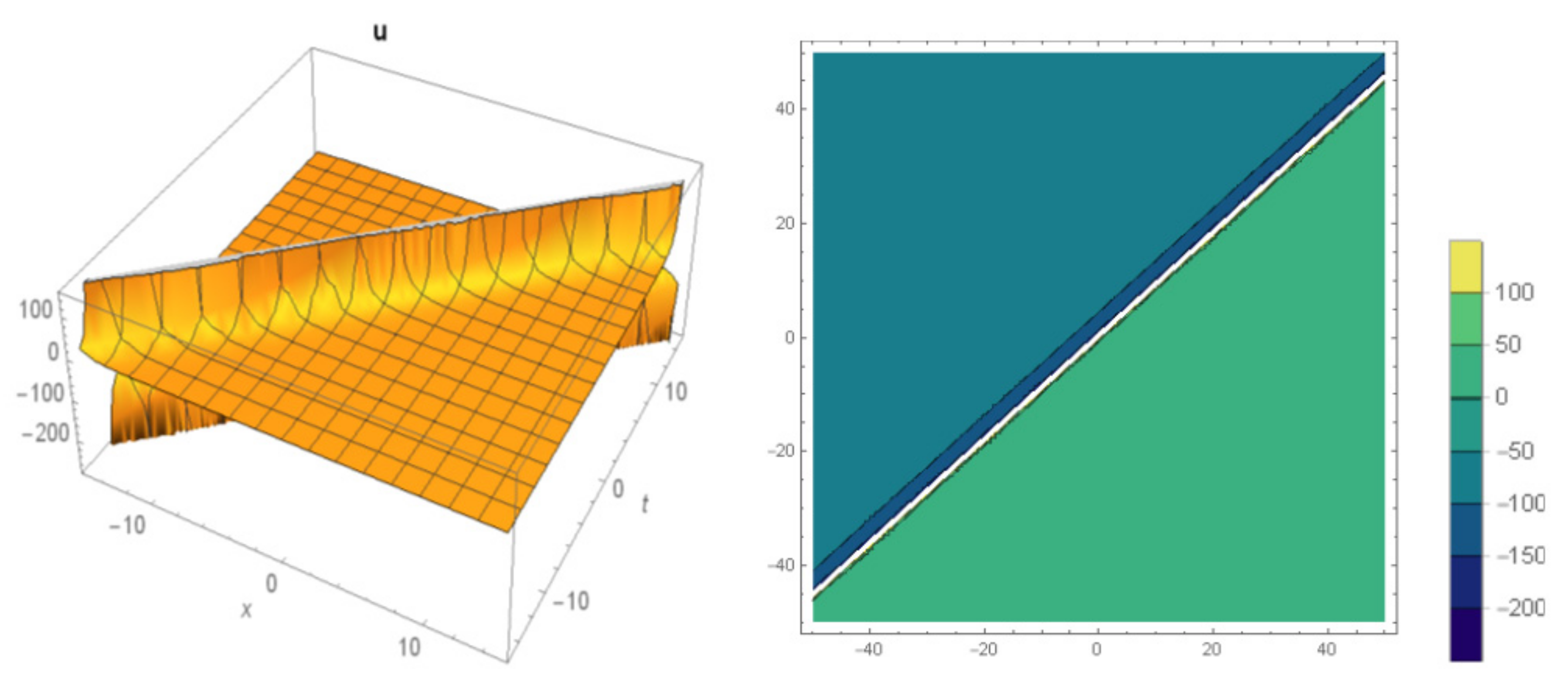
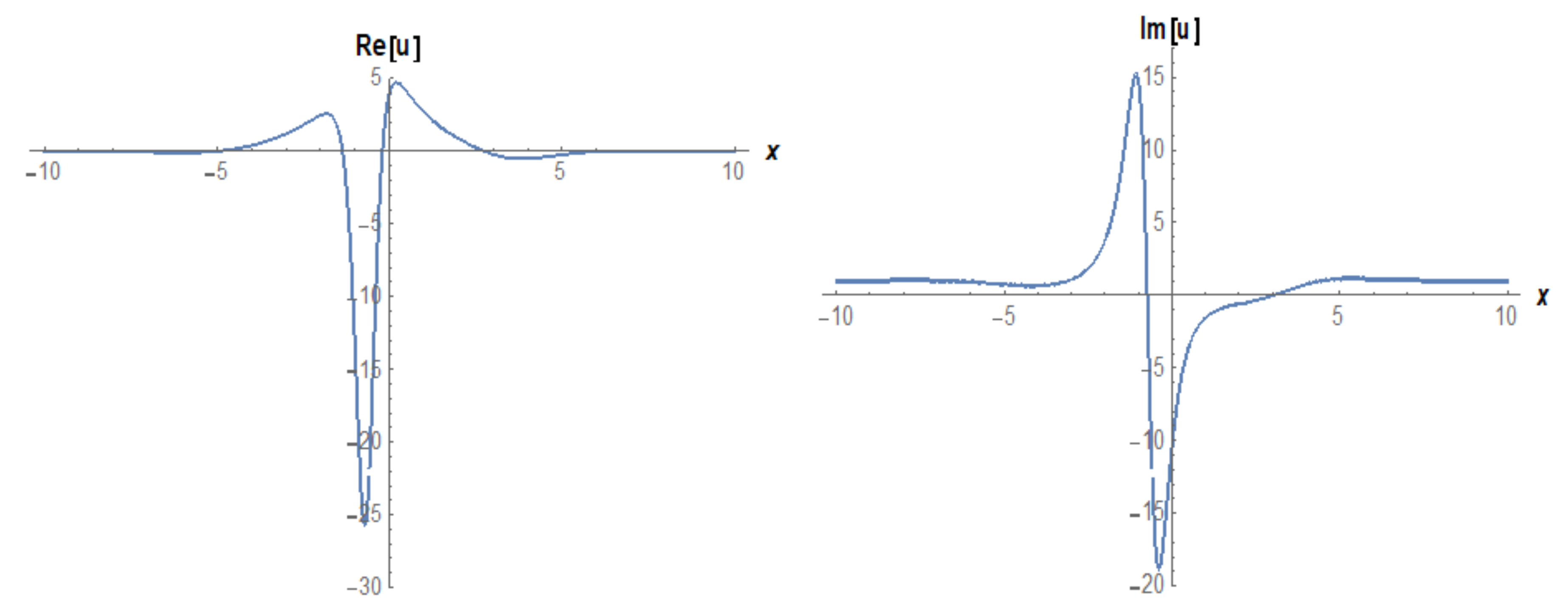
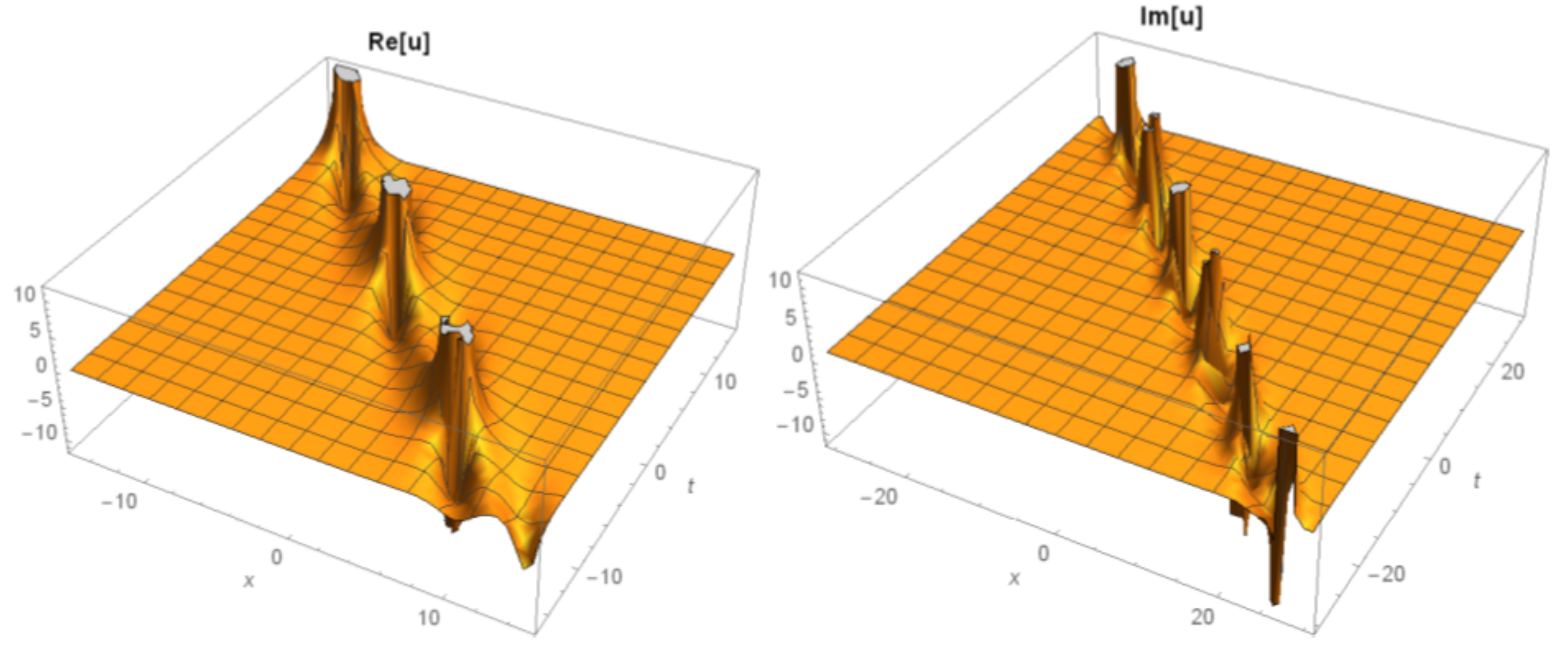
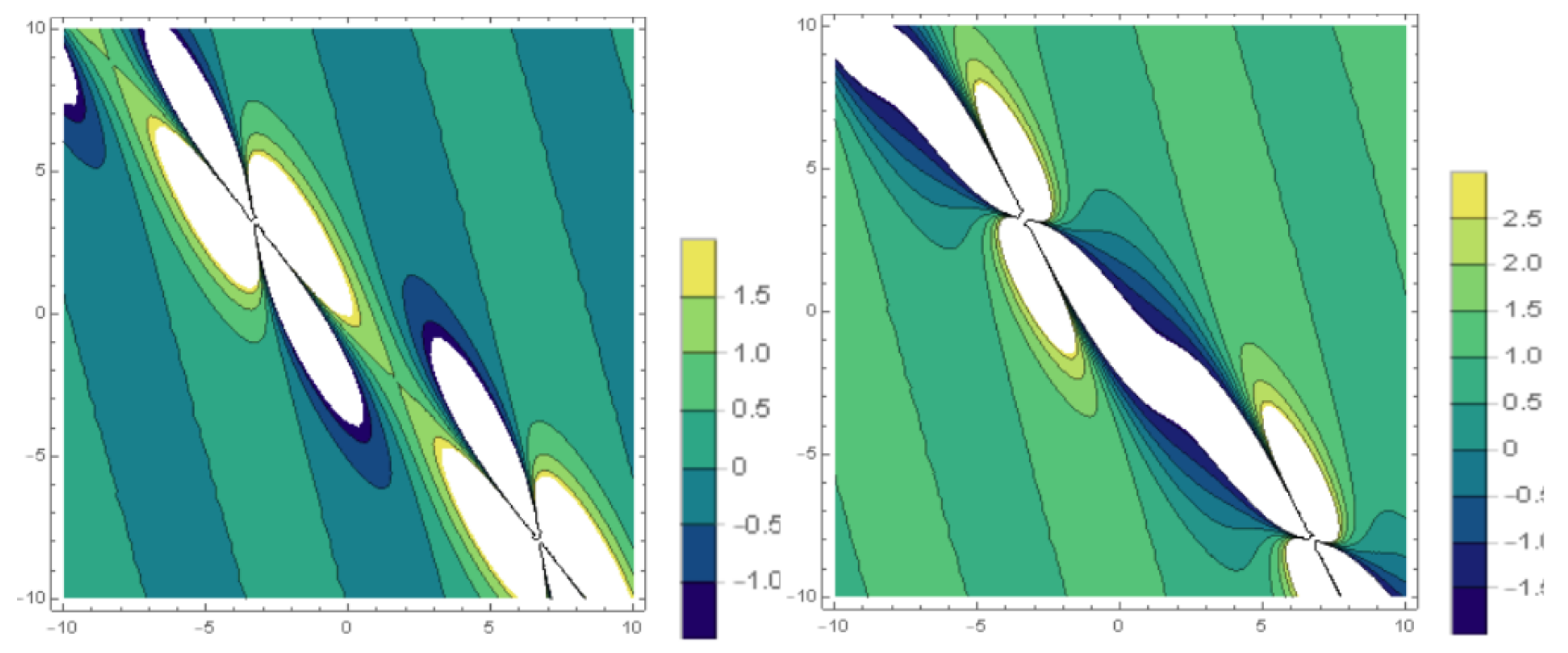
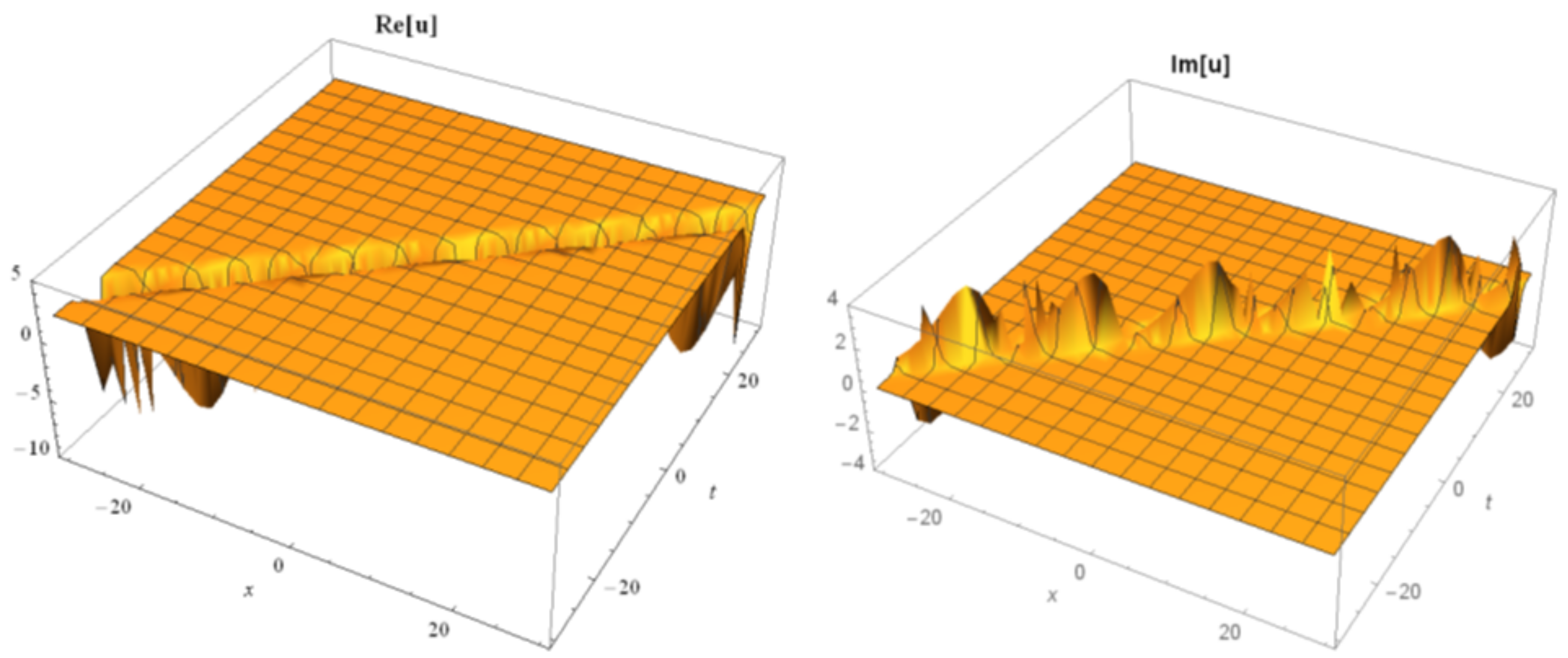
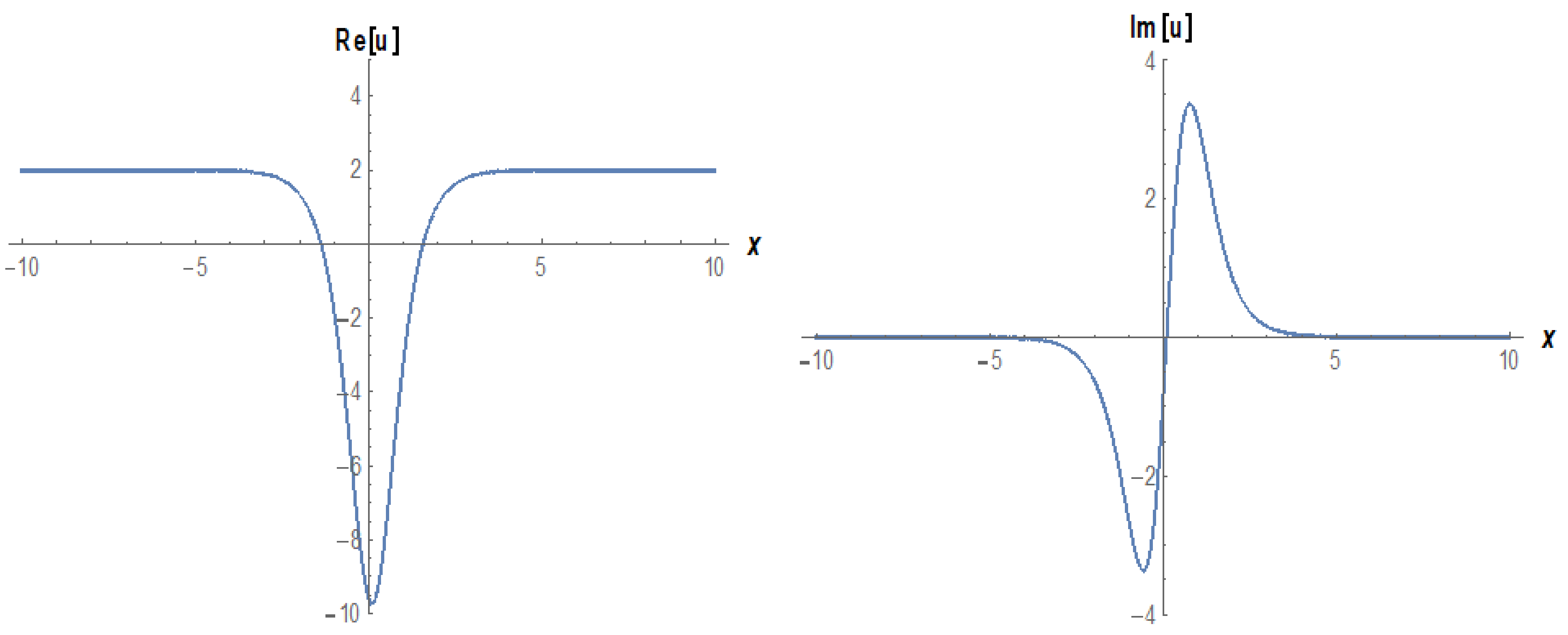
3. Implementation of the BSEFM
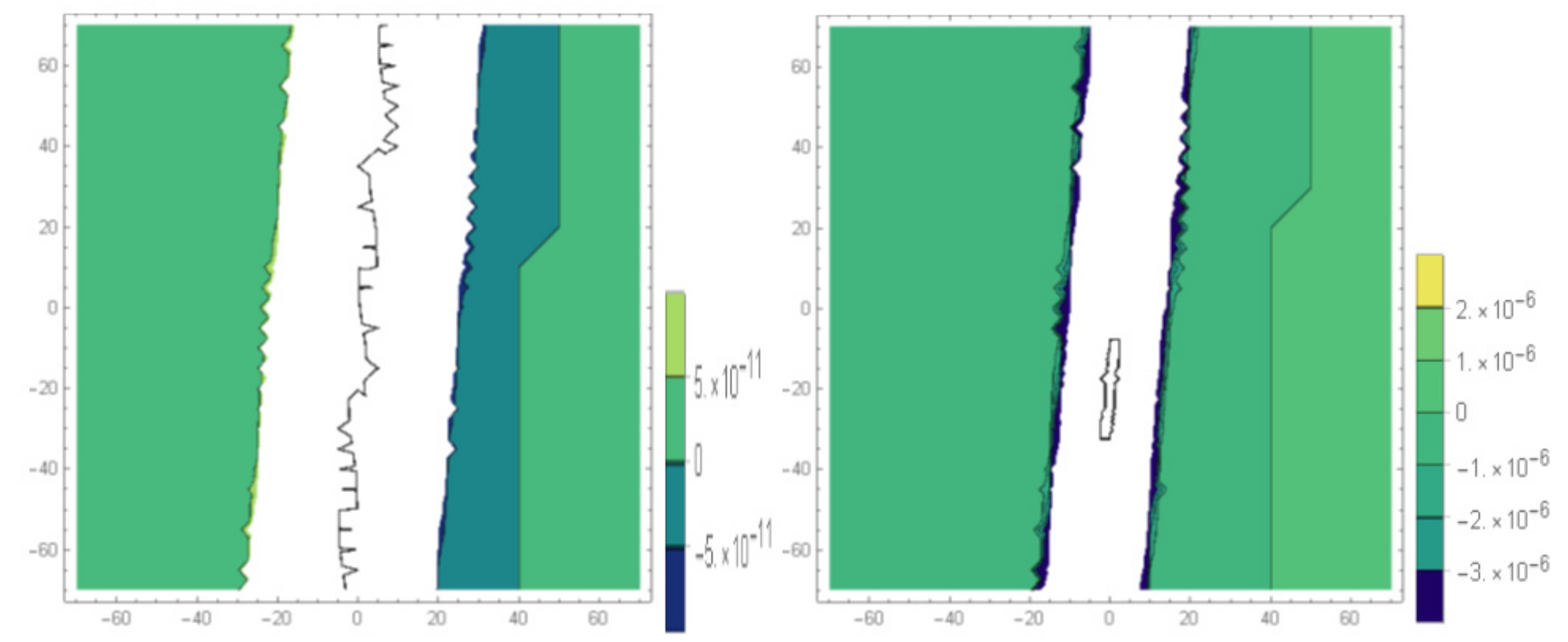
4. Comparison and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgements
Conflicts of Interest
References
- Qi, F.-H.; Huang, Y.-H.; Wang, P. Solitary-wave and new exact solutions for an extended (3+1)-dimensional Jimbo–Miwa-like equation. Appl. Math. Lett. 2020, 100, 106004. [Google Scholar] [CrossRef]
- Cao, B. Solutions of Jimbo-Miwa Equation and Konopelchenko-Dubrovsky Equations. arXiv 2009, arXiv:0902.3308. [Google Scholar]
- Behera, S.; Ray, S.S. An operational matrix based scheme for numerical solutions of nonlinear weakly singular partial integro-differential equations. Appl. Math. Comput. 2020, 367, 124771. [Google Scholar] [CrossRef]
- Syam, M.I. The solution of Cahn-Allen equation based on Bernoulli sub-equation method. Results Phys. 2019, 14, 102413. [Google Scholar] [CrossRef]
- Mendo, L. An asymptotically optimal Bernoulli factory for certain functions that can be expressed as power series. Stoch. Process. Their Appl. 2019, 129, 4366–4384. [Google Scholar] [CrossRef] [Green Version]
- Rani, D.; Mishra, V. Numerical inverse Laplace transform based on Bernoulli polynomials operational matrix for solving nonlinear differential equations. Results Phys. 2020, 16, 102836. [Google Scholar] [CrossRef]
- Lee, J.Y.; Jeon, W. Exact solution of Euler-Bernoulli equation for acoustic black holes via generalized hypergeometric differential equation. J. Sound Vib. 2019, 452, 191–204. [Google Scholar] [CrossRef]
- Arqub, O.A.; Maayah, B. Modulation of reproducing kernel Hilbert space method for numerical solutions of Riccati and Bernoulli equations in the Atangana-Baleanu fractional sense. Chaos Solitons Fractals 2019, 125, 163–170. [Google Scholar]
- Rahimkhani, P.; Ordokhani, Y.; Babolian, E. Numerical solution of fractional pantograph differential equations by using generalized fractional-order Bernoulli wavelet. J. Comput. Appl. Math. 2017, 309, 493–510. [Google Scholar] [CrossRef]
- Yang, S.L. An identity of symmetry for the Bernoulli polynomials. Discret. Math. 2008, 308, 550–554. [Google Scholar]
- Dilcher, K.; Vignat, C. General convolution identities for Bernoulli and Euler polynomials. J. Math. Anal. Appl. 2016, 435, 1478–1498. [Google Scholar]
- Dilcher, K.; Straub, A.; Vignat, C. Identities for Bernoulli polynomials related to multiple Tornheim zeta functions. J. Math. Anal. Appl. 2019, 476, 569–584. [Google Scholar] [CrossRef] [Green Version]
- Rahimkhani, P.; Ordokhani, Y.; Babolian, E. Fractional-order Bernoulli wavelets and their applications. Appl. Math. Model. 2016, 40, 8087–8107. [Google Scholar] [CrossRef]
- Ren, Q.; Tian, H. Numerical solution of the static beam problem by Bernoulli collocation method. Appl. Math. Model. 2016, 40, 8886–8897. [Google Scholar] [CrossRef] [Green Version]
- Jamei, M.M.; Beyki, M.R.; Koepf, W. An extension of the Euler-Maclaurin quadrature formula using a parametric type of Bernoulli polynomials. Bull. Des. Sci. Mathématiques 2019, 156, 102798. [Google Scholar]
- Rahimkhani, P.; Ordokhani, Y.; Babolian, E. Fractional-order Bernoulli functions and their applications in solving fractional Fredholem–Volterra integro-differential equations. Appl. Numer. Math. 2017, 122, 66–81. [Google Scholar] [CrossRef]
- Biswas, A.; Mirzazade, M.; Triki, H.; Zhou, Q.; Ullah, M.Z.; Moshokoa, S.P.; Belic, M. Perturbed resonant 1-soliton solution with an-ti-cubic nonlinearity by Riccati-Bernoulli sub-ODE method. Optik 2018, 156, 346–350. [Google Scholar]
- Keshavarz, E.; Ordokhani, Y.; Razzaghi, M. The Bernoulli wavelets operational matrix of integration and its applications for the solution of linear and nonlinear problems in calculus of variations. Appl. Math. Comput. 2019, 351, 83–98. [Google Scholar] [CrossRef]
- Zeghdane, R. Numerical solution of stochastic integral equations by using Bernoulli operational matrix. Math. Comput. Simul. 2019, 165, 238–254. [Google Scholar]
- Marinov, T.T.; Vatsala, A.S. Inverse problem for coefficient identification in the Euler–Bernoulli equation. Comput. Math. Appl. 2008, 56, 400–410. [Google Scholar] [CrossRef] [Green Version]
- Islam, N.; Asaduzzaman, M.; Ali, S. Exact wave solutions to the simplified modified Camassa-Holm equation in mathematical physics. AIMS Math. 2020, 5, 26–41. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Solitary wave solutions for modified forms of Degasperis–Procesi and Camassa–Holm equations. Phys. Lett. A 2006, 352, 500–504. [Google Scholar] [CrossRef]
- Baskonus, H.M.; Bulut, H. On the complex structures of Kundu-Eckhaus equation via improved Bernoulli sub-equation function method. Waves Random Complex Media 2015, 25. [Google Scholar] [CrossRef]
- Ihan, E.; Kiymaz, I.O. A generalization of truncated M-fractional derivative and applications to fractional differential equations. Appl. Math. Nonlinear Sci. 2020, 5, 171–188. [Google Scholar]
- Pandey, P.K.; Jaboob, S.S.A. A finite difference method for a numerical solution of elliptic boundary value problems. Appl. Math. Nonlinear Sci. 2018, 3, 311–320. [Google Scholar] [CrossRef] [Green Version]
- Durur, H.; Ilhan, E.; Bulut, H. Novel Complex Wave Solutions of the (2+1)-Dimensional Hyperbolic Nonlinear Schrödinger Equation. Fractal Fract. 2020, 4, 41. [Google Scholar] [CrossRef]
- Eskitascioglu, E.I.; Aktas, M.B.; Baskonus, H.M. New Complex and Hyperbolic Forms for Ablowitz-Kaup-Newell-Segur Wave Equation with Fourth Order. Appl. Math. Nonlinear Sci. 2019, 4, 105–112. [Google Scholar]
- Conte, R.; Musette, M. Elliptic General Analytic Solutions. Stud. Appl. Math. 2009, 123, 63–81. [Google Scholar] [CrossRef]
- Contel, R.; Ng, T.W. Meromorphic solutions of a third order nonlinear differential equation. J. Math. Phys. 2010, 51, 033518. [Google Scholar] [CrossRef] [Green Version]
- Gao, W.; Yel, G.; Baskonus, H.M.; Cattani, C. Complex solitons in the conformable (2+1)-dimensional Ablowitz-Kaup-Newell-Segur equation. AIMS Math. 2020, 5, 507–521. [Google Scholar] [CrossRef]
- Ismael, H.F.; Bulut, H.; Baskonus, H.M.; Gao, W. Newly modified method and its application to the coupled Boussinesq equation in ocean engineering with its linear stability analysis. Commun. Theor. Phys. 2020, 72, 115002. [Google Scholar] [CrossRef]
- Liu, J.-G.; Yang, X.-J.; Feng, Y.-Y. Analytical solutions of some integral fractional differential–difference equations. Mod. Phys. Lett. B 2020, 34, 2050009. [Google Scholar] [CrossRef]
- Silambarasan, R.; Baskonus, H.M.; Rajasekaran, V.A.; Dinakaran, M.; Balusamy, B.; Gao, W. Longitudinal strain waves propagating in an infinitely long cylindrical rod composed of generally incompressible materials and it’s Jacobi elliptic function solutions. Math. Comput. Simul. 2020, 182, 566–602. [Google Scholar] [CrossRef]
- Ghanbari, B.; Günerhan, H.; Ilhan, O.A.; Baskonus, H.M. Some new families of exact solutions to a new extension of nonlinear Schrödinger equation. Phys. Scr. 2020, 95, 075208. [Google Scholar] [CrossRef]
- Berna, F.B. Analysis of fractional Klein–Gordon–Zakharov equations using efficient method. Num. Method. Partial Dif. Eq. 2020. [Google Scholar] [CrossRef]
- Houwe, A.; Sabi’U, J.; Hammouch, Z.; Doka, S.Y. Solitary pulses of a conformable nonlinear differential equation governing wave propagation in low-pass electrical transmission line. Phys. Scr. 2020, 95, 045203. [Google Scholar] [CrossRef]
- Cordero, A.; Jaiswal, J.P.; Torregrosa, J.R. Stability analysis of fourth-order iterative method for finding multiple roots of non-linear equations. Appl. Math. Nonlinear Sci. 2019, 4, 43–56. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.-G.; Yang, X.-J.; Feng, Y.-Y. Characteristic of the algebraic traveling wave solutions for two extended (2 + 1)-dimensional Kadomtsev–Petviashvili equations. Mod. Phys. Lett. A 2019, 35, 2050028. [Google Scholar] [CrossRef]
- Ozer, O. Fundamental units for real quadratic fields determined by continued fraction conditions. AIMS Math. 2020, 5, 2899–2908. [Google Scholar] [CrossRef]
- Gao, W.; Senel, M.; Yel, G.; Baskonus, H.M.; Senel, B. New complex wave patterns to the electrical transmission line model arising in network system. AIMS Math. 2020, 5, 1881–1892. [Google Scholar] [CrossRef]
- Yang, X.-J.; Gao, F. A new technology for solving diffusion and heat equations. Therm. Sci. 2017, 21, 133–140. [Google Scholar] [CrossRef]
- Hosseini, K.; Samavat, M.; Mirzazadeh, M.; Ma, W.X.; Hammouch, Z. A New $$(3+ 1) $$-dimensional Hirota Bilinear Equation: Its Bäcklund Transformation and Rational-type Solutions. Regul. Chaotic Dyn. 2020, 25, 383–391. [Google Scholar] [CrossRef]
- Gao, W.; Ismael, H.F.; Husien, A.M.; Bulut, H.; Baskonus, H. Optical Soliton solutions of the Nonlinear Schrödinger and Resonant Nonlinear Schrödinger Equation with Parabolic Law. Appl. Sci. 2020, 10, 219. [Google Scholar] [CrossRef] [Green Version]
- Uddin, M.F.; Hafez, M.G.; Hammouch, Z.; Baleanu, D. Periodic and rogue waves for Heisenberg models of ferromag-netic spin chains with fractional beta derivative evolution and obliqueness. Waves Random Complex Media 2020. [Google Scholar] [CrossRef]
- Cattani, C.; Sulaiman, T.A.; Baskonus, H.M.; Bulut, H. On the soliton solutions to the Nizhnik-Novikov-Veselov and the Drinfel’d-Sokolov systems. Opt. Quantum Electron. 2018, 50, 138. [Google Scholar] [CrossRef]
- Khader, M.M.; Saad, K.M.; Hammouch, Z.; Baleanu, D. A spectral collocation method for solving fractional KdV and KdV-Burger’s equations with non-singular kernel derivatives. Appl. Numer. Math. 2020. [Google Scholar] [CrossRef]
- Yokus, A.; Sulaiman, T.A.; Baskonus, H.M.; Atmaca, S.P. On the exact and numerical solutions to a nonlinear model aris-ing in mathematical biology. ITM Web Conf. 2018, 22, 8815363. [Google Scholar] [CrossRef] [Green Version]
- Sulaiman, T.A.; Yokus, A.; Gulluoglu, N.; Baskonus, H.M.; Bulut, H. Regarding the Numerical and Stability Analysis of the Sharma-Tosso-Olver Equation. ITM Web Conf. 2018, 22, 102555. [Google Scholar] [CrossRef] [Green Version]
- Baskonus, H.M.; Cattani, C.; Ciancio, A. Periodic, Complex and Kink-type Solitons for the Nonlinear Model in Microtu-bules. J. Appl. Sci. 2019, 21, 34–45. [Google Scholar]
- Weisstein, E.W. Concise Encyclopedia of Mathematics; CRC Press: New York, NY, USA, 2002. [Google Scholar]















Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baskonus, H.M.; Ercan, M. Extraction Complex Properties of the Nonlinear Modified Alpha Equation. Fractal Fract. 2021, 5, 6. https://0-doi-org.brum.beds.ac.uk/10.3390/fractalfract5010006
Baskonus HM, Ercan M. Extraction Complex Properties of the Nonlinear Modified Alpha Equation. Fractal and Fractional. 2021; 5(1):6. https://0-doi-org.brum.beds.ac.uk/10.3390/fractalfract5010006
Chicago/Turabian StyleBaskonus, Haci Mehmet, and Muzaffer Ercan. 2021. "Extraction Complex Properties of the Nonlinear Modified Alpha Equation" Fractal and Fractional 5, no. 1: 6. https://0-doi-org.brum.beds.ac.uk/10.3390/fractalfract5010006




