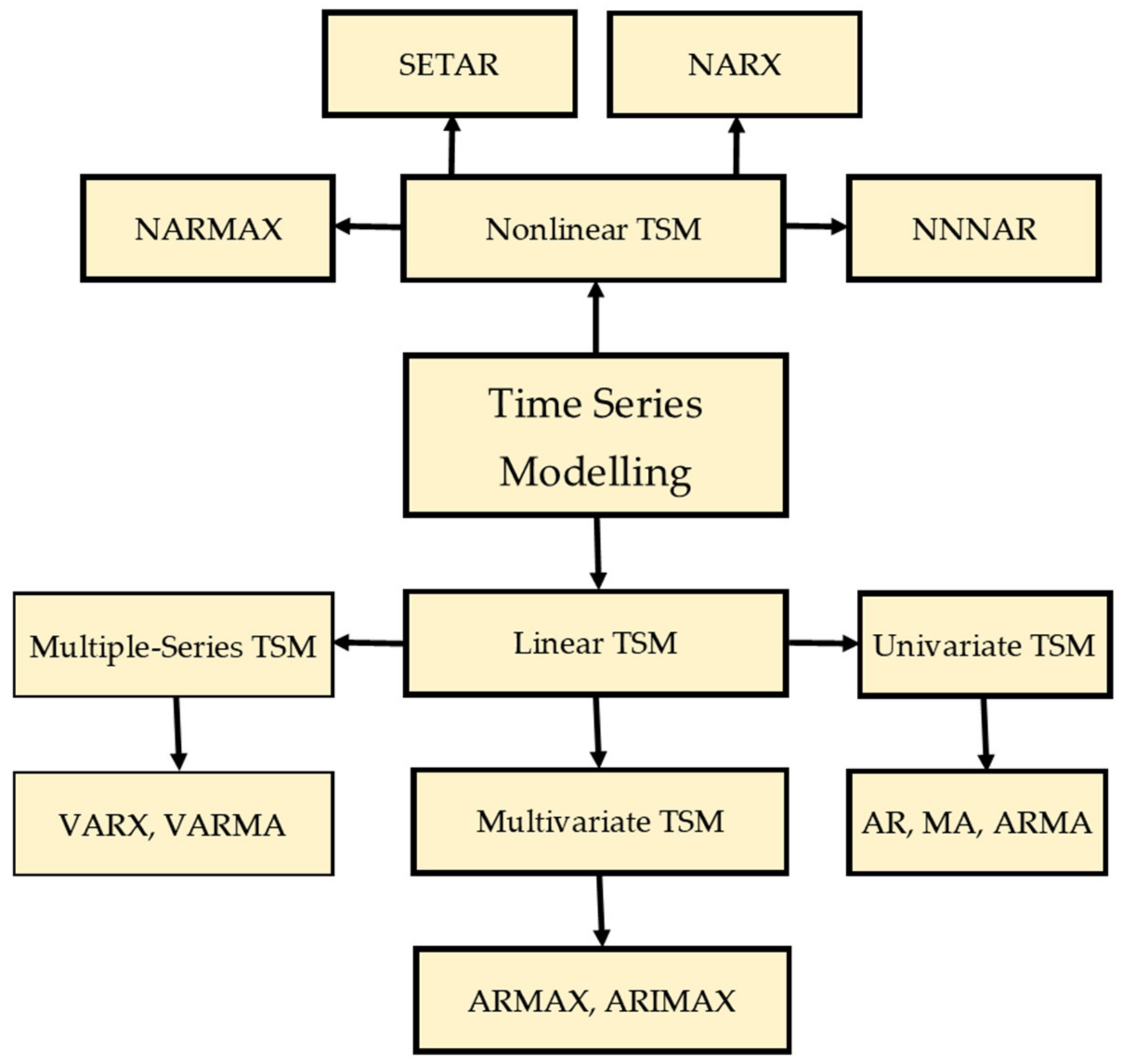
Figure 1.
Classification of time series models. TSM, time series model; AR, autoregressive; MA, moving average; ARMA, autoregressive moving average; ARMAX, autoregressive moving average with exogenous variables; ARIMAX, autoregressive integrated moving average with exogenous variables; VARX, vector autoregressive with exogenous variables; VARMA, vector autoregressive moving average; NARX, nonlinear autoregressive with exogenous variables; NARMAX, nonlinear autoregressive moving average with exogenous variables; SETAR, self-exciting threshold autoregressive; NNNAR, neural network nonlinear autoregressive.
Figure 1.
Classification of time series models. TSM, time series model; AR, autoregressive; MA, moving average; ARMA, autoregressive moving average; ARMAX, autoregressive moving average with exogenous variables; ARIMAX, autoregressive integrated moving average with exogenous variables; VARX, vector autoregressive with exogenous variables; VARMA, vector autoregressive moving average; NARX, nonlinear autoregressive with exogenous variables; NARMAX, nonlinear autoregressive moving average with exogenous variables; SETAR, self-exciting threshold autoregressive; NNNAR, neural network nonlinear autoregressive.
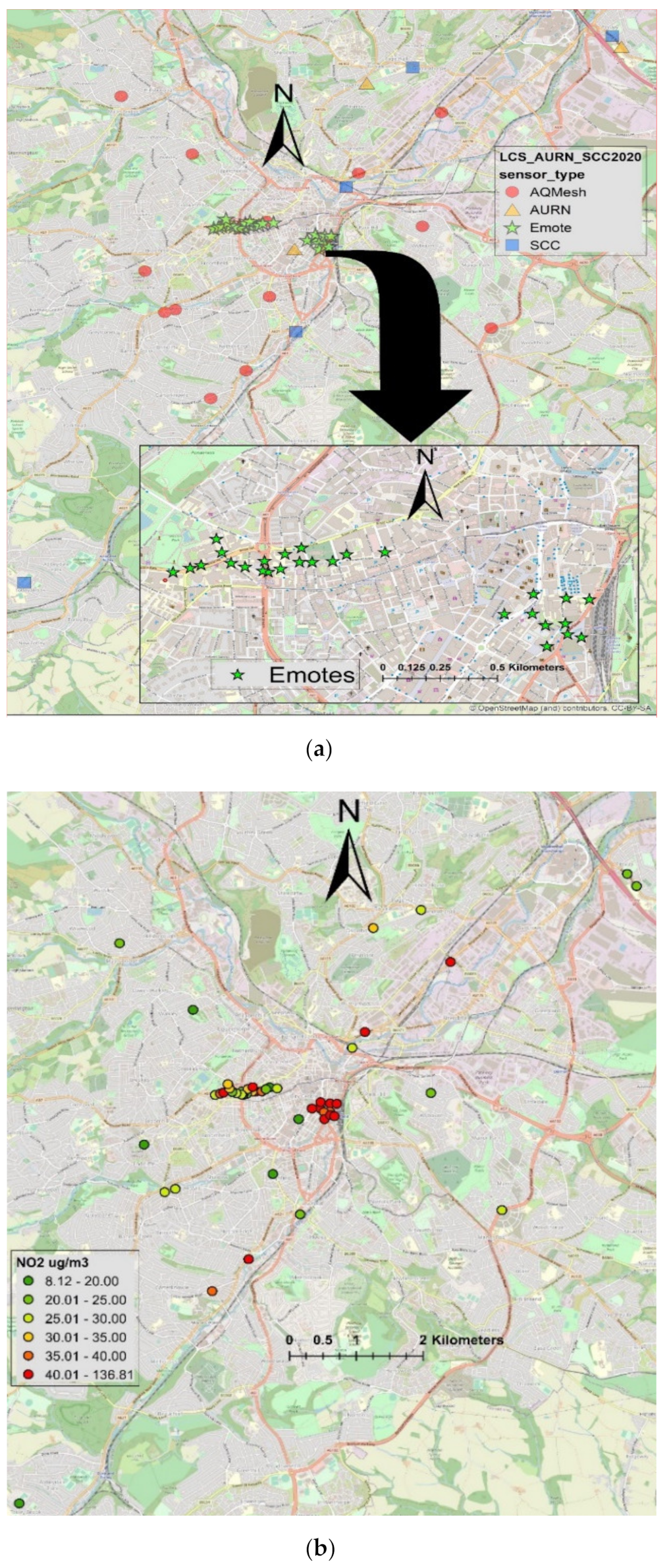
Figure 2.
(a) The locations of air quality monitoring stations (AQMSs) in Sheffield; (b) annual mean NO2 levels (µg/m3) measured by low-cost sensors (LCSs) and Automatic Urban and Rural Network (AURN) and Sheffield City Council (SCC) AQMSs in Sheffield from August 2019 to September 2020.
Figure 2.
(a) The locations of air quality monitoring stations (AQMSs) in Sheffield; (b) annual mean NO2 levels (µg/m3) measured by low-cost sensors (LCSs) and Automatic Urban and Rural Network (AURN) and Sheffield City Council (SCC) AQMSs in Sheffield from August 2019 to September 2020.
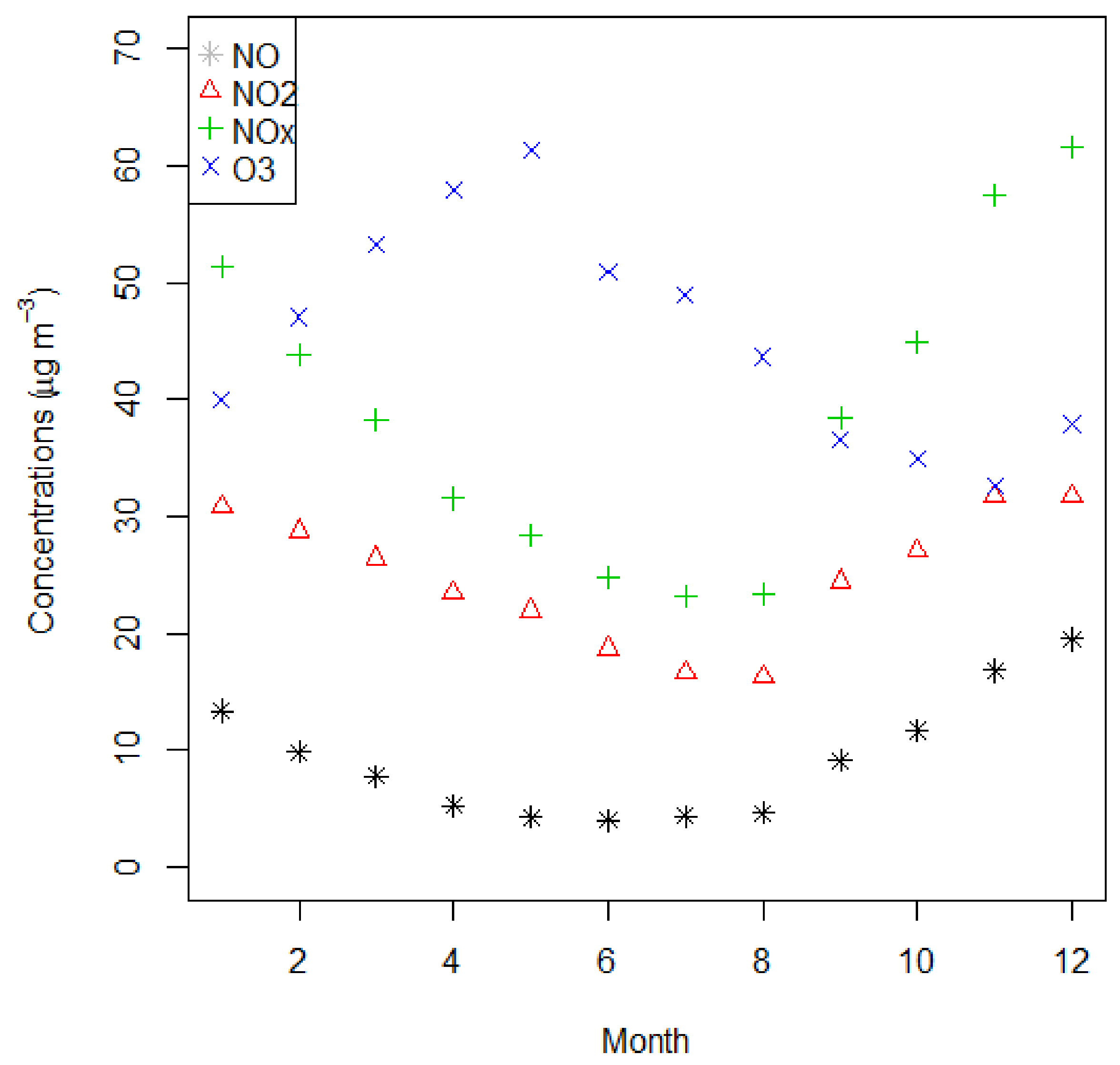
Figure 3.
Monthly average concentrations (µg/m3) of NO, NO2, NOx and O3 in different months of the year from the Devonshire Green AQMS in Sheffield, 2014–2019.
Figure 3.
Monthly average concentrations (µg/m3) of NO, NO2, NOx and O3 in different months of the year from the Devonshire Green AQMS in Sheffield, 2014–2019.
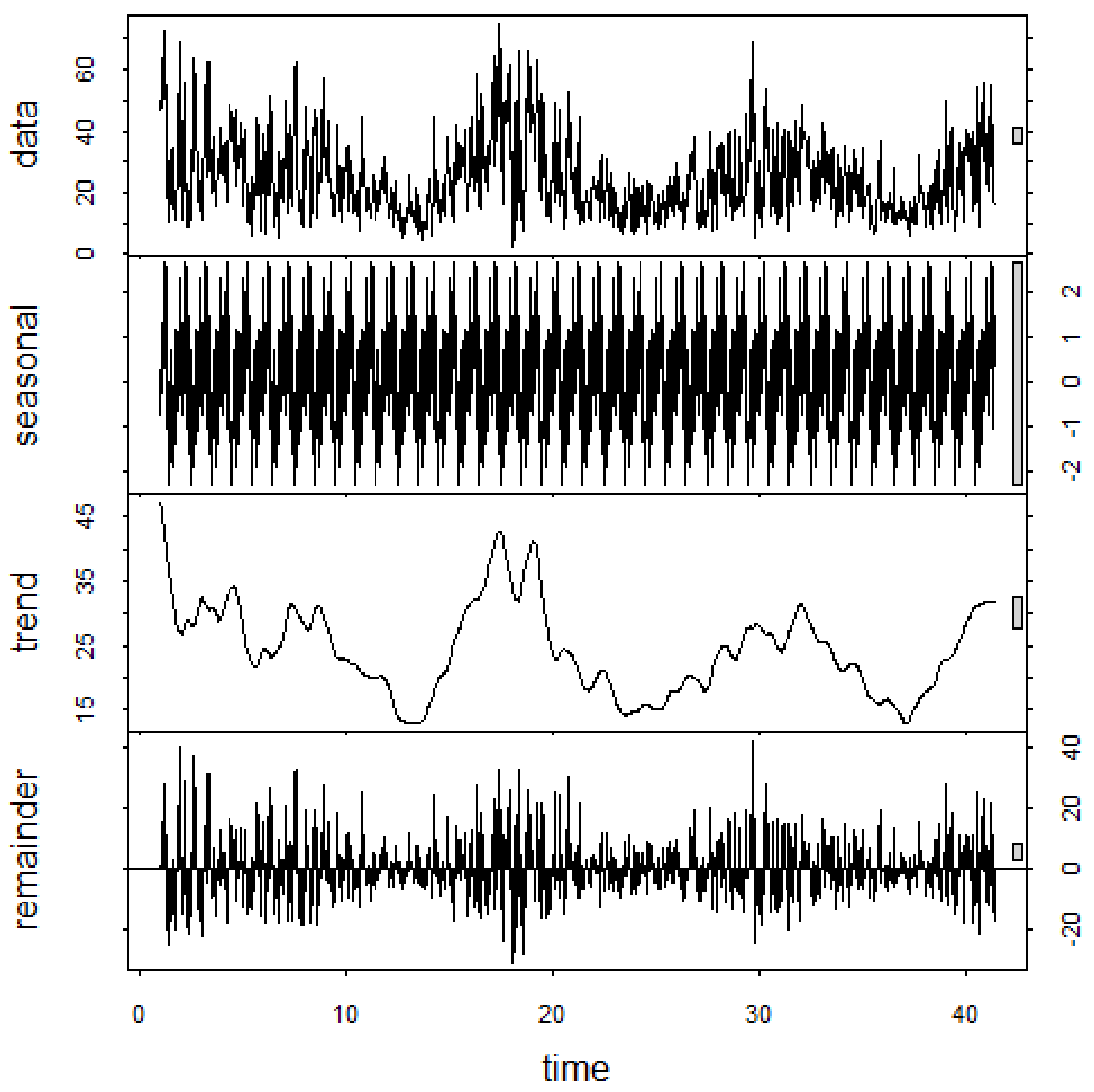
Figure 4.
Three additive components obtained from seasonal-trend decomposition based on loess (STL), decomposition of NO2 concentration (µg/m3) collected at the Devonshire Green AQMS, Sheffield.
Figure 4.
Three additive components obtained from seasonal-trend decomposition based on loess (STL), decomposition of NO2 concentration (µg/m3) collected at the Devonshire Green AQMS, Sheffield.
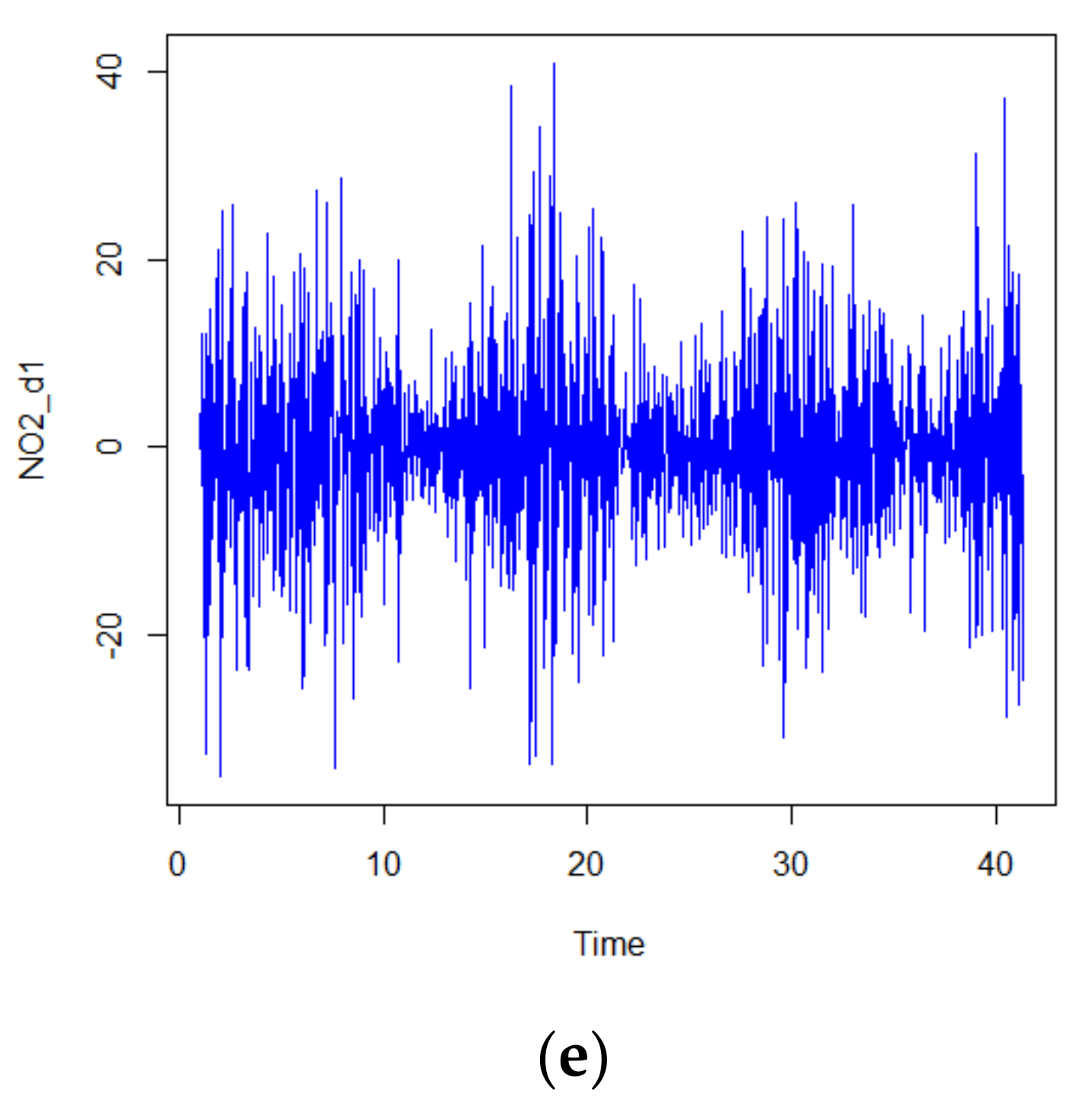
Figure 5.
Auto-correlation function (ACF) plot of the NO2 (µg/m3) time series (not differenced) (a), differenced once (b) and differenced twice (c); partial ACF plot (d) and once-differenced NO2 plot of oscillating pattern around zero with no visible strong trend (e) showing that the series is stationary. NO2 concentrations used here were collected at the Devonshire Green AQMS, Sheffield.
Figure 5.
Auto-correlation function (ACF) plot of the NO2 (µg/m3) time series (not differenced) (a), differenced once (b) and differenced twice (c); partial ACF plot (d) and once-differenced NO2 plot of oscillating pattern around zero with no visible strong trend (e) showing that the series is stationary. NO2 concentrations used here were collected at the Devonshire Green AQMS, Sheffield.
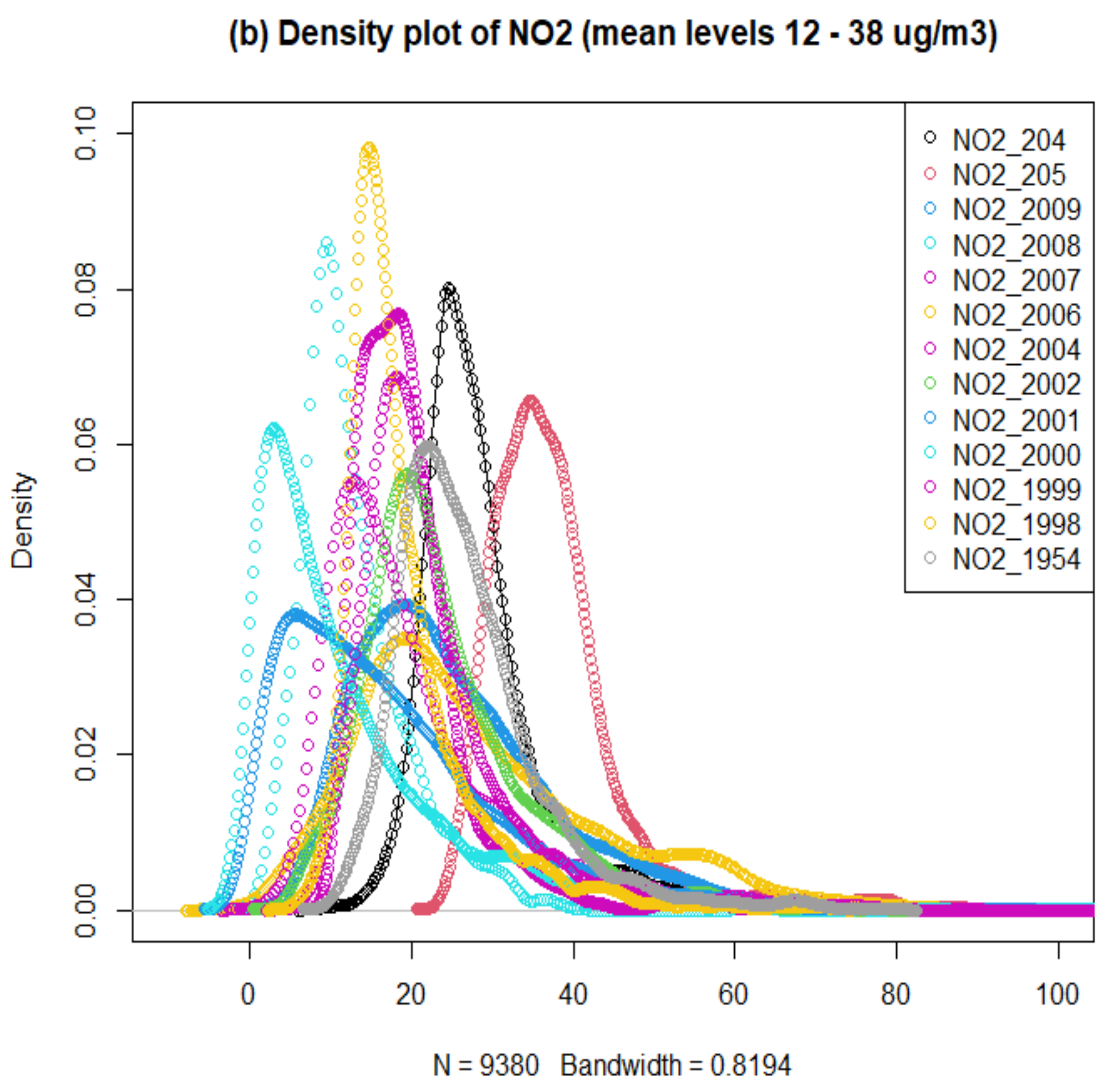
Figure 6.
Different density plots of hourly NO2 concentrations (µg/m3) measured by Envirowatch E-MOTEs, August 2019–September 2020 in Sheffield.
Figure 6.
Different density plots of hourly NO2 concentrations (µg/m3) measured by Envirowatch E-MOTEs, August 2019–September 2020 in Sheffield.
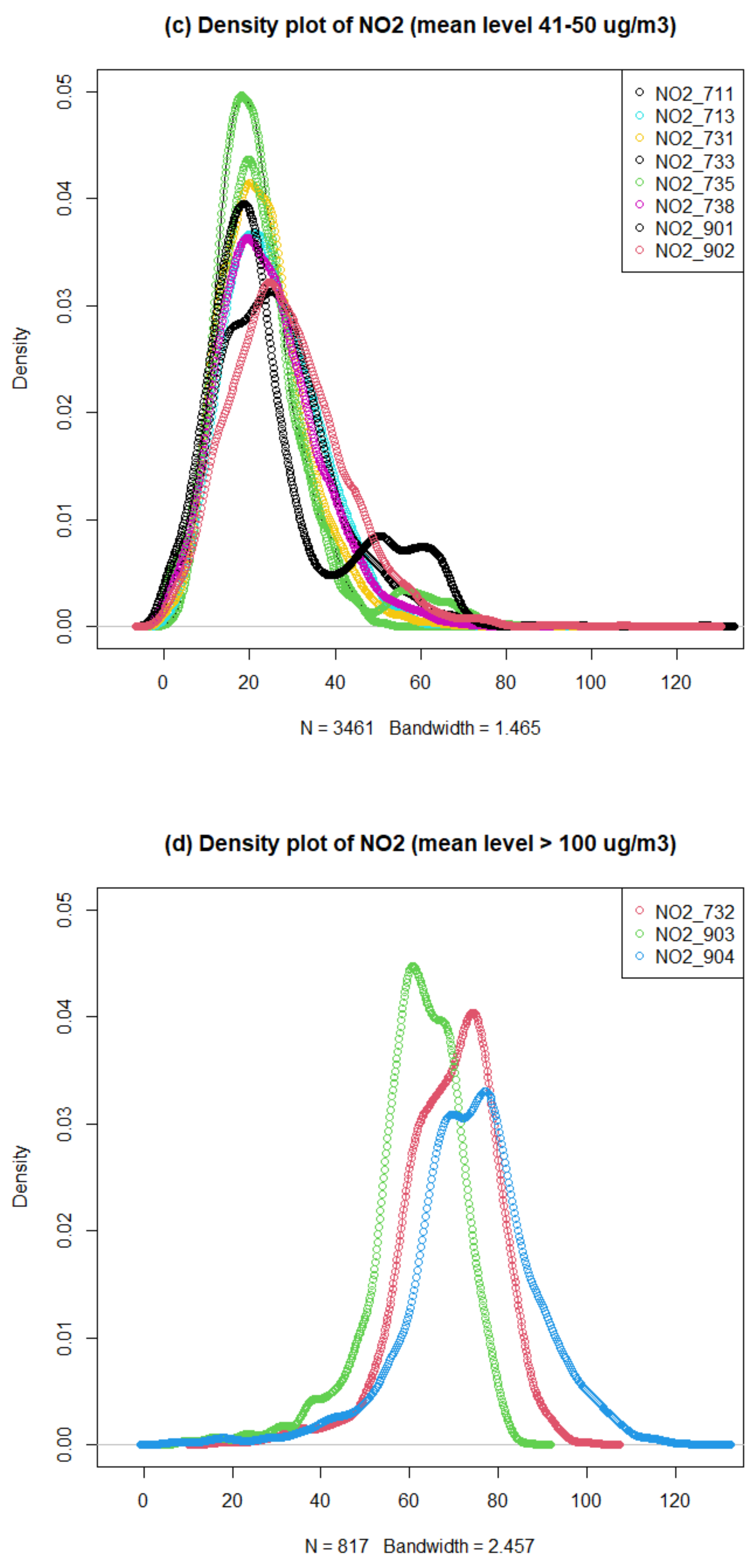
Figure 7.
Density plots of hourly NO2 concentrations (µg/m3) measured by AQMesh pods from August 2019 to September 2020 in Sheffield.
Figure 7.
Density plots of hourly NO2 concentrations (µg/m3) measured by AQMesh pods from August 2019 to September 2020 in Sheffield.
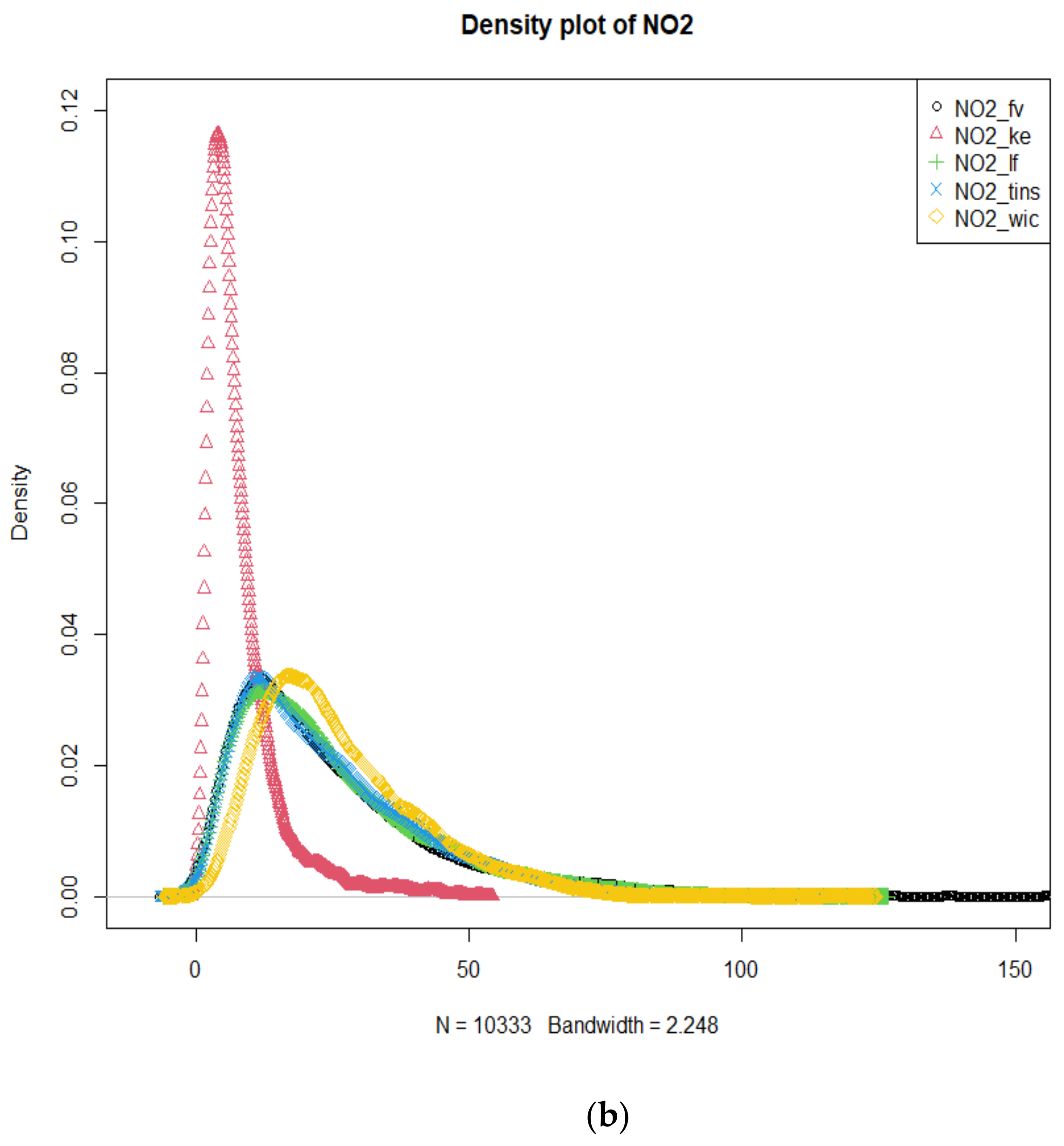
Figure 8.
Density plots of NO2 concentrations (µg/m3) measured by: (a) AURN sites-Barnsley road (brn), Tinsley (tin) and Devonshire Green (dg); and (b) SCC sites-Firvale (fv), King Ecgbert (ke), Lowfield (lf), Tinsley (tins) and Wicker (wic), from August 2019–September 2020.
Figure 8.
Density plots of NO2 concentrations (µg/m3) measured by: (a) AURN sites-Barnsley road (brn), Tinsley (tin) and Devonshire Green (dg); and (b) SCC sites-Firvale (fv), King Ecgbert (ke), Lowfield (lf), Tinsley (tins) and Wicker (wic), from August 2019–September 2020.
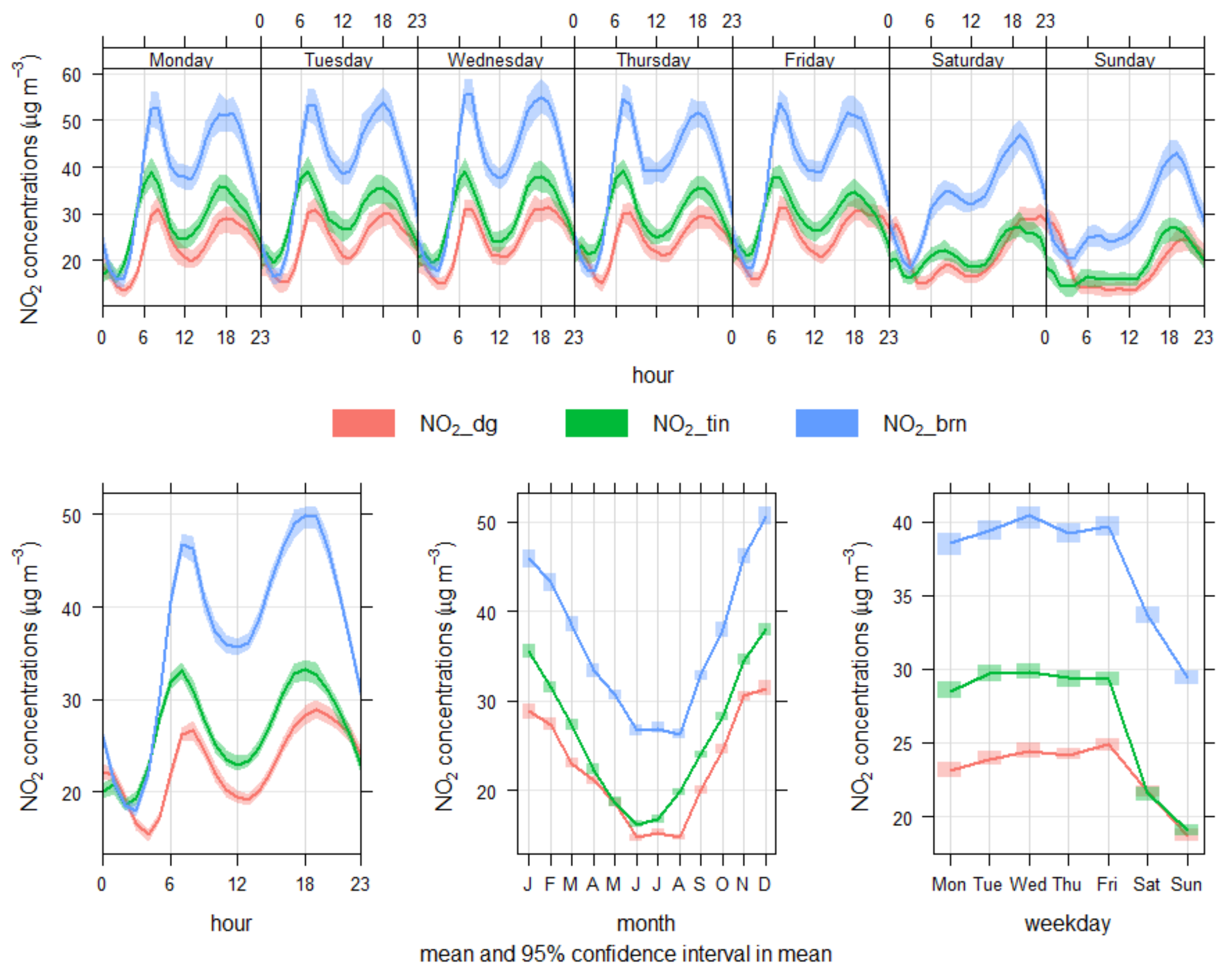
Figure 9.
Time variation plots of NO2 concentrations (µg/m3) in Sheffield at the three AURN AQMS: Barnsley, Tinsley and Devonshire Green.
Figure 9.
Time variation plots of NO2 concentrations (µg/m3) in Sheffield at the three AURN AQMS: Barnsley, Tinsley and Devonshire Green.
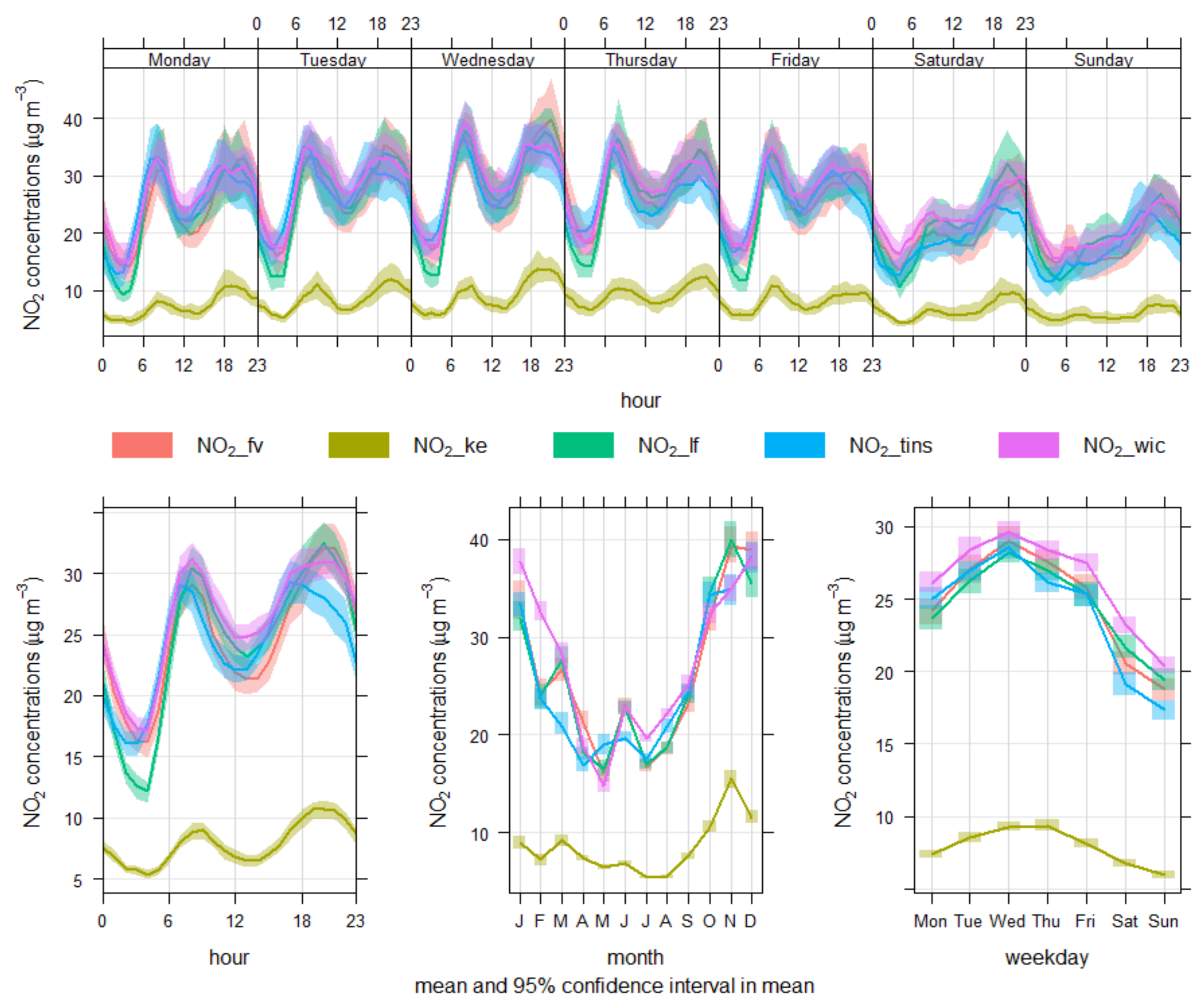
Figure 10.
Time variation plots of NO2 concentrations (µg/m3) measured at SCC sites: Firvale, King Ecgbert, Lowfield, Tinsley and Wicker, from August 2019–September 2020.
Figure 10.
Time variation plots of NO2 concentrations (µg/m3) measured at SCC sites: Firvale, King Ecgbert, Lowfield, Tinsley and Wicker, from August 2019–September 2020.
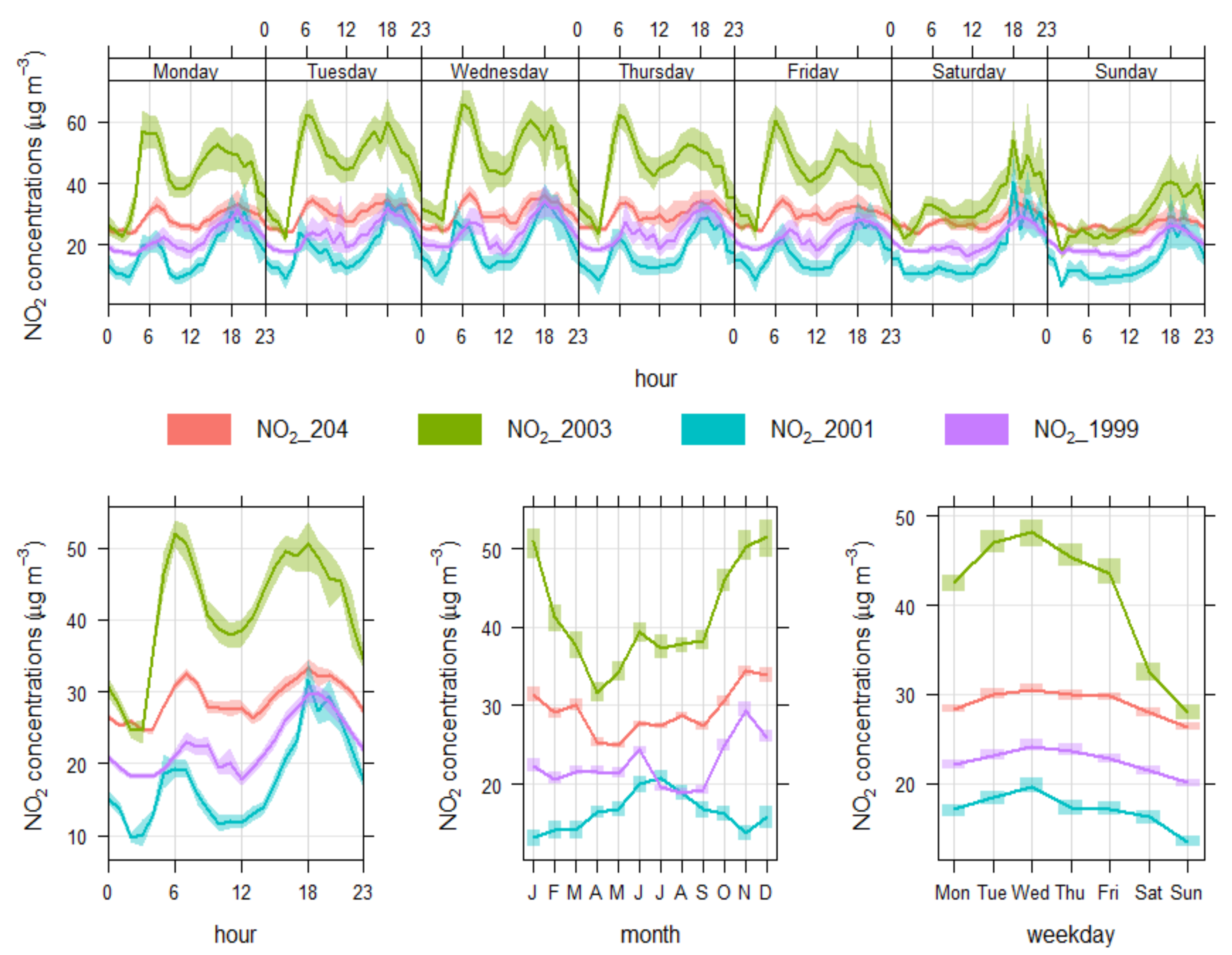
Figure 11.
Time variation plots of NO2 concentrations (µg/m3) measured by Envirowatch E-MOTEs.
Figure 11.
Time variation plots of NO2 concentrations (µg/m3) measured by Envirowatch E-MOTEs.
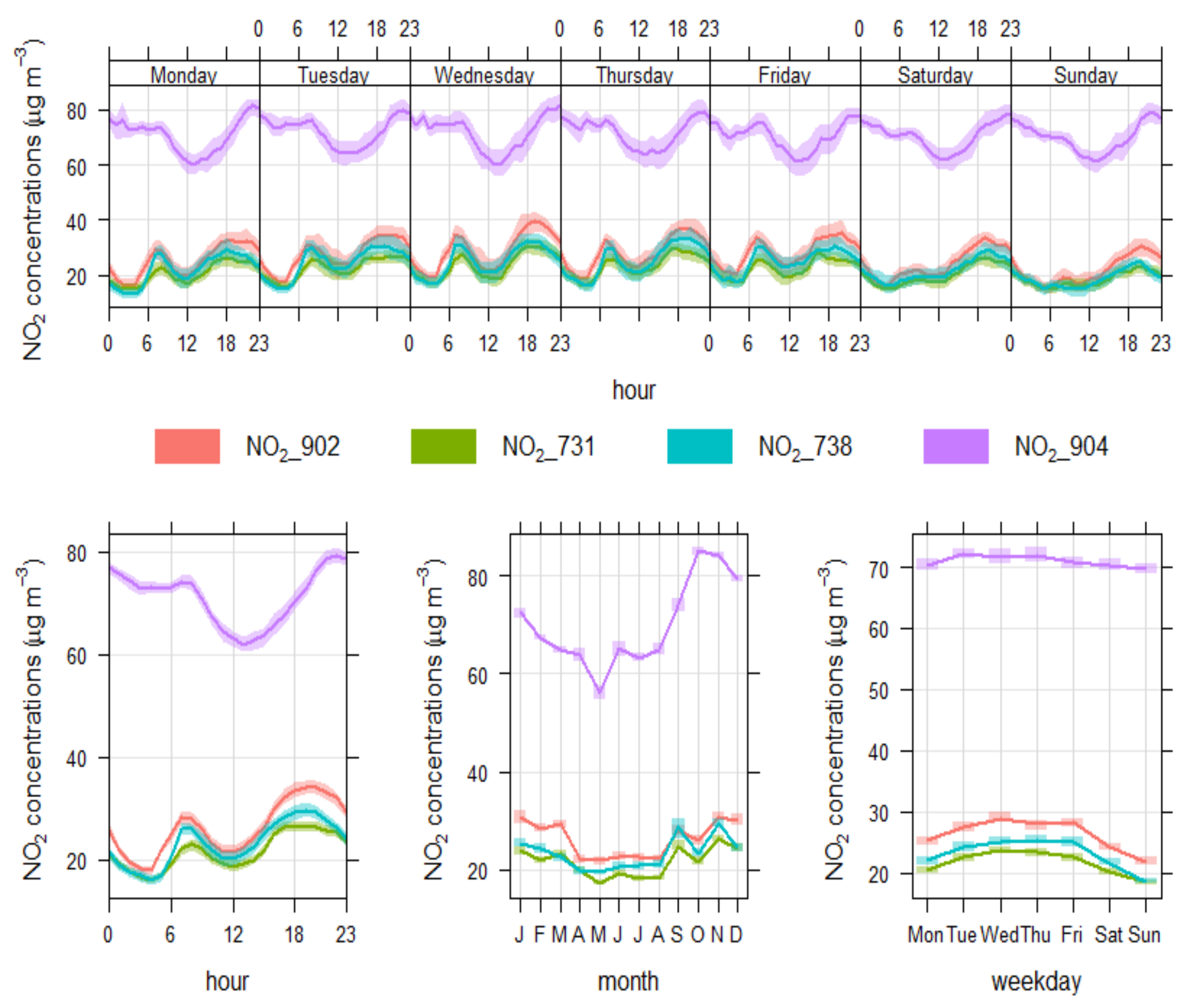
Figure 12.
Time variation plots of NO2 concentrations (µg/m3) measured by AQMesh pods.
Figure 12.
Time variation plots of NO2 concentrations (µg/m3) measured by AQMesh pods.
Figure 13.
Long-term temporal trend for NO2 concentrations (µg/m3) (2000–2019) at the Sheffield Tinsley site, one of the AURN sites. *** shows that the trend is highly significant.
Figure 13.
Long-term temporal trend for NO2 concentrations (µg/m3) (2000–2019) at the Sheffield Tinsley site, one of the AURN sites. *** shows that the trend is highly significant.
Figure 14.
Long-term temporal trend for NO2 concentrations (µg/m3) (2014–2019) at the Sheffield Devonshire Green site. *** shows that the trend is highly significant.
Figure 14.
Long-term temporal trend for NO2 concentrations (µg/m3) (2014–2019) at the Sheffield Devonshire Green site. *** shows that the trend is highly significant.
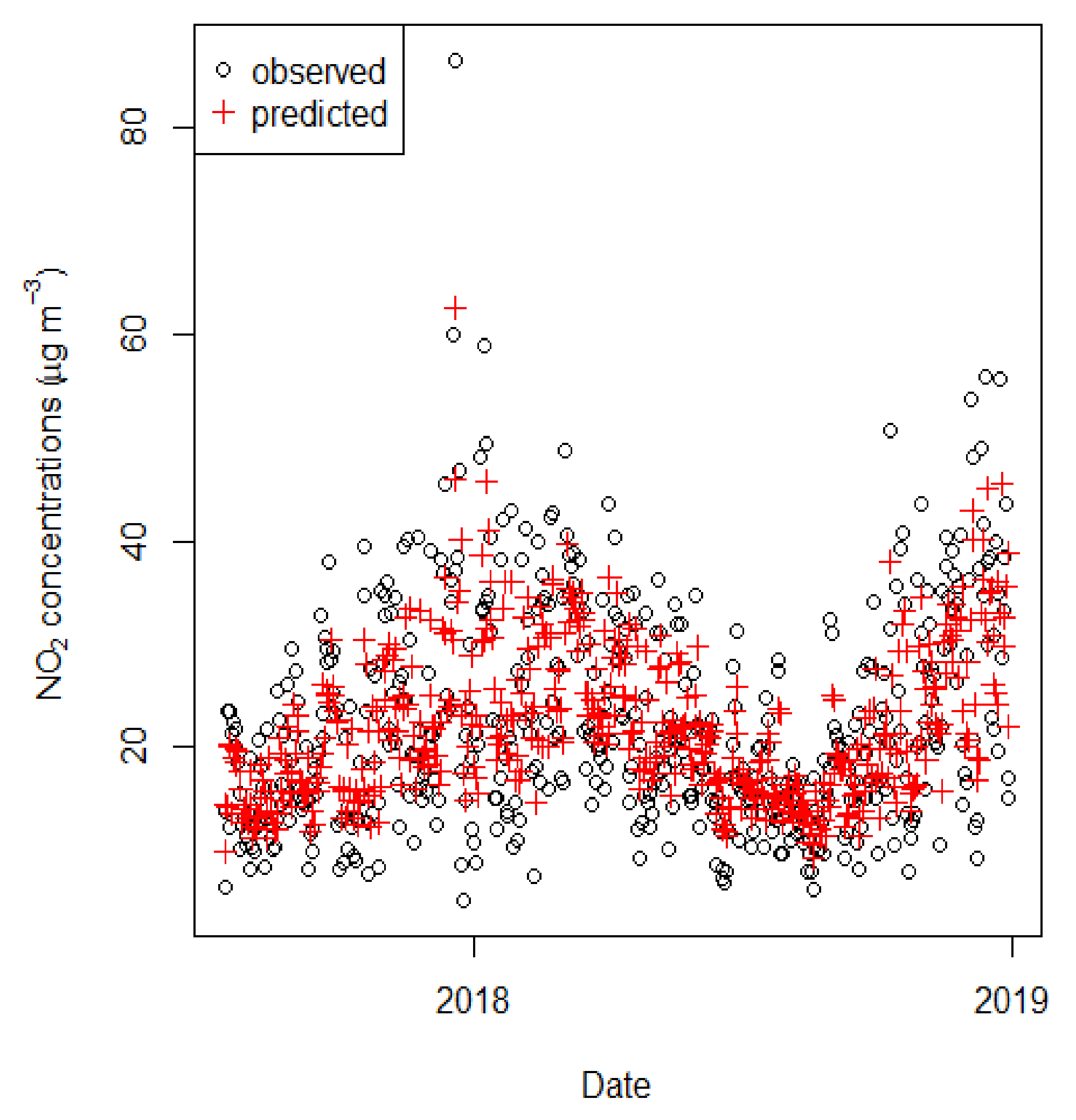
Figure 15.
Predicted vs. observed daily average NO2 concentrations (µg/m3) using the ARIMA (1,1,1) model. Model performance was assessed against held-out testing data, which was not used for model fitting. No exogenous variable was used in the model. The solid line represents the 1:1 relationship, whereas the dashed lines represent the 1:0.5 and 1:2 relationships, between observed and predicted concentrations. The dashed lines show the points that are within a factor of two (FAC2).
Figure 15.
Predicted vs. observed daily average NO2 concentrations (µg/m3) using the ARIMA (1,1,1) model. Model performance was assessed against held-out testing data, which was not used for model fitting. No exogenous variable was used in the model. The solid line represents the 1:1 relationship, whereas the dashed lines represent the 1:0.5 and 1:2 relationships, between observed and predicted concentrations. The dashed lines show the points that are within a factor of two (FAC2).
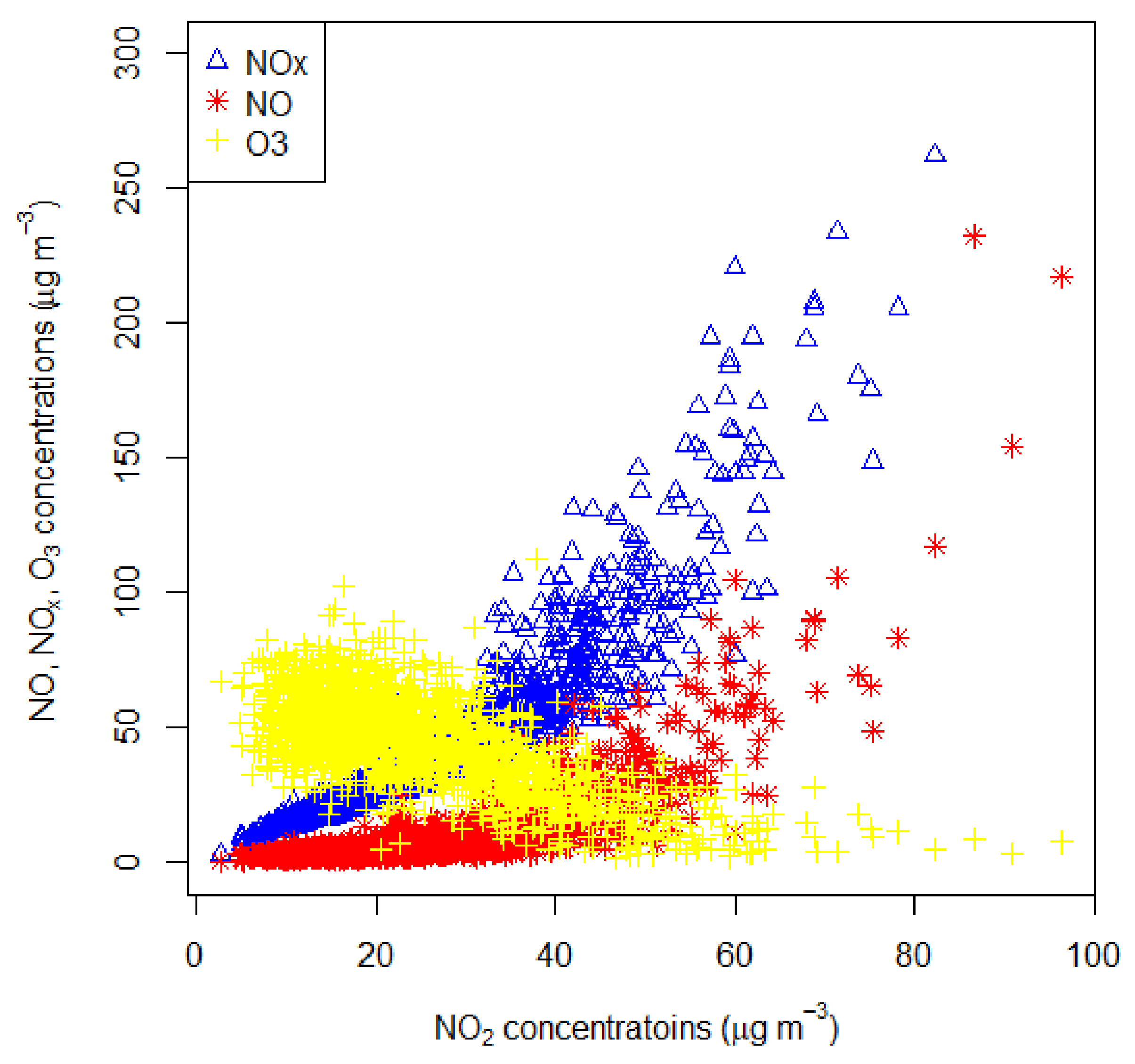
Figure 16.
Scatter plot showing the association of NO2 with NO, NOx and O3 concentrations (µg/m3) at the Devonshire Green AQMS in Sheffield.
Figure 16.
Scatter plot showing the association of NO2 with NO, NOx and O3 concentrations (µg/m3) at the Devonshire Green AQMS in Sheffield.
Table 1.
Names, IDs and annual mean NO2 concentrations (µg/m3) measured by low-cost sensors (AQMesh and Envirowatch E-MOTEs) and AURN and Sheffield City Council sites from August 2019 to September 2020.
Table 1.
Names, IDs and annual mean NO2 concentrations (µg/m3) measured by low-cost sensors (AQMesh and Envirowatch E-MOTEs) and AURN and Sheffield City Council sites from August 2019 to September 2020.
| Site Name | Sensor Type | Sensor ID | NO2 (µg/m3) |
|---|
| Brightside Lane | AQMesh | 2003150 | 41.3 |
| Saville Street | AQMesh | 2005150 | 46.9 |
| Cundy Street | AQMesh | 2007150 | 19.8 |
| off Endcliffe Crescent | AQMesh | 2008150 | 12.7 |
| Sharrow Vale Rd | AQMesh | 2009150 | 25.1 |
| Abbeydale Rd | AQMesh | 2450206 | 43.7 |
| London Rd | AQMesh | 2001150 | 14.6 |
| Prince of Wales Rd | AQMesh | 2006150 | 28.2 |
| Maltravers Rd | AQMesh | 2004150 | 20.8 |
| Hunter’s Bar School | AQMesh | 2450204 | 29.0 |
| Malin Bridge PS | AQMesh | 1999150 | 22.6 |
| Broad Lane | AQMesh | 1998150 | 19.2 |
| Carter Knowle Bridge | AQMesh | 2450205 | 37.6 |
| Tinsley | AURN | SHE | 22.9 |
| Devonshire Green | AURN | SHDG | 19.1 |
| Barnsley Road | AURN | SHBR | 32.1 |
| Regent Court, E-camp | E_MOTE | 711 | 41.7 |
| Leavygreave Road, E-camp | E_MOTE | 712 | 34.2 |
| Gell Street, E-camp | E_MOTE | 701 | 21.1 |
| Upper Hanover/Henderson’s building | E_MOTE | 702 | 28.7 |
| Behind Jessop West | E_MOTE | 703 | 23.7 |
| Diamond/Bio-incubator | E_MOTE | 704 | 34.2 |
| Broad Lane/St George’s Terrace | E_MOTE | 713 | 44.9 |
| Portobello Street, Mappin Street | E_MOTE | 714 | 37.6 |
| 28 Portobello Street, EC | E_MOTE | 705 | 20.8 |
| Howard Street, CC | E_MOTE | 731 | 41.2 |
| Arundel Gate/Genting Club | E_MOTE | 732 | 115.6 |
| Arundel Gate/Surrey Street | E_MOTE | 733 | 43.5 |
| Harmer Lane/Pond Street | E_MOTE | 901 | 44.2 |
| Harmer Lane/Sheaf Street | E_MOTE | 902 | 49.9 |
| Pond Street/Sheaf Building | E_MOTE | 736 | 38.3 |
| Howard Street/Science Park | E_MOTE | 734 | 39.0 |
| Paternoster Rows | E_MOTE | 735 | 42.4 |
| Sheaf Street/Sheaf Square | E_MOTE | 903 | 107.2 |
| Railway Station Taxi rank | E_MOTE | 904 | 136.8 |
| Upper Hanover St/Info. Commons | E_MOTE | 707 | 26.6 |
| Leavygreave Road/Favell Road | E_MOTE | 708 | 25.7 |
| Hounsfield Rd/Hicks Building | E_MOTE | 709 | 24.9 |
| Sheffield Children’s Hospital | E_MOTE | 710 | 28.2 |
| Robert Hadfield Building | E_MOTE | 706 | 25.2 |
| Brook Hill/Firth Court1 | E_MOTE | 737 | 39.3 |
| Brook Hill/Firth Court2 | E_MOTE | 738 | 42.9 |
| Arts Tower Concourse | E_MOTE | 739 | 34.3 |
| Arts Tower Concourse/Library | E_MOTE | 740 | 33.2 |
| Firvale | SSC | GH1 | 25.0 |
| Tinsley | SSC | GH2 | 24.1 |
| Lowfield | SSC | GH3 | 24.6 |
| Wicker | SSC | GH4 | 25.9 |
| King Ecgbert | SSC | GH5 | 8.1 |
Table 2.
Autoregressive integrated moving average (ARIMA) model specification and corresponding Akaike’s information criterion (AIC) values of NO2 time series (µg/m3), where p represents the order of the autoregressive, d represents the difference and q represents the MA.
Table 2.
Autoregressive integrated moving average (ARIMA) model specification and corresponding Akaike’s information criterion (AIC) values of NO2 time series (µg/m3), where p represents the order of the autoregressive, d represents the difference and q represents the MA.
| AIC | p | d | q |
|---|
| 8910.88 | 1 | 1 | 1 |
| 9104.28 | 1 | 2 | 1 |
| 8910.53 | 2 | 1 | 1 |
| 8912.42 | 2 | 1 | 2 |
| 8944.8 | 1 | 0 | 0 |
| 8941.53 | 1 | 0 | 1 |
| 8904.29 | 3 | 1 | 1 |
| 8905.83 | 4 | 1 | 1 |
Table 3.
Comparing the performances of different models, including both linear and nonlinear models, using the testing dataset (cross validation). MBE, MAE and RMSE are expressed in µg/m3. r is the value of correlation coefficient.
Table 3.
Comparing the performances of different models, including both linear and nonlinear models, using the testing dataset (cross validation). MBE, MAE and RMSE are expressed in µg/m3. r is the value of correlation coefficient.
| Model | FAC2 | MBE | MAE | RMSE | r |
|---|
| SETAR | 0.90 | −0.13 | 8.28 | 10.56 | 0.44 |
| NNET | 0.89 | −0.29 | 8.12 | 10.45 | 0.45 |
| ARIMA | 0.91 | −0.26 | 6.46 | 8.61 | 0.59 |
Table 4.
Estimating the parameters of the ARIMA (1,1,1) model for the NO2 concentrations (µg/m3) training dataset.
Table 4.
Estimating the parameters of the ARIMA (1,1,1) model for the NO2 concentrations (µg/m3) training dataset.
| ARIMA Model Applied to Log_NO2 with p, d and q, Order of 1, 1, 1 |
|---|
| Coefficients | AR1 (ϕ) | MA1 (θ) |
| | 0.5362 | −0.9511 |
| S.E. | 0.0296 | 0.0117 |
| Sigma square (σ2) estimated as 0.148: log likelihood = −556.75, AIC = 1117.5 |
Table 5.
Estimating the parameters of the ARIMAX (1,1,1) model for the NO2 concentrations (µg/m3) training dataset, with NO as exogenous variable.
Table 5.
Estimating the parameters of the ARIMAX (1,1,1) model for the NO2 concentrations (µg/m3) training dataset, with NO as exogenous variable.
| ARIMAX Model Applied to Log_NO2 with p, d and q, Order of 1, 1, 1 and Xreg as NO |
|---|
| Coefficients | AR1 (ϕ) | MA1(θ) | XREG |
| | 0.2533 | −0.9689 | 0.4133 |
| Sigma square (σ2) estimated as 0.056: log likelihood = 20.82, AIC = −31.64 |
Table 6.
Model statistics showing the value of several metrics in assessed the model performance by comparing observed and predicted NO2 concentrations (µg/m3) for testing and training data, using NO as exogenous variables. MBE, MAE and RMSE are expressed in µg/m3.
Table 6.
Model statistics showing the value of several metrics in assessed the model performance by comparing observed and predicted NO2 concentrations (µg/m3) for testing and training data, using NO as exogenous variables. MBE, MAE and RMSE are expressed in µg/m3.
| Statistics | FAC2 | MBE | MAE | RMSE | r |
|---|
| Training data | 0.96 | 0.07 | 5.53 | 7.11 | 0.85 |
| Testing data | 0.88 | −6.84 | 7.81 | 10.15 | 0.70 |
Table 7.
Estimating the parameters of the ARIMAX (1,1,1) model for the NO2 concentrations (µg/m3) training dataset, with NO and O3 as exogenous variables.
Table 7.
Estimating the parameters of the ARIMAX (1,1,1) model for the NO2 concentrations (µg/m3) training dataset, with NO and O3 as exogenous variables.
| ARIMAX MODEL Applied to log_NO2 with p, d and q, Order of 1, 1, 1 and Xreg as NO and O3 |
|---|
| Coefficients | AR1 (ϕ) | MA1(θ) | XREG2 (NOx) | XREG3 (O3) |
| | 0.21 | −0.985 | 0.839 | −0.108 |
| Sigma square (σ2) estimated as 0.014: log likelihood = 866.86, AIC = −1721.73 |
Table 8.
Statistical metrics assessing the model performance by comparing observed and predicted concentrations for both the training and testing datasets, using NO and O3 as exogenous variables. MBE, MAE and RMSE are expressed in µg/m3.
Table 8.
Statistical metrics assessing the model performance by comparing observed and predicted concentrations for both the training and testing datasets, using NO and O3 as exogenous variables. MBE, MAE and RMSE are expressed in µg/m3.
| Statistics | FAC2 | MBE | MAE | RMSE | r |
|---|
| Training data | 0.65 | −10.25 | 10.45 | 11.75 | 0.90 |
| Testing data | 0.73 | −7.94 | 9.34 | 9.90 | 0.84 |