Dynamic Analysis of Composite Wind Turbine Blades as Beams: An Analytical and Numerical Study
Abstract
:1. Introduction
2. Dynamic Modelling of Composite Wind Turbine Blades
2.1. Analytical Model
2.2. Finite Element Model
3. Results
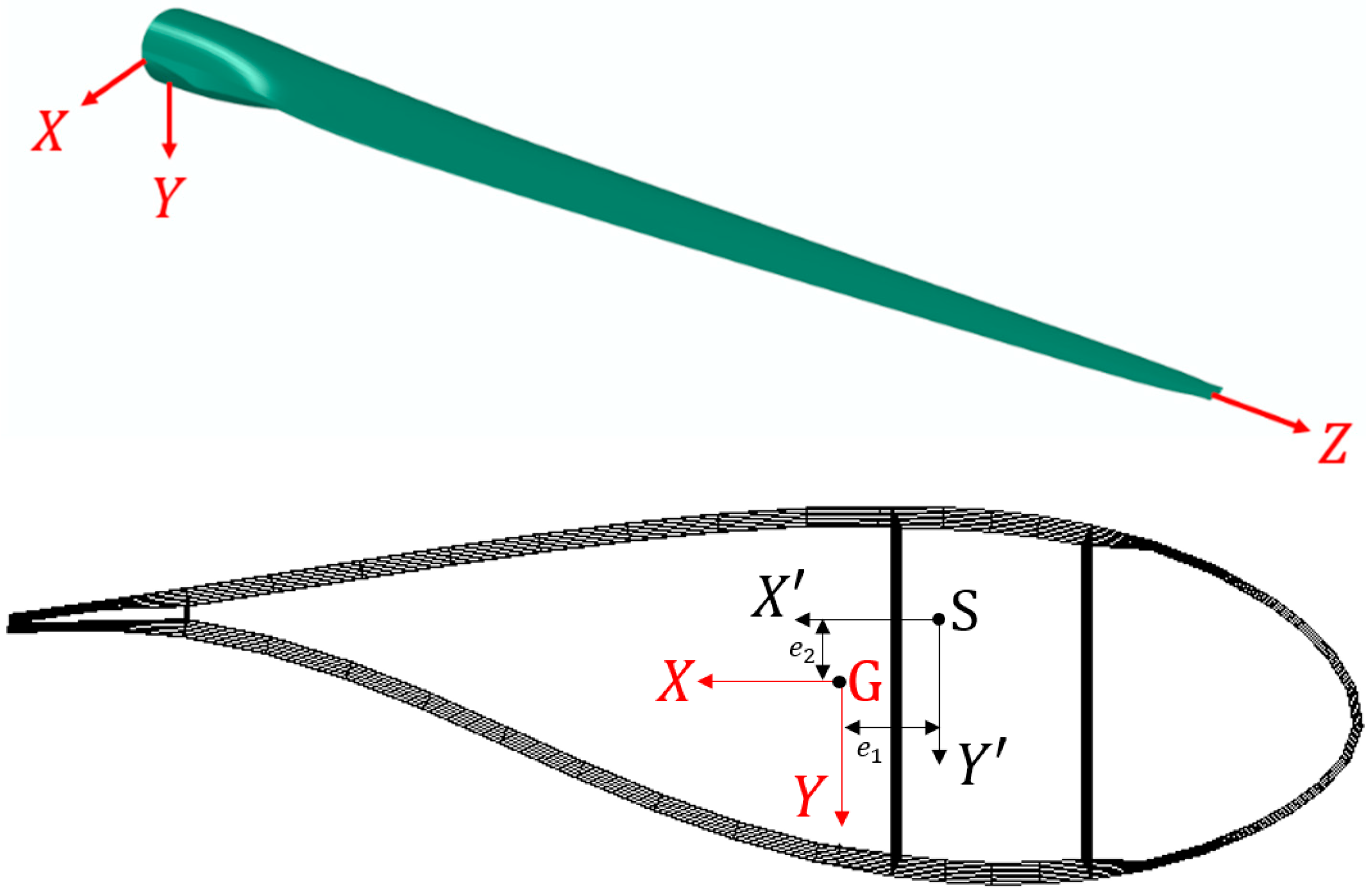
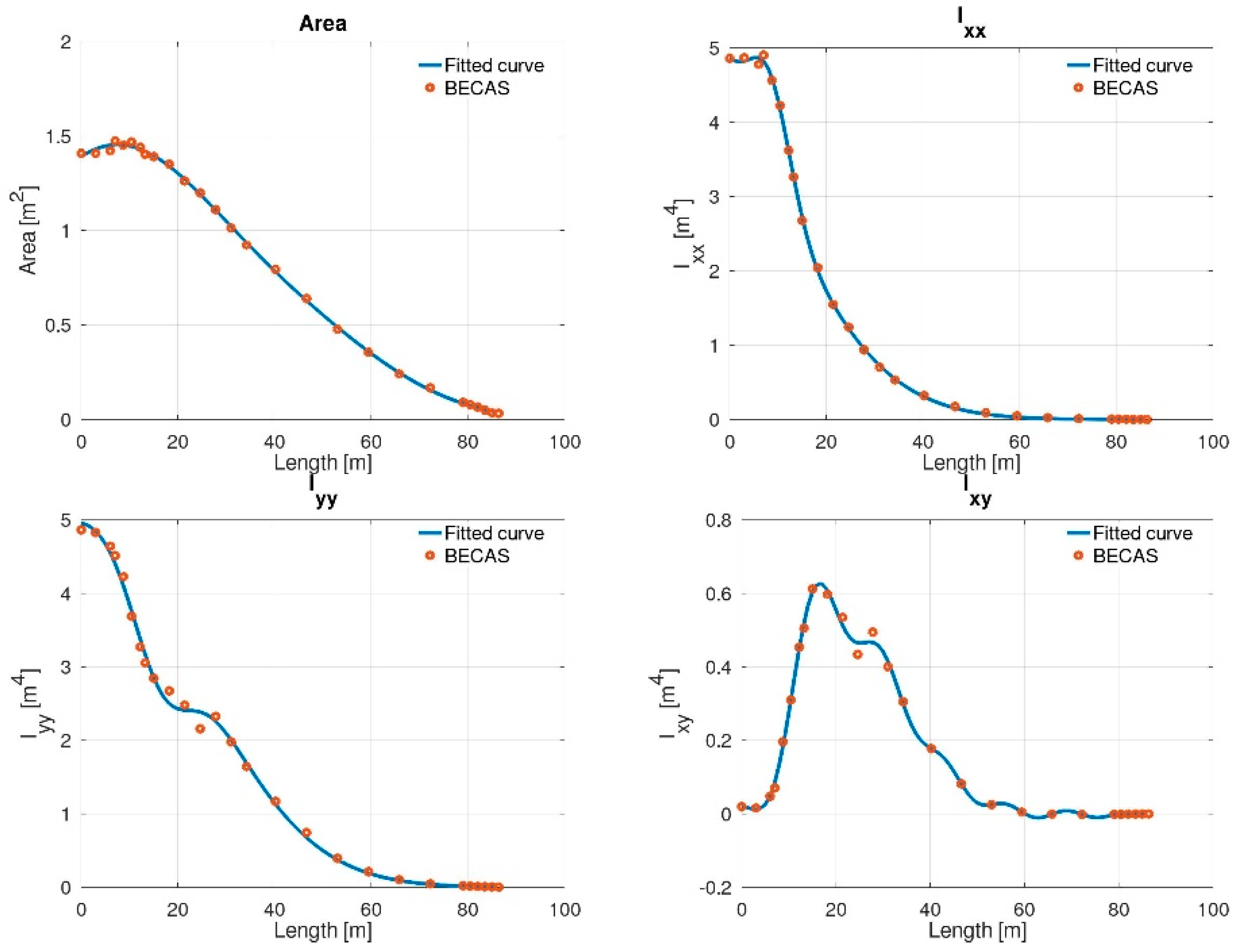
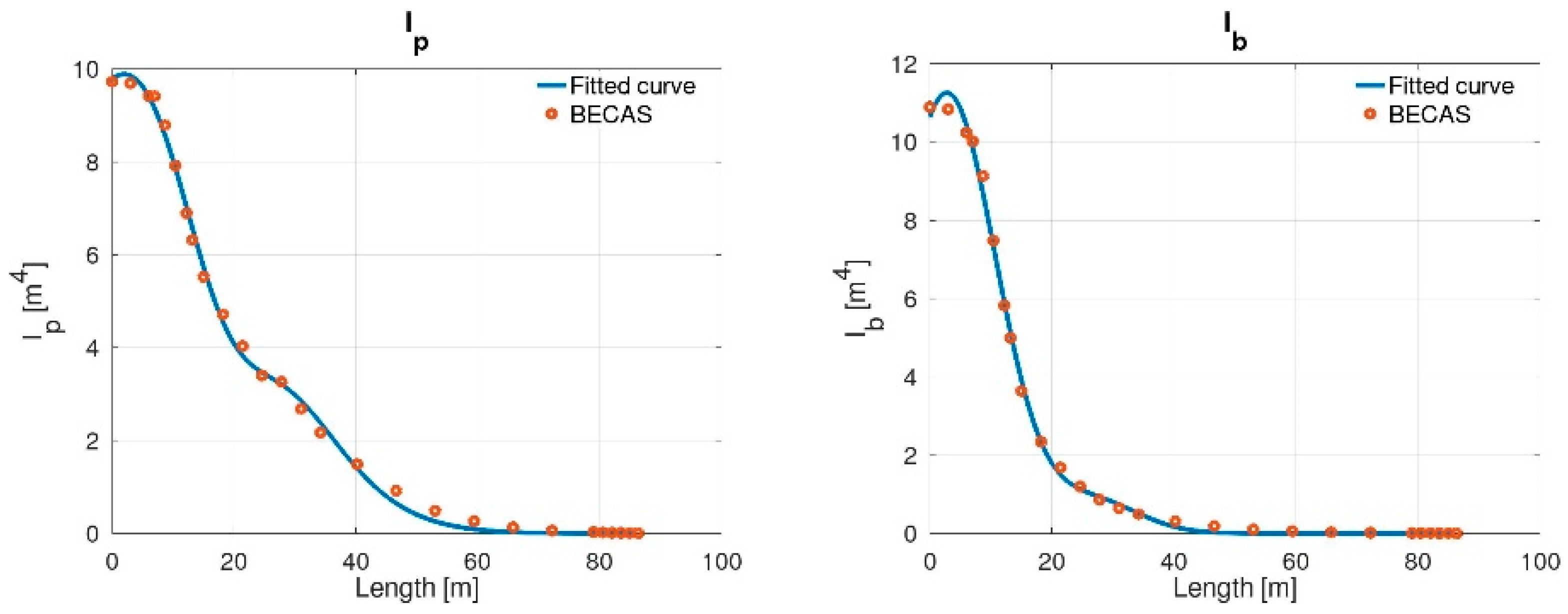
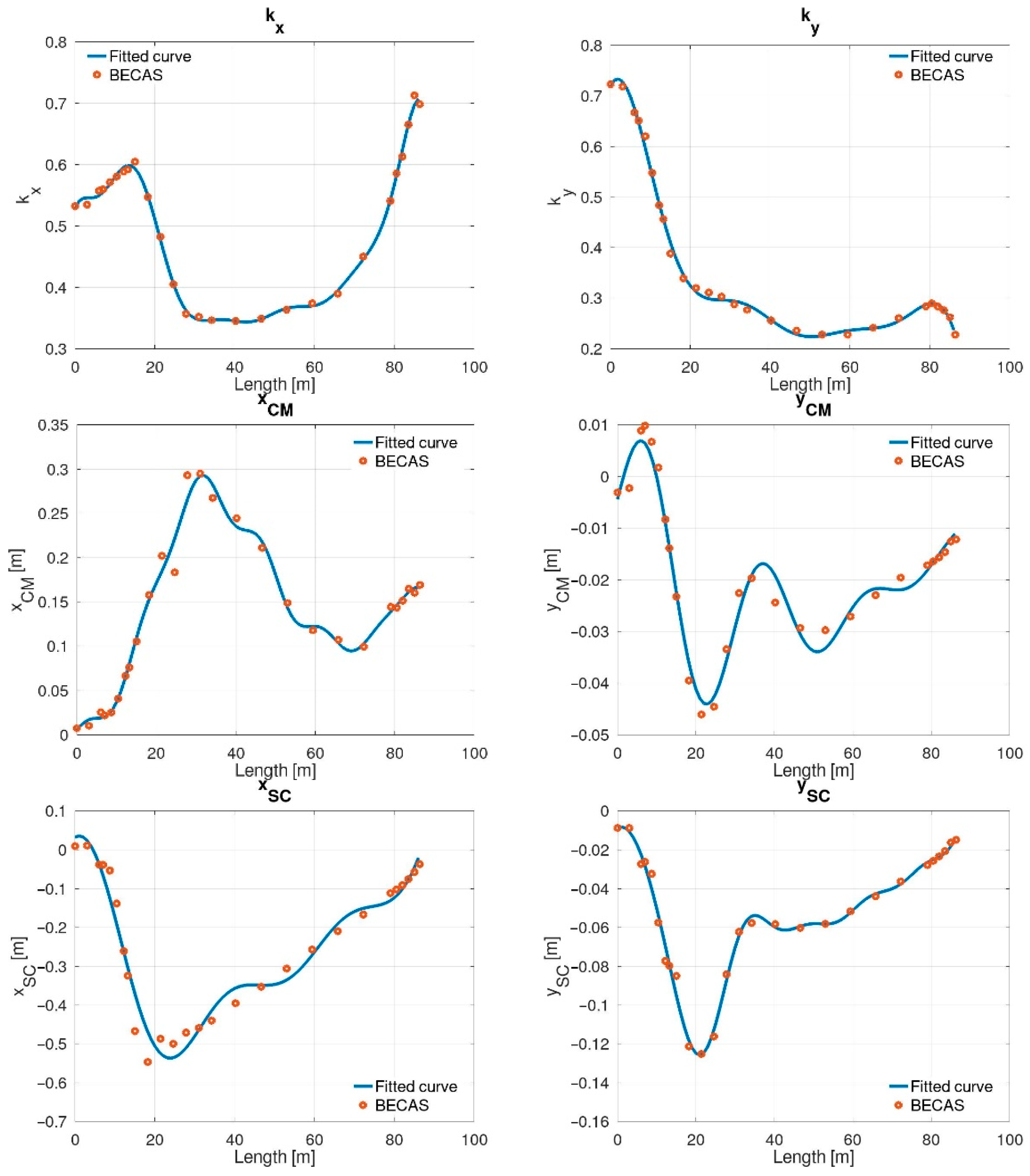
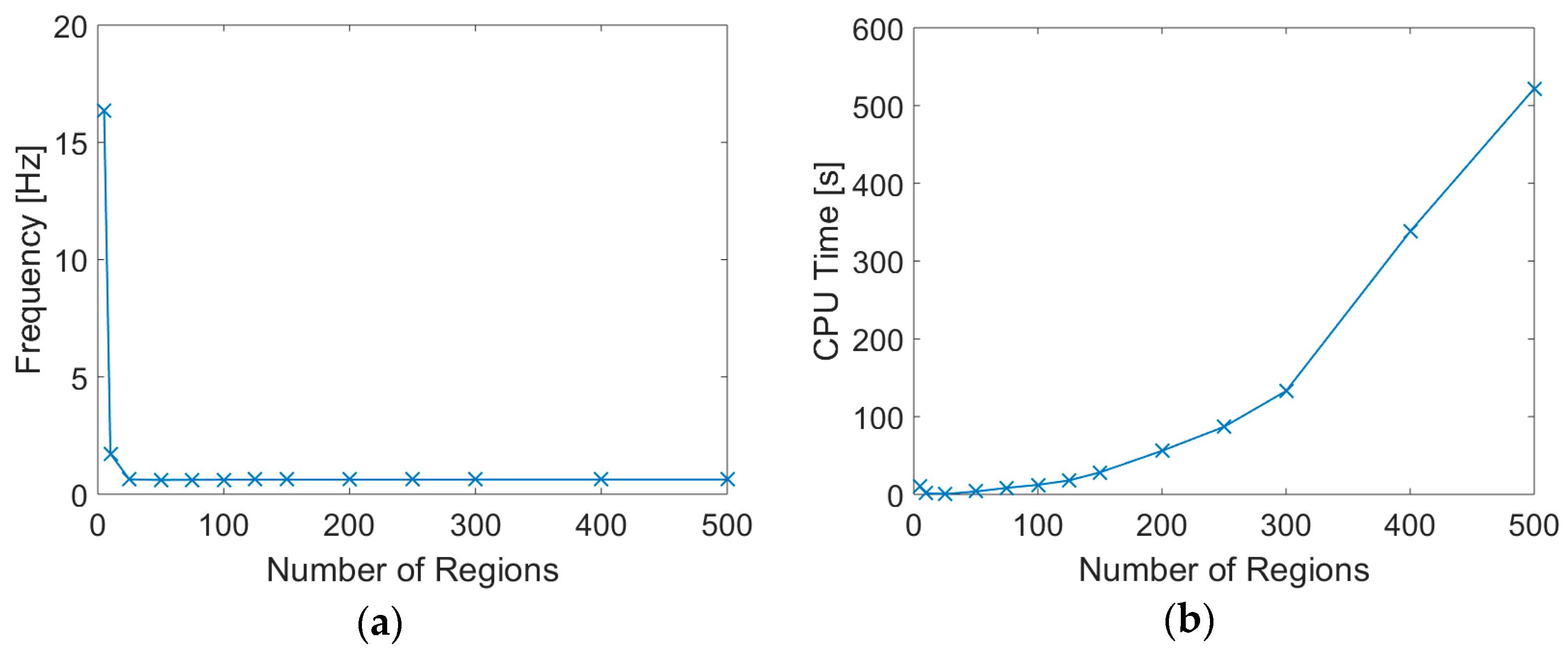
3.1. Structural Properties of the Blade
3.2. Modal Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix B
References
- Thomsen, O.T. Sandwich Materials for Wind Turbine Blades—Present and Future. J. Sandw. Struct. Mater. 2009, 11, 7–26. [Google Scholar] [CrossRef]
- Schubel, P.; Crossley, R.J. Wind Turbine Blade Design. Energies 2012, 5, 3425–3449. [Google Scholar] [CrossRef] [Green Version]
- Brøndsted, P.; Lilholt, H.; Lystrup, A. Composite materials for wind power turbine blades. Annu. Rev. Mater. Res. 2005, 35, 505–538. [Google Scholar] [CrossRef]
- Malek, S.; Raney, J.R.; A Lewis, J.; Gibson, L.J. Lightweight 3D cellular composites inspired by balsa. Bioinspir. Biomim. 2017, 12, 026014. [Google Scholar] [CrossRef] [PubMed]
- E Theotokoglou, E.; Balokas, G. Computational analysis and material selection in cross-section of a composite wind turbine blade. J. Reinf. Plast. Compos. 2014, 34, 101–115. [Google Scholar] [CrossRef]
- Kong, C.; Bang, J.; Sugiyama, Y. Structural investigation of composite wind turbine blade considering various load cases and fatigue life. Energy 2005, 30, 2101–2114. [Google Scholar] [CrossRef]
- Ozyildiz, M.; Muyan, C.; Coker, D. Strength Analysis of a Composite Turbine Blade Using Puck Failure Criteria. J. Phys. Conf. Ser. 2018, 1037, 042027. [Google Scholar] [CrossRef]
- Baumgart, A. A mathematical model for wind turbine blades. J. Sound Vib. 2002, 251, 1–12. [Google Scholar] [CrossRef]
- Bechly, M.; Clausen, P.D. Structural design of a composite wind turbine blade using finite element analysis. Comput. Struct. 1997, 63, 639–646. [Google Scholar] [CrossRef]
- Post, N.; Case, S.; Lesko, J. Modeling the variable amplitude fatigue of composite materials: A review and evaluation of the state of the art for spectrum loading. Int. J. Fatigue 2008, 30, 2064–2086. [Google Scholar] [CrossRef]
- Chang, L.; Yu, Y.; Liu, T. Aeroelastic Flutter and Sliding Mode Control of Wind Turbine Blade. Shock. Vib. 2020, 2020, 8846529. [Google Scholar] [CrossRef]
- Guo, S.; Li, Y.; Chen, W. Analysis on dynamic interaction between flexible bodies of large-sized wind turbine and its response to random wind loads. Renew. Energy 2020, 163, 123–137. [Google Scholar] [CrossRef]
- Bazilevs, Y.; Hsu, M.-C.; Kiendl, J.; Wüchner, R.; Bletzinger, K. 3D simulation of wind turbine rotors at full scale. Part II: Fluid-structure interaction modeling with composite blades. Int. J. Numer. Methods Fluids 2011, 65, 236–253. [Google Scholar] [CrossRef]
- Roul, R.; Kumar, A.; Roul, R. Fluid-Structure Interaction of Wind Turbine Blade Using Four Different Materials: Numerical Investigation. Symmetry 2020, 12, 1467. [Google Scholar] [CrossRef]
- Júnior, C.J.F.; Cardozo, A.C.P.; Júnior, V.M.; Neto, A.G. Modeling wind turbine blades by geometrically-exact beam and shell elements: A comparative approach. Eng. Struct. 2019, 180, 357–378. [Google Scholar] [CrossRef] [Green Version]
- Cardenas, D.; Escárpita, A.A.; Elizalde, H.; Aguirre, J.J.; Ahuett, H.; Marzocca, P.; Probst, O.; Ahuett-Garza, H. Numerical validation of a finite element thin-walled beam model of a composite wind turbine blade. Wind. Energy 2011, 15, 203–223. [Google Scholar] [CrossRef]
- Nabi, S.M.; Ganesan, N. Comparison of beam and plate theories for free vibrations of metal matrix composite pre-twisted blades. J. Sound Vib. 1996, 189, 149–160. [Google Scholar] [CrossRef]
- Kim, T.; Hansen, A.M.; Branner, K. Development of an anisotropic beam finite element for composite wind turbine blades in multibody system. Renew. Energy 2013, 59, 172–183. [Google Scholar] [CrossRef] [Green Version]
- Kosmatka, J.B.; Friedmann, P.P. Vibration analysis of composite turbopropellers using a nonlinear beam-type finite-element approach. AIAA J. 1989, 27, 1606–1614. [Google Scholar] [CrossRef]
- Vo, T.; Thai, H.-T.; Aydogdu, M. Free vibration of axially loaded composite beams using a four-unknown shear and normal deformation theory. Compos. Struct. 2017, 178, 406–414. [Google Scholar] [CrossRef]
- Kunz, D.L. Survey and comparison of engineering beam theories for helicopter rotor blades. J. Aircr. 1994, 31, 473–479. [Google Scholar] [CrossRef]
- Hodges, D.H. Review of composite rotor blade modeling. AIAA J. 1990, 28, 561–565. [Google Scholar] [CrossRef]
- Eipakchi, H.; Sohani, F. Analytical solution for modal analysis of Euler-Bernoulli and Timoshenko beam with an arbitrary varying cross-section. Math. Model. Eng. 2018, 4, 164–174. [Google Scholar] [CrossRef]
- Barr, S.M.; Jaworski, J.W. Optimization of tow-steered composite wind turbine blades for static aeroelastic performance. Renew. Energy 2019, 139, 859–872. [Google Scholar] [CrossRef]
- Capuzzi, M.; Pirrera, A.; Weaver, P.M. Structural design of a novel aeroelastically tailored wind turbine blade. Thin-Walled Struct. 2015, 95, 7–15. [Google Scholar] [CrossRef] [Green Version]
- Patni, M.; Minera, S.; Groh, R.M.J.; Pirrera, A.; Weaver, P.M. On the accuracy of localised 3D stress fields in tow-steered laminated composite structures. Compos. Struct. 2019, 225, 111034. [Google Scholar] [CrossRef]
- Yucel, A.; Arpaci, A.; Tüfekci, E. Coupled axial-flexural-torsional vibration of Timoshenko frames. J. Vib. Control. 2013, 20, 2366–2377. [Google Scholar] [CrossRef]
- Otero, A.D.; Ponta, F.L. Structural Analysis of Wind-Turbine Blades by a Generalized Timoshenko Beam Model. J. Sol. Energy Eng. 2010, 132, 011015. [Google Scholar] [CrossRef]
- Malcolm, D.J.; Laird, D.L. Modeling of Blades as Equivalent Beams for Aeroelastic Analysis. ASME 2003 Wind Energy Symp. 2003, 2003, 293–303. [Google Scholar] [CrossRef] [Green Version]
- Sayyad, A.S.; Ghugal, Y.M. Bending, buckling and free vibration of laminated composite and sandwich beams: A critical review of literature. Compos. Struct. 2017, 171, 486–504. [Google Scholar] [CrossRef]
- Hajianmaleki, M.; Qatu, M.S. Vibrations of straight and curved composite beams: A review. Compos. Struct. 2013, 100, 218–232. [Google Scholar] [CrossRef]
- Kant, T.; Marur, S.R.; Rao, G. Analytical solution to the dynamic analysis of laminated beams using higher order refined theory. Compos. Struct. 1997, 40, 1–9. [Google Scholar] [CrossRef]
- Savoia, M.; Tullini, N. Beam theory for strongly orthotropic materials. Int. J. Solids Struct. 1996, 33, 2459–2484. [Google Scholar] [CrossRef]
- Nath, S.K.D. A Finite Difference Solution of a Simply Supported Beam of Orthotropic Composite Materials Using Displacement Potential Formulation. Chin. J. Eng. 2014, 2014, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Z.; Chen, M.; Xie, K. NURBS-based free vibration analysis of axially functionally graded tapered Timoshenko curved beams. Appl. Math. Mech. 2020, 41, 1–20. [Google Scholar] [CrossRef]
- Eroglu, U. Large deflection analysis of planar curved beams made of Functionally Graded Materials using Variational Iterational Method. Compos. Struct. 2016, 136, 204–216. [Google Scholar] [CrossRef]
- Tufekci, E.; Eroglu, U.; Aya, S.A. Exact solution for in-plane static problems of circular beams made of functionally graded materials. Mech. Based Des. Struct. Mach. 2016, 44, 476–494. [Google Scholar] [CrossRef]
- Hadji, L.; Khelifa, Z.; El Abbes, A.B. A new higher order shear deformation model for functionally graded beams. KSCE J. Civ. Eng. 2015, 20, 1835–1841. [Google Scholar] [CrossRef]
- Eroglu, U.; Tüfekci, E. Small-Amplitude free vibrations of straight beams subjected to large displacements and rotation. Appl. Math. Model. 2018, 53, 223–241. [Google Scholar] [CrossRef]
- Bagheri, S.; Nikkar, A.; Ghaffarzadeh, H. Study of nonlinear vibration of Euler-Bernoulli beams by using analytical approximate techniques. Lat. Am. J. Solids Struct. 2014, 11, 157–168. [Google Scholar] [CrossRef] [Green Version]
- Bauchau, O.A.; Hong, C.H. Nonlinear Composite Beam Theory. J. Appl. Mech. 1988, 55, 156–163. [Google Scholar] [CrossRef] [Green Version]
- Foraboschi, P. Analytical Solution of Two-Layer Beam Taking into Account Nonlinear Interlayer Slip. J. Eng. Mech. 2009, 135, 1129–1146. [Google Scholar] [CrossRef]
- Monetto, I. Analytical solutions of three-layer beams with interlayer slip and step-wise linear interface law. Compos. Struct. 2015, 120, 543–551. [Google Scholar] [CrossRef]
- Eroglu, U.; Tüfekci, E. Some closed-form solutions for buckling of straight beams with varying cross-section by Variational Iteration Method with Generalized Lagrange Multipliers. Int. J. Eng. Appl. Sci. 2018, 10, 159–175. [Google Scholar] [CrossRef]
- Banerjee, J.R.; Williams, F.W. Coupled Bending-Torsional Dynamic Stiffness Matrix of an Axially Loaded Timoshenko Beam Element. Int. J. Solids Struct. 1994, 31, 749–762. [Google Scholar] [CrossRef]
- Freund, J.; Karakoç, A. Warping displacement of Timoshenko beam model. Int. J. Solids Struct. 2016, 92, 9–16. [Google Scholar] [CrossRef]
- Freund, J.; Karakoç, A. Shear and torsion correction factors of Timoshenko beam model for generic cross sections. Res. Eng. Struct. Mater. 2016, 2. [Google Scholar] [CrossRef]
- Malcolm, D.J.; Laird, D.L. Extraction of equivalent beam properties from blade models. Wind. Energy 2007, 10, 135–157. [Google Scholar] [CrossRef]
- Hodges, D.H.; Yu, W. A rigorous, engineer-friendly approach for modelling realistic, composite rotor blades. Wind. Energy 2007, 10, 179–193. [Google Scholar] [CrossRef]
- Yu, W.; Blair, M. GEBT: A general-purpose nonlinear analysis tool for composite beams. Compos. Struct. 2012, 94, 2677–2689. [Google Scholar] [CrossRef]
- Cesnik, C.E.S.; Hodges, D.H. VABS: A New Concept for Composite Rotor Blade Cross-Sectional Modeling. J. Am. Helicopter Soc. 1997, 42, 27–38. [Google Scholar] [CrossRef]
- Blasques, J.P.A.A.; Stolpe, M. Multi-material topology optimization of laminated composite beam cross sections. Compos. Struct. 2012, 94, 3278–3289. [Google Scholar] [CrossRef] [Green Version]
- Eaton, J.W.; Bateman, D.; Hauberg, S.; Wehbring, R. GNU Octave Version 5.2.0 Manual: A High-Level Interactive Language for Numerical Computations. 2019. Available online: https://www.gnu.org/software/octave/doc/v5.2.0/ (accessed on 23 December 2020).
- Bak, C.; Zahle, F.; Bitsche, R.; Kim, T.; Yde, A.; Henriksen, L.C.; Hansen, M.H.; Blasques, J.P.A.A.; Gaunaa, M.; Natarajan, A. The DTU 10-MW Reference Wind Turbine; Sound/Visual Production (Digital); DTU Library: Copenhagen, Denmark, 2013; Available online: https://orbit.dtu.dk/en/publications/the-dtu-10-mw-reference-wind-turbine (accessed on 23 December 2020).




| Mode | Analytical Nat. Frequency [Hz] | FEM Nat. Frequency [Hz] | Mode Type | Error [%] |
|---|---|---|---|---|
| 1 | 0.63 | 0.61 | Flapwise bending | 3.17 |
| 2 | 0.98 | 0.95 | Edgewise bending | 3.06 |
| 3 | 1.76 | 1.76 | Flapwise bending | 0 |
| 4 | 2.88 | 2.84 | Edgewise bending | 1.39 |
| 5 | 3.66 | 3.60 | Flapwise bending | 1.64 |
| 6 | 5.81 | 5.70 | Coupled flapwise-edgewise bending | 1.89 |
| 7 | 5.89 | 5.73 | Torsional | 2.72 |
| 8 | 6.28 | 6.13 | Coupled flapwise-edgewise bending | 2.39 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tüfekci, M.; Genel, Ö.E.; Tatar, A.; Tüfekci, E. Dynamic Analysis of Composite Wind Turbine Blades as Beams: An Analytical and Numerical Study. Vibration 2021, 4, 1-15. https://0-doi-org.brum.beds.ac.uk/10.3390/vibration4010001
Tüfekci M, Genel ÖE, Tatar A, Tüfekci E. Dynamic Analysis of Composite Wind Turbine Blades as Beams: An Analytical and Numerical Study. Vibration. 2021; 4(1):1-15. https://0-doi-org.brum.beds.ac.uk/10.3390/vibration4010001
Chicago/Turabian StyleTüfekci, Mertol, Ömer Ekim Genel, Ali Tatar, and Ekrem Tüfekci. 2021. "Dynamic Analysis of Composite Wind Turbine Blades as Beams: An Analytical and Numerical Study" Vibration 4, no. 1: 1-15. https://0-doi-org.brum.beds.ac.uk/10.3390/vibration4010001






