1. Introduction
In this paper, we estimate Approximate Dynamic Factor Models (ADFMs) with incomplete panel data. Data incompleteness covers, among others, two scenarios:
(i) public holidays, operational interruptions, trading suspensions, etc. cause the absence of single elements,
(ii) mixed-frequency information, e.g., monthly and quarterly indicators, results in systematically missing observations and temporal aggregation. To obtain balanced panel data without any gaps, we relate each irregular times series to an artificial, high-frequency counterpart following Stock and Watson [
1]. Depending on the relation, the artificial analogs are categorized as stock, flow and change in flow variables. In the literature, the above scenarios of data irregularities are handled in [
1,
2,
3,
4,
5,
6,
7].
The gaps in
(i) and
(ii) are permanent, as they cannot be filled by any future observations. In contrast, publication delays cause temporary lacks until the desired information is available. The numbers of (trading) days, public holidays, weeks, etc. per month change over time. Therefore, calendar irregularities, the chosen time horizon, and different publication conventions further affect the panel data pattern. In a following paper,
incomplete data refers to any collection of stock, flow and change in flow variables [
1,
4].
Factor models with cross-sectionally correlated errors are called approximate, whereas factor models without any cross-sectional correlation are called exact. In Approximate (Static) Factor Models with identically and independently distributed (iid) factors, Stock and Watson [
8] showed that unobserved factors can be consistently estimated using Principal Component Analysis (PCA). Moreover, the consistent estimation of the factors leads to a consistent forecast. Under additional regularity assumptions, these consistency results remain valid even for Approximate Factor Models with time-dependent loadings. In the past, Approximate Static Factor Models (ASFMs) were extensively discussed in the literature [
9,
10,
11,
12,
13,
14,
15].
Dynamic Factor Models (DFMs) assume time-varying factors, whose evolution over time is expressed by a Vector Autoregression Model (VAR). For Exact Dynamic Factor Models (EDFMs), Doz et al. [
16] showed that these models may be regarded as misspecified ADFMs. Under this misspecification and in the maximum likelihood framework, they proved the consistency of the estimated factors. Therefore, cross-sectional correlation of errors is often ignored in recent studies [
7,
17,
18,
19,
20]. However, cross-sectional error correlation cannot be excluded in empirical applications. The estimation of DFMs is not trivial due to the hidden factors and high-dimensional parameter space. Shumway and Stoffer [
21] and Watson and Engle [
22] elegantly solved this problem by employing an Expectation-Maximization Algorithm (EM) and the Kalman Filter (KF)-Kalman Smoother (KS). By incorporating loading restrictions, Bork [
23] further developed this estimation procedure for factor-augmented VARs. Asymptotic properties of the estimation with KS and EM for approximate dynamic factor models have recently been investigated by Barigozzi and Luciani [
24]. For EDFMs, Reis and Watson [
25] treated serial autocorrelation of errors at first. For the same model framework, Bańbura and Modugno [
20] provided a Maximum-Likelihood Estimation (MLE) using the EM and KF for incomplete data. It should be noted that Jungbacker et al. [
26] proposed a computationally more effective estimation procedure, which involves, however, a more complex time-varying state-space representation.
This paper also aims at the estimation of ADFMs for incomplete panel data in the maximum likelihood framework. It contributes to the existing estimation methodology in the following manner: First, we explicitly allow for iid cross-sectionally correlated errors similar to Jungbacker et al. [
26] but do not undertake any adaptations for an underlying DFMs. In contrast, Bańbura and Modugno [
20] consider serial error correlation instead and assume zero cross-sectional correlation. Second, our MLE does not combine an EM and the KF. We instead propose the alternating use of two EMs and employ conditional factor moments in closed form. The first EM reconstructs missing panel data for each relevant variable by using a relation between low-frequency observations and their artificial counterparts of higher frequency [
1]. The second EM performs the actual MLE based on the full data and is similar to Bork [
23] and Bańbura and Modugno [
20]. Our estimation approach for incomplete panel data deals with a more simple state-space representation of DFMs, which is invariant with respect to any chosen relationship between low-frequency observations and their artificial counterparts of higher frequency. In contrast, the approaches by Bańbura and Modugno [
20] and Jungbacker et al. [
26] usually deal with more complex underlying DFMs and require adjustments, even if a relationship between observations of low-frequency and high-frequency changes for a single variable only. There exist different types of possible relations between observations of low-frequency and high-frequency in the literature and we refer to
Section 2.2 for more details. Third, our paper addresses a model selection problem for the factor dimension and autoregressive order. For this, we propose a two-step approach and investigate its performance in a Monte Carlo study. The choice of the factor dimension is inspired by Bai and Ng [
27] and the choice of the autoregressive lag is based on the Akaike Information Criterion (AIC) adjusted for the hiddenness of the factors as in Mariano and Murasawa [
28]. It should be noted that our paper does not provide any statistical inference on ADFMs for incomplete panel data.
As an application, we develop a framework for forecasting weekly returns using the estimated factors to determine their main driving indicators of different frequencies. We also empirically construct prediction intervals for index returns taking into account uncertainties arising from the estimation of the latent factors and model parameters. Our framework is able to trace the expected behavior of the index returns back to the initial observations and their high-frequency counterparts. In the empirical study, weekly prediction intervals of the Standard & Poor’s 500 (S&P500) returns are determined for support of asset and risk management. Thus, we detect the drivers of its expected market development and define two dynamic trading strategies to profit from the gained information. For this, our prediction intervals serve as the main ingredient of the two trading strategies.
The remainder of this paper is structured as follows.
Section 2 introduces ADFMs. For known model dimensions and autoregressive order, we derive here our estimation procedure for complete and incomplete data sets.
Section 3 proposes a selection procedure for the optimal factor dimension and autoregressive order.
Section 4 summarizes the results of a Monte Carlo study, where we examine the performance of our estimation method and compare it with the benchmark of Bańbura and Modugno [
20] across different sample sizes, factor dimensions, autoregressive orders and proportions of missing data. In
Section 5, we present our forecasting framework for a univariate return series using the estimated factors in an autoregressive setup. We also discuss the construction of empirical prediction intervals and use them to specify our two dynamic trading strategies.
Section 6 contains our empirical study and
Section 7 concludes. Finally note that all computations have been done in Matlab. Our Matlab codes and data are available as supplementary materials.
3. Model Selection for Unknown Dimensions and Autoregressive Orders
The ADFM (
1)–(2) for complete panel data and its estimation require knowledge of the factor dimension
K and autoregressive order
p. In empirical analyses, both must be determined. For this, we propose a two-step model selection method. For static factor models, Bai and Ng [
27] thoroughly investigated the selection of the optimal factor dimension
and introduced several common model selection procedures which were reused in, e.g., [
23,
25,
37,
38,
39,
40]. In this paper, we deploy the following modification of Bai and Ng [
27]:
where
denotes an upper limit for factor dimension
K and
covers the estimated residual variance of Model (
1) ignoring any autoregressive factor dynamics. Bai and Ng [
27] (p. 199, Theorem 2) showed that panel criteria in the form of (
16) consistently estimate the true factor dimension, if their assumptions A-D are satisfied, PCA is used for factor estimation and the penalty function obeys for
:
The penalty function
in (17) coincides with the 2
nd panel criterion in Bai and Ng [
27] (p. 201) except for
. For empirical studies, Bai and Ng [
27] suggest
as scaling of the penalty in (17) with
as minimum of (
18) for fixed
regarding
and
. Therefore, their penalty depends on the variance that remains, although the upper limit of the factor dimension was reached. If we use
, the setting
for all
is a trivial solution for SFM (
1). Furthermore, it yields
and thus, overrides the penalty. For any
, the choice of
affects
and hence, the penalty in (17). To avoid any undesirable degree of freedom arising from the choice of
, we therefore propose
for a non-negative multiplier
m and
denoting the empirical residual variance, if Model (
1) is estimated using the PPCA of Tipping and Bishop [
29].
Irrespective of whether PCA or PPCA is deployed, the error variance decreases, when the factor dimension increases. Thus,
holds. The non-negativity of
m causes that
in (
19) and the penalty in (17) are non-negative. This guarantees that large
K is punished. Unlike
, the strictness of
depends on
m instead of
. Hence, the strictness of the penalty and upper limit of the factor dimension are separated from each other. The panel criteria of Bai and Ng [
27] are asymptotically equivalent as
, but may differently behave for finite samples [
25,
27]. For a better understanding of how
m influences the penalty function, we exemplarily consider various multipliers
in
Section 4. Finally, we answer why
instead of
or any alternative is used. For
, the term
in (
19) coincides with the negative slope of the straight line through the points
and
, i.e., we linearize the decay in
over the interval
and then, take its absolute value for penalty adjustment. In other words, for
the term
in (
19) describes the absolute value of the decay in
per unit in dimension. In the empirical study of
Section 6, we also use
, since this provides a decent dimension reduction, but it is not such restrictive that changes in the economy are ignored. In total, neither our proposal of
nor the original version in Bai and Ng [
27] affects the asymptotic behavior of the function
such that
in (17) consistently estimates the true dimension. Please note that we neglect the factor dynamics and treat DFMs as SFMs in this step.
In a next step, our model selection approach derives the optimal autoregressive order
for any fixed
using AIC. As factors are unobservable, we replace the log-likelihood
of Model (2) by the conditional expectation
in the usual AIC. Furthermore, Equation (2) can be rewritten as a stationary VAR(1) process
, whose covariance matrix
has a similar representation to (
3). When we run the EM for a fixed
K and a prespecified range of the autoregressive orders, the optimal
satisfies
with
as upper lag length to be tested [
41]. For
, we use the maximum likelihood estimates of matrices
M,
D and
. Like
, the criterion
truncates the infinite series for
. Alternatively,
can explicitly be computed, see Lemma A.2.7 in [
41]. Further, the vector
comprises the first
p observations of
X. For
, Model (
1)–(2) is regarded as SFM. In particular, the objective function of the selection criterion (
20) for SFMs is
. Thereafter, we choose an optimal factor dimension
by using (17) and ignoring the autoregressive structure in (2). An algorithm for the overall model selection procedure is provided in Algorithm A1.
4. Monte Carlo Simulation
In this section, we analyze the two-step estimation method for ADFM (
1)–(2) for complete and incomplete panel data within a Monte Carlo (MC) simulation study. Among other things, we address the following questions:
(i) does the data sample size (i.e., length and number of time series) affect the estimation quality?
(ii) to what extent does data incompleteness deteriorate the estimation quality?
(iii) do the underlying panel data types (i.e., stock, flow and change in flow variables) matter?
(iv) does our model selection procedure detect the true factor dimension and lag order, even for
and
?
(v) how does our two-step approach perform compared to the estimation method of Bańbura and Modugno [
20]?
(vi) are factor means and covariance matrices more accurate for the closed-form factor distributions (
4) instead of the standard KF and KS?
Before we answer the previous questions, we explain how our random samples are generated. For
with
, let
stand for the uniform distribution on the interval
and let
be a diagonal matrix with elements
. For fixed data and factor dimensions
, let
and
represent arbitrary orthonormal matrices. Then, we receive the parameters of the ADFM (
1)–(2) in the following manner:
The above ADFMs have cross-sectionally, but not serially correlated shocks. To prevent us from implicitly constructing SFMs with eigenvalues of
close to zero, the eigenvalues of
lie within the range
. The division by
p balances the sum of all eigenvalues regarding the autoregressive order
p. For simplicity reasons, we consider matrices
with positive eigenvalues. However, this assumption, the restriction to eigenvalues in the range
and the division by
p can be skipped. If matrices
meet the covariance-stationarity conditions, we simulate factor samples
and panel data
using Equations (
1) and (2). Otherwise, all matrices
are drawn again until the covariance-stationarity conditions are met. Similarly, we only choose matrices
W of full column rank
K.
So far, we have complete panel data. Let be the ratio of gaps arising from missing observations and low-frequency time series, respectively. To achieve incomplete data we remove elements from each time series. For stock variables, we randomly delete values to end up with irregularly scattered gaps. At this stage, flow and change in flow variables serve as low-frequency information, which is supposed to have an ordered pattern of gaps. Therefore, an observation is made at time with and . Please note that an observed (change in) flow variable is a linear combination of high-frequency data.
In
Table A1,
Table A2,
Table A3,
Table A4,
Table A5,
Table A6,
Table A7,
Table A8 and
Table A9 the same
applies to all univariate columns in
X such that gaps of (change in) flow variables occur at the same time. If the panel data contains a single point in time without any observation, neither our closed-form solution nor the standard KF provide factor estimates. To avoid such scenarios, i.e., empty rows of the observed panel data
, each panel data in the second (third) column of
Table A1,
Table A2,
Table A3 and
Table A4 comprises
times series modeled as stock variable and
time series treated as (change in) flow variable. To ensure at least one observation per row of
, we check each panel data sample, before we proceed. If there is a zero row in
, we reapply our missing data routine based on the complete data
X.
Note that estimated factors are unique except for an invertible, linear transformation. For a proper quality assessment across diverse estimation methods, we must take this ambiguity into account as in [
4,
8,
16,
20,
42]. Let
F and
be the original and estimated factors, respectively. If the estimation methodology works, it holds:
. The solution
justifies the trace
of Stock and Watson [
8] defined by
The trace lies in with lower (upper) limits indicating a poorly (perfectly) estimated factor span.
Eventually, we choose for the termination criteria:
and
, i.e., we have the same
and
as in the empirical application of
Section 6. Furthermore, we use constant interpolation for incomplete panel data, when we initialize the set
. In
Table A1,
Table A2 and
Table A3, we consider for known factor dimension
K and lag order
p, if the standard KF and KS should be used for estimating factor means
and covariance matrices
instead of the closed-form distributions (
4). To be more precise,
Table A1 shows trace
means (each based on 500 MC simulations) when we combine the EM updates (
6)–(
10) with the standard KF and KS. For the same MC paths,
Table A2 provides trace
means, when we use Equation (
4) instead.
A comparison of
Table A1 and
Table A2 shows: First, both estimation methods offer large trace
values regardless the data type, i.e., the mix of stock, flow and change in flow variables does not affect the trace
. Second, the larger the percentage of gaps the worse the trace
. Third, the trace
increases for large samples (i.e., more or longer time series). Fourth, for larger
K and
p the trace
, ceteris paribus, deteriorates. Fifth, our estimation method based on closed-form factor moments appears more robust than the Kalman approach. For instance, in
Table A1 for
and 40% of missing data the trace
is NaN, which is an abbreviation for
Not a Number, i.e., there was at least one MC path the Kalman approach could not estimate. By contrast, the respective trace
in
Table A2 is 0.94 and so, all 500 MC paths were estimated without any problems. The means in
Table A1 and
Table A2 are pretty close, this is why
Table A3 divides the means in
Table A2 by their counterparts in
Table A1. Hence, ratios larger than one indicate that our estimation method outperforms the Kalman approach, while ratios less than one do the opposite. Since all ratios in
Table A3 are at least one, our method is superior.
For the sake of simplicity, we proceed with stock variables only, i.e., we treat all incomplete time series as stock variables in
Table A4, which compares the single-step estimation method from Bańbura and Modugno [
20] (abbreviated by BM) with our closed-form factor moments, two-step approach (abbreviated by CFM). At first glance, one step less speaks in favor of the single-step ansatz. However, one step less comes with a price, i.e., its state-space representation. Whenever a switch between data types occurs, the state-space representation of the overall model in [
20] calls for adjustments. Furthermore, the inclusion of mixed-frequency information requires a regular scheme as for months and quarters. E.g., for weeks and months with an irregular pattern, the state-space representation in [
20] becomes tremendous or calls for a recursive implementation of the temporal aggregation (
11) as in Bańbura and Rünstler [
18]. By contrast, our two-step approach permits any data type and calendar structure through the linear relation (
11) and leaves the overall model untouched. This is easy and reduces the risk of mistakes. Moreover, the estimation of factor moments in closed form is computationally cheaper than a KF-KS-based estimation. Because of this, our approach can be more than 5-times faster than the corresponding procedure in [
20]. According to
Table A4, our approach is 5.5 times faster than its BM counterpart for complete panel data with
and
. For missing panel data in the range of [10%, 40%], ceteris paribus, our closed-form approach is 3.3–3.7 times faster than the KF-KS approach in [
20].
Bańbura and Modugno [
20] first derived their estimation method for EDFMs. Thereafter, they followed the argumentation in Doz et al. [
16] to admit weakly cross-sectionally correlated shocks
. Since Doz et al. [
16] provided asymptotic results, we would like to assess how the method of [
20] performs for finite samples with cross-sectionally correlated shocks. With a view to
Table A4 we conclude: First, the general facts remain valid, i.e., for more missing data the trace
means worsen. Similarly, for larger
K and
p, the trace
means, ceteris paribus, deteriorate. By contrast, for larger panel data the trace
means improve. Second, for simple factor dynamics, i.e., small
K and
p, or sufficiently large panel data, cross-sectional correlation of the idiosyncratic shocks does not matter, if the ratio of missing data is low. This is in line with the argumentation in [
16,
20]. However, for small panel data, e.g.,
and
, with 40% gaps and factor dimensions
cross-sectional error correlation matters. This is why our two-step estimation method outperforms the one-step approach of [
20] in such scenarios.
Next, we focus on our two-step model selection procedure. Here, we address the impact of the multiplier
m in Equation (
19) on the estimated factor dimension. For
Table A5,
Table A6,
Table A7,
Table A8 and
Table A9, we set
in Algorithm A1. Since
Table A5 and
Table A6 treat ADFMs with
and
, the upper limits
and
are set. In
Table A7,
Table A8 and
Table A9, we have trace
means, estimated factor dimension and lag orders of ADFMs with
and
. Therefore, we specify
and
in these cases. For efficiency reasons, the criterion (17) tests factor dimensions in the range
instead of the overall range
. A comparison of
Table A5 and
Table A6 shows that multipliers
and
detect the true factor dimension and hence, support that the true lag order is identified. In doing so, larger panel data increases the estimation quality, i.e., trace
means increase, while estimated factor dimensions and lag orders converge to the true ones. By contrast, more gaps deteriorate the results.
For a better understanding of the meaning of
m, we have a look at ADFMs with
in
Table A7,
Table A8 and
Table A9 and conclude: First, multiplier
is too strict, since it provides 12 for the estimated factor dimension, which is the lower limit of our tests. Fortunately, the criterion (
20) for estimating the autoregressive order tends to the true one, even though the estimated factor dimension is too small. Second, for
the slope argumentation after Equation (17) yields
, which properly estimates the true factor dimension for all scenarios in
Table A8. As a consequence, the trace
means in
Table A8 clearly dominate their analogs in
Table A7. Third, we consider
in
Table A9 for some additional sensitivity analyses. If 40% of the panel data is missing,
overshoots the true factor dimension, which is reflected in slightly smaller trace
means than in
Table A8. For lower ratios of missing observations, our two-step estimation method with
also works well, i.e., it delivers large trace
means and the estimated factor dimensions and lag orders tend towards the true values. With
Table A7,
Table A8 and
Table A9 in mind, we recommend for empirical studies to have
m rather too small than too big.
5. Modeling Index Returns
The preceding sections show how to condense information in large, incomplete panel data in the form of factors with known distributions. In the past, factor models were popular for nowcasting and forecasting of Gross Domestic Products (GDPs) and the construction of composite indicators [
4,
12,
14,
15,
17,
18,
28,
43].
Now, we show how estimated factors may support investing and risk management. Let
be the returns, e.g., of the S&P 500 price index. The panel data
, delivers additional information on the financial market, related indicators, the real economy, etc. Like Bai and Ng [
44], we construct interval estimates instead of point estimates for the future returns. However, our prediction intervals are empirically derived, since we cannot take their asymptotic ones in the presence of missing observations.
Uncertainties arising from the estimation of factors and model parameters shall affect the interval size. Additionally, we intend to disclose the drivers of the expected returns supporting plausibility assessments. As any problem resulting from incomplete data was solved before, we assume coincident updating frequencies of factors and returns. Let the return dynamics satisfy an Autoregressive Extended Model (ARX)
with
and
. The VAR
in (2) requires the latter constraint, as otherwise for
the ARX parameters are not identifiable. Thus, for sample length
,
and
, we consider the following regression model
where
and
are constants and
denotes the factor at time
t in Model (
1)–(2). Then, we collect the regression parameters of (
21) in the joint vector
.
The OLS estimate
of
is asymptotically normal with mean
and covariance matrix
depending on
and the design matrix resulting from (
21) [
30] (p. 215) and its parameters can be consistently estimated. Subsequently, we assess the uncertainty caused by the estimation of
. For this, the asymptotic distribution with consistently estimated parameters is essential, since an unknown parameter vector
is randomly drawn from it [
41] (Algorithm 4.2.1) for the construction of prediction intervals of
. The factors are unique up to an invertible, linear transformation
as shown by
The unobservable factor
must be extracted from
X which may be distorted by estimation errors. To cover the inherent uncertainty, we apply (
4) and obtain for (
21)
with
as square root matrix of
and
for all
. The vector
and error
are independent for all
.
When we empirically construct prediction intervals for
, uncertainties due to factor and ARX parameter estimation shall drive the interval width. To implement this in a Monte Carlo approach, let
C be the number of simulated
using Equation (
22). After Algorithm A2 determined the factor distribution (
4), for each trajectory
a random sample
enters the OLS estimate of
such that the distribution of
depends on
c. Therefore, we capture both estimation risks despite their nonlinear relation.
The orders
are selected using AIC based on the estimated factor means. To take the factor hiddenness into account, we approximate the factor variance by the distortion of
. Then, let the periods and frequencies of
and
be coincident. Besides
, this prevents from a run-up period before
offering additional information in terms of
. For chosen
from Model (
1)–(2), the optimal pair
can be computed using an adjusted AIC. Here we refer to Ramsauer [
41] for more details. Finally, a prediction interval for
can be generated in a Monte-Carlo framework by drawing
from the asymptotic distribution of
, the factors
from (
4) and using (
21).
The mean and covariance matrix of the OLS estimate
are functions of the factors such that the asymptotic distribution of
in Ramsauer [
41] (Algorithm 4.2.1) depends on
. If we neglect the
impact on the mean and covariance matrix of
for a moment, e.g., in case of a sufficiently long sample and little varying factors, we may decompose the forecasted returns as follows
with
and
for all
.
If neither the returns
nor any transformation of
are part of the panel data
X, the distinction between the four pillars in (
23) is more precise. In Equation (
23), there are four drivers of
.
AR Nature covers the autoregressive return behavior, whereas
Factor impact maps the information extracted from the panel data
X. Therefore, both affect the direction of
. By contrast, the latter treat estimation uncertainties. Therefore,
Factor Risk reveals the distortion caused by
and hence, indicates the variation inherent in the estimated factors. This is of particular importance for data sets of small size or with many gaps. Finally,
AR Risk incorporates deviations from the expected trend, since it adds the deviation of the ARX residuals.
The four drivers in (
23) support the detection of model inadequacies and the construction of extensions, since each driver can be treated separately or as part of a group. For instance, a comparison of the pillars
AR Nature and
Factor Impact shows, whether a market has an own behavior such as a trend and seasonalities or is triggered by exogenous events. Next, we trace back the total contribution of
Factor Impact to its single constituents such that the influence of a single signal may be analyzed. For this purpose, we store the single constituents of
Factor Risk, sort all time series in line with the ascendingly ordered returns and then, derive prediction intervals for both (i.e., returns and their single drivers). This procedure prevents us from discrepancies due to data aggregation and ensures consistent expectations of
and its drivers.
All in all, the presented approach for modeling the 1-step ahead returns of a financial index offers several advantages for asset and risk management applications: First, it admits the treatment of incomplete data. E.g., if macroeconomic data, flows, technical findings and valuation results are included, data and calendar irregularities cannot be neglected. Second, for each low-frequency signal a high-frequency counterpart is constructed (nowcasting) to identify, e.g., structural changes in the real economy at an early stage. Third, the ARX Model (
21) links the empirical behavior of an asset class with exogenous information to provide interval and point estimations. Besides the expected return trend, the derived prediction intervals measure estimation uncertainties. In addition, investors take a great interest in the market drivers, as those indicate its sustainability. For instance, if increased inflows caused by an extremely loose monetary policy trigger a stock market rally and an asset manager is aware of this, he cares more about an unexpected change in monetary policy than poor macroeconomic figures. As soon as the drivers are known, alternative hedging strategies can be developed. In our example, fixed income derivatives might also serve for hedging purposes instead of equity derivatives.
The prediction intervals cover the trend and uncertainty of the forecasted returns. Therefore, we propose some simple and risk-adjusted dynamic trading strategies incorporating them. For simplicity, our investment strategies are restricted to a single financial market and a bank account. For
, let
be the ratio of the total wealth invested with an expected return
over the period
. The remaining wealth
is deposited on the bank account for an interest rate
. Let
and
be lower and upper limits, respectively, of the
-prediction interval for the same period. Then, a trading strategy based on the prediction intervals is given by
If the prediction interval is centered around zero, except for lateral movements, no clear trend is indicated. Regardless of the interval width, Strategy (
24) takes a neutral allocation (i.e., 50% market exposure and 50% bank account deposit). As soon as the prediction interval is shifted to the positive (negative) half-plane, the market exposure increases up to 100% (decreases down to 0%). Depending on the interval width, the same shift size results in different proportions
, i.e., for large intervals with a high degree of uncertainty, a shift to the positive (negative) half-plane causes a smaller increase (decrease) in
compared to tight ones indicating low uncertainty. Besides temporary uncertainties, the prediction level
affects the interval size and so, the market exposure
. Therefore, we have: The higher the level
, the lower and rarer are deviations from the neutral allocation.
Strategy (
24) is not always appropriate for applications in practice due to investor-specific risk preferences and restrictions. For all
, Strategy (
24) can therefore be accordingly adjusted
with
from Equation (
24).
with
are the lower and upper limits, respectively, of the market exposure which may not be exceeded.
reflects the risk appetite of the investor.
The max-min-construction in Equation (
25) defines a piecewise linear function bounded below (above) by
(
). Within these limits the term
drives the market exposure
. For
changes in
are scaled-up (i.e., increased amplitude of
versus
). Furthermore, the limits are reached more likely. This is why,
refers to a risk-affine investor. By contrast,
reduces the amplitude of
and thus, of
. Therefore,
covers a risk-averse attitude. As an example, we choose
and
which implies:
such that short sales are possible.
6. Empirical Application
This section applies the developed framework to the S&P500 price index. Diverse publication conventions and delays require us to declare, when we run our updates. From a business perspective the period between the end of trading on Friday and its restart on Monday is reasonable. On the one hand, there is plenty of time after the day-to-day business is done. On the other hand, there is enough time left to prepare changes in existing asset allocations triggered by the gained information, e.g., the weekly prediction intervals, until the stock exchange reopens. In this example, we have a weekly horizon such that the obtained prediction intervals cover the expected S&P500 log-return until next Friday. For the convenience of the reader, we summarize the vintage data of weekly, monthly or quarterly frequencies in
Appendix E. Here, we mention some characteristics of the raw information, explain the preprocessing of inputs and state the data types (stock, flow or change in flow variable) of the transformed time series. Some inputs are related with each other, therefore, we group them into US Treasuries, US Corporates, US LIBOR, Foreign Exchange Rates and Gold, Demand, Supply, and Inflation, before we analyze the drivers of the predicted log-returns. This improves the clarity of our results, in particular, when we illustrate them.
The overall sample ranges from 15 January 1999 to 5 February 2016 and is updated weekly. We set a rolling window of 364 weeks, i.e., seven years, such that the period from 15 January 1999 until 30 December 2005 constitutes our in-sample period. Based on this, we construct the first prediction interval for the S&P500 log-return from 30 December 2005 until 6 January 2006. Then, we shift the rolling window by one week and repeat all steps (incl. model selection and estimation) to derive the second prediction interval. Finally, we proceed until the sample end is reached. As the length of the rolling window is kept, the estimated contributions remain comparable, when time goes by. Furthermore, our prediction intervals react on structural changes, e.g., crises, more quickly compared to an increasing in-sample period. As upper limits of the factor dimension, factor lags and return lags we choose and , respectively. For the termination criteria, we have: and . To avoid any bias caused by simulation each prediction interval relies on trajectories.
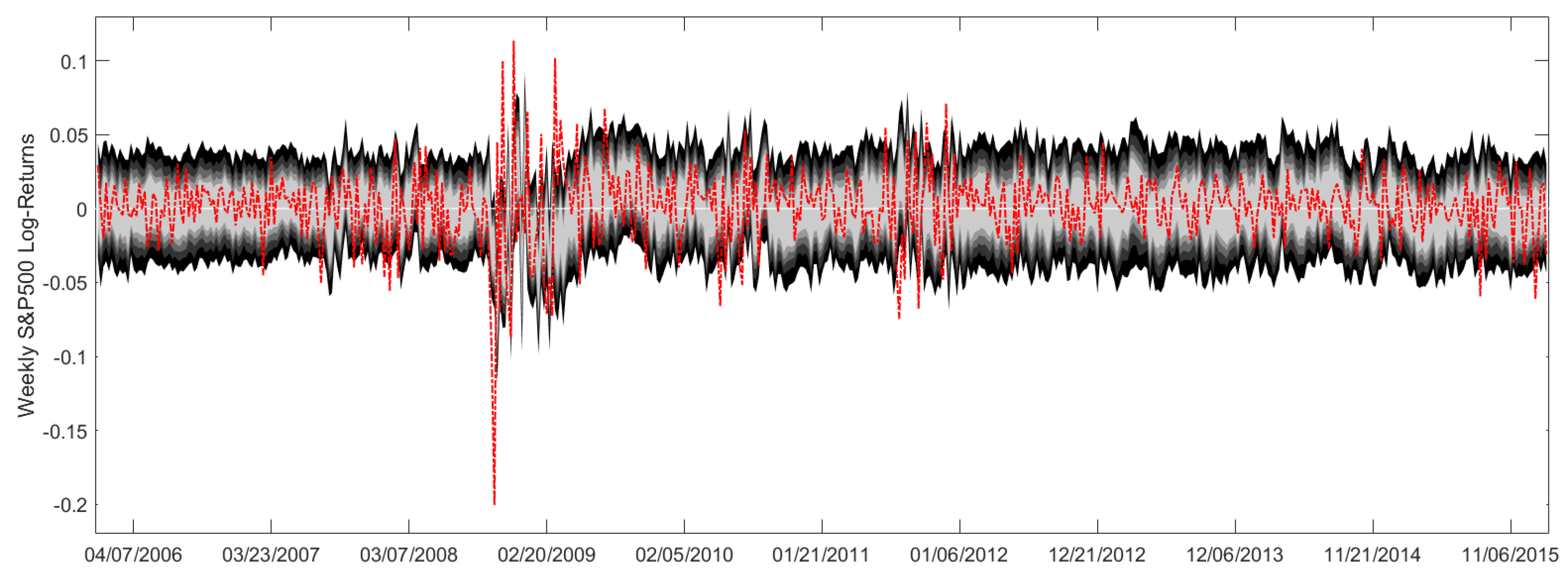
For the above settings, we receive the prediction intervals in
Figure A1 for weekly S&P500 log-returns. To be precise, the light gray area reveals the 50%-prediction intervals, while the black areas specify the 90%-prediction intervals. Here, each new, slightly darker area corresponds to prediction levels increased by 10%. In addition, the red line shows the afterwards realized S&P500 log-returns. Please note that the prediction intervals cover the S&P500 returns quite well, as there is a moderate number of interval outliers. However, during the financial crisis in 2008/2009 we have a cluster of interval outliers, which calls for further analyses. Perhaps, the inclusion of regime-switching concepts may remedy this circumstance.
As supplement to
Figure A1,
Figure A2 breaks the means of the predicted S&P500 log-returns down into the contributions of our panel data groups. In contrast to
Figure A1, where Factor and AR Risks widened the prediction intervals, both do not matter in
Figure A2. This makes sense, as we average the predicted returns, whose Factor and AR Risks are assumed to have zero mean. Dark and light blue colored areas detect how financial data affects our return predictions. In particular, during the financial crisis in 2008/2009 and in the years 2010–2012, when the United States (US) Federal Reserve intervened on capital markets in the form of its quantitative easing programs, financial aspects mainly drove our return predictions. Since the year 2012, the decomposition is more scattered and changes quite often, i.e., macroeconomic and financial events matter.
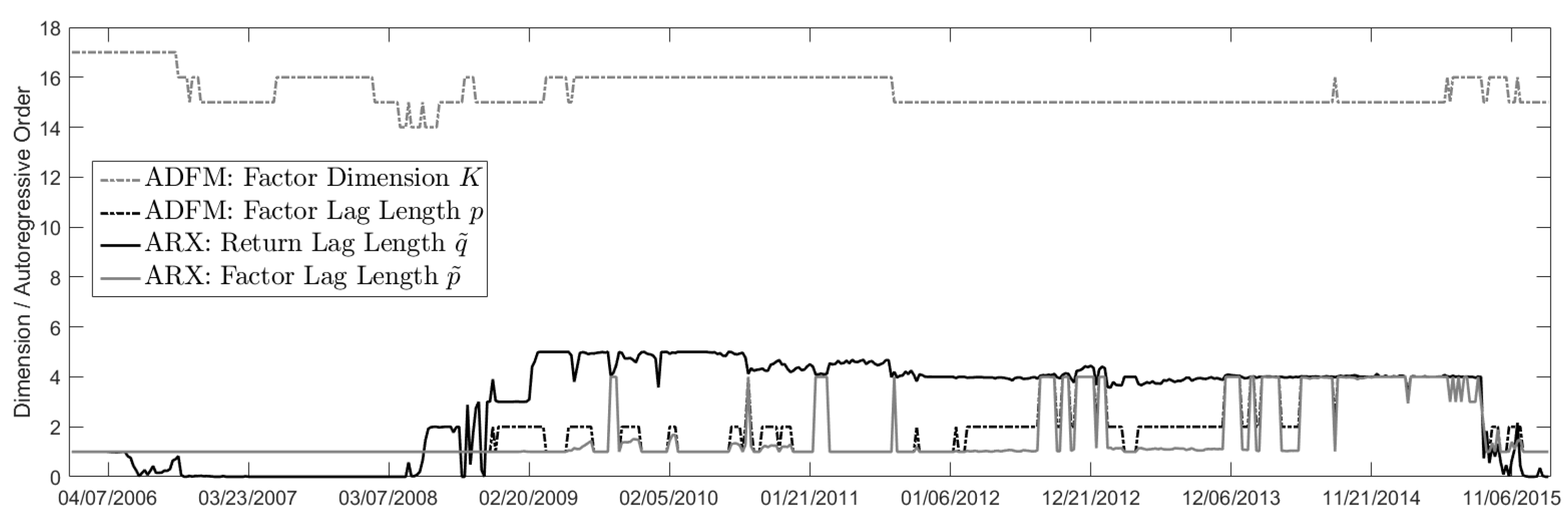
Figure A3 also supports the hypothesis that exogenous information increasingly affected the S&P500 returns in recent years. Although the factor dimension stayed within the range [15, 16] and we have for the autoregressive return order
, from mid-2013 until mid-2015 the factor lags
p and
increased. This indicates a more complex ADFM and ARX modeling.
Next, we focus on the financial characteristics of the presented approach. Therefore, we verify whether the Trading Strategies (
24) and (
25) may benefit from the proper mapping of the prediction intervals. Here, we abbreviate Trading Strategy (
24) based on the 50%-prediction intervals by Prediction Level PL 50, while (PL) 60 is its analog using the 60%-prediction intervals, etc. For simplicity, our cash account does not offer any interest rate, i.e.,
for all times
and transaction costs are neglected. In total,
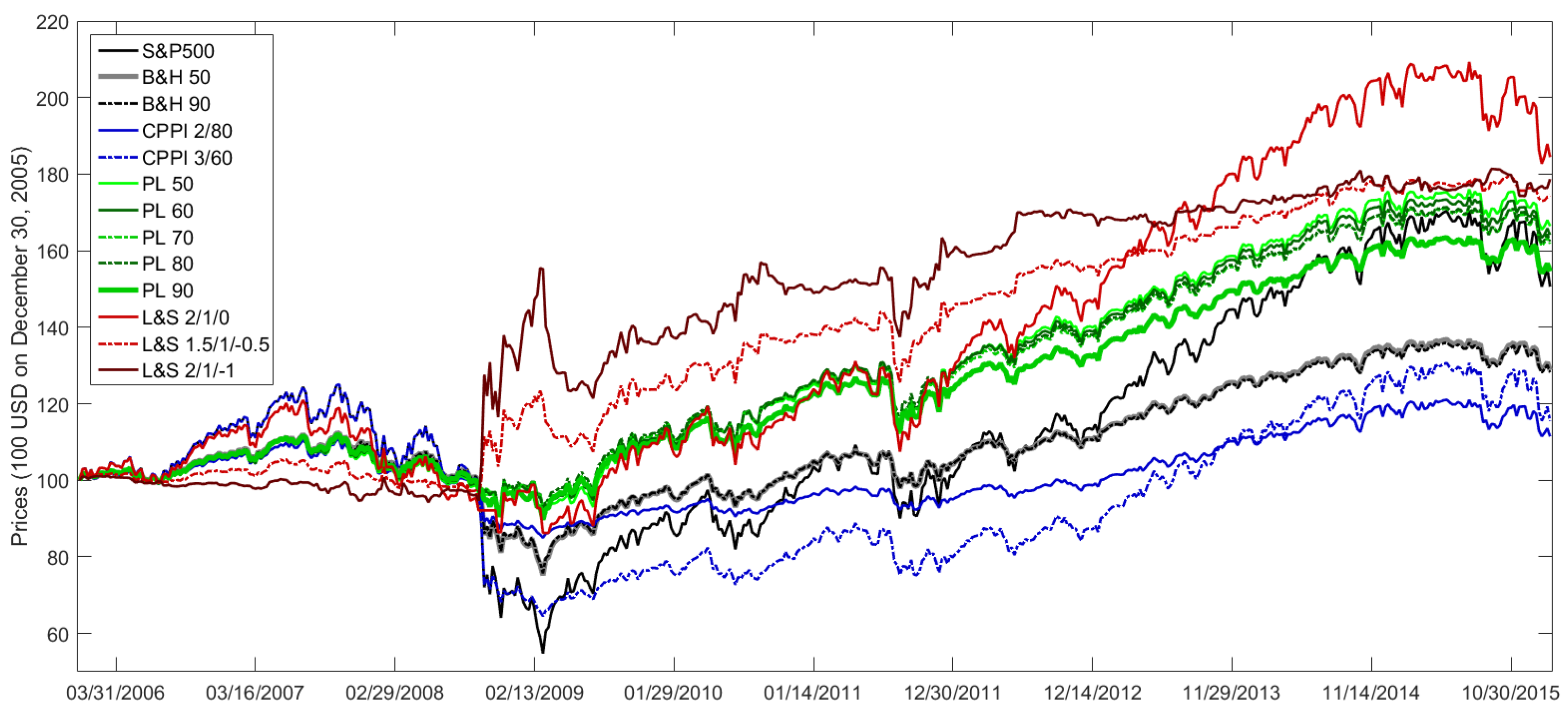
Figure A4 illustrates how an initial investment of 100 United States Dollar (USD) on December 30, 2005 in the trading strategies PL 50 until PL 90 with weekly rebalancing would have evolved. Hence, it shows a classical backtest.
In addition, we analyze how Leverage & Short Sales (L&S) change the risk-return profile of Trading Strategy (
24). Again, we have for the cash account:
and there are zero transaction costs. That is, how the risk-return profile of Trading Strategy (
25) deviates from the one in (
24) and what the respective contribution of parameters
and
is. In
Figure A4, L&S 2/1/0 stands for Trading Strategy (
25) with weekly rebalancing based on PL 50 with parameters
and
. The trading strategy L&S 2/1/−1 is also based on PL 50, but has the parameters
and
.
In
Figure A4, the strategy S&P500 reveals how a pure investment in the S&P500 would have performed. Moreover,
Figure A4 shows the price evolution of two Buy&Hold (B&H) and two Constant Proportion Portfolio Insurance (CPPI) strategies with weekly rebalancing. Hence, the Buy&Hold strategies serve as Constant Mix strategies. Here, B&H 50 denotes a Buy&Hold strategy with rebalanced S&P500 exposure on average of PL 50. Similarly, B&H 90 invests the averaged S&P500 exposure of PL 90. In
Figure A4, CPPI 2/80 stands for a CPPI strategy with multiplier 2 and floor 80%. The floor of a CPPI strategy denotes the minimum repayment at maturity. For any point in time before maturity, the cushion represents the difference between the current portfolio value and the discounted floor. Here, discounting does not matter, since
holds. The multiplier of a CPPI strategy constitutes to what extent the positive cushion is leveraged. As long as the cushion is positive, the cushion times the multiplier, which is called exposure, is invested in the risky assets. Because of
, there is no penalty, if the exposure exceeds the current portfolio value. To avoid borrowing money, the portfolio value at a given rebalancing date caps the risky exposure in this section. As soon as the cushion is zero or becomes negative, the total wealth is deposited on the bank account with
for the remaining time to maturity. Further information about CPPI strategies is stated in, e.g., Black and Perold [
45]. Similarly, CPPI 3/60 stands for a CPPI strategy with multiplier 3 and floor 60%.
Besides
Figure A4,
Table A10 lists some common performance and risk measures for all trading strategies. Then, we conclude: First, for higher prediction levels the Log-Return (Total, %) of its PL strategy decreases. E.g., compare PL 50 and PL 90. By definition, a high prediction level widens the intervals such that shifts in their location have less impact on the stock exposure
in (
24). As shown in
Figure A5, all PL strategies are centered around a level of 50%, but PL 50 adjusts its stock exposure more often and to a bigger extent than PL 90. Second, all PL strategies have periods of time with a lasting stock exposure
or
. Over our out-of-sample period, PL 50 invests on average 51% of its wealth in the S&P 500, but it outperformed B&H 50 by far. Hence, changing our asset allocation by
in (
24) really paid off.
Except for the L&S strategies, PL 50 has the highest Log-Return (Total, %) and therefore, appears very attractive. However, the upside usually comes with a price. This is why we next focus on the volatilities of our trading strategies. In this regard, CPPI 2/80 offers with 0.93% the lowest weekly standard deviation. With its allocation in
Figure A5 in mind, this makes sense, as CPPI 2/80 was much less exposed to the S&P500 than all others. Please note that
Figure A5 also shows how CPPI 3/60 was hit by the financial crisis in 2007/2008, when its S&P500 exposure dramatically dropped from 100% on 3 October 2008 to 21% on 13 March 2009. For PL strategies, we get for the volatility an opposite picture compared to the Log-Return (Total, %), i.e., the higher the prediction level, the lower the weekly standard deviation is. This sounds reasonable, as PL 90 makes smaller bets than PL 50. For L&S strategies,
Table A10 confirms that leveraging works as usual. Both, i.e., return and volatility, increased at the same time.
The Sharpe Ratio links the return and volatility of a trading strategy. Except for L&S 1.5/1/−0.5, the PL strategies offer the largest Sharpe Ratios. Therefore, PL 80 has the biggest weekly Sharpe Ratio of 7.39%. As supplement,
Table A11 reveals that the Sharpe Ratios of PL 80 and PL 90 are significantly different to those of S&P500, CPPI 2/80 and CPPI 3/60. The differences within or between the PL and L&S strategies are not significant. The Omega Measure compares the upside and downside of a strategy. Based on
Table A10, L&S 1.5/1/−0.5 and L&S 2/1/−1 have the largest Omega Measures given by 134.92% and 132.39%. The Omega Measures of the PL strategies lie in the range [121.34%, 124.94%], which are larger than those of the benchmark strategies in the range [103.86%, 111.16%]. The differences between all Omega Measures are not significant, see Table 4.16 in [
41].
Similar to the volatility, CPPI 2/80 has the smallest 95% Value at Risk and 95% Conditional Value at Risk. The PL strategies have more or less the same weekly 95% VaR, since all lie in the range
. However, their 95% CVaR ranges from −3.19% to −2.78% and so, reflects that PL 50 makes bigger bets than PL 90. For L&S strategies, there is no pattern how leveraging and short selling affects the 95% VaR and CVaR. Finally, we consider the Maximum Drawdown based on the complete out-of-sample period. Please note that
Figure A4 and
Figure A5 and
Table A10 confirm that CPPI 3/60 behaves like the S&P500, until it was knocked out by the financial crises in 2007/2008. This is why its Maximum Drawdown of −48.43% is close to the −56.24% of the S&P500. By contrast, the Maximum Drawdowns of the PL strategies lie in the range of [−19.91%, −17.37%], which is less than half. They are even smaller than the Maximum Drawdown of CPPI 2/80, which is −23.18%. For L&S strategies, short sales admit us to gain from a drop on the stock market, while leveraging boosts profits and losses. In total, this yields a scattered picture for their Maximum Drawdowns.
With the financial figures in mind, we recommend PL 50 for several reasons: First, it provides a decent return, which is steadily gained over the total period. Second, it has an acceptable volatility and a moderate downside. Please note that all PL strategies, L&S 1.5/1/−0.5 and L&S 2/1/−1 are positively skewed, which indicates a capped downside. The normalized histograms of the log-returns for all trading strategies can be found in Figure 4.6 from Ramsauer [
41].
If we repeat the previous analysis for complete panel data, we can verify whether the inclusion of mixed-frequency information really pays off. Instead of all 33 time series in
Appendix E, we restrict ourselves to US Treasuries, Corporate Bonds, London Interbank Offered Rate (LIBOR) and Foreign Exchange (FX)&Gold. Therefore, we have 22 time series without any missing observations. Again, we keep our rolling window of 364 weeks and gradually shift it over time, until we reach the sample end. For the upper limit of the factor dimension, we set
. At this stage, there are no obvious differences between the prediction intervals for incomplete and complete panel data [
41] (Figure 4.7). If we break the means of the predicted log-returns in
Figure A6 down into the contributions of the respective groups as shown in
Figure A6, we have a different pattern than in
Figure A2. E.g.,
Figure A2 detects supply as main driver at the turn of the year 2009/2010, whereas
Figure A6 suggests US Treasuries and Corporate Bonds. However, in the years 2010–2012 US Treasuries gained in importance in
Figure A6, which also indicates the interventions of the US Federal Reserve through its quantitative easing programs.
Next, we analyze the impact of the prediction intervals on Trading Strategies (
24) and (
25). Besides PL and L&S strategies of
Figure A4 based on 33 variables,
Figure A7 shows their analogs arising from 22 complete time series. Please note that the expression PL 50 (no) in
Figure A7 is an abbreviation for PL 50 using panel data with no gaps. The same holds for L&S 2/1/0, etc. Besides the prices in
Figure A7,
Table A12 lists their performance and risk measures. The S&P exposure of the single strategies based on the 22 complete time series can be found in Figure 4.11 from Ramsauer [
41]. Thus, we conclude: First, PL 50 (no) has a total log-return of 30.22%, which exceeds all other PL (no) strategies, but is much less than 50.93% of PL 50. Similarly, the L&S (no) strategies have a much lower log-return than their L&S counterparts. Second, PL 50 (no) changes its S&P500 exposure more often and to a larger extent than PL 90 (no). Third, the standard deviations of PL (no) strategies exceed their PL analogs such that their Sharpe Ratios are about half of the PL Sharpe Ratios. As shown in
Table A13, the Sharpe Ratios of PL and PL (no) strategies are significantly different. Fourth, PL (no) strategies are dominated by their PL versions in terms of Omega Measure. Table 4.19 in [
41] shows that such differences are not significant. Fifth, the 95% VaR and CVaR of the PL (no) strategies are slightly worse than of the PL alternatives, but their Maximum Drawdowns almost doubled in the absence of macroeconomic signals. Except for PL 50 (no), the returns of all PL (no) strategies, are negatively skewed [
41] (Figure 4.12). This indicates that large profits were removed and big losses were added, respectively. All in all, we therefore suggest the inclusion of macroeconomic variables.
Eventually, we consider the Root-Mean-Square Error (RMSE) for weekly point forecasts of the S&P500 log-returns. We replace sampled factors and ARX coefficients by their estimates to predict the log-return of next week. In this context, an ARX based on incomplete panel data has a RMSE of 0.0272, while an ARX restricted to 22 variables provides a RMSE of 0.0292. Please note that a constant forecast
yields a RMSE of 0.0259, the RMSEs of Autoregressive Models (ARs) with orders from 1–12 lie in the range
and the RMSEs of Random Walks with and without drift are 0.0380 and 0.0379, respectively. Therefore, our model is mediocre in terms of RMSE. Since the RMSE controls the size, but not the direction of the deviations,
Figure A8 illustrates the deviations
of our ARX based on all panel data and the AR(3), which was best regarding RMSE. As
Figure A8 shows, the orange histogram has 4 data points with
. Our ARX predictions for 10/17/2008, 10/31/2008, 11/28/2008 and 03/13/2009 were too conservative, which deteriorated its RMSE. If we exclude these four dates, our mixed-frequency ARX has a RMSE of 0.0251, which beats all other models.
For comparing the predictive ability of competing forecasts, we perform a conditional Giacomini-White test. Our results rely on the MATLAB implementation available at
http://www.execandshare.org/CompanionSite/site.do?siteId=116 (accessed on 13 December 2020) of the test introduced in Giacomini and White [
46]. Furthermore, we consider the squared error loss function. We conclude: First, the inclusion of macroeconomic data in our approach is beneficial at a 10%-significance level. A comparison of our method based on incomplete panel data vs. complete financial data only provides a
p-value of 0.06 and a test statistic of 5.61. In this context, forecasting with macroeconomic variables outperforms the forecasting relying on pure financial data by more than 50% of the time. Second, there are not any significant differences between our approach and an AR(3) or a constant forecast
. By comparing our approach with an AR(3), we observe a p-value of 0.364. Similarly, we have a
p-value of 0.355 compared to the constant forecast
. Unfortunately, this also holds true, if we remove the four previously mentioned outliers from our prediction sample.
Finally, we verify the quality of our interval forecasts with respect to the Ratio of Interval Outliers (RIO) and Mean Interval Score (MIS) for prediction intervals in
Table A14. For the respective definitions, we refer to Gneiting and Raftery [
47], Brechmann and Czado [
48] and Ramsauer [
41]. In this context, the inclusion of mixed-frequency information provides some statistical improvements. Except for the 50%-prediction intervals, we have more outliers in
Table A14, when the ARX relies on 22 complete time series than all 33 variables. Thus, the macroeconomic indicators make our model more cautious. Except for the 90%-prediction intervals based on complete panel data, all Ratios of Interval Outliers are below the aimed threshold. In contrast to RIO counting the number of interval outliers, MIS takes into account by how much the prediction intervals are exceeded. In this regard, the ARX using incomplete panel data dominates the ARX restricted to the 22 time series. All in all, this underpins again the advantages arising from the inclusion of macroeconomic information.